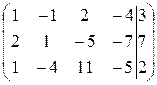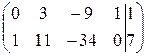Как найти неотрицательные базисные решения систем

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Что означает фраза “ранг матрицы равен $r$”? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.

Решить СЛАУ $ left < begin& 3x_1-6x_2+9x_3+13x_4=9\ & -x_1+2x_2+x_3+x_4=-11;\ & x_1-2x_2+2x_3+3x_4=5. end right.$. Если система является неопределённой, указать базисное решение.

Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$ left( begin 3 & -6 & 9 & 13 & 9 \ -1 & 2 & 1 & 1 & -11 \ 1 & -2 & 2 & 3 & 5 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ -1 & 2 & 1 & 1 & -11 \ 3 & -6 & 9 & 13 & 9 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 3 & 4 & -6 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright) $$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:

На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:

$$ left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright) $$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=5$, а вторая строка соответствует уравнению $3x_3+4x_4=-6$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$ left( begin 1 & 2 & 5 & 2 & -3\ 0 & 3 & -6 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 5 & 2 & -3\ 0 & 1 & -2 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 9 & 2 & -1/3\ 0 & 1 & -2 & 0 & -4/3 endright). $$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:

Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left <begin& x_1=frac<2><3>;\ & x_2=-4;\ & x_3=-frac<10><3>;\ & x_4=1. endright.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac<1><3>x_4$ и $x_3=-2-frac<4><3>x_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-2-frac<4><3>x_4right)+13x_4=9. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

Похожий пример уже был решен в теме “метод Крамера” (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.

$$ left( begin 1 & -2 & 4 & 0 & 2 & 0\ 4 & -11 & 21 & -2 & 3 & -1\ -3 & 5 & -13 & -4 & 1 & -2 end right) begin phantom <0>\ II-4cdot I\ III+3cdot Iend rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -3 & 5 & -2 & -5 & -1\ 0 & -1 & -1 & -4 & 7 & -2 end right) rightarrow \ rightarrow left|begin & text<поменяем местами вторую и третью>\ & text<строки, чтобы диагональным элементом>\ & text <второй строки стало число (-1).>endright|rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & -3 & 5 & -2 & -5 & -1 end right) begin phantom <0>\ phantom<0>\ III-3cdot Iend rightarrow \ rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & 0 & 8 & 10 & -26 & 5 end right). $$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод “ступенек”, что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

$$ left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 8 & 5 & -10 & 26 end right) begin phantom <0>\ phantom<0>\ III:8end rightarrow left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I-4cdot III \ II+III\ phantom<0>end rightarrow \ left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & -1 & 0 & -11/8 & 11/4 & -15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin phantom <0>\ IIcdot (-1)\ phantom<0>end rightarrow left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I+2cdot II \ phantom<0>\ phantom<0>end rightarrow\ rightarrowleft( begin 1 & 0 & 0 & 1/4 & -1/2 & -15/2\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) $$

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

П.1. Базисные и опорные решения

Рассмотрим линейную систему из m уравнений с n переменными

(2.1)

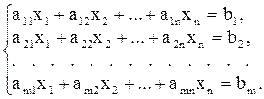
В дальнейшем будет интересен случай, когда n > m.

Будем полагать, что в системе (2.1) все уравнения являются независимыми, что в свою очередь означает r = m, где r – ранг матрицы системы
A = (a_ij).

Рассмотрим одну из таких систем

Составим расширенную матрицу системы и проведем несложные преобразования

В данном случае r = 2, число переменных n = 3. Очевидно, что такая система имеет бесконечно много решений.

Перейдем от последней матрицы к системе уравнений

Выразим переменные х₁ и х₃ через переменную х₂

Рассмотрим столбцы перед переменными х₁ и х₃, как векторы и . Данные векторы образуют базис в двумерном пространстве. Отсюда название переменных х₁ и х₃ – базисные переменные.

В общем случае базисных переменных в системе из m независимых уравнений с n переменными будет m.

Определение 2.1. Базисными переменными системы m линейных уравнений с n переменными (m

Число базисных решений равно количеству неупорядоченных подмножеств из n элементов (число неизвестных) по m (число базисных неизвестных), т.е. это число равно

,

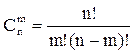
где n! = n × (n – 1) ×…× 3 × 2 × 1; m! = m × (m – 1) ×…× 2 × 1.

В данном примере число базисных решений определяется следующим образом

.

Среди базисных решений выделяют вырожденные решения, в которых нулевыми являются не только свободные решения, но и некоторые базисные.

Обратимся к примерам 1.1 и 1.2, рассмотренным в предыдущем параграфе. В системе ограничений одной и другой задачи присутствует требование неотрицательности переменных х₁, …, х_n. Это требование не является случайным, поскольку в экономических моделях, связанных с решением систем линейных уравнений, неизвестные величины соответствуют некоторым конкретным экономическим показателям, которые могут быть только неотрицательными. Неотрицательные базисные решения назовем опорными*.

Рассмотрим отыскание опорных решений на примере.

П р и м е р 2.1. Найти все опорные решения системы линейных уравнений:

Решение. Столбец свободных переменных не содержит отрицательных компонент. Если бы в каком-то уравнении были отрицательные свободные члены, нужно было бы умножением обеих частей уравнения на (– 1) сделать свободный член соответствующего уравнения положительным. Составим расширенную матрицу системы

и определим первый разрешающий элемент так, чтобы в последнем столбце в результате элементарных преобразований не появились отрицательные компоненты. Очевидно, разрешающий элемент должен быть положительным. В первом столбце все компоненты положительные. Какой из них можно взять в качестве разрешающего? Составим отношения 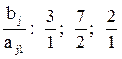(j = 1, 2, 3). Если за разрешающий элемент выбрать тот из элементов первого столбца, которому соответствует минимальное отношение, то в столбце свободных членов после преобразований не будет отрицательных компонент – это элемент а₃₁ = 1. Получим

.

Во втором столбце первоначальной матрицы за разрешающий можно взять только элемент а₂₂ = 1 (он единственный положительный элемент этого столбца)

.

В третьем столбце за разрешающий можно взять а₃₃ = 11, т. к. :

.

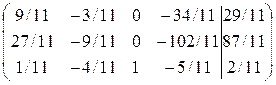
В четвертом столбце все элементы отрицательные и разрешающий элемент выбрать нельзя.

Остановимся на первом варианте и продолжим процесс далее

.

Очевидно, ранг матрицы равен 2, базисные неизвестные – х₁ и х₄; свободные – х₂ и х₃. Общее решение: (7 – 11х₂ + 34 х₃; х₂; х₃; 1 – 3х₂ + 9х₃).

Базисное решение (7; 0; 0; 1) является опорным.

В данном случае существует 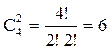базисных решений, соответствующих базисным переменным: х₁х₂; х₁х₃; х₁х₄; х₂х₃; х₂х₄; х₃х₄. Вариант х₁х₄ уже был рассмотрен.

Вернемся к матрице системы, полученной после преобразований:

.

Варианты х₁х₃; х₂х₃; х₃х₄ невозможны, т.к. в столбце, соответствующем х₃, нет положительных компонент, и х₃ не может войти в базис. Введем в базис х₂: , значит разрешающий элемент а₁₂ = 3. Получим

.

Базисное решение – опорное.

Проверим последний вариант х₂х₄: в четвертом столбце последней матрицы разрешающим может быть только элемент а₁₂ = 1/3 > 0, но тогда из базиса уйдет неизвестная х₂ и получим базисные переменные х₁х₄, что уже было рассмотрено.

Итак, опорные решения: (7; 0; 0; 1) и .

Сформулируем общее правило выбора разрешающего элемента при отыскании опорного решения для определенного столбца j.

1. Приводим систему уравнений к виду, когда в столбце свободных членов нет отрицательных чисел.

2. В выбранном столбце j в «конкурсе» на звание «разрешающий элемент» участвуют только положительные элементы.

3. Каждый элемент в столбце свободных членов, делим на соответствующий ему элемент столбца j.

4. Выбираем из полученных соотношений наименьшее (Q_j).

5. Элемент, для которого отношение, полученное в пункте 3, наименьшее, является разрешающим элементом.

Последнее изменение этой страницы: 2017-04-12; Просмотров: 1799; Нарушение авторского права страницы

Решение систем линейных уравнений методом Жордана-Гаусса

Разрешенная система уравнений

Уравнение имеет решение: если хотя бы один из коэффициентов при неизвестных отличен от нуля. В этом случае любой -мерный вектор называется решением уравнения, если при подстановке его координат уравнение обращается в тождество.

Общая характеристика разрешенной системы уравнений

Дать характеристику системе уравнений.

Решение:

1. Входит ли в состав системы линейных уравнений противоречивое уравнение? (Если коэффициенты , в этом случае уравнение имеет вид: и называется противоречивым.)

• Если система содержит противоречивое, то такая система несовместна и не имеет решения

2. Найти все разрешенные переменные. (Неизвестная называется разрешенной для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит (т.е. входит с коэффициентом, равным нулю).

• В нашем примере неизвестная входит в первое уравнение с коэффициентом единица, во второе уравнение не входит, то есть является первой разрешенной .
• Аналогично — содержится только во втором уравнении а только в первом.

3. Является ли система уравнений разрешенной? (Система уравнений называется разрешенной, если каждое уравнение системы содержит разрешенную неизвестную, среди которых нет совпадающих)

• Наша система является разрешенной т.к. каждое уравнение содержит в себе разрешенные неизвестные )

Разрешенные неизвестные, взятые по одному из каждого уравнения системы, образуют полный набор разрешенных неизвестных системы. (в нашем примере это )

Разрешенные неизвестные, входящие в полный набор, называют также базисными ( ), а не входящие в набор — свободными ( ).

В общем случае разрешенная система уравнений имеет вид:

!На данном этапе главное понять что такое разрешенная неизвестная (входящая в базис и свободная).

Общее Частное Базисное решения

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

• Базисное решение (вектор) называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
• Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена (имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена (имеет бесконечное множество решений).

Решение:

1. Проверяем является ли система разрешенной?

• Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения.

• В нашем случае мы можем включить в набор разрешенных неизвестных из первого уравнения — и , а из второго уравнения только . То есть набор может состоять из ( ) или ( ).

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор.

• допустим мы включили в набор неизвестные и , тогда общее решение будет выглядеть так:

4. Находим частное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

• Пусть , , , тогда из общего решения находим:

Ответ: частное решение (один из вариантов)

5. Находим базисное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

• , то из общего решения получаем , и базисное решение:

Элементарные преобразования линейных уравнений

Системы линейных уравнений приводятся к равносильным разрешенным системам с помощью элементарных преобразований.

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число, а остальные уравнения оставить без изменения, то получится система, равносильная данной. (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое, а все остальные уравнения оставить без изменения, то получится система, равносильная данной. (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число, а все остальные уравнения оставить без изменения, то получится система, равносильная данной.

Формулы пересчета коэффициентов системы

Если у нас есть система уравнений и мы хотим преобразовать ее в разрешенную систему уравнений в этом нам поможет метод Жордана-Гаусса.

Преобразование Жордана с разрешающим элементом позволяет получить для системы уравнений разрешенную неизвестную в уравнении с номером . (пример 2).

Преобразование Жордана состоит из элементарных преобразований двух типов:

1. Уравнение с разрешающим элементом делится на этот элемент (умножается на )
2. Уравнение с разрешающим элементом умножается на подходящие множители и прибавляется ко всем другим уравнениям для того, чтобы исключить неизвестную .

Допустим мы хотим сделать неизвестную в нижнем уравнении разрешенной неизвестной. Для этого мы должны разделить на , так чтобы сумма .

Пример 2 Пересчитаем коэффициенты системы

При делении уравнения с номером на , его коэффициенты пересчитываются по формулам:

Чтобы исключить из уравнения с номером , нужно уравнение с номером умножить на и прибавить к этому уравнению.

Теорема (4) О сокращении числа уравнений системы.

Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной.

Теорема (5) О несовместимости системы уравнений.

Если система уравнений содержит противоречивое уравнение, то она несовместна.

Алгоритм метода Жордана-Гаусса

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
5. Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти: два общих и два соответствующих базисных решения

Решение:

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

Равносильная система с разрешенными неизвестными и имеет вид:

Теперь можем записать Общее решение:

Приравниваем свободные переменные и нулю и получаем: .

Базисное решение:

Для того чтобы найти второе общее и соответствующее ему базисное решение, в полученной разрешенной системе в каком-либо уравнении необходимо выбрать какой-либо другой разрешающий элемент. (дело в том, что линейное уравнение может содержать несколько общих и базисных решений). Если разрешенная система уравнений, равносильная исходной системе содержит неизвестных и уравнений, то число общих и соответствующих базисных решений исходной системы равно числу сочетаний и . Количество сочетаний можно вычислить по формуле:

В нашем случае выбран разрешающий элемент (-1) в первом уравнении при (строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными и :

Записываем второе общее решение:

И соответствующее ему базисное решение:

[spoiler title=”источники:”]

http://lektsia.com/8x32c1.html

http://www.grandars.ru/student/vysshaya-matematika/metod-gaussa.html

[/spoiler]

Метод Жордана Гаусса — история возникновения

Метод Жордана-Гаусса, то есть способ полного исключения неизвестных, применяют в алгебре для решения следующих задач:

• квадратные системы линейных алгебраических уравнений;
• поиск обратной матрицы;
• определение координат вектора в заданном базисе;
• поиск ранга матрицы.

Рассматриваемый метод представляет собой модифицированную теорию Гаусса. Методика получила название в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана.

Метод Жордана-Гаусса — способ решения линейных уравнений, предполагающий полное исключение неизвестных.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Предпосылки для возникновения метода Гаусса появились еще до нашей эры. Объяснение этого способа можно найти в древней китайской книге под названием «Математика в девяти книгах». Труд был написан приблизительно в 150 году до нашей эры. Трактат является сборником разных задач по математике и способов их решений.

В Европе впервые начал изучать данный метод Исаак Ньютон. В процессе исследований древней литературы по математике ученый пришел к выводу о том, что отсутствует способ решения систем уравнений, которые предусматривают большое количество переменных.

Ньютон разработал схему решения в своем труде, который был представлен общественности в 1707 году. Данную методику активно использовали в разных пособиях и арифметических справочниках в течение последующих 100 лет.

Немецкий ученый К.Ф. Гаусс в 1810 году модернизировал способ Ньютона. Усовершенствованная методика была опубликована вместе с другими разработками исследователя. В результате метод преобразования в треугольную матрицу завоевал популярность и получил название в честь ученого.

Во второй половине ХІХ века ученый Жордан доработал способ Гаусса. Таким образом удалось получить способ приведения к диагональной матрице. Интересным фактом является точно такое же открытие другого ученого, однако название методики в настоящее время содержит имена Гаусса и Жордана.

Метод Жордана-Гаусса получил широкое распространение. Кроме поиска ответов к примерам по математике, данный способ необходим для решения инженерных задач, содержащих большое число неизвестных. В процессе решения систем уравнений, полученных из инженерно-технических задач, в первую очередь выбирают максимально большие по модулю переменные. Это позволяет минимизировать погрешность. Затем из матрицы по очереди убирают ненужные переменные.

Занимаясь расчетами инженерно-технических задач рассматриваемым способом, целесообразно использовать разные алгоритмы программирования. В результате полученные ответы характеризуются минимальной погрешностью.

Отличия рассматриваемого метода от метода Гаусса заключаются в том, что в последнем к нулям приводится только нижняя часть матрицы. Метода Жордана-Гаусса предполагает, что к нулям нужно привести также и верхнюю часть матрицы.

Обе методики позволяют определить базисное и общее решения системы уравнений. В случае базисного решения системы уравнений каждая свободная переменная обладает нулевым значением.  При общем решении системы уравнений основные переменные выражают через свободные переменные.

Практическое применение для решения систем линейных уравнений

Существует простой алгоритм действий для решения задач методом Жордана-Гаусса. Он состоит из следующих этапов:

1. Выбор первого с левой стороны столбца матрицы, содержащего, как минимум, одно отличное от нуля значение.
2. Когда самое верхнее число в данном столбце является нулем, следует заменить полностью первую строку матрицы на другую строку матрицы, в которой в аналогичном столбце отсутствует нуль.
3. Каждый элемент, находящийся в первой строке, необходимо поделить на верхний элемент выбранного столбца.
4. Из оставшихся строк требуется отнять первую строку, умноженную на первый элемент соответствующей строки для получения первым элементом каждой строки (за исключением первой) нуля.
5. Аналогичные действия предусмотрены для матрицы, которая получена из начальной матрицы путем удаления первой строки и первого столбца.
6. Процедуру повторяют n-1 раз. В результате получается верхняя треугольная матрица.
7. С целью оставить в предпоследней строке лишь 1 на главной диагонали, нужно отнять из предпоследней строки последнюю строку, которую умножили на соответствующий коэффициент.
8. В случае последующих строк предыдущий шаг повторяют. Таким образом, формируется единичная матрица и решение на месте свободного вектора (для него предусмотрены аналогичные преобразования).

Расширенный алгоритм действий, позволяющий найти обратную матрицу, целесообразно рассмотреть на примере решения задачи. Предположим, что:

(A=begin{pmatrix} a_{11} & a_{12} & cdots & a_{1n} \ a_{21} & a_{22} & cdots & a_{2n} \ vdots & vdots & ddots & vdots \ a_{n1} & a_{n2} & cdots & a_{nn} end{pmatrix} quad a_{ii} ne 0 quad I=begin{pmatrix} 1 & 0 & cdots & 0 \ 0 & 1 & cdots & 0 \ vdots & vdots & ddots & vdots \ 0 & 0 & cdots & 1 end{pmatrix})

Прямой ход (алгоритм образования нулей под главной диагональю) предполагает в первую очередь деление первой строки матрицы А на (a_{11},) что даст в результате:

({a_{11}}) (a_{1j}^1 )(= frac{a_{1j} }{a_{11} },)

j — столбец матрицы А.

Далее необходимо повторить действия для матрицы I. Запишем формулу:

(b_{1s}^1 = frac{b_{1s} }{a_{11} }),

s — столбец матрицы I.

Таким образом:

(A=begin{pmatrix} 1 & a_{12}^1 & cdots & a_{1n}^1 \ a_{21} & a_{22} & cdots & a_{2n} \ vdots & vdots & ddots & vdots \ a_{n1} & a_{n2} & cdots & a_{nn} end{pmatrix} qquad I=begin{pmatrix} b_{11}^1 & 0 & cdots & 0 \ 0 & 1 & cdots & 0 \ vdots & vdots & ddots & vdots \ 0 & 0 & cdots & 1 end{pmatrix})

Для того чтобы нуль образовался в первом столбце, потребуется:

({displaystyle a_{2j}^{1}=a_{2j}-a_{1j}^{1}a_{21} ,dots , a_{nj}^{1}=a_{nj}-a_{1j}^{1}a_{n1}})

В случае матрицы І следует повторить действия по формулам:

({displaystyle b_{2s}^{1}=b_{2s}-b_{1s}^{1}a_{21} ,dots , b_{ns}^{1}=b_{ns}-b_{1s}^{1}a_{n1}})

В результате:

({displaystyle A={begin{pmatrix}1&a_{12}^{1}&cdots &a_{1n}^{1}\0&a_{22}^{1}&cdots &a_{2n}^{1}\vdots &vdots &ddots &vdots \0&a_{n2}^{1}&cdots &a_{nn}^{1}end{pmatrix}}qquad I={begin{pmatrix}b_{11}^{1}&0&cdots &0\b_{21}^{1}&1&cdots &0\vdots &vdots &ddots &vdots \b_{n1}^{1}&0&cdots &1end{pmatrix}}})

Можно записать уравнения:

(a_{ij}^k=frac{a_{ij}^k}{a_{ii} } qquad a_{ij}^k=a_{ij}^{k-1}-a_{kj}^k a_{ik}^{k-1})

С их помощью необходимо повторить действия, учитывая условия:

(k = 1 rightarrow n,i = k + 1 rightarrow n,j = 1 rightarrow n)

Повтор операций для матрицы І по формулам:

(b_{ik}^k=frac{b_{ik}^k}{a_{ii} } qquad b_{is}^k=b_{is}^{k-1}-b_{ks}^k a_{ik}^{k-1})

Следует принять во внимание, что:

(k=1 to n,; i=k+1 to n,; s=1 to n)

В результате:

({displaystyle A={begin{pmatrix}1&a_{12}^{1}&cdots &a_{1n}^{1}\0&1&cdots &a_{2n}^{2}\vdots &vdots &ddots &vdots \0&0&cdots &1end{pmatrix}}qquad I={begin{pmatrix}b_{11}^{1}&0&cdots &0\b_{21}^{2}&b_{22}^{2}&cdots &0\vdots &vdots &ddots &vdots \b_{n1}^{n}&b_{n2}^{n}&cdots &b_{nn}^{n}end{pmatrix}}})

Если использовать обратный ход, то есть алгоритм образования нулей над главной диагональю, в первую очередь нужно воспользоваться формулой:

(a_{ij}^{k-1}=a_{ij}^{k-1}-a_{ij}^k a_{ik}^i,)

В данном случае необходимо учитывать, что:

(k=n to 1,; i=1 to k-1,; j=1 to n)

Затем требуется повторить действия для матрицы І, по формуле:

(b_{is}^{k-1}=b_{is}^{k-1}-b_{is}^k a_{ik}^i)

Выполняется условие:

(k=n to 1,; i=1 to k-1,; s=1 to n)

В итоге получим, что:

(A=begin{pmatrix} 1 & 0 & cdots & 0 \ 0 & 1 & cdots & 0 \ vdots & vdots & ddots & vdots \ 0 & 0 & cdots & 1 end{pmatrix} qquad I=A^{-1})

Произвольный способ выбора разрешающих элементов

Особенность данного способа решения состоит в том, что столбы матрицы системы перебираются в определенной последовательности. В каждой колонке необходимо выбрать какой-то элемент с нулевым значением. Данный элемент называют разрешающим. Предположим, что в текущем столбце разрешающим элементом является:

( displaystyle{a_{ij}}.)

Когда (displaystyle{a_{ij}neq{1}}), умножив строку (displaystyle{r_i} на displaystyle{frac{1}{a_{ij}}}), требуется привести разрешающий элемент к значению 1. На следующем этапе предполагаются действия со строками. Это позволит обнулить каждый ненулевой элемент j-го столбца, за исключением разрешающего элемента.

Далее следует перейти к следующему столбцу. В процессе из каждой строки можно позаимствовать разрешающий элемент лишь единожды. Строки, которые являются нулевыми, исключаются по мере их возникновения. В том случае, когда разрешающий элемент станет невозможно выбрать, алгоритм прекращается.

Можно подробно рассмотреть этот способ. Сначала работать необходимо в первой колонке матрицы системы. Здесь требуется выбрать произвольный ненулевой элемент (displaystyle{a_{i1}neq{0}}), который является разрешающим. Если (displaystyle{a_{i1}neq{1}}), то следует умножить строку  (displaystyle{r_i} ) с разрешающим элементом на (displaystyle{frac{1}{a_{i1}}}).

В результате разрешающий элемент станет равен 1. При  (displaystyle{a_{i1}=1}) не требуется выполнять умножение. Используя строку  (displaystyle{r_i}), нужно обнулить другие ненулевые элементы первого столбца. Из строки  (displaystyle{r_i} ) выбирать разрешающие элементы в последующих шагах запрещено. Допустимо из некой строки выбирать разрешающий элемент только один раз.

На втором шаге нужно перейти к следующей колонке матрицы системы. Необходимо проверить наличие или отсутствие в этом столбце ненулевого элемента, который не принадлежит строке, имеющей разрешающий элемент, выбранный на предыдущем шаге.

Когда такой разрешающий элемент во втором столбце отсутствует, можно переходить к третьей, четвертой колонке и так далее. Переход следует закончить после нахождения столбца с нужным элементом, либо при отсутствии искомого столбца в матрице системы. В результате алгоритм будет завершен.

Предположим, что искомый столбец найден, и в нем присутствует разрешенный элемент.  Данный элемент нужно обозначить (displaystyle{b_{nk}}). Далее по аналогии с первым шагом, если (displaystyle{b_{nk}neq{1}}), необходимо умножить строку (displaystyle{r_n}) с разрешающим элементом на (displaystyle{frac{1}{b_{nk}}}). Затем следует обнулить другие ненулевые элементы k-го столбца.

Запрещено выбирать разрешающие элементы из строк, в которых были обнаружены разрешающие элементы на первом и втором этапе алгоритма. Когда обнуление завершено, можно переходить к следующему столбцу и так далее. Как только выбор разрешающего элемента станет невозможен, алгоритм закончится.

Выбор разрешающих элементов на главной диагонали матрицы системы

Данный способ предполагает использование метода прямоугольника. Результатом является диагональная матрица, то есть квадратная матрица с элементами, расположенными вне главной диагонали и равными нулю.

В качестве примера можно рассмотреть решение системы линейных уравнений:

 Данную систему можно представить в виде матрицы:

 Векторы-столбцы базисного решения являются единичными векторами, которые образуют базис, а соответствующие им переменные называются базисными. Для получения единичных векторов применяют метод Жордана-Гаусса. Опорным решением называют базисное неотрицательное решение. Базисное решение системы линейных уравнений возможно в том случае, когда свободные переменные ((m>n)) принимают нулевые значения.

Предположим, что имеется система линейных уравнений. Необходимо определить три базисных решения с помощью метода Жордана-Гаусса, а также назвать, какие из них являются опорными.

Система имеет вид:

 В определенной последовательности необходимо выбирать разрешающий элемент, расположенный на главной диагонали матрицы. Разрешающий элемент равен (2).
На его месте получаем 1, а в самом столбце следует записать нули. Другие элементы матрицы, в том числе, элементы столбца B, вычисляются, согласно правилу прямоугольника.

В процессе нужно выбрать четыре числа, которые расположены в вершинах прямоугольника и в любом случае содержат разрешающий элемент.

(НЭ = СЭ – (А*В)/РЭ)

(РЭ )— разрешающий элемент (2);

А и В — элементы матрицы, которые формируют прямоугольник с элементами СТЭ и РЭ.

Записать расчеты для каждого элемента можно в виде таблицы:

 Таблицу допустимо представить в таком виде:

 Разрешающий элемент равен (-1.5). Можно записать расчет каждого элемента в виде таблицы:

 Разрешающий элемент равен (-0.67). По результатам пересчета общее решение системы примет следующий вид:

Нужные переменные Х4 и Х5 можно рассматривать, как свободные переменные, чтобы выразить с их помощью базисные переменные. Для этого данные переменные следует приравнять к нулю. Таким образом, получим базисное решение системы.

 В связи с тем, что в базисном решении отсутствуют отрицательные значения, полученное решение можно считать опорным. Для того чтобы получить частное решение, требуется задать какие-либо значения Х4 и Х5. Например, они равны 1. Тогда:

Примеры решения систем линейных алгебраических уравнений методом Гаусса-Жордана

Нахождение неотрицательных базисных решений системы

Так как не всякое базисное решение является опорным, то возникают вычислительные затруднения при нахождении опорных решений системы обычным методом Гаусса. Приходится находить все базисные решения и из них выбирать опорные. Существует алгоритм, позволяющий сразу находить опорные решения.

1. При заполнении исходной таблицы Гаусса все свободные члены делают неотрицательными.
2. Ключевой элемент выбирается специальным образом:
1. а) в качестве ключевого столбца выбирают любой столбец коэффициентов при неизвестных, если в нем есть хотя бы один положительный элемент;
2. б) в качестве ключевой строки берется та, у которой отношение свободного члена к положительному элементу ключевого столбца минимально.

На пересечении ключевой строки и ключевого столбца находится ключевой элемент. Далее проводят обычное преобразование Жордана.

Однородные системы линейных уравнений

Пусть дана однородная система

Рассмотрим соответствующую неоднородную систему

С помощью матриц

эти системы можно записать в матричном виде.

A`x = . (8.3)

A`x = `b. (8.4)

Справедливы следующие свойства решений однородной и неоднородной систем.

Теорема 8.23. Линейная комбинация решений однородной системы (8.1) является решением однородной системы.

Доказательство. Пусть `x, `y и `z — решения однородной системы. Рассмотрим `t = α`x + β`y + γ`z, где α, β и γ — некоторые произвольные числа. Так как `x, `y и `z являются решениями, то A`x = , A`y = и A`z = . Найдем A`t.

A`t = A · (α`x + β`y + γ`z) = A · α`x + A · β`y + A · γ`z =

= αA`x + βA`y + γA`z = α + β + γ = .

A`t = Þ`t является решением системы.

Теорема 8.24. Разность двух решений неоднородной системы (8.2) является решением однородной системы (8.1).

Доказательство. Пусть `x и `y — решения системы. Рассмотрим `t = `x – `y.

A`x = `b, A`y = `b

A`t = A (`x – `y) = A`x – A`y = `b – `b =.

`t = `x + `y является решением однородной системы.

Теорема 8.25. Сумма решения однородной системы с решением неоднородной системы есть решение неоднородной системы.

Доказательство. Пусть `x — решение однородной системы, `y — решение неоднородной системы. Покажем, что `t = `x + `y — решение неоднородной системы.

A`x = , A`y = `b

A`t = A (`x + `y) = A`x + A`y = `b + = `b.

A`t = `b Þ`t является решением неоднородной системы.

Совместность однородной системы

Рассмотрим однородную систему

Однородная система всегда совместна, так как имеет тривиальное (нулевое) решение x₁ = x₂ = … = x_n = 0. Выясним, когда данная система имеет нетривиальное решение.

Теорема 8.26. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система имеет нетривиальное решение. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, не все равные нулю, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде

Следовательно, система векторов—столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т. е. r(A) < n.

Следствие. Однородная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A) < n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.

Совместность однородной системы

Рассмотрим однородную систему

Однородная система всегда совместна, так как имеет тривиальное (нулевое) решение x₁ = x₂ = … = x_n = 0. Выясним, когда данная система имеет нетривиальное решение.

Теорема 8.26. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система имеет нетривиальное решение. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, не все равные нулю, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде

Следовательно, система векторов—столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т. е. r(A) < n.

Следствие. Однородная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A) < n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.

Общее решение однородной системы

Система (8.1) всегда имеет тривиальное решение. Если ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных, то система (8.1) имеет нетривиальные решения.

1) r(A) = n — система (8.1) имеет только тривиальное решение:

2) r(A) = r < n — система (8.1) имеет нетривиальные решения.

Количество свободных переменных во втором случае будет равно n – r, а базисных r. Давая свободным переменным произвольные значения, мы будем получать различные решения системы (8.1), т. е. любому вектору размерности n – r

(с_{r + 1}, c_{r + 2}, …, c_n)

будет соответствовать решение системы (8.1)

(с₁, c₂, …, c_r, c_{r + 1}, …, c_n).

Определение 8.51. Фундаментальной системой решений однородной системы (8.1) называется максимальная линейно независимая система решений системы (8.1). Фундаментальная система содержит n – r линейно независимых решений системы (8.1).

Чтобы получить фундаментальную систему решений, нужно в (n – r)-мерном пространстве взять линейно независимую систему из n – r векторов и по ним построить соответствующие решения системы (8.1). Полученные решения будут образовывать фундаментальную систему решений `x<sub>1</sub>, `x₂, …, `x<sub>n-r</sub>. Так как эта система максимальна, то любое решение системы (8.1) можно представить в виде линейной комбинации решений фундаментальной системы `x = α₁`x<sub>1</sub> ‌ α<sub>2</sub>`x₂ ‌ … ‌ α_n-r`x_n-r. Полученное выражение является общим решением однородной системы (8.1).

Пример 8.25.

x₁, x₂ — базисные, x₃, x₄, x₅ — свободные. Два последних уравнения линейно выражаются через два первых, поэтому их можно отбросить:

ì3x₁ + x₂ – 8x₃ + 2x₄ + x₅ = 0, í î2x₁ – 2x₂ – 3x₃ – 7x₄ + 2x₅ = 0.

Выразим базисные переменные.

Умножим первое уравнение на 2 и сложим со вторым. Результат разделим на 8.

Умножим первое уравнение на 2, второе на -3 и сложим полученные уравнения. Результат разделим на 8.

В качестве значений свободных переменных возьмем координаты векторов трехмерного единичного базиса.

(1,0,0), `x1 =	æ è			;		; 1; 0; 0	ö ø	;
(0,1,0), `x2 =	æ è			; –		; 0; 1; 0	ö ø	; — фундаментальная система решений,
(0,0,1), `x3 =	æ è	–		; –		; 0; 0; 1	ö ø	.

`x = α<sub>1</sub>`x₁ + α₂`x<sub>2</sub> + α<sub>3</sub>`x₃ — общее решение однородной системы.

Сумма общего решения однородной системы (8.1) с любым решением неоднородной системы (8.2) является общим решением неоднородной системы (8.2).

Применение линейной алгебры в экономике

Производственные показатели

Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в следующей таблице.

Вид изделий	Количество изделий	Расход сырья, кг/изд.	Норма времени изготовления, ч/изд.	Цена изделийя, ден. ед./изд.

Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.

По приведенным данным составим четыре вектора, характеризующие весь производственный цикл:

`q = (20, 50, 30, 40) — вектор ассортимента;

`s = (5, 2, 7, 4) — вектор расхода сырья;

= (10, 5, 15, 8) — вектор затрат рабочего времени;

`p = (30, 15, 45, 20) — ценовой вектор.

Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента на три других вектора:

S = `q`s = 100 + 100 + 210 + 160 = 570 кг,

Т = `q = 1220 ч, P = `q`p = 3500 ден. ед.

Расход сырья

Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:

Вид сырья 1 2 3 4

Вид изделия.

Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно, 60, 50, 35 и 40 ед.

Составим вектор—план выпуска продукции:

`q = (60, 50, 35, 40).

Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду: этот вектор затрат вычисляется как произведение вектора `q на матрицу А:

Конечный продукт отрасли

Отрасль состоит из n предприятий, выпускающих по одному виду продукции каждое: обозначим объем продукции i-го предприятия через х_i. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Пусть а_ij — доля продукции i-го предприятия, потребляемая j-м предприятием для обеспечения выпуска своей продукции объема х_j. Найдем величину у_i — количество продукции i-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле

Введем в рассмотрение квадратную матрицу порядка n, описывающую внутреннее потребление отрасли

A = (a_ij); i,j = 1, 2, …, n.

Тогда вектор конечного продукта является решением матричного уравнения

`x – A`x = `y

с использованием единичной матрицы Е получаем

(E – A)`x = `y

Пример 8.26. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют, соответственно, вид

Получим вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из трех предприятий:

Прогноз выпуска продукции

Пусть C = (c_ij); i = 1, 2, …, m, j = 1, 2, …, n, — матрица затрат сырья t видов при выпуске продукции n видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор

`q = (q₁, q₂, …, q_m)

вектор-план `x = (x₁, x₂, …, x_n) выпуска продукции определяется из решения системы m уравнений с n неизвестными:

C`x<sup>T</sup> = `x^T,

где индекс «T» означает транспонирование вектора-строки в вектор-столбец.

Пример 8.27. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства представлены следующими данными:

Вид сырья	Расход сырья по видам продукции, вес. ед./изд.	Запас сырья, вес. ед.

Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.

Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в планировании микроэкономики предприятий.

Обозначим неизвестные объемы выпуска продукции через х₁, х₂ и х₃. Тогда при условии полного расхода запасов каждого вида сырья можно записать балансовые соотношения, которые образуют систему трех уравнений с тремя неизвестными:

Решая эту систему уравнений любым способом, находим, что при заданных запасах сырья объемы выпуска продукции составят по каждому виду соответственно (в условных единицах):

x₁ = 150, x₂ = 250, x₃ = 100.

---