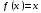Одномерные отображения
Неподвижная точка — точка, кот зад отобр переводит в неё же, иными сл, реш ур .
К прим, отобр имеет неподв точки x=1 и x=-3, т к f(1)=1 и f(3)=3.
Неподв есть не у всякого отобр — например, отобр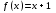
Периодические точки – Точки, возвращающиеся в себя после конечного числа итераций, т е, решение ур 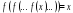
неподвижные точки — это периодические точки периода 1).
Теорема Шарковского. Пусть I – отрезок на числовой прямой, а f: I → I – непрерывное
отображение. Если f имеет точку периода p и , то найдется точка периода q
Пр1.Непрерывное отображение f: [1,5] → [1, 5], имеющее период 5, но не имеющее периода 3 Пусть f задано в точках 1, 2, 3, 4, 5 так :
а на промежуточные отрезки распространено по линейности (рис). а на промежуточные
отрезки распространено по линейности (рис. 1). Орбита точки x = 1 имеет вид 1, 3, 4, 2, 5, 1, …, т. е. f обладает периодом 5. Из графиков видим что нет орбиты периода 3
пр2 Непрерывное отображение f: [1,7] → [1, 7], спериод 7, не имеющее периоды 5 и 3.
Орбита точки x = 1 имеет вид 1, 4, 5, 3, 6, 2, 7, 1, т е имеет период 7
Из последнего рис решение уравнения есть только неподвижная точка. Значит, точек предыдущих периодов нет.
Задачи на одномерные отображения
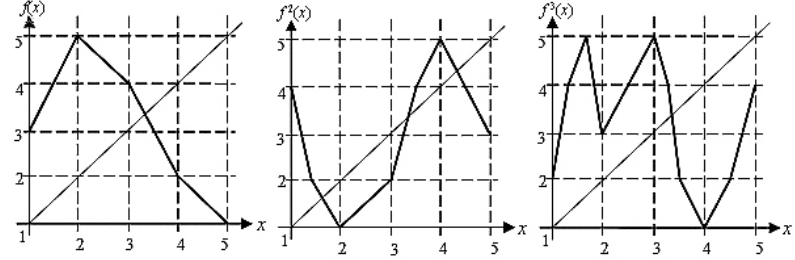
пр Найти неподвижную точку отображения промежутка [0, 1] в себя, заданного ф-лой:
РЕШ: Неподвижная точка отображения промежутка [0, 1] соотв т пересеч графика
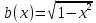
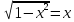
графиком явл окружность в ц нач к=т и с рад = 1ед измерения Неподвижная точка получ путем поворота т (1; 0) на угол 45◦, вокруг центра
1)Функция y = sign x не имеет обратной.
2) Дано уравнение 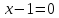
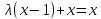
3) Для каждого из следующих множеств указать пример непрерывного отображенияч этого множества в себя без неподвижных точек:
а) числовая прямая; б) полуинтервал (0,1]; в) пара отрезков [-2,-1] и [1,2].
4) указать пример разрывного (т.е. не непрерывного) отображения отрезка [0,1] в себя, не имеющего неподвижных точек
5)На числовой прямой R заданы функции. Какая из них отображает отрезок [0,1] в себя?
6) Пусть f – непрерывная функция на отрезке , отображающая каждый конец отрезка в себя, т. е.
. Пусть g – непрерывная функция, отображающая отрезок
в себя. Докажите, что тогда на этом отрезке найдется такая точка x0, что
. Сохранится ли это в силе, если g – произвольная непрерывная функция на
?
7). Докажите, что непрерывное отображение f отрезка на (весь) отрезок
, содержащий в себе отрезок А, имеет неподвижную точку. Верно ли это, если образ
отрезка А не совпадает с В, а только лежит в нем?
8).Пусть f –непрерывное отображение отрезка на себя. Докажите, что отображение
(композиция отображения f с самим собой) имеет по крайней мере две неподвижных точки. Верно ли это, если f отображает отрезок
в себя, но не на себя?
9) Показать, что отображение оси Ох в себя имеет единственную неподвижную точку. В качестве приближенного значения корня уравнения
взять 3й член посл-ти
, полученной методом итерации, и оценить величину погрешности.
10) Отображение А на полупрямой переводит каждую точку
в
. Является ли оно сжимающим и имеет ли неподвижную точку?
Логистическое отображение (квадратичное отображение) – это полиномиальное отображение, описывающее изменение численности популяции с течением времени. 2 вида записи
|
Отобр Фейгенбаума |
отобр Ферхюльста |
описывает два эффекта:
1)когда численность популяции xn мала, она размножается со скоростью, пропорциональной этой численности, т к если
2) скорость размножения падает, возрастает конкуренция и смертность (нелинейное ограничение роста ) :
1)Найдите неподвижные точки логистического отображения и иссл их устойивость в зависимости от λ отв и
2). Найдите в явном виде элементы 2- цикла логистического отображения В каком интервале параметра λ существует 2й- цикл ?
3)Построить с помощью компьютера итерационные диаграммы для логистического отображения для значений параметра Какой процесс будет устанавливаться в каждом случае по прошествии достаточно большого времени ?
7)пример разрывного (т.е. не непрерывного) отобр отр [0,1] в себя, не имеющ неподвижных точек.
Инволюции
Непрерывное отображение f отрезка [0,1] в себя называют инволюцией, если оставляет неподв каждую точку отрезка. Иначе, это значит, что функция f обратна самой себе.
—————————————————————————————————————–
1)Проверить что следующие функции являются инволюциями
2)Доказать что каждая нетривиальная инволюция имеет только 1 непод точку
3)Пусть f – непрерывная функция на отрезке , отобр каждый конец отрезка в себя, т.е.
. Пусть g – любая непрер функция, отобр отрезок
в себя. До, что тогда на этом отрезке найдется такая т x0, что
. Сохранится ли это утверждение в силе, если g – произвольная непрерывная функция на
?
Теорема о неподвижной точке.
Допустим, что некоторый шар заполнен песком. Если мы встряхнем этот шар, то все песч немн изменят свое положение. Но, оказывается, что есть такая песчинка, которая останется неподвижной.Пусть А – отрезок тонкой резинки. Б его деформир как уг, но без разрывов и склеивания. И в таком деформир виде заставим его занимать на пл=ти то же место, что и раньше (или часть места). Оказ, что при этом хотя бы одна точка займёт свое первона место.
Эти 2 примера дают понятие т о неподвижной точке. Л.Брауэра и причис к важн т в матем. Ещё прим этой т: если круг повернуть вокруг ц на угол 30о, то единств неподв точкой б центр круга.Но если то же отобр рассм на окружн, то она не б иметь неподвижных точек.
Каждое пост отобр произв пр=ва в себя имеет одну неподвижную т. А отобр некот множества в себя м иметь, а может и не иметь этой точки.
: Точка х, обл свойством, что f(x)=x, наз неподвижной точкой отображения.
Т БРАУЭРА: Каждое непрерывное отображение прямолинейного отрезка в себя имеет хотя бы 1 неподвижную точку.
Интуитивное доказательство
ДОК: В на прямой, содержащей этот отрезок, к-ты так, что отрезок превр в замкн промеж [a, b].
Тогда рассматриваемое отображение будет непрерывной функцией f, отображающей промежуток в себя (f :[a,b]→[a,c]). Опр новую ф q:[a,b]→R с усл, что q(x)=f(x) –x для x € [a,b] . Таким обр, функция q равна, взятому с определенным знаком, расстоянию между точкой Х и её образом f(x).
Если f(x) x, то f(x) – x= q 0, а если f(x)
а) Если неподвижен какой-н из концов промежeжутка, то доказывать нечего, т.к. этот конец и будет неподвижен точно.
б) Доп, что ни один из концов промежутка не неподвижен. Т к f(a) и f(b) принадлежат [a,b], то f(a)a и f(b)0 (f(a) – а = q0) и q (b)
Функция q непрерывна= она принимает все значения между q(a) и q(b). Следовательно, в некой точке х € [a, b] функция g(х) = 0. Эта точка и является искомой неподвижной точкой отображения .Ч т д.
Т Бореука-Улама для окружности. Пусть f : C R – непрерывная функция на окружности C. Тогда существует пара точек – антиподов x, x* такая, что f (x) = f (x*).
Следствие: на любой большой окружности земного шара (например, на экваторе) найдется пара антиподов, в которых температура воздуха одинакова.
Т (о блинах). Если A и B – ограниченные фигуры на плоскости, то существует прямая, которая делит каждую из этих фигур на две части равной площади.
Итерационный метод как применение сжатых отображений
Метод простой итерации – для уточнения корня уравнение f(x) = 0 (1) заменяется эквивалентным уравнением (2) Т е из
следует
и наоборот. Привести (1) к (2) можно многими способами, например,
, где
– непрерывная произвольная знакопостоянная функция. Геометрически на интервале отделения корня уравнение (1) представляется в виде двух пересекающихся линий
и y = x
Условия сходимости достаточное f(x)- непрерывно дифференцируемая, при этом
должна переводить отрезок [a,b] в себя.
Итерационная последовательность
Пример найти корень уравнения на отрезке [0,1]
1 способ но
не непрерывно дифференцируема на [0,1]
Условие сжимаемости не выполнено
2 способ переводит [0,1] в себя и
Условие сжимаемости выполнено
Непрерывные отображения на квадрате
Задается уравнениями
Интуитивное доказательство теоремы Брауэра
Теорема о неподвижной точке формулируется для отрезка, квадрата. Она верна для круга и всякого выпуклого многоугольника
Лемма Шпернера — комбинаторный аналог теоремы Брауэра о неподвижной точке, один из основных результатов комбинаторной топологии. Утверждает, что при любой Шпернеровской раскраске вершин в триангуляции n-мерного симплекса найдётся ячейка триангуляции, вершины которой покрашены во все цвета. В 1мер сл, лемма Шпернера м рассм как дискр аналог т Больцано Коши.- если большой отрезок разбит на подотр и в вершинах отр расст 1 и 2, то при усл, что в верш большого отрезка стоят разные зн, сущ отрезок подразби, в верш кот стоят разные зн.
Есть триангуляция треугольника T. Вершины отмечены числами 1, 2 и 3 соот. Все вершины триангуляции от этими же числами с соблюдением след граничных условий: если такая вершина лежит на стороне треугольника T, то она получена в качестве отметки одно из тех 2 чисел, кот соотв концам этой стороны. Тогда есть хотя бы 1 грань с 3 разными отметками вершин (хорошая грань). Есть нечетное число хороших граней. , возможны пути 3 типов: 1) от гранич ребра (1,2) к хорошей грани (или в обратном направлении, что несущ), 2) от гранич ребра (1,2) к др такому же ребру, 3) от хорошей грани к другой такой же грани
Задачи на двумерные отображения и неподвижные точки
6) . К остову треугольника (рис.) применяется одно из следующих отображений: 1) каждый угол треугольника, состоящий из 4 граней, загибается внутрь, 2) весь треугольник поворачивается вокруг центра на угол 120 против часовой стрелки. В каждом из этих слу найтит неподвижные и почти неподвижные точки
двумерное отображение Эно
может служить для описания динамики ряда простых физических систем, таких как частица в вязкой среде под действием импульсных толчков, интенсивность которых зависит от координаты.
Параметр b характеризует степень диссипативности Параметр a -нелинейность (эквивалентен параметру λ в отображении Фейгенбаума).
1) Найти неподвижные точки отображения Эно
Отв
2) При выполнении какого условия в отображении появляются устойчивая и неустойчивая точки?
двумерное отображение с кубической нелинейностью Холмса
1. Найти аналитически координаты неподвижных точек периода 1 двумерного отображения Холмса и определить область их существования
метод простой итерации для системы двух уравнений
Рассмотрим систему двух уравнений
разными способами преобразуем к виду
Итерационный процесс
Достаточные условия сходимости
ф)(х, у) и ф2(х, у) определены и непрерывно дифференцируемы в заданной области;
начальные приближения х0, у0 и все последующие х,„ у„ принадлежат заданной области;
в рассматриваемой области выполняются неравенства:
или
Пример решить систему 2 уравнений
Преобразуем
Ограничимся положительным решением. Из рис за начальное приближение положительного решения системы можно принять
Точное решение системы имеет вид
Литература
1)Шашкин. Неподвижные точки, сер. Популярные лекции по математике, М.Наука,1989
2) Прошин Ю.Н., Шакиров М.А., Моделирование и визуализация нелинейных динамических систем, КФУ, Институт физики, 2017 г
3) Лемма Шпернера и справедливое деление, автореферат дипломной работы, СГУ им Чернышевского, каф. Компьютерной алгебры и теории чисел, Свратов, 2017
4) Данилов В.И., Лекции о неподвижных точках. —Российская экономическая школа, М, 2006 г
5) А.П. КузнецовА.В. Савин Л.В. Тюрюкина Введение в физику нелинейных отображений
6) Старостина В.В., Тепляков В.В. Вокруг теоремы Шарковского
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 ноября 2022 года; проверки требует 1 правка.
Отображение с тремя неподвижными точками
Неподвижная точка в математике — точка, которую заданное отображение переводит в неё же, иными словами, решение уравнения 
К примеру, отображение 




Неподвижные точки есть не у всякого отображения — скажем, отображение 
Точки, возвращающиеся в себя после определённого числа итераций, то есть, решения уравнения
,
называются периодическими (в частности, неподвижные точки — это периодические точки периода 
Притягивающие неподвижные точки[править | править код]
Неподвижная точка 





.
При этом обычно требуют, чтобы результат каждой итерации не покидал некоторой большей окрестности точки 

В частности, достаточным условием, чтобы точка была притягивающей, является условие 
Метод Ньютона[править | править код]
Одним из применений идеи притягивающей неподвижной точки является метод Ньютона: решение уравнения оказывается притягивающей неподвижной точкой некоторого отображения, и потому может быть найдено как предел очень быстро сходящейся последовательности чисел, полученных его повторным применением.
Наиболее известным примером применения этого метода является нахождение квадратного корня из числа 
.
См. также[править | править код]
- Теорема Банаха о неподвижной точке
- Теорема Брауэра о неподвижной точке
- Особая точка дифференциального уравнения
- Теорема Шаудера — Тихонова
- Комбинатор неподвижной точки
- Теорема Клини о неподвижной точке
- Теорема о неподвижных точках нормальных функцийruen
Литература[править | править код]
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1976. — Гл. 2, п. 4.
- Красносельский М. А., Забрейко П. П. Геометрические методы нелинейного анализа. — М.: Наука, 1975. — Гл. 5.
- Agarwal R. P., Meehan M., O’Regan D. Fixed Point Theory and Applications. — Cambridge University Press, 2001. — ISBN 0-521-80250-4.
- Borisovich Yu. G., Gel’man B. D., Myshkis A. D., Obukhovskii V. V. Multivalued mappings // Journal of Soviet Mathematics, 1984. — Vol. 24, Issue 6, pp 719—791.
- Fitzpatrick P. M., Petryshyn W. V. Fixed point theorems for multivalued noncompact acyclic mappings // Pacific Journal of Mathematics, 54:2, 1974.
- Шашкин Юрий Алексеевич, Неподвизжные Точки. — М.: Наука, 1989.
Теорема о неподвижной точке
Определение 1.7. Элемент множества
называют неподвижной точкой отображения
, если
.
Элемент упорядоченного множества
называют наименьшей неподвижной точкой отображения
, если он является наименьшим элементом множества всех неподвижных точек отображения
.
Теорема 1.7 (теорема о неподвижной точке). Любое непрерывное отображение индуктивного упорядоченного множества
в себя имеет наименьшую неподвижную точку.
Обозначим через наименьший элемент множества
. Полагаем
и
для любого
, т.е.
означает результат n-кратного применения
к
. Рассмотрим последовательность элементов
(1.7)
Докажем, что последовательность (1.7) неубывающая. Используем метод математической индукции. Для элемента , как наименьшего элемента множества
, имеем
. Пусть для некоторого натурального
верно соотношение
. Согласно теореме 1.6, отображение
монотонно, и поэтому
т.е. соотношение верно и для номера . Согласно методу математической индукции,
для любого
, т.е. последовательность (1.7) неубывающая. Следовательно, по определению индуктивного упорядоченного множества, она имеет точную верхнюю грань. Обозначим ее через
(1.8)
Докажем теперь, что если у неубывающей последовательности отбросить любое конечное число начальных членов, то ее точная верхняя грань не изменится.
Действительно, если а есть точная верхняя грань неубывающей последовательности , то
для всякого
. В частности, фиксируя произвольно
, для любого
имеем
, т.е. а будет верхней гранью подпоследовательности
.
Докажем, что а является точной верхней гранью этой подпоследовательности. Пусть — какая-то ее верхняя грань, т.е.
для любого
. Так как последовательность
неубывающая, то
для каждого
. Поскольку
, то в силу транзитивности отношения порядка
и тем самым
для любого
, т.е.
есть верхняя грань всей последовательности
. Поскольку
, то
и
. Следовательно,
— точная верхняя грань последовательности
.
В силу непрерывности получаем
Но
Таким образом, доказано, что является неподвижной точкой отображения
.
Покажем теперь, что найденная неподвижная точка является наименьшей. Пусть для некоторого имеем
. Так как
, а отображение
, будучи непрерывным, монотонно, то
и т.д.
Следовательно, для любого имеем
, т.е. элемент
есть верхняя грань последовательности
. Поскольку элемент
(как точная верхняя грань) есть наименьший элемент на множестве всех верхних граней этой последовательности, то
. Таким образом, мы доказали, что произвольная неподвижная точка отображения
не меньше элемента
, то есть
— наименьшая неподвижная точка отображения
.
Нахождение неподвижной точки
Поиск неподвижной точки отображения можно рассматривать как задачу решения уравнения
(1.9)
Теорему о неподвижной точке можно трактовать таким образом: для непрерывного отображения индуктивного упорядоченного множества в себя уравнение
имеет решение, т.е. существует такой
, что выполняется равенство
причем множество всех решений этого уравнения имеет наименьший элемент. Этот элемент и будет наименьшей неподвижной точкой отображения
.
Отметим, что доказательство теоремы о неподвижной точке конструктивное: оно дает метод получения неподвижной точки. Для ее нахождения надо построить последовательность вида (1.7) и найти ее точную верхнюю грань.
Пример 1.20. Приведем простой пример вычисления наименьшей неподвижной точки. В качестве индуктивного упорядоченного множества возьмем отрезок
с естественным числовым порядком
. Согласно примеру 1.19, это индуктивное упорядоченное множество.
Рассмотрим на этом множестве уравнение . Можно показать, что для индуктивного упорядоченного множества
любая монотонная функция
, непрерывная в смысле определения из курса математического анализа, непрерывна и в смысле данного выше определения. Действительно, для любой неубывающей последовательности
на множестве
справедливо равенство
. В силу непрерывности функции
в смысле определения из курса математического анализа имеем
Так как функция монотонна, то
— неубывающая последовательность и
В итоге получаем
Следовательно, правая часть данного уравнения непрерывна.
Заметим, что если бы в правой части стояла линейная функция с отрицательным коэффициентом при , то условие непрерывности функции в смысле приведенного выше определения было бы уже нарушено, поскольку такая функция не является монотонной в смысле определения 1.6.
Наименьшим элементом рассматриваемого множества является число 0. Вычисляем:
получая последовательность приближений к наименьшей неподвижной точке.
Можно проверить (например, с помощью метода математической индукции), что
Предел этой последовательности равен . Таким образом, наименьшая неподвижная точка отображения
, определяемого правой частью уравнения, равна
. Это единственная в данном случае неподвижная точка отображения
, что, конечно, очевидно и без теоремы 1.7 о неподвижной точке. Но здесь мы нарочно рассмотрели простой пример, показав, как можно решать подобные уравнения, основываясь на доказательстве теоремы. Мы не будем пока приводить более сложные примеры, так как интересные приложения теоремы о неподвижной точке имеются в теории графов и теории автоматов, и вернемся к этой теореме при решении задачи о путях в ориентированных графах.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

http://profbeckman.narod.ru/
Графические методы исследования отображений основаны на построении
диаграмм.
Диаграмма – графическое представление данных линейными отрезками или геометрическими фигурами, позволяющее быстро оценить соотношение нескольких величин. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации.
Диаграмма Верхулста (паутина) – визуальный инструмент, применяемый в исследованиях качественного поведения одномерных итерированных функций (например, логистического отображения). Используется для изучения долгосрочного влияния начального условия при длительных итерациях.
Построение диаграмм в теории нелинейной динамики используют процесс рекурсии.
Рекурсия – процесс, с помощью которого предыдущий результат используется как вход для следующего результата. При рекурсии компьютерная подпрограмма вызывает сама себя.
Рекурсия – способ организации вычислений, при котором процедура или функция в ходе выполнения обращается сама к себе; это определение через себя, сведение общего случая к аналогичным частным случаям.
Пример. Рекурсивное определение понятия факториала N! (N 0)
1, при N 0
Здесь факториал N! выражается через факториал (N–1)!, т.е. через себя, поэтому данное определение N! является рекурсивным.
Рис. 12. Две диаграммы для последовательности an=frac12an−1+2.
При создании паутинной диаграммы для рекурсивной формулы an=f(an−1), действуйте следующим образом.
1. Графа (в той же прямоугольной системе координат) уравнения y=f(x) и y=x.
2. Начинают с точки (a1,0).
3. Проводят линию вертикально до встречи с исследуемой кривой y=f(x).
4. Проводят линию горизонтально до
встречи с исследуемой кривой y=x.
5.Возвращаются к шагу 3.
Рассмотрим диаграммы паутины для некоторых простых случаев и их результирующие графы. На рис. 12 представлены две диаграммы для последовательности an=frac12an−1+2. На обеих этих диаграммах наклон рекурсивной функции меньше единицы, и итерации паутины приближаются к пересечению функции с линией y=x Эта последовательность сходится к значению 4, решению уравнения x=f(x). Уравнение x=f(x)
называется уравнением с фиксированной точкой, а
его решение является фиксированной точкой
рекурсивного уравнения. Если первый член последовательности был решением уравнения с фиксированной точкой, то последовательность была бы постоянной.
Диаграммы паутины трёх связанных уравнений (рис. 14) демонстрирует, что в первом

http://profbeckman.narod.ru/
циклическое поведение возможно, а второй и третий графики показывают, что небольшие изменения в уравнении могут привести к тому, что итерации либо приближаются, либо расходятся с неподвижной точкой.
Рис. 13. Две диаграммы для последовательности an=2an−1−4.
Возможное поведение последовательности может быть весьма непредсказуемым. Хотя значения последовательности, изображенной ниже, полностью определяются рекурсивной формулой и явно ограничены, но они не сходятся к неподвижной точке и не являются циклическими. Фактически, за исключением того, что все значения находятся между нулем и единицей, долгосрочное поведение этой системы кажется довольно хаотичным.
На диаграммах рис. 13 наклон рекурсивной функции больше единицы, и итерации паутины расходятся от пересечения функции с линией y=x. Значения этой последовательности неограниченны.
Рис. 14. Диаграммы паутины трёх связанных уравнений.
Арифметические последовательности могут показывать только один тип конечного поведения, неограниченность (если общая разница не равна нулю). Геометрические последовательности могут быть либо неограниченными, либо сходятся к неподвижной точке. Ни арифметические, ни геометрические последовательности не проявят циклического или хаотического поведения. Классическим примером последовательности, которая показывает все эти конечные поведения, является логистическая последовательность.
Если f(x)=x для некоторого x из X (т. е. период орбиты x равен 1), то x – неподвижная точка итерированной последовательности. Множество неподвижных точек часто обозначается как Fix(f). Существует ряд теорем о неподвижной точке которые гарантируют существование неподвижных точек в различных ситуациях, например, теорема Банаха о неподвижной точке и теорема Брауэра о неподвижной точке.
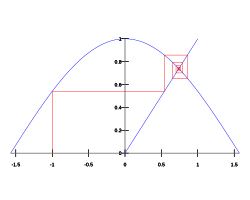
Рис. 15. Графическое нахождение особых точек.
Особенно удобным способом графического представления орбиты вещественнозначной функции f является паутинная диаграмма.
Для данной итерированной функции f:R→R график состоит из диагональной (x=y) линии и кривой, представляющей y=f(x). Изучение поведения х0 ведут этапами.
http://profbeckman.narod.ru/
1.Находят точку на функциональной кривой с x-координатой х0: точка (х0.
2.Проводят горизонтальную прямую от этой точки до диагональной линии.
3.Строят вертикальную линию от точки на диагонали до функциональной кривой. При необходимости повторяют шаг 2.
На участке паутины устойчивая неподвижная точка соответствует внутренней
спирали, а неустойчивая неподвижная точка – внешней спирали. Эти спирали будут стремиться к точке, где диагональ y=x пересекает график функции. Орбита периода 2 представлена прямоугольником, в то время как более длительные циклы производят более сложные замкнутые контуры. На хаотичной орбите будет отображаться «заполненная» область, указывающая на бесконечное количество неповторяющихся значений.
Диаграммы паутины позволяют итерировать функцию полностью графическими средствами и без прибегания к аналитическим или численным методам. Рассмотрим приведенную ниже функцию f(x). Начиная с точки x0, мы можем найти следующая итерация функции x1=f(x0), просто рисуя вертикальную линию на график функции; x1 можно пометить на вертикальной оси, вычерчивая горизонтальную линию из точки пересечения.
Чтобы найти x2=f(x1), нужно переместить точку x1, отмеченную на вертикальной оси (рис.15, на ту же точку на горизонтальной оси. Это осуществляют путём нахождения пересечения горизонтальной линии с линией y=x. Так как горизонтальная линия имеет уравнение y=x1, это пересечение произойдёт в точке (x0, x1) (рис. 15а) Затем проведя вертикальную линию вниз к горизонтальной оси отмечают точку x1. Имея точку x1 на горизонтальной оси, можно найти точку x2=f(x1) проведя вертикальную линию до графика функции (рис. 15б). Этот процесс можно повторить для создания «паутинной диаграммы», которая показывает позиции последующих итераций функции (рис. 15в)
В этом примере мы видим, что итераты фиксируются в 2-цикле (который отмечен синим).
Рис. 16.
х 0,739.
На паутинных диаграммах хорошо видна динамика орбит, особенно если на отрезках показаны стрелки, обозначающие направления движения.
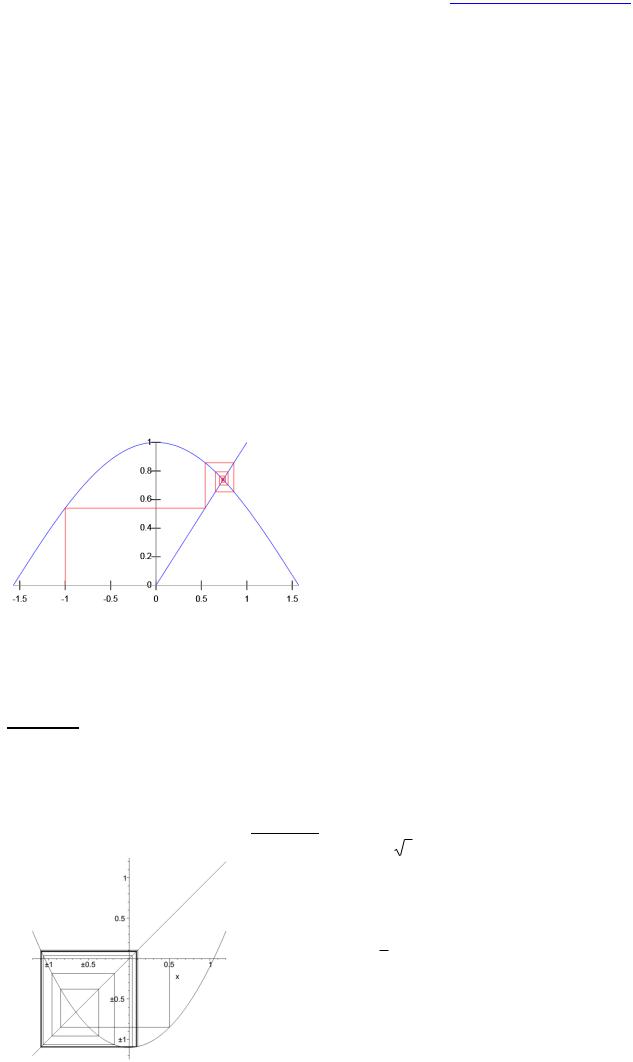
Пример 1. Функция f(x)=x2 (рис. 17). Если начальная точка х0=0 или х0=1, т.е. х0 принимает значения неподвижных точек f, то орбиты постоянны. Если х0>1, то орбита стремится к + . Если 0<x0<1 или -1<x0<0, то орбита сходится к неподвижной точке 0. Если х0=1, то орбита принимает вид: [-1 1 1 1…], т.е. орбита является в конечном итоге периодической. Если х0<0, то xn . В этом случае говорят, что орбита расходится. В данном примере неподвижная точка 0 является притягивающей, а неподвижная точка – отталкивающей.
Пример 2. Функция f(x)=x2-1 (рис. 18). Две неподвижные
|
точки равны |
x |
1 |
5 |
. Обе они отталкивающие, т.к. |
|
2 |
||||
|
|f‘(x)|=2|x|>1 в |
обоих |
случаях. Любая неподвижная точка |
f(2)(x)=(x2-1)2-1=x4-2x2 есть точка периода 2 функции f(x). В этом случае орбиты принимают вид: [x0 x1 x0 x1 x0]. Неподвижные точки f(2)(x) суть корни полинома х4-2х2–х и
равны 0, -1 и (1 
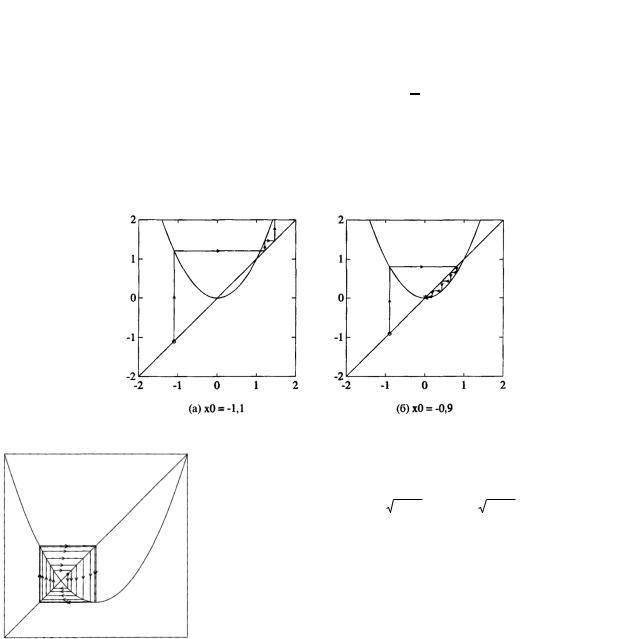
http://profbeckman.narod.ru/
же неподвижными точками f(x), поэтому они обладают периодическими орбитами наименьшего периода 1. Орбиты двух новых точек, 0 и 1: [0 -1 0 -1 0…] и -1 0 -1 0 -1 …], имеют наименьший период 2.
Рис. 17. Паутина диаграммы итераций x0=0,5 при x2 +1,1: итераты сходятся к двум циклам в {p+, p–}≈ {0,0916, -1,0916}.
Функции х2 и х2-1 – частные случаи отображения х2+с которое часто встречается в теории нелинейной динамики. Хотя f(x)=x2+c – всего-навсего квадратичная функция, она применяется во всех областях теории, например, во множествах Мандельброта и Жюлиа, которые получаются в результате рассмотрения того же квадратичного полинома, но только с использованием комплексных чисел, вместо действительных.
Рис. 18. Функция f(x)=x2: а – х0=1,1: б – х0=-0,9
Рис. 19. Функция f(x)=x2-1; x0=-0,5.
Пусть х – действительное число. Для любого значения с неподвижные точки, которые суть решения уравнения
|
х2+с=х, имеют вид: |
1 |
1 4c |
, |
1 |
1 4c |
. Неподвижные |
|
|
2 |
2 |
||||||
точки будут действительными числами только, если 1-4с 0. Алгебраически несложно показать, что если с 1/4, то – < < . Кроме того, f(- )= . Орбиты для х0> и x0<- не представляют интереса, т.к. для этих случаев все они стремятся к + . Далее будем полагать, что с 1/4 и – <х0< . Для f(x0)<+ , если -2 с, то – f(x0). Три возможных случая, соответствующих –
2<c 1/4, с=-2 и с<-2, приведены на рис.5.
Пусть I – замкнутый интервал [- , ]. В случае -2 с 1/4, если х0 I, то f(x0) I и вся орбита целиком находится в I. Если с<-2 и x0 I, то возможны два случая: либо орбита остаётся в I или же в конечном счёте некоторое значение х0 становится меньше – и тогда орбиты устремляются к + .

http://profbeckman.narod.ru/
Рис. 20: а –2<c 1/4, б – c=-2, в – c<2.
|
Когда |
-3/4<c<1/4, неподвижная точка является притягивающей, т.к. |
|||||
|
f ‘( ) |
1 |
1 и все орбиты (начинающиеся в I) сходятся к . По мере того как с |
||||
|
1 4c |
||||||
убывает и становится меньше -3/4, величина |f‘( )| возрастает и становится больше 1, т.е. становится отталкивающей. В то же время функция f(2) доставляет пару притягивающих неподвижных точек, которые приводят к появлению цикла с периодом 2 для f (рис. 21 и 22). Этот феномен наблюдался в примере 2. Говорят, что система претерпевает бифуркацию удвоения периода, когда с переходит через значение -3/4.
Рис. 21. Бифуркация удвоения периода.
Другая бифуркация удвоения периода возникает при с=-5/4. Когда с становится меньше этого значения, орбиты начинают притягиваться циклом с периодом 4. По мере того как с убывает, мы последовательно встречаем притягивающие периодические орбиты длины 8, 16 и так далее. С помощью удвоения периода система погружается в хаос.
Рис. 22. Увеличенное изображение графика f(x)=x2-0,9.
Частный случай с=-2 заслуживает особенного внимания. При этом =2, а I=[-2, 2]. Как следует из рис. 21б, график y=f(x) для х I в точности заполняет квадрат IxI, в том смысле, что
не существует меньшего квадрата со сторонами, параллельными осям координат, который был бы полностью содержал данный график. То же самое верно для y=f(2)(x), y=f(3)(x),…
Прямая у=x пересекает график y=f(n) точно 2n раз в квадрате IxI. Каждое пересечение есть не что иное, как неподвижная точка функции f(n) и, следовательно, периодическая точка с

http://profbeckman.narod.ru/
периодом n (не обязательно наименьшим). Для с=-2 существуют периодические орбиты функции f с периодами длины 2, 3, 4,…
Рис. 23. Графики f, f(2) и f(3) при с=-2.
Графически особые точки находят с помощью построения Ламерея (лестница Ламереля, рис. 24). С этой целью на графике исследуемой зависимости строят прямую, выходящую из начала координат под углом 45о. Неподвижные точки – точки пересечения исследуемой кривой с прямой линией. Далее из
некоторой начальной точки х0 строят вертикальную линии до пресечения с кривой и точку пересечения горизонтальной линией проецируют на прямую (метод линеаризации, функциональный масштаб, метод особых точек), из точки на прямой вновь проводят вертикаль до пересечения с прямой и т.д. Непрерывная кривая превращается в набор дискретных точек на прямой (кривая линеаризуется). Аналогично можно поступить с плоскостью или объёмом. Устойчивость неподвижной точки определятся по углу наклона касательной к кривой в точке её пересечения с прямой (рис. 25).
Неподвижные точки могут быть устойчивыми или неустойчивыми, аттракторами, репеллерами или нейтральными. Так, на рис. 25 точка x* (неподвижная, если x*=f(x*)) неустойчивая, точки x** и x*** – устойчивые (Точка x* – неустойчива, если |f′(x*)|>1.
Точки x**, x*** – устойчивы, если |f′(x**, x***)|<1).
Рис. 24. Особые точки отображений: а – построение прямой xn+1=xn и нахождение особых точек; б – построение Ламерея («лестница Ламерея»).
Рис. 25. Графическая оценка устойчивости точек: углы **, ***<45o, угол >45o.
В линейной системе с дискретным временем
xn+1=Bxn (17)
равновесное решение x=0 является единственным равновесием.
Существует важное различие между решениями систем непрерывного времени и решениями систем дискретного времени относительно состояния инвариантных линий, определяемых собственными векторами. Реальные собственные векторы, связанные с вещественными собственными значениями для систем разностных
Теорема Брауэра о неподвижной точке – это теорема о неподвижной точке в топологии , названная в честь LEJ (Бертуса) Брауэра . Он утверждает, что для любой непрерывной функции, отображающей компактное выпуклое множество в себя, существует точка такая, что . Простейшие формы теоремы Брауэра относятся к непрерывным функциям из отрезка вещественных чисел в себя или из замкнутого круга в себя. Более общий вид , чем второй для непрерывных функций из выпуклого компакта в евклидове пространства к самому себе.


Среди сотен теорем о неподвижной точке особенно хорошо известна теорема Брауэра, отчасти благодаря ее использованию во многих областях математики. В своем первоначальном поле, этот результат является одним из основных теорем , характеризующих топологию евклидовы пространства, наряду с теоремой Жордана , в теореме волосатой шара и теоремы Борсука-Улама . Это дает ему место среди основных теорем топологии. Теорема также используется для доказательства глубоких результатов о дифференциальных уравнениях и рассматривается в большинстве вводных курсов по дифференциальной геометрии . Он появляется в маловероятных областях, таких как теория игр . В экономике, теорема о неподвижной точке Брауэра и его расширение, то Какутани с фиксированной точкой теоремы , играет центральную роль в доказательстве существования в общем равновесии в рыночной экономике , как развитый в 1950 нобелевских призерах Kenneth Arrow и Жерар Дебре .
Теорема была впервые изучена в связи с работой над дифференциальными уравнениями французских математиков Анри Пуанкаре и Шарля Эмиля Пикара . Доказательство таких результатов, как теорема Пуанкаре – Бендиксона, требует использования топологических методов. Эта работа конца XIX века открыла несколько последовательных версий теоремы. Общий случай был впервые доказан в 1910 году Жаком Адамаром и Луитценом Эгбертусом Яном Брауэром .
Заявление
Теорема имеет несколько формулировок в зависимости от контекста, в котором она используется, и степени ее обобщения. Самым простым иногда называют следующее:
-
- В самолете
- Каждая непрерывная функция из замкнутого круга в себя имеет по крайней мере одну неподвижную точку.
Это можно обобщить на произвольную конечную размерность:
-
- В евклидовом пространстве
- Всякая непрерывная функция от замкнутого шара в виде евклидова пространства в себя имеет неподвижную точку.
Немного более общая версия выглядит следующим образом:
-
- Выпуклый компакт
- Каждая непрерывная функция из выпуклого компактного подмножества K евклидова пространства в сам K имеет неподвижную точку.
Еще более общая форма более известна под другим названием:
-
- Теорема Шаудера о неподвижной точке
- Каждая непрерывная функция из выпуклого компакта K в виде банаховом пространстве к K само имеет неподвижную точку.
Важность предварительных условий
Теорема верна только для множеств, которые являются компактными (в частности, ограниченными и замкнутыми) и выпуклыми (или гомеоморфными выпуклым). Следующие примеры показывают, почему предварительные условия важны.
Ограниченность
Рассмотрим функцию
которая является непрерывной функцией от самого себя. Поскольку он сдвигает каждую точку вправо, у него не может быть фиксированной точки. Пространство выпуклое и замкнутое, но не ограниченное.
Закрытость
Рассмотрим функцию
которая является непрерывной функцией от открытого интервала (−1,1) к себе. В этом интервале каждая точка сдвигается вправо, поэтому у него не может быть фиксированной точки. Пространство (−1,1) выпукло и ограничено, но не замкнуто. Функция F имеет иметь фиксированную точку для отрезка [-1,1], а именно : F (1) = 1.
Выпуклость
Выпуклость не является строго обязательной для BFPT. Поскольку задействованные свойства (непрерывность, неподвижность точки) инвариантны относительно гомеоморфизмов , BFPT эквивалентен формам, в которых требуется, чтобы область была замкнутым единичным шаром . По той же причине это справедливо для любого множества, гомеоморфного замкнутому шару (и, следовательно, замкнутого , ограниченного, связного , без дырок и т. Д.).
В следующем примере показано, что BFPT не работает для доменов с дырами. Рассмотрим функцию , которая является непрерывной функцией от единичной окружности к самой себе. Поскольку -x ≠ x выполняется для любой точки единичной окружности, f не имеет неподвижной точки. Аналогичный пример работает для n- мерной сферы (или любой симметричной области, не содержащей начала координат). Единичная окружность замкнута и ограничена, но в ней есть отверстие (и поэтому она не выпуклая). Функция f действительно имеет фиксированную точку для единичного диска, поскольку она берет начало координат в себя.

Формальное обобщение BFPT для областей «без дырок» может быть получено из теоремы Лефшеца о неподвижной точке .
Примечания
Непрерывная функция в этой теореме не обязана быть биективной или даже сюръективной .
Иллюстрации
Теорема имеет несколько иллюстраций из “реального мира”. Вот несколько примеров.
- Возьмите два листа миллиметровой бумаги одинакового размера с системами координат на них, положите один на стол, скомкайте (не разрывая и не порвав) второй и положите его любым способом поверх первого так, чтобы он смялся. бумага не выходит за пределы плоской. Тогда будет по крайней мере одна точка смятого листа, которая будет находиться непосредственно над соответствующей ей точкой (то есть точкой с теми же координатами) плоского листа. Это является следствием случая n = 2 теоремы Брауэра, примененного к непрерывной карте, которая присваивает координатам каждой точки смятого листа координаты точки плоского листа непосредственно под ним.
- Возьмем обычную карту страны и предположим, что эта карта выложена на столе внутри этой страны. На карте всегда будет точка «Вы здесь», которая представляет собой ту же точку в стране.
- В трех измерениях следствием теоремы Брауэра о фиксированной точке является то, что независимо от того, сколько вы перемешиваете коктейль в стакане (или думаете о молочном коктейле), когда жидкость успокоится, какая-то точка в жидкости окажется. в том же самом месте в стакане, что и до того, как вы предприняли какое-либо действие, предполагая, что конечное положение каждой точки является непрерывной функцией ее исходного положения, что жидкость после перемешивания содержится в пространстве, первоначально занятом ею, и что стакан (и форма перемешиваемой поверхности) сохраняют выпуклый объем. Заказ коктейля « взбалтывать, а не перемешивать» нарушает условие выпуклости («встряхивание» определяется как динамическая серия невыпуклых инерционных состояний удержания в свободном свободном пространстве под крышкой). В этом случае теорема неприменима, и, таким образом, все точки распределения жидкости потенциально смещаются из исходного состояния.
Интуитивный подход
Объяснения, приписываемые Брауэру
Предполагается, что эта теорема возникла из наблюдения Брауэра над чашкой кофе. Если перемешать, чтобы растворить кусок сахара, окажется, что всегда есть точка, в которой нет движения. Он пришел к выводу, что в любой момент на поверхности есть точка, которая не движется. Фиксированная точка не обязательно является точкой, которая кажется неподвижной, поскольку центр турбулентности немного перемещается. Результат не является интуитивно понятным, поскольку исходная фиксированная точка может стать подвижной, когда появится другая фиксированная точка.
Говорят, что Брауэр добавил: «Я могу сформулировать этот великолепный результат по-разному, я беру горизонтальный лист и еще один идентичный, который я сминаю, сплющиваю и кладу на другой. на другом листе “. Брауэр «выравнивает» лист, как утюг, не удаляя складок и складок. В отличие от примера с кофейной чашкой, пример скомканной бумаги также демонстрирует, что может существовать более одной фиксированной точки. Это отличает результат Брауэра от других теорем о неподвижной точке, таких как теоремы Стефана Банаха , которые гарантируют единственность.
Одномерный случай
В одном измерении результат интуитивно понятен и легко доказывается. Непрерывная функция f определена на отрезке [ a , b ] и принимает значения в том же интервале. Сказать, что эта функция имеет фиксированную точку, означает сказать, что ее график (темно-зеленый на рисунке справа) пересекает график функции, определенной на том же интервале [ a , b ], который отображает x в x (светло-зеленый).
Интуитивно понятно, что любая непрерывная линия от левого края квадрата до правого края обязательно должна пересекать зеленую диагональ. Чтобы доказать это, рассмотрим функцию g, которая отображает x в f ( x ) – x . Это ≥ 0 на a и ≤ 0 на b . По теореме промежуточного значения , г имеет нуль в [ с , Ь ]; этот ноль – неподвижная точка.
Говорят, что Брауэр выразил это следующим образом: «Вместо того, чтобы исследовать поверхность, мы докажем теорему о куске струны. Давайте начнем со струны в развернутом состоянии, а затем перегибаем ее. Давайте сплющим перевернутую струну. Опять же, точка нити не изменила своего положения по отношению к своему исходному положению на развернутой нити “.
История
Теорема Брауэра о неподвижной точке была одним из первых достижений алгебраической топологии и является основой более общих теорем о неподвижной точке, которые важны в функциональном анализе . Случай n = 3 был впервые доказан Пирсом Болем в 1904 году (опубликован в Journal für die reine und angewandte Mathematik ). Позже это было доказано Л.Е. Брауэром в 1909 году. Жак Адамар доказал общий случай в 1910 году, а Брауэр нашел другое доказательство в том же году. Поскольку все эти ранние доказательства были неконструктивными косвенными доказательствами , они противоречили интуиционистским идеалам Брауэра . Хотя существование неподвижной точки не является конструктивным в смысле конструктивизма в математике , теперь известны методы приближения неподвижных точек, гарантированные теоремой Брауэра.
Предыстория
Для потоков в неограниченной области или в области с «дырой» теорема неприменима.
Теорема применима к любой области в форме диска, где она гарантирует наличие неподвижной точки.
Чтобы понять предысторию теоремы Брауэра о неподвижной точке, необходимо пройти через дифференциальные уравнения . В конце 19 века старая проблема стабильности Солнечной системы вернулась в центр внимания математического сообщества. Для ее решения потребовались новые методы. Как заметил Анри Пуанкаре , который работал над проблемой трех тел , нет никакой надежды найти точное решение: «Нет ничего более подходящего, чтобы дать нам представление о сложности проблемы трех тел и вообще всех проблем. динамики, где нет единого интеграла и расходятся ряды Болина ». Он также отметил, что поиск приближенного решения не более эффективен: «чем больше мы стремимся получить точные приближения, тем больше будет отклоняться результат в сторону возрастающей неточности».
Он изучил вопрос, аналогичный вопросу о движении поверхности чашки кофе. Что вообще можно сказать о траекториях на поверхности, оживляемой постоянным потоком ? Пуанкаре обнаружил, что ответ можно найти в том, что мы теперь называем топологическими свойствами в области, содержащей траекторию. Если эта область компактна , т.е. одновременно замкнута и ограничена , то траектория либо становится стационарной, либо приближается к предельному циклу . Пуанкаре пошел дальше; если область такого же типа, как диск, как в случае с чашкой кофе, обязательно должна быть фиксированная точка. Эта неподвижная точка инвариантна относительно всех функций, которые ставят в соответствие каждой точке исходной поверхности ее положение через короткий интервал времени t . Если область представляет собой круглую полосу или если она не закрыта, то это не обязательно так.
Чтобы лучше понять дифференциальные уравнения, родился новый раздел математики. Пуанкаре называл это анализом . Французская универсальная энциклопедия определяет его как ветвь, которая «рассматривает свойства объекта, которые остаются неизменными, если он постоянно деформируется, без разрывов». В 1886 году Пуанкаре доказал результат, эквивалентный теореме Брауэра о неподвижной точке, хотя связь с предметом этой статьи еще не была очевидна. Чуть позже он разработал один из фундаментальных инструментов для лучшего понимания ситуации анализа, теперь известный как фундаментальная группа или иногда группа Пуанкаре. Этот метод можно использовать для очень компактного доказательства обсуждаемой теоремы.
Метод Пуанкаре был аналогичен методу Эмиля Пикара , современного математика, обобщившего теорему Коши – Липшица . Подход Пикарда основан на результате, который позже будет формализован другой теоремой о неподвижной точке , названной в честь Банаха . Вместо топологических свойств области в этой теореме используется тот факт, что рассматриваемая функция является сжатием .
Первые доказательства
На заре 20-го века интерес к анализу места не остался незамеченным. Однако необходимость теоремы, эквивалентной обсуждаемой в этой статье, еще не была очевидна. Пирс Бол , латвийский математик, применил топологические методы к изучению дифференциальных уравнений. В 1904 году он доказал трехмерный случай нашей теоремы, но его публикация не была замечена.
Наконец, именно Брауэр дал этой теореме первый патент на благородство. Его цели отличались от целей Пуанкаре. Этот математик был вдохновлен основами математики, особенно математической логикой и топологией . Его первоначальный интерес заключался в попытке решить пятую проблему Гильберта . В 1909 году во время путешествия в Париж он встретил Анри Пуанкаре , Жака Адамара и Эмиля Бореля . Последовавшие за этим обсуждения убедили Брауэра в важности лучшего понимания евклидовых пространств и положили начало плодотворному обмену письмами с Адамаром. Следующие четыре года он сосредоточился на доказательстве некоторых великих теорем по этому вопросу. В 1912 году он доказал теорему о волосатом шаре для двумерной сферы, а также тот факт, что каждое непрерывное отображение двумерного шара в себя имеет фиксированную точку. Эти два результата сами по себе не были новостью. Как заметил Адамар, Пуанкаре показал теорему, эквивалентную теореме о волосатом шарике. Революционным аспектом подхода Брауэра было его систематическое использование недавно разработанных инструментов, таких как гомотопия , лежащая в основе концепции группы Пуанкаре. В следующем году Адамар обобщил обсуждаемую теорему на произвольную конечную размерность, но использовал другие методы. Ганс Фройденталь комментирует соответствующие роли следующим образом: «По сравнению с революционными методами Брауэра методы Адамара были очень традиционными, но участие Адамара в рождении идей Брауэра больше похоже на акушерку, чем на простого зрителя».
Подход Брауэра принес свои плоды, и в 1910 году он также нашел доказательство, справедливое для любой конечной размерности, а также другие ключевые теоремы, такие как инвариантность размерности. В контексте этой работы Брауэр также обобщил теорему Жордана о кривой на произвольную размерность и установил свойства, связанные со степенью непрерывного отображения . Этот раздел математики, первоначально задуманный Пуанкаре и развитый Брауэром, изменил свое название. В 1930-х годах место анализа превратилось в алгебраическую топологию .
Прием
Джон Нэш использовал теорему теории игр, чтобы доказать существование профиля равновесной стратегии.
Теорема доказала свою ценность более чем одним способом. В течение 20 века было разработано множество теорем о неподвижной точке и даже раздел математики, названный теорией о неподвижной точке . Теорема Брауэра, вероятно, самая важная. Он также входит в число основополагающих теорем о топологии топологических многообразий и часто используется для доказательства других важных результатов, таких как теорема о жордановой кривой .
Помимо теорем о неподвижной точке для более или менее сжимающих функций, многие прямо или косвенно вытекают из обсуждаемого результата. Непрерывное отображение замкнутого шара евклидова пространства на его границу не может быть тождественным на границе. Точно так же теорема Борсука – Улама утверждает, что непрерывное отображение n- мерной сферы в R n имеет пару антиподальных точек, которые отображаются в одну и ту же точку. В конечномерном случае теорема Лефшеца о неподвижной точке предоставила с 1926 года метод подсчета неподвижных точек. В 1930 году теорема Брауэра о неподвижной точке была обобщена на банаховы пространства . Это обобщение известно как теорема Шаудера о неподвижной точке , результат, обобщенный С. Какутани на многозначные функции . Встречается также теорема и ее варианты вне топологии. Его можно использовать для доказательства теоремы Хартмана-Гробмана , которая описывает качественное поведение некоторых дифференциальных уравнений вблизи определенных положений равновесия. Точно так же теорема Брауэра используется для доказательства центральной предельной теоремы . Теорема также может быть найдена в доказательствах существования решений некоторых дифференциальных уравнений в частных производных .
Затронуты и другие области. В теории игр , Джон Нэш использовал теорему доказать , что в игре Hex есть выигрышная стратегия для белого. В области экономики П. Бич объясняет, что некоторые обобщения теоремы показывают, что ее использование полезно для некоторых классических задач теории игр и в целом для равновесий ( закон Хотеллинга ), финансовых равновесий и неполных рынков.
Знаменитость Брауэра связана не только с его топологической работой. Доказательства его великих топологических теорем неконструктивны , и неудовлетворенность Брауэра этим отчасти и заставила его сформулировать идею конструктивности . Он стал создателем и ревностным защитником способа формализации математики, известного как интуиционизм , который в то время выступал против теории множеств . Брауэр отказался от своего первоначального доказательства теоремы о неподвижной точке. Первый алгоритм аппроксимации неподвижной точки был предложен Гербертом Скарфом . Тонкий аспект алгоритма Скарфа заключается в том, что он находит точку, которая почти фиксируется функцией f , но в целом не может найти точку, которая близка к реальной фиксированной точке. На математическом языке, если ε выбрано очень маленьким, алгоритм Скарфа может использоваться для поиска точки x, такой что f ( x ) очень близка к x , т . Е .. Но алгоритм Скарфа не может быть использован для нахождения точки x, такой, что x очень близок к фиксированной точке: мы не можем гарантировать, где. Часто это последнее условие подразумевается под неформальной фразой «приближение к фиксированной точке».
Очертания доказательств
Доказательство с использованием степени
Первоначальное доказательство Брауэра 1911 года основывалось на понятии степени непрерывного отображения . Современные версии доказательства также можно найти в литературе.
Обозначим через замкнутый единичный шар с центром в нуле. Предположим просто, что непрерывно дифференцируемо. Регулярное значение из является точка , так что якобиан из неособ в каждой точке прообраза . В частности, по теореме об обратной функции , каждая точка прообраза лежит в (внутренности ). Степени на обычное значении определяются как сумма знаков якобиевого детерминанта из над прообразами Under :
Степень – это, грубо говоря, количество «листов» прообраза f, лежащих на небольшом открытом множестве вокруг p , причем листы подсчитываются противоположно, если они противоположно ориентированы. Таким образом, это обобщение номера намотки на более высокие размеры.
Степень удовлетворяет свойству гомотопической инвариантности : пусть и – две непрерывно дифференцируемые функции, и для . Предположим, что точка является регулярным значением для всех t . Тогда .
Если неподвижной точки границы нет , то функция
хорошо определен, и

определяет гомотопию от функции идентичности к ней. Функция идентичности имеет степень один в каждой точке. В частности, функция идентичности имеет степень один в начале координат, поэтому также имеет степень один в начале координат. Как следствие, прообраз не пустой. Элементы – это в точности неподвижные точки исходной функции f .
Это требует некоторой работы, чтобы сделать его полностью общим. Определение степени необходимо распространить на особые значения f , а затем на непрерывные функции. Более современное появление теории гомологии упрощает построение степени, и поэтому оно стало стандартным доказательством в литературе.
Доказательство с использованием гомологии
Доказательство использует наблюдение , что граница по п -дисков D п является S п -1 , то ( п – 1) – сфера .
Предположим, от противного, что непрерывная функция f : D n → D n не имеет неподвижной точки. Это означает, что для каждой точки x в D n точки x и f ( x ) различны. Поскольку они различны, для каждой точки x в D n мы можем построить уникальный луч от f ( x ) до x и следовать за лучом, пока он не пересечет границу S n −1 (см. Иллюстрацию). Называя эту точку пересечения F ( x ), мы определяем функцию F : D n → S n −1, отправляющую каждую точку в круге в соответствующую ей точку пересечения на границе. Как частный случай, когда x сам находится на границе, точка пересечения F ( x ) должна быть x .
Следовательно, Р представляет собой особый тип непрерывной функции известна как ретракции : каждая точка области значений (в данном случае S п -1 ) является неподвижной точкой F .
Интуитивно кажется маловероятным, что может быть втягивание D n на S n −1 , а в случае n = 1 невозможность более очевидна, потому что S 0 (т. Е. Конечные точки замкнутого интервала D 1 ) не даже подключен. Случай n = 2 менее очевиден, но может быть доказан с помощью основных аргументов, включающих фундаментальные группы соответствующих пространств: ретракция индуцирует сюръективный групповой гомоморфизм от фундаментальной группы D 2 к группе S 1 , но последний группа изоморфна Z, а первая группа тривиальна, поэтому это невозможно. Случай n = 2 также может быть доказан от противного на основе теоремы о ненулевых векторных полях .
Однако при n > 2 доказать невозможность ретракции сложнее. Один из способов – использовать группы гомологий : гомологии H n −1 ( D n ) тривиальны, а H n −1 ( S n −1 ) бесконечны циклическими . Это показывает, что ретракция невозможна, потому что снова ретракция индуцирует инъективный групповой гомоморфизм от последней к первой группе.
Доказательство с использованием теоремы Стокса.
Чтобы доказать, что непрерывная карта имеет неподвижные точки, можно предположить, что она гладкая, потому что, если карта не имеет неподвижных точек, то ее свертка с подходящим смягчителем (гладкой функцией с достаточно малой опорой и целой функцией) даст гладкая функция без неподвижных точек. Как и в доказательстве с использованием гомологий, проблема сводится к доказательству отсутствия плавного возврата с шара на его границу . Если это форма объема на границе , то по теореме Стокса ,
приводя к противоречию.
В более общем плане это показывает, что не существует гладкого ретракции с любого непустого гладкого ориентируемого компактного многообразия на его границу. Доказательство с использованием теоремы Стокса тесно связано с доказательством с использованием гомологий, потому что форма порождает группу когомологий де Рама, которая изоморфна группе гомологий по теореме де Рама .

Комбинаторное доказательство
BFPT можно доказать с помощью леммы Спернера . Приведем схему доказательства для частного случая , в котором е является функцией от стандартного п – симплекс , к самому себе, где
Для каждой точки также Следовательно, сумма их координат равна:
Следовательно, в соответствии с принципом ячейки для каждого должен быть такой индекс , чтобы th координата была больше или равна th координате его изображения при f :
Более того, если он лежит на k- мерной суб-грани, то по тому же аргументу, индекс может быть выбран из числа k + 1 координат, которые не равны нулю на этой суб-грани.
Теперь мы используем этот факт для построения раскраски Спернера. Для каждой триангуляции цвета каждой вершины есть такой индекс , что
По построению это раскраска Спернера. Следовательно, по лемме Шпернера существует n -мерный симплекс, вершины которого раскрашены всем набором из n + 1 доступных цветов.
Поскольку f непрерывен, этот симплекс можно сделать сколь угодно малым, выбрав сколь угодно точную триангуляцию. Следовательно, должна быть точка, удовлетворяющая условию разметки во всех координатах: для всех
Поскольку сумма координат и должна быть равной, все эти неравенства фактически должны быть равенствами. Но это значит, что:
То есть неподвижная точка
Доказательство Хирша
Есть также быстрое доказательство, сделанное Моррисом Хиршем , основанное на невозможности дифференцируемой ретракции. Косвенное доказательство начинается, отметив , что отображение F может быть аппроксимировано с помощью гладкого отображения удерживающего свойства не фиксируя точку; это можно сделать, например, с помощью аппроксимационной теоремы Вейерштрасса . Затем определяется ретракция, как указано выше, которая теперь должна быть дифференцируемой. Такая ретракция должна иметь неособое значение по теореме Сарда , которая также не является сингулярной для ограничения на границу (что и есть тождество). Таким образом, прообраз будет 1-многообразием с краем. Граница должна содержать по крайней мере две конечные точки, обе из которых должны лежать на границе исходного шара, что невозможно при ретракции.
Р. Брюс Келлог, Тьен-Иен Ли и Джеймс А. Йорк превратили доказательство Хирша в вычислимое доказательство, заметив, что ретракт фактически определен везде, кроме неподвижных точек. Почти для любой точки q на границе (при условии, что это не неподвижная точка) существует одно многообразие с краем, упомянутое выше, и единственная возможность состоит в том, что оно ведет от q к фиксированной точке. Проследить такой путь от q до фиксированной точки – это простая численная задача, поэтому метод по существу вычислим. дал концептуально аналогичную версию доказательства гомотопии, которая распространяется на широкий круг связанных проблем.
Доказательство использования ориентированной области
Вариант предыдущего доказательства не использует теорему Сарда и выглядит следующим образом. Если – плавный отвод, рассматривается плавная деформация и гладкая функция
Дифференцируя под знаком интеграла, нетрудно проверить, что φ ′ ( t ) = 0 для всех t , поэтому φ – постоянная функция; противоречие, поскольку φ (0) – n -мерный объем шара, а φ (1) равен нулю. Геометрическая идея состоит в том, что φ ( t ) является ориентированной площадью g t ( B ) (то есть мерой Лебега образа шара через g t с учетом кратности и ориентации) и должна оставаться постоянной (как это очень ясно в одномерном случае). С другой стороны, когда параметр t переходит из 0 в 1, отображение g t непрерывно преобразуется из тождественного отображения мяча в ретракцию r , что является противоречием, поскольку ориентированная область тождества совпадает с объемом мяч, в то время как ориентированная область r обязательно равна 0, так как его изображение является границей шара, набора нулевой меры.
Доказательство с использованием игрового гекса
Совершенно иное доказательство, данное Дэвидом Гейлом , основано на игре Hex . Основная теорема о Hex заключается в том, что ни одна игра не может закончиться ничьей. Это эквивалентно теореме Брауэра о неподвижной точке для размерности 2. Рассматривая n- мерные версии Hex, можно в общем доказать, что теорема Брауэра эквивалентна теореме об определенности для Hex.
Доказательство с использованием теоремы Лефшеца о неподвижной точке
Теорема Лефшеца о неподвижной точке гласит, что если непрерывное отображение f конечного симплициального комплекса B в себя имеет только изолированные неподвижные точки, то количество неподвижных точек, подсчитанных с кратностями (которые могут быть отрицательными), равно числу Лефшеца
и, в частности, если число Лефшеца не равно нулю, то f должна иметь неподвижную точку. Если B – шар (или, в более общем смысле, стягиваемый), то число Лефшеца равно единице, потому что единственной ненулевой группой гомологий является: и f действует как тождество на этой группе, поэтому f имеет неподвижную точку.
Доказательство в слабой логической системе
В обратной математике теорема Брауэра может быть доказана в системе WKL 0 , и наоборот, в базовой системе RCA 0 из теоремы Брауэра для квадрата следует слабая лемма Кенига , так что это дает точное описание силы теоремы Брауэра.
Обобщения
Теорема Брауэра о неподвижной точке является отправной точкой для ряда более общих теорем о неподвижной точке .
Прямое обобщение на бесконечные измерения, то есть использование единичного шара произвольного гильбертова пространства вместо евклидова пространства, неверно. Основная проблема здесь в том, что единичные шары бесконечномерных гильбертовых пространств не компактны . Например, в гильбертовом пространстве ℓ 2 суммируемых с квадратом вещественных (или комплексных) последовательностей рассмотрим отображение f : ℓ 2 → ℓ 2, которое отправляет последовательность ( x n ) из замкнутого единичного шара 2 в последовательность ( y n ) определяется
Нетрудно проверить, что это отображение непрерывно, имеет свой образ в единичной сфере 2 , но не имеет неподвижной точки.
Обобщения теоремы Брауэра о неподвижной точке на бесконечномерные пространства поэтому все включают предположение компактности, а также часто предположение выпуклости . См. Теоремы о неподвижной точке в бесконечномерных пространствах для обсуждения этих теорем.
Существует также конечномерное обобщение на более широкий класс пространств: если является произведением конечного числа цепных континуумов, то каждая непрерывная функция имеет фиксированную точку, где цепной континуум является (обычно, но в этом случае не обязательно метрическим ) компактным Хаусдорфово пространство, каждое открытое покрытие которого имеет конечное открытое измельчение , такое что тогда и только тогда, когда . Примеры цепных континуумов включают компактные связные линейно упорядоченные пространства и, в частности, отрезки действительных чисел.

Теорема Какутани о неподвижной точке обобщает теорему Брауэра о неподвижной точке в другом направлении: она остается в R n , но рассматривает полунепрерывные сверху многозначные функции (функции, которые присваивают каждой точке множества подмножество множества). Также требуется компактность и выпуклость набора.
Теорема Лефшеца о неподвижной точке применяется к (почти) произвольным компактным топологическим пространствам и дает условие в терминах особых гомологий, которое гарантирует существование неподвижных точек; это условие тривиально выполняется для любого отображения в случае D n .
Эквивалентные результаты
Существует несколько теорем о неподвижной точке, которые представлены в трех эквивалентных вариантах: вариант алгебраической топологии , комбинаторный вариант и вариант покрытия множества. Каждый вариант можно доказать отдельно, используя совершенно разные аргументы, но каждый вариант также можно свести к другим вариантам в своем ряду. Кроме того, каждый результат в верхней строке можно вывести из результата, находящегося под ним в том же столбце.
| Алгебраическая топология | Комбинаторика | Установить покрытие |
|---|---|---|
| Теорема Брауэра о неподвижной точке | Лемма Спернера | Лемма Кнастера – Куратовского – Мазуркевича. |
| Теорема Борсука – Улама. | Лемма Такера | Теорема Люстерника – Шнирельмана. |
Смотрите также
- Теорема Банаха о неподвижной точке
- Бесконечные композиции аналитических функций
- равновесие по Нэшу
- Теорема Пуанкаре – Миранды – эквивалент теоремы Брауэра о неподвижной точке
- Топологическая комбинаторика
Примечания
использованная литература
- Чоу, Шуй Ни; Маллет-Парет, Джон; Йорк, Джеймс А. (1978). «Нахождение нулей карт: методы гомотопии, конструктивные с вероятностью единица» . Математика вычислений . 32 (143): 887–899. DOI : 10.1090 / S0025-5718-1978-0492046-9 . Руководство по ремонту 0492046 .
- Гейл, Д. (1979). “Игра шестиугольника и теорема Брауэра о неподвижной точке”. Американский математический ежемесячник . 86 (10): 818–827. DOI : 10.2307 / 2320146 . JSTOR 2320146 .
- Хирш, Моррис В. (1988). Дифференциальная топология . Нью-Йорк: Спрингер. ISBN 978-0-387-90148-0. (Доказательство Хирша, использующее отсутствие дифференцируемой ретракции, см. на стр. 72–73)
- Истрэшеску, Василий И. (1981). Теория неподвижной точки . Математика и ее приложения. 7 . Дордрехт – Бостон, Массачусетс: Д. Рейдел. ISBN 978-90-277-1224-0. Руководство по ремонту 0620639 .
- Карамардян, С., Под ред. (1977). Неподвижные точки: алгоритмы и приложения . Академическая пресса. ISBN 978-0-12-398050-2.
- Келлог, Р. Брюс; Ли, Тянь-Иен; Йорк, Джеймс А. (1976). «Конструктивное доказательство теоремы Брауэра о неподвижной точке и результаты вычислений». Журнал СИАМ по численному анализу . 13 (4): 473–483. Bibcode : 1976SJNA … 13..473K . DOI : 10.1137 / 0713041 . Руководство по ремонту 0416010 .
- Леони, Джованни (2017). Первый курс в пространствах Соболева: Издание второе . Аспирантура по математике . 181 . Американское математическое общество. стр. 734. ISBN 978-1-4704-2921-8
- Соболев, Владимир И. (2001) [1994], “Теорема Брауэра” , Энциклопедия математики , EMS Press
внешние ссылки
- Теорема Брауэра о неподвижной точке для треугольников при разрезании узла
- Теорема Брауэра из PlanetMath с прилагаемым доказательством.
- Реконструкция Брауэра на MathPages
- Теорема Брауэра о неподвижной точке в математических изображениях.