Как найти неправильную дробь
Неправильная дробь – это один из форматов записи обыкновенной дроби. Как и у любой обыкновенной дроби, у нее есть число над чертой (числитель) и под ней – знаменатель. Если числитель больше знаменателя, это и есть отличительный признак неправильности дроби. В эту форму можно перевести смешанную обыкновенную дробь. Десятичную тоже можно представить в неправильной обыкновенной форме записи, но лишь в том случае, если перед разделительной запятой стоит число, отличное от нуля.

Инструкция
В смешанном формате обыкновенной дроби числитель и знаменатель отделены от целой части пробелом. Чтобы перевести такую запись в неправильную форму, сначала умножьте ее целую часть (число, стоящее перед пробелом) на знаменатель дробной части. Полученное значение прибавьте к числителю. Рассчитанная таким способом величина будет числителем неправильной дроби, а в ее знаменатель поставьте знаменатель смешанной дроби без каких-либо изменений. Например, обыкновенную смешанную дробь 5 7/11 в формате обыкновенной неправильной можно записать так: (5*11+7)/11 = 62/11.
Для перевода десятичной дроби в неправильный обыкновенный формат записи определите количество разрядов после запятой, отделяющей целую часть от дробной – оно равно числу цифр справа от этой запятой. Полученное число используйте в качестве показателя степени, в которую вам нужно возвести десятку, чтобы рассчитать знаменатель неправильной дроби. Числитель получается без каких-либо расчетов – просто уберите запятую из десятичной дроби. Например, если исходная десятичная дробь равна 12,585, в числителе соответствующей ей неправильной должно стоять число 10³ = 1000, а в знаменателе – 12585: 12,585 = 12585/1000.
Как и любые обыкновенные дроби, неправильные можно и нужно сокращать. Для этого после получения результата описанными в предыдущих двух шагах способами попытайтесь подобрать наибольший общий делитель для числителя и знаменателя. Если это удастся сделать, разделите на найденное значение числа по обе стороны дробной черты. Для примера из второго шага таким делителем будет число 5, поэтому неправильную дробь можно сократить: 12,585 = 12585/1000 = 2517/200. А для примера из первого шага общего делителя нет, поэтому сокращать результирующую неправильную дробь не нужно.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
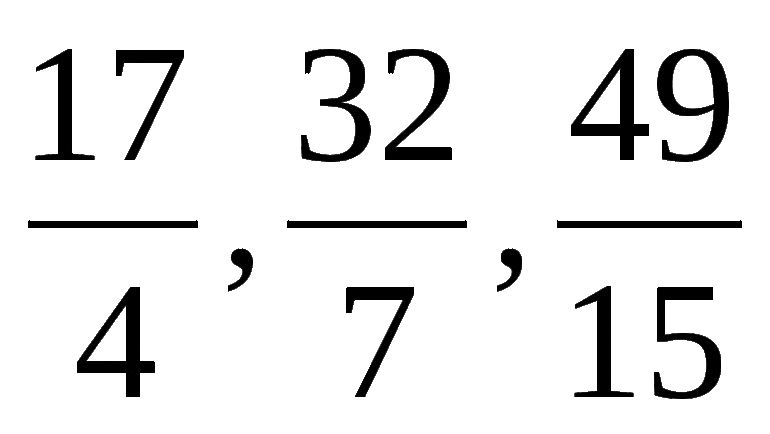
Общие сведения
Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.
В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.
Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 – это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.
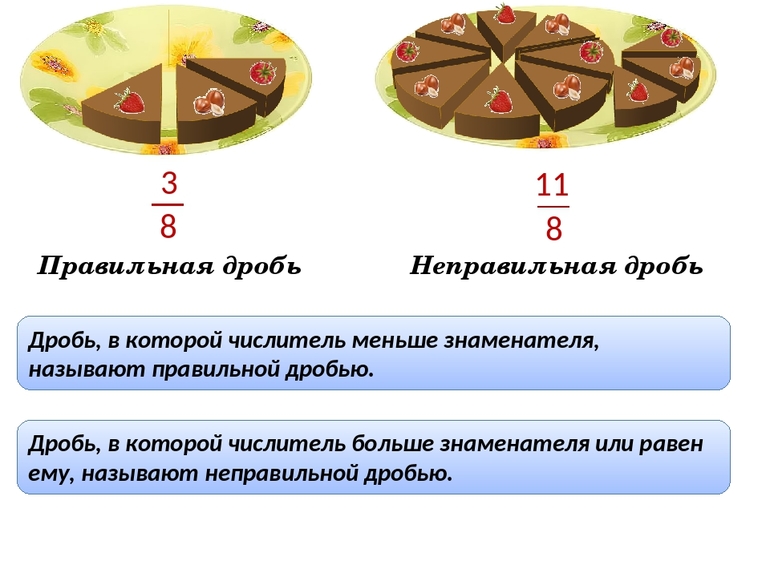
Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:
- Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.
- Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.
- Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5
Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.
Так как, по сути, дроби – это числа, только чаще всего не целые, над ними можно выполнять любые операции. Для того чтобы школьника научить правильно решать дроби, в 5 классе, кроме теоретического материала несколько уроков уделяют практике. На ней, кроме непосредственного выполнения арифметических операций, учат преобразовывать дробные отношения из одного вида в другой.
Суть отношения
Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.
Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.
Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.
Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.
Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:
- натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
- суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.
Как и любое число, дробь может быть положительной и отрицательной. В первом случае она обозначает изменение чего-то в сторону увеличения, а во втором — уменьшения. Например, -6 / 5 может обозначать недостачу равную шесть пятых.
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.
Превращение дробей
По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).
Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём – 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.
Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:
- перемножить единицы целой части со знаменателем дробного числа;
- сложить полученное произведение и числитель дроби;
- результат сложения записать в числитель, а знаменатель оставить без изменений.

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.
Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.
Выполнение действий
Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.
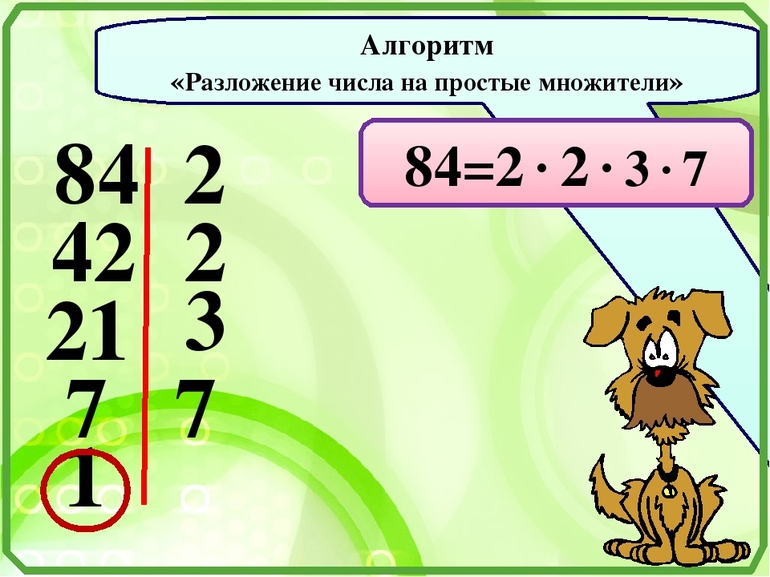
Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.
Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:
- исследовать числитель и знаменатель на возможность сокращения;
- определить наименьший общий знаменатель (НОЗ) среди делителей;
- найти дополнительные множители;
- выполнить умножение числителей на найденные аргументы;
- в знаменатель записать НОЗ, а в числитель сумму или разность произведений делимых.
Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).

Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).
Возведение в степень и извлечение корня выполняют способом разделения. То есть, делимое от делителя возводится или извлекается отдельно: (s / m) j = sj / mj и √(s / m) = √s / √m. Например, 3 / 2 * 9 / 6 : 7 / 5 * (3 / 2)3. С какого действия начинать решение не принципиально, но следует обратить внимание, что 9 / 6 можно сократить на три. В итоге получится 9 / 6 = 3 / 2. Далее, решение будет выглядеть следующим образом: 3 / 2 * 3 / 2 : 7 / 5 * 3 3 / 23 = (3 * 3) / (2 * 2): 7 / 5 * 27 / 8 = 9 / 4 * 5 / 7 * 27 / 8 = (9 * 5 * 27) / (4* 7 * 8) = 1215 / 224 = 5 (95 / 224).
Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 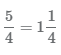 :
:
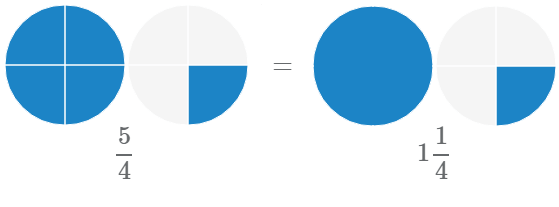
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 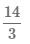 в смешанное число выполните следующие шаги:
в смешанное число выполните следующие шаги:
- 1 Разделим числитель на знаменатель 14 ÷ 3, в результате получим 4 целых и 2 в остатке.
- 2 Число 4 будет целой частью смешанного числа.
-
3 Остаток от деления 2 будет числителем дроби, а знаменатель останется прежним, равным 3. В результате получаем
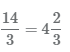
Рассмотрим на примерах как переводить неправильные дроби в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 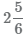 в неправильную дробь выполните следующие шаги:
в неправильную дробь выполните следующие шаги:
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Перейти к содержанию
Правильная и неправильная дроби
Опубликовано 04.06.2021
Дадим определение правильной и неправильной дроби. Эти понятия часто используются в математике. Как понять – какая дробь правильная, а какая неправильная – даем определения. Пример правильной дроби и пример неправильной дроби – в этом материале.
Правильная дробь
Определение правильной дроби:
Дробь, в которой числитель меньше знаменателя, называется правильной. Например,
– правильная дробь.
Неправильная дробь
Определение неправильной дроби:

Дробь, в которой числитель равен знаменателю или больше его, называется неправильной дробью. Например,
,
– неправильные дроби.
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, ![]() .
.
![]() .
.
Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.

Как выделить целую часть из неправильной дроби
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток – числителем, а делитель – знаменателем. Например, .

( 8 оценок, среднее 4.25 из 5 )
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
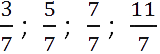
Обратите внимание, что в двух первых дробях (
и
)
числители меньше знаменателей. Такие дроби называют правильными.
Запомните!
![]()
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь
всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
имеет числитель равный знаменателю (такие дроби
равны единицы), а дробь
имеет числитель больший знаменателя. Такие
дроби называют неправильными.
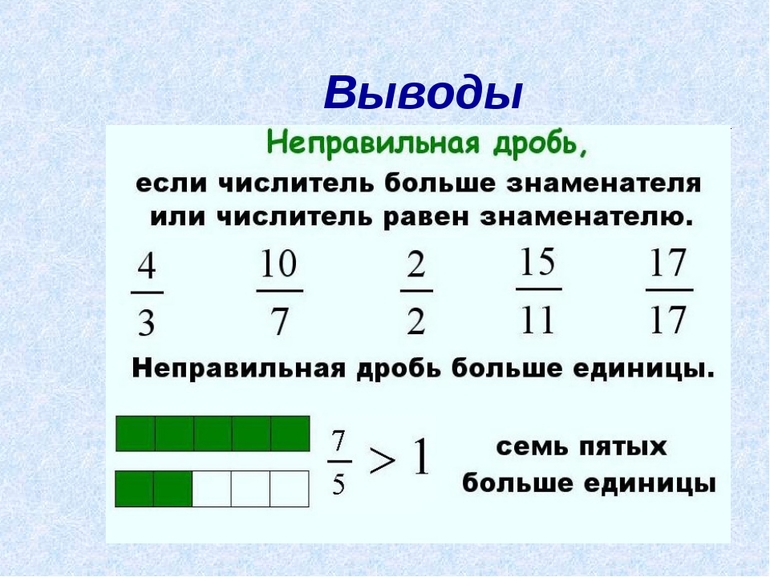
Запомните!
![]()
У неправильной дроби числитель равен или больше знаменателя.
Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
.
- Разделим в столбик числитель на знаменатель.
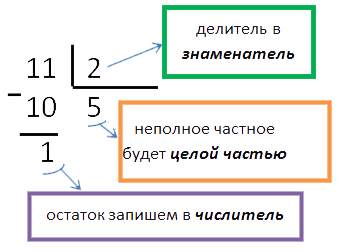
- Теперь запишем ответ.
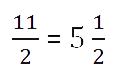
Запомните!
![]()
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
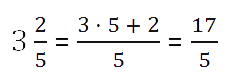
Любое смешанное число можно представить как сумму целой и дробной части.
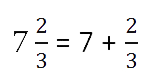
Запомните!
![]()
Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
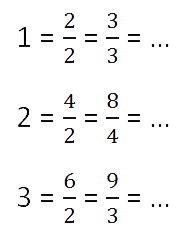
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
7 сентября 2020 в 18:33
Ксюша Островская

Профиль
Благодарили: 0
Сообщений: 1

Ксюша Островская
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 сентября 2020 в 20:33
Ответ для Ксюша Островская
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
= 55 : 66 = 5 : 6.
0
Спасибо
Ответить
14 декабря 2016 в 16:32
Руслан Потапов

Профиль
Благодарили: 0
Сообщений: 2

Руслан Потапов
Профиль
Благодарили: 0
Сообщений: 2
50
найдите числитель неправильной обыкновенной
дроби.равной смешанному числу.
помогите пожалуйста решением.
0
Спасибо
Ответить
15 декабря 2016 в 16:45
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
я думаю что это дродь
0
Спасибо
Ответить
15 декабря 2016 в 16:46
Ответ для Руслан Потапов
Амина Гилазиева

Профиль
Благодарили: 0
Сообщений: 2

Амина Гилазиева
Профиль
Благодарили: 0
Сообщений: 2
а числитель 71
0
Спасибо
Ответить
16 декабря 2016 в 19:33
Ответ для Руслан Потапов
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Чушь полная, конечно.
0
Спасибо
Ответить
18 октября 2016 в 10:44
Светлана Черемисова

Профиль
Благодарили: 0
Сообщений: 1

Светлана Черемисова
Профиль
Благодарили: 0
Сообщений: 1
Найдите целые значения а, при которых дробь принимает целые значения:
0
Спасибо
Ответить
18 октября 2016 в 18:00
Ответ для Светлана Черемисова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
±2.
0
Спасибо
Ответить
2 апреля 2016 в 19:01
Валерия Аралушкина

Профиль
Благодарили: 0
Сообщений: 1

Валерия Аралушкина
Профиль
Благодарили: 0
Сообщений: 1
Вычитание дроби из единицы и вычитание дроби из натурального числа.
5-7/10 10-3/5 9-5/9 7-5/11 8-2/5
Помогите я не очень понимаю как это делать!
0
Спасибо
Ответить
3 апреля 2016 в 12:22
Ответ для Валерия Аралушкина
Марина Доценко

Профиль
Благодарили: 0
Сообщений: 1

Марина Доценко
Профиль
Благодарили: 0
Сообщений: 1
5-7/10=5/1-7/10=50/10-7/10=43/10=4 целых и 3/10.
10-3/5=10/1-3/5=50/5-3/5=47/5=9 целых 2/5
9-5/9=9/1-5/9=81/9-5/9=76/9=8 целых 4/9
7-5/11=7/1-5/11=77/11-5/11=72/11=6 целых 6/11
8-2/5=8/1-2/5=40/5-2/5=38/5=7целых 3/5
0
Спасибо
Ответить
11 января 2016 в 23:48
Алинчик Плышевская

Профиль
Благодарили: 0
Сообщений: 1

Алинчик Плышевская
Профиль
Благодарили: 0
Сообщений: 1
Привет, помогите понять как сложить и вычетать смешаные числа?
0
Спасибо
Ответить
12 января 2016 в 19:05
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
смотри:
Сложение дробейСложение дробей с одинаковыми знаменателями.Определение. Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | б | = | + б |
| С | С | С |
Примеры сложения дробей с одинаковыми знаменателямиПример 1. Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2. Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.Определение. Чтобы сложить две обыкновенные дроби, следует:привести дроби к наименьшему общему знаменателю;сложить числители дробей, а знаменатель оставить без изменений;сократить полученную дробь;Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.Примеры сложения обыкновенных дробейПример 3. Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4. Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чиселОпределение. Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.Примеры сложения смешанных чиселПример 5. Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6. Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробейВычитание дробей с одинаковыми знаменателями.Определение. Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | – | б | = | – б |
| С | С | С |
Примеры вычитания дробей с одинаковыми знаменателямиПример 7. Найти разность двух дробей с одинаковыми знаменателями:
| 3 | – | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8. Найти разность двух дробей с одинаковыми знаменателями:
| 8 | – | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.Определение. Чтобы вычесть из одной обыкновенной дроби другую, следует:привести дроби к наименьшему общему знаменателю;из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений;сократить полученную дробь.
Примеры вычитания обыкновенных дробейПример 9. Найти разность двух дробей:
| 5 | – | 1 | = | 5 | – | 1·3 | = | 5 | – | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10. Найти разность двух дробей:
| 3 | – | 1 | = | 3·3 | – | 1·5 | = | 9 | – | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.Определение. Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю;если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь.
Примеры вычитания смешанных чиселПример 11. Найти разность двух смешанных чисел:
| 2 | 1 | – | 1 | 1 | = | 2 | 1·3 | – | 1 | 1·2 | = | (2 — 1) | + | 3 | – | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12. Найти разность двух смешанных чисел:
| 3 | 1 | – | 1 | 3 | = | 3 | 1·4 | – | 1 | 3·3 | = | 3 | 4 | – | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | – | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13. Найти разность двух смешанных чисел:
| 1 | 1 | – | 3 | 2 | = | 1 | 1 | – | 3 | 2·2 | = | 1 | 1 | – | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | – | 3 | = | -2 | – | 3 | = | -2 | – | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Смотрите также:Онлайн калькулятор дробейУпражнения на тему сложение и вычитание двух смешанных чиселДробиВиды дробей (обыкновенная правильная, неправильная, смешанная, десятичная)Основное свойство дробиСокращение дробиПриведение дробей к общему знаменателюПреобразование неправильной дроби в смешанное числоПреобразование смешанного числа в неправильную дробьСложение и вычитание дробейУмножение дробейДеление дробейСравнение дробейПреобразование десятичной дроби в обыкновенную дробьОнлайн калькуляторы дробейОнлайн упражнения с дробями
0
Спасибо
Ответить
12 января 2016 в 19:06
Ответ для Алинчик Плышевская
Janina Kutovska

Профиль
Благодарили: 0
Сообщений: 2

Janina Kutovska
Профиль
Благодарили: 0
Сообщений: 2
![]()
0
Спасибо
Ответить
8 сентября 2015 в 23:36
Лариса Краснова

Профиль
Благодарили: 0
Сообщений: 1

Лариса Краснова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 14:12
Ответ для Лариса Краснова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
=25 ? + = 25 ? = 25 ? = 24=24,25
0
Спасибо
Ответить
8 сентября 2015 в 18:48
Никита Парфёнов

Профиль
Благодарили: 0
Сообщений: 1

Никита Парфёнов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
5 сентября 2016 в 9:14
Ответ для Никита Парфёнов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В таком виде не ясна задача и решить её не возмонжо.
0
Спасибо
Ответить
8 сентября 2015 в 0:32
Sparkiss Princess

Профиль
Благодарили: 0
Сообщений: 1

Sparkiss Princess
Профиль
Благодарили: 0
Сообщений: 1
Всем привет! Помогите пожалуйста в решении примеров со смешанными дробями!
1.) 2
? 51
:11 · (21
? 9,8 : 2,8 · 4
) +
2.) 48
? ( 66,4 — 66,25) · (1
+
) + 28, 2: 5 ? 44, 2
3.) 12
? 0,5 ? 5
· 1
: (
+ 1
· 1,5) · 0,62
4.) 7, 025 ? (11
+ 22
? 33
) · 7,8 + (65
? 64) : 0,5
5.) 97
? 3
? 8,5 ? ( 2
+ 28,2 : 2) · 0,2 ·
22,5
Заранее спасибо! ![]()
0
Спасибо
Ответить
5 сентября 2016 в 14:21
Ответ для Sparkiss Princess
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Принцип решения таких примеров сводится к большой внимательности и применения нескольких простейших правил:
1) Последовательность действий в первую очередь действие в скобках, далее умножение/деление, далее сложение/вычитание
2) Правила перевода обыкновенных дробей в десятичные. Подробно можно почитать вот здесь: http://math-prosto.ru/index.php?page=pages/convert-decimal/convert-decimal2.php
3)Действия с десятичными дробями. О них можно подробнее почитать здесь: math-prosto.ru/index.php?page=pages/decimal/decimal1.php
В случаях, когда решение осложняется периодическими дробями, можно воспользоваться обратными действиями и перевести десятичные дроби в обыкновенные. Подробнее можно прочесть здесь http://math-prosto.ru/index.php?page=pages/decimal/decimal1.php
0
Спасибо
Ответить
5 апреля 2015 в 12:10
Кристина Тишина

Профиль
Благодарили: 0
Сообщений: 1

Кристина Тишина
Профиль
Благодарили: 0
Сообщений: 1
[1
*0,27-3
*0,15] ? 1500*[ ? 0,1]3
0
Спасибо
Ответить
14 апреля 2016 в 10:27
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Преобразуем и решим.
(1 · -3 · ) ?1500 · (-0,001)=( ?) +1,5=( ? )+1,5= ? +1,5= ?0,14+1,5=1,36
Ответ:1,36
0
Спасибо
Ответить
14 апреля 2016 в 10:28
Ответ для Кристина Тишина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Решил пойти с конца форума и ответить на неотвеченные задачи =) Камни не кидайте, что так долго отвечал =)
0
Спасибо
Ответить
