Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция 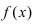
- – она определена в этой точке и ее некоторой
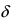 -окрестности;
-окрестности; - – существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
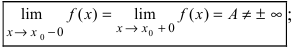
– предел функции в точке 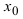 равен значению функции в исследуемой точке, т.е.
равен значению функции в исследуемой точке, т.е. 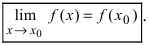
Пример:
Найти область непрерывности функции 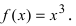
Решение:
Данная функция непрерывна 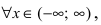 так как в каждой точке указанного интервала функция определена, в каждой точке существуют конечные и равные лево- и правосторонние пределы, а предел функции в каждой точке равен значению функции в этой точке.
так как в каждой точке указанного интервала функция определена, в каждой точке существуют конечные и равные лево- и правосторонние пределы, а предел функции в каждой точке равен значению функции в этой точке.
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
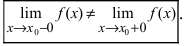
Пример:
Доказать, что функция 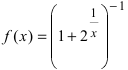 в точке
в точке 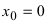 имеет разрыв первого рода.
имеет разрыв первого рода.
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 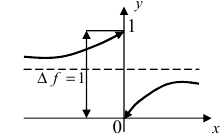 Рис. 64. График функции
Рис. 64. График функции 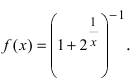 Область определения функции:
Область определения функции: 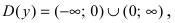 т.е. точка
т.е. точка 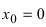 является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке:
является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 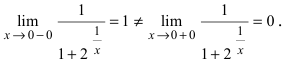 Следовательно, в изучаемой точке данная функция терпит разрыв первого рода.
Следовательно, в изучаемой точке данная функция терпит разрыв первого рода.
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция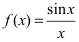 имеет в точке
имеет в точке 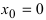 устранимый разрыв.
устранимый разрыв.
Решение:
В точке 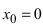 функция имеет неопределенность
функция имеет неопределенность 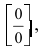 поэтому эта точка является точкой, подозрительной на разрыв. Вычислив в этой точке лево- и правосторонний пределы
поэтому эта точка является точкой, подозрительной на разрыв. Вычислив в этой точке лево- и правосторонний пределы 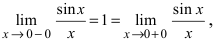 убеждаемся, что данная точка является точкой устранимого разрыва.
убеждаемся, что данная точка является точкой устранимого разрыва.
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 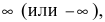 т.е. в такой точке функция терпит бесконечный разрыв.
т.е. в такой точке функция терпит бесконечный разрыв.
Пример:
Исследовать на непрерывность функцию 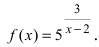
Решение:
Найдем область определения этой функции: 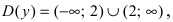 т.е. точка
т.е. точка
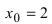 является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке:
является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 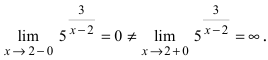 Так как левосторонний предел конечен, а правосторонний предел бесконечен, то в изучаемой точке данная функция терпит разрыв II рода.
Так как левосторонний предел конечен, а правосторонний предел бесконечен, то в изучаемой точке данная функция терпит разрыв II рода.
Пример:
Исследовать на непрерывность функцию 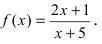
Решение:
Найдем область определения этой функции: 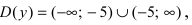 т.е. точка
т.е. точка 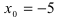 является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке:
является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 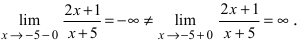 Так как левосторонний и правосторонний пределы бесконечены, то в изучаемой точке данная функция терпит разрыв II рода.
Так как левосторонний и правосторонний пределы бесконечены, то в изучаемой точке данная функция терпит разрыв II рода.
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 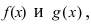 которые определены в некоторой
которые определены в некоторой 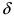 -окрестности точки
-окрестности точки 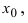 в которой лево- и правосторонние пределы равны между собой. Так как функции
в которой лево- и правосторонние пределы равны между собой. Так как функции 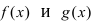 непрерывны в некоторой
непрерывны в некоторой 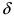 -окрестности точки
-окрестности точки 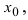 то выполняются равенства:
то выполняются равенства: 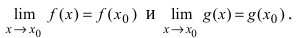 В силу того, что существуют конечные пределы обеих функций, то по теореме о пределе суммы двух функций имеем, что
В силу того, что существуют конечные пределы обеих функций, то по теореме о пределе суммы двух функций имеем, что 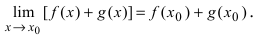 Аналогично теорема доказывается для суммы (разности) любого конечного числа непрерывных функций. Нижеприведенные теоремы доказываются так же, как и теорема.
Аналогично теорема доказывается для суммы (разности) любого конечного числа непрерывных функций. Нижеприведенные теоремы доказываются так же, как и теорема.
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 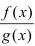 при условии, что во всех точках общей области определения функция
при условии, что во всех точках общей области определения функция 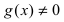 , есть непрерывная функция.
, есть непрерывная функция.
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию 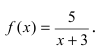
Решение:
Согласно схеме исследования функции на непрерывность имеем:
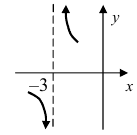
Рис. 65. Поведение графика функции 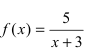 в малой окрестности точки разрыва второго рода
в малой окрестности точки разрыва второго рода 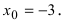
Из рисунка видно, что график функции 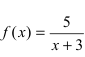 —неограниченно приближается к вертикальной прямой
—неограниченно приближается к вертикальной прямой 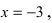 нигде не пересекая эту прямую.
нигде не пересекая эту прямую.
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 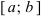 .
.
Определение: Замкнутый интервал 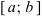 будем называть сегментом.
будем называть сегментом.
Приведем без доказательства свойства непрерывных функций на сегменте 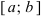 .
.
Теорема: Если функция 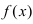 непрерывна на сегменте
непрерывна на сегменте 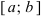 , то она достигает своего наименьшего (
, то она достигает своего наименьшего (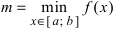 ) и наибольшего (
) и наибольшего (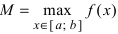 ) значения либо во внутренних точках сегмента, либо на его концах.
) значения либо во внутренних точках сегмента, либо на его концах.
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
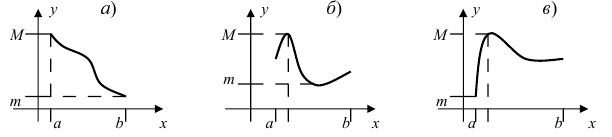
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 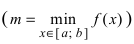 и наибольшего
и наибольшего 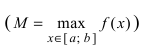 значений на концах сегмента
значений на концах сегмента 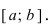 На графике б) функция достигает своего наименьшего
На графике б) функция достигает своего наименьшего 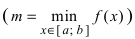 и наибольшего значения
и наибольшего значения 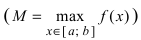 во внутренних точках сегмента
во внутренних точках сегмента 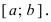 На графике в) функция достигает своего наименьшего значения
На графике в) функция достигает своего наименьшего значения 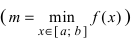 на левом конце сегмента
на левом конце сегмента 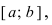 а наибольшего значения
а наибольшего значения 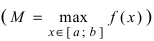 во внутренней точке сегмента
во внутренней точке сегмента 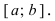
Тб. Если функция 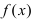 непрерывна на сегменте
непрерывна на сегменте 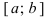 и достигает своего наименьшего (
и достигает своего наименьшего (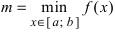 ) и наибольшего (
) и наибольшего (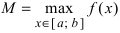 ) значений, то для любого вещественного числа С, удовлетворяющего неравенству
) значений, то для любого вещественного числа С, удовлетворяющего неравенству 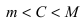 , найдется хотя бы одна точка
, найдется хотя бы одна точка 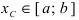 такая, что
такая, что 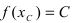 .
.
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67). 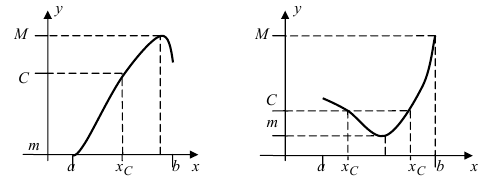
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 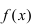 непрерывна на сегменте
непрерывна на сегменте 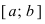 и на его концах принимает значения разных знаков, то найдется хотя бы одна точка
и на его концах принимает значения разных знаков, то найдется хотя бы одна точка 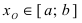 такая, что
такая, что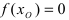 .
.
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
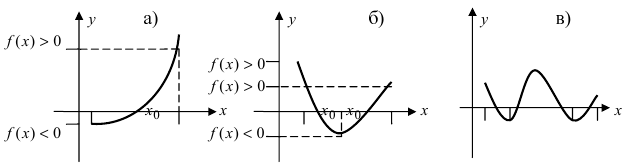
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x – произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) – величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a – text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b – text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) – точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) – точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) – точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) – левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) – подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} – text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) – точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) – точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) – точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Функция f(x) является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0, т.е.: limx→x0-0f(x)=limx→x0+0f(x)=f(x0)
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Дана функция f(x)=16(x-8)2-8. Необходимо доказать ее непрерывность в точке х0= 2.
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов хn, сводящуюся к х0 =2·(хn<2). Например, такой последовательностью может быть:
-2, 0, 1, 112, 134, 178, 11516,…, 110231024,…→2
Соответствующая последовательность значений функций выглядит так:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8.667; 2.667; 0.167; -0.958; -1.489; -1.747; -1.874;…;-1.998;…→-2
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к -2, значит limx→2-016(x-8)2-8=-2.
Определим существование предела справа: используем последовательность аргументов хn, сводящуюся к х0= 2 (хn>2). Например, такой последовательностью может быть:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Соответствующая последовательность функций:
f(6); f(4); f(3); f212; f214; f218; f2116;…; f211024;…==-7.333; -5.333; -3.833; -2.958; -2.489; -2.247; -2.247; -2.124;…; -2.001;…→-2
на рисунке обозначена синим цветом.
И эта последовательность сводится к -2, тогда limx→2+016(x-8)2-8=-2.
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f(x)=16x-82-8 в точке х0= 2, при этом limx→216(x-8)2-8=-2.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
limx→2-0f(x)=limx→2+0f(x)=f(2)=16(2-8)2-8=-2 что свидетельствует о непрерывности заданной функции в заданной точке.
Покажем графически:
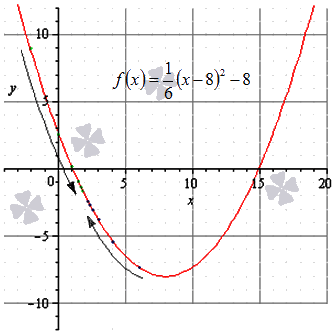
Ответ: Непрерывность функции f(x)=16(x-8)2-8 в заданной части доказано.
Устранимый разрыв первого рода
Функция имеет устранимый разрыв первого рода в точке х0, когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
limx→x0-0f(x)=limx→x0+0f(x)≠f(x0)
Задана функция f(x)=x2-25x-5. Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции: D(f(x))⇔Dx2-25x-5⇔x-5≠0⇔x∈(-∞; 5)∪(5; +∞)
В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. х0= 5. Исследуем функцию на непрерывность в этой точке.
Выражение x2-25x-5 упростим: x2-25x-5=(x-5)(x+5)x-5=x+5.
Определим пределы справа и слева. Поскольку функция g(x)=x+5 является непрерывной при любом действительном x, тогда:
limx→5-0(x+5)=5+5=10limx→5+0(x+5)=5+5=10
Ответ: пределы справа и слева являются равными, а заданная функция в точке х0= 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Функция имеет неустранимый разрыв первого рода в точке х0, когда пределы справа и слева не являются равными, т.е.: limx→x0-0f(x)≠limx→x0+0f(x). Точка х0 здесь – точка скачка функции.
Задана кусочно-непрерывная функция f(x)=x+4, x<-1,x2+2, -1≤x<12x, x≥1. Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке х0=-1 или в точке х0=1.
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки х0=-1 заданная функция есть f(x)=x+4, тогда в силу непрерывности линейной функции: limx→-1-0f(x)=limx→-1-0(x+4)=-1+4=3;
- непосредственно в точке х0=-1 функция принимает вид: f(x)=x2+2, тогда: f(-1)=(-1)2+2=3;
- на промежутке (-1; 1) заданная функция есть: f(x)=x2+2. Опираясь на свойство непрерывности квадратичной функции, имеем: limx→-1+0f(x)=limx→-1+0(x2+2)=(-1)2+2=3limx→1-0f(x)=limx→1-0(x2+2)=(1)2+2=3
- в точке х0=-1 функция имеет вид: f(x)=2x и f(1)=2·1=2.
- справа от точки х0 заданная функция есть f(x)=2x. В силу непрерывности линейной функции: limx→1+0f(x)=limx→1+0(2x)=2·1=2
Ответ: в конечном счете мы получили:
- limx→-1-0f(x)=limx→-1+0f(x)=f(-1)=3 – это означает, что в точке х0=-1 заданная кусочная функция непрерывна;
- limx→-1-0f(x)=3, limx→1+0f(x)=2 – таким образом, в точке х0=1 определён неустранимый разрыв первого рода (скачок).
Нам остается только подготовить чертеж данного задания.
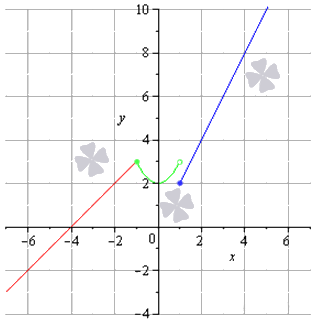
Разрыв второго рода (бесконечный разрыв)
Функция имеет разрыв второго рода в точке х0, когда какой-либо из пределов слева limx→x0-0f(x) или справа limx→x0+0f(x) не существует или бесконечен.
Задана функция f(x)=1x. Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: x∈(-∞; 0)∪(0; +∞).
Найдем пределы справа и слева от точки х0= 0.
Зададим произвольную последовательность значений аргумента, сходящуюся к х0 слева. К примеру:
-8; -4; -2; -1; -12; -14;…; -11024;…
Ей соответствует последовательность значений функции:
f(-8); f(-4); f(-2); f(-1); f-12; f-14;…; f-11024;…==-18;-14; -12; -1; -2; -4;…; -1024;…
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда limx→0-0f(x)=limx→0-01x=-∞.
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х0 справа. К примеру: 8; 4; 2; 1; 12; 14;…; 11024;…, и ей соответствует последовательность значений функции:
f(8); f(4); f(2); f(1); f12; f14;…; f11024;…==18; 14; 12; 1; 2; 4;…; 1024;…
Эта последовательность – бесконечно большая положительная, а значит limx→0+0f(x)=limx→0+01x=+∞.
Ответ: точка х0= 0 – точка разрыва функции второго рода.
Проиллюстрируем:
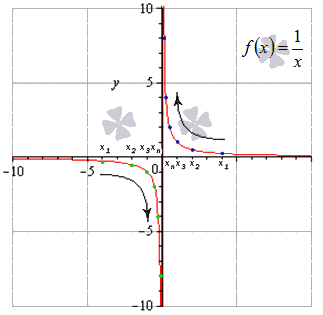
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)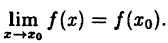
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 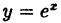 в точке х = 1.
в точке х = 1.
Решение:
Чтобы доказать, что функция 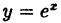 непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):
непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):
Таким образом, доказано, что функция 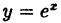 непрерывна в точке х = 1.
непрерывна в точке х = 1.
Замечание:
Формулу (10.1) можно записать в виде
(10.2) 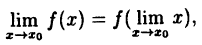
так как 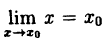 . Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.
. Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 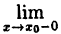 f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.
f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему: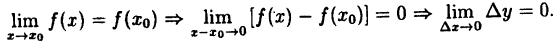
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3) 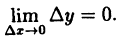
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим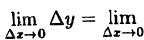 (3x²∆x 4- 3x∆x² + ∆x³) = 0.
(3x²∆x 4- 3x∆x² + ∆x³) = 0.
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.

Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
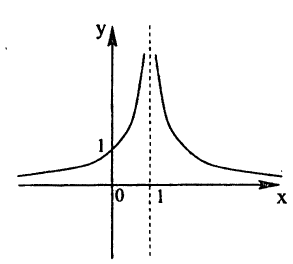
Так, например, функция 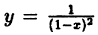 (рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.
(рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.
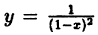
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е. 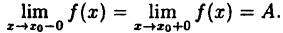
Пример:
Исследовать на непрерывность функцию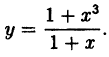
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность  . В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:
. В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить: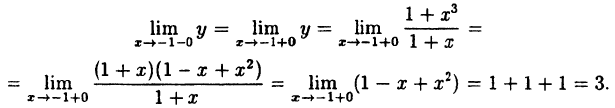
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =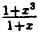 = 3.
= 3.
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию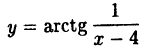 (рис. 90).
(рис. 90).
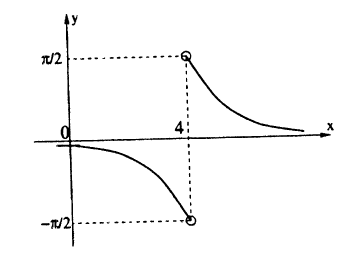
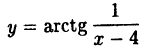
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —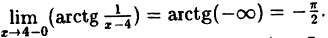 .
.
Предел справа — 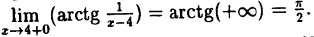 .
.
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 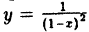 , представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.
, представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀: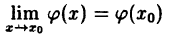 и
и 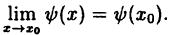
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е.  f(x) — f(x₀).
f(x) — f(x₀).
Доказательство: f(x) =
f(x) = [ϕ(x) ∙ ψ(x)] =
[ϕ(x) ∙ ψ(x)] =  ϕ(x) ∙
ϕ(x) ∙  ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).
ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).
Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 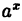 , тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция
, тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция 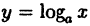 непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов
непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов 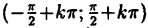 и терпит разрыв II рода в точках
и терпит разрыв II рода в точках 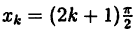 (k = 0; ±1; ±2;…).
(k = 0; ±1; ±2;…).
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить 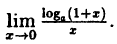
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида  . Выполним преобразование
. Выполним преобразование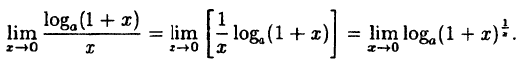
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( f(x)= f (
f(x)= f ( x)).
x)).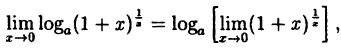
но 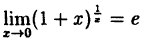 — второй замечательный предел.
— второй замечательный предел.
Следовательно,
(10.4) 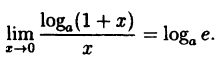
В частности, при а = е
(10.5) 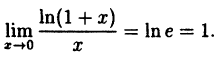
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить 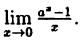
Решение:
Здесь мы имеем дело с неопределенностью вида  . Для нахождения предела сделаем замену переменной, положив
. Для нахождения предела сделаем замену переменной, положив 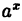 — 1 = t. Тогда
— 1 = t. Тогда 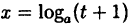 . При х → 0 также и t → 0.
. При х → 0 также и t → 0.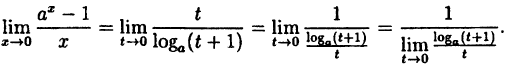
Так как на основании результата, полученного в предыдущем примере, 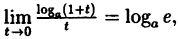 то
то
(10.6) 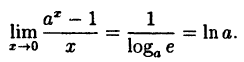
В частности, если а = е, имеем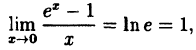
т.е. у = 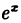 — 1 и y = x — эквивалентные бесконечно малые функции при х → 0.
— 1 и y = x — эквивалентные бесконечно малые функции при х → 0.
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
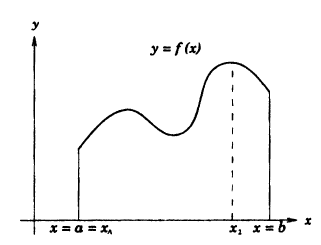
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
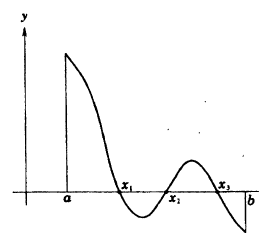
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
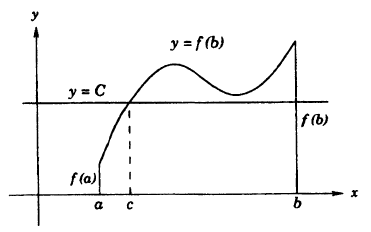
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 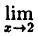 f(x) =
f(x) = 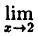 4x²= 16;
4x²= 16;
3) этот предел равен значению функции в точке х = 2
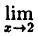 f(x) = f(2) = 16.
f(x) = f(2) = 16.
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств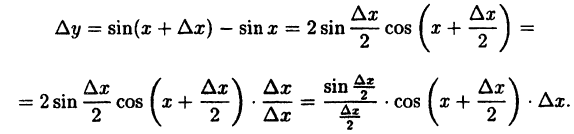
Так как 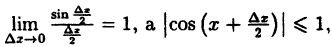 то при любом х имеем
то при любом х имеем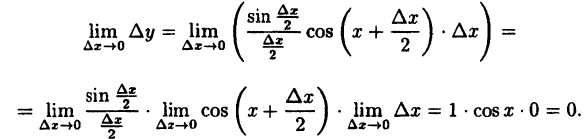
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
Пример:
Исследовать на непрерывность функцию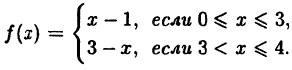
Решение:
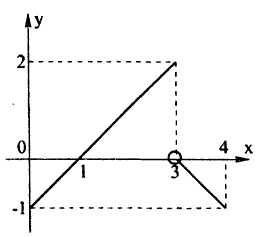
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :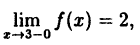
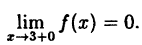
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию 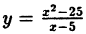
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что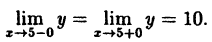
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию 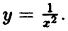
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию 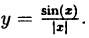
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева 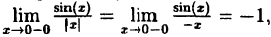
предел справа 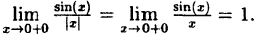
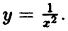
Пример:
Исследовать на непрерывность функцию 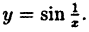 .
.
Решение:
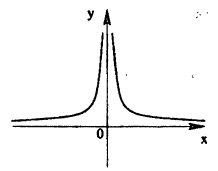
Функция 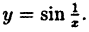 определена для всех значений х, кроме x = 0.B этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II рода, так как при х → 0 как справа, так и слева, функция
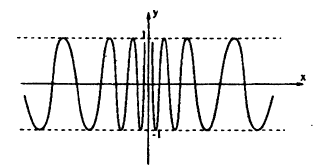
определена для всех значений х, кроме x = 0.B этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II рода, так как при х → 0 как справа, так и слева, функция 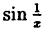 , колеблясь между -1 и 1, не приближается ни к какому числовому значению. График ее приведен на рис. 96.
, колеблясь между -1 и 1, не приближается ни к какому числовому значению. График ее приведен на рис. 96.
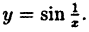
Пример:
Исследовать на непрерывность функцию 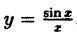
Решение:
Функция 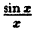 не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева:
не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева: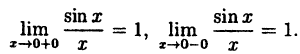
Если доопределить функцию 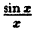 в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
f(х) =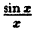 , если х ≠ 0; f(0) = 1.
, если х ≠ 0; f(0) = 1.
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций




Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Учреждение
образования «Белорусская государственная
сельскохозяйственная
академия»


Кафедра
высшей математики
Методические
указания
по
изучению темы «Непрерывность функций
одной переменной»
студентами
бухгалтерского факультета заочной
формы получения
образования
(НИСПО)
Горки,
2013
Непрерывность
функций одной переменной
-
Односторонние
пределы
Пусть
функция
![]()
определена на множестве
![]() .
.
Введём понятие односторонних пределов
функции при
![]() .
.
Будем рассматривать такие значения х,
что
![]()
. Это означает, что
![]() ,
,
оставаясь всё время слева от
![]() .
.
Если при этом существует предел функции
![]()
при
![]()
то он называется левым
пределом
этой функции в точке
![]()
( или при
![]() )
)
и обозначается
![]() .
.
Пусть
теперь
![]() ,
,
оставаясь всё время справа от
![]() ,
,
т.е. оставаясь больше
![]() .
.
Если при этом существует предел функции
![]() ,
,
то он называется правым
пределом
этой функции в точке
![]()
и обозначается
![]() .
.
Левый
и правый пределы называются односторонними
пределами
функции в точке.
Если
существуют односторонние пределы
функции в точке и они равны между собой,
то функция имеет тот же предел в этой
точке:
![]()
![]()
![]() .
.
Если
односторонние пределы функции в точке
![]()
существуют, но не равны между собой, то
предел функции в этой точке не существует.
-
Непрерывность
функции в точке
Пусть
функция
![]()
определена
на некотором множестве D.
Пусть независимая переменная х
переходит от одного своего (начального)
значения
![]()
к другому (конечному) значению
![]()
.
Разность
конечного и начального значений
называется приращением
величины х
и обозначается
![]() .
.
Приращение может быть как положительным,
так и отрицательным. В первом случае
величина х
при переходе от
![]()
к х
увеличивается, а во втором случае –
уменьшается.
Если
независимая переменная х
получает некоторое приращение
![]() ,
,
то функция
![]()
получает приращение
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Приращением
функции
![]()
в
точке
![]()
называется разность
![]() ,
,
где
![]()
– приращение независимой переменной.
Можно
дать несколько определений непрерывности
функции в точке.
-
Функция
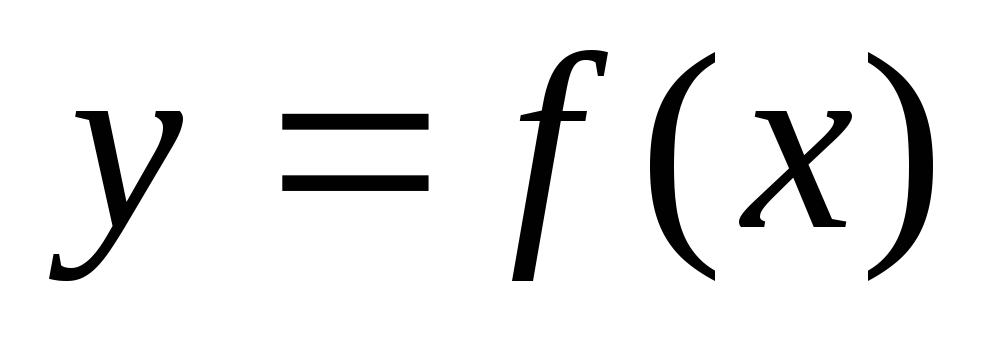
называется
непрерывной
в
точке
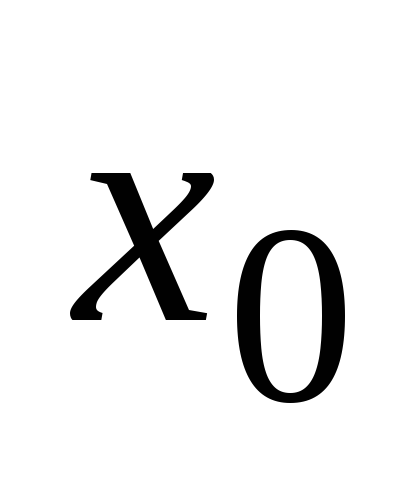 ,
,
если она определена в окрестности точки
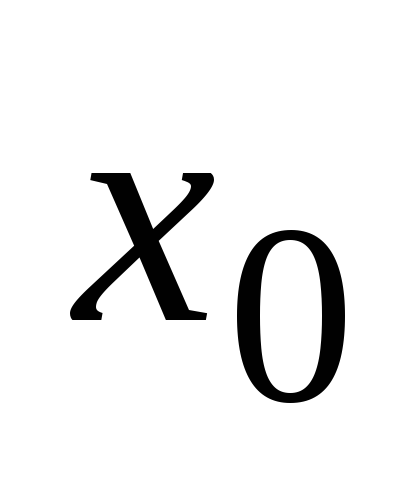
и

т.е.
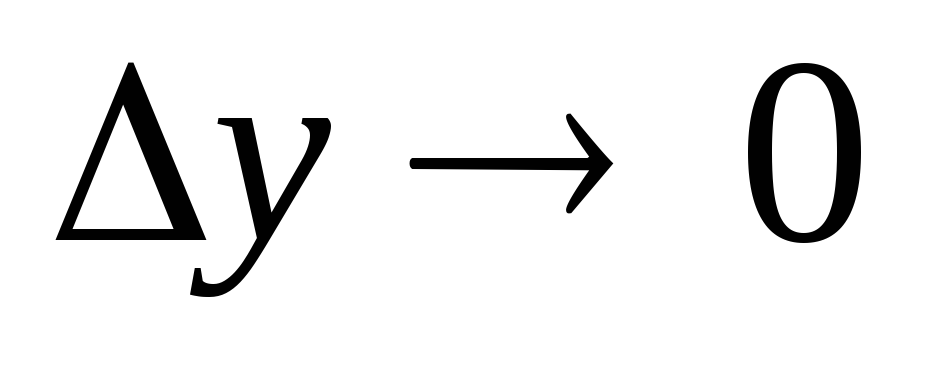
при
 .
.
Это означает, что функция непрерывна
в токе
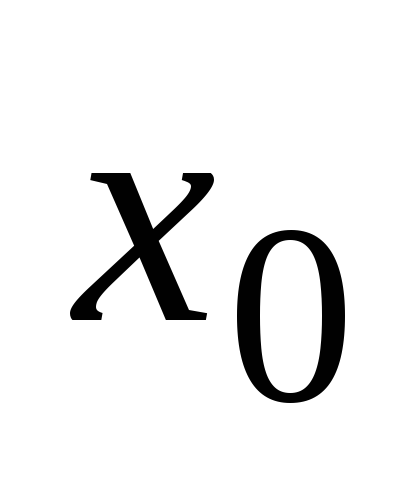 ,
,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции. -
Функция
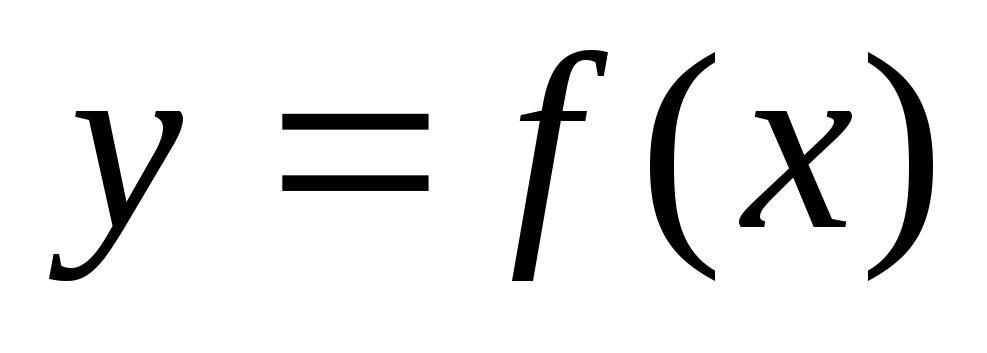
называется непрерывной
в
точке
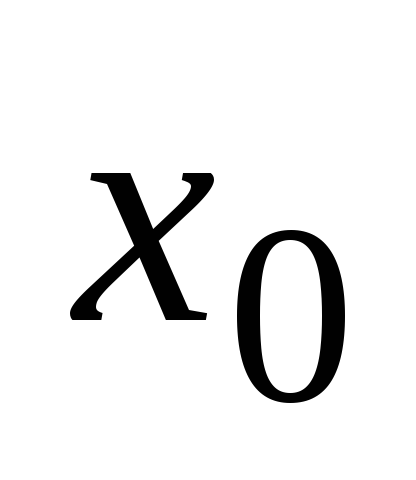 ,
,
если предел функции при

равен значению функции в этой точке:
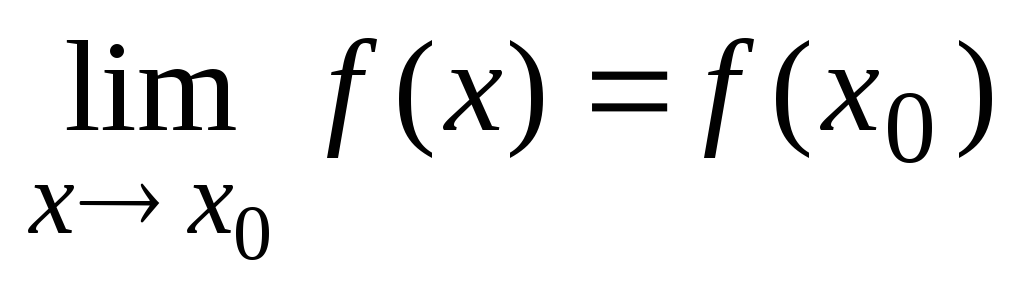 .
.

-
Функция
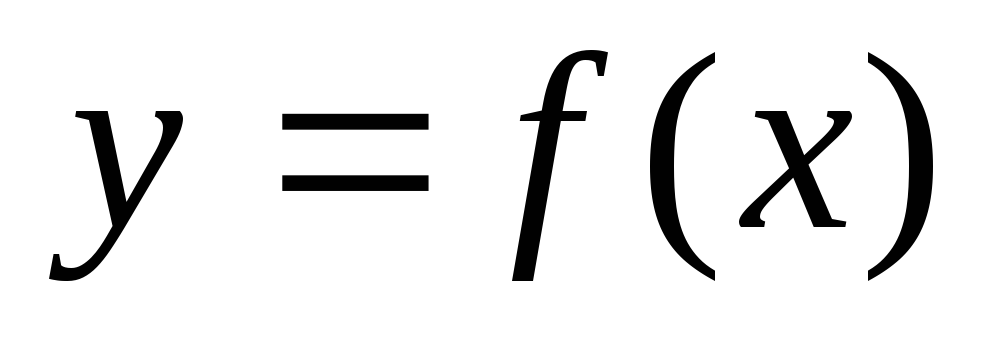
называется непрерывной
в точке
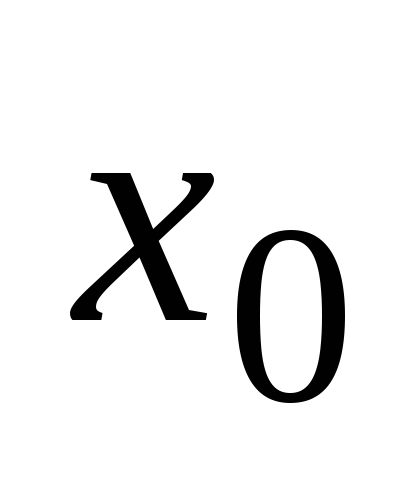 ,
,
если существуют левый и правый пределы
этой функции при
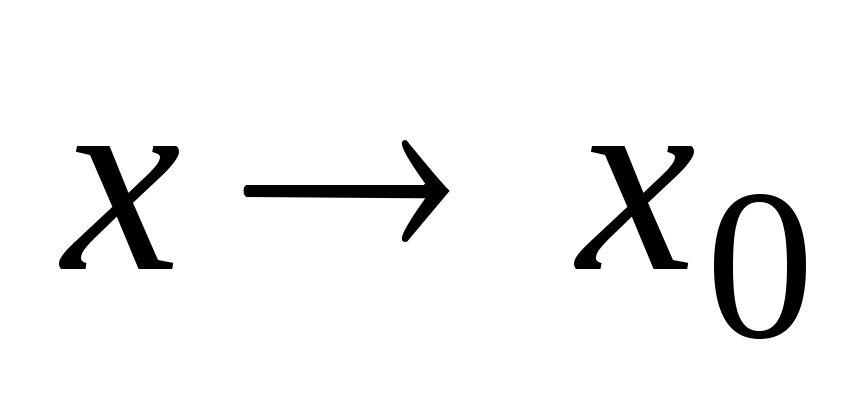
и если эти пределы равны между собой
и равны значению функции в этой точке:
![]() .
.
Функция
называется непрерывной
в интервале,
если она непрерывна в каждой точке этого
интервала. Геометрически непрерывность
функции
![]()
в замкнутом интервале означает, что
график функции представляет собой
сплошную линию без разрывов.
Непрерывные
на отрезке функции обладают важными
свойствами, которые выражаются следующими
утверждениями.
![]()
Если
функция
![]()
непрерывна
на отрезке [a,
b],
то она ограничена на этом отрезке.
![]()
Если
функция
![]()
непрерывна
на отрезке [a,
b],
то она достигает на этом отрезке своего
наименьшего и наибольшего значений.
![]()
Если
функция
![]()
непрерывна
на отрезке [a,b]
и
![]() ,
,
то каким бы ни было число С,
заключённое между числами А
и В,
найдётся точка
![]() ,
,
что
![]() .
.
Из
этого утверждения следует, что если
функция
![]()
непрерывна на [a,
b]
и на концах этого отрезка принимает
значения разных знаков, то на этом
отрезке существует хотя бы одна точка
c,
в которой функция обращается в нуль.
Справедливо
следующее утверждение: если
над непрерывными функциями производить
арифметические действия, то в результате
получается непрерывная функция.
Пример
1.
Исследовать
на непрерывность функцию
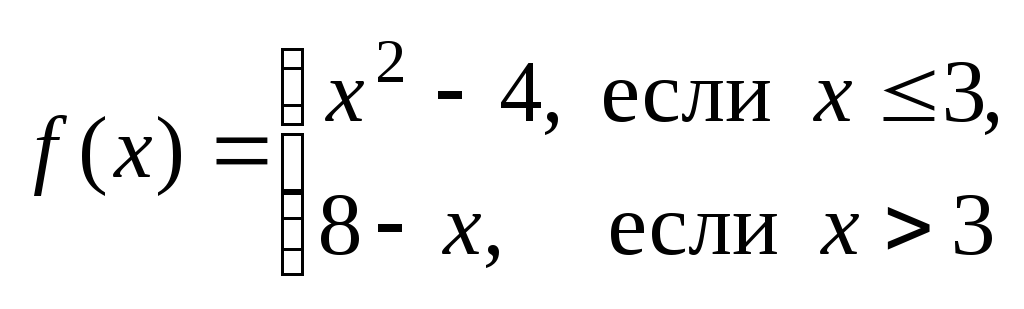
в
точке
![]() .
.
Решение.
Значение функции при
![]() есть
есть
![]() .
.
Вычислим односторонние пределы функции
в точке
![]() :
:
![]() ,
,
![]() .
.
Так
как односторонние пределы при
![]()
равны между собой и равны значению
функции в этой точке, то данная функция
непрерывна в точке
![]() .
.
3.
Непрерывность элементарных функций
Рассмотрим
функцию
![]() .
.
Эта постоянная функция непрерывна в
любой точке
![]() ,
,
так как
![]() .
.
Функция
![]()
также непрерывна в каждой точке
![]() ,
,
так как
![]() .
.
Так как
![]() ,
,
то на основании приведённого утверждения
об арифметических операциях над
непрерывными функциями
![]()
будет непрерывной. Непрерывными будут
такжен функции
![]()
.
Аналогично
можно показать непрерывность остальных
элементарных функций.
Таким
образом, любая
элементарная функция непрерывна в своей
области определения, т.е. область
определения элементарной функции
совпадает с областью её непрерывности.
-
Непрерывность
сложной и обратной функций
Пусть
функция
![]()
непрерывна в точке
![]() ,
,
а функция
![]()
непрерывна в точке
![]() .
.
Тогда сложная функция
![]()
непрерывна в точке
![]() .
.
Это означает, что если сложная функция
составлена из непрерывных функций, то
она также будет непрерывной, т.е.
непрерывная
функция от непрерывной функции есть
функция непрерывная.
Это определение распространяется на
конечное число непрерывных функций.
Из
этого определения следует, что под
знаком непрерывной функции можно
переходить к пределу:
![]() .
.
Это
означает, что если функция непрерывна,
то знак предела и знак функции можно
поменять местами.
Пусть
функция
![]()
определена, строго монотонна и непрерывна
на отрезке [a,
b].
Тогда обратная ей функция
![]()
определена, строго монотонна и непрерывна
на отрезке [A,
B],
где
![]() .
.
-
Точки
разрыва и их классификация
Как
уже известно, что если функция
![]()
определена на множестве D
и в точке
![]()
выполняется условие
![]() ,
,
то функция непрерывна в этой точке. Если
же это условие непрерывности не
выполняется, то в точке х0
функция имеет разрыв.
Точка
![]()
называется точкой
разрыва первого рода
функции
![]() ,
,
если в этой точке функция имеет конечные
односторонние пределы, не равные друг
другу, т.е.
![]() .
.
При этом величина
![]()
называется
скачком
функции
![]()
в точке
![]() .
.

Точка
![]()
называется точкой
устранимого разрыва
функции
![]() ,
,
если односторонние пределы функции в
этой точке равны друг другу и не равны
значению функции в этой точке, т.е.
![]() В
В
этом случае для устранения разрыва в
точке
![]()
нужно положить
![]()
Точка
х0
называется точкой
разрыва второго рода
функции
![]() если
если
хотя бы один из односторонних пределов
![]()
или
![]()
в этой точке либо не существует, либо
равен бесконечности.
Пример
2.
Исследовать
на непрерывность функцию
![]()
.
Решение.
Функция определена и непрерывна на всей
числовой прямой, за исключением точки
![]() .
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции в точке
![]() :
:
![]() ,
,
![]() .
.
Так
как в точке
![]()
односторонние пределы равны между
собой, а функция в этой точке не определена,
то точка
![]()
является точкой устранимого разрыва.
Чтобы устранить разрыв в этой точке,
необходимо доопределить функцию, положив
![]() .
.
Пример
3.
Исследовать
на непрерывность функцию
![]() .
.
Решение.
Функция определена и непрерывна на всём
множестве действительных чисел, кроме
![]() .
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции при
![]() :
:
![]() ,
,
![]() .
.
Так
как данная функция в точке
![]()
имеет конечные односторонние пределы,
не равные друг другу, то эта точка
является точкой разрыва первого рода.
Скачок функции в точке
![]()
равен
![]() .
.
Вопросы
для самоконтроля знаний
-
Что
называется приращением аргумента и
приращением функции? -
Что
называется левосторонним (левым)
пределом функции? -
Что
называется правосторонним (правым)
пределом функции? -
Какая
функция называется непрерывной в точке,
в интервале? -
Какая
точка называется точкой разрыва функции? -
Какая
точка называется точкой разрыва первого
рода? -
Какая
точка называется точкой разрыва второго
рода? -
Какая
точка называется точкой устранимого
разрыва?
Задания
для самостоятельной работы
Исследовать
функции на непрерывность:
-
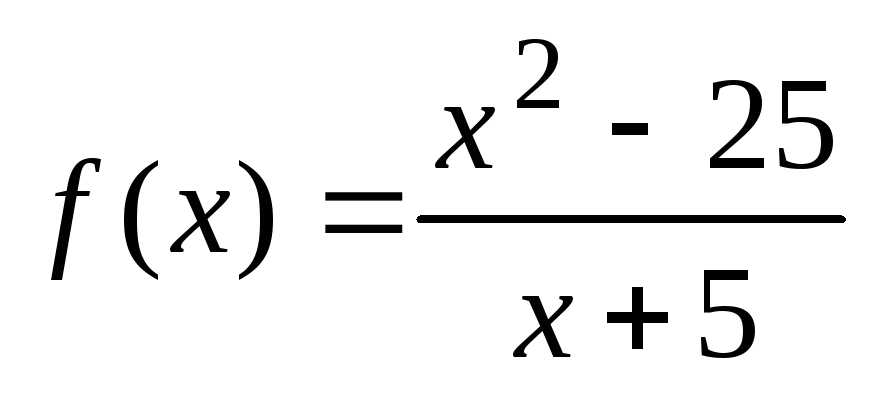 ;
;
2)
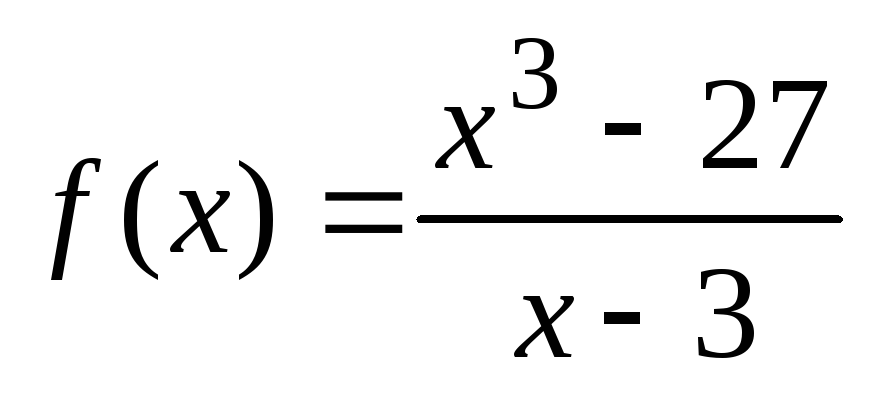 ;
;
3)
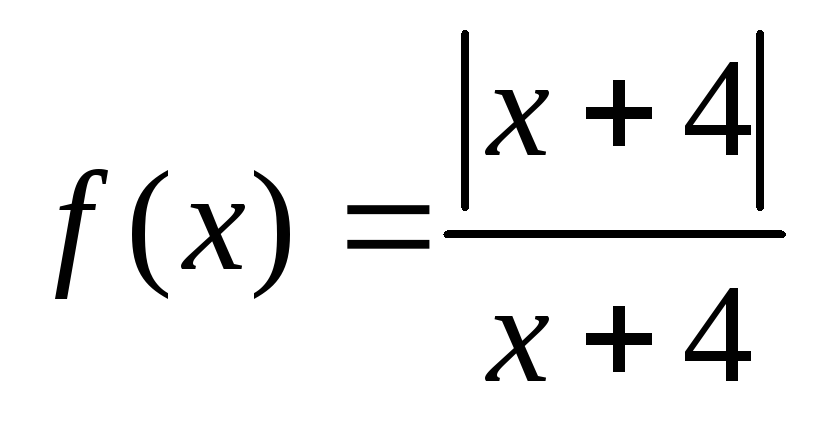 ;
;
![]()
в
точке
![]() .
.
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
