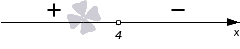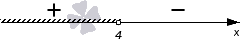Понятие решения неравенства с одной переменной
Решением неравенства с одной переменной называют такое множество всех значений этой переменной, при подстановке которых в это неравенство вместо неизвестного получается верное числовое неравенство.
При решении неравенств используются свойства неравенств (см. §36 этого справочника), из которых следует:
- если перенести какое-либо слагаемое неравенства в другую часть, знак неравенства не изменится;
- если разделить обе части неравенства на одно и то же положительное число, знак не изменится; при делении на одно и то же отрицательное число знак нужно поменять.
Например: Решить неравенство $5x-12 gt 3x+4$
$5x-12 gt 3x+4$
Переносим 12 вправо со знаком +
$5x gt 3x+4+12$
Переносим 3x влево со знаком –
$2x gt 16$
Делим на 2 обе части неравенства
Получаем ответ: $x gt 8 или x in (8;+infty)$
Ответом является бесконечное множество решений – все действительные числа больше 8. Эти решения образуют открытый луч (см. §16 данного справочника)
Изображение множества решений неравенства с одной переменной на числовой прямой
Подробно о числовой прямой и видах числовых промежутков на ней рассказано в §16 данного справочника. Здесь мы изобразим числовые промежутки как решения неравенств на более простых примерах.
|
Отрезок |
|
 |
$3 le x le 5 или x in [3;5]$ |
|
Интервал |
|
 |
$3 lt x lt 5 или x in (3;5)$ |
|
Полуинтервал |
|
 |
$3 lt x le 5 или x in (3;5]$ |
 |
$3 le x lt 5 или x in [3;5)$ |
|
Луч |
|
 |
$x ge 3 или x in [3, +infty)$ |
 |
$x le 5 или x in (-infty,5]$ |
|
Открытый луч |
|
 |
$x gt 3 или x in (3,+infty)$ |
 |
$x lt 5 или x in (-infty,5)$ |
Примеры
Пример 1. Решите неравенство, изобразите множество его решений на числовой прямой, укажите вид полученного числового промежутка:
$а) 2x+4 ge 3x-8$
$2x-3x ge -8-4 $
$-x ge -12 |:(-1) $
$x le 12 или x in (-infty;12]$ – луч
$б) 5(x+2) lt 8(x-1)$
$5x+10 lt 8x-8 $
$5x-8x lt -8-10$
$-3x lt -18 |:(-3)$
$x gt 6 или x in (6;+ infty)$ – открытый луч
$в) frac{x+2}{2} – frac{x+3}{5} le 1 | times 10$
$5(x+2)-2(x+3) le 10 $
$5x-2x le 10-10+6$
$3x le 6 |:3$
$x le 2 или x in (-infty;2]$ – луч
$г) x^2 ge (x-3)(x+2)+10$
$x^2 ge x^2-x-6+10 $
$x ge 4 или x in [4;+ infty)$- луч
Пример 2. Длина стороны прямоугольника 7 см. Какой должна быть длина другой стороны, чтобы периметр прямоугольника был меньше периметра квадрата со стороной 5 см?
Пусть x неизвестная сторона прямоугольника.
Периметр прямоугольника: $P_{rec} = 2(7+x)$
Периметр квадрата: $P_{sq} = 4 cdot 5 = 20$
По условию:
$$ 2(7+x) lt 20 |:2 $$
$$ 7+x lt 10 $$
$$ x lt 3 $$
Т.к. речь идёт о стороне прямоугольника, которая не может быть равной 0 или отрицательной, получаем: $0 lt x lt 3$ (см)
Ответ: $0 lt x lt 3$ см
Пример 3. Турист отправился на моторной лодке по течению реки и должен вернуться обратно не позже, чем через 5 часов. На какое расстояние может отъехать турист, если скорость течения 3 км/ч, а скорость лодки в стоячей воде 15 км/ч.
Заполним таблицу:
По течению
18
$frac{s}{18}$
s
Против течения
12
$frac{s}{12}$
s
По условию:
$$frac{s}{18} + frac{s}{12} le 5 | times 36 $$
$$ 2s+3s le 180 $$
$$ 5s le 180 $$
$$ s le 36 $$
Турист не должен отъезжать дальше, чем на 36 км.
Ответ: не более 36 км.
План урока:
Целые неравенства
Неравенства первой степени
Неравенства второй степени
Метод интервалов
Неравенства высоких степеней
Дробно-рациональные неравенства
Целые неравенства
Неравенства по своей сути очень похожи на уравнения. Аналогично понятию целого уравнения существует понятие целого неравенства. Так называют то нер-во, в котором используются сложение и умножение, вычитание и деление, возведение в степень, но в котором нет деления на выражения с переменной. Другими словами, ни в одном знаменателе в целом нер-ве не должно быть переменных величин.
Приведем примеры целых нер-в:
14х4 + 13х2⩽ 91х3 + 2
у3 – 7 > 1/5
(z + 1)/8 <z15 + 4z9
Если бы переменная могла быть в знаменателе, то знаменатель мог бы обращаться в ноль при некоторых ее значениях, что недопустимо в математике.Но так как в целых нер-вах переменная не находиться в знаменателе, то она может принимать любое значение.
Любое целое нер-во можно преобразовать так, чтобы в одной его части (обычно правой) стоял ноль, а в другой части – некоторый многочлен Р(х).
Пример. Преобразуйте нер-во
(х3 + 7)(2х – 3) >4х(х2 – 5х + 9)
к виду Р(х) > 0, где Р(х) – это многочлен.
Решение. Раскроем скобки в каждой части нер-ва:
(х3 + 7)(2х – 3) >4х(х2 – 5х + 9)
2х4 – 3х3 + 14х – 21 > 4x3– 20х2 + 36х
Перенесем слагаемые влево и приведем подобные слагаемые:
2х4 – 3х3 + 14х – 21 – 4x3+ 20х2 – 36х > 0
2х4 – 7х3 + 20х2 – 22х – 21 > 0
Ответ:2х4 – 7х3 + 20х2 – 22х – 21 > 0
Как и в случае с уравнениями, у нер-в есть степени. Она равна степени многочлена, стоящего в одной из его частей. Так, степень неравенства в рассмотренном только что примере равна 4, ведь степень полинома 2х4 – 7х3 + 20х2 – 22х – 21 равна 4.
Неравенства первой степени
В общем виде неравенства первой степени выглядит так:
ах + b> 0
где а и b– некоторые числа, а х – переменная.
Естественно, вместо знака «>»могут стоять знаки «<», «⩾» и«⩽». Приведем примеры нер-в первой степени:
5х – 12 > 0
– 4,52у + 63 ⩾ 0
34z+ 9 < 0
Для решения такого нер-ва свободный член (коэффициент b) переносят в другую часть нер-ва, а потом делят нер-во на коэффициент а. Здесь важно помнить, что при делении нер-ва на отрицательное число оно меняет знак!
Пример. Решите нер-во
5х – 15 > 0
Решение:
5х – 15 > 0
5х > 15
х > 15/5
х > 3
Напомним, что решения нер-в традиционно записывают в виде числовых промежутков. Запись х > 3 аналогична записи х∈(3; + ∞). На числовой прямой этот промежуток выглядит так (отмечен штриховкой):
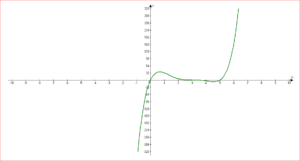
Для наглядности построим график функции у = 5х – 15 и отметим промежуток, на котором она больше нуля:
Заметим, что неравенство строгое, а потому само число 3 в его решение не входит. Из-за этого в записи (3; + ∞) первая скобка – круглая.
Ответ:(3; + ∞)
Пример. Решите нер-во
– 3х – 9 ⩾0
Решение:
– 3х – 9 ⩾0
– 3х ⩾9
х ⩽ 9/(– 3) (обратите внимание, из-за деления на отрицательное число изменился знак нер-ва!)
х ⩽ – 3
х∈(– ∞; – 3]
Также построим график у = – 3х – 9 и убедимся, что мы не ошиблись:
Неравенство нестрогое, и число – 3 входит в ответ, поэтому поле него в промежутке стоит квадратная скобка.
Ответ:(– ∞; – 3]
Неравенства второй степени
Неравенства второй степени в общем виде записываются так:
ах2 + bx + c> 0
Примерами таких нер-в являются
5х2 – 3х + 19 > 0
– 12у2 + 1,23у + 64 ⩾ 0
462z2 + 3z– 54 < 0
В левой части такого нер-ва стоит квадратичная функция. Вспомним два важных момента:
- Ветви параболы у = ах2 + bx + c смотрят вверх, если коэффициент а > 0, и смотрят вниз, если а < 0.
- Чтобы найти нули функции у = ах2 + bx + c, надо решить квадратное ур-ние ах2 + bx + c = 0. Если его дискриминант (D) больше нуля, то есть два нуля. Если D = 0, то есть только один ноль. Если D< 0, то парабола не пересекает ось Ох.
В соответствии с этим возможно 6 случаев расположения графика квадратичной функции на координатной плоскости, в зависимости от значений старшего коэффициента a и дискриминанта D:
При решении нер-в 2-ой степени обязательно возникает один из этих случаев. Поэтому для решения нер-ва
ах2 + bx + c> 0
надо решить ур-ние ах2 + bx + c = 0 и проанализировать положение графика квадратичной функции относительно оси Ох.
Пример. Найдите промежуток, на котором справедливо нер-во
2х2 – 5х + 2 < 0
Решение. Найдем корни ур-ния 2х2 – 5х + 2 = 0.
D = b2– 4ас = (– 5)2 – 4•2•2 = 25 – 16 = 9
х1 = (5 – 3)/4 = 0,5
х2 = (5 + 3)/4 = 2
Коэффициент а параболы положителен, поэтому ее ветви смотрят вверх. Сам график будет выглядеть так:
Однако нам достаточно и схематичного изображения параболы и ее нулей на координатной прямой:
Нули функции разбивают прямую на три промежутка. На каждом из них знак квадратичной функции неизменен. Отметим эти знаки:
В нер-ве стоит знак «<». Значит, нам нужен промежуток от 0,5 до 2, на котором ф-ция отрицательна (парабола ниже оси Ох). Нер-во строгое, а потому сами числа 0,5 и 2 не входят в промежуток. Такие «выколотые точки» обозначают белыми кружочками:
Ответ: (0,5; 2)
Пример. Решите нер-во
– 2х2 + 9х – 9 ≤ 0
Решение. Сначала находим нули параболы, решая ур-ние
– 2х2 + 9х – 9 = 0
D = b2– 4ас = 92 – 4•(– 2)•(– 9) = 81 – 72 = 9
х1 = (– 9 – 3)/ (– 4) = 3
х2 = (– 9 + 3)/ (– 4) = 1,5
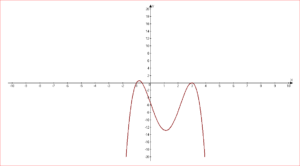
Коэффициент а параболы отрицательный, поэтому ее ветви смотрят вниз. Отметим на координатной прямой нули ф-ции и схематично график параболы, а также промежуток, на котором она неположительна:
Так как нер-во нестрогое, то сами нули ф-ции входят в ответ, а потому скобки рядом с нулями – квадратные. В итоге х∊(– ∞; 1,5]∪[3; + ∞).
Ответ: х∊(– ∞; 1,5]∪[3; + ∞).
Пример Решите нер-во
х2 – 2х + 1 > 0
Решение. Решим квадратное ур-ние
х2 – 2х + 1 = 0
D = b2– 4ас = (– 2)2 – 4•1•1 = 4 – 4 = 0
Дискриминант равен нулю, поэтому у ур-ния лишь 1 корень.
х1 = – b/2a = – (– 2)/2 = 1
Парабола будет касаться прямой Ох в единственной точке, при этом ветви параболы должны смотреть вверх:
Получается, что ф-ция положительна на всей координатной прямой, кроме точки х = 1, где она обращается в ноль. Соответственно, в ответе надо указать объединение промежутков: х∊(– ∞; 1)∪(1; + ∞).
Ответ: (– ∞; 1)∪(1; + ∞).
Пример. Найдите решение нер-ва
– 5х2 + х – 100 < 0
Решение. Попытаемся найти корни ур-ния
– 5х2 + х – 100 = 0
D = b2– 4ас = 12 – 4•(– 5)•(– 100) = 1 – 2000 = – 2001
Дискриминант меньше нуля, поэтому корней не будет. Вся парабола будет находиться ниже оси Ох, так как ее ветви должны смотреть вниз из-за отрицательного коэффициента а = – 5.
Видно, что при любых значениях х левая часть нер-ва меньше нуля, то есть нер-во справедливо при х∊(– ∞; + ∞).
Ответ: (– ∞; + ∞).
Метод интервалов
Ясно, что знак произведения зависит от знаков множителей. Так, если мы перемножаем три отрицательных числа и два положительных, то мы получим отрицательное произведение:
(– 1)•(– 2)•(– 3)•4•5 = – 120
Если же отрицательных множителей два или четыре, то итоговое произведение получится положительным:
(– 1)•(– 2)•3•4•5 = 120
(– 1)•(– 2)•(– 3)•(–4)•5 = 120
Вообще можно заметить, что если в произведении находится нечетное количество множителей (1, 3, 5, 7…), то и всё произведение отрицательно. Если же количество отрицательных множителей четно (0, 2, 4, 6, 8…), то произведение положительно. Дело в том, что при умножении отрицательных чисел действует правило «минус на минус дает плюс», то есть два минуса как бы «самоуничтожаются». Поэтому при перемножении четного количества отрицательных чисел все минусы попарно сократятся. Из этого правила есть одно исключение – если хотя бы один множитель равен нулю, то и всё произведение равно нулю, независимо от количества отрицательных сомножителей.
Пример. Справедливо ли нер-во
(– 12)•453•62,36•725•(– 975)•(– 812,99) < 0
Решение. Для ответа на вопрос нет смысла вычислять значение выражения слева. Оно представляет собой произведение, в котором 3 отрицательных множителя. 3 – это нечетное число, а потому и всё произведение отрицательно. Значит, нер-во справедливо.
Ответ: справедливо.
Далее рассмотрим нер-во, где слева стоит произведение скобок. В каждой из скобок записано выражение вида (х – а), например:
(х – 1)(х – 2)(х – 3)(х – 4) < 0
Произведение слева отрицательно, если отрицательна либо одна, либо три скобки. Определим, какие знаки принимают выражения в скобках при разных значениях х. В первой скобке записано выражение х – 1, поэтому рассмотрим нер-во
х – 1 > 0
Перенеся единицу вправо, получим, что
х > 1
Графически это можно показать так:
Аналогично, рассматривая нер-ва
х – 2 > 0
x – 3 > 0
х – 4 > 0
можно показать, какие значения принимает каждая из скобок при различных х:
Видно, что скобки (х – 1), (х – 2), (х – 3) и (х – 4) изменяют знаки с «–» на «+» при «перескоке» через точки 1, 2, 3 и 4. Отметим их все вместе на одной прямой и укажем знаки скобок на каждом из образовавшихся промежутков:
Получили 5 промежутков. Если выражение выделено красным, то оно отрицательно на промежутке, а если синим – то положительно. Напомним, что произведение отрицательно, если в его состав входит нечетное количество (1, 3, 5…) отрицательных множителей. На рисунке видно, что на промежутке (1; 2) отрицательны 3 множителя, а на промежутке (3; 4) – один множитель. Следовательно, именно на них всё произведение
(х – 1)(х – 2)(х – 3)(х – 4)
оказывается отрицательным. Соответственно на других промежутках произведение положительно. Это можно отметить так:
Штриховкой отмечены промежутки, где произведение отрицательно. Получается, что решением нер-ва является объединение промежутков (1; 2)∪(3; 4). Сами точки 1, 2, 3 и 4 исключены из решения, так как нер-во строгое. Если бы нер-во было нестрогим, то на рисунке точки были бы закрашены, а скобки в промежутке были бы квадратными.
Убедимся в верности этого решения, выбрав произвольное число из каждого промежутка и подставив его в произведение.
Из промежутка (– ∞; 1) возьмем значение х = 0:
(0 – 1)(0 – 2)(0 – 3)(0 – 4) = (– 1)•(– 2)(– 3)•(– 4) = 24 > 0
Из следующего промежутка возьмем х = 1,5:
(1,5 – 1)(1,5 – 2)(1,5 – 3)(1,5 – 4) = 0,5•(– 0,5)•(– 1,5)•(– 2,5) < 0
Примечание. Здесь мы не стали вычислять точное значение произведения, а просто посчитали, что в нем 3 отрицательных множителя. Следовательно, всё произведение отрицательно, то есть меньше нуля.
Из интервала (2; 3) возьмем число 2,5:
(2,5 – 1)(2,5 – 2)(2,5 – 3)(2,5 – 4) = 1,5•0,5•(– 0,5)•(– 1,5) > 0
Из промежутка (3; 4) выберем х = 3,5:
(3,5 – 1)(3,5 – 2)(3,5 – 3)(3,5 – 4) = 3,5•1,5•0,5•(– 0,5) < 0
Наконец, из последнего интервала (4; + ∞) возьмем число 5:
(5 – 1)(5 – 2)(5 – 3)(5 – 4) = 4•3•2•1 > 0
Для решения нер-ва мы просто нашли, при каких значениях выражение слева принимает нулевые значения, а потом расставили знаки в полученных интервалах. Данный способ называется методом интервалов.
Пример. Решите неравенство методом интервалов:
(у – 5)(– 2у + 6)(у + 4) ≥0
Решение. Вынесем из второй скобки множитель (– 2):
(у – 5)(– 2)(у – 3)(у + 4) ≥ 0
Поделим нер-во на число (– 2). Напомним, что при делении нер-ва на отрицательную величину его знак меняется на противоположный:
(у – 5)(у – 3)(у + 4) ≤ 0
Используем метод интервалов. Отметим на координатной прямой точки, при которых каждая скобка обращается в ноль (это 5, 3 и (– 4)), и расставим знаки над получившимися промежутками:
Определить эти знаки можно, просто выбрав произвольное число из промежутка и подставив его в левую часть. Так, выберем из промежутка (– ∞; – 4) число (– 5) и получим:
(– 5 – 5)(– 5 – 3)(– 5 + 4) = (– 10)•(– 8)•(– 1) < 0
Из промежутка (–4; 3) выберем число 0:
(0 – 5)(0 – 3)(0 + 4) = (– 5)•(– 3)•(4) > 0
Из промежутка (3; 5) возьмем число 4:
(4 – 5)(4 – 3)(4 + 4) = (– 1)•1•8 < 0
Из множества (5; + ∞) возьмем шестерку:
(6 – 5)(6 – 3)(6 + 4) = 1•3•10 > 0
Итак, выражение слева меньше или равно нулю при у∊(– ∞; – 4]∪[3; 5].
Ответ: (– ∞; – 4]∪[3; 5].
Обратим внимание, что в рассмотренных примерах знаки на промежутках чередовались. Это значит, что достаточно было определить знак на одном промежутке, а дальше просто менять их при переходе через отмеченные точки. Есть один частный случай, когда такое чередование НЕ происходит. Такое возможно, если в двух скобках находится одинаковые выражения.
Пример. Решите нер-во
(z – 5)(3z – 15)(7 – z) ≤ 0
Решение. Вынесем из второй скобки множитель 3, а из третьей – (– 1):
(z – 5)•3•(z – 5)•(– 1)•(z – 7) ≤ 0
Делим нер-во на (– 3):
(z – 5)(z – 5)(z – 7) ≥ 0
Обратите внимание – мы получили две одинаковые скобки (z – 5). Отметим на прямой нули левого выражения (это числа 5 и 7), а также знаки промежутков:
Для расстановки знаков подставим в выражение слева числа:
при z = 4 (4 – 5)(4 – 5)(4 – 7) = (– 1)•(– 1)•(– 3) < 0
при z = 6 (6 – 5)(6 – 5)(6 – 7) = 1•1•(– 1) < 0
при z = 8 (8 – 5)(6 – 5)(8 – 7) = 3•3•1> 0
Получилось, что на соседних интервалах (– ∞; 5) и (5; 7) знаки совпадают, а не чередуются. Так произошло из-за того, что при переходе через точку z = 5 знак поменяла не одна, а сразу 2 скобки (х – 5).
При записи ответа надо учесть, что в задании дано нестрогое нер-во. Поэтому в ответ надо включить как промежуток [7; + ∞), так и число 5, которое обращает в ноль произведение в левой части.
Ответ: 5∪[7; + ∞).
Неравенства высоких степеней
Напомним, что если некоторое число а – корень многочлена Р(х) (то есть оно является корнем ур-ния Р(х) = 0), то этот многочлен можно представить как произведение двучлена (х – а) и какого-то другого многочлена Р1(х). Другими словами, зная корни многочлена, можно разложить его на множители. За счет этого можно решать нер-ва высоких степеней.
Пример. Решите нер-во
х3 – 3х2 – х + 3 < 0
Решение. Найдем корни многочлена, стоящего в левой части, то есть решим ур-ние
х3 – 3х2 – х + 3 = 0
Попробуем подобрать корни, начав с целых чисел. Напомним, что все целые корни должны быть делителем свободного члена, то есть в данном случае числа 3. Поэтому «кандидатами» являются числа 1, (– 1), 3 и (– 3). Подставляя их в ур-ние, находим, что оно имеет три корня: 1, (– 1) и 3:
13 – 3•12 – 1 + 3 = 1 – 3 – 1 + 3 = 0
(– 1)3 – 3•(– 1)2 – (– 1) + 3 = – 1 – 3 + 1 + 3 = 0
33 – 3•32 – 3 + 3 = 27 – 27 – 3 + 3 = 0
Число (– 3) не подходит, ведь при его подстановке в левую часть ноль не получается:
(– 3)3 – 3•(– 3)2 – (– 3) + (– 3) = – 27 +27 + 3 + 3 = 6
Напомним, что у ур-ния 3-ей степени не может быть более 3 корней, поэтому других корней у ур-ния нет.
Зная корни, мы можем разложить многочлен на множители:
х3 – 3х2 – х + 3 = (х – 1)(х + 1)(х – 3).
В справедливости такого разложения можно убедиться, раскрыв скобки в правой части этого равенства. Теперь можно переписать исходное нер-во
х3 – 3х2 – х + 3 < 0
(х – 1)(х + 1)(х – 3) < 0
Найдем его решение методом интервалов:
Убедимся в том, что мы правильно расставили знаки, подставляя в нер-во произвольные числа из промежутков:
при х = – 2 имеем (– 2 – 1)(– 2 + 1)(– 2 – 3) = (– 3)•(– 1)•(– 5) < 0
при х = 0 получится (0 – 1)(0 + 1)(0 – 3) = (– 1)•1•(– 3) > 0
при х = 2 имеем (2 – 1)(2 + 1)(2 – 3) = 1•3•(– 1) < 0
при х = 4 получится (4 – 1)(4 + 1)(4 – 3) = 3•5•1 > 0
Получаем, что левая часть отрицательна при х∊(– ∞; – 1)∪(1; 3).
Ответ:(– ∞; – 1)∪(1; 3).
Пример. Решите нер-во
х3 + 2х – 3 > 0
Решение. Рассмотрим ур-ние
х3 + 2х – 3 = 0
Подбором можно определить лишь один его корень – единицу:
13 + 2•1 – 3 = 0
Поделим исходный многочлен на (х – 1):
Подробнее в уроке 2
Получили, что х3 + 2х – 3 = (х – 1)(х2 + 2х + 3)
Можно ли разложить на множители квадратный трехчлен х2 + 2х + 3? Попытаемся решить ур-ние
х2 + 2х + 3 = 0
D = b2– 4ас = 42 – 4•2•3 = 16 – 24 = – 8
Получили, что корней нет. Это значит, что функция у = х2 + 2х + 3 не пересекает ось Ох, и, так как коэффициент а этого трехчлена положителен, то выражение х2 + 2х + 3 больше нулю при любом х.
Это можно показать и иначе, если выделить полный квадрат из трехчлена:
х2 + 2х + 3 = х2 + 2х + 1 + 2 = (х + 1)2 + 2
Перепишем исходное нер-во с учетом разложения многочлена на множители:
х3 + 2х + 3 > 0
(х – 1)(х2 + 2х + 3) > 0
Так как выражение х2 + 2х + 3 положительно при любом значении х, то мы можем поделить неравенство на него:
х – 1 > 0
Отсюда получаем, что х∊(1; + ∞).
Ответ: (1; + ∞).
Пример. Укажите наименьшее целое решение неравенства
4х3 + 4х2 – 7х + 2 > 0
Решение. Попытаемся найти корень многочлена 4х3 + 4х2 – 7х + 2. Целый корень должен быть делителем двойки (свободного члена), то есть возможны варианты 1 и (–1), 2 и (– 2). Из них подходит только – 2:
4•(– 2)3 + 4•(– 2)2 – 7•(– 2) + 2 = – 32 + 16 + 14 + 2 = 0
Значит, можно поделить исходный многочлен на х + 2:
Подробнее в уроке 2
Можно записать, что 4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1).
Далее разложим получившийся при делении квадратный трехчлен на множители, для чего приравняем его к нулю:
4х2 – 4х + 1 = 0
D = b2– 4ас = (– 4)2 – 4•4•1 = 16 – 16 = 0
Получается, что есть лишь один корень.
х = – b/(2a) = – (– 4)/(2•4) = 0,5
Если у квадратного трехчлена дискриминант равен нулю, то это значит, что он является полным квадратом какого-то выражения. Действительно:
4х2 – 4х + 1 = (2х)2 – 2•2х•1 + 12 = (2х – 1)2
Тогда можно записать:
4х3 + 4х2 – 7х + 2 = (х + 2)(4х2 – 4х + 1) = (х + 2)(2х – 1)2 =
= (х + 2)(2х – 1)(2х – 1)
Перепишем с учетом этого исходное нер-во:
4х3 + 4х2 – 7х + 2 > 0
(х + 2)(2х – 1)(2х – 1) > 0
Вынесем множитель 2 из двух последних скобок и поделим нер-во на них:
(х + 2)•2•(х – 0,5)•2•(х – 0,5) > 0
(х + 2)(х – 0,5)(х – 0,5) > 0
Решим его методом интервалов:
Снова из-за двух одинаковых скобок (х – 0,5) на соседних промежутках (– 2; 0,5) и (0,5; 2) получили один и тот же знак. Функция положительна на них, однако она равна нулю при х = 0,5, поэтому это число из решения неравенства исключается. Получаем, что х∈(– 2; 0,5)∪(0,5; + ∞).
Нам надо указать наименьшее целое решение. Самым малым целым числом из множества (– 2; 0,5)∪(0,5; + ∞) является (– 1).
Ответ: (– 1).
Дробно-рациональные неравенства
До сих пор мы рассматривали целые нер-ва. Однако, по аналогии с уравнениями, существуют ещё и дробно-рациональные нер-ва. В них выражение с переменной может стоять в знаменателе. Приведем примеры дробно-рациональных нер-в:
Любое такое нер-во можно представить в виде
где Р(х) и Q(х) – некоторые многочлены. Естественно, вместо знака «>» может стоять и другой знак. Для примера преобразуем к такому виду нер-во
Перенесем все слагаемые влево:
Далее приведем левую часть к общему знаменателю:
Осталось раскрыть скобки:
В итоге и в числителе, и в знаменателе стоят многочлены.
Рассмотрим нер-ва
а/b>0 и ab> 0
Докажем, что они равносильны друг другу. Возможны 5 случаев:
- И а, и b являются положительными числами. Тогда оба нер-ва верны, ведь и произведение, и отношение двух положительных чисел само положительно:
10•5 = 50 > 0
10/5 = 2 > 0
- Оба числа, а и b, отрицательны, тогда снова оба нер-ва справедливы, ведь при умножении и делении двух отрицательных чисел получается положительное число. Например:
(– 10)•(– 5) = 50 > 0
(– 10)/(– 5) = 2 > 0
- Только одно из чисел положительно, а другое отрицательно, тогда их произведение, как и частное, меньше нуля, и нер-ва неверны:
(– 10)•5 = – 50< 0
(– 10):5 = – 2 < 0
- Число a равно нулю. Тогда выражения ab и a/b также равны нулю, а потому рассматриваемые нер-ва неверны:
0•5 = 0
0/5 = 0
- Число b равно нулю. Тогда произведение ab равно нулю, а дробь а/b не имеет смысла (из-за нуля в знаменателе). То есть нер-ва а/b> 0 и ab> 0 снова одновременно неверны.
Получили, что при любых значениях а и b нер-ва а/b> 0 и ab> 0 либо одновременно справедливы, либо одновременно несправедливы. Это значит, что они равносильны.
Это значит, что от дробно-рационального нер-ва можно перейти к равносильному ему целому нер-ву.
Пример. Решите нер-во
Решение:
Исходному нер-ву равносильно иное нер-во:
(х – 1)(х – 2)(х – 3)(х – 4)> 0
Решим его методом интервалов:
Получаем, что х∊(1; 2)∪(3; 4).
Ответ: (1; 2)∪(3; 4).
Пример. Решите нер-во
Решение. В числителе и знаменателе находятся квадратные трехчлены. Их можно разложить на корни, если знать их корни. Найдем их.
х2 – 9х + 14 = 0
D = b2– 4ас = (– 9)2 – 4•1•14 = 84 – 56 = 25
х1 = (9 – 5)/2 = 2
х2 = (9 + 5)/2 = 7
Так как корни равны 2 и 7, то можно записать, что
х2 – 9х + 14 = (х – 2)(х – 7)
Аналогично разложим знаменатель
х2 – 14х + 45 = 0
D = b2– 4ас = (– 14)2 – 4•1•45 = 196 – 180 = 16
х1 = (14 – 4)/2 = 5
х2 = (14 + 4)/2 = 9
х2 – 14х + 45 = (х – 5)(х – 9)
Перепишем исходное нер-во:
Ему равносильно другое нер-во:
(х – 2)(х – 7)(х – 5)(х – 9) > 0
Его можно решить методом интервалов:
Получаем, что х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).
Ответ: х∊(– ∞; 2)∪(5; 7)∪(9; + ∞).
Обратим внимание на одну особенность метода интервала в случаях, когда решается дробно-рациональное нер-во. Она касается нестрогих нер-в (со знаками «≤» и «≥»). В целых нестрогих нер-вах сами точки, при которых выражение слева обращается в ноль, включаются в решение. Но при рассмотрении дроби важно понимать, что ее знаменатель не может быть равным нулю. Поэтому при нестрогом нер-ве в ответ надо включить точки, обращающие в ноль числитель, но при этом исключить точки, обращающие в ноль знаменатель.
Пример. Решите нер-во
Числитель обращается в ноль в точках (– 2) и 4, а знаменатель – в точках (– 7) и 8. Так как нер-во нестрогое, то числа 4 и (– 2) будут входить в решение (на координатной прямой мы отметим их закрашенным кружочком), а числа (– 7) и 8 – нет (их отметим как «выколотые точки»):
В итоге получаем, что дробь неотрицательна при х∊(– ∞; – 7)∪[– 2; 4]∪(8; – ∞).
Ответ: (– ∞; – 7)∪[– 2; 4]∪(8; – ∞).
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 – в первом, и a=0 – во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
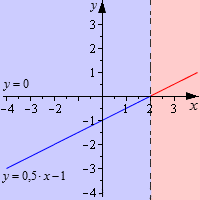
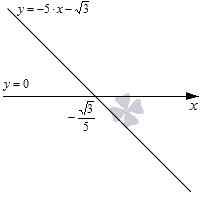
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Решить неравенство -5·x-3>0 при помощи графика.
Решение
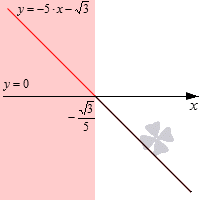
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох -5·x-3>0 получим значение -35. Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Неравенство с одной переменной — это два выражения с переменной, соединенные знаком неравенства ((gt; ; lt; ; leq; ; geq)).
Решением неравенств с одной переменной называется такое значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство — это значит найти все его решения или доказать, что их нет, т.е. найти множество решений неравенства.
Решением неравенства с одной переменной, как правило, является числовой промежуток или совокупность промежутков.
Числовой промежуток — это множество чисел, удовлетворяющих одному из условий, перечисленных в первом столбце таблицы.
| Числовые промежутки | Обозначение | Название |
|---|---|---|
| (a lt x lt b) | ((a; b)) | Открытый промежуток, интервал |
| (x gt a) | ((a; +infty)) | |
| (x lt a) | ((-infty; a)) | |
| x — любое | ((-infty;+infty)) | |
| (a leq x leq b) | ([a;b]) | Закрытый промежуток, отрезок |
| (a lt x leq b) | ((a; b]) | Полуоткрытый промежуток, полуинтервал |
| (a leq x lt b) | ([a; b)) | |
| (x leq a) | ((-infty; a]) | |
| (x geq a) | ([a; +infty)) |
Равносильными (эквивалентами) называются неравенства, имеющие одно и то же множество решений (в частности, не имеющие решений).
Чтобы получить неравенство, равносильное данному, можно производить действия, вытекающие из свойств числовых неравенств:
- к обеим частям неравенства прибавлять одно и то же число;
- умножать обе части неравенства на одно и то же число;
- умножать обе части неравенства на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Схема решения неравенств первой степени (линейных) с одной переменной
| (a cdot x geq b) | |||
|---|---|---|---|
| (a neq 0) |
(a = 0) (0 cdot x geq b) |
||
|
(a gt 0) (x ge frac{b}{a}) (x in left[frac{b}{a}; +inftyright)) |
(a lt 0) (x le frac{b}{a}) (x in left(-infty; frac{b}{a}right]) |
(b gt 0) нет решений |
(b le 0) ( x ) — любое число (x in (-infty; +infty) ) |
В случае строгого неравенства (ax gt b) схема аналогична, но все неравенства таже строгие, а интервалы — открытые.
Метод интервалов при решении неравенств
Этот метод удобен для решения неравенства вида ( P(x) gt 0 ; (lt; ; geq; ; leq) ), или ( frac{P(x)}{Q(x)} gt 0 ; (lt; ; geq; ; leq) ),
где P(x) и Q(x) — многочлены, раскладываемые на множетели.
-
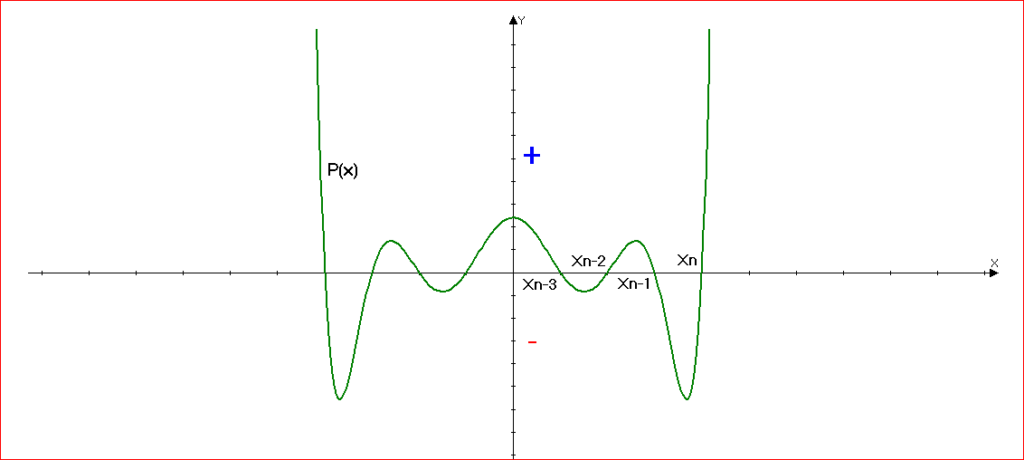
Рассмотрим неравенство ( P(x) gt 0 ), и пусть многочлен ( P(x) ) раскладывается на множетели следующим образом:
(P(x)=(x-x_1)(x-x_2)…(x-x_n) gt 0) , где (x_1, x_2, …x_n) – корни данного многочлена и (n geq 2).Предположим, что все эти корни разные.
Знак левой части неравенства зависит от комбинации знаков линейных множителей и меняется в каждой из точек (x_1, x_2, …x_n).
Допустим, что (x_1 lt x_2 lt x_3 lt … lt x_n).
При (x gt x_n) все линейные множетели положительны, и вся левая часть тоже.
При (x_{n-1} lt x lt x_n) меняет знак только последний множитель, значит, и все выражение отрицательно.
При (x_{n-2} lt x lt x_{n-1}) отрицательны два последних множителя, значит левая часть опять положительна (т.к. «минус» умножить на «минус» получим «плюс») и т.д.Эти рассуждения позволяют сразу найти все решения неравенства, если воспользоваться числовой прямой.
отметим на числовой прямой числа (x_1, x_2, …x_n) и проведём через них кривую (как показано на рисунке).В общем виде нельзя показать, как эта кривая пересечет прямую в точках (x_1 и x_2), т.к. мы не знаем, четно или нечетно n.
Если кривая проведена именно таким образом, то участки кривой, лежащие над числовой прямой, соответствует решению неравенства (P(x)gt 0),
а участки кривой, лежащие под осью – решение неравенства (P(x)lt 0),
(в случае строго неравенства берутся открытые промежутки, в случае нестрого — закрытые).Так в нашем случае:
(P(x)gt 0) при (x in …(x_{n-2};x_{n-1})bigcup{(x_n;+infty)} )
(P(x)leq 0) при (x in …[x_{n-3};x_{n-2}]bigcup{[x_{n-1};x_n]} )Пример
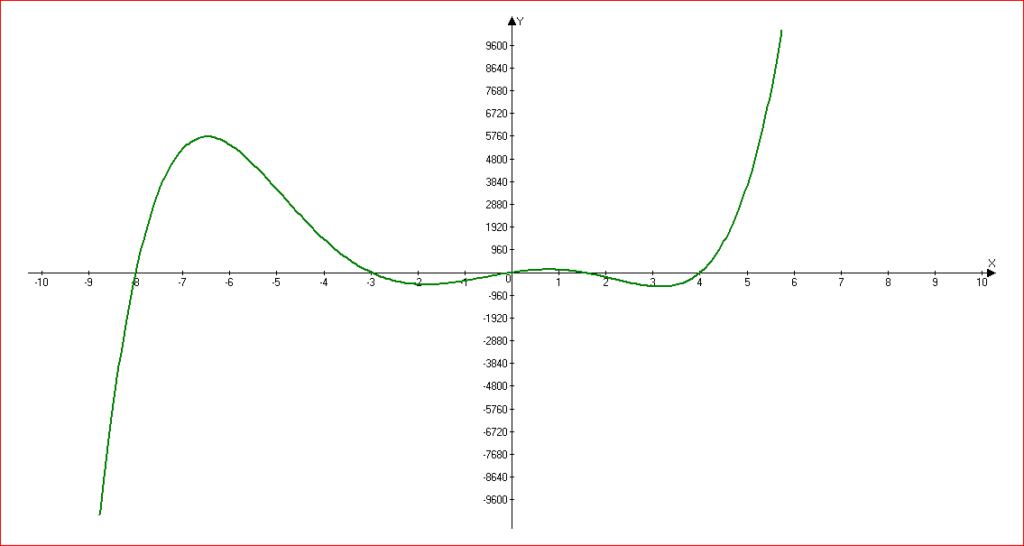
( x(x-4)(x+8)(x-1,5)(2x+6)geq 0 )
при (x in [-8; -3] bigcup [0; 1.5] bigcup [4; +infty) ) -
Пусть теперь среди множителей встречаются одинаковые (кратные).
Их произведение тогда можно записать с помощью степени в виде ((x-a)^2) или ((x+b)^3) и т.д.Если в разложении P(x) входит множитель вида ((x-a)^m), где m нечетно,
мы можем заменить его при решении неравенства множителем ((x-a)), т.к. у них знак один и тот же.Если в разложении P(x) входит множитель вида ((x-a)^m), где m четно,
то в нестрогом неравенстве его можно просто опустить, т.к. он положителен и никак не влияет на знак.
В случае строгого неравенства просто опустить множитель ((x-a)^2, ;; (x-a)^4) и т.д. нельзя,
т.к. мы должны включить в множество решений неравенства точку (x=a), для которой (P(x)=0).Пример
-
( x(x-3)^3 cdot (x-5) gt 0 )
т.к. корень x = 3 имеет кратность 3 (нечетная), то знак меняется.
решение: ( x in (0; 3) bigcup (5; +infty) ) -
( x(x-3)^2 cdot (x-5) leq 0 )
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
решение: ( x in [0; 3] bigcup [3; 5] ) или ( x in [0; 5] ) -
( x(x-3)^2 cdot (x-5) lt 0 )
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
решение: ( x in (0; 3) bigcup (3; 5) )
-
( x(x-3)^3 cdot (x-5) gt 0 )
-
В разложение многочлена входит квадратный трёхчлен, который не имеет действительных корней, а значит, не раскладывается на линейные множители.
В этом случае он нигде не обращается в нуль и не меняет знак, следовательно, его можно отбросить, если этот трёхчлен принимает только положительные значения.
Если же квадратный трёхчлен принимает только отрицательные значения, то его тоже можно отбросить, но при этом поменять знак неравенства на противоположный.Пример
( (x+3) cdot (x^2 + 3x + 10) gt 0 )
Т.к. трехчлен не имеет действительных корней ( (D lt 0) ) и коэффициент при (x^2) положителен,
то этот трёхчлен принимает положительные значения для всех ( x ),
т.е. решение исходного неравенства равносильно решению неравенства ( x+3 gt 0 ).
Откуда ( x gt -3 ). -
Пусть надо решить неравенство вида:
( frac{P(x)}{Q(x)} gt 0 ;; (lt, ; geq, ; leq) )
где ( P(x) ) и ( Q(x) ) — многочлены, которые можно разложить на множители.Поскольку на знак выражения не влияет, находится ли множитель в числителе или в знаменателе,
то это неравенство можно заменить неравенством (P(x) cdot Q(x)gt 0),
т.е. решение свести к первому случаю, но при этом обязательно исключить точки, в которых (Q(x)=0).
Если неравенство не строгое, то значения ( x ), при которых (Q(x)=0),
могут войти в множество решений неравенства (P(x) cdot Q(x)geq 0);
в этом случае их необходимо исключить из ответа, т.к. они не входят в ОДЗ исходного неравенства.
В случае же строгого неравенства этого можно не опасаться.Пример
$$ frac{x(x+5)}{(x-3)(x+7)^2}leq 0 $$
т.к. ( (x+7)^2 geq 0 ), то исходное неравенство равносильно следующей системе:
$$ begin{cases}
x(x+5)(x-3) leq 0 \
x neq 3 \
x neq -7
end{cases} $$решение выглядит так:
ответ: (x in (-infty; -7) bigcup (-7;-5) bigcup [0;3)). -
Прежде чем применить метод интервалов, необходимо привести линейные множители к виду (x-a),
разделив обе части неравенства на коэффициент при ( x ) (в каждой скобке).
многочлены при этом нужно разложить на множители.Пример
$$ (5x+3)(6-2x)(x^2-2x-3) geq 0 $$
Преобразуем выражение и получим:
$$ (x+frac{3}{5})(3-x)(x+1)(x-3) geq 0 $$
Ответ: (x in [-1; -3/5] bigcup [3; 3] ).
Выражение с одной переменной, содержащее знак неравенства, называется неравенством с одной переменной. Например:
23х+11<11x+5; 6x–10; х>9
Неравенства такого вида называют линейными неравенствами с одной переменной, так как х в них в первой степени.
Вспомним, что в зависимости от знака неравенства, их называют строгие знаки (< и >) или нестрогие знаки (≤ и ≥).
Решением неравенства с одной переменной является значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или доказать, что решений нет.
При решении неравенства с одной переменной пользуются следующими свойствами.
Свойства неравенств
- Если из одной части неравенства перенести слагаемое в другую часть, поменяв при этом знак слагаемого на противоположный, то получится равносильное ему неравенство;
- Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится равносильное ему неравенство.
Рассмотрим решение линейных неравенств с одной переменной на примерах.
Пример №1. Решить неравенство:
6х–13<x–3
Перенесем слагаемые из одной части в другую, изменяя знаки у слагаемых, которые будем переносить, на противоположные:
6х–x < –3+13
Теперь приведем подобные слагаемые в каждой части неравенства: 5х<10. Дальше разделим обе части неравенства на число 5 (коэффициент при х), получим: х<2. Множество решений данного неравенства состоит из всех чисел, которые меньше минус двух. Ответ можно записать в виде неравенства х<2, либо в виде числового промежутка (–∞;-2). Вспомним, что около знака «бесконечность» всегда ставится круглая скобка, а так как неравенство строгое (знак «меньше»), то и у числа два также ставится «круглая» скобка). Это множество чисел можно показать на числовом луче (точка, которая показывает число 2, будет «выколотая», так как неравенство строгое):
Пример №2. Решить неравенство:
12–2х≤х–6
Выполним перенос слагаемых:
–х–2х–6–12
Приведем подобные слагаемые: –3х–18. Разделим обе части неравенства на минус три и изменим знак неравенства на противоположный: х≥6. Значит, множество решений данного неравенства – это все числа, которые больше или равны 6. Ответ можно записать, как в виде нестрогого (знак «больше или равно») неравенства х≥6, так и в виде числового промежутка [6;+), (видим около числа 6 «квадратную» скобку), показав его на числовом луче, где точка, обозначающая число 6, закрашена, ее называют «приколотой» точкой, так как неравенство нестрогое.
В рассмотренных примерах мы получали неравенства, у которых коэффициент при переменной не равен нулю. Но есть случаи, когда получается неравенство вида 0•х>a или 0•х<a (возможны и нестрогие знаки). В этом случае неравенство либо не имеет решений, либо решением является любое число.
Пример №3. Решить неравенство:
3х–15<3x–56
Выполняя перенос слагаемых и приведение подобных, получим неравенство:
0х<–41
Данное неравенство при любом значении х будет иметь вид 0<–41, что является неверным. Значит, оно не имеет решений, следовательно, и данное по условию неравенство не имеет решений.
Пример №4. Решить неравенство:
5х+24>5x+14
Выполним все необходимые действия, получим:
0х>–10
Данное неравенство при любом значении х будет иметь вид 0>–10, а это верное неравенство, значит х – любое число. Следовательно, ответ в данном неравенстве – «х – любое число».
Алла Василевская | Просмотров: 4k