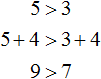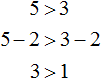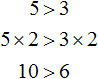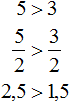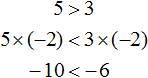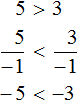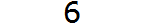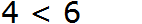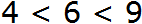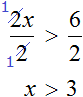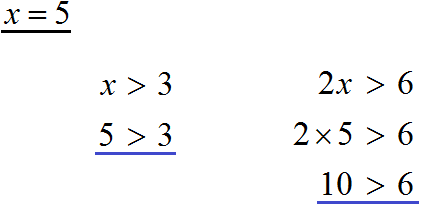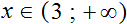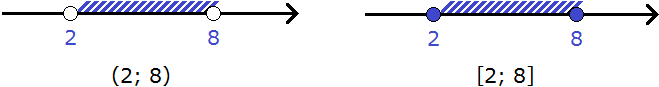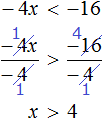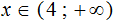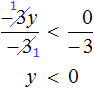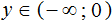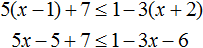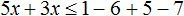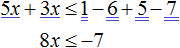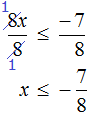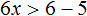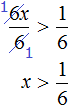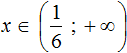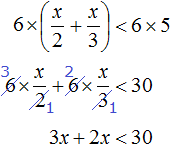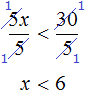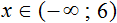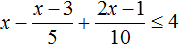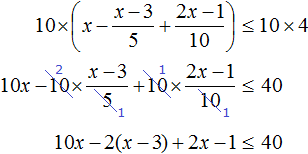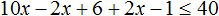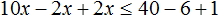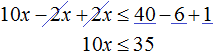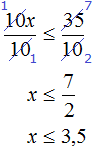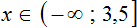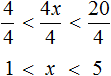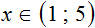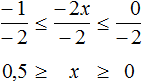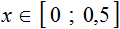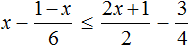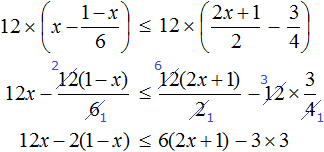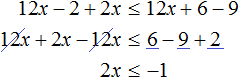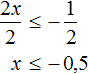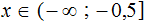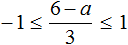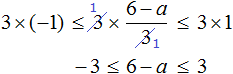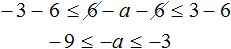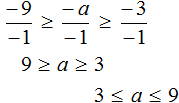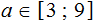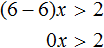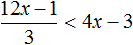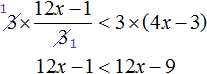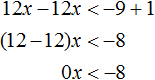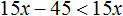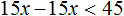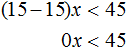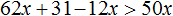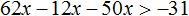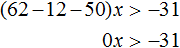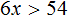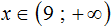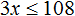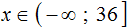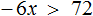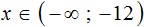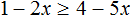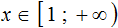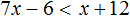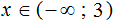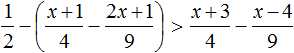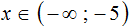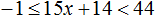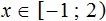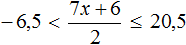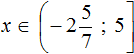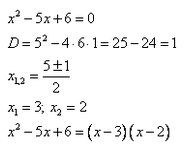Как найти неравенство которое не имеет решений

Сегодня посмотрим один вид задания №13 первой части ОГЭ, которое вызывает наибольшие трудности у девятиклассников.

Само задание звучит следующим образом:

Укажите неравенство, которое не имеет решений:

1) x²+x+36<0

2) x²+x+36>0

3) x²+x-36<0

4) x²+x-36>0

Это стандартное полное квадратное неравенство.

Если левая часть квадратного неравенства имеет корни, то неравенство всегда имеет решение.

Если левая часть не имеет корней, то неравенство либо имеет бесконечное множество решений, либо не имеет решений.

Значит, чтобы неравенство не имело решений необходимо выполнение нескольких условий, первое из которых: левая часть не имеет корней.

На этом этапе уже можно отсеять варианты 3) и 4)

Осталось теперь определить, какое из оставшихся неравенство имеет бесконечное множество решений, а какое не имеет решений.

Для этого изобразим решение на числовой прямой. Функция “у=x²+x+36” парабола. Ветки параболы смотрят вверх (a>0). Т.к. функция не имеет корней, то парабола не пересекает числовую прямую, а значит располагается выше оси.

Значит при любом значении х: x²+x+36>0.

А вот x²+x+36<0 не имеет решений

ОТВЕТ: 1

ПС Обратите внимание, что при отрицательном дискриминанте УРАВНЕНИЕ не имеет решений, на НЕРАВЕНСТВО либо не имеет решений, либо имеет бесконечное число решений. Поэтому выбор ответа требует дополнительного исследования функции.

Продолжение следует…

Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность

(✿◠‿◠)

Метод интервалов, решение неравенств

Определение квадратного неравенства

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

Квадратное неравенство можно решить двумя способами:

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Неравенство примет вид:

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Решение линейных неравенств

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.

Типы неравенств

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

Решение линейных неравенств

Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов это:

Если a ≠ 0, тогда решением будет единственный корень — х₀;

Для этого найдем значения функции в точках на промежутке;

Как решаем:

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Ответ: (−∞, −√3 : 5) или x

Источник

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Смысл жирной точки в том, что сама точка входит в ответ.

Таблица числовых промежутков

Алгоритм решения линейного неравенства

a x b a x ≤ b a x > b a x ≥ b

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

Квадратные неравенства

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№5. Решить неравенство x 2 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

3 ( x + 8 ) − 5 x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

x = − 37 5 = − 37 5 = − 7,4

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

Алгоритм решения системы неравенств

Примеры решений систем неравенств:

№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 4 на графике жирная, так как знак неравенства нестрогий.

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Графическая интерпретация решения:

№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения:

Графическая интерпретация решения:

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Графическая интерпретация решения первого неравенства:

Решаем методом интервалов.

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Источник

Общие сведения о неравенствах

Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.

Определения и свойства

Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, 5 > 3

Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.

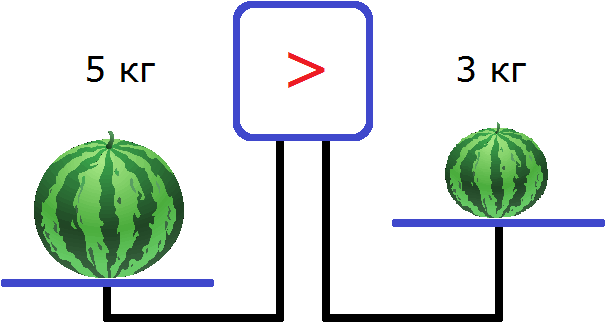
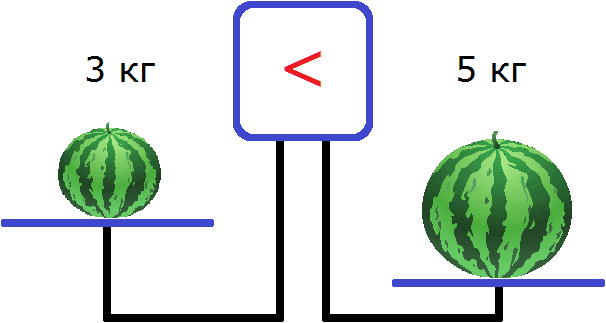
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:

Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.

Свойство 1.

Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.

Например, прибавим к обеим частям неравенства число 4. Тогда получим:

Видим, что левая часть по-прежнему больше правой.

Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2

Видим, что левая часть по-прежнему больше правой.

Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.

Видим, что левая часть по-прежнему больше правой.

Свойство 2.

Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.

Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:

Видим, что левая часть по-прежнему больше правой.

Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2

Видим, что левая часть по-прежнему больше правой.

Свойство 3.

Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.

Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1

Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.

Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.

Неравенство 8 не является верным, поскольку не выполняется условие «8 меньше, чем 6».

Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:

Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.

Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.

Строгие и нестрогие неравенства

Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:

Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.

Двойное неравенство

Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.

Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.

Сначала записываем 6

Слева записываем, что это число больше, чем число 4

Справа записываем, что число 6 меньше, чем число 9

Неравенство с переменной

Неравенство, как и равенство может содержать переменную.

Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.

Значение переменной, при котором неравенство становится верным, называется решением неравенства.

Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.

Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:

Как решать неравенства

Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.

Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.

А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.

Пример 1. Решить неравенство 2x > 6

Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.

В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.

Итак, разделим обе части неравенства на 2.

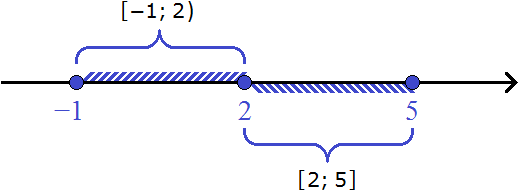
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.

Отметим, что неравенство x > 3 является строгим. « Переменная x строго больше трёх».

Видим, что в обоих случаях получается верное неравенство.

После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:

Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.

Числовые промежутки

Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.

Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8

Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.

Границы могут принадлежать числовому промежутку либо не принадлежать ему.

Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.

Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.

На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.

Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:

В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.

На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.

Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.

Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.

На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:

На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.

На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.

С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:

То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.

Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:

В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.

А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.

Существуют разновидности числовых промежутков. Рассмотрим каждый из них.

Числовой луч

Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее

Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.

На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:

Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.

Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.

Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3

Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.

Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:

В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.

Открытый числовой луч

Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.

На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:

Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.

Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:

На письме открытый числовой луч, заданный неравенством x , обозначается следующим образом:

Запишем ответ к неравенству x с помощью обозначения открытого числового луча:

В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x Граница 2 не принадлежит множеству решений, поскольку неравенство x является строгим.

Отрезок

Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:

На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:

Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:

Интервал

Изобразим интервал на координатной прямой:

На письме интервал, заданный неравенством a обозначается следующим образом:

Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 с помощью этого обозначения:

Полуинтервал

Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.

В ситуации с полуинтервалом a ≤ x ему (полуинтервалу) принадлежит левая граница.

А в ситуации с полуинтервалом a ему принадлежит правая граница.

Изобразим полуинтервал 2 ≤ x на координатной прямой:

Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x принадлежит множеству его решений.

А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x не принадлежит множеству его решений.

На письме полуинтервал, заданный неравенством a ≤ x обозначается следующим образом:

Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x с помощью этого обозначения:

Изобразим полуинтервал 2 на координатной прямой:

Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 не принадлежит множеству его решений.

А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 принадлежит множеству его решений.

Изображение числовых промежутков на координатной прямой

Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.

Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5

Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:

Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой

Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.

Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.

Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:

Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.

Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:

Пример 4. Изобразить числовой промежуток, заданный неравенством −5

Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.

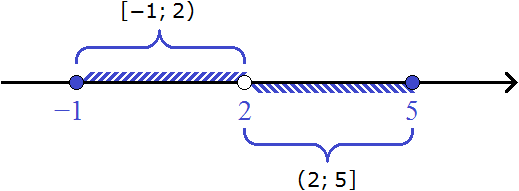
Пример 5. Изобразить на координатной прямой числовые промежутки [−1; 2) и [2; 5]

В этот раз изобразим на координатной прямой сразу два промежутка. Промежуток [−1; 2) является полуинтервалом, промежуток [2; 5] — отрезком.

У полуинтервала [−1; 2) левая граница принадлежит ему, а правая нет.

А у отрезка [2; 5] обе границы принадлежат ему.

Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]

Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.

В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.

А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.

Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:

Примеры решения неравенств

Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax ), будем называть линейным неравенством с одной переменной.

Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2

Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b

Пример 1. Решить неравенство x − 7

Прибавим к обеим частям неравенства число 7

Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x и обозначается как ( −∞ ; a)

На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:

Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4

Получилось верное числовое неравенство. Значит решение верное.

Пример 2. Решить неравенство −4x

Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 3. Решить неравенство 3y + 1 > 1 + 6y

Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:

Приведём подобные слагаемые:

Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Решениями неравенства y являются все числа, меньшие нуля. Изобразим множество решений неравенства y на координатной прямой и запишем ответ в виде числового промежутка:

Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)

Раскроем скобки в обеих частях неравенства:

Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:

Приведем подобные слагаемые:

Разделим обе части получившегося неравенства на 8

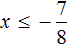
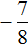
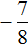
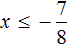
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.

Изобразим множество решений неравенства 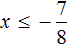на координатной прямой и запишем ответ в виде числового промежутка:

Пример 5. Решить неравенство

Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:

Теперь перенесем 5 из левой части в правую часть, изменив знак:

Изобразим множество решений неравенства 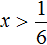на координатной прямой и запишем ответ в виде числового промежутка:

Пример 6. Решить неравенство

Умножим обе части на 6

Решениями неравенства x являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x строгим.

Изобразим множество решений неравенства x на координатной прямой и запишем ответ в виде числового промежутка:

Пример 7. Решить неравенство

Умножим обе части неравенства на 10

В получившемся неравенстве раскроем скобки в левой части:

Перенесем члены без x в правую часть

Приведем подобные слагаемые в обеих частях:

Разделим обе части получившегося неравенства на 10

Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.

Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 8. Решить неравенство 4

Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.

Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4

Решениями неравенства 1 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 является строгим.

Изобразим множество решений неравенства 1 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 9. Решить неравенство −1 ≤ −2x ≤ 0

Разделим все члены неравенства на −2

Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.

Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 10. Решить неравенство

Умножим обе неравенства на 12

Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:

Разделим обе части получившегося неравенства на 2

Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.

Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:

Пример 11. Решить неравенство

Умножим все части неравенства на 3

Теперь из каждой части получившегося неравенства вычтем 6

Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:

Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.

Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:

Когда решений нет

Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:

Пример 2. Решить неравенство

Умножим обе части неравенства на 3

В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:

Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x не имеет решений.

Ответ: решений нет.

Когда решений бесконечно много

Пример 1. Решить неравенство 5(3x − 9)

Раскроем скобки в правой части неравенства:

Перенесём 15x из правой части в левую часть, изменив знак:

Приведем подобные слагаемые в левой части:

А если приведённое равносильное неравенство 0x имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) имеет те же решения.

Ответ можно записать в виде числового промежутка:

В этом выражении говорится, что решениями неравенства 5(3x − 9) являются все числа от минус бесконечности до плюс бесконечности.

Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x

Раскроем скобки в левой части неравенства:

Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:

Приведём подобные слагаемые:

А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.

Запишем ответ в виде числового промежутка:

Задания для самостоятельного решения

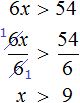
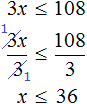
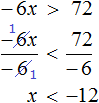
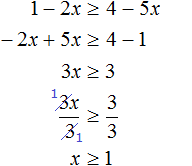
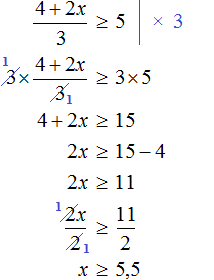
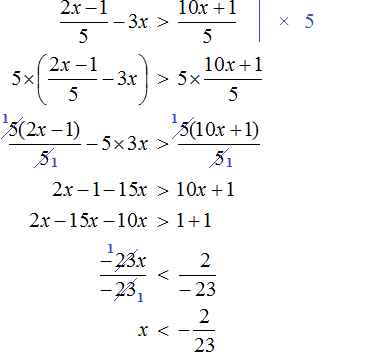
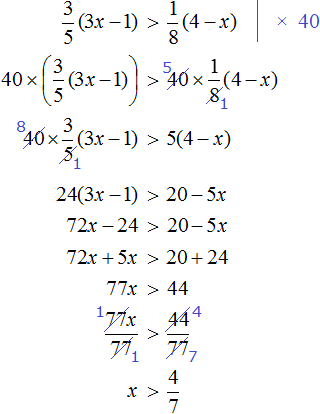
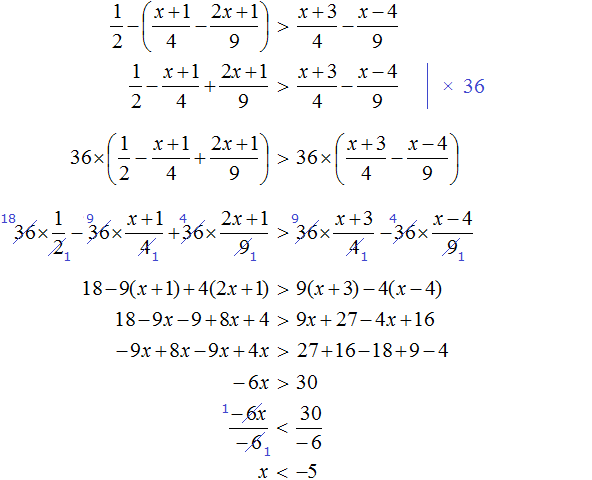
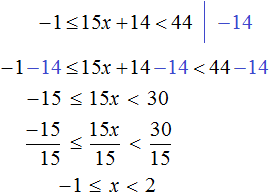
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Adblock
detector

Неравенство	Графическое решение	Форма записи ответа
x c

3) система не имеет решений

Решением системы является отрезок, изображённый под номером 1.

Решите систему неравенств

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

Решением системы является отрезок, изображённый под номером 2.

Правильный ответ указан под номером 2.

Решите систему неравенств

Используя тот факт, что знаменатель первого неравенства всегда больше нуля, преобразуем систему неравенств:

А куда делся знаменатель в первой части? Его можно просто так выкидывать?

Никита, знаменатель в первом уравнении всегда больше ноля, поэтому мы его не учитываем.

Решите систему неравенств

На каком из рисунков изображено множество её решений?

В ответе укажите номер правильного варианта.

Правильный ответ указан под номером 3.

Найдите наибольшее значение , удовлетворяющее системе неравенств

Значит, наибольшее значение удовлетворяющее данной системе неравенств −3.

и определите, на каком рисунке изображено множество его решений.

В ответе укажите номер правильного варианта.

Решение неравенства изображено на рис. 1.

Правильный ответ указан под номером 1.

Решите систему неравенств

Преобразуем систему неравенств:

Аналоги к заданию № 338522: 341418 Все

Укажите решение системы неравенств:

Данное решение соответствует варианту 2).

Аналоги к заданию № 348461: 348486 Все

Решение какого из данных неравенств изображено на рисунке?

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Решим каждое из неравенств.

1) &nbsp — решений нет.

2) &nbsp

3) &nbsp верно для всех

4) &nbsp

На рисунке изображено решение четвёртого неравенства.

Источник

Метод интервалов, решение неравенств

О чем эта статья:

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
3. D

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.

Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.

Когда квадратный трехчлен корней не имеет (D

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.

Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

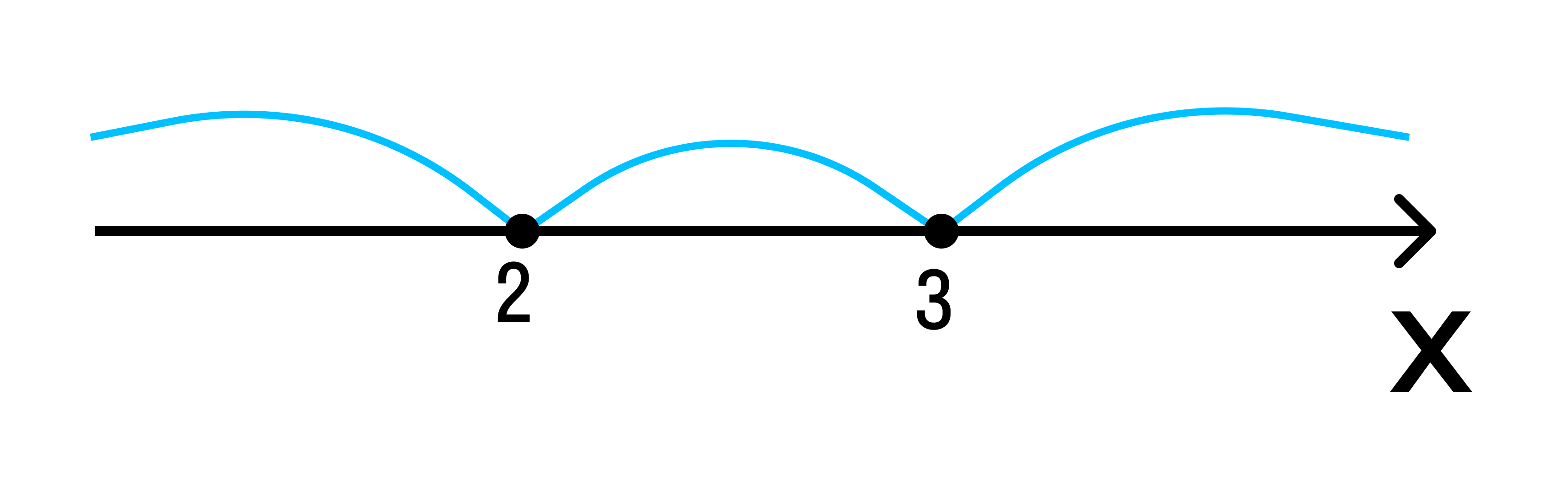
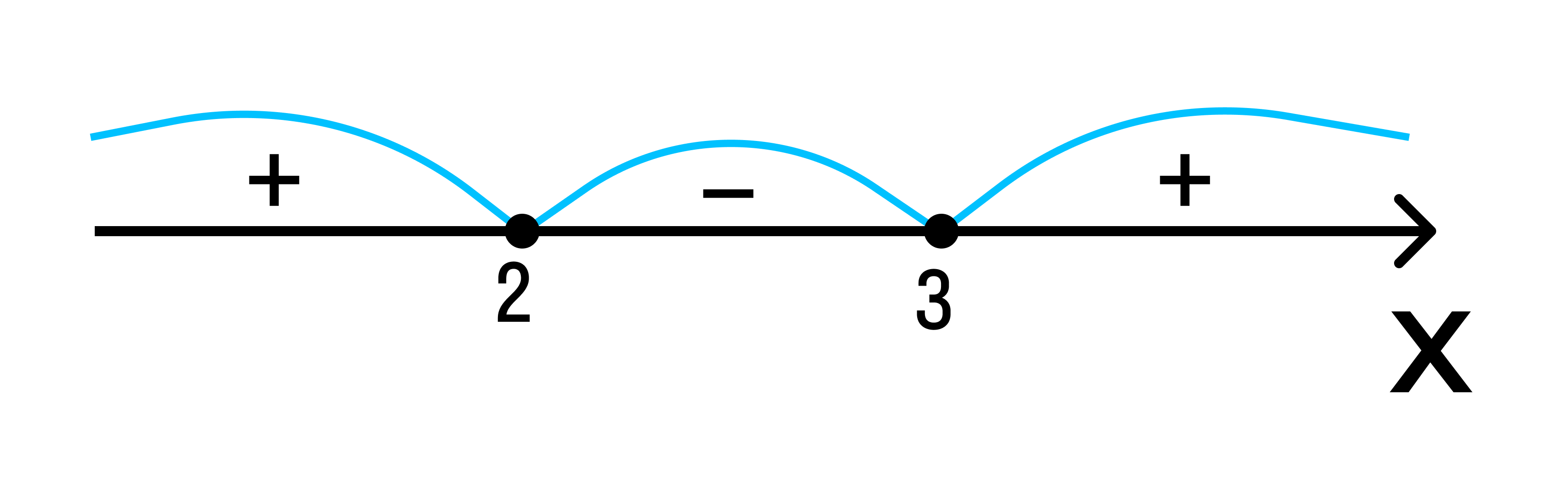
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• (25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Решение линейных неравенств

О чем эта статья:

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.

Типы неравенств

1. Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
2. a > b и b > и

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

1. Если а > b , то b а.
2. Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

1. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

1. Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

• 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

1. Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

• Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

1. Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

• Разделим обе части на минус два 2x > 9 ⇒ 2x : –2 > 9 : -2 ⇒ x
  
  

  Решение линейных неравенств

  Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

  Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак c , где x — переменная, a, c — некоторые числа.

  Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x 0 — в первом и ax > c — во втором;

• допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

• Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
• Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов это:

• введение функции y = ax + b;
• поиск нулей для разбиения области определения на промежутки;
• отметить полученные корни на координатной прямой;
• определение знаков и отмечание их на интервалах.

Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

• найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

• начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
• определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

Как решаем:

1. В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

1. Определим знаки на промежутках.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

1. Выполним решение со знаком >. Штриховку сделаем над положительным промежутком.

По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

• во время решения ax + b 0 произвести определение промежутка, где график изображается выше Ох;
• во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

• Так как коэффициент при x отрицательный, данная прямая является убывающей.
• Координаты точки пересечения с Ох равны −√3 : 5.
• Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
• Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x

Источник

Adblock
detector