Содержание:
Неравенство треугольника:
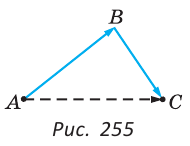
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС <АВ + ВС. Докажем это.
Теорема (о неравенстве треугольника).
Любая сторона треугольника меньше суммы двух других его сторон.
Дано: 
Доказать: АС <АВ+ВС, АВ<АС+ВС, ВС < АВ+АС.
Доказательство:
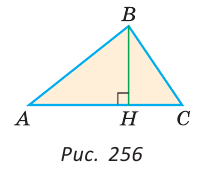
Пусть АС — наибольшая сторона  АВС. Проведем высоту ВН. Из прямоугольного
АВС. Проведем высоту ВН. Из прямоугольного  АНВ следует АН<АВ (катет меньше гипотенузы). Аналогично из
АНВ следует АН<АВ (катет меньше гипотенузы). Аналогично из  СНВ НС<ВС. Сложив неравенства, получим АН+НС<АВ+ВС. Откуда АС<АВ+ВС. Два других неравенства АВ<АС+ВС и ВС
СНВ НС<ВС. Сложив неравенства, получим АН+НС<АВ+ВС. Откуда АС<АВ+ВС. Два других неравенства АВ<АС+ВС и ВС
Для сторон 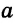 ,
, 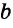 и
и 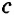 треугольника можно записать неравенства:
треугольника можно записать неравенства: 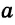 <
<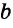 +
+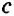 ,
, 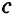 <
<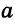 +
+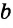 ,
,
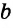 <
<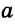 +
+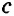 . Каждое из трех указанных неравенств называется неравенством треугольника.
. Каждое из трех указанных неравенств называется неравенством треугольника.
Следствие 1.
Если для точек А, В и С верно, что АВ=АС+ВС, то эти точки лежат на одной прямой. При этом точка С лежит между точками А и В.
Следствие 2.
Длина отрезка, соединяющего концы незамкнутой ломаной, меньше длины ломаной.
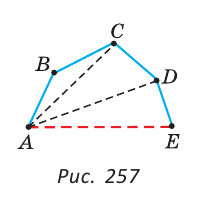
На рисунке 257 изображена незамкнутая ломаная ABCDE.
Докажем, что АЕ<АВ+ВС+CD+DE. Соединим точку А с точками С и D отрезками. По неравенству треугольника АС<АВ+ВС и AD<АС+CD. Значит, AD<АВ+ВС+CD. Так как по неравенству треугольника АЕ
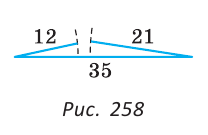
Чтобы доказать, что данные три числа не могут быть длинами сторон треугольника, достаточно убедиться, что большее из этих чисел не меньше суммы двух других чисел. Например, треугольника со сторонами 21, 12, 35 не существует, так как не выполняется неравенство треугольника: 35>12+21 (рис. 258).
Замечание. Из неравенств треугольника 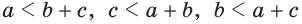 следует, что
следует, что 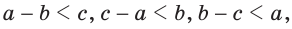 то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 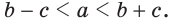
Пример:
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
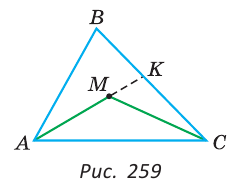
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС < АВ + ВС. Продлим сторону AM до пересечения со стороной ВС в точке К. Из  МКС по неравенству треугольника МС<МК+КС. Тогда AM + МС<АК + КС (1). Из
МКС по неравенству треугольника МС<МК+КС. Тогда AM + МС<АК + КС (1). Из  АВК по неравенству треугольника АК < АВ + ВК, значит, АК + КС<АВ + ВС (2). Из неравенств (1) и (2) следует, что AM + МС < АВ + ВС. Утверждение доказано.
АВК по неравенству треугольника АК < АВ + ВК, значит, АК + КС<АВ + ВС (2). Из неравенств (1) и (2) следует, что AM + МС < АВ + ВС. Утверждение доказано.
Пример:
Доказать, что медиана треугольника меньше полусуммы двух соседних сторон.
Доказательство:
Докажем, что для медианы ВМ треугольника ABC справедливо неравенство: ВМ < 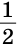 (АВ + ВС) (рис.260).
(АВ + ВС) (рис.260).
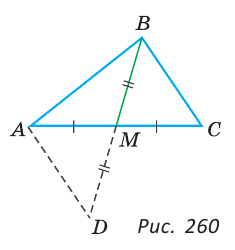
Продлим медиану ВМ на ее длину, MD = ВМ, BD = 2ВМ. Треугольники AMD и СМВ равны по первому признаку равенства треугольников (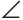 AMD =
AMD =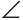 CMB как вертикальные), откуда AD = BC. В
CMB как вертикальные), откуда AD = BC. В  ABD по неравенству треугольника BD (АВ + ВС). Утверждение доказано.
ABD по неравенству треугольника BD (АВ + ВС). Утверждение доказано.
Теоремы о соотношениях между сторонами и углами треугольника.
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство.
1) Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что  C >
C >  B (рис. 108, а).
B (рис. 108, а).
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
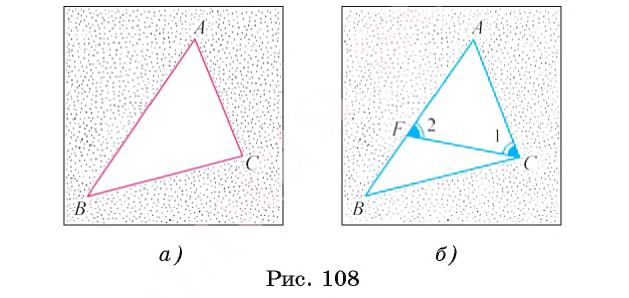
3) Так как АF < АВ, то точка F лежит между точками А и В. Отсюда следует, что  l является частью угла ВСА, а, значит,
l является частью угла ВСА, а, значит,  ВСА >
ВСА >  1.
1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно,  2 >
2 >  B.
B.
5) Так как треугольник FАС является равнобедренным, то  1 =
1 =  2.
2.
Таким образом,  BСА >
BСА >  1,
1,  1 =
1 =  2 и
2 и  2 >
2 >  B.
B.
Отсюда получаем, что  ВСА >
ВСА >  B.
B.
Теорема доказана.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Доказательство.
1) Пусть в треугольнике АBС  С >
С >  B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ < АС.
3) Если АВ = АС, то данный треугольник АBС является равнобедренным, а, значит,  B =
B =  C. Если АВ < АС, то по теореме 1
C. Если АВ < АС, то по теореме 1  B >
B >  C.
C.
В каждом из этих случаев получаем противоречие с условием:  C >
C >  B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Теорема доказана.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Доказательство.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Теорема доказана.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
Доказательство.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ < АС + СВ (рис. 109, а).
2) Отложим на луче АС отрезок CF, равный стороне ВС (рис. 109, б).
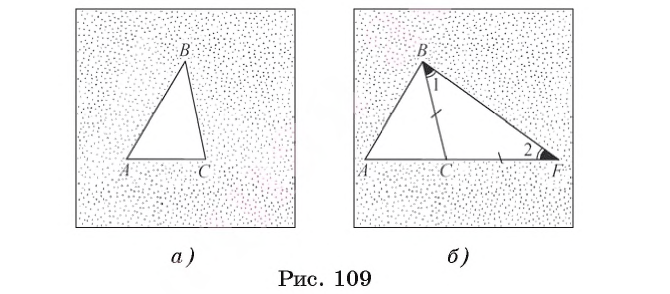
3) В равнобедренном треугольнике ВСF угол 1 равен углу 2, а в треугольнике АВF  АВF >
АВF >  l, следовательно, верно неравенство
l, следовательно, верно неравенство  АВF >
АВF >  2.
2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ < АF. Но так как АF = АС + СF, то АВ < АС + СВ.
Теорема доказана.
Следствие 1. Для любых трех точек А, В, С, не лежащих на одной прямой, справедливы следующие три неравенства, которые называются неравенствами треугольника:
АВ < АС + СB; АС < АВ + ВС; АВ < ВА+АС.
Следствие 2. Длина каждой стороны треугольника больше разности длин двух других его сторон.
Признаки равенства прямоугольных треугольников
На основании первого и второго признаков равенства треугольников можно доказать следующие признаки равенства прямоугольных треугольников.
Теорема 1 (о равенстве прямоугольных треугольников по двум катетам). Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
Так как в прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны, то по первому признаку равенства треугольников следует утверждение данной теоремы.
Теорема доказана.
Например, пусть ABCD — квадрат, а точки О и F — середины сторон АВ и AD соответственно (рис. 112, а). Тогда прямоугольные треугольники OAD и FAB равны. Действительно, поскольку каждый угол квадрата прямой, а его стороны равны, то АD =АВ и АО = АF, т. е. эти треугольники равны по двум катетам.
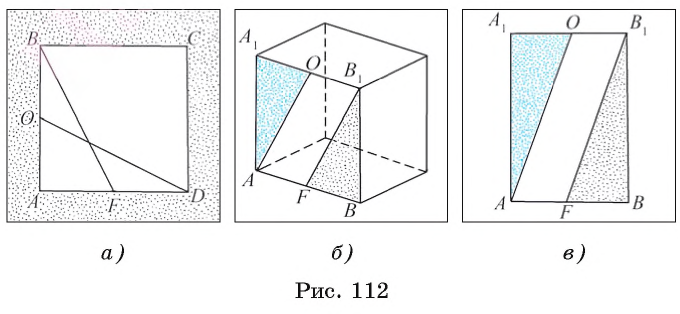
Пусть точки О и F — середины ребер А1В1 и АВ соответственно прямоугольного параллелепипеда (рис. 112, б). Тогда равны прямоугольные треугольники АА1O и В1ВF, содержащиеся в грани АA1B1B прямоугольного параллелепипеда. Действительно, так как каждый угол прямоугольника АA1B1B прямой (рис. 112, в), а противоположные стороны равны, то верны равенства  АA1О =
АA1О = FBВ1= 90°, АА1=ВВ1 и А1O = ВF, т. е. треугольники равны по двум катетам.
FBВ1= 90°, АА1=ВВ1 и А1O = ВF, т. е. треугольники равны по двум катетам.
Теорема 2 (о равенстве прямоугольных треугольников по катету и прилежащему острому углу). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.
Доказательство.
Учитывая условие теоремы и тот факт, что прямые углы равны, получаем, что катет и два прилежащих к нему угла одного прямоугольного треугольника соответственно равны катету и двум прилежащим к нему углам второго прямоугольного треугольника. Следовательно, по второму признаку равенства треугольников эти треугольники равны.
Теорема доказана.
Докажем еще два признака равенства прямоугольных треугольников.
Теорема 3 (о равенстве прямоугольных треугольников по гипотенузе и острому углу). Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
1) Пусть в прямоугольных треугольниках АBС и А1В1С1 равны гипотенузы АВ и А1В1, а также  А=
А= A1. Докажем, что треугольники ABC и А1В1С1 равны (рис. 113, а).
A1. Докажем, что треугольники ABC и А1В1С1 равны (рис. 113, а).
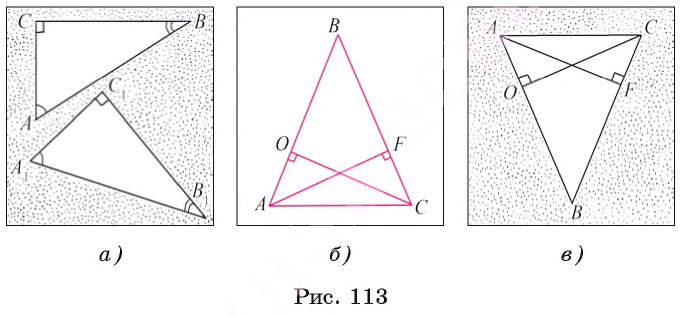
2) Так как сумма градусных мер углов любого треугольника равна 180°, то в треугольнике ABC  B = 90° –
B = 90° –  A и в треугольнике А1В1С1
A и в треугольнике А1В1С1  B1 = 90° –
B1 = 90° –  A1. Так как
A1. Так как  A =
A =  A1, то
A1, то  B =
B =  B1.
B1.
3) Таким образом, гипотенуза AB и два прилежащих к ней угла треугольника ABC соответственно равны гипотенузе А1В1 и двум прилежащим к ней углам треугольника А1В1С1. Следовательно, на основании второго признака равенства треугольников получаем, что  АВС =
АВС =  А1В1С1.
А1В1С1.
Теорема доказана.
Например, пусть отрезки СО и AF — высоты равнобедренного треугольника ABC с основанием АС. Тогда  АОС =
АОС =  CFA по гипотенузе и острому углу.
CFA по гипотенузе и острому углу.
Действительно, АС — общая гипотенуза этих треугольников, а  OAC =
OAC =  FCA, поскольку углы при основании равнобедренного треугольника ABC равны (рис. 113, б, в).
FCA, поскольку углы при основании равнобедренного треугольника ABC равны (рис. 113, б, в).
Теорема 4 (о равенстве прямоугольных треугольников по гипотенузе и катету). Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
1) Пусть в прямоугольных треугольниках АСВ и А1С1 В1  C=
C= С1, AB=А1В1 и AC=А1C1 (рис. 114, a).
С1, AB=А1В1 и AC=А1C1 (рис. 114, a).
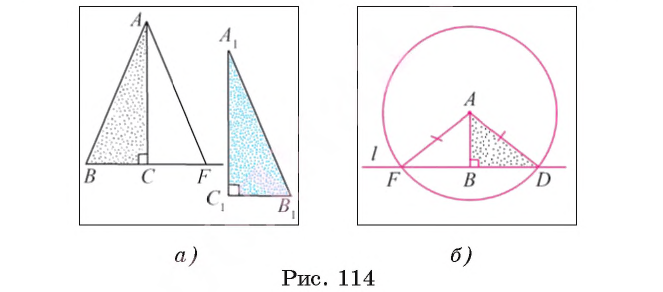
2) На луче, противоположном лучу СB, отложим отрезок СF, равный отрезку С1В1. Тогда треугольники А1В1С1 и АСF равны по двум катетам.
3) Следовательно, АF =А1В1=АВ, т. е. треугольник АВF является равнобедренным и  B =
B =  F. Таким образом, прямоугольные треугольники АСВ и АСF равны по гипотенузе и острому углу. Кроме того, АCF = А1С1В1, значит, треугольник АСВ равен треугольнику А1С1В1.
F. Таким образом, прямоугольные треугольники АСВ и АСF равны по гипотенузе и острому углу. Кроме того, АCF = А1С1В1, значит, треугольник АСВ равен треугольнику А1С1В1.
Теорема доказана.
Например, пусть прямая l пересекает окружность, центром которой является точка А, в точках D и F (рис. 114, б). Отрезок АВ — перпендикуляр, проведенный из точки А к прямой l. Тогда треугольники ABF и ABD равны по гипотенузе и катету. Действительно, AF = AD как радиусы окружности, отрезок АВ — общий катет этих треугольников.
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
- Серединный перпендикуляр к отрезку
- Второй и третий признаки равенства треугольников
- Параллельные прямые
- Соотношения между сторонами и углами треугольника
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 января 2023 года; проверки требуют 4 правки.
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния.
Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон (или равносильная формулировка — длина наибольшей стороны меньше суммы длин двух других сторон).
Евклидова геометрия[править | править код]

Длина любой стороны треугольника не превосходит сумму длин двух других.
Неравенство
выполняется в любом треугольнике 
Причём равенство 



Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из неё выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.
Нормированное пространство[править | править код]
Пусть 



Гильбертово пространство[править | править код]
В гильбертовом пространстве, неравенство треугольника является следствием неравенства Коши — Буняковского.
Метрическое пространство[править | править код]
Пусть 



Вариации и обобщения[править | править код]
Сильное неравенство треугольника
Обратное неравенство треугольника[править | править код]
Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:
Неравенство треугольника для трёхгранного угла[править | править код]
Каждый плоский угол выпуклого трёхгранного угла меньше суммы двух других его плоских углов.
Произвольное число точек[править | править код]
Обозначим 




См. также[править | править код]
- Неравенство четырёхугольника
- Теорема о внешнем угле треугольника
Примечания[править | править код]
- ↑ Шилов Г. Е. Математический анализ. Специальный курс. — М.: Физматлит, 1961. — C. 28
Неравенство треугольника – определение и вычисление с примерами решения
Содержание:
Неравенство треугольника:
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

Замечание. Из неравенств треугольника 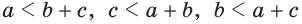 следует, что
следует, что 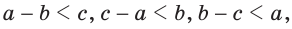 то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 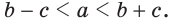
Пример:
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС  B (рис. 108, а).
B (рис. 108, а).
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF  1.
1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно,  2 >
2 >  B.
B.
5) Так как треугольник FАС является равнобедренным, то  1 =
1 =  2.
2.
Таким образом,  BСА >
BСА >  1,
1,  1 =
1 =  2 и
2 и  2 >
2 >  B.
B.
Отсюда получаем, что  ВСА >
ВСА >  B.
B.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
1) Пусть в треугольнике АBС  С >
С >  B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ  C.
C.
В каждом из этих случаев получаем противоречие с условием:  C >
C >  B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ  l, следовательно, верно неравенство
l, следовательно, верно неравенство  АВF >
АВF >  2.
2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Теорема о неравенстве треугольника
Понятие термина неравенство треугольника и его сторон
Определение: неравенство треугольника в геометрии, математическом анализе и смежных дисциплинах — это свойство, при котором длина любой стороны треугольника всегда меньше суммы длин двух других его сторон.
Теорема о неравенстве треугольников вытекает из теоремы о соотношении сторон и углов треугольника: против большей стороны в треугольнике лежит больший угол и, наоборот, против большего угла лежит большая сторона.
А В > А С > В С , ∠ С > ∠ В > ∠ А .
Теорема о неравенстве треугольника
Основная формулировка: каждая сторона треугольника меньше суммы двух других сторон.
Доказать: А В А С + С В .
Проведем C D = C B , A C + C D = A D . ∠ 1 = ∠ 2 .
В треугольнике АВD требуется доказать, что АВ
Пользуясь теоремой о соотношении углов и сторон: А В A D = A C + C B .
Что и требовалось доказать.
Формула и следствие
Для любых трех точек А, В, С, не лежащих на одной прямой справедливы неравенства:
Длина каждой стороны треугольника больше разности длин двух других его сторон.
По теореме о неравенстве треугольника:
Примеры решения задач
Существует ли треугольник со сторонами: 1 м , 2 м , 3 м .
Решение: по теореме о неравенстве треугольника 3 = 2 + 1 ⇒ 3 = 3
Ответ: такого треугольника не существует.
Существует ли треугольник со сторонами: 3 м , 4 м , 5 м .
Ответ: такой треугольник существует.
Краткие упражнения для самостоятельной работы
Одна сторона треугольника равна 2, другая 5. Какой может быть третья сторона, если известно, что ее длина тоже целое число?
Периметр равнобедренного треугольника равен 13, при этом две его стороны отличаются по длине на 4. Чему могут быть равны эти стороны?
Одна сторона треугольника равна 12, другая 5. Чему может быть равна самая короткая сторона этого треугольника? Самая длинная? Средняя по длине?
Неравенство треугольника
теория по математике 📈 планиметрия
Каждая сторона любого треугольника меньше суммы двух других сторон.
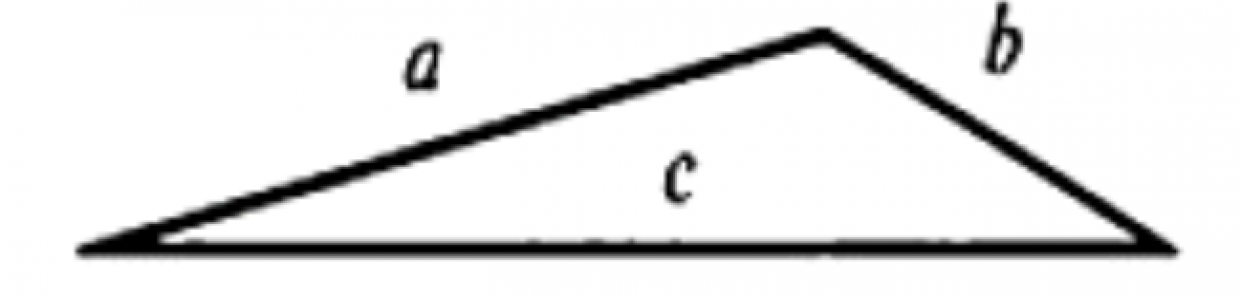
На данном рисунке показан произвольный треугольник, стороны которого обозначены для удобства буквами а, b, c. Так, в соответствии с неравенством треугольника:
Можно ли построить треугольник со сторонами 12, 18 и 23 см?
Для ответа на вопрос данной задачи нужно проверить каждую сторону на верность неравенства: 12
Существует ли треугольник со сторонами 19, 21 и 11 см?
Для ответа на вопрос данной задачи нужно также проверить каждую сторону на верность неравенства: 19 Даниил Романович | Просмотров: 862 | Оценить:
[spoiler title=”источники:”]
http://wika.tutoronline.ru/geometriya/class/7/teorema-o-neravenstve-treugolnika
[/spoiler]
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Неравенство треугольника
Теорема
Каждая сторона треугольника меньше суммы двух других сторон.
Доказательство:
Дано:  АВС.
АВС.
Доказать: АВ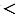 ВС + АС.
ВС + АС.
Доказательство:
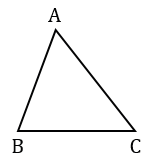
Сделаем дополнительное построение. Отложим на продолжении стороны ВС отрезок СD, равный стороне АС.
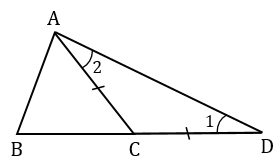
По построению СD = АС, следовательно,  АСD – равнобедренный с основанием АD, тогда
АСD – равнобедренный с основанием АD, тогда 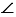 1 =
1 = 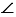 2 (углы при основании), при этом в
2 (углы при основании), при этом в  АВD
АВD 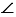 ВАD
ВАD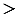
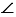 2, следовательно,
2, следовательно, 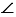 ВАD
ВАD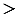
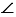 1.
1.
В треугольнике против большего угла лежит большая сторона, значит, АВ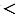 ВD. При этом ВD = ВС + СD, а учитывая то, что по построению СD = АС получим, ВD = ВС + АС, поэтому АВ
ВD. При этом ВD = ВС + СD, а учитывая то, что по построению СD = АС получим, ВD = ВС + АС, поэтому АВ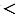 ВС + АС. Что и требовалось доказать.
ВС + АС. Что и требовалось доказать.
Следствие
Каждое из неравенств АВ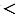 АС+СВ, АС
АС+СВ, АС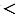 АВ+ВС, ВС
АВ+ВС, ВС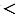 ВА+АС, называется неравенством треугольника.
ВА+АС, называется неравенством треугольника.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 250,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 292,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 304*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 306,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 773,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 818,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 858,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1176,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1232,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Неравенство треугольника


4.3
Средняя оценка: 4.3
Всего получено оценок: 507.
4.3
Средняя оценка: 4.3
Всего получено оценок: 507.
Любая фигура имеет некие рамки, пропорции длин сторон. В реальной жизни они помогают определить, можно ли изготовить треугольное основание определенных пропорций, насколько возможно создать линзу той или иной формы или может ли удержаться табуретка на треугольном, квадратном или любом другом основании. В теоретической геометрии пропорции, как правило, применяют для решения задач на доказательство или для определения правильности условия задачи.
Теорема о неравенстве треугольника
Именно с этой теоремы должно начинаться любое решение задачи. Но, как правило, это действие опускают. Считается, что составитель задач не может предложить условие с несуществующим треугольником.
Теорема о неравенстве сторон треугольника гласит, что каждая сторона треугольника всегда меньше или равна сумме двух других его сторон.
По факту, любая сторона треугольника всегда меньше суммы двух других его сторон. Равенство возможно, только если все три вершины треугольника лежат на одной линии. Можно ли считать такую фигуру треугольником – вопрос философов, а не математиков. Поэтому в формулировке ставится знак больше или равно.
Доказать это определение можно двумя способами: через аксиому Евклида или через высоту треугольника. Последний способ более логичен, тогда как второй – короче. Какой выбрать – решает доказывающий.
Доказательство через аксиому
Существует аксиома, которая говорит, что для трех точек А, В, С не лежащих на одной прямой справедливо утверждение: АВ< ВС+АС.
Эти точки можно принять за вершины треугольника, тогда расстояния между точками это стороны треугольника.
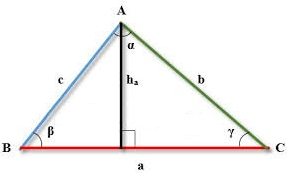
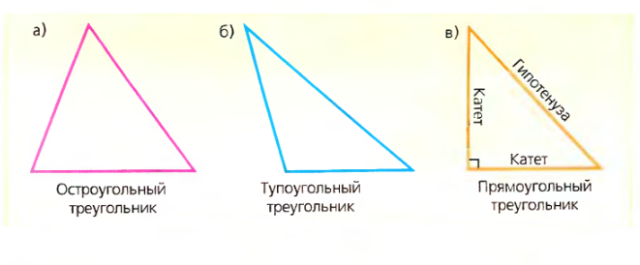
В произвольном треугольнике АВС проведем высоту АН. Высота разобьет произвольный треугольник на два прямоугольных. Тогда для каждого из прямоугольных треугольников в виде неравенств запишем, что катет всегда меньше гипотенузы.
Гипотенуза всегда больше катета потому, что в треугольнике действует отношение сторон и углов. Поэтому напротив наибольшего угла всегда находится наибольшая сторона. А в треугольнике наибольшим углом всегда является угол в 90 градусов.
ВН<АВ и НС<АС
Сложим два неравенства. Для этого нужно сложить правые части неравенств и левые с сохранением знака.
Например:
6<8
1<5
6+1<8+5
7<13, как видно неравенство все еще верно. Теперь проделаем ту же операцию с соотношением сторон в треугольнике:
ВН+НС<АВ+АС
ВН+НС=ВС
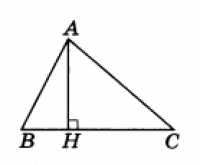
Значит, ВС<АВ+АС, то есть сторона меньше суммы двух других сторон, что и требовалось доказать. Высоту можно провести к любой стороне и повторить аналогичное доказательство. Как видно, все просто и ясно. Самое трудное: это разобраться в сложении неравенств.

Что мы узнали?
Мы узнали о теореме неравенства треугольников. Доказали ее различными способами, а также поговорили о том, для чего в мире нужны понятия пропорций в фигурах.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Ариадна Калашникова
5/5
-

Антон Кривых
4/5
-

Иван Тумба
5/5
-

Dorian Gray
5/5
-

Иван Красавский
5/5
-

Михаил Колесников
4/5
-

Антон Сковскикх
5/5
-

Дмитрий Познахарёв
5/5
-

Анастасия Уманец
4/5
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 507.
А какая ваша оценка?





