Проценты
- Нахождение процентов от числа
- Нахождение числа по его процентам
- Процентное отношение двух чисел
- Перевод процентов в десятичную дробь
Процент — это одна сотая часть числа. Отсюда следует, что два процента — это две сотых, двадцать процентов — двадцать сотых и так далее.
Слово процент
обозначается знаком %
. Так, 43% какого либо числа означает 43 процента, то есть 
%
не пишется, он может быть записан в условии задачи и в окончательном результате.
Величина, от которой вычисляются проценты (например, цена, длина, количество конфет и т. д.), составляет 100 своих сотых долей, то есть 100%.
Чтобы найти один процент от числа, надо разделить это число на 100.
Пример 1. Найти один процент от числа 300.
Решение:
300 : 100 = 3.
Ответ: Один процент от 300 равен 3.
Пример 2. Найти один процент от числа 27,5.
Решение:
27,5 : 100 = 0,275.
Ответ: Один процент от 27,5 равен 0,275.
Нахождение процентов от числа
Чтобы найти некоторое число процентов от данного числа, нужно данное число разделить на 100 и умножить на число процентов.
Задача 1. В том году в магазине к новому году купили 200 ёлок. В этом году количество купленных ёлок увеличилось на 120%. Сколько ёлок купили в этом году?
Решение: Сначала надо найти 120% от 200, для этого 200 надо разделить на 100, так мы найдём 1%, а затем полученный результат умножить на 120:
(200 : 100) · 120 = 240.
Число 240 — это 120% от 200. Значит, в этом году количество проданных ёлок увеличилось на 240 штук. То есть, количество ёлок, проданных в этом году равно:
200 + 240 = 440 (ёлок).
Ответ: В этом году купили 440 ёлок.
Задача 2. В коробке 28 конфет, 25% конфет с клубничной начинкой. Сколько конфет с клубничной начинкой в коробке?
Решение:
Ответ: В коробке 7 конфет с клубничной начинкой.
Нахождение числа по его процентам
Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на 100.
Задача. Цена метра сукна снизилась на 24 руб., что составило 15% цены. Сколько стоил метр сукна до снижения?
Решение:
Ответ: Метр сукна стоил 160 рублей.
Процентное отношение двух чисел
Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Задача. Завод по годовому плану должен выпустить продукции на сумму 1 250 000 руб. За 1-ый квартал он выпустил её на сумму 450 000 руб. На сколько процентов выполнен заводом годовой план за 1-ый квартал?
Решение:
Ответ: За 1-ый квартал план выполнен на 36%.
Перевод процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на 100.
Пример 1. Представить 25% в виде десятичной дроби.
Решение:
25 : 100 = 0,25.
Ответ: 25% — это 0,25.
Пример 2. Выразить 100% десятичной дробью.
Решение:
100 : 100 = 1.
Ответ: 100% — это 1.
Пример 3. Выразить 230% десятичной дробью.
Решение:
230 : 100 = 2,3.
Ответ: 230% — это 2,3.
Из данных примеров следует, что для перевода процентов в десятичные дроби, надо в числе, стоящем перед знаком %
, перенести запятую на два знака влево.
Муниципальное казённое
общеобразовательное
учреждение «Дивеевская школа-интернат»
Нахождение нескольких процентов от числа.
9 класс
Учитель
математики:
Комкова Г.А.
2016-2017 уч.год
Тема : Нахождение
нескольких процентов от числа.
Цель урока: обобщить и систематизировать знания по теме
«Проценты», отработать навык решения задач на проценты.
Задачи :
Образовательные:
– формировать умение
вычислять несколько процентов от числа;
– применять данные
умения в повседневной жизни;
– повышать
экономическую грамотность школьников.
Коррекционно -развивающие:
– развивать
зрительную и слуховую память, произвольное внимание, наглядно-образное мышление
обучающихся;
– развивать
аналитико-синтетическую деятельность обучающихся в процессе работы над задачей;
– способствовать овладению
приёмами самоконтроля;
– формировать у обучающихся
познавательный интерес к математике через использование ИКТ;
Воспитательные:
– расширять знания
детей об окружающем мире;
– воспитывать чувство
радости, удовлетворённости результатами работы;
– способствовать
сохранению здоровья обучающихся.
Ход урока.
I.Организация начала урока. (слайд 2)
Учитель: Здравствуйте, ребята! Сегодняшний
урок я хочу начать словами французского философа Ж.Ж. Руссо (1712–1778
гг.): «Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы
умные, как много хорошего умеете, если будете постоянно работать над собой,
ставить новые цели и стремиться к их достижению…»
Я желаю вам уже сегодня на уроке убедиться в этих словах .
– Вы готовы к работе?
– Какое сегодня число, месяц и
день недели?
-Сегодня … декабря, день недели среда.
– Какой сейчас урок?
– Сейчас урок математики.
– Какой урок по счету?
– Урок по счету …….
II. Проверка домашнего задания.
–Открываем домашние тетради.
-Что было задано на дом?
-На дом был задан №.
-Сейчас мы проверим, как вы справились с
этой работой.
-Молодцы! Все справились с этим заданием.
III. Постановка цели и задач урока.
Тема сегодняшнего урока «Нахождение нескольких
процентов от числа». Мы закрепим умения находить несколько
процентов от числа, пользоваться этим при покупке различных товаров и будем
решать задачи на проценты.
Откройте свои тетради, запишите число,
классная работа, тему урока.
Слово
“процент” происходит от латинских слов pro centum, что
буквально означает “со ста“, «на сто». Широко начали использовать проценты
в Древнем Риме, но идея процентов возникла много раньше – вавилонские
ростовщики уже умели находить проценты в v веке.
IV.Актуализация опорных знаний.
1.Что такое процент? (слайд 3)
– Процентом называют одну сотую часть числа.
Так как 1% равен сотой части величины, то вся величина равна 100%.
2. Где мы встречаемся с процентами в повседневной
жизни? (слайд 4)
– в
магазине (особенно во время предпраздничных скидок),
– на
работе (повышение и понижение зарплаты),
– в банке
(оформление кредита),
– в
интернете.
3. Выразите заштрихованную часть
круга в процентах (слайд 5,6)
4. Для каждой фразы из левого столбца
подберите соответствующую фразу в правом: (слайд 7)
Все учащиеся школы- 100%.
Половина учащихся школы- 50%.
Четверть-25%.
Десятая часть-10%.
5. Выберите для каждого процента в левом
столбце соответствующую ему дробь (слайд 8).
½-50%
¾-75%
9/10-90%
¼-25%
7. Определите сотую часть величины (слайд
9)
8. Найдите 1% от каждого числа (слайд
10)
200р., 9000м; 5370кг; 867,2; 84,7
V. Работа над новым материалом.
1.Давайте
вспомним, как найти несколько процентов от числа.
Чтобы найти несколько процентов от числа, надо это
число сначала разделить на 100, а потом умножить на количество процентов. (слайд 11)
2.Решение
примеров.
№452(1,2ст.) стр.86
VI. Физкультминутка.
А теперь ребята встали!
Быстро
руки вверх подняли, в стороны, вперёд, назад,
Повернулись
вправо, влево,
Тихо сели
– вновь за дело.
3.Решение задачи. (слайд 12)
Месячный заработок семьи из 4 человек составляет 35000 рублей.
Из них платят:
за электроэнергию –
2% – ? руб.
за воду – 3% – ? руб.
за газ, отопление – 8% – ? руб.
Сколько рублей у семьи на другие расходы?
После решения обсуждается вопрос:
Как можно сократить расходы? (экономить электроэнергию, выключать
краны)
4.
Поговорим об энергосбережении. (слайд 13, 14)
Что вы понимаете под энергосбережением?
Энергосберегающие лампочки потребляют в 5 раз меньше
энергии, чем лампы накаливания. (слайд 15)
5.
Решение задачи (слайд 16)
Расход
семьи Ивановых за электричество составлял 542 рубля в месяц. После замены ламп
накаливания на энергосберегающие лампы они сэкономили 40% денег потраченных
ранее. Сколько рублей в месяц стали платить Ивановы за использованное
электричество?
542:100х40=216,8
542-216,8=325,2
VII. Самостоятельная работа.
·
Покупатель
приобрёл в магазине в кредит на 1 год телевизор стоимостью15000 руб. Процентная
ставка по кредиту -16%. Какой будет полная стоимость телевизора с учётом уплаченных
процентов?
·
Вкладчик
положил в банк на 1 год 5100 рублей. Процентная ставка по вкладу 7% годовых.
Какую сумму получит вкладчик в банке в конце года хранения?
VIII. «Распродажа в магазине». (слайд 17)
Ребята,
скоро праздник «Новый год». И в преддверии этого праздника магазины устраивают
распродажи. Сейчас мы с вами поиграем в игру “Распродажа в магазине”.
Около
доски стоит стол с различными товарами. На товарах прикреплены ценники, в
которых зачеркнута старая цена, нужно внести изменения в ценники.
Вывешивается
объявление:
“Праздничная
распродажа. Цены снижены”.
1. Первоначальная цена кроссовок
2100 рублей. Сколько будут стоить кроссовки, если на них скидка 20 % ?
2100:100х20=420
2100-420=1680
Сделайте новый ценник.
2. Сколько будут стоить сапоги
после снижения цены на 30 %, если их первоначальная стоимость составляла
3400 рублей ?
3400:100х30=1020
3400-1020=2380
Сделайте новый ценник.
3. Сколько будут стоить туфли,
если магазин снизил цену на 20 %? Первоначальная стоимость туфель 3200 рублей.
3200:100х20=640
3200-640=2560
Сделайте новый ценник.
4.
В январе
домашние тапочки стоили 400 рублей. Цена понизилась на 10 %. Сколько
рублей будут стоить тапочки?
400:100х10=40
400-40=360
Сделайте новый ценник.
IX.Домашнее задание (слайд
18)
№456(1ст.)
стр.87
X. Рефлексия. (слайд 19)
Подведение итогов
урока: Наш урок подходит к концу. Давайте подведем его итог и выясним,
какие новые знания вы получили и чему научились? А поможет нам в этом ряд
вопросов.
Учитель: А я довольна всеми вами. Вы хорошо
работали на уроке! Я рада вашему успеху.
Цель
разработки заключается в интеграции предмета математики и практической
деятельностью. Во время выполнения заданий учащиеся знакомятся с интересными фактами
из жизни. Эта разработка способствует расширению и углублению знаний о
процентах и их нахождении, в занимательной форме показывает взаимосвязь
математики с жизненными ситуациями, развивает стремление познать новое,
расширяет кругозор детей, воспитывает интерес к урокам математики.
Магазин «Сапожок».
- Первоначальная цена кроссовок
2100 рублей. Сколько будут стоить кроссовки, если в магазине на все
кроссовки скидка 20 % ? Сделайте новый ценник. - Сколько будут стоить сапоги
после снижения цены на 30 %, если их первоначальная
стоимость составляла 3400
рублей ? Сделайте новый ценник.
- Сколько будут стоить туфли,
если магазин снизил цену сначала на 20 %, а затем ещё на 20 % ?
Первоначальная стоимость туфель 3200 рублей. Сделайте новый
ценник.
- В январе домашние тапочки
стоили 400 рублей. В феврале цена понизилась на 20 %, а в марте
повысилась на 30 %. Сколько стоят тапочки в марте?
Сделайте новый ценник.
Магазин «Башмачок».
- Первоначальная цена кроссовок
2400 рублей. Сколько будут стоить кроссовки, если в магазине на все
кроссовки скидка 30 % ? Сделайте новый ценник.
- Сколько будут стоить сапоги
после снижения цены на 20 %, если их первоначальная стоимость
составляла 2900 рублей ? Сделайте новый ценник.
- Сколько будут стоить туфли,
если магазин снизил цену на 40 % ? Первоначальная стоимость туфель
3200 рублей. Сделайте новый ценник.
- В январе домашние тапочки
стоили 400 рублей. В феврале цена повысилась на 20 %, а в марте
понизилась на 30 %. Сколько стоят тапочки в марте?
Сделайте новый ценник.
Покупатели (1 группа).
- Первоначальная цена кроссовок
в магазине «Сапожок» 2100 рублей. Сколько будут стоить кроссовки, если в
магазине «Сапожок» на все кроссовки скидка 20 % ?
Первоначальная
цена кроссовок в магазине «Башмачок» 2400 рублей.
Сколько будут стоить кроссовки, если в магазине «Башмачок» на все
кроссовки скидка 30 %?
Какой магазин вы выберете для покупки кроссовок?
- Сколько будут стоить туфли,
если магазин «Сапожок» снизил цену сначала на 20 %, а затем
ещё на 20 % ? Первоначальная стоимость туфель 3200 рублей.
Сколько будут
стоить туфли, если магазин «Башмачок» снизил цену на 40 % ?
Первоначальная
стоимость туфель
3200 рублей.
Какой магазин вы
выберете для покупки туфель?
Покупатели (2 группа).
- Сколько будут стоить сапоги в
магазине «Сапожок» после снижения цены на 30 %, если их первоначальная
стоимость составляла 3400 руб?
Сколько будут
стоить сапоги в магазине «Башмачок» после снижения цены на 20 %, если их
первоначальная
стоимость составляла 2900 руб?
Какой магазин вы выберете для покупки сапог?
2. В
январе в магазине «Сапожок» домашние тапочки стоили 400 рублей.
В феврале цена понизилась на 20 %, а в марте повысилась на 30 %.
Сколько стоят тапочки в магазине «Сапожок» в марте?
В
январе в магазине «Башмачок» домашние тапочки стоили 400 рублей.
В
феврале цена повысилась на 20 %, а в марте понизилась на 30 %.
Сколько стоят тапочки в магазине «Башмачок» в марте?
Какой магазин вы выберете для покупки домашних тапочек?
5. Проводится
совместная проверка и анализ результатов.
6.Каждой группе
выдаётся своя табличка с названием ( кассир Сбербанка, бухгалтер ЕИРЦ,
квартиросъёмщик (группа №1), квартиросъёмщик (группа №2)) и соответствующие
карточки
с заданиями.
Каждый ученик решает задачи самостоятельно, но имеет право
проконсультироваться с
учениками
из своей группы..
Как найти несколько процентов от числа?
|
Как найти несколько процентов от числа? |
|
| Просмотров: 807 | Добавил: (08.11.2019) (Изменено: 08.11.2019) |
|
Всего ответов: 2 |
|
Обсуждение вопроса:Всего ответов: 2 Порядок вывода комментариев:
0 Люсси 1. Число разделить на 100. Почему на 100? Потому что процент — это одна сотая часть числа. И для того, чтобы найти несколько процентов, для начала нужно найти 1 %( процент). Число мы делим на 100 и таким образом мы находим 1%(процент) числа. 2. Получившийся результат умножить на количество процентов. Таким образом мы увидим какую часть от числа мы искали.
0 Тамми Чтобы найти проценты от числа, надо: 1) перевести % в десятичную дробь (для этого следует разделить количество процентов на 100); 2) умножить эту дробь на данное в задаче число. |
|
Время чтения: 15 минут
В задании 3 ты можешь встретить различные задачи на части. Давай разберемся, какие типы задач могут встречаться и как их решать!
В основном существует 2 типа задач: нахождение части от числа и нахождение числа по его части. Подробно разберем каждый из них.
Нахождение части от числа 🍕
Для нахождения части от числа необходимо целое умножить на дробь, соответствующую этой части.
Нахождение числа по его части🍎
Для нахождения числа по его части необходимо часть разделить на соответствующую дробь.
🚩Сохрани формулы, чтобы не потерять👇
Изменение числа 📊
Часто встречаются задачи, где исходное число уменьшают/увеличивают НА некоторое число, либо В несколько раз. Что нужно делать в этом случае?
Предлог НА означает операцию сложения или вычитания:
- Число 5 увеличили на 2: 5 + 2 = 7
- Число 9 уменьшили на 4: 9 – 4 = 5
Предлог В означает операцию умножения или деления:
- Число 4 увеличили В 3 раза: 4 * 3 = 12
- Число 15 уменьшили в 5 раз: 15 : 5 = 3
Решение задач с помощью уравнений👩🏫
Встречаются более сложные типы задач, для которых удобнее всего составить уравнение и решить его.
Алгоритм:
- За неизвестное (x), берут искомое число;
- Записывают уравнение по условию задачи;
- Находят значение х.
Задание 1 (см. картинку ниже): Если от задуманного числа отнять 220, то получится число, которое в пять раз меньше задуманного. Найдите задуманное число.
Решение:
- Обозначим задуманное число как x.
- “Если от задуманного числа отнять 220” – эту фразу можно записать в виде: x – 220.
- “Число, которое в пять раз меньше задуманного” – это значит, что задуманное число нужно разделить на 5: x/5.
- Получается следующее уравнение: x – 220 = x/5
Аналогичным образом решается Задание 2 (листай карусель ниже)
Разбор заданий из вариантов ВПР🥴
Давай посмотрим, каким типы задач могут встретиться тебе в Задании №3 и как их решать! Ниже представлено несколько примеров для ознакомления.
Больше различных заданий ты найдешь на сайте РЕШУ ВПР: https://math6-vpr.sdamgia.ru/?redir=1
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #6класс #алгебра #часть от числа #арифметика #средняяшкола
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Инструменты для вычислений и измерений
- Проценты
Процентом от некоторой величины называется одна сотая ее часть и обозначают один процент так: 1%.
Чтобы найти процент от некоторой величины, нужно разделить эту величину на 100.
Пример:
1% от 200 т равен 2 т, так как 200 : 100 = 2.
1% от 5 км равен 50 м, т.к. 1 км = 1 000 м, тогда 5 км = 5 000 м, а 5 000 м : 100 = 50 м.
Величина, от которой вычисляются проценты составляет 100 своих сотых долей, т.е. 100 %.
Например, если говорят, что учащийся выполнил 100% домашнего задания, значит, он выполнил все домашнее задание, которое ему было задано.
Пример:
15% = 15 : 100 = 0,15;
60% = 60 : 100 = 0,60 = 0,6;
700% = 700 : 100 = 7;
23,5% = 23,5 : 100 = 0,235.
Обратите внимание: если у числа на конце справа стоит меньше двух нулей, то деление выполняем по правилу деления десятичных дробей на 100, т.е. перемещая запятую влево на две цифры, учитывая то, что у натурального числа запятую мы подразумеваем на конце справа.
Любую десятичную дробь или любое натуральное можно записать в процентах.
Для этого нужно десятичную дробь или натуральное число умножить на 100 и к результату приписать знак %.
Пример:
3,5 = 3,5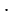
0,07 = 0,07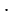
9 = 9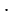
Обратите внимание: когда мы умножаем десятичную дробь на 100, то перемещаем запятую вправо на две цифры.
Чтобы найти несколько процентов от числа, нужно это число разделить на 100, а затем, полученный результат, умножить на число, стоящее перед знаком %.
Пример:
1) Найти 15% от числа 800.
800 : 100 = 8 – 1% от числа 800.
8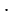
2) Найти 6% от числа 375.
375 : 100 = 3,75 – 1% от числа 375.
3,75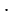
| × | 3 | 7 | 5 |
| 6 | |||
| 2 | 2 | 5 | 0 |
Чтобы найти число по его процентам, нужно разделить число, соответствующее известным процентам от числа, на число стоящее перед знаком % и полученный результат умножить на 100 или можно представить проценты в виде десятичной дроби и разделить значение процентов на эту дробь.
Пример:
Найдите число, если 20% этого числа равны 80?
1 способ:
1) 80 : 20 = 4 – 1% от числа.
2) 4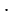
2 способ:
1) 20% = 0,2
2) 80 : 0,2 = 800 : 2 = 400.
Ответ: 400.
Советуем посмотреть:
Микрокалькулятор
Скорость
Единицы измерения длины.
Единицы измерения массы
Диаграммы
Графики
Инструменты для вычислений и измерений
Правило встречается в следующих упражнениях:
5 класс
Задание 1572,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1584,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1646,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 1101,
Мерзляк, Полонский, Якир, Учебник
Номер 1102,
Мерзляк, Полонский, Якир, Учебник
Номер 1105,
Мерзляк, Полонский, Якир, Учебник
Номер 1113,
Мерзляк, Полонский, Якир, Учебник
Номер 1115,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 501,
Мерзляк, Полонский, Якир, Учебник
Номер 650,
Мерзляк, Полонский, Якир, Учебник
Номер 1193,
Мерзляк, Полонский, Якир, Учебник
Номер 1291,
Мерзляк, Полонский, Якир, Учебник
Задание 106,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 993,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1230,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1231,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1258,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1548,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 99,
Мерзляк, Полонский, Якир, Учебник
Номер 387,
Мерзляк, Полонский, Якир, Учебник
Номер 471,
Мерзляк, Полонский, Якир, Учебник
Номер 903,
Мерзляк, Полонский, Якир, Учебник
Номер 979,
Мерзляк, Полонский, Якир, Учебник
Номер 980,
Мерзляк, Полонский, Якир, Учебник
Номер 1027,
Мерзляк, Полонский, Якир, Учебник
Номер 1041,
Мерзляк, Полонский, Якир, Учебник
Номер 1103,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 173,
Мерзляк, Полонский, Якир, Учебник
Номер 197,
Мерзляк, Полонский, Якир, Учебник
Номер 222,
Мерзляк, Полонский, Якир, Учебник
Номер 266,
Мерзляк, Полонский, Якир, Учебник
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Номер 346,
Мерзляк, Полонский, Якир, Учебник




