Несмещенная оценка выборочной дисперсии
Краткая теория
Пусть из генеральной совокупности в результате
независимых наблюдений над количественным
признаком
извлечена повторная выборка объема
:
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить
на дробь
.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через
:
Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:
Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Задача
Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма
частот:
Вычислим
среднюю:
Средняя квадратов:
Несмещенная
выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть
пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
Задача 55. Из генеральной совокупности извлечена выборка объема N, заданная вариантами ХI и соответствующими им частотами. Найти несмещенную оценку генеральной средней.
|
Варианта ХI |
2 |
5 |
7 |
10 |
|
Частота Ni |
16 |
12 |
8 |
14 |
Решение. Множество всех объектов, подлежащих изучению, называется Генеральной совокупностью. Множество случайно отобранных объектов называется выборочной совокупностью или Выборкой.
Для оценки неизвестных параметров теоретического распределения служат статистические оценки. Статистическая оценка, определяемая одним числом, называется Точечной оценкой.
Точечная статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется Несмещенной оценкой. Статистическая оценка, математическое ожидание которой не равно оцениваемому параметру является Смещенной.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
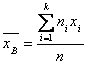 (1),
(1),
Где ХI – варианта выборки (элемент выборки); Ni – частота варианты ХI (число наблюдений варианты ХI); ![]() – объем выборки (число элементов совокупности).
– объем выборки (число элементов совокупности).
Объем данной выборки равен ![]() .
.
Далее по формуле (1) вычисляем несмещенную оценку генеральной средней:
![]()
Задача 56. По выборке объема N=41 найдена смещенная оценка генеральной дисперсии ![]() . Найти несмещенную оценку дисперсии генеральной совокупности.
. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
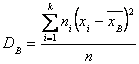
Несмещенной оценкой генеральной дисперсии является «исправленная дисперсия»
![]() или
или 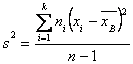
Таким образом, мы получаем искомую несмещенную оценку дисперсии генеральной совокупности:
![]()
Задача 57. Найти доверительный интервал для оценки с надежностью P=0,95 неизвестного математического ожидания A нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение S=5, выборочная средняя ![]() , а объем выборки N=25.
, а объем выборки N=25.
Решение. Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр.
Для оценки математического ожидания A нормально распределенного количественного признака Х по выборочной средней ![]() при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал
![]() ,
,
Где ![]() – точность оценки, T – значение аргумента функции Лапласа
– точность оценки, T – значение аргумента функции Лапласа ![]() (приложение, таблица 2).
(приложение, таблица 2).
В данной задаче T находим из условия ![]() . По таблице 2 определяем
. По таблице 2 определяем ![]() . Таким образом, T=1,96.
. Таким образом, T=1,96.
Далее получаем
![]()
Или ![]()
Задача 58. По данным N=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений ![]() и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью
и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью ![]() =0,99.
=0,99.
Решение. Оценкой математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал
![]() .
.
По таблице 3 приложения, по заданным N и ![]() находим
находим ![]() =3,36.
=3,36.
Таким образом
![]()
Окончательно получаем
![]()
Задача 59. Из генеральной совокупности извлечена выборка объема N. Оценить с надежностью ![]() =0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
=0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
|
Значение признака ХI |
-2 |
1 |
1 |
3 |
4 |
5 |
|
Частота Ni |
2 |
1 |
2 |
2 |
2 |
1 |
Решение. Объем данной выборки равен ![]()
![]()
По данным задачи находим выборочную среднюю:
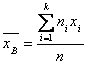
![]()
Далее находим исправленное среднее квадратическое отклонение S:
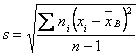
![]()
Для оценки математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал
![]() .
.
По таблице 3 приложения по заданным N и ![]() находим
находим ![]() =2,26.
=2,26.
Таким образом
![]()
Окончательно получаем
![]()
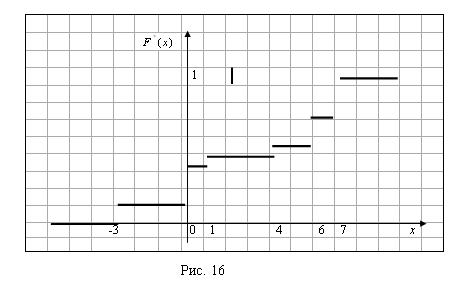
Задача 60. Построить полигон частот и эмпирическую функцию по данному распределению выборки:
|
Варианты ХI |
-3 |
0 |
1 |
4 |
6 |
7 |
|
Частоты Ni |
3 |
6 |
1 |
2 |
5 |
1 |
Решение. Полигоном частот называют ломаную, отрезки которой соединяют точки ![]() ;
; ![]() ;…;
;…;![]() , где ХI – варианты выборки, Ni – соответствующие им частоты.
, где ХI – варианты выборки, Ni – соответствующие им частоты.
Полигон частот для данного распределения изображен на рисунке 15.

Рис. 15
Эмпирической функцией распределения (функцией распределения выборки) называют функцию ![]() , определяющую для каждого значения X относительную частоту события
, определяющую для каждого значения X относительную частоту события ![]() :
:
![]() ,
,
Где ![]() – число вариант, меньших Х; N – объем выборки.
– число вариант, меньших Х; N – объем выборки.
Из определения следует, что ![]() .
.
Найдем эмпирическую функцию распределения.
Объем данной выборки равен ![]() =18.
=18.
Если ![]() , то
, то ![]() =0 (так как -3 – наименьшая варианта). Если
=0 (так как -3 – наименьшая варианта). Если ![]() , то значение
, то значение ![]() , а именно
, а именно ![]() наблюдалось 3 раза, следовательно,
наблюдалось 3 раза, следовательно, ![]() . При
. При ![]() значения
значения ![]() , а именно
, а именно ![]() и
и ![]() наблюдались 3+6=9 раз, следовательно,
наблюдались 3+6=9 раз, следовательно, ![]() .
.
Аналогично получаем, что при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() ; при
; при ![]() функция распределения
функция распределения ![]() . Далее, если
. Далее, если ![]() , то
, то ![]() (так как 7 – наибольшая варианта).
(так как 7 – наибольшая варианта).
Таким образом, эмпирическая функция распределения равна:

График полученной эмпирической функции распределения изображен на рисунке 16.
Задача 61. Найти методом сумм асимметрию и эксцесс по заданному распределению выборки объема N=100:
|
Варианта ХI |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
84 |
|
Частота Ni |
2 |
4 |
6 |
8 |
12 |
30 |
18 |
8 |
7 |
5 |
Решение. Асимметрия ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
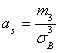 ,
,
Где ![]() – центральный эмпирический момент третьего порядка, вычисляемый по формуле:
– центральный эмпирический момент третьего порядка, вычисляемый по формуле: 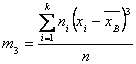
Эксцесс ![]() эмпирического распределения определяется равенством:
эмпирического распределения определяется равенством:
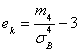 ,
,
Где ![]() – центральный эмпирический момент четвертого порядка, вычисляемый по формуле:
– центральный эмпирический момент четвертого порядка, вычисляемый по формуле: 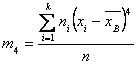
Асимметрия и эксцесс служат для оценки отклонения эмпирического распределения от нормального. Для нормального распределения эти характеристики равны нулю. Поэтому, если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Кроме того, если эксцесс положительный, то распределение будет островершинным; если отрицательный, то распределение будет плосковершинным по сравнению с нормальным распределением.
Для практического расчета асимметрии и эксцесса непосредственно пользоваться вышеуказанными формулами довольно затруднительно, поэтому воспользуемся методом сумм. Составим расчетную таблицу 1, для этого:
1) Запишем варианты в первый столбец.
2) Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца.
3) В качестве ложного нуля С выберем варианту (68), которая имеет наибольшую частоту (в качестве С можно взять любую варианту, расположенную примерно в середине столбца); в клетках строки, содержащей ложный нуль, запишем нули; в четвертом столбце над и под уже помещенным нулем запишем еще по одному нулю.
4) В оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты:
2; 2+4=6; 6+6=12; 12+8=20; 20+12=32.
Сложив все накопленные частоты, получим число B1=72, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты:
5; 5+7=12; 12+8=20; 20+18=38.
Сложив все накопленные частоты, получим число A1=75, которое поместим в нижнюю клетку третьего столбца.
5) Аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца. Сложив все накопленные частоты, расположенные над нулем, получим число B2=70, которое поместим в верхнюю клетку четвертого столбца. Сумма накопленных частот, расположенных под нулем, равна числу A2=59, которое поместим в нижнюю клетку четвертого столбца.
6) Для заполнения столбца 5 запишем нуль в клетке строки, содержащей ложный нуль (68); над этим нулем и под ним поставим еще по два нуля. В клетках над нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 сверху вниз; в итоге будем иметь следующие накопленные частоты:
2; 2+8=10; 10+20=30.
Сложив накопленные частоты, получим число B3=42, которое поместим в верхнюю клетку пятого столбца. В клетках под нулями запишем накопленные частоты, для чего просуммируем частоты столбца 4 снизу вниз; в итоге будем иметь следующие накопленные частоты:
5; 5+17=22.
Сложив накопленные частоты, получим число A3=27, которое поместим в нижнюю клетку пятого столбца.
7) Аналогично заполняется столбец 6, причем суммируют частоты столбца 5.
В итоге получим расчетную таблицу 1:
Расчетная таблица 1
|
1 |
2 |
3 |
4 |
5 |
6 |
|
ХI |
Ni |
B1=72 |
B2=70 |
B3=42 |
B4=14 |
|
48 |
2 |
2 |
2 |
2 |
2 |
|
52 |
4 |
6 |
8 |
10 |
12 |
|
56 |
6 |
12 |
20 |
30 |
0 |
|
60 |
8 |
20 |
40 |
0 |
0 |
|
64 |
12 |
32 |
0 |
0 |
0 |
|
68 |
30 |
0 |
0 |
0 |
0 |
|
72 |
18 |
38 |
0 |
0 |
0 |
|
76 |
8 |
20 |
37 |
0 |
0 |
|
80 |
7 |
12 |
17 |
22 |
0 |
|
84 |
5 |
5 |
5 |
5 |
5 |
|
N=100 |
A1=75 |
A2=59 |
A3=27 |
A4=5 |
Теперь найдем Di (I=1, 2, 3) и si (I=1, 2, 3, 4):
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Найдем условные моменты первого, второго, третьего и четвертого порядков:
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
Найдем далее центральные эмпирические моменты третьего и четвертого порядков, учитывая, что шаг ![]() (разность между двумя соседними вариантами):
(разность между двумя соседними вариантами):
![]() ;
;

Так как дисперсия ![]() , то выборочное среднее квадратическое отклонение
, то выборочное среднее квадратическое отклонение ![]() .
.
Учитывая определения асимметрии и эксцесса, окончательно получаем:
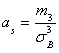
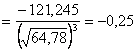 ;
; 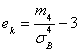
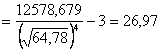 .
.
| < Предыдущая | Следующая > |
|---|
3.1Определение оценки и ее качество
Дана выборка ![]()
генеральной случайной величины Х.
Обозначим через ![]()
числовую характеристику или параметр,
связанный со случайной величиной Х.
По данным выборки требуется найти
приближенное значение ![]() .
.
Определяется функция ![]()
от выборочных значений. Эта функция
называется оценкой.
В известном смысле значения оценки ![]()
должны быть близки к значению ![]()
Качество оценки
определяется не по одной выборке, а по
всему мыслимому набору выборок, то есть
по случайной выборке ![]()
Поэтому оценка ![]()
является случайной величиной.
По разным выборкам
мы будем получать различные значения
оценки ![]() ,
,
но в среднем эти значения должны быть
равны величине ![]()
Оценка ![]()
называется несмещенной,
если ее математическое ожидание равно
истинному значению:
![]()
Чем больше объем
выборки, тем оценка ![]()
должна лучше оценивать истинное значение
![]()
Чаще всего отклонение значений оценки
от истинного значения должно быть мало
при больших объемах выборки.
Оценка называется
состоятельной,
если при увеличении объема выборки
вероятность того, что оценка мало
отличается от истинного значения,
приближается к единице. Запишем это в
виде предельного соотношения:
![]() ,
,
для любого ![]()
Разброс значений
случайной величины будет тем меньше,
чем меньше ее дисперсия. Нам бы хотелось,
чтобы разброс значений оценки был
минимальным.
Несмещенная оценка
называется эффективной,
если она имеет наименьшую дисперсию
среди всех несмещенных оценок данной
истинной величины.
3.2 Оценки моментов
В математической
статистике моменты генеральной случайной
величины Х
называются еще теоретическими
моментами.
Напомним их определение.
Центральный
момент k-го
порядка:
![]()
Начальный
момент k-го
порядка:
![]()
Центральные моменты
выражаются через начальные.
В роли величины ![]()
выступает момент. При построении оценки
используется обобщенная выборочная
случайная величина ![]()
построенная по выборке:
-


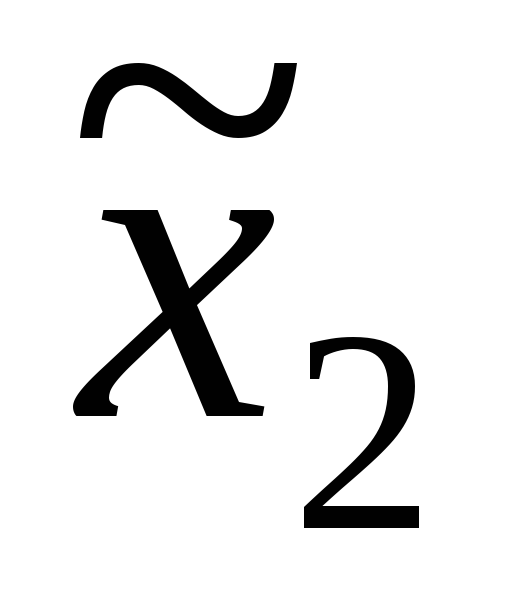





 ,
,
Выборочная случайная
величина является дискретной. Начальный
момент k-го
порядка случайной величины ![]()
![]()
По необработанной
выборке ![]()
имеем:
![]()
Введем обозначение:
![]()
Согласно теореме
Чебышева [2, §6], имеем:
![]() для любого
для любого ![]()
Поэтому если
истинная величина ![]()
то в роли ее оценки будем брать ![]()
то есть ![]()
Оценка ![]()
обозначается ![]()
она еще называется выборочным
(эмпирическим)
моментом
k–го
порядка. Эти
оценки являются состоятельными.
Аналогично вводятся
и оценки центральных моментов:
![]()
Для необработанной
выборки ![]()
![]()
Эти оценки также
являются состоятельными. Из свойств
математического ожидания вытекает
несмещенность
оценок начальных моментов:

Выборочные
центральные моменты являются смещенными.
Докажем смещенность выборочной дисперсии
(центрального момента второго порядка).
Для выборочной дисперсии вводится
специальное обозначение:
![]()
Мы рассматриваем
эту оценку как случайную величину.
Раскроем квадрат под знаком суммы:
![]()
Найдем математическое
ожидание каждого из слагаемых:
![]()
![]()
![]()
![]()
![]()
Тогда ![]()
Оценка ![]()
корректируется с целью получения
несмещенной оценки:
![]()
Несмещенная
оценка дисперсии:
![]()
Пример 1.
По выборке 2, 3, 2, 5, 3, 2 найти оценку
математического ожидания (выборочное
математическое ожидание).
Объем выборки п
равен 6.
Найдем сумму всех
выборочных значений:
![]()
Находим оценку
математического ожидания:
![]()
Пример 2.
По выборке найти несмещенную оценку
дисперсии:
-

0
2
3
5

10
14
15
11
Объем выборки
равен ![]()
Найдем оценку
математического ожидания:
![]()
Найдем сумму
квадратов отклонений от выборочного
математического ожидания:
![]()
![]()
Находим несмещенную
оценку дисперсии:
![]()
Можно считать, что
![]()
где Х
– генеральная случайная величина.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
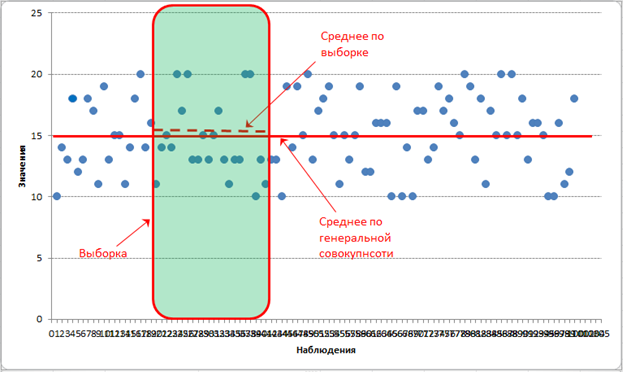
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
![]()
Выборочная несмещенная дисперсия:
![]()
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. В знаменателе несмещенной оценки n-1 вместо n.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.
До новых встреч на блоге statanaliz.info.
Поделиться в социальных сетях:
Содержание:
Оценки и методы их получения:
Приближенные значения параметров, входящих в законы распределения, определяемые каким-либо способом по выборкам, называются оценками или статистиками. Оценки бывают точечными и интервальными. Точечные оценки представляются одним числом, интервальные – двумя числами 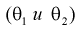
Метод моментов
Пусть генеральная случайная величина X имеет плотность распределения 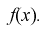
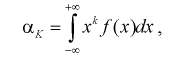 (8.1)
(8.1)
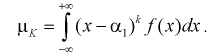 (8.2)
(8.2)
По выборке 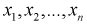 определяем выборочные начальные и центральные моменты:
определяем выборочные начальные и центральные моменты:
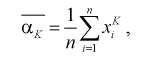 (8.3)
(8.3)
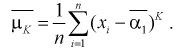 (8.4 )
(8.4 )
Метод моментов состоит в том, что генеральные моменты (8.1, 8.2), в которые входят оцениваемые параметры, приблизительно приравниваются к соответствующим выборочным моментам (8.3), (8.4). Составляется система уравнений:
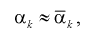 (8.5)
(8.5)
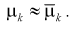 (8.6)
(8.6)
Решая систему (8.5), (8.6), находим оцениваемые параметры.
Особо важную роль играет 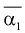 – выборочный начальный момент 1-го по рядка, он называется выборочным средним и обозначается
– выборочный начальный момент 1-го по рядка, он называется выборочным средним и обозначается 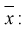
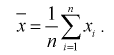 (8.7)
(8.7)
Следующим по важности выборочным моментом является выборочный центральный момент 2-го порядка 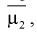 который называется выборочной дисперсией и обозначается
который называется выборочной дисперсией и обозначается 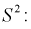
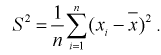 (8.8)
(8.8)
Наиболее часто используются две формулы метода моментов.
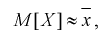 (8.9)
(8.9)
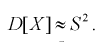 (8.10)
(8.10)
Сформулируем метод моментов в общем виде.
Пусть 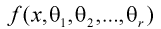 плотность распределения случайной величины
плотность распределения случайной величины 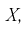 где
где 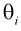 – неизвестные параметры. Чтобы найти оценки
– неизвестные параметры. Чтобы найти оценки 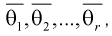 выражаем первые
выражаем первые 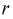 начальных или центральных моментов случайной величины X через параметры
начальных или центральных моментов случайной величины X через параметры 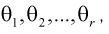 затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из
затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из 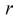 уравнений с
уравнений с 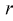 неизвестными, откуда и получаем
неизвестными, откуда и получаем 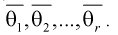
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 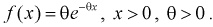 По выборке
По выборке 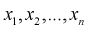 методом моментов найти оценку параметра
методом моментов найти оценку параметра 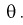
1. Определяем 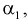 используя (8.1):
используя (8.1):
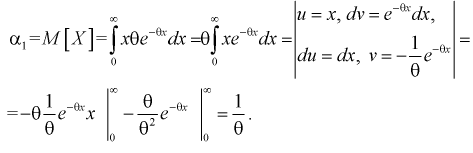
2. По (8.3) или (8.7) находим выборочный начальный момент 1-го порядка или 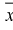 и составляем выражение вида (8.5) или (8.9):
и составляем выражение вида (8.5) или (8.9):
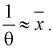
3. Заменяя в п. 2 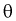 на оценку
на оценку 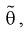 составим уравнение:
составим уравнение: 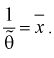
4. Откуда определим оценку параметра 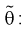
Метод наибольшего правдоподобия
Этот метод предложен математиком Фишером в 1912 г.
Пусть 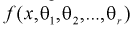 – плотность распределения генеральной случайной величины X, где
– плотность распределения генеральной случайной величины X, где 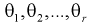 – неизвестные параметры. Согласно методу, наилучшими оценками
– неизвестные параметры. Согласно методу, наилучшими оценками 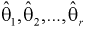 параметров
параметров 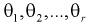 являются такие, для которых функция правдоподобия L принимает наибольшее значение.
являются такие, для которых функция правдоподобия L принимает наибольшее значение.
Для непрерывной случайной величины
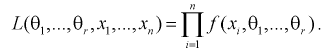 (8.11)
(8.11)
Для дискретной случайной величины
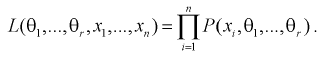 (8.12)
(8.12)
Здесь 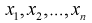 – выборка из генеральной случайной величины X.
– выборка из генеральной случайной величины X.
Априорные выборочные значения 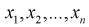 – являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности
– являются независимыми случайными величинами, закон распределения которых совпадает с законом распределения генеральной случайной величины X. Тогда правую часть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) можно рассматривать как плотность распределения вероятности  мерного вектора
мерного вектора 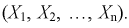 Согласно методу, для наилучших оценок
Согласно методу, для наилучших оценок 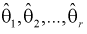 случайный вектор
случайный вектор 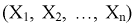 будет иметь наибольшую плотность распределения. То есть надо найти такие оценки
будет иметь наибольшую плотность распределения. То есть надо найти такие оценки 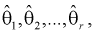 для которых функция правдоподобия L – максимальна. Для этого составляют и решают такую систему уравнений:
для которых функция правдоподобия L – максимальна. Для этого составляют и решают такую систему уравнений:
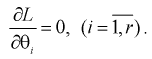 (8.13)
(8.13)
Так как функция и ее логарифм достигают экстремума в одной точке, то часто для упрощения решения задачи используют логарифмическую функцию правдоподобия. В случае логарифмической функции правдоподобия составляется система следующих уравнений:
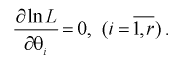 (8.14)
(8.14)
Пример:
Пусть генеральная случайная величина X имеет показательный закон распределения с плотностью 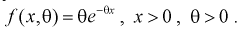 По выборке
По выборке 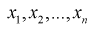 методом наибольшего правдоподобия найти оценку параметра
методом наибольшего правдоподобия найти оценку параметра 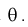
1. Так как нам необходимо оценить один параметр 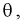 то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):
то надо составить и решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):
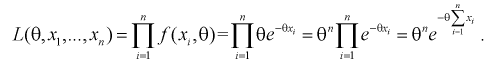
2. Составим логарифмическую функцию правдоподобия:
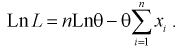
3. Для определения максимума логарифмической функции правдоподобия составляем и решаем следующее уравнение:
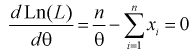
Откуда оценка 0 параметра 0 определяется так:
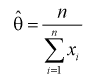
При сравнение это выражение с оценкой 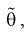 полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.
полученной по методу моментов (см. раздел 8.1), мы понимаем, что они одинаковы. Методы, рассмотренные нами, как видим, абсолютно разные. Это свидетельствует о их достоверности.
Свойства оценок
Пусть  – выборка из генеральной совокупности. Обозначим оценку параметра
– выборка из генеральной совокупности. Обозначим оценку параметра 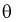 через
через 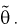 Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от
Ранее мы показали, что эта оценка определяется с помощью различных методов по полученной выборке , т. е. являляется функцией от 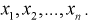
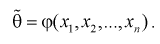
Так как любая выборка типа 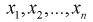 – случайна, то и выборочные функции
– случайна, то и выборочные функции 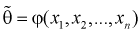 – тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
– тоже являются случайными. Следовательно, она тоже имеет свои характеристики.
1. Оценка 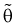 называется несмещенной, если ее математическое ожидание совпадает с самим оцениваемым параметром:
называется несмещенной, если ее математическое ожидание совпадает с самим оцениваемым параметром:
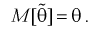
В противном случае оценка называется смещенной.
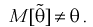
Полную погрешность 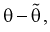 возникшую от замены 0 на 0, можно представить так:
возникшую от замены 0 на 0, можно представить так:
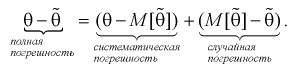
Таким образом, если оценка несмещенная, то систематическая погрешность равна нулю, т. е. 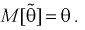
Наиболее опасна систематическая ошибка, если она заранее неизвестна или среднее квадратичное отклонение не очень большое. Среднее значение случайной ошибки 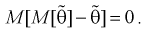
Мы уже отмечали, что 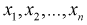 – независимые случайные величины, имеющие тот же закон распределения, что и
– независимые случайные величины, имеющие тот же закон распределения, что и 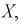 генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:
генеральная случайная величина, в частности, выборочное математическое ожидание и дисперсия имеет те же числовые характеристики, т. е. справедливы тождества:
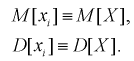 (*)
(*)
Проверим смещенность оценки математического ожидания выборочной средней 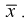 Используя обычные свойства математического ожидания, найдем
Используя обычные свойства математического ожидания, найдем 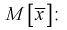
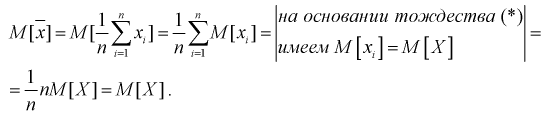
Обозначим 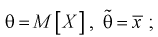 видим, что
видим, что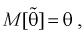 значит, выборочное среднее
значит, выборочное среднее 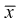 является несмещенной оценкой математического ожидания.
является несмещенной оценкой математического ожидания.
Проверим смещенность оценки дисперсии выборочной дисперсией 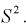 Найдем математическое ожидание от выборочной дисперсии:
Найдем математическое ожидание от выборочной дисперсии:
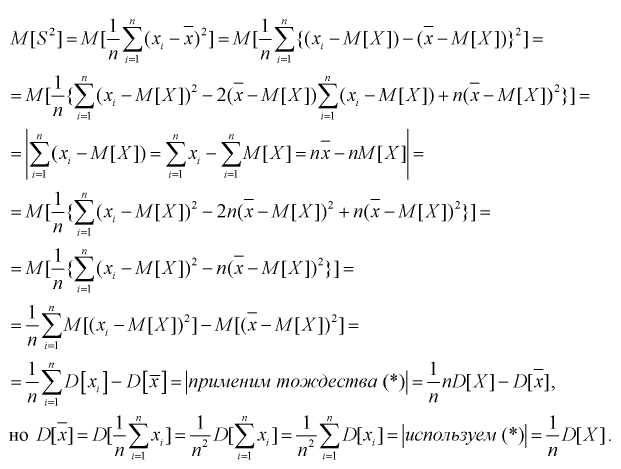
То есть дисперсия выборочной средней в 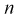 раз меньше дисперсии генеральной случайной величины. Тогда
раз меньше дисперсии генеральной случайной величины. Тогда
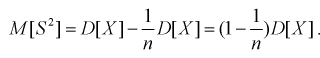
Обозначим 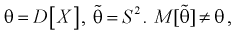 значит, выборочная дисперсия
значит, выборочная дисперсия 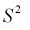 является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия
является смещенной оценкой дисперсии. Можно отметить, что выборочная дисперсия 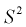 является асимптотически несмещенной оценкой, т. к. при
является асимптотически несмещенной оценкой, т. к. при 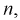 стремящемся к бесконечности, смещение стремится к нулю.
стремящемся к бесконечности, смещение стремится к нулю.
При решении практических задач часто используется несмещенная оценка дисперсии – это модифицированная выборочная дисперсия:
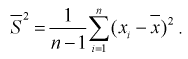
Найдем математическое ожидание от 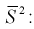
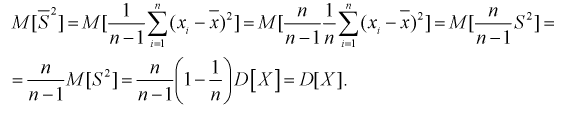
Обозначим 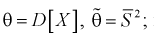 как видим,
как видим, 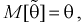 значит, оценка
значит, оценка 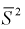 уже несмещенная. При малых
уже несмещенная. При малых 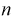 этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии – когда известно математическое ожидание:
этой формулой пользоваться лучше (при и > 30 оценки совпадают). На практике используют еще одну несмещенную оценку дисперсии – когда известно математическое ожидание:
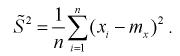
Найдем 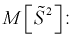
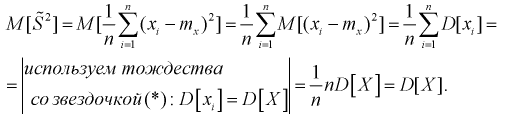
Обозначим 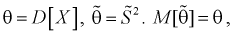 значит, оценка
значит, оценка 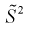 несмещенная.
несмещенная.
2. Оценка 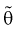 параметра
параметра 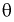 называется состоятельной, если она сходится по вероятности к параметру
называется состоятельной, если она сходится по вероятности к параметру 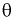 , т. е. если
, т. е. если 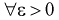 выполняется:
выполняется:
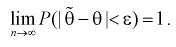
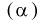
Условие 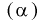 на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:
на практике проверить трудно. Поэтому для проверки состоятельности оценок применяют более простые условия:
а) 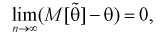
б) 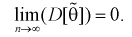
Как видим, оценка 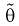 будет состоятельной, если при
будет состоятельной, если при 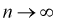 смещение устраняется и дисперсия оценки стремится к нулю.
смещение устраняется и дисперсия оценки стремится к нулю.
Пример:
Проверим состоятельность оценки математического ожидания выборочной средней 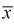 . Ранее мы показали, что
. Ранее мы показали, что 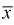 является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем
является несмещенной оценкой математического ожидания, т. е. условие а) выполняется и без вычисления предела. Проверим условие б), найдем 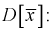
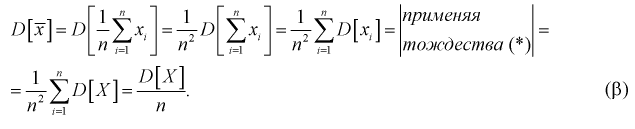
Видим, что при 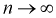 предел
предел 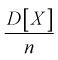 будет стремиться к нулю, значит условие б) выполняется. Следовательно,
будет стремиться к нулю, значит условие б) выполняется. Следовательно, 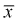 является состоятельной оценкой математического ожидания.
является состоятельной оценкой математического ожидания.
3. Несмещенная оценка 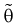 параметра
параметра 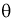 называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки
называется эффективной, если она имеет наименьшую дисперсию среди всех оценок при одном и том же объеме выборки 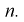
Для определения наименьшей дисперсии эффективной оценки 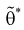 параметра
параметра 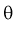 применяется формула Рао-Крамера:
применяется формула Рао-Крамера:
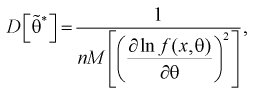 (8.15)
(8.15)
где 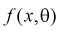 – плотность распределения генеральной случайной величины X.
– плотность распределения генеральной случайной величины X.
Отметим, если оценка 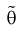 смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки
смещенная, то малость ее дисперсии еще не говорит о ее эффективности. Например, если в качестве оценки 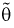 взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
взять любую постоянную величину с, то ее дисперсия будет равна нулю, а ошибка может быть какой угодно большой.
Пример:
Задана нормальная случайная величина 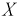 с плотностью распределения
с плотностью распределения
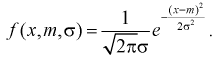
Проверим эффективность оценки математического ожидания выборочной средней 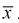 .
.
Найдем дисперсию эффективной оценки параметра 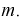 Обозначим эффективную оценку
Обозначим эффективную оценку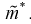 Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим
Чтобы воспользоваться формулой Рао-Крамера (8.15), вычислим
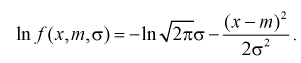
Найдем производную:
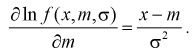
Подставим полученное выражение в (8.15):
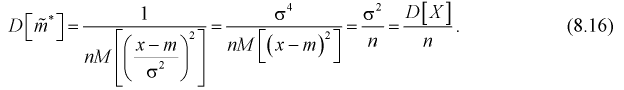
Ранее мы показали, что такую же дисперсию имеет 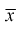 (см. формулу
(см. формулу 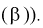
Видим, что правые части формул (8.16) и 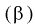 совпадают, следовательно, выборочное среднее
совпадают, следовательно, выборочное среднее 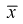 является эффективной оценкой параметра
является эффективной оценкой параметра 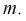
Отметим, что оценки, полученные методом наибольшего правдоподобия, являются состоятельными. Если существуют эффективная оценка, то метод наибольшего правдоподобия позволяет найти ее, но не всегда оценки, полученные этим методом, являются несмещенными.
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
