Как найти несмещенную выборочную дисперсию – Сайт, где вы сможете решить свои вопросы

Несмещенная оценка выборочной дисперсии

Краткая теория

Пусть из генеральной совокупности в результате

независимых наблюдений над количественным
признаком

извлечена повторная выборка объема

При этом

Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию

.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой

,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:

Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить

на дробь

.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через

Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:

Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:

Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:

При достаточно больших значениях

объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно

Пример решения задачи

Задача

Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.

Сумма
частот:

Вычислим
среднюю:

Средняя квадратов:

Несмещенная
выборочная дисперсия:

Ответ:

Кроме этой задачи на другой странице сайта есть

пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда

Источник

Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».

Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.

Понятие о сплошном и выборочном наблюдении

С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.

Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.

Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.

В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.

Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.

У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.

Выборочная несмещенная дисперсия

И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?

Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.

Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.

Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.

Отклонение выборочной средней от генеральной показано на рисунке.

Среднее арифметическое в выборке и в генеральной совокупности

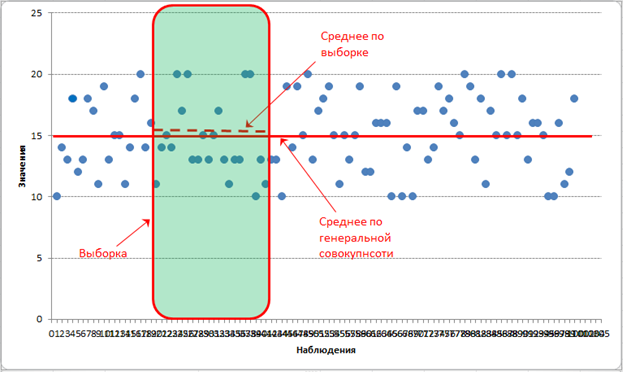
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.

Выборочная смещенная дисперсия:

Выборочная несмещенная дисперсия:

Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.

Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.

Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.

При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.

Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.

Из данной статьи неплохо бы усвоить следующее.

1. Формула генеральной дисперсии в выборке дает смещенную оценку.

2. В знаменателе несмещенной оценки n-1 вместо n.

3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.

4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.

До новых встреч на блоге statanaliz.info.

Поделиться в социальных сетях:

Источник

Генеральная и выборочная дисперсия

Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:

размах вариации;
среднее абсолютное отклонение;
дисперсия.

Разберем понятие дисперсии, ее виды и свойства.

Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.

Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.

В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.

Дисперсию также делят на два вида в зависимости от используемых данных:

генеральная дисперсия;
выборочная дисперсия.

Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.

Выборочная дисперсия, определение, формулы для вычисления

Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как ({overline y}_в).

Выборочная дисперсия (D_в) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки (y_1,;y_2,;…y_n) от ее среднего значения ({overline y}_в).

Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.

Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:

Формула 1

(D_в=frac{{displaystylesum_{i=1}^n}(y_i-{overline y}_в)}n)

В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.

Формула 2

(D_в=frac{{displaystylesum_{i=1}^k}(y’_i-{overline y}_в)cdot n_i}n)

где (y’_i )— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;

(n_i )— частота.

Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.

Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:

Формула 3

(D_в=frac{{displaystylesum_{i=1}^n}{(y_i-{overline y}_в)}^2}{n-1})

Примечание 1

Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.

Генеральная дисперсия, определение, что является оценкой, формулы для вычисления

Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности (X — {overline x}_г.)

Генеральная дисперсия (D_г) есть среднее арифметическое отклонение квадратов разности признаков (x_1,;x_2,;…x_n) генеральной совокупности X от их среднего значения ({overline x}_г).

Примечание 2

Иногда генеральную дисперсию называют теоретической.

Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:

Формула 4

(D_г=frac{{displaystylesum_{i=1}^N}{(x_i-{overline x}_г)}^2}N)

и для сформированного вариационного ряда:

Формула 5

(D_г=frac{{displaystylesum_{i=1}^K}{(x’_i-{overline x}_г)}^2cdot n_i}N)

Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.

Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.

Оценки параметров распределения

Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.

Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.

Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.

Формула 6

(delta=sqrt D)

Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).

Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:

Формула 7

(D=Mleft[X-M(X)right]^2)

для непрерывной:

Формула 8

(D=int_{-infty}^infty(x-M{(x))}^2cdot f(x)dx)

где f(x) — функция распределения случайной величины.

Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.

Примеры решения задач

Пример 1

Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.

Решение.

Сначала вычислим выборочное среднее значение:

({overline x}_в=frac{210+200+195+205+190+200}6=200;B.)

Теперь найдем выборочную дисперсию:

(D_в=frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=frac{250}6approx42.)

Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель (frac n{n-1} (n=6):)

(D_и=frac n{n-1}cdot D_в=frac65cdotfrac{250}6=50.)

Примечание 3

Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.

Пример 2

Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.

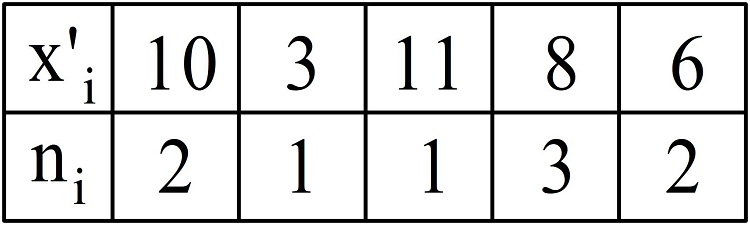
Решение.

Вычислим выборочную несмещенную дисперсию:

(D_в=frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9cdotfrac98=frac{398}8approx50.)

Теперь найдем среднеквадратическое отклонение:

(delta=sqrt{D_в}=sqrt{frac{398}8}=frac{sqrt{199}}2approx7.)

Источник

Т.к.
X₁,
X₂,…,X_n
– независимые, одинаково распределенные
случайные величины, то все они имеют
один и тот же закон распределения
вероятностей и одинаковые числовые
характеристики.

Среднее
выборочное

удовлетворяет
всем накладываемым к статистическим
оценкам требованиям, т.е. дает несмещенную,
эффективную и состоятельную оценку.
Действительно:

. (3.7)

Это
равенство следует из того, что все
значения x_i
распределены одинаково с математическим
ожиданием
.
Поэтому
является несмещенной оценкой
.

В
то же время эта оценка является
состоятельной:
согласно
закону больших чисел, при увеличении
n,
величина
сходится по вероятности к математическому
ожиданию. Говорят, выборочное среднее
обладает свойством
статистической
устойчивости.

Оценим
по данным выборки неизвестную нам
генеральную дисперсию D_Г.
Поступим аналогично, т.е. в качестве
оценки D_Г
возьмем D_В.
Можно доказать, что математическое
ожидание D_В
равно

Таким
образом, D_В
оказывается смещенной оценкой генеральной
дисперсии, давая заниженное
значение D_Г.
Это значит, что при малых п,
ее использование приведет к систематическим
ошибкам. Для
несмещенной оценки D_Г
достаточно взять величину
,
которую называютисправленной
дисперсией
и обозначают s².
Тогда

Т.о.,
математическое ожидание исправленной
дисперсии действительно равно дисперсии
генеральной совокупности и, значит, s²
– состоятельная оценка генеральной
дисперсии.

На
практике для оценки генеральной дисперсии
применяют исправленную дисперсию при
.
В остальных случаях,
отклонениеD_В
от D_Г
малозаметно. Поэтому при больших
значениях n
ошибкой “смещения” 1/n
можно пренебречь: т.к. при
коэффициент,
т.е.s²
– состоятельная оценка.

Итак, несмещенная
оценка для дисперсии имеет вид

(3.8)

для
выборки, заданной последовательностью
значений или таблицей относительных
частот.

Пусть
некоторая случайная величина X
имеет математическое ожидание MX=m
и дисперсию
DX=.
В ходе эксперимента получена случайная
выборка из n
независимых испытаний случайной величины
X.
Тогда справедливы следующие утверждения.

1)
Среднее выборочное
служит несмещенной и состоятельной
оценкой математического ожиданияMX.

2)
Если случайная величина X
распределена по нормальному закону с
параметрами N(m,),
то среднее выборочное
также распределено нормально и имеет
минимальную дисперсию
:
т.е.
.
Поэтому среднее выборочное– эффективная и состоятельная оценка
математического ожидания.

3)
Выборочная дисперсия
является
смещенной оценкой генеральной дисперсии.
Несмещенной оценкой генеральной
дисперсииявляется
«исправленная» дисперсия,
для получения которой необходимо
умножитьна так называемуюпоправку
Бесселя
.
Тогда

«Исправленная»
выборочная дисперсия
является состоятельной оценкой
генеральной дисперсии.

Если
известно m
– математическое ожидание случайной
величины X,
то выборочная дисперсия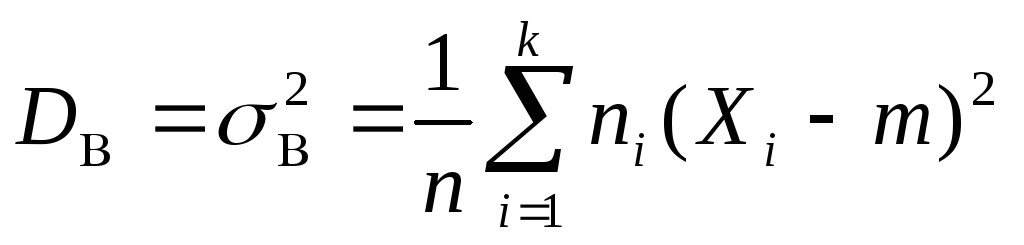является несмещенной, состоятельной
и эффективной оценкой генеральной
дисперсии.
Относительная
частота
является
несмещенной и состоятельной оценкой
вероятностиP(X=x_i).
Эмпирическая функция распределения
–
накопленная относительная частота –
является несмещенной и состоятельной
оценкой теоретической функции
распределенияF(x)=P(X<x).

Задача
5. Найти
несмещенные оценки математического
ожидания и дисперсии по таблице выборки:

x_i	2	6	12
n_i	3	10	7

Решение:

Из
таблицы имеем объем выборки n
= 20. Несмещенная оценка математического
ожидания есть среднее выборочное
:

Для
вычисления несмещенной оценки дисперсии
сначала найдем выборочную дисперсию,
а затем несмещенную оценку – s²_:

, .

х_i	2	6	12
	0.15	0.5	0.35

Задача 6.
Найти несмещенные числовые характеристики
выборки, заданной таблицей:

Решение:

Среднее
выборочное
является несмещенной оценкой генерального
среднего, а для вычисления несмещенной
дисперсиипредварительно вычислим смещенную
дисперсию

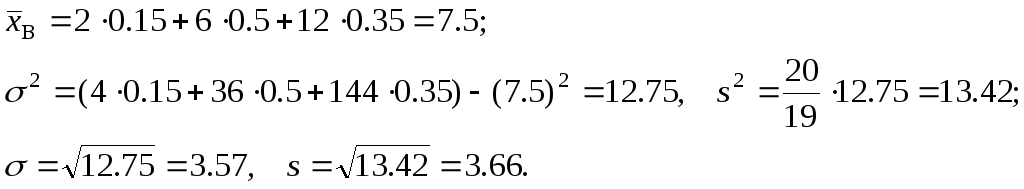
Легко видеть, что
задачи 5 и 6 задают одну и ту же выборку,
но в задаче 5 она задается таблицей
абсолютных частот, а в задаче 6 – таблицей
относительных частот:

На
практике если значение вариант x_i
– большие числа, то для облегчения
расчетов их представляют в виде суммы
некоторого постоянного числа с
и условной варианты u_i,
как дополнения до
,
т.е..
Это значит, что задан некий новый
вариационный ряд для величиныU,
определенный по выборочным данным u_i.
Поскольку выбор с
произволен, то лучше взять за с
значение, близкое к
.
Тогда,,
а дисперсия не изменится, т.е.,
так как по свойствам дисперсии

,
где C
– const.
Тогда

.
Аналогично
вычисляется несмещенная оценка дисперсии:

. (3.9.)

Если
первоначальные варианты представлены
десятичными дробями, то их умножают на
постоянное число с=10^k,
где k
– количество десятичных знаков. Тогда
условные варианты имеют вид
,
то есть дисперсия увеличилась в
раз, согласно свойству дисперсии. Поэтому,
а.

Аналогично,
. (3.10)

Задача
7. Из генеральной
совокупности извлечена выборка. Найти
несмещенную оценку генеральной средней
и генеральной дисперсии.

x_i	3250	3270	3280
n_i	2	5	3

Решение:
1. Найдем
условную варианту и составим для нее
ряд распределений:

Пусть
с=3270,
тогда
,

u_i	-20	0	10
n_i	2	5	3

2.
Т.к. объем выборки n=10,
то
;.

3.
Найдем выборочную дисперсию для
первоначальной варианты с помощью
условной варианты:
.

4.
Найдем «несмещенную выборочную дисперсию»
– несмещенную оценку генеральной
дисперсии:
.

То,
что выбор постоянной с
не влияет на значение дисперсии, следует
из соответствующего свойства, известного
теории вероятностей. Поэтому выбор
постоянной с
весьма условен и определяется удобством
расчета. Особенно это очевидно при очень
малых значениях V:
например, если среднеквадратичное
отклонение порядка 10^-7,
а выборочное среднее порядка 10⁷,
то затруднительно непосредственно
вычислить дисперсию, т.к. незначительная
разница будет меньше погрешности
округления на микрокалькуляторе. Т.о.,
на практике исходят из критерия удобства
дальнейших расчетов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки. Виды выборочных дисперсий:

смещённая;
несмещённая, или исправленная

Содержание

1 Определения
2 Замечание
3 Свойства выборочных дисперсий
4 См. также

Определения[править | править код]

Пусть $X_{1},ldots ,X_{n},ldots$ — выборка из распределения вероятности. Тогда

выборочная дисперсия — это случайная величина

$S_{n}^{2}={frac {1}{n}}sum limits _{{i=1}}^{n}left(X_{i}-{bar {X}}right)^{2}={frac {1}{n}}sum limits _{{i=1}}^{n}X_{i}^{2}-left({frac {1}{n}}sum limits _{{i=1}}^{n}X_{i}right)^{2}$ ,

где символ ${bar {X}}$ обозначает выборочное среднее;

несмещённая (исправленная) дисперсия — это случайная величина

$S^{2}={frac {1}{n-1}}sum limits _{{i=1}}^{n}left(X_{i}-{bar {X}}right)^{2}$ .

Замечание[править | править код]

Очевидно,

$S^{2}={frac {n}{n-1}}S_{n}^{2}$ .

Свойства выборочных дисперсий[править | править код]

Выборочная дисперсия является теоретической дисперсией выборочного распределения. Более точно, пусть ${hat {F}}(x)$ — выборочная функция распределения данной выборки. Тогда для любого фиксированного $omega in Omega$ функция ${hat {F}}(omega ,x)$ является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна $S_{n}^{2}(omega )$ .