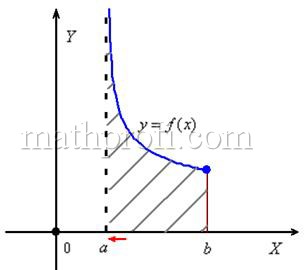
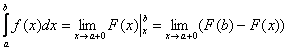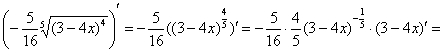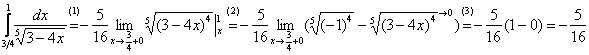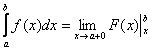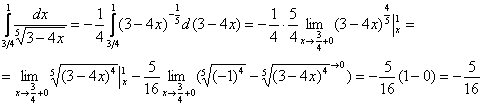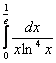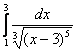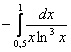Как найти несобственный интеграл 2 рода - Сайт, где вы сможете решить свои вопросы

Это интегралы от неограниченных (сверху и / или снизу) функций. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: . Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв: 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или разрывы даже есть внутри.

На практике гораздо чаще и одинаково часто встречаются первые два варианта, и сейчас я подброшу монетку… так, начинаем, со Случая 1, когда подынтегральной функции не существует в точке .

Сразу пример, чтобы было понятно: 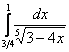. Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Проверим заодно и верхний предел: . Здесь всё хорошо. И вообще, обязательно анализируем весь знаменатель, а то, может статься, точки разрыва есть и внутри отрезка (и это не выдумки). В нашем примере знаменатель обращается в ноль в единственной точке, а значит, вопрос закрыт.

Принципиально этот случай выглядит так:

И здесь почти всё так же, как в интеграле первого рода. Если интеграл 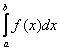существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!).

Осталось модифицировать формулу Ньютона-Лейбница, я приведу упрощённый по сравнению с учебниками вариант, без лишних букв:

«Добавка» символизирует тот факт, что к точке разрыва мы приближаемся справа (красная стрелка на чертеже). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

Разделаемся с демонстрационным интегралом:

Пример 35
Вычислить несобственный интеграл или установить его расходимость.

Во-первых, ПИСЬМЕННО констатируем тот факт, что подынтегральная функция терпит бесконечный разрыв в точке . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

И приём стар, как чешуя динозавра: сначала всегда можно найти неопределённый интеграл.

Особенно, если пример не прост и особенно в кубе, если вы «чайник».

Проведём замену: , откуда выражаем оставшийся кусок исходного интеграла, сиротливый дифференциал:

Проверка:
, в чём мы и хотели убедиться.

Теперь вычислим несобственный интеграл, сначала решение, затем комментарии:

(1) Используем формулу

(2) и её продолжение , где при подстановке нижнего предела интегрирования вместо «икс» мы формально подставляем «икс».

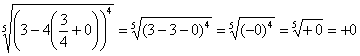
(3) Но самое главное: как выяснить, куда стремится , если ? Всё просто. Мысленно либо на черновике подставляем под корень и проводим упрощения: – в результате получено бесконечно малое положительное значение, поэтому .

Результат получился отрицательным, и в этом нет криминала, просто соответствующая криволинейная трапеция расположена под осью .

Решение можно оформить и по-другому. Например, провести ту же замену прямо в несобственном интеграле с пересчётом новых пределов интегрирования. Ну и совсем шикарно обыденно – это с ходу подвести под знак дифференциала:

А сейчас два интеграла для самостоятельного решения:

Пример 36
Вычислить несобственные интегралы или установить их расходимость
а) 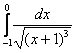, б)

В образце я привёл прямое решение с подведением под знак дифференциала и подробно закомментировал что, к чему и почему стремится. Обязательно разберитесь!

Случай 2. Если подынтегральной функции не существует в точке .

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит так:

Здесь всё так же, за исключением того, что предел у нас стремится к значению слева:

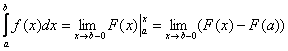
Такой предел называют левосторонним, и бесконечно малая отрицательная «добавка» означает, что к точке «бэ» мы подбираемся по оси именно слева.

Пример 37
Вычислить несобственный интеграл или установить его расходимость.

Очевидно, что подынтегральная функция терпит бесконечный разрыв в точке , но не пренебрегаем и проверяем, что больше разрывов нет! – по той причине, что знаменатель обращается в ноль в единственной точке.

Интеграл решим методом подведения под знак дифференциала:

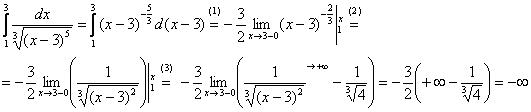
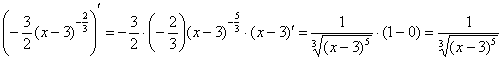
(1) Берём интеграл и используем формулу . Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку:
, ОК.

(2) Представляем первообразную в более удобном виде.

(3) Подставляем в неё пределы интегрирования: , формально считая, что вместо «икс» мы подставляем «икс».

Как выяснить, что при дробь ? Приём тот же самый: мысленно либо на черновике подставляем под корень и проводим упрощения:
, а единица, делённая на бесконечно малое и положительное значение – это «плюс» бесконечность: .
И на завершающем шаге бесконечность меняет знак:

Будьте очень внимательны в знаках! Да, конечно, несобственный интеграл расходится, но и – это две разные вещи, и если вы недосмотрите за знаками, то допустите серьезную ошибку.

Следующие интегралы для самостоятельного рассмотрения:

Пример 38
Вычислить несобственные интегралы или установить их расходимость.
а) , б)

В образце решения я опять использовал «быстрый» способ, но если вам трудно, то, конечно, сначала лучше найти неопредёленный интеграл.

И в заключение курса коротко о более редких случаях:

2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования

2.4. Что делать, если оба предела интегрирования бесконечны?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Как уже отмечалось выше для
неограниченной на отрезке [a,
b]
ф-и интеграл Римана смысла не имеет.
Обобщим понятие определенного интеграла
на ф-ю f(x)
неограниченную на полуинтервале [a,
b),
но ограниченную и интегрируемую на
любом отрезке [a,
b-ε],
0<ε<a.
Рассмотрим ф-ю F(ε)=.(1)

Перейдем
в (1) формально к пределу при ε→0

F(ε)=
=.(2).

Символ
=называют несобственным интегралом 2-го
рода. При этом, если предел (1) конечный,
то несобственный интеграл 2-го рода
называют сходящимся. Если предел
бесконечный или не сущ., то расходящимся.
Точкуx=b
называют особой.

Аналогично
определяются несобственные интегралы
2-го рода, если особой точкой является
левый конец отрезка [a,
b]
или внутренняя точка x=c
отрезка [a,
b].

==,

=(+).(3)

Величины
ε1
и ε2
→0 независимо друг от друга.

Пример
1. Исследовать
на сходимость интеграл.

Решение.
Пусть α=1. Тогда
==-ln(b-x)
=(ln(b-a)-lnε)=∞
=> ряд расходится.

Пусть
α≠1. Тогда
===(–)
=> Сходится, если α<1. Расходится, если
α>1.

Вывод:
при α<1 интеграл сходится, при α≥1
интеграл расходится.

При
некоторых ограничениях на ф-ю f(x)
несобственный интеграл 2-го рода сводится
к несобственному интегралу 1-го рода.

Пусть
f(x)
непрерывна на [a,
b)
и b
– особая точка. В интеграле
сделаем замену.

==.(4)

Перейдем
в (4) к пределу при ε→+0. Получим

=.(5)

Таким образом
данная замена переводит несобственный
интеграл 2-го рода в несобсвенный интеграл
1-го рода. Ясно, что если интеграл в левой
части (5) существует, то существует и
интеграл в правой части (5), и наоборот.
Все признаки сходимости, доказанные
для несобственного интеграла 1-го рода,
справедливы (с нек. исправлениями) и для
интеграла 2-го рода. Правила интегрирования
также остаются прежними.

Пример
2. Вычислить
несобственный интеграл.

Согласно
(2) имеем
===(xlnx-x)
=
=(-1-εlnε+ε)=-1-=-1-=-1.

Пример
3. Исследовать
на сходимость интеграл.

Доопределим
подыинтегральную ф-ю в точке x=0,
т.е. положим
=0.
Особой точкой являетсяx=1.
Найдем предел
=x=1.
Это означает эквивалентность функций
в точке x=1,
т.е.
~приx→1.
Согласно предельному признаку сравнения
интеграла
иведут себя одинаково. Но интегралрасходится (см. пр. 1), => и данный интеграл
расходится.

П 18. Главное значение несобственного интеграла.

Пусть
ф-я f(x)
определена на всей числовой оси и
интегрируема на любом конечном отрезке
числовой оси. Тогда

=(1)
–

несобственный
интеграл 1-го рода. Напомним, что a
и b
стремятся к ∞ независимо друг от друга.
Положим теперь b=-a.
Если существует предел
,
то говорят, что несобственный интеграл
сходится по Коши, а его значение называют
главным значением несобственного
интеграла по Коши и обозначают

V.P.=.(2)

Ясно,
что если интеграл (1) сходится, то он
сходится к этому же значению по Коши.
Однако интеграл (1) может расходится, но
иметь главное значение по Коши.

Пример
1.
– расходится (см. пр.2 §9). Найдем его
главное значение.

V.P.==-(cosa-cos(-a))=0.

Теорема
1. Если
ф-я f(x)
нечетная и интегрируема по Риману на
любом конечном отрезке, то ее главное
значение равно нулю.

Док-во.
=+==–==0,
т.к.f(t)
нечетная V.P.==0.
Теорема доказана.

Если
любая особая точка c
внутренняя для отрезка [a,
b],
то главное значение интеграла по Коши
можно ввести и для несобственного
интеграла 2-го рода.

V.P.=(+).(3)

Пример
2. Интеграл
,a<c<b
расходится (см. пр.1 §12). Найдем его главное
значение.
V.P.=(+)=(ln|x-c|+ln|x-c|)=(lnε-ln|a-c|+ln(b-c)-lnε)=
.

Пример
3. Интеграл
расходится. Найдем его главное значение.V.P.=
(+)=-(+)=-(-++1-)=-∞.
Главное значение данного интеграла не
существует.

Источник

Содержание:

Несобственный интеграл – Основные понятия и теоремы
Свойства несобственного интеграла
Несобственные интегралы
Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
Интегралы от неограниченных функций (несобственные интегралы II типа)

Несобственный интеграл – Основные понятия и теоремы

Пусть функция определена на промежутке и интегрируема на отрезке при любом . Если существует предел

(1.1)

то его называют несобственным интегралом от функции по промежутку и обозначают символом

(1.2)

Символ (1.2) также называется несобственным интегралом. Если предел (1.1) существует, то несобственный интеграл называется сходящимся, в противном случае — расходящимся.

Аналогично определяется несобственный интеграл с бесконечным нижним пределом:

(1.3)

Интегралы (1.2) и (1.3) называются несобственными интегралами по неограниченному множеству.

Пусть функция определена на промежутке , интегрируема на отрезке при любом и не ограничена в левой полуокрестности точки . Тогда интеграл (1.4)

называют несобственным интегралом от неограниченной функции и по определению полагают

(1.5)

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Если предел (1.5) существует, то несобственный интеграл (1.4) называется сходящимся, в противном случае — расходящимся.

Аналогично определяется несобственный интеграл по промежутку .

Обозначим через один из символов и сформулируем определение несобственного интеграла в общем случае.

Пусть функция определена на промежутке и интегрируема на каждом отрезке. Если существует предел

(1.6)

то его называют несобственным интегралом от функции по промежутку и обозначают символом

(1.7)

Несобственный интеграл по промежутку , где — один из символов определяется аналогично. Далее все утверждения будем формулировать для промежутка . Они очевидным образом переносятся на интегралы по промежутку .

Несобственные интегралы возникают в задачах на геометрические приложения интегрального исчисления: при вычислении площадей неограниченных фигур; объемов тел и площадей поверхностей вращения, если вращающаяся фигура неограничена.

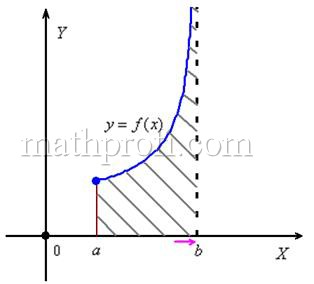
Пусть функция непрерывна и неотрицательна в промежутке . Рассмотрим фигуру

(1.8)

которую назовем неограниченной криволинейной трапецией.

Если несобственный интеграл сходится, то площадью фигуры называется число

(1.9)

Возможно вам будут полезны данные страницы:

Объем тела, образованного вращением фигуры вокруг оси равен несобственному интегралу

(1.10)

Площадь поверхности, полученной вращением непрерывной кривой

вокруг оси , вычисляется по формуле

(1.11)

Формулы (1.10), (1.11), как и формула (1.9), применимы при условии сходимости соответствующих несобственных интегралов.

При решении геометрических задач используются и несобственные интегралы от неограниченных функций.

Свойства несобственного интеграла

3. При любом

Свойства 1 и 2 называют линейными, а свойство 3 — аддитивностью.

Теорема 1.1 (о замене переменной в несобственном интеграле). Пусть выполнены следующие условия:

1) непрерывно дифференцируемая и строго монотонная функция отображает промежуток в промежуток , где и при

2) функция непрерывна в промежутке . Тогда интегралы

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

(1.12)

Теорема 1.2 (об интегрировании по частям в несобственном интеграле). Пусть функции и непрерывно дифференцируемы на промежутке и существует .

Тогда интегралы

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

(1.13)

где

Определенный интеграл считается неуместным, если выполнено хотя бы одно из следующих условий: Поля интеграции бесконечны. Например, бесконечный разрыв. Функция не ограничена вблизи некоторых точек области интегрирования.

Примеры с решением

Вычислить несобственный интеграл или установить его расходимость.

Пример 1.

Решение:

Вычислим несобственный интеграл по определению:

Следовательно, данный интеграл интеграл сходится.

Пример 2.

Решение: По определению несобственного интеграла с бесконечным верхним пределом имеем

Следовательно, данный интеграл интеграл расходится.

Пример 3.

Решение:

По определению несобственного интеграла с бесконечным нижним пределом имеем

Итак, интеграл сходится и равен 1.

Пример 4.

Решение:

Интеграл является несобственным, поскольку верхний предел бесконечен. Рассмотрим два случая.

1). Пусть Тогда по определению имеем

2). Пусть . Тогда Итак, интеграл сходится при и расходится при

Пример 5.

Решение:

Данный интеграл является несобственным, поскольку подынтегральная функция не определена в точке и . По определению несобственного интеграла от неограниченной функции имеем

Итак, данный интеграл сходится и равен

Пример 6.

Решение:

Подынтегральная функция не ограничена в правой полуокрестности нижнего предела. Поэтому данный интеграл – несобственный. Рассмотрим два случая.

1). Пусть . По определению несобственного интеграла от неограниченной функции имеем

2). Пусть . Тогда

Итак, интеграл сходится при и расходится при

Пример 7.

Решение:

Применим к данному интегралу формулу интегрирования по частям: Пример 1.8.

Данный интеграл является несобственным, поскольку

подынтегральная функция не определена в точке

и . Воспользуемся формулой замены переменной в несобственном интеграле. Положим . Имеем

Заметим, что в результате замены переменной несобственный интеграл преобразовался в определенный интеграл от непрерывной функции по отрезку.

Пример 8.

Найти площадь фигуры, ограниченной графиком функции и прямой .

Решение:

Функция непрерывна и неотрицательна в промежутке . Поэтому заданная фигура является неограниченной криволинейной трапецией вида (1.8). Площадь фигуры находится по формуле (1.9):

Для вычисления интеграла применим формулу (1.13) интегрирования по частям. Положим Тогда . Функции и непрерывно дифференцируемы в промежутке и существует

По формуле (1.13) имеем

Пример 9.

Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной графиком функции

и прямыми

Решение: Функция непрерывна, неотрицательна в промежутке (1,2] и не ограничена на нем, так как . Поэтому объем тела вращения выражается через несобственный интеграл:

Итак,

Несобственные интегралы

Понятие «несобственные интегралы» связано с нарушением условий теоремы 23.1 о существовании определенного интеграла. В зависимости от того, какая именно условие существования нарушена, рассматривают несобственные интегралы I и II типов.

Различают следующие случаи:

1) вместо конечного отрезка рассматриваются бесконечные пол интервалы или интервал
2) вместо подынтегральной функции, которая является непрерывной или ограниченной на отрезке интегрирования и имеет конечное число точек разрыва первого рода, рассматривают функцию, имеет на этом отрезке бесконечный разрыв, то есть разрыв второго рода.

Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)

Пусть функция определена и непрерывна на промежутке Тогда согласно теореме 23.1 она интегрируема на любом отрезке где – произвольное действительное число, большее Итак, существует определенный интеграл от этой функции на отрезке

где

то есть является первоначальной для подынтегральной функции

Несобственным интегралом I типа функции на промежутке называется предел определенного интеграла при условии, что верхняя граница интегрирования стремится к плюс бесконечности, то есть

Если граница конечна, то несобственный интеграл I типа называется сходящимся, или говорят, что он совпадает. Если граница в соотношении (25.1) является бесконечной или вовсе не существует, то несобственный интеграл I типа называется расходящимся, то есть разбегается.

С учетом формулы Ньютона-Лейбница соотношение (25.1) можно записать так:

где применяется обозначения:

Аналогично определяется несобственный интеграл I типа для случая, когда вместо отрезка интегрирования рассматривается интервал с бесконечной нижней границей.

Пусть функция определена и непрерывна на промежутке тогда для любого действительного существует определенный интеграл:

Несобственным интегралом I типа функции на промежутке называется предел определенного интеграла при условии, что нижняя граница интегрирования стремится к минус бесконечности, то есть

где применяется обозначение

Пусть функция определена и непрерывна на промежутке Тогда представим интеграл на этом промежутке как сумму двух несобственных интегралов на промежутках и

Если в соотношении (25.4) обе границы существуют, то несобственный интеграл I типа с бесконечными пределами совпадает.

С учетом формулы Ньютона-Лейбница несобственный интеграл на промежутке определяется соотношением:

Общий порядок нахождения несобственного интеграла I типа состоит из двух шагов:

1) вычисляем определенный интеграл от на где – переменная нижняя граница интегрирования ( – переменная верхний предел интегрирования)
2) находим границу определенного интеграла при

Под исследованием несобственных интегралов на сходимость понимают установления факта его сходимости или разногласия. Для этого во многих случаях бывает достаточна не вычислять самый интеграл (а он может быть таким, что и «не берется»), а сравнить его с несобственным интегралом, сходимость (или расхождение) которого известна.

Приведем признаки сравнения несобственных интегралов (которые примем без доказательства).

Теорема 25.1. Если функции и для всех связанные соотношением и несобственный интеграл совпадает, то совпадает и несобственный интеграл при этом

Теорема 25.2. Если функции и для всех связанные соотношением и несобственный интеграл расходится, то расходится и несобственный интеграл

Несобственный интеграл от функции сходимость или расхождение которого известна заранее, называется эталонным интегралом, а – эталонной функцией.

В предыдущих теоремах рассматривались несобственные интегралы от неотъемлемых функций. Для знакопеременной функции на бесконечном промежутке справедлива следующая теорема.

Теорема 25.3. Если несобственный интеграл от модуля заданной функции совпадает, то совпадает и интеграл от самой функции

В этом случае несобственный интеграл от на называется абсолютно сходящимся.

Рассмотрим некоторые примеры несобственных интегралов I типа. Одним из таких интегралов является интеграл Эйлера-Пуассона:

Этот интеграл нельзя представить в виде конечного числа элементарных функций, поэтому по общему алгоритму проблему вычисления интеграла Эйлера – Пуассона решить невозможно. Докажем, что этот интеграл совпадает, применив теорему 25.1.

Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции (рис. 25.1):

Рис. 25.1

Сравним функции и Обе функции положительные на числовой оси, и для выполняется неравенство тогда относительно функций и имеет место соотношение:

Следовательно, применить теорему 25.1 можно только на промежутке
Исследуем на сходимость интеграл от эталонной функции на

Эталонный интеграл совпадает на промежутке тогда по признаку сравнения сходится есть интеграл Поскольку несобственный интеграл отличается от несобственного интеграла постоянной, равной площади криволинейной трапеции для то интеграл Эйлера-Пуассона тоже является сходящимся.

В главе 26 будет доказано, что:

При исследовании вопроса о сходимости несобственных интегралов I типа часто в роли эталонного интеграла принимают интеграл вида:

Свойства этого интеграла зависят от значений параметра

Интеграл (25.8) при разбегается:

Следовательно, несобственный интеграл от степенной функции совпадает, если и расходится, если

Исследовать на сходимость несобственный интеграл I типа:

По определению:

Мы доказали, что несобственный интеграл совпадает, поскольку соответствующая граница равна конечном числу.

Исследовать на сходимость несобственный интеграл I типа:

По определению имеем:

Эта граница не существует, поскольку не существует следовательно, заданный несобственный интеграл расходится.

Исследовать на сходимость несобственный интеграл I типа:

По определению:

то есть данный интеграл расходится.

Интегралы от неограниченных функций (несобственные интегралы II типа)

Пусть на имеет конечное число точек разрыва второго рода. Это означает, что хотя бы одна из односторонних пределов функции в этих точках равна бесконечности, то есть при приближении к точкам разрыва функция неограниченно приходит или растет. Такие точки называются особыми точками функции. На рис. 25.2 приведены примеры расположения особых точек c на отрезке Так, особой точкой может быть как левый, так и правый конец отрезка, а также любая внутренняя точка. В геометрическом смысле прямая является вертикальной асимптотой графика функции

Рис. 25.2

Выберем некоторое положительное число и рассмотрим, соответственно, отрезки (рис. 25.2 а, б и в), на которых подынтегральная функция ограничена и непрерывная, следовательно, существует определенный интеграл от этой функции.

Несобственным интегралом II типа от функции на промежутке где при функция имеет разрыв второго рода, называется предел определенного интеграла на промежутке при условии, что стремится к нулю:

Аналогично определяют несобственные интегралы II типа для случая, когда особой точкой является верхняя граница отрезка интегрирования:

а также для случая, когда особая точка является внутренней точкой отрезка интегрирования:

Несобственный интеграл II типа называется сходящимся, если существуют конечные границы в правых частях формул (25.10) – (25.12). В противном случае их называют расходящимися.

Порядок исчисления несобственных интегралов II типа принципиально ничем не отличается от порядка определения несобственных интегралов I типа: вычисляют определенный интеграл на конечном отрезке и находят его границу при условии, что или Если для подынтегральной функции не существует первоначальная в виде конечной суммы элементарных функций, то для исследования несобственных интегралов II типа на сходимость применяются признаки сравнения их с эталонными интегралами, то есть такими, о которых заранее известно, совпадают они или разбегаются. Часто в качестве эталонных берут несобственные интегралы от степенных функций:

и его обобщения:

где

Для первого и второго эталонных интегралов особой точкой является нижняя граница отрезка интегрирования, а для третьего – верхний предел.

Проведем исследование на сходимость первого интеграла с (25.13):

Если то

Следовательно, несобственный интеграл II типа совпадает при и расходится при

Определим, совпадает ли несобственный интеграл

Его подынтегральная функция имеет разрыв второго рода в точке то есть ее особой точкой является верхняя граница отрезка интегрирования. По определению имеем:

Заданный интеграл совпадает, потому соответствующая граница равна конечном числу.

Исследуем на сходимость несобственный интеграл

Подынтегральная функция непрерывна на промежутке по исключением точки в которой знаменатель равен нулю, следовательно, в окрестности этой точки функция не ограничена, поэтому интеграл записываем в таком виде:

Если каждый интеграл в правой части совпадает, то выходной интеграл тоже будет совпадать.

Рассмотрим первый интеграл:

Поскольку первый интеграл расходится, то нет необходимости вычислять второй. Окончательно делаем вывод, что заданный несобственный интеграл расходится.

Лекции:

Определенный интеграл и объем фигур вращения
Уравнение гиперболы
Уравнение эллипса
Степенные ряды
Случайные события и вероятность
Свойства пределов функции
Решение пределов со степенями
Теория сплайнов примеры решения
Жорданова форма матрицы
Скрещивающиеся прямые

Источник

Интегралы с бесконечным промежутком интегрирования

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен, а подынтегральная функция ограничена на нем — в противном случае множество сумм Дарбу не будет ограниченным. При решении задач встречаются случаи, когда одно или оба из этих условий не выполняются, т. е. когда промежуток интегрирования бесконечен или подынтегральная функция не ограничена. Такие интегралы называются несобственными. Различают несобственные интегралы 1-го и 2-го рода в зависимости от того, имеем ли мы дело с бесконечностью промежутка интегрирования или с неограниченностью подынтегральной функции.

Геометрический смысл несобственного интеграла

Хотя несобственные интегралы и нельзя рассматривать как разделяющие числа для сумм Дарбу, иногда им можно придать определенный смысл с помощью дополнительного предельного перехода. Начнем со случая, когда промежутком интегрирования является луч [a,+infty) . Предположим, что функция y=f(x) интегрируема на каждой конечной части луча, т. е. что для любого c>a существует интеграл $textstyle{I(c)= intlimits_{a}^{c} f(x),dx}$ . За значение интеграла $textstyle{intlimits_{a}^{+infty} f(x),dx}$ естественно принять предел функции I(c) , когда с стремится к +infty , т. е. когда промежуток интегрирования стремится заполнить весь луч [a,+infty) (рис. 18).

Может, однако, случиться, что этот предел не существует. Поэтому будем различать два случая:

а) Если предел $lim_{cto+infty}I(c)$ существует и конечен, то несобственный $textstyle{intlimits_{a}^{+infty} f(x),dx}$ интеграл называют сходящимся, а значение этого предела — значением несобственного интеграла. В этом случае

$intlimits_{a}^{+infty} f(x),dx= lim_{cto+infty}intlimits_{a}^{c} f(x),dx,.$

(1)

б) Если предел в правой части равенства (1) не существует, говорят, что несобственный интеграл $textstyle{intlimits_{a}^{+infty} f(x),dx}$ расходится.

При аналогичных предположениях относительно функции y=f(x) можно рассмотреть случай, когда верхний предел фиксирован, а нижний предел стремится к -infty:

$intlimits_{-infty}^{b}f(x),dx= lim_{cto-infty} intlimits_{c}^{b} f(x),dx,.$

(2)

Если предел, стоящий в правой части равенства (2), конечен, то несобственный интеграл $textstyle{intlimits_{-infty}^{b} f(x),dx}$ называют сходящимся, в противном случае его называют расходящимся.

Наконец, можно определить и несобственный интеграл вида $textstyle{ intlimits_{-infty}^{+infty} f(x),dx= intlimits_{mathbb{R}}f(x),dx}$ . Будем считать, что функция y=f(x) интегрируема на всей числовой прямой (mathbb{R}) . Выберем на прямой произвольную точку . Эта точка разобьет прямую на два луча: (-infty,a] и [a,+infty) . Если существуют несобственные интегралы

$intlimits_{-infty}^{a} f(x),dx,,qquad intlimits_{a}^{+infty} f(x),dx,,$

то говорят, что существует и несобственный интеграл $textstyle{intlimits_{-infty}^{+infty} f(x),dx}$ . В этом случае полагают

$intlimits_{-infty}^{+infty} f(x),dx= intlimits_{-infty}^{a} f(x),dx+ intlimits_{a}^{+infty} f(x),dx,.$

(3)

где несобственные интегралы, содержащиеся в правой части равенства (3), определены соответственно равенствами (1) и (2). Легко проверить, что значение интеграла не зависит от выбора точки .

Пример 1. Вычислить несобственный интеграл $intlimits_{1}^{+infty} frac{dx}{1+x^2}$ с бесконечным верхним пределом.

Решение. Подынтегральная функция $y=frac{1}{1+x^2}$ всюду непрерывна и, следовательно, интегрируема в любом конечном промежутке. Имеем:

$begin{aligned}intlimits_{1}^{+infty} frac{dx}{1+x^2} &= lim_{bto+infty}intlimits_{1}^{b} frac{dx}{1+x^2}= left.{lim_{bto+infty} operatorname{arctg}x}right|_{1}^{b}= lim_{bto+infty}bigl(operatorname{arctg}b- operatorname{arctg}1bigr)=\ &=lim_{bto+infty}operatorname{arctg}b- frac{pi}{4}= frac{pi}{2}- frac{pi}{4}= frac{pi}{4},.end{aligned}$

Значит, окончательно имеем $intlimits_{1}^{+infty} frac{dx}{1+x^2}= frac{pi}{4}$ .

Пример 2. Вычислить несобственный интеграл от синуса $intlimits_{-infty}^{pi/2}sin{x},dx$ .

Решение. Имеем:

$intlimits_{-infty}^{pi/2}sin{x},dx= lim_{ato-infty}intlimits_{a}^{pi/2}sin{x},dx= left.{-lim_{ato-infty}cos{x}}right|_{a}^{pi/2}= -lim_{ato-infty}!left(cosfrac{pi}{2}- cos{a}right)= lim_{ato-infty}cos{a},.$

Так как $lim_{ato-infty}cos{a}$ не существует, то несобственный интеграл $intlimits_{-infty}^{pi/2}sin{x},dx$ расходится.

Запись вычислений несобственных интегралов можно упростить, предварительно найдя первообразную для подынтегральной функции y=f(x) . Именно, если F(x) —первообразная функция для f(x) , то

$intlimits_{a}^{+infty}f(x),dx= lim_{bto+infty} intlimits_{a}^{b}f(x),dx= lim_{bto+infty} Bigl[F(b)-F(a)Bigr].$

Предположим, что существует предел $lim_{bto+infty}F(b)$ . Введем обозначение: $lim_{bto+infty}F(b)= F(+infty)$ . Тогда

$intlimits_{a}^{+infty}f(x),dx= F(+infty)-F(a)= Bigl.{F(x)}Bigr|_{a}^{+infty}.$

Аналогично,

$intlimits_{-infty}^{b}f(x),dx= F(b)-F(-infty)= Bigl.{F(x)}Bigr|_{-infty}^{b},$ где $F(-infty)= lim_{ato-infty}F(a)$

Наконец,

$intlimits_{-infty}^{+infty}f(x),dx= F(+infty)-F(-infty)= Bigl.{F(x)}Bigr|_{-infty}^{+infty}.$

Пример 3. Вычислить несобственный интеграл $intlimits_{-infty}^{+infty} frac{dx}{1+x^2}$ .

Решение. Имеем:

$intlimits_{-infty}^{+infty} frac{dx}{1+x^2}= Bigl.{}Bigr|_{-infty}^{+infty}= lim_{bto+infty}operatorname{arctg}b- lim_{ato-infty}operatorname{arctg}a= frac{pi}{2}-left(-frac{pi}{2}right)=pi,.$

Пример 4. Исследовать на сходимость несобственный интеграл $intlimits_{1}^{+infty}frac{dx}{x^{alpha}}$ .

Решение. Если alpha=1 , то $intlimits_{1}^{+infty}frac{dx}{x}= Bigl.{ln|x| }Bigr|_{1}^{+infty}= lim_{bto+infty}ln|b|- ln1= +infty,.$ .

Если alphane1 , то $intlimits_{1}^{+infty} frac{dx}{x^{alpha}}= left.{frac{x^{-alpha+1}}{-alpha+ 1}}right|_{1}^{+infty}= frac{1}{1-alpha} lim_{bto+infty} b^{1-alpha}- frac{1}{1-alpha},.$ .

Сходимость или расходимость интеграла $textstyle{intlimits_{1}^{+infty} frac{dx}{x^{alpha}}}$ зависит от того, существует или нет предел $lim_{bto+infty} b^{1-alpha}$ . Если alpha>1 , тo $lim_{bto+infty} b^{1-alpha}=0$ ; если alpha<1 , то $lim_{bto+infty} b^{1-alpha}=+infty$ . Таким образом, $textstyle{intlimits_{1}^{+infty} frac{dx}{x^{alpha}}}$ сходится, если alpha>1 , и расходится, если alphageqslant1 .

При исследовании на сходимость несобственных интегралов оказываются полезными следующие утверждения:

а) Если сходится интеграл $intlimits_{a}^{+infty} f(x),dx$ , то при A>a сходится и интеграл $intlimits_{A}^{+infty}f(x),dx$ . При этом

$intlimits_{a}^{+infty}f(x),dx= intlimits_{a}^{A}f(x),dx+ intlimits_{A}^{+infty}f(x),dx,.$

б) Если сходятся интегралы $intlimits_{a}^{+infty} f(x),dx$ и $intlimits_{a}^{+infty} g(x),dx$ , то и интеграл $intlimits_{a}^{+infty} bigl(lambda f(x)+mu g(x)bigr)dx$ сходится, причем

$intlimits_{a}^{+infty} bigl(lambda f(x)+mu g(x)bigr)dx= lambda intlimits_{a}^{+infty}f(x),dx+ mu intlimits_{a}^{+infty}g(x),dx,.$

Признаки сходимости несобственных интегралов 1-го рода

В дальнейшем мы будем обычно иметь дело с несобственными интегралами от неотрицательных функций. Если функция y=f(x) неотрицательна на луче [a;+infty) , то функция $textstyle{F(x)= intlimits_{a}^{x}f(x),dx}$ возрастает на этом луче. Поэтому она имеет предел при xto+infty в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение:

а) Для сходимости несобственного интеграла $intlimits_{a}^{+infty} f(x),dx$ от неотрицательной функции y=f(x), aleqslant x<+infty , необходимо и достаточно, чтобы функция $F(x)= intlimits_{a}^{x}f(x),dx$ была ограничена, т. е. чтобы нашлось такое число , что $intlimits_{a}^{x}f(x),dx leqslant M$ для всех xin[a,+infty) .

Непосредственно найти такое число бывает довольно сложно, поэтому во многих случаях оказывается полезным следующее утверждение:

б) Если на луче [a,+infty) выполняется неравенство 0leqslant f(x)leqslant g(x) и интеграл $intlimits_{a}^{+infty} g(x),dx$ сходится, то сходится и интеграл $intlimits_{a}^{+infty} f(x),dx$ .

В самом деле, из f(x)leqslant g(x) следует, что для любого имеем:

$intlimits_{a}^{x}f(x),dxleqslant intlimits_{a}^{x} g(x),dx,.$

Но функция $Y(x)= intlimits_{a}^{x}g(x),dx$ возрастает, и потому ее предел при xto+infty не меньше любого из ее значений: Y(x)leqslant Y(+infty) . Поэтому для всех xin[a,+infty) имеем: $intlimits_{a}^{x}f(x),dx leqslant M$ , где M=Y(+infty) . А тогда на основании предыдущего утверждения интеграл $intlimits_{a}^{+infty}f(x),dx$ сходится.

Из доказанного вытекает, что если 0leqslant f(x)leqslant g(x) при xin[a,+infty) и интеграл $intlimits_{a}^{+infty}f(x),dx$ расходится, то расходится и интеграл $intlimits_{a}^{+infty}g(x),dx$ — в противном случае в соответствии с утверждением б) интеграл $intlimits_{a}^{+infty}f(x),dx$ сходился бы.

Пример 5. Исследуем на сходимость интеграл $intlimits_{a}^{+infty} frac{dx}{1+x^3}$ .

Решение. Мы имеем $0leqslant frac{1}{1+x^3}<frac{1}{x^3}$ при xgeqslant1 . Но интеграл $intlimits_{a}^{+infty}frac{dx}{x^3}$ сходится (см. пример 4). Поэтому сходится и исходный интеграл.

Пример 6. Исследуем на сходимость интеграл $intlimits_{a}^{+infty} frac{dx}{1+sqrt{x}}$ .

Решение. Так как $frac{1}{1+sqrt{x}}> frac{1}{3sqrt{x}}>0$ при xgeqslant1 , а интеграл $intlimits_{a}^{+infty}frac{dx}{3sqrt{x}}$ расходится (см. пример 4 при alpha=1/2 ), то расходится и заданный интеграл.

Несобственные интегралы 2-го рода

Рассмотрим теперь случай, когда промежуток интегрирования [a,b] конечен, но подынтегральная функция y=f(x) не ограничена на нем. Строение таких функций может быть очень сложным. Мы ограничимся рассмотрением случая, когда можно указать конечное множество особых точек c_1,c_2,ldots,c_n , таких, что в сколь угодно малых окрестностях этих точек функция f(x) не ограничена, но после удаления этих окрестностей получаем промежутки, на которых функция интегрируема.

Геометрический смысл несобственного интеграла 2-го рода

Сначала изучим случай, когда множество особых точек состоит лишь из точки . В этом случае f(x) не ограничена на всем отрезке [a,b] , но интегрируема на любом из отрезков [a,b-varepsilon] (рис. 19). За значение интеграла $intlimits_{a}^{b} f(x),dx$ естественно принять предел $lim_{varepsilon to+0} intlimits_{a}^{b-varepsilon}f(x),dx$ , если этот предел существует.

Введем следующее определение:

Пусть функция y=f(x) не ограничена на отрезке [a,b] , но интегрируема на любом из отрезков [a,b-varepsilon] , где varepsilon>0 . Несобственный интеграл $intlimits_{a}^{b} f(x),dx$ называют сходящимся, если существует предел $lim_{varepsilonto+0} intlimits_{a}^{b-varepsilon}f(x),dx$ . Значение этого предела и называют значением интеграла $intlimits_{a}^{b}f(x),dx$ . Если же этот предел не существует, то интеграл называют расходящимся.

Аналогично, если функция не ограничена на отрезке [a;b] , но интегрируема на любом отрезке [a-varepsilon;b] , то полагаем

$intlimits_{a}^{b}f(x),dx= lim_{varepsilonto+0} intlimits_{a+varepsilon}^{b}f(x),dx,.$

Наконец, если единственная особая точка лежит внутри отрезка [a;b] , то положим

$intlimits_{a}^{b}f(x),dx= lim_{varepsilonto+0} intlimits_{a}^{c-varepsilon}f(x),dx+ lim_{varepsilonto+0} intlimits_{c+varepsilon}^{b}f(x),dx,.$

Пусть F(x) — первообразная для функции f(x) . Положим

$F(a+0)= lim_{varepsilonto+0} F(a+varepsilon),qquad F(b-0)= lim_{varepsilonto+0} F(b-varepsilon)$

(если эти пределы существуют). Тогда для сходящихся интегралов, у которых особыми являются лишь точки и , имеем:

$intlimits_{a}^{b} f(x),dx= F(b-0)-F(a+0).$

Если функция F(x) непрерывна в точках и , то получаем:

$intlimits_{a}^{b} f(x),dx= F(b)-F(a).$

Аналогично обстоит дело и в случае, когда подынтегральная функция не ограничена в любой окрестности некоторой внутренней точки отрезка [a;b] .

Пример 7. Вычислим несобственный интеграл второго рода $intlimits_{0}^{1} frac{dx}{sqrt{1-x^2}}$ .

Решение. Этот интеграл является несобственным, так как функция $y=frac{1}{sqrt{1-x^2}}$ не ограничена в любой окрестности точки x=1 . Поскольку первообразная для функции равна arcsin{x} , то, пользуясь определением несобственного интеграла, получаем:

$intlimits_{0}^{1} frac{dx}{sqrt{1-x^2}}= Bigl.{ lim_{varepsilonto+0} arcsin{x}}Bigr|_{0}^{1-varepsilon}= lim_{varepsilonto+0} arcsin(1-varepsilon)- arcsin0,,$

откуда, учитывая непрерывность функции arcsin{x} , окончательно получаем

$intlimits_{0}^{1} frac{dx}{sqrt{1-x^2}}= Bigl.{arcsin{x}}Bigr|_{0}^{1}= frac{pi}{2}-0= frac{pi}{2},.$

Пример 8. Вычислить интеграл $intlimits_{2}^{4} frac{2x,dx}{sqrt[LARGE{3}]{x^2-9}}$ .

Решение. Подынтегральная функция внутри данного промежутка интегрирования имеет одну особую точку x=3 . Найдем первообразную для подынтегральной функции:

$int frac{2x,dx}{sqrt[LARGE{3}]{x^2-9}}= frac{3}{2} sqrt[LARGE{3}]{(x^2-9)^2}+C.$

Так как функция $F(x)= frac{3}{2} sqrt[LARGE{3}]{(x^2-9)^2}$ непрерывна в точке x=3 , то имеем

$intlimits_{2}^{4} frac{2x,dx}{sqrt[LARGE{3}]{x^2-9}}= left.{frac{3}{2} sqrt[LARGE{3}]{(x^2-9)^2}}right|_{2}^{4}= frac{3}{2}bigl(sqrt[LARGE{3}]{49}- sqrt[LARGE{3}]{25}bigr).$

Пример 9. Вычислить $intlimits_{-3}^{3} frac{dx}{sqrt{9-x^2}}$ .

Решение. В данном случае подынтегральная функция имеет две особые точки x_1=-3 и x_2=3 . Пользуясь определением несобственного интеграла и учитывая непрерывность первообразной, получаем, что

$intlimits_{-3}^{3} frac{dx}{sqrt{9-x^2}}= left.{arcsinfrac{x}{3}}right|_{-3}^{3}= frac{pi}{2}- left(-frac{pi}{2}right)= pi,.$

Пример 10. Исследуем на сходимость интеграл $intlimits_{0}^{1} frac{dx}{x}$ .

Решение. Имеем: $intlimits_{0}^{1} frac{dx}{x}= lim_{varepsilonto+0} intlimits_{varepsilon}^{1} frac{dx}{x}= lim_{varepsilonto+0} bigl(ln1-lnvarepsilonbigr)= -lim_{varepsilonto+0} lnvarepsilon= +infty$ . Значит, данный интеграл расходится.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определённый интеграл называется несобственным, если выполняется по крайней мере одно из следующих условий.

Область интегрирования является бесконечной. Например, является бесконечным промежутком .
Функция является неограниченной в окрестности некоторых точек области интегрирования.

Если интервал [a,b] конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.

Несобственные интегралы I рода[править | править код]

Несобственный интеграл первого рода

Пусть f(x) определена и непрерывна на интервале и ${displaystyle forall A>a exists int limits _{a}^{A}f(x)dx}$ . Тогда:

Если $exists lim_{A to +infty}intlimits_{a}^{A} f(x)dx = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{+infty} f(x)dx$ и интеграл называется несобственным интегралом Римана первого рода. В этом случае $I=intlimits_{a}^{+infty} f(x)dx$ называется сходящимся.
Если не существует конечного $lim_{A to +infty}intlimits_{a}^{A} f(x)dx$ ( или ), то интеграл $intlimits_{a}^{+infty} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Пусть f(x) определена и непрерывна на множестве от и $forall B < b Rightarrow exists intlimits_{B}^{b} f(x)dx$ . Тогда:

Если $exists lim_{B to -infty}intlimits_{B}^{b} f(x)dx = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{-infty}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана первого рода. В этом случае $I=intlimits_{-infty}^{b} f(x)dx$ называется сходящимся.
Если не существует конечного $lim_{B to -infty}intlimits_{B}^{b} f(x)dx$ ( или ), то интеграл $intlimits_{-infty}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

$intlimits_{-infty}^{+infty} f(x)dx = intlimits_{-infty}^{c} f(x)dx + intlimits_{c}^{+infty} f(x)dx$ , где с — произвольное число.

Геометрический смысл несобственного интеграла I рода[править | править код]

Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.

Примеры[править | править код]

${displaystyle int limits _{-infty }^{-1}{1 over x^{2}}dx=lim _{ato -infty }int limits _{a}^{-1}{1 over x^{2}}dx=lim _{ato -infty }{Bigl .}-{frac {1}{x}}{Bigr |}_{a}^{-1}=1+lim _{ato -infty }{frac {1}{a}}=1+0=1}$

Несобственные интегралы II рода[править | править код]

Несобственный интеграл Римана второго рода

Пусть f(x) определена на (a,b] , терпит бесконечный разрыв в точке x = a и $forall delta > 0 Rightarrow exists intlimits_{a + delta}^{b} f(x)dx = mathcal{I}(delta)$ . Тогда:

Если $exists lim_{delta to 0+0} mathcal{I}(delta) = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если $lim_{delta to 0+0} mathcal{I}(delta) = infty ; (pminfty$ или , то обозначение сохраняется, а $mathcal{I}=intlimits_{a}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Пусть f(x) определена на [a,b) , терпит бесконечный разрыв при x = b и $forall delta > 0 Rightarrow exists intlimits_{a}^{b-delta} f(x)dx = mathcal{I}(delta)$ . Тогда:

Если $exists lim_{delta to 0+0} mathcal{I}(delta) = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если $lim_{delta to 0+0} mathcal{I}(delta) = infty ; (pminfty$ или , то обозначение сохраняется, а $mathcal{I}=intlimits_{a}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Если функция f(x) терпит разрыв во внутренней точке отрезка [a;b] , то несобственный интеграл второго рода определяется формулой:

${displaystyle int limits _{a}^{b}f(x)dx=int limits _{a}^{c}f(x)dx+int limits _{c}^{b}f(x)dx.}$

Геометрический смысл несобственных интегралов II рода[править | править код]

Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.

Пример[править | править код]

$intlimits_{0}^{1} {dx over x} = lim_{delta to 0+0} Bigl. ln |x| Bigr|_{0+delta }^1 = 0 - lim_{delta to 0+0} ln delta = + infty$

Отдельный случай[править | править код]

Пусть функция f(x) определена на всей числовой оси и имеет разрыв в точках .

Тогда можно найти несобственный интеграл $intlimits_{-infty }^{+infty} f(x)dx = intlimits_{-infty }^{x_1} f(x)dx + sum_{j=1}^{k-1} {intlimits_{x_j}^{x_{j+1}} f(x)dx}+ intlimits_{x_k}^{+infty} f(x)dx$

Критерий Коши[править | править код]

1. Пусть f(x) определена на множестве от и ${displaystyle forall A>a exists int limits _{a}^{A}f(x)dx}$ .

Тогда $mathcal{I}=intlimits_{a}^{+infty} f(x)dx$

сходится ${displaystyle Leftrightarrow forall varepsilon >0 exists A(varepsilon )>a:forall (A_{2}>A_{1}>A)Rightarrow left|,int limits _{A_{1}}^{A_{2}}f(x)dxright|<varepsilon }$

2. Пусть f(x) определена на (a,b] и ${displaystyle forall delta >0 exists int limits _{a+delta }^{b}f(x)dx}$ .

Тогда $mathcal{I}=intlimits_{a}^{b} f(x)dx$

сходится ${displaystyle Leftrightarrow forall varepsilon >0Rightarrow exists delta (varepsilon )>0:forall (0<delta _{1}<delta _{2}<delta )Rightarrow left|,int limits _{a+delta _{1}}^{a+delta _{2}}f(x)dxright|<varepsilon }$

Абсолютная сходимость[править | править код]

Интеграл $intlimits_{a}^{+infty} f(x)dx left(intlimits_{a}^{b} f(x)dxright)$ называется абсолютно сходящимся, если $intlimits_{a}^{+infty} |f(x)|dx left(intlimits_{a}^{b} |f(x)|dxright)$ сходится.
Если интеграл сходится абсолютно, то он сходится.

Условная сходимость[править | править код]

Интеграл $intlimits_{a}^{+infty} f(x)dx$ называется условно сходящимся, если $intlimits_{a}^{+infty} f(x)dx$ сходится, а $intlimits_{a}^{+infty} |f(x)|dx$ расходится.

См. также[править | править код]

Интеграл Римана
Интеграл Лебега
Метод Самокиша — численный метод для вычисления интегралов с особенностями.

Литература[править | править код]

Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.

Источник

П 18. Главное значение несобственного интеграла.

Несобственный интеграл – Основные понятия и теоремы

Свойства несобственного интеграла

Примеры с решением

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Пример 7.

Пример 8.

Пример 9.

Несобственные интегралы

Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)

Интегралы от неограниченных функций (несобственные интегралы II типа)

Интегралы с бесконечным промежутком интегрирования

Признаки сходимости несобственных интегралов 1-го рода

Несобственные интегралы 2-го рода

Несобственные интегралы I рода[править | править код]

Геометрический смысл несобственного интеграла I рода[править | править код]

Примеры[править | править код]

Несобственные интегралы II рода[править | править код]

Геометрический смысл несобственных интегралов II рода[править | править код]

Пример[править | править код]

Отдельный случай[править | править код]

Критерий Коши[править | править код]

Абсолютная сходимость[править | править код]

Условная сходимость[править | править код]

См. также[править | править код]

Литература[править | править код]

Вам также может понравиться

Длина окружности как найти диаметр онлайн калькулятор

Как найти песню dance monkey

Как найти клиентов оптовиков

Добавить комментарий Отменить ответ