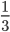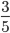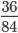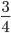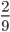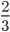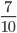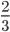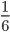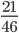Дроби делятся на сократимые и несократимые дроби. Рассмотрим подробнее какую дробь называются сократимой и какую дробь называют несократимой.
Сократимая дробь, определение и примеры.
Определение:
Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель не равный нулю и единице.
Например:
Докажите, что дробь (frac{20}{35}) является сократимой.
Решение:
Распишем числитель и знаменатель на простые множители, найдем их наибольший общий делитель (НОД).
20=2⋅2⋅5
35=5⋅7
Так как у числителя и знаменателя повторяется множитель 5, это число и будет их наибольшим общим делителем.
НОД(20, 35)=5
Сократим дробь на НОД.
(frac{20}{35}=frac{4 times 5}{7 times 5}=frac{4}{7})
Из сократимой дроби (frac{20}{35}) получили несократимую дробь (frac{4}{7}).
Несократимая дробь, определение и примеры.
Какие же дроби несократимые или что значит несократимая дробь? Ответ на вопрос кроется в определении.
Определение:
Несократимая дробь – это дробь у которой числитель и знаменатель имеют только один общий делитель равный единице, то есть числитель и знаменатель являются взаимно-простыми числами.
Рассмотрим пример:
Докажите, что дробь (frac{137}{149}) является несократимой дробью.
Решение:
Число 137 является простым, так как оно делиться на 1 и на само себя.
Число 149 является простым, так как оно делиться на 1 и на само себя.
У числителя 137 и знаменателя 149 нет общих делителей, поэтому дробь (frac{137}{149}) является несократимой.
Правило несократимой дроби.
Правило:
- Нужно расписать на простые множители числитель и знаменатель.
- Нужно посмотреть есть ли у числителя и знаменателя общие множители. Если множители есть, то сократить дробь.
- Оставшиеся множители перемножить и записать полученную несократимую дробь.
Пример:
Запишите сократимую дробь в виде несократимой обыкновенной дроби (frac{55}{100}).
Решение:
По правилу несократимой дроби распишем числитель и знаменатель на простые множители.
55=5⋅11
100=5⋅2⋅2⋅5
Видим, что у числителя и знаменателя есть общий множитель равный 5, поэтому сокращаем дробь на 5.
(frac{55}{100}=frac{5 times 11}{5 times 20}=frac{11}{20})
Ответ: получили несократимую дробь (frac{11}{20}).
Неправильные сократимые и несократимые дроби.
Чтобы перевести неправильную сократимую дробь в неправильную несократимую дробь, мы пользуемся теми же правилами, что и для правильной сократимой дроби. Рассмотрим пример:
Запишите неправильную сократимую дробь в виде неправильной несократимой дроби (frac{32}{20}).
Решение:
Разложим числитель и знаменатель на простые множители.
32=2⋅2⋅2⋅2⋅2
20=5⋅2
Общий множитель у числителя и знаменателя равен 2. Распишем
(frac{32}{20}=frac{2 times 2 times 2 times 2 times 2}{5 times 2}=frac{16 times 2}{5 times 2}=frac{16}{5})
Ответ: получили несократимую неправильную дробь (frac{16}{5}).
Вопросы по теме:
Как узнать сократима ли дробь?
Ответ: чтобы узнать сократима ли дробь для начала нужно расписать числитель и знаменатель на простые множители, а потом посмотреть если у них общие множители, если есть, то дробь сократима, иначе – несократима. Рассмотрим пример.
Определите сократима ли дробь (frac{16}{25}).
Решение:
Распишем числитель и знаменатель на простые множители.
16=2⋅2⋅2⋅2
25=5⋅5
Видно, что у числителя и знаменателя нет общих множителей (одинаковых множителей), следовательно, дробь несократима.
Пример:
Сколько несократимых правильных дробей: а) (frac{8}{25}) б) (frac{6}{4}) в) (frac{13}{5}) г) (frac{36}{44}).
Решение:
а) У числителя и знаменателя дроби (frac{8}{25}) (8=2⋅2⋅2, 25=5⋅5) нет общих множителей, поэтому это правильная несократимая дробь. По условию это дробь нам подходит.
б) У числителя и знаменателя дроби (frac{6}{4}) (6=2⋅3, 4=2⋅2, (frac{6}{4}=frac{2 times 3}{2 times 2}=frac{3}{2}) ) есть общий множитель равный 2, поэтому это дробь сократимая и еще неправильная, потому что числитель больше знаменателя. По условию задания эта дробь нам не подходит.
в) Числитель и знаменатель дроби (frac{13}{5}), 5 и 13 простые числа, поэтому общих множителей кроме 1 у них нет, дробь несократимая. Так как числитель больше знаменателя дробь неправильная, поэтому по условию задания нам она не подходит.
г) Числитель и знаменатель дроби (frac{36}{44}) (36=2⋅2⋅3⋅3, 44=2⋅2⋅11) имеют общий множитель равный 4, поэтому дробь (frac{36}{44}=frac{4 times 9}{4 times 11}=frac{9}{11}) является сократимой, правильной. Нам по условию задания не подходит.
Ответ: (frac{8}{25}) несократимая, правильная дробь.
Пример:
Сколько имеется правильных несократимых дробей со знаменателем: а) 145 б) 123 в) 133 г) 115.
Решение:
а) Распишем на простые множители знаменатель 145:
145=5⋅29
Нужно исключить все числа от 1 до 144 кратные 5 и 29.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140.
На 29 делится: 29, 58, 87, 116.
В сумме получаем 32 числа, которые имеют общий множитель с число 145. Всего у нас чисел 144.
144-32=112
Ответ: 112 правильных несократимых дробей со знаменателем 145.
б) Распишем на простые множители знаменатель 123:
123=3⋅41
В диапазоне чисел от 1 до 122 исключаем числа кратные 3 и 41.
На число 3 делится, поэтому не могут находиться в числителе: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120.
На 41 делится: 41, 82.
В сумме получаем 40+2=42 числа, которые имеют общий множитель с число 123, поэтому мы их исключим. Всего у нас чисел 122.
122-42=80
Ответ: 80 правильных несократимых дробей со знаменателем 123.
в) Распишем на простые множители знаменатель 133:
133=7⋅19
Числа от 1 до 132 исключаем, они делятся на 7 и 19, для того чтобы получить все несократимые дроби от (frac{1}{133}) до (frac{132}{133}).
Число 7 кратно: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126. Всего 18 чисел.
Число 19 кратно:19, 38, 57, 76, 95, 114. Всего 6 чисел.
132-18-6=108
Ответ: 108 правильных несократимых дробей со знаменателем 133.
г) Распишем на простые множители знаменатель 115:
115=5⋅23
Числа от 1 до 114 исключаем.
На 5 делится: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110. Всего 22 числа.
На 23 делится число: 23, 46, 96, 92. Всего 4 чисел.
114-22-4=88
Ответ: 88 правильных несократимых дробей со знаменателем 115.
Нестандартная задача по математике:
Когда нельзя сокращать сократимую обыкновенную дробь?
Ответ: когда сократимая обыкновенная дробь является номером углового дома или квартала.
Данная статья посвящена рассмотрению сократимых и несократимых дробей. Приведем примеры, дадим определения сократимых и несократимых дробей. Выясним, как определить, можно ли сократить конкретную дробь.
Сократимые и несократимые дроби
Все обыкновенные дроби вида ab можно разделить на сократимые и несократимые. Разделение объясняется соответственно наличием или отсутствием общих для числителя и знаменателя дроби делителей. Приведем определения.
Обыкновенная сократимая дробь – такая дробь, для числителя и знаменателя которой существует положительный общий делитель, отличный от единицы.
Обыкновенная несократимая дробь – такая дробь, числитель и знаменатель которой являются взаимно простыми числами, то есть имеют единственный общий положительный делитель, равный единице.
Приведем примеры сократимых и несократимых дробей.
Дробь 1545 – сократимая. Действительно, как числитель, так и знаменатель можно разделить на 5. Другими словами, числитель и знаменатель этой дроби имеют общий делитель.
Другие примеры сократимых дробей – 1212, 366, 832
Дробь 712 – несократимая, так как ее числитель и знаменатель являются взаимно простыми числами.
Другие несократимые дроби – 914, 1112, 833.
Проверка дроби на сократимость
Часто с первого взгляда на конкретную дробь сложно сказать, является она сократимой или несократимой. Конечно, исключения составляют простые случаи, когда по признакам делимости сразу можно выявить общий делитель числителя и знаменателя.
К примеру, по признаку делимости на 10 сразу можно сказать, что дробь 470540 сократима, так как числитель и знаменатель имеют общий делитель, равный 10. Так же, дробь 384428 является сократимой по признаку делимости на 2.
Но как быть с более сложными случаями, когда признаки делимости не могут помочь? Например, когда нужно узнать, сократима ли дробь 288329342439. Для таких случаев существует общий метод проверки дроби на сократимость.
Вычисляем наибольший общий делитель числителя и знаменателя дроби.
- Если НОД равен единице, то дробь является несократимой.
- Если НОД отличен от единицы, то дробь сократима.
Посмотрим на практическое применение этого правила.
Выясним, сократима ли обыкновенная дробь 495539. Для этого вычислим НОД числителя и знаменателя, применяя алгоритм Евклида.
539=495·1+44495=44·11+1144=11·4
Отсюда НОД(495, 539)=11. Следовательно, числитель и знаменатель дроби не являются взаимно простыми числами, и дробь сократима.
В математических выкладках, если при вычислениях получилась сократимая дробь, принято производить ее сокращение и записывать в виде несократимой дроби.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:
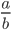
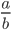
где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений —
на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.
3 : 3 =1
15 : 3 = 5
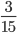
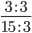
Сокращение выполнено: 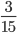
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.
4 : 2 = 2
16 : 2 = 8
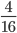
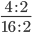
Сокращение выполнено: 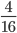
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 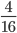
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
-
— несократимая дробь, так как по свойствам НОД мы знаем, что:
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1
36 : 12 = 3
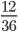
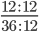
Сокращение выполнено: 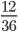
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3
25 : 5 = 5
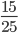
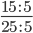
Сокращение выполнено: 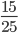
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
- Найдите НОД числителя и знаменателя дроби.
- Разделите числитель и знаменатель дроби на НОД.
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
- Например, дана дробь
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.
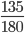
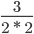
Сокращение выполнено: 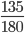
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9
18 : 9 = 2
81 : 9 = 9
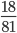
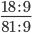
Сокращение выполнено: 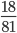
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:
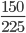
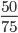
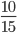
Сокращение выполнено: 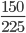
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7
240 : 24 = 10
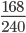
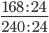
Сокращение выполнено: 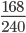
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2
540 : 180 = 3
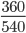
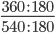
Сокращение выполнено: 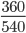
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1
2520 : 420 = 6
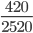
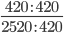
Сокращение выполнено. Дробь приведена к несократимому виду: 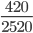
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21
3450 : 75 = 46
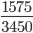
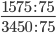
Сокращение выполнено. Дробь приведена к несократимому виду: 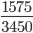
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Сократимые и несократимые дроби
Все обыкновенные дроби делятся на сократимые и несократимые дроби. Такое разделение дробей зависит от наличия или отсутствия общих делителей числителя и знаменателя, отличных от единицы.
Определение 1
Сократимая обыкновенная дробь — это дробь, у которой числитель и знаменатель имеют положительный отличный от единицы общий делитель.
Пример 1
Например, обыкновенная дробь $frac{4}{20}$ является сократимой, т.к. числитель $4$ и знаменатель $20$ делятся на $4$, т.е. имеют положительный общий делитель $4$, отличный от единицы. Сократимыми также являются дроби $frac{3}{12}$, $frac{7}{7}$. Легко увидеть, что числитель $3$ и знаменатель $12$ имеют отличный от единицы положительный общий делитель $3$, а числа $7$ и $7$ имеют общий делитель $7$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Несократимая обыкновенная дробь — это дробь, у которой числитель и знаменатель являются взаимно простыми, т.е. имеют единственный общий положительный делитель — единицу.
Пример 2
Например, дроби $frac{3}{5}$, $frac{11}{4}$, $frac{171}{5}$, $frac{18}{35}$ являются несократимыми, т.к. числитель и знаменатель каждой из них — взаимно простые числа.
Правила проверки дроби на сократимость
В самых простых случаях проверить дробь на сократимость можно с помощью признаков делимости.
Например, легко увидеть, что дробь $frac{230}{450}$ сократима, т.к. ее числитель и знаменатель имеют общий делитель $10$. Или с помощью признака делимости на $2$ можно утверждать, что дробь $frac{368}{6824}$ сократима.
В более сложных случаях с помощью признаков делимости сложно выяснить, сократима ли данная дробь. Например, сложно определить, сократима дробь $frac{240671}{357893}$. В таких случаях удобно использовать общий метод проверки дроби на сократимость.
«Сократимые дроби» 👇
Правило проверки обыкновенной дроби на сократимость
Вычислить наибольший общий делитель (НОД) числителя и знаменателя данной дроби:
- если $НОД=1$, то дробь является несократимой;
- если $НОДne 1$, то дробь является сократимой.
Пример 3
Проверить на сократимость обыкновенную дробь $frac{203}{861}$.
Решение.
Проверим, являются ли числитель $203$ и знаменатель $861$ взаимно простыми числами. Для этого найдем НОД числителя и знаменателя и проверим, равен ли он единице.
НОД вычислим по алгоритму Евклида:
$frac{861}{203}=4$(остаток $49$)
$frac{203}{49}=4$ (остаток $7$)
$frac{49}{7}=7$ (остаток $0$)
$frac{33}{25}=1$ (остаток $8$)
$frac{25}{8}=3$ (остаток $1$)
Таким образом, НОД($861, 203)=7$. Итак, числитель и знаменатель данной дроби не являются взаимно простыми числами, поэтому $frac{203}{861}$ — сократимая дробь.
Ответ: дробь $frac{203}{861}$ — сократимая.
Сокращение дробей
Чтобы сократить дробь, нужно ее числитель и знаменатель разделить на их общий положительный отличный от единицы делитель. В результате сокращения дроби получают новую дробь, равную исходной, но с меньшим числителем и знаменателем.
Например, сократим обыкновенную дробь $frac{7}{21}$ на $7$, т.к. $7div 7=1$ и $21div 7=3$. В результате сокращения получим дробь $frac{1}{3}$, для которой $frac{7}{21}=frac{7cdot 1}{7cdot 3}=frac{1}{3}$.
Приведение обыкновенных дробей к несократимому виду
Обычно дроби сокращают для получения несократимых дробей, которые равны исходным сократимым дробям. Несократимую дробь можно получить в результате сокращения исходной сократимой дроби на наибольший общий делитель ее числителя и знаменателя — наибольшее число, на которое можно сократить данную дробь.
Дробь $frac{a:НОДleft(a, bright)}{b:НОДleft(a, bright)}$ — несократимая, т.к. $a:НОДleft(a, bright)$ и $b:НОДleft(a, bright)$ — взаимно простые числа.
Таким образом, для приведения обыкновенной дроби к несократимому виду необходимо ее числитель и знаменатель разделить на их НОД.
Под фразой «сократите дробь» чаще всего подразумевают приведение исходной дроби к несократимому виду. Т.е. именно деление числителя и знаменателя на их НОД, а не деление на любой их общий делитель.
Правило сокращения дробей
-
Найти НОД числителя и знаменателя дроби.
-
Разделить числитель и знаменатель дроби на их НОД, в результате чего получают несократимую дробь, равную исходной.
Пример 4
Сократить дробь $frac{187}{231}$.
Решение.
Воспользуемся правилом сокращения дробей:
-
Найдем НОД($187, 231$).
Наиболее удобным является алгоритм Евклида:
[231=187cdot 1+44][187=44cdot 4+11][44=11cdot 4]
Таким образом, НОД($187, 231)=11$.
-
Разделим числитель и знаменатель дроби $frac{187}{231}$ на $11$, в результате чего получим несократимую дробь, равную исходной дроби:
[frac{187}{231}=frac{17cdot 11}{21cdot 11}=frac{17}{21}.]
Ответ: $frac{187}{231}=frac{17}{21}$
Иногда для сокращения дробей (в более простых случаях) применяют способ textit{разложения дроби на простые множители}, после чего убираются все общие множители из числителя и знаменателя. Этот способ вытекает из правила сокращения дробей, т.к. НОД равен произведению всех общих простых множителей числителя и знаменателя.
Пример 5
Сократить дробь $frac{720}{960}$.
Решение.
Разложим числитель и знаменатель на простые множители:
Рисунок 1.
Получим $frac{720}{960}=frac{2cdot 2cdot 2cdot 2cdot 3cdot 3cdot 5}{2cdot 2cdot 2cdot 2cdot 2cdot 2cdot 3cdot 5}$.
Избавимся от общих множителей в числителе и знаменателе (для удобства их часто зачеркивают):
[frac{720}{960}=frac{2cdot 2cdot 2cdot 2cdot 3cdot 3cdot 5}{2cdot 2cdot 2cdot 2cdot 2cdot 2cdot 3cdot 5}=frac{3}{2cdot 2}=frac{3}{4}.]
Ответ: $frac{720}{960}=frac{3}{4}$.
Также можно использовать еще один способ сокращения дроби — последовательное сокращение. Т.е. на каждом шаге проводят сокращение дроби на общий делитель числителя и знаменателя, который легко определяется, например, по признакам делимости.
Пример 6
Сократить дробь $frac{5000}{21150}$.
Решение.
Легко увидеть, что общим множителем числителя и знаменателя дроби является число $10$. После сокращения дроби $frac{5000}{21150}$ на $10$ получим $frac{500}{2115}$.
Далее сократим дробь $frac{500}{2115}$ на $5$, исходя из признака делимости на $5$. Получим $frac{100}{423}$ — несократимую дробь. Сокращение завершено.
Ответ: $frac{5000}{21150}=frac{100}{423}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В математике несократимая (приведённая) дробь — обыкновенная дробь вида 




Обыкновенные дроби[править | править код]
Каждое ненулевое рациональное число единственным образом может быть представлено в виде несократимой дроби вида 



Для приведения обыкновенной дроби 

Для целого числа n представлением в виде несократимой дроби является
Вариации и обобщения[править | править код]
Свойства несократимости, существующие для обыкновенных дробей, сохраняются для произвольного факториального кольца, то есть кольца, в котором справедлив аналог основной теоремы арифметики. Всякую дробь из элементов факториального кольца (с ненулевым знаменателем) можно представить в несократимом виде, причём однозначно с точностью до делителей единицы данного кольца.
Кольцо гауссовых чисел состоит из комплексных чисел вида 




Многочлены с коэффициентами из некоторого кольца также образуют факториальное кольцо — кольцо многочленов. рациональные функции, то есть дроби, в числителях и знаменателях которых стоят многочлены. Делителями единицы здесь будут ненулевые числа (как многочлены нулевой степени). Неоднозначность представления можно устранить, потребовав, чтобы многочлен в знаменателе был приведённым.
Однако над произвольным кольцом элемент кольца частных, вообще говоря, не обязан иметь единственное, с точностью до делителей единицы, представление в виде несократимой дроби, поскольку основная теорема арифметики справедлива не во всяком кольце[4]. Рассмотрим, к примеру, комплексные числа вида 


У второй и третьей дробей и числитель, и знаменатель — простые числа для указанного кольца, поэтому обе дроби несократимы.
Примечания[править | править код]
- ↑ Гусев, Мордкович, 2013, с. 29—30.
- ↑ Выгодский, 2006, с. 81—82.
- ↑ Weisstein, Eric W. Irreducible Fraction (англ.) на сайте Wolfram MathWorld.
- ↑ Жиков В.В. Основная теорема арифметики // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 3. — С. 112—117.
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
- Гусев В. А., Мордкович А. Г. Математика: учебно-справочное пособие. — М.: Астрель, 2013. — 671 с. — (Справочник школьника). — ISBN 978-5-271-07165-2.
Ссылки[править | править код]
- Weisstein, Eric W. Reduced Fraction (англ.) на сайте Wolfram MathWorld.
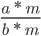
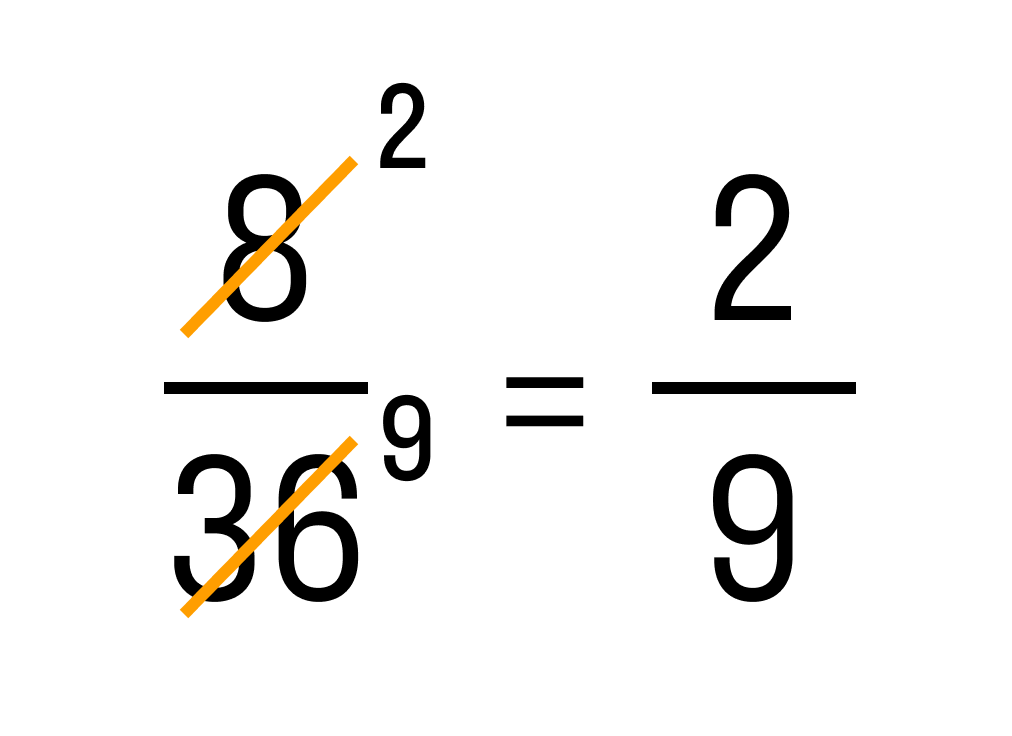
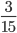
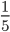
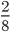

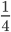
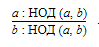 — несократимая дробь, так как по свойствам НОД мы знаем, что:
— несократимая дробь, так как по свойствам НОД мы знаем, что: