Как найти нетривиальное решение однородной системы

Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений

Пример 2 . Найти общее решение и фундаментальную систему решений системы
Решение.

Задание . Исследовать и решить систему линейных уравнений.
Пример 4

Задание . Найти общее и частное решения каждой системы.
Решение. Выпишем основную матрицу системы:

5	-2	9	-4	-1
1	4	2	2	-5
6	2	11	-2	-6
x1	x2	x3	x4	x5

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-5). Добавим 2-ую строку к 1-ой:

0	-22	-1	-14	24
1	4	2	2	-5
6	2	11	-2	-6

Умножим 2-ую строку на (6). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

0	-22	-1	-14	24
0	22	1	14	-24
6	2	11	-2	-6

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

0	22	1	14	-24
6	2	11	-2	-6

Найдем ранг матрицы.

0	22	1	14	-24
6	2	11	-2	-6
x1	x2	x3	x4	x5

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	22	14	-1	-24
6	2	-2	-11	-6
x1	x2	x4	x3	x5

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
22x₂ = 14x₄ – x₃ – 24x₅
6x₁ + 2x₂ = – 2x₄ – 11x₃ – 6x₅
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄,x₅, то есть нашли общее решение:
x₂ = 0.64x₄ – 0.0455x₃ – 1.09x₅
x₁ = – 0.55x₄ – 1.82x₃ – 0.64x₅
Находим фундаментальную систему решений, которая состоит из (n-r) решений.
В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.
Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.
Достаточно придать свободным неизвестным x₃,x₄,x₅ значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x₁,x₂.
Простейшим определителем, отличным от нуля, является единичная матрица.

Задача . Найти фундаментальный набор решений однородной системы линейных уравнений. Решение

Задача . Найти общее решение системы. Проанализировать его структуру (указать базис пространства решений однородной системы, установить размерность пространства). Решение Пример 3
Пример 4

Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.

Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.

Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи” вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left < begin& 2x_1-3x_2-x_3-x_4=0;\ & -4x_1+5x_2+3x_4=0. end right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.

Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:

Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?

Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:

Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.

Кстати сказать, чтобы не писать каждый раз выражения вроде “$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$”, пишут все значения переменных в матрицу-столбец: $left(begin 1 \ -1 \ 2 \ 3 end right)$. Эту матрицу тоже называют решением СЛАУ.

Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.

Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.

Этот случай уже был рассмотрен в теме “Базисные и свободные переменные. Общее и базисное решения СЛАУ”. По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.

Что такое базисные и свободные переменные? показатьскрыть

Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза “ранг матрицы равен $r$”. Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Фундаментальная система решений однородной СЛАУ.

С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$. $varphi_$.

Часто вместо словосочетания “фундаментальная система решений” используют аббревиатуру “ФСР”. Если решения $varphi_1$, $varphi_2$. $varphi_$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:

$$ X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_cdot varphi_, $$

где $C_1$, $C_2$. $C_$ – произвольные постоянные.

Что значит “линейно независимые решения”? показатьскрыть

В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.

Решения $varphi_1$, $varphi_2$, $ldots$, $varphi_n$ называются линейно зависимыми, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что выполняется следующее равенство:

$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+ldots+alpha_ncdot varphi_n=O $$

при условии, что среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.

Если же указанное выше равенство возможно лишь при условии $alpha_1=alpha_2=ldots=alpha_n=0$, то система решений называется линейно независимой.

Буква “$O$” в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $varphi_1=left(begin 1 \-1 \2 \3 endright)$ – решение данной СЛАУ. Точно так же можно показать, что $varphi_2=left(begin 16 \ 11 \ -4 \ 3 endright)$, $varphi_3=left(begin -5 \ -4 \ 2 \ 0 endright)$, $varphi_4=left(begin 7 \ 5 \ -2 \ 1endright)$ – решения данной системы.

Примем $alpha_1=-1$, $alpha_2=0$, $alpha_3=4$, $alpha_4=3$. Выясним, чему же равно выражение $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4$:

$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4= -1cdot left(begin 1 \-1 \2 \3 endright)+ 0cdot left(begin 16 \ 11 \ -4 \ 3 endright)+ 4cdot left(begin -5 \ -4 \ 2 \ 0 endright)+ 3cdot left(begin 7 \ 5 \ -2 \ 1endright)=\ =left(begin -1+0-20+21\ 1+0-16+15 \ -2+0+8-6 \ -3+0+0+3endright)= left(begin 0\ 0\ 0\0endright). $$

Итак, существуют такие значения констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, не все одновременно равные нулю, что выполняется равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4=O$. Вывод: совокупность решений $varphi_1$, $varphi_2$, $varphi_3$, $varphi_4$ – линейно зависима.

Для сравнения: равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2=O$ возможно лишь при условии $alpha_1=alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $varphi_1$, $varphi_2$ является линейно независимой.

Если система является неопределённой, указать фундаментальную систему решений.

Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$ left( begin 3 & -6 & 9 & 13 & 0 \ -1 & 2 & 1 & 1 & 0 \ 1 & -2 & 2 & 3 & 0 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ -1 & 2 & 1 & 1 & 0 \ 3 & -6 & 9 & 13 & 0 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 3 & 4 & 0 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright). $$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:

На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:

$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:

$$ left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright) $$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=0$, а вторая строка соответствует уравнению $3x_3+4x_4=0$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$ left( begin 1 & 2 & 2 & -3\ 0 & 3 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 2 & -3\ 0 & 1 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 2 & -1/3\ 0 & 1 & 0 & -4/3 endright). $$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:

Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-frac<4><3>x_4right)+13x_4=0. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin 1 & 0 \0 & 1endright)$. Таблица будет выглядеть так:

Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$. Если $x_2=1$, $x_4=0$, то:

Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:

Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:

Найденные значения $x_1=-frac<1><3>$ и $x_3=-frac<4><3>$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:

Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin x_1 \x_2 \x_3 \x_4 endright)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:

$$ varphi_1=left(begin 2 \1 \0 \0 endright);; varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright). $$

Совокупность $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:

$$ X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Общее решение: $left <begin& x_1=2x_2-frac<1><3>x_4;\ & x_2in R;\ & x_3=-frac<4><3>x_4;\ & x_4 in R. endright.$. Или так: $X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$.

Записать ФСР однородной СЛАУ

зная общее решение. Записать общее решение с помощью ФСР.

Общее решение уже было получено в теме “метод Крамера” (пример №4). Это решение таково:

Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.

Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.

Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.

Совокупность $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:

$$ X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Фундаментальная система решений: $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$. Общее решение: $X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$, где $C_1$ и $C_2$ – произвольные константы.

Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.

Однородные СЛАУ. Фундаментальная система решений

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=Theta$ всегда совместна, так как $X=Theta$ всегда является ее решением.

Заметим, что если $x_<1>, x_<2>$ – это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=lambda_ <1>x_<1>+lambda_ <2>x_<2>$$ $$A Y=Aleft(lambda_ <1>x_<1>+lambda_ <2>x_<2>right)=lambda_ <1>A x_<1>+lambda_ <2>A x_<2>=lambda_ <1>Theta+lambda_ <2>Theta=Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $left<begin 3 x-2 y=-1 \ x+3 y=7 endright.$ ненулевые решения.

$$Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $left<begin x_<1>+x_<2>-3 x_<4>-x_<5>=0 \ x_<1>-x_<2>+2 x_<3>-x_<4>=0 \ 4 x_<1>-2 x_<2>+6 x_<3>+3 x_<4>-4 x_<5>=0 \ 2 x_<1>+4 x_<2>-2 x_<3>+4 x_<4>-7 x_<5>=0 endright.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=left(begin 1 & 1 & 0 & -3 & -1 \ 1 & -2 & 2 & -1 & 0 \ 4 & -2 & 6 & 3 & -4 \ 2 & 4 & -2 & 4 & -7 endright)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей – четыре первых, от четвертой – две первых:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & -6 & 6 & 15 & 0 \ 0 & 2 & -2 & 10 & -5 endright)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 9 & -3 \ 0 & 0 & 0 & 12 & -4 endright)$$

От четвертой строки отнимем $frac<4><3>$ третьей и третью строку умножим на $frac<1><3>$ :

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 \ 0 & 0 & 0 & 0 & 0 endright)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 endright)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A simleft(begin 1 & 1 & 0 & -6 & 0 \ 0 & -2 & 2 & 5 & 0 \ 0 & 0 & 0 & 3 & -1 endright)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_<2>, x_<4>$ – независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>, x_<3>, x_<5>$ – зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ – количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $left<begin x_<1>=-1+6 cdot 0=-1 \ x_<3>=1-frac<5> <2>cdot 0=1 \ x_<5>=3 cdot 0=0 endright.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что =12, x_<3>=-5, x_<5>=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

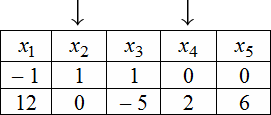
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_<1>=left(begin -1 \ 1 \ 1 \ 0 \ 0 endright), X_<2>=left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>left(begin -1 \ 1 \ 1 \ 0 \ 0 endright)+C_<2>left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

[spoiler title=”источники:”]

http://math1.ru/education/sys_lin_eq/fsr1.html

http://www.webmath.ru/poleznoe/formules_5_6.php

[/spoiler]

Совместность однородной системы

Рассмотрим однородную
систему

.

Однородная
система всегда совместна,
так как всегда имеет тривиальное
(нулевое) решение .
Выясним, когда данная система имеет
нетривиальное решение.

Теорема
1. Однородная
система имеет нетривиальное решение
тогда и только тогда, когда ранг
матрицы,
составленной из коэффициентов при
неизвестных, меньше числа неизвестных.

Доказательство.
Пусть система совместна. Это может быть
тогда и только тогда, когда найдутся
числа с₁, с₂,
…, с_n,
при подстановке которых в систему мы
получим mтождеств.
Эти m тождеств
можно записать в виде

.

Следовательно,
система векторов-столбцов матрицы А линейно
зависима.
А это может быть тогда и только тогда,
когда ранг
системы векторов-столбцов
меньше n,
т.е. r(A)<n.

Следствие. Квадратная
однородная система имеет нетривиальное
решение тогда и только тогда,
когда определитель
матрицы,
составленной из коэффициентов при
неизвестных, равен нулю.

Доказательство.
Так как r(A)<n,
то столбцы матрицы линейно зависимы и,
следовательно, определитель матрицы
равен нулю.

№17

Основные
определения.

Пусть
К – поле. Элементы поля К мы будем
называть скалярами. Под полем К можно
понимать или поле действительных чисел
или поле комплексных чисел.

Определение.
Матрицей размера  над
полем К называется таблица элементов
поля К, имеющую  строк
и  столбцов.

Обозначение:

.

Определение.
Элементы  называются
элементами матрицы, где  i – номер
строки, в которой находится элемент ,
j – номер столбца.

Определение. Матрица размеров :

 называется
строкой длины .

Определение.
Матрица размеров :

 называется
столбцом высоты .

Определение.
Матрица размеров  называется
квадратной матрицей –
го порядка.

Определение.
Матрица, все элементы которой равны
нулю, называется нулевой.

В
квадратной матрице выделяют две
диагонали, как диагонали квадрата:
главную диагональ и побочную диагональ.

Главную
диагональ образуют элементы ,
т.е. элементы с одинаковыми нижними
индексами.

Побочную
диагональ образуют элементы .

Определение.
Квадратная матрица, в которой все
элементы вне главной диагонали равны
0, называется диагональной:

.

Определение.
Матрица В размера  называется
транспонированной по отношению к матрице
А размера ,
если к – й столбец матрицы В
состоит из элементов к – й строки матрицы
А, для всех.

Обозначение: .

Определение.
Процесс (процедура) получения
транспонированной матрицы из данной
называется транспонированием матрицы.

Пример:

, .

Определение.
Две матрицы  и  называются
равными, если они имеют одинаковые
размеры и для всех значений индексов
выполняется равенство .

Свойства
опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

№18

Рангом системы
строк (столбцов) матрицы  с  строк
и  столбцов
называется максимальное число линейно
независимых строк
(столбцов). Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы.

Ранг
матрицы —
наивысший из порядков миноров этой
матрицы, отличных от нуля.

Обычно
ранг матрицы  обозначается  ()

Элементарными
преобразованиями строк называют:

• перестановка
  местами любых двух строк матрицы;

• умножение
  любой строки матрицы на константу , ;

• прибавление
  к любой строке матрицы другой строки.

В
некоторых курсах линейной алгебры
перестановка строк матрицы не выделяется
в отдельное элементарное преобразование
в силу того, что перестановку местами
любых двух строк матрицы можно получить,
используя умножение любой строки
матрицы на константу ,  и
прибавление к любой строке матрицы
другой строки, умноженной на константу , .

Аналогично
определяются элементарные
преобразования столбцов.

Элементарные
преобразования обратимы.

Обозначение  указывает
на то, что матрица  может
быть получена из  путём
элементарных преобразований (или
наоборот).

Вычисление ранга
матрицы с помощью миноров

Ранг
матрицы находится либо методом окаймления
миноров, либо методом элементарных
преобразований. При вычислении ранга
матрицы первым способом следует
переходить от миноров низших порядков
к минорам более высокого порядка. Если
уже найден минор D k-го порядка матрицы
А, отличный от нуля, то требуют вычисления
лишь миноры (k+1)-го порядка, окаймляющие
минор D, т.е. содержащие его в качестве
минора. Если все они равны нулю, то ранг
матрицы равен k.

Пример
1. Найти
методом окаймления миноров ранг матрицы

.

Решение. Начинаем
с миноров 1-го порядка, т.е. с элементов
матрицы А. Выберем, например, минор
(элемент) М₁ =
1, расположенный в первой строке и первом
столбце. Окаймляя при помощи второй
строки и третьего столбца, получаем
минор M₂ = ,
отличный от нуля. Переходим теперь к
минорам 3-го порядка, окаймляющим М₂.
Их всего два (можно добавить второй
столбец или четвертый). Вычисляем
их:  = 0.
Таким образом, все окаймляющие миноры
третьего порядка оказались равными
нулю. Ранг матрицы А равен двум.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #

  09.06.201514.68 Mб41P.N.Bibilo_Osnovy_yazika_VHDL(2007)1.djvu

• #
• #
• #

Условие нетривиальной совместности однородной системы линейных уравнений

Решением системы называется совокупность n значений неизвестных

при подстановке которых все уравнения системы обращаются в тождества.

Система линейных уравнений может быть записана в матричном виде:

где A — матрица системы, b — правая часть, x — искомое решение, A_p — расширенная матрица системы:

.

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.

Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

.

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.

ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.
Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы
e₁ , e₂ , . e_n-r образуют ее фундаментальную систему решений (Ae_i =0, i=1,2, . n-r), то любое решение x системы Ax=0 можно записать в виде

где c₁ , c₂ , . c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

матрица исследуемой однородной системы, ранг которой r

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.

Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.

Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.

Следствие из теоремы Кронекера-Капелли

Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.

Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.

Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:

Способ №1. Вычисление рангов по определению.

Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:

$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$

Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.

Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.

Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.

Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.

Способ №2. Вычисление ранга методом элементарных преобразований.

Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.

Ответ: Заданная СЛАУ совместна и определена.

$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom<0>\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom<0>\phantom<0>\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom<0>\phantom<0>\phantom<0>\ r_4-r_3\phantom<0>endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$

Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.

Ответ: система несовместна.

Приводим расширенную матрицу системы к ступенчатому виду:

$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset> <rightarrow>$$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom<0>\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom<0>\ phantom<0>\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom<0>\ phantom<0>\phantom <0>\ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$

Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.

Ответ: система является неопределённой.

Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.

Нетривиальная совместность однородной системы

Нетривиальная совместность однородной системы

• Нетривиальная совместимость однородных систем. В.1) однородная линейная система, т.е. Система + B12 ^ 2 + ••• + UlnXn = 0, + a22 ^ 2 + ••• + CL2nXn = 0 . + ash2x2 + … + ashpxn = 0. Помните, что все эти системы совместимы. Когда существует так называемое очевидное (или нулевое) решение x -x2 -…- xn-0 3).

• При каких условиях однородная система имеет значение? C.7) Решение (то есть «важный сустав»). Эта проблема решается очень легко. создание Нетривиальное решение системы C.7) эквивалентно линейному Зависимость столбца матрицы C.2) (из-за линейной зависимости столбца.

В дополнение к указанным тривиальным решениям. Людмила Фирмаль

Матрица C.2) означает, что числа x1, x2, …, xn существуют. Все равны нулю, и выполняется уравнение C.7)). Однако линейная зависимость по основной малой теореме 1.6 Столбец матрицы С.2) встречается только тогда, когда: Не все столбцы этой матрицы являются базовыми.

• Это значит Только если порядок минорных миноров матрицы C.2) мал Количество столбцов n. Следующая теорема достигнута. Теорема 3.1. Однородная система С.7) неочевидна Только если ранг r матрицы C.2) меньше Количество столбцов n. 3) На самом деле C.7) Заменить ноль в системе для всех неизвестных 1, x2, …, xn, составьте все уравнения в этой системе тождеств.

Результат не очевиден для равномерной квадратной системы 4) Интеграционное решение только для определителей Неизвестный коэффициент равен нулю. На самом деле, в случае квадратной равномерной системы C.7) Если m = n, ранг r матрицы C.2) меньше, чем число m = n.

Только если определитель этой матрицы равен нулю. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Макеты страниц