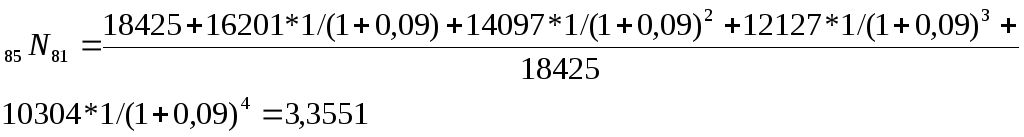«Нетто» и «брутто» — слова, которые мы чаще всего связываем с едой или физическими величинами. Однако подобные определения встречаются и в страховании. Mafin Media рассказывает об одном из таких — нетто-ставке.
Что это такое
Нетто-ставка — основная часть брутто-ставки, необходимая для покрытия текущих и будущих выплат и создания страховых резервов. Фактически это страховой тариф без учета дополнительных нагрузок (в частности, расходов на оплату услуг страховых агентов и брокеров).
Нетто-ставка, по сути, отражает убыточность того или иного страхового продукта и определяется с помощью актуарных расчетов при сложении двух составляющих:
- рисковой ставки — основной части нетто-ставки;
- рисковой надбавки — той части, которая должна покрыть возможное превышение количества страховых случаев относительно их среднего значения.
Как выглядит формула нетто-ставки
В упрощенном варианте ее можно представить так:
Здесь:
Tn — нетто-ставка
To — рисковая ставка
Tp — рисковая надбавка
В свою очередь, составляющие нетто-ставки рассчитываются таким образом:
Sb — среднее страховое возмещение по одному договору страхования при наступлении страхового случая
S — средняя страховая сумма
q — вероятность наступления страхового случая
Rb —средний разброс страхового возмещения
Kδ — количество договоров страхования за определенный период
α(y) — коэффициент, зависящий от гарантии безопасности
Как это работает на практике
Представим, что стоимость автомобиля в среднем составляет 500 000 руб., ремонт обычно обходится страховой компании (СК) в 40 000 руб., а частота ДТП за год равна примерно 0,001 (то есть в аварию попадает каждый тысячный автомобилист).
Значит, рисковая ставка по данному страховому продукту (например, КАСКО) будет рассчитываться следующим образом:
Получается, чистая нетто-ставка (ее основная часть) равна 8%, или 8 руб. на 100 руб. страховой суммы.
Добавим еще несколько переменных и попробуем посчитать рисковую надбавку. Допустим, что гарантия безопасности равна 0,95, а зависящий от нее коэффициент — 1,5 (обычно такие показатели в страховых компаниях рассчитываются по отдельным таблицам).
При этом средний разброс страхового возмещения составляет 5 000 руб., а всего СК успела заключить 5 000 договоров. Тогда на выходе мы получаем такое число:
То есть рисковая надбавка составила 5,4%, или 5,4 руб. на 100 руб. страховой суммы. Выходит, совокупная нетто-ставка по этому страховому продукту равна 13,4%.
Подберите самые выгодные условия по ОСАГО
Введите номер авто — данные заполнятся автоматически
или нажмите «Рассчитать», если еще не получили его
Утверждены
Распоряжением Федеральной службы
Российской Федерации по надзору
за страховой деятельностью
от 8 июля 1993 г. N 02-03-36
МЕТОДИКИ
РАСЧЕТА ТАРИФНЫХ СТАВОК ПО РИСКОВЫМ ВИДАМ СТРАХОВАНИЯ
Учитывая сложность оценки страховых рисков и расчета страховых тарифов для начинающих страховую деятельность страховых организаций, Федеральная служба России по надзору за страховой деятельностью рекомендует использовать предлагаемые методики расчета страховых тарифов по рисковым видам страхования.
Под рисковыми в настоящих методиках понимаются виды страхования, относящиеся к видам страховой деятельности иным, чем страхование жизни:
не предусматривающие обязательства страховщика по выплате страховой суммы при окончании срока действия договора страхования;
не связанные с накоплением страховой суммы в течение срока действия договора страхования.
Прилагаемые методики могут быть использованы при подготовке документов, представляемых страховыми организациями для получения государственных лицензий на проведение страховой деятельности, осуществления текущего контроля за обеспечением финансовой устойчивости страховых операций. Если страховая организация использует иные способы оценки страхового риска и размеров страховых тарифов, обоснованность применяемых методик должна быть подтверждена использованием математических методов, учитывающих специфику страховых операций.
Определение основных понятий,
использованных в методике
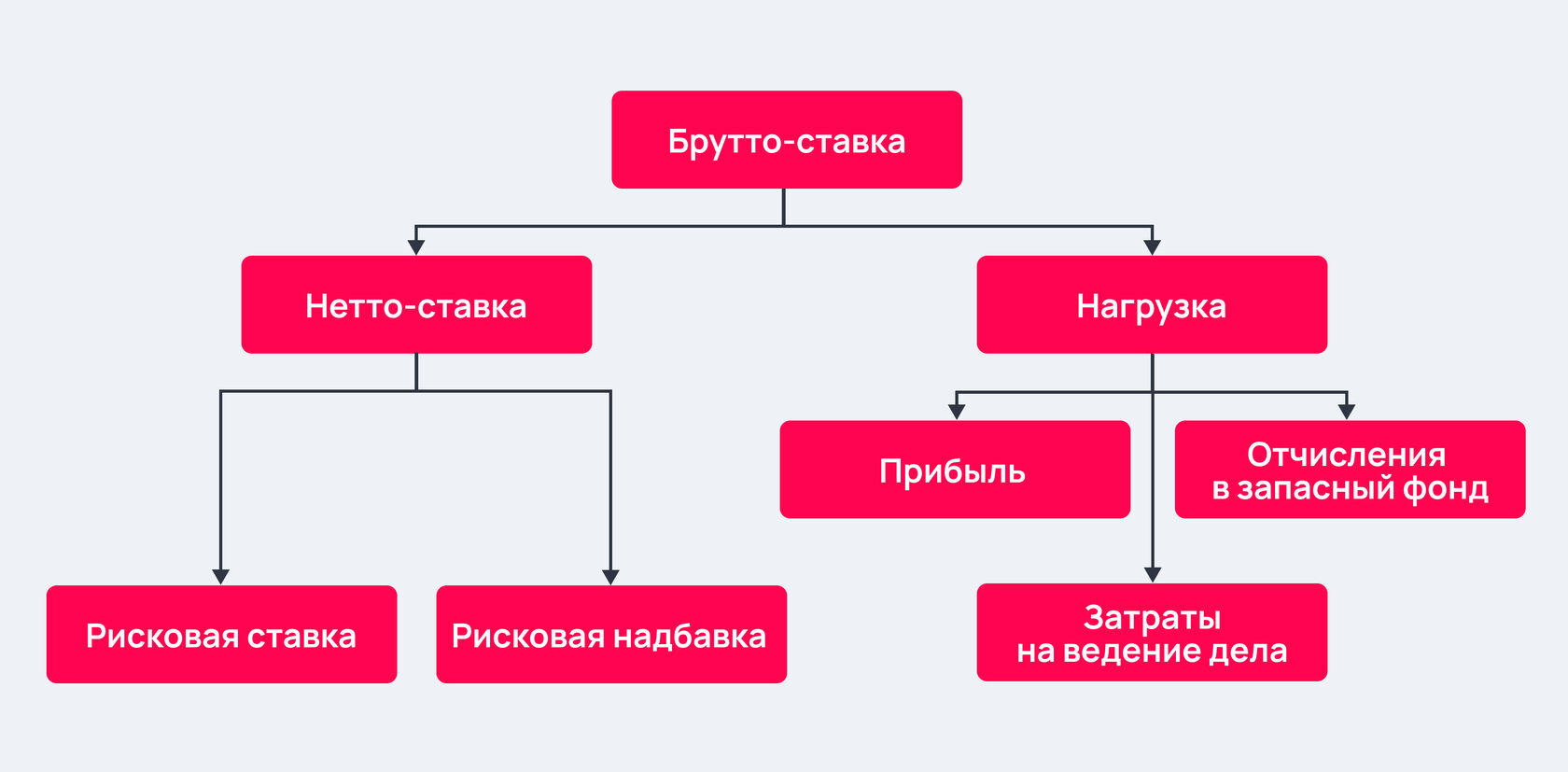
Страховой тариф (брутто – тариф) – ставка страхового взноса с единицы страховой суммы или объекта страхования. Страховой тариф состоит из нетто – ставки и нагрузки.
Нетто – ставка страхового тарифа – часть страхового тарифа, предназначенная для обеспечения текущих страховых выплат по договорам страхования.
Нагрузка – часть страхового тарифа, предназначенная для покрытия затрат на проведение страхования и создания резерва (фонда) предупредительных мероприятий. В составе нагрузки может быть предусмотрена прибыль от проведения страховых операций.
Методика (I) расчета тарифных ставок
по массовым рисковым видам страхования “*”
——————————–
“*” Под массовыми рисковыми видами страхования в настоящих методиках понимаются виды страхования, предположительно охватывающие значительное число субъектов страхования и страховых рисков, характеризующихся однородностью объектов страхования и незначительным разбросом в размерах страховых сумм.
Предлагаемая методика пригодна для расчета тарифных ставок для рисковых видов страхования и применима при следующих условиях:
1) существует статистика либо какая-то другая информация по рассматриваемому виду страхования, что позволяет оценить следующие величины:
q – вероятность наступления страхового случая по одному договору страхования,
S – среднюю страховую сумму по одному договору страхования,
Sв – среднее возмещение по одному договору страхования при наступлении страхового случая;
2) предполагается, что не будет опустошительных событий, когда одно событие влечет за собой несколько страховых случаев;
3) расчет тарифов проводится при заранее известном количестве договоров n, которые предполагается заключить со страхователями.
При наличии статистики по рассматриваемому виду страхования за величины q, S, Sв принимаются оценки их значений:
M
q = ---------, (1)
N
N
SUM Si
i=1
S = -----------, (2)
N
M
SUM Sвk
k=1
Sв = -----------, (3)
M
где N – общее количество договоров, заключенных за некоторый период времени в прошлом;
M – количество страховых случаев в N договорах;
Si – страховая сумма при заключении i-го договора,
i = 1, 2, …, N;
Sвk – страховое возмещение при k-м страховом случае,
k = 1, 2, …, M.
При страховании по новым видам рисков при отсутствии фактических данных о результатах проведения страховых операций, т.е. статистики по величинам q, S и Sв, эти величины могут оцениваться экспертным методом либо в качестве них могут использоваться значения показателей – аналогов. В этом случае должны быть представлены мнения экспертов либо пояснения по обоснованности выбора показателей – аналогов q, S, Sв, а отношение средней выплаты к средней страховой сумме (Sв / S) рекомендуется принимать не ниже:
0,3 – при страховании от несчастных случаев и болезней, в медицинском страховании;
0,4 – при страховании средств наземного транспорта;
0,6 – при страховании средств воздушного и водного транспорта;
0,5 – при страховании грузов и имущества, кроме средств транспорта;
0,7 – при страховании ответственности владельцев автотранспортных средств и других видов ответственности и страховании финансовых рисков.
Нетто – ставка Tn состоит из двух частей – основной части Tо и рисковой надбавки Tр:
Tn = Tо + Tр. (4)
Основная часть нетто – ставки (Tо) соответствует средним выплатам страховщика, зависящим от вероятности наступления страхового случая q, средней страховой суммы S и среднего возмещения Sв. Основная часть нетто – ставки со 100 руб. страховой суммы рассчитывается по формуле:
Sв
Tо = 100 x ------- x q (руб.). (5)
S
Рисковая надбавка Tр вводится для того, чтобы учесть вероятные превышения количества страховых случаев относительно их среднего значения. Кроме q, S и Sв, рисковая надбавка зависит еще от трех параметров: n – количества договоров, отнесенных к периоду времени, на который проводится страхование, среднего разброса возмещений Rв и гарантии гамма – требуемой вероятности, с которой собранных взносов должно хватить на выплату возмещения по страховым случаям.
Возможны два варианта расчета рисковой надбавки.
1. Рисковая надбавка может быть рассчитана для каждого риска. В этом случае
─────────────────────
┐ / 2
│ / 1 Rв
Tр = Tо x альфа (гамма) x │/ ----- [1 - q + (---) ], (6)
n x q Sв
где альфа (гамма) – коэффициент, который зависит от гарантии безопасности гамма. Его значение может быть взято из таблицы.
┌─────────┬──────────┬──────────┬───────────┬──────────┬─────────┐ │ гамма │ 0,84 │ 0,90 │ 0,95 │ 0,98 │ 0,9986 │ ├─────────┼──────────┼──────────┼───────────┼──────────┼─────────┤ │ альфа │ 1,0 │ 1,3 │ 1,645 │ 2,0 │ 3,0 │ └─────────┴──────────┴──────────┴───────────┴──────────┴─────────┘
Rв - среднеквадратическое отклонение возмещений при
наступлении страховых случаев. При наличии статистики выплат
2
страховых возмещений дисперсия выплат R оценивается следующим
в
образом:
2 1 M 2 1 M 2 M 2
R = ----- x SUM (S - S ) = ----- x SUM S - ----- x S , (7)
в M - 1 k=1 вk в M - 1 k=1 вk M - 1 в
где Sвk – страховое возмещение при k-м страховом случае,
k = 1, 2, …, M;
M – количество страховых случаев в N договорах;
Sв – среднее возмещение по одному договору страхования при наступлении страхового случая.
Если у страховой организации нет данных о величине Rв, допускается вычисление рисковой надбавки по формуле:
┐ ──────────
│ / 1 - q
Tр = 1,2 x Tо x альфа (гамма) x │ / ----------. (8)
│/ nq
2. В том случае, когда страховая организация проводит страхование по нескольким видам рисков (j = 1, 2, …, m), рисковая надбавка может быть рассчитана по всему страховому портфелю, что позволяет несколько уменьшить ее размер:
Tр = Tо x альфа (гамма) x мю, (9)
где мю – коэффициент вариации страхового возмещения, который соответствует отношению среднеквадратического отклонения к ожидаемым выплатам страхового возмещения. Если j-й риск
характеризуется вероятностью его наступления gj, средним возмещением Sвj и среднеквадратическим отклонением возмещений Rвj, то
┐ ───────────────────────────────────────────────
│ / m 2 2
│ / SUM [S x n x q x (1 - q ) + R x n x q ]
│/ j=1 вj j j j вj j j
мю = -----------------------------------------------------. (10)
m
SUM Sвj x nj x qj
j=1
При неизвестной величине Rвj среднеквадратического отклонения выплат при наступлении j-го риска соответствующее слагаемое в числителе формулы (10) допускается заменять величиной:
2
1,44 x S x n x q x (1 - q ). (11)
вj j j j
Если не известна ни одна из величин Rвj, то мю вычисляется по формуле:
┐ ───────────────────────────────
│ / m 2
│ / SUM x S x n x q x (1 - q )
│/ j=1 вj j j j
мю = 1,2 x -------------------------------------. (12)
m
SUM Sвj x nj x qj
j=1
Формулы (6), (9) и (10) для вычисления рисковой надбавки тем точнее, чем больше величины n x q и nj x qj. При n x q ” 10 и nj x qj ” 10 формулы (6), (9) и (10) носят приближенный характер.
Если о величинах q, S, Sв нет достоверной информации, например, в случае когда они оцениваются не по формулам (1) – (3) с использованием страховой статистики, а из других источников, то рекомендуется брать
альфа (гамма) = 3.
Брутто – ставка Tдельта рассчитывается по формуле:
Tn x 100
Tдельта = -------------, (13)
100 - f
где Tn – нетто – ставка;
f(%) – доля нагрузки в общей тарифной ставке.
Рассмотрим несколько примеров применения методики.
1. Допустим, что страховая компания заключает договоры имущественного страхования. Пусть вероятность наступления страхового случая q1 = 0,01, средняя страховая сумма составляет S1= 500 тыс. руб., среднее возмещение при наступлении страхового события Sв1 = 375 тыс. руб., количество договоров n1 = 10000, доля нагрузки в структуре тарифа f1 = 30%. Данных о разбросе возможных возмещений нет.
Тогда основная часть нетто – ставки со 100 руб. страховой суммы по формуле (5):
Sв1 375
Tо1 = 100 x ----- x q1 = 100 x --- x 0,01 = 0,75 (руб.).
S1 500
Рассчитаем рисковую надбавку. Пусть страховая компания с вероятностью гамма1 = 0,95 предполагает обеспечить непревышение возможных возмещений над собранными взносами, тогда из таблицы альфа = 1,645 рисковая надбавка по формуле (8):
(1 - q1)
Tр1 = 1,2 x Tо1 x альфа (гамма) x -------- = 1,2 x 0,75 x
n1 x q1
1 - 0,01
x 1,645 x ------------ = 0,15 (руб.).
10000 x 0,01
Нетто – ставка со 100 руб. страховой суммы по формуле (4):
Tn1 = Tо1 + Tр1 = 0,90 (руб.).
Брутто – ставка со 100 руб. страховой суммы по формуле (13):
Tn1 x 100 0,90 x 100
Tдельта1 = ------------ = ------------- = 1,29 (руб.).
100 - f1 100 - 30
2. Другая страховая компания проводит страхование граждан от несчастных случаев. При этом средняя страховая сумма S2 = 140 тыс. руб., среднее возмещение при наступлении страхового события Sв2 = 56 тыс. руб., вероятность наступления риска q2 = 0,04, количество договоров n2 = 3000, нагрузка f2 = 30%. Средний разброс возмещений Rв2 = 30 тыс. руб.
По формулам (5), (6), (4), (11) получаем:
Sв2 56
Tо2 = 100 x ----- x q2 = 100 x --- x 0,04 = 1,6 (руб.),
S2 140
───────────────────
┐ / 2
│ / Rв2
│ / 1 - q2 + (-----)
│ / Sв2
Tр2 = Tо2 x альфа (гамма) x │ / ------------------- =
│/ n2 x q2
┐ ────────────────────
│ / 2
│ / 30
│ / 1 - 0,04 + (----)
│ / 56
= 1,6 x 1,645 x │ / -------------------- = 0,27 (руб.),
│/ 3000 x 0,04
Tn2 = Tо2 + Tр2 = 1,6 + 0,27 = 1,87 (руб.),
Tn2 x 100 1,87 x 100
Tдельта2 = ----------- = ------------ = 2,67 (руб.).
100 - f2 100 - 30
3. Допустим, что страховая компания проводит виды страхования, описанные в предыдущих примерах, т.е. в ее портфеле есть разнородные риски. В этом случае основные части нетто – ставок будут такими же, как в примерах 1 и 2. Для расчета рисковых надбавок определяем коэффициент мю, используя формулу (10), учитывая, что средний разброс выплат по 1 риску неизвестен:
┐ ───────────────────────────────────────────────────────────────────────────
│ / 2 2 2
│ / 1,44 x S x n x q x (1 - q ) + S x n x q x (1 - q ) + R x n x q
│/ в1 1 1 1 в2 2 2 2 в2 2 2
мю = ------------------------------------------------------------------------------- =
Sв1 x n1 x q1 + Sв2 x n2 x q2
┐ ────────────────────────────────────────────────────────────────────────────────────────────
│ / 2 2 2
│/ 1,44 x 375 x 10000 x 0,01 x (1 - 0,01) + 56 x 3000 x 0,04 x (1 - 0,04) + 30 x 3000 x 0,04
= ------------------------------------------------------------------------------------------------ =
375 x 10000 x 0,01 + 56 x 3000 x 0,04
= 0,102.
Рисковая надбавка по формуле (9)
Tр = Tо x альфа (гамма) x мю = Tо x 1,645 x 0,102 = 0,17 x Tо,
нетто – ставка для любого вида страхования, составляющего страховой портфель,
Tn = Tо + 0,17 x Tо = 1,17 x Tо.
Нетто – ставка со 100 руб. страховой суммы:
при имущественном страховании
Tn1 = 1,17 x 0,75 = 0,88 (руб.),
при страховании граждан от несчастных случаев
Tn2 = 1,17 x 1,6 = 1,87 (руб.).
Соответствующие брутто – ставки со 100 руб. страховой суммы:
Tдельта1 = 1,26 руб.
Tдельта2 = 2,67 руб.
Методика (II) расчета тарифных ставок
по массовым рисковым видам страхования
Данную методику целесообразно использовать по массовым видам страхования на основе имеющейся страховой статистики за определенный период времени или при отсутствии таковой использовать статистическую информационную базу (демографическая статистика, смертность, инвалидность, производственный травматизм и т.д.).
Определение страхового тарифа на основе страховой статистики за несколько лет осуществляется с учетом прогнозируемого уровня убыточности страховой суммы на следующий год.
Предлагаемая методика применима при следующих условиях:
1) имеется информация о сумме страховых возмещений и совокупной страховой сумме по рискам, принятым на страхование, за ряд лет;
2) зависимость убыточности от времени близка к линейной.
Расчет нетто – ставки производится в следующей последовательности:
а) по каждому году рассчитывается фактическая убыточность страховой суммы (y) как отношение страхового возмещения к общей страховой сумме застрахованных рисков (Sв / S)
Таблица 1
┌─────────────┬────────────────┬───────────────┬─────────────────┐ │ Год │Общая страховая │ Страховое │ Фактическая │ │ │ сумма (S) │возмещение (Sв)│убыточность (yi) │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1988 │ 2278 │ 410 │ 0,18 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1989 │ 2942 │ 765 │ 0,26 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1990 │ 2755 │ 799 │ 0,29 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1991 │ 3094 │ 1114 │ 0,36 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1992 │ 3346 │ 1305 │ 0,39 │ └─────────────┴────────────────┴───────────────┴─────────────────┘
б) на основании полученного ряда исходных данных рассчитывается прогнозируемый уровень убыточности страховой суммы, для чего используется модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения:
*
y = a + a x i, (1)
i 0 1
*
где y - выравненный показатель убыточности страховой суммы,
i
a0, a1 - параметры линейного тренда,
i - порядковый номер соответствующего года.
Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными:
n n
a0 x n + a1 x SUM i = SUM yi,
i=1 i=1
(2)
n n 2 n
a x SUM i + a x SUM i = SUM y x i,
0 i=1 1 i=1 i=1 1
где n – число анализируемых лет.
Коэффициенты данной системы уравнений находятся с помощью таблицы 2:
Таблица 2
┌───────────┬──────────┬───────────────┬─────────────────────────┐ │ Год │ i │ Фактическая │ Расчетные показатели │ │ │ │ убыточность ├─────────────┬───────────┤ │ │ │ (yi) │ yi x i │ 2 │ │ │ │ │ │ i │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1988 │ 1 │ 0,18 │ 0,18 │ 1 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1989 │ 2 │ 0,26 │ 0,52 │ 4 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1990 │ 3 │ 0,29 │ 0,87 │ 9 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1991 │ 4 │ 0,36 │ 1,44 │ 16 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1992 │ 5 │ 0,39 │ 1,95 │ 25 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ │ 15 │ 1,48 │ 4,96 │ 55 │ └───────────┴──────────┴───────────────┴─────────────┴───────────┘
Подставив полученные в таблице 2 данные в систему уравнений (2), получим:
a0 x 5 + a1 x 15 = 1,48,
(3)
a0 x 15 + a1 x 55 = 4,96.
Решив систему уравнений (3), получаем следующие значения:
a0 = 0,14,
a1 = 0,052,
на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в уравнение (1).
Таким образом, ожидаемая убыточность на 1993 год с учетом тренда исходных данных составит:
y6 = a0 + a1 x 6,
y6 = 0,14 + 0,052 x 6 = 0,452 руб. со 100 руб. страховой суммы, т.е. это и является основной частью нетто – ставки;
в) для определения рисковой надбавки необходимо по следующей формуле рассчитать среднее квадратическое отклонение фактических значений убыточности от выравненных значений:
┐ ──────────────────
│ / n * 2
│ / SUM x (y - y )
│ / i=1 i i (4)
сигма = │ / -----------------.
│/ n - 1
Используемые для определения рисковой надбавки показатели приведены в таблице 3:
Таблица 3
┌──────┬────┬───────────┬────────────┬──────────────┬────────────┐ │ Годы │ I │Фактическая│ Выравненная│ Отклонения │ Квадраты │ │ │ │убыточность│ убыточность│ выравненной │ отклонений │ │ │ │ (y ) │ * │ убыточности │ * 2 │ │ │ │ i │ (y ) │от фактической│ (y - y ) │ │ │ │ │ i │ * │ i i │ │ │ │ │ │ (y - y ) │ │ │ │ │ │ │ i i │ │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1988 │ 1 │ 0,18 │ 0,192 │ +0,012 │ 0,000144 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1989 │ 2 │ 0,26 │ 0,244 │ -0,016 │ 0,000256 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1990 │ 3 │ 0,29 │ 0,296 │ +0,006 │ 0,000036 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1991 │ 4 │ 0,36 │ 0,348 │ -0,012 │ 0,000144 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1992 │ 5 │ 0,39 │ 0,400 │ +0,010 │ 0,000100 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │Сумма │ │ │ │ │ 0,000680 │ └──────┴────┴───────────┴────────────┴──────────────┴────────────┘
Подставив рассчитанные показатели в формулу (4), получим:
┐ ──────────
│ / 0,00068
сигма = │ / ---------- = 0,013;
│/ 5 - 1
г) нетто – ставка рассчитывается следующим образом:
Tn = y6 + бета (гамма; n) x сигма,
где бета (гамма; n) – коэффициент, используемый для исчисления размера рисковой надбавки. Величина бета (гамма; n) зависит от заданной гарантии безопасности гамма (той вероятности, с которой собранных взносов хватит на выплаты страховых возмещений) и n – числа анализируемых лет и может быть взята из таблицы 4.
Таблица 4
┌──────┬───────────┬──────────┬───────────┬───────────┬──────────┐ │гамма │ 0,8 │ 0,9 │ 0,95 │ 0,975 │ 0,99 │ │ n │ │ │ │ │ │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 3 │ 2,972 │ 6,649 │ 13,640 │ 27,448 │ 68,740 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 4 │ 1,592 │ 2,829 │ 4,380 │ 6,455 │ 10,448 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 5 │ 1,184 │ 1,984 │ 2,850 │ 3,854 │ 5,500 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 6 │ 0,980 │ 1,596 │ 2,219 │ 2,889 │ 3,900 │ └──────┴───────────┴──────────┴───────────┴───────────┴──────────┘
Допустим, страховая компания считает необходимым с уровнем вероятности гамма = 0,9 быть уверена в том, что собранной суммы взносов будет достаточно для выплаты страховых возмещений. Тогда из таблицы 4 при гамма = 0,9 для n = 5, бета = 1,984.
Нетто – ставка со 100 руб. страховой суммы
Tn = 0,452 + 1,984 x 0,013 = 0,48 (руб.).
Брутто – ставка (Tдельта) определяется по следующей формуле:
Tn x 100
Tдельта = ----------,
100 - f
где Tn – нетто – ставка,
f(%) – доля нагрузки в общей тарифной ставке.
При условии, что нагрузка определена страховой организацией в размере 30% от брутто – ставки, рассчитывается брутто – ставка:
0,48 x 100
Tдельта = ------------ = 0,69 (руб.).
100 - 30
Брутто – ставка со 100 руб. страховой суммы равна 0,69 руб.
Расчет нетто- и брутто-ставки в
имущественном страховании
Показатель убыточности страховой суммы
математически выражает вероятность
ущерба в виде той доли совокупной
страховой суммы, которая выбывает из
страхового портфеля ежегодно или за
тарифный период в связи с наступлением
страховых случаев и возмещением ущерба.
Эта доля составляет основу для построения
нетто-ставки:
,
где q-убыточность,f-сумма
страхового возмещения, b-страховая
сумма застрахованных объектов
Методика расчета нетто-ставок сводится
к определению среднего показателя
убыточности страховой суммы за тарифный
период (5 или 10 лет) с поправкой на величину
рисковой надбавки.
Среднее значение убыточности находят
по формуле:
,
где n-количество лет
Далее рассчитывается среднее
квадратическое отклонение по формуле:
Затем рассчитывается коэффициент
вариации:
Значение коэффициента вариации более
30% свидетельствует о неустойчивости
динамического ряда.
Нетто-ставка рассчитывается по
формуле:
.
В страховании L называется
рисковая надбавка.
Если динамический ряд неустойчив, то
оценивают значение показателя убыточности
за 10 лет. Если и в этом случае исследуемый
ряд неустойчив, то нетто-ставку
рассчитывают так:
Брутто-ставка рассчитывается по
формуле:
,
где Н-удельный вес нагрузки в брутто-ставке.
Н определяется на основе фактических
накладных расходов страховщика за
последние 1-2 года.
Пример: Определите размер нетто- и
брутто-ставки в имущественном страховании.
если Н=20%?
|
Годы |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Убыточность |
17 |
16 |
16 |
15 |
15 |
;
;
-
год
(q-q)
(q-q)2
1
1.2
1.44
2
0.2
0.04
3
0.2
0.04
4
-0.8
0.64
5
-0.8
0.64
;
N=15,8+0,84=16,64;
Пример: Определите размер нетто- и
брутто-ставки в имущественном страховании.
если Н=20%?
|
Годы |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Убыточность |
38 |
45 |
40 |
50 |
54 |
;
;
;
N=45,4+6,54=51,94;
Методика расчета нетто-ставок по
страхованию на дожитие
Расчет единовременных нетто-ставок по
страхованию на дожитие производится
по формуле:
,где
–
нетто-ставка по страхованию на дожитие
для лиц в возрасте х лет сроком на n
лет,
lx+n
– число лиц доживающих до окончания
срока страхования (из таблицы),
lx –
число лиц доживших до возраста х лет
(из таблицы),
S-страховая сумма,
V- коэффициент дисконтирования
Пример: Страхователь мужчина
(женщина) в возрасте 45 лет заключает
договор по страхованию на дожитие сроком
15 лет. Страховая сумма составляет 100 тыс
руб. Определите размер единовременной
нетто-ставки при норме дисконта 10%
годовых?
мужчина
женщина
Пример: В возрасте 30 лет мужчина
заключает договор по страхованию на
дожитие до 50 лет. Страховая сумма=100 тыс
руб. Определите размер единовременной
нетто-ставки при норме дисконта 20%
годовых?мужчина
Методика расчета единовременных
нетто-ставок по страхованию на случай
смерти
,
где
N-единовременная нетто-ставка
для лиц в возрасте х сроком на n
лет,
dx–
количество лиц умерших при переходе от
возраста х к возрасту х+1 лет,
dx
=lx+1-lx.
Пример: Женщина в возрасте 35 лет
заключает договор страхования на случай
смерти сроком 5 лет. Страховая сумма=100000
руб. Норма дисконта=10%. Определите размер
единовременной нетто –ставки?
=
[(94937-94806)*1/(1+0,1) +
(94806-94665)*1/(1+0,1)2 +
(94665-94513)*1/(1+0,1)3 +
(94513-94349)*1/(1+0,1)4 +
(94349-94172)*1/(1+0,1)5 ] /
94937=(119.09+116.53+114.20+112.01+109.90)/94937=
=0.0060
Пример: Мужчина 55 лет заключил
договор страхования на случай смерти
сроком 5 лет. Страховая сумма=100000 руб.
Норма дисконта=10%. Определите размер
единовременной нетто –ставки?
=
[0,909*1368+0,826*1454+0,751*1553+0,683*1661+0,621*1772]
/ 76035=0.0769
Методика построения нетто-ставок по
страхованию пенсий
Единовременная нетто-ставка по страхованию
пожизненной ренты N,
которая выплачивается застрахованному
лицу в начале каждого страхового года,
называется пренумеранда и
рассчитывается следующим образом:
,
где w-пожизненное страхование
(расчет до 85 лет).
Если рента выплачивается не пожизненно,
а в течение определенного числа лет
в начале каждого страхового года
Если рента выплачивается не пожизненно,
а в течение определенного числа лет
в конце каждого страхового года
(постнумеранда)
Пример: Мужчина в возрасте 50 лет
заключает договор по страхованию ренты
сроком на 3 года. Определите единовременную
нетто-ставку, если условиями договора
предусмотрена выплата ренты в начале
каждого страхового года в сумме 10000руб.
Норма дисконта=9%.
Пример: Женщина в возрасте 48 лет
заключает договор по страхованию ренты
сроком на 3 года. Определите единовременную
нетто-ставку, если условиями договора
предусмотрена выплата ренты в конце
каждого страхового года в сумме 15000руб.
Норма дисконта=9%.
Пример: Определите единовременную
нетто-ставку пожизненной ренты, если
договор страхования заключает мужчина
в возрасте 81 года и в начале каждого
страхового года ему будет выплачиваться
10000руб. Норма дисконта=9%.
Соседние файлы в папке страх
- #
- #
14.02.201598.3 Кб9~WRL2314.tmp
- #
- #
- #
- #
- #
- #
Содержание
- – Что показывает нетто ставка?
- – Как рассчитать нетто тариф?
- – Чем отличается брутто тариф и нетто тариф?
- – Для чего предназначена нетто часть страхового тарифа?
- – Чему равна брутто ставка?
- – Как определить страховую сумму формула?
- – Как определить страховую сумму?
- – Как найти брутто премию?
- – Что влияет на брутто премию?
- – Что означает слова нетто?
- – Что означает нетто и брутто?
- – Что такое рисковая надбавка?
- – Какие формы страхования вы знаете?
- – Что означает понятие страхователь?
Это основная часть брутто-ставки, предназначенная для формирования страхового фонда, используемого для текущих страховых выплат и создания страховых резервов.
Что показывает нетто ставка?
Нетто–ставка представляет собой процент, который отражает вероятность убытка, рассчитанную на основе соотношения ущерба к совокупной страховой сумме застрахованных объектов.
Как рассчитать нетто тариф?
Методика расчета нетто–ставки как составляющей части тарифа по каждому виду или однородным объектам страхования сводится к определению среднего показателя убыточности страховой суммы за тарифный период с поправкой на величину рисковой надбавки. Нетто–ставка равна: убыточность страховой суммы плюс рисковая надбавка.
Чем отличается брутто тариф и нетто тариф?
Размер брутто – ставки устанавливается в рублях и копейках с единицы страховой суммы либо в процентах к совокупной страховой сумме. Нетто – ставка – основная часть страхового тарифа. Она служит для формирования страхового фонда, предназначенного для страховых выплат страхователям.
Для чего предназначена нетто часть страхового тарифа?
Страховой тариф состоит из нетто-ставки и нагрузки. Нетто-ставка страхового тарифа – часть страхового тарифа, предназначенная для обеспечения текущих страховых выплат по договорам страхования. … В составе нагрузки может быть предусмотрена прибыль от проведения страховых операций.
Чему равна брутто ставка?
Брутто–ставка – это тарифная ставка взносов по страхованию, представляющая сумму нетто-ставки, обеспечивающей выплату страхового возмещения (страховой суммы), и надбавки (нагрузки) к ней, предназначенной для покрытия других расходов, связанных с проведением страхования.
Как определить страховую сумму формула?
Иначе говоря, размер страхового возмещения будет рассчитан по следующей формуле: Страховое возмещение = страховой ущерб х страховая сумма : страховая стоимость. Страховое возмещение — сумма, выплачиваемая страхователю в целях покрытия нанесенного ущерба имуществу при наступлении страхового случая.
Как определить страховую сумму?
В имущественном страховании страховая сумма определяется действительной фактической стоимостью имущества на момент заключения договора страхования в месте его нахождения. В имущественном страховании она не должна превышать страховой стоимости объекта страхования.
Как найти брутто премию?
Брутто–премия состоит из нетто-премии и нагрузки. Брутто–премия рассчитывается как произведение страховой суммы на брутто-ставку.
Что влияет на брутто премию?
Размер брутто–премии зависит от величины страховой суммы, уровня риска и периода действия договора. Для упрощения расчетов, связанных с определением размера страховой премии (брутто–премии), в страховании используют понятие страхового тарифа. Существует два варианта выражения страхового тарифа – в рублях и в процентах.
Что означает слова нетто?
Нетто — (итал. netto — «чистый») — антоним брутто, означает нечто очищенное от лишнего — масса товара без упаковки, чистый доход за вычетом всех удержаний, встречается как часть сложных слов («нетто-»).
Что означает нетто и брутто?
Прежде всего, нетто и брутто – это термины из экономики, которые происходят из итальянского языка. «Брутто» дословно переводится как «плохой или грязный», «нетто» же наоборот – «чистый». В логистике под весом нетто или net weight понимают массу товара без какой-либо упаковки и тары.
Что такое рисковая надбавка?
НАДБАВКА РИСКОВАЯ — Метод обеспечения финансовой устойчивости результатов страховых операций путем включения в страховые тарифы соответствующей дополнительной фиксированной суммы (обычно в процентах от нетто ставки).
Какие формы страхования вы знаете?
Но существует и другая точка зрения, в соответствии с которой на практике выделяют следующие виды страхования:
- личное страхование: – страхование жизни; …
- имущественное страхование: – страхование имущества; …
- страхование ответственности: …
- специальные виды страхования:
Что означает понятие страхователь?
Страхователь (или полисодержатель) — это юридическое лицо или дееспособное физическое лицо, заключившее со страховщиком договор страхования либо являющееся страхователем в силу закона.
Интересные материалы:
Как восстановить номер Киевстар если нет PUK кода?
Как восстановить пак код Киевстар?
Как восстановить пак код мтс украина?
Как восстановить пин код Если забыл?
Как восстановить пин код Эцп?
Как восстановить резервные коды в Инстаграм?
Как восстановить защитный код стрелки?
Как возобновить идентификационный код?
Как вставить фрагмент кода на сайт?
Как вставить HTML код в гугл сайт?
Галина Викторовна Бирюкова
Эксперт по предмету «Страхование»
Задать вопрос автору статьи
Понятие и структура брутто-премии
Определение 1
Брутто-премия – это определенная условиями договора страхования сумма денежных средств, которую обязан уплатить страхователь страховой компании за определенный период времени.
В структуре брутто-премии выделяют нетто-премию и нагрузку.
Нетто-премия необходима для выполнения обязательств страховой компании по договорам страхования. Может состоять из следующих элементов:
- рисковой премии, предназначенной для покрытия ущерба при наступлении страхового случая;
- рисковой надбавки, необходимой для возмещения повышенного ущерба в случае возможного увеличения вероятности наступления рискового события;
- сберегательного взноса, используемого только в страховании жизни и предназначенного для накопления определенной суммы денежных средств в течение срока действия договора с последующей выплатой.
Рисковая премия присутствует всегда в составе нетто-премии и предназначена для формирования страхового резервного фонда, а рисковая надбавка учитывается при расчете нетто-премии по усмотрению страховой компании и идет на формирование запасного фонда.
Нагрузка, входящая в структуру брутто-премии, представляет собой затраты страховой компании на осуществление своей деятельности и ее прибыль.
Затраты включают в себя традиционные издержки, характерные для любого предприятия (заработная плата, аренда, командировочные расходы, коммунальные платежи и т.д.) и специфические издержки, которые применимы только к страховой отрасли (выплата комиссионных вознаграждений страховым агентам и брокерам, осуществление предупредительных мероприятий, проведение экспертиз с целью определения размера ущерба и т.д.).
Замечание 1
В зависимости от вида страхования, а также затрат страховой компании на осуществление своей деятельности, соотношение нетто-премии и нагрузки могут быть различными. Чаще всего в общей величине брутто-премии 70-80% составляет нетто-премия, остальное – нагрузка.
«Как рассчитать брутто-премию в страховании» 👇
В общем случае брутто-ставку $Тб$ равна:
$Тб = Тн / (100 – Н) • 100$, где:
$Тн$ – нетто-ставка,
$Н$ – нагрузка, определенная в процентах от брутто-ставки.
Если нагрузка определена в рублях, то брутто-ставка равна:
$Тб = Тн + Н$
При расчете брутто-премии наиболее важное значение имеет определение оптимального размера нетто-премии, т.к. от этого зависит последующая платежеспособность и финансовая устойчивость страховщика. Поэтому ее расчету уделяют повышенное внимание.
Расчет нетто-ставки по рисковым видам страхования
Определение 2
Нетто-ставка – это показатель, равный величине нетто-премии, рассчитанной на одну единицу (обычно 100 рублей) страховой суммы.
Методика расчета нетто-ставки по рисковым видам страхования подразумевает наличие достаточного объема статистических данных, необходимых для осуществления точных расчетов, прогнозируется заключение большого количество договоров (на один и тот же срок), а также предполагается отсутствие событий, которые могут повлечь за собой выплаты сразу по нескольким страховым случаям.
В соответствии с методикой формула для вычисления нетто-ставки $Тн$ имеет вид:
$Тн = То + Тр$, где:
$То$ – рисковая премия (часть) нетто-ставки,
$Тр$ – рисковая надбавка.
Рисковая премия рассчитывается следующим образом:
$То = Q • Sb ⁄ S • 100$, где:
$Q$ – вероятность, с которой возможно наступление страхового события,
$Sb$ – средний размер страховой выплаты,
$S$ – средний размер страховой суммы.
$Q = M ⁄ N$, где:
$M$ – количество произошедших страховых событий,
$N$ – количество заключенных за определенный период времени договоров.
Средний размер страховой выплаты равен отношению суммы выплат по всем договорам к количеству договоров:
$Sb = (∑Sbi ) ⁄ M$
Средний размер страховой суммы равен отношению суммарной величине страховых сумм по всем договорам к количеству этих договоров:
$S = (∑Si ) ⁄ N$
Рисковая надбавка $Тр$ равна:
$Тр = То • α(γ) • √ ((1 – Q + (Rb ⁄ Sb )^2) / (N • Q))$, где:
$Rb$ – среднеквадратичное отклонение средней страховой выплаты,
$α(γ)$ – коэффициент, который зависит от выбранной страховой компанией вероятности γ того, что взносов хватит для покрытия ущерба. Значение берется из таблицы:
Рисунок 1. Значения коэффициентов. Автор24 — интернет-биржа студенческих работ
Расчет нетто-ставки по страхованию жизни
К основным факторам, влияющим на размер нетто-ставки при страховании жизни, можно отнести:
- возраст и пол страхуемого лица;
- срок действия договора и порядок уплаты взносов;
- прогнозируемая доходность средств, поступивших в страховой резервный фонд страхования жизни, в случае их инвестирования.
Расчет нетто-ставки основан на данных таблиц о смертности населения определенного возраста и средней продолжительности жизни.
Для начала рассчитываются необходимые показатели
Вероятность наступления смерти в заданный год жизни $Qx$ вычисляется по формуле:
$Qx = Bx ⁄ Lx$, где:
$Bx$ – количество человек, которое умирает в период от $x$ до $x + 1$ лет,
$Lx$ – общее количество человек, доживших до х лет;
Вероятность, с которой человек доживет до заданного возраста, $Px$ равна:
$Px = L(x+1) ⁄ Lx$, или:
$Px = 1 – Qx$
С учетом того, что договоры по данному виду страхования имеют длительный период действия, а средства, поступающие от страхователя, могут использоваться страховой компанией для инвестирования с целью получения дополнительного дохода, для корректировки итоговой нетто-ставки используют множитель $V^n$ равный:
$V_n = 1 ⁄ (1+i)_n$, где:
$i$ – норма доходности от инвестирования,
$n$ – количество лет, на которое вкладываются средства.
В итоге размер нетто-премии ${Ex}_n$ на дожитие будет равен:
${Ex}_n = (L(x+n) • V_n) / Lx • S$, где:
$L(x+n)$ – количество человек, доживших до завершения срока, на который заключен договор,
$n$ – срок, на который заключен договор,
$S$ – величина страховой суммы.
Нетто-ставка на возможность смерти ${Az}_n$ равна:
${Az}_n = (Bx ∙ V + B(x+1) ∙ V_2 + ⋯ +B (x+n-1) ∙ V_n) / Lx ∙ 100$, где:
$Bx, B(х+1)…B(x+n-1)$ – количество человек, умирающих в период с $х$ лет до $х+1$, рассчитанное по каждому году срока действия договора.
При заключении договора комбинированного страхования и на дожитие, и на возможность смерти нетто-ставка будет равна:
$Тн = {Ex}_n + {Az}_n$
Такой метода расчета нетто-ставки применим при условии, что вся сумма страхового платежа вносится сразу за весть период страхования. Если же страхователь желает разделить сумму взноса на несколько частей, равное количеству лет страхования, то размер ежегодного платежа $P^x$ будет равен:
$Р_x = {Ed}_x / α_x$, где:
${Ed}_x$ – размер рассчитанного единовременного платежа,
$α_х$ – коэффициент рассрочки, который представляет собой стоимость платежей в размере одной денежной единицы. Фактически данный показатель по величие близок к значению количества лет, на которые заключается договор, но получается чуть ниже него. В итоге величина ежегодных платежей превышает значение, равное простому делению единовременного взноса на количество лет страхования. В этом случае страховщик возмещает потери, которые он несет от невозможности инвестировать всю сумму сразу и получить от этого доход.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме