Определение видимости точек, прямых и плоских фигур.
Видимость
— это изображение на чертеже только
тех точек, прямых и поверхностей
(плоскостей) предметов, которые расположены
ближе к наблюдателю. Изображение
предметов с учетом видимости улучшает
восприятие их формы и размещения в
пространстве.
Определение
видимости — это определение точек
предмета, лежащих на одном луче
проецирования (называемых конкурирующими),
и обозначение на чертеже только тех из
них, которые расположены по этому лучу
ближе к наблюдателю.
в
F’
С’
Г
Рис. 3.16
Если
необходимо указать невидимые точки, их
обозначения на плоскости проекций, где
проекции точек совпадают, заключают в
круглые скобки. Невидимые линии
изображаются на чертеже штриховыми
линиями.
Определение
видимости осуществляется как при
центральном, так и при параллельном
проецировании.
Граничными точками
видимости называются точки, разделяющие
зоны видимости и невидимости прямых и
поверхностей (плоскостей).
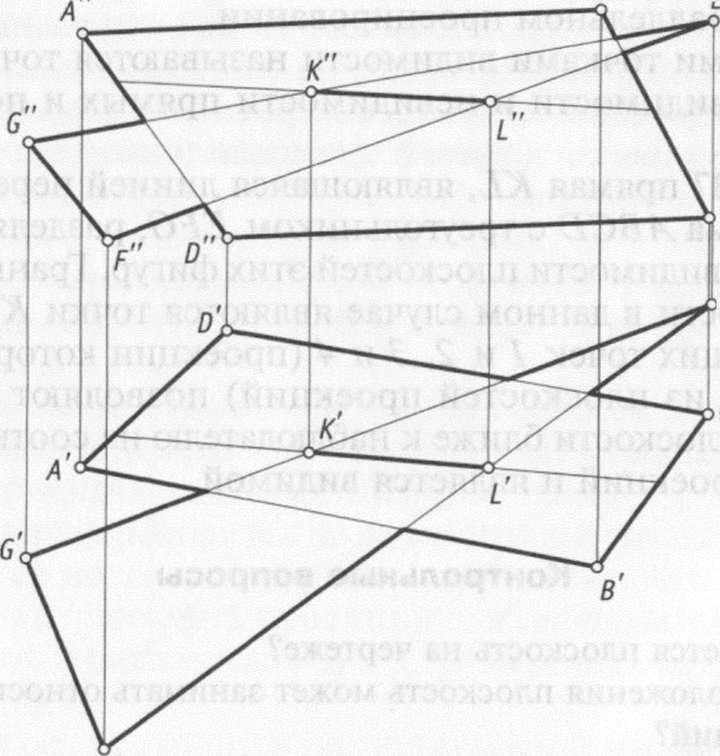
На
рис. 3.17 прямая АХ, являющаяся линией
пересечения параллелограмма ABCD с
треугольником EFG, разделяет зоны видимости
и невидимости плоскостей этих фигур.
Граничными точками видимости в данном
случае являются точки К и L, а пары
конкурирующих точек 1 и 2, 3 и 4 (проекции
которых совпадают на одной из
плоскостей проекций) позволяют определить,
какая часть плоскости ближе к наблюдателю
на соответствующей плоскости проекций
и является видимой.
Контрольные
вопросы
-
Как задается
плоскость на чертеже? -
Какие
положения плоскость может занимать
относительно плоскостей проекций? -
Как определить
на чертеже восходящую и нисходящую
плоскости общего положения? -
Какие положения
занимают горизонтально-проецирующая,
фрон- тально-проецирующая и
профильно-проецирующая плоскости? -
Как определить
углы между проецирующими плоскостями
и плоскостями проекций? -
Где располагается
проекция любой точки, находящейся в
проецирующих плоскостях? -
Какие положения
занимают плоскости уровня? -
Как определяются
углы наклона плоскости уровня к
плоскостям проекций? -
Каково условие
принадлежности точки плоскости? -
Дайте определения
горизонтали, фронтали и профильной
прямой плоскости. -
Каковы условия
параллельности прямой и плоскости? -
Как могут
располагаться две плоскости относительно
друг друга?
Глава 4. Способы преобразования чертежа
Использование
частных положений прямых линий и плоских
фигур относительно плоскостей проекций
значительно упрощает построение чертежа
и позволяет отобразить натуральные
размеры прямых линий, плоских фигур,
расположенных на одной плоскости
проекций, и расстояний между ними. Для
такого преобразования чертежа используют:
-
введение
дополнительных плоскостей проекций
таким образом, чтобы прямая линия или
плоская фигура, не изменяя своего
положения в пространстве, оказалась в
каком-либо частном положении в новой
системе плоскостей проекций — способ
перемены плоскостей проекций; -
изменение
положения прямой линии или плоской
фигуры посредством поворота вокруг
некоторой оси таким образом, чтобы
прямая или плоская фигура оказалась в
частном положении относительно
неизменной системы плоскостей проекций
— способ вращения.
Преобразование
чертежа (для достижения необходимого
результата) при определении натуральных
размеров отрезков и углов может
осуществляться многократно одним или
разными способами.
Способ
перемены плоскостей проекций.
При использовании способа перемены
плоскостей проекций (рис. 4.1) положение
точек, линий, плоских фигур, поверхностей
в пространстве остается неизменным, а
система щ, п2 дополняется плоскостями,
образующими с щ или п2, или между собой
системы двух взаимно-перпендикулярных
плоскостей, принимаемых за плоскости
проекций.
Рис. 4.1
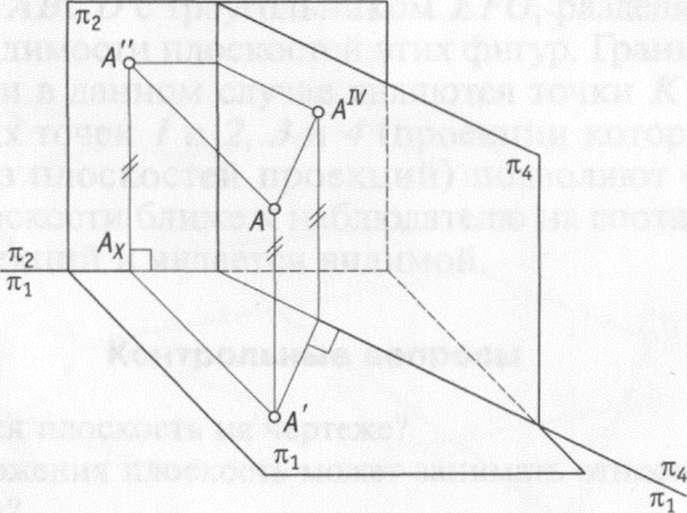
При введении
дополнительной плоскости проекций
проводят новую ось системы проекций
(рис. 4.2), разделяющую две плоскости
проекций в новой системе проекций. При
этом новую ось проводят либо параллельно,
либо перпендикулярно проекциям прямых,
чтобы получить частное положение этих
прямых в новой системе проекций.
При построении в
новой системе плоскостей следует
соблюдать те же условия положения
наблюдателя, которые были установлены
в первоначальной системе проекций.
Если новая ось
проводится на горизонтальной плоскости,
значит, изменяется положение фронтальной
плоскости проекций и дополнительная
плоскость проекций для наблюдателя
становится фронтальной. Наблюдатель
при этом перемещается в горизонтальной
плоскости.
Если
новая ось проводится на фронтальной
плоскости, значит, изменяется положение
горизонтальной плоскости проекций и
дополнительная плоскость проекций для
наблюдателя становится горизонтальной.
Наблюдатель при этом перемещается в
фронтальной плоскости.
Таким образом,
наблюдатель может рассматривать предметы
с любой стороны.
Дополнительные
плоскости по мере построения обозначают
тг4, 7с5и т.д. Обозначения дополнительных
плоскостей представляют собой как бы
числитель и знаменатель дроби,
разделительной чертой которой является
ось проекций, причем их обозначения
располагаются по ту сторону оси, где
должны размещаться соответствующие
проекции.
На
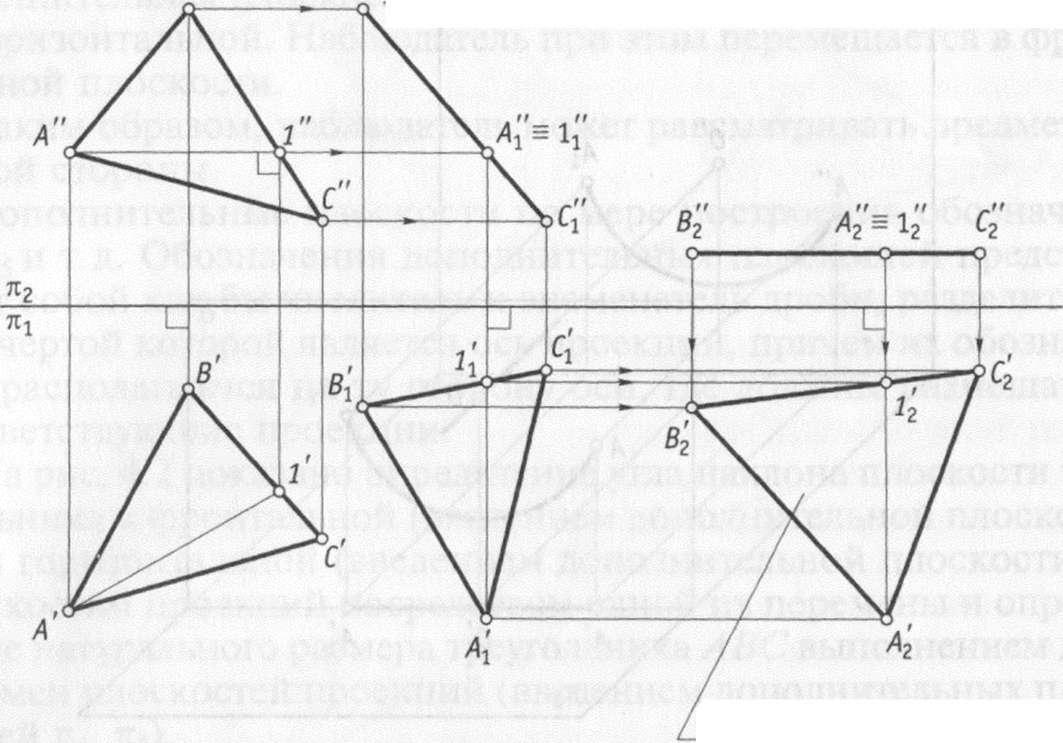
рис. 4.2 показано определение угла наклона
плоскости треугольника к фронтальной
(введением дополнительной плоскости
я6) и горизонтальной (введением
дополнительной плоскости я4) плоскостям
проекций посредством одной их перемены
и определение натурального размера
треугольника ЛВС выполнением двух
перемен плоскостей проекций (введением
дополнительных плоскостей я4, тс5).
Способ
вращения.
При вращении вокруг некоторой неподвижной
прямой — оси вращения — каждая точка
вращаемой фигуры перемещается в
плоскости, перпендикулярной этой оси
(т.е. плоскости вращения).
Точка
вращаемой фигуры перемещается по
окружности, центр которой находится в
точке пересечения оси вращения этой
фигуры с плоскостью вращения, называемой
центром вращения, а радиус этой окружности
равен расстоянию от вращаемой точки до
центра вращения и называется радиусом
вращения.
Если какая-либо
из точек данной системы находится на
оси вращения, то при ее вращении эта
точка считается неподвижной.
Ось
вращения может быть задана или выбрана.
В последнем случае ее выгодно располагать
перпендикулярно одной из плоскостей
проекций, так как при этом упрощаются
построения.
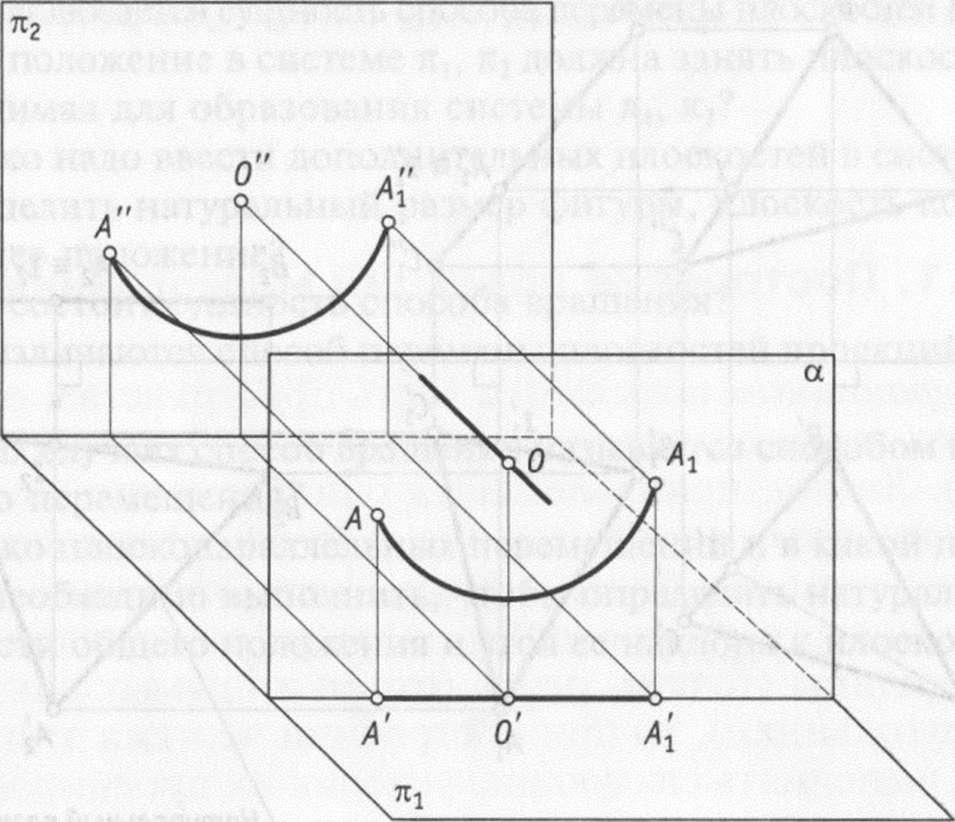
Действительно,
если ось вращения перпендикулярна,
например, плоскости тс2, то плоскость,
в которой происходит вращение точки,
параллельна плоскости п2. Следовательно,
траектория этой точки на плоскость п2
проецируется в виде окружности без
искажения, а на плоскость 7Cj — в виде
отрезка прямой линии (рис. 4.3).
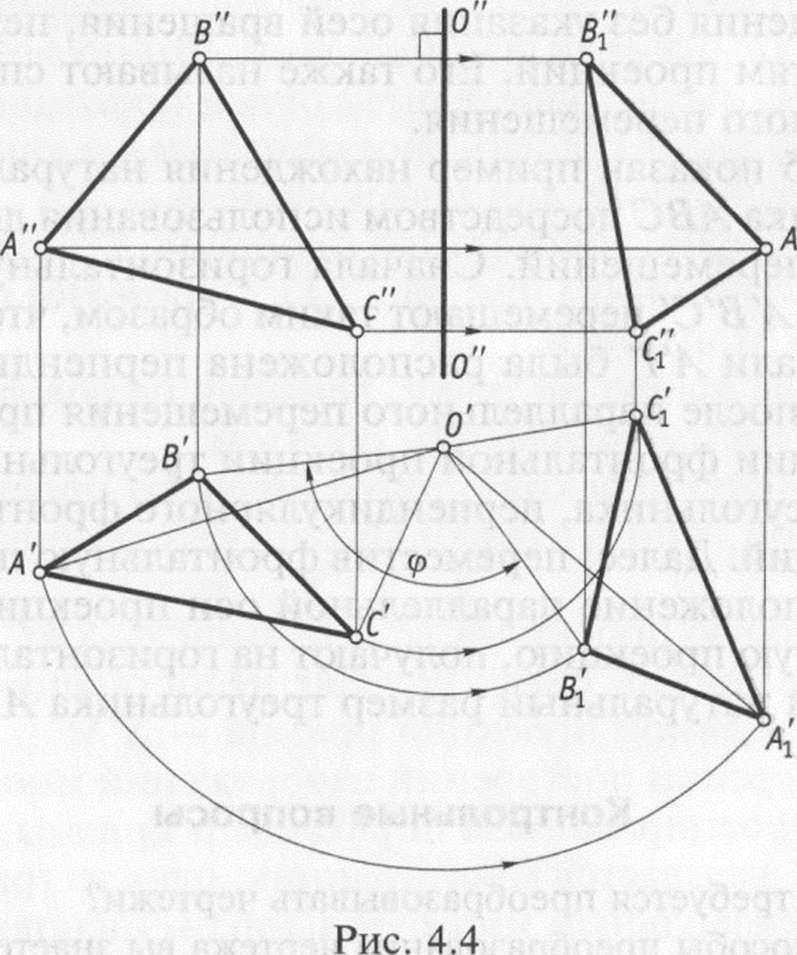
На
рис. 4.4 показан поворот треугольника
ABC вокруг выбранной оси О на угол ср.
Если
вращать отрезок прямой линии или плоскую
фигуру вокруг оси, перпендикулярной
плоскости проекций, то проекция на эту
плоскость не изменится ни по виду, ни
по размеру, изменится лишь положение
этой проекции относительно оси проекций.
Что же касается проекции на плоскость,
параллельную оси вращения, все ее точки
(за исключением, конечно, точек, проекции
которых расположены на оси вращения)
перемещаются по прямым, параллельным
оси проекций, и, следовательно, изменяются
ее форма и размер. В этом случае можно
не указывать проек цию оси вращения, не
устанавливать радиус вращения, а, не
изменяя вид и размер одной из проекций
заданной плоской фигуры, переместить
ее в требуемое положение и построить
другую проекцию с помощью линий,
параллельных оси проекций.
Рис. 4.3
33
Натуральный размер
Рис. 4.5
Данный
способ преобразования чертежа получил
название способа вращения без указания
осей вращения, перпендикулярных
плоскостям проекций. Его также называют
способом плоскопараллельного перемещения.
На
рис. 4.5 показан пример нахождения
натурального размера треугольника ABC
посредством использования двух
плоскопараллельных перемещений. Сначала
горизонтальную проекцию треугольника
А’В’С’ перемещают таким образом, чтобы
проекция его горизонтали AT была
расположена перпендикулярно оси
проекций, и после параллельного
перемещения проекций точек при построении
фронтальной проекции треугольника
получают плоскость треугольника,
перпендикулярного фронтальной плоскости
проекций. Далее, переместив фронтальную
проекцию треугольника в положение
параллельной оси проекций и построив
горизонтальную проекцию, получают на
горизонтальной плоскости проекций
натуральный размер треугольника ЛВС.
Контрольные
вопросы
-
Для чего требуется
преобразовывать чертежи? -
Какие способы
преобразования чертежа вы знаете? -
В чем заключается
сущность способа перемены плоскостей
проекции? -
Какое
положение в системе щ9 к2 должна занять
плоскость я3 проекций, вводимая для
образования системы я4, Я|? -
Сколько
надо ввести дополнительных плоскостей
в систему яь тс2, чтобы определить
натуральный размер фигуры, плоскость
которой занимает общее положение? -
В чем состоит
сущность способа вращения? -
Чем различаются
способ перемены плоскостей проекций
и способ вращения? -
В каких случаях
способ вращения называется способом
плоскопараллельного перемещения? -
Сколько
плоскопараллельных перемещений и в
какой последовательности необходимо
выполнить, чтобы определить натуральный
размер плоскости общего положения и
угол ее наклона к плоскостям проекций?
Преподаватель который помогает студентам и школьникам в учёбе.
Определение видимости в начертательной геометрии с примерами
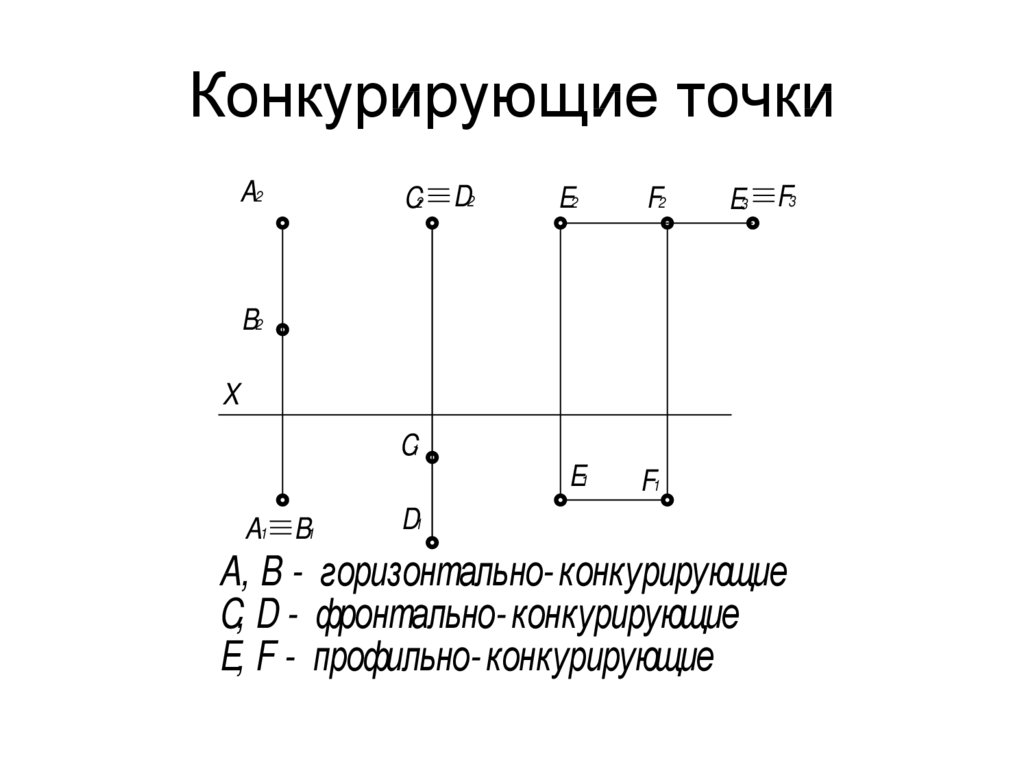
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
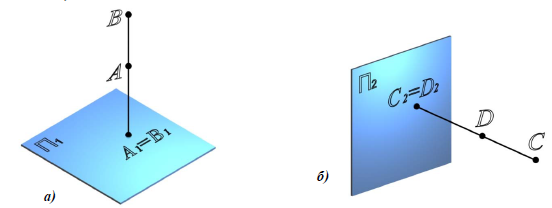
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
Рис. 7.1. Конкурирующие точки:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D – невидима).
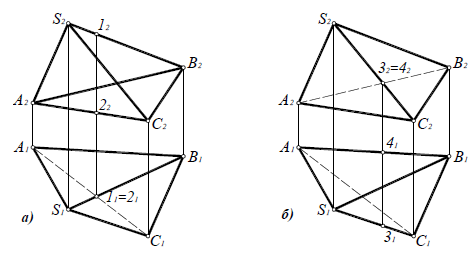
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
- Заказать чертежи
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.
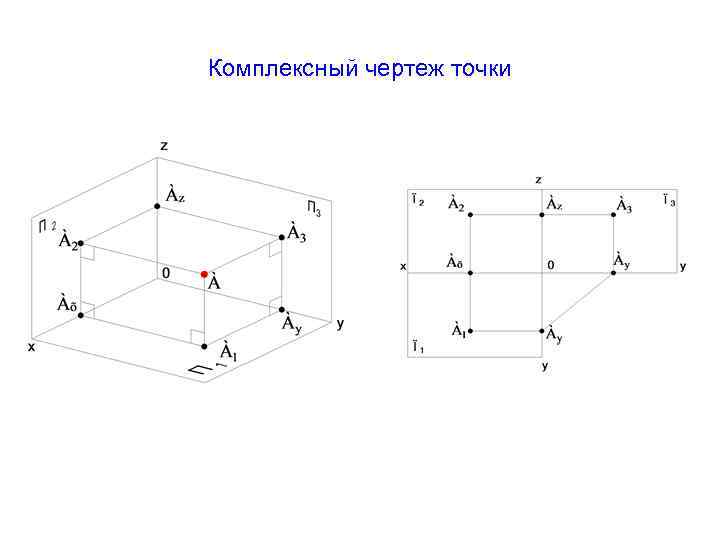
Комплексный чертеж и координаты точки
Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.
Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.
Рисунок 1. Координаты точки
Как найти точки на чертеже
Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.
Как правильно расставлять точки
Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.
Видимые и невидимые точки
Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.
Рисунок 2. Видимые и невидимые точки
Точки сопряжения
В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.
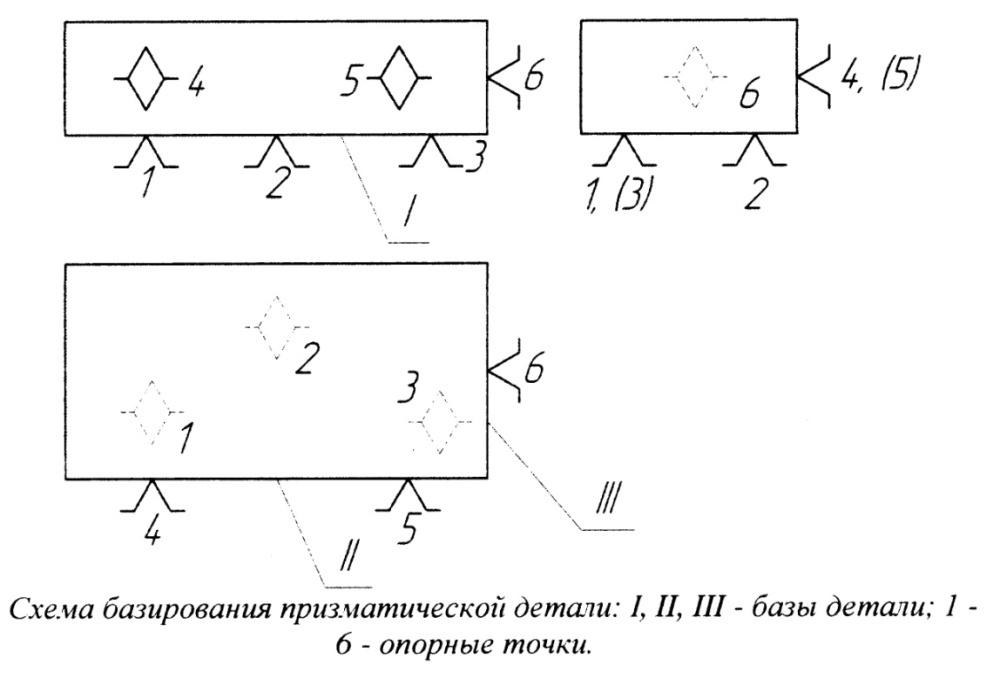
Опорные точки на чертеже
Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.
Рисунок 3. Опорные точки на чертеже
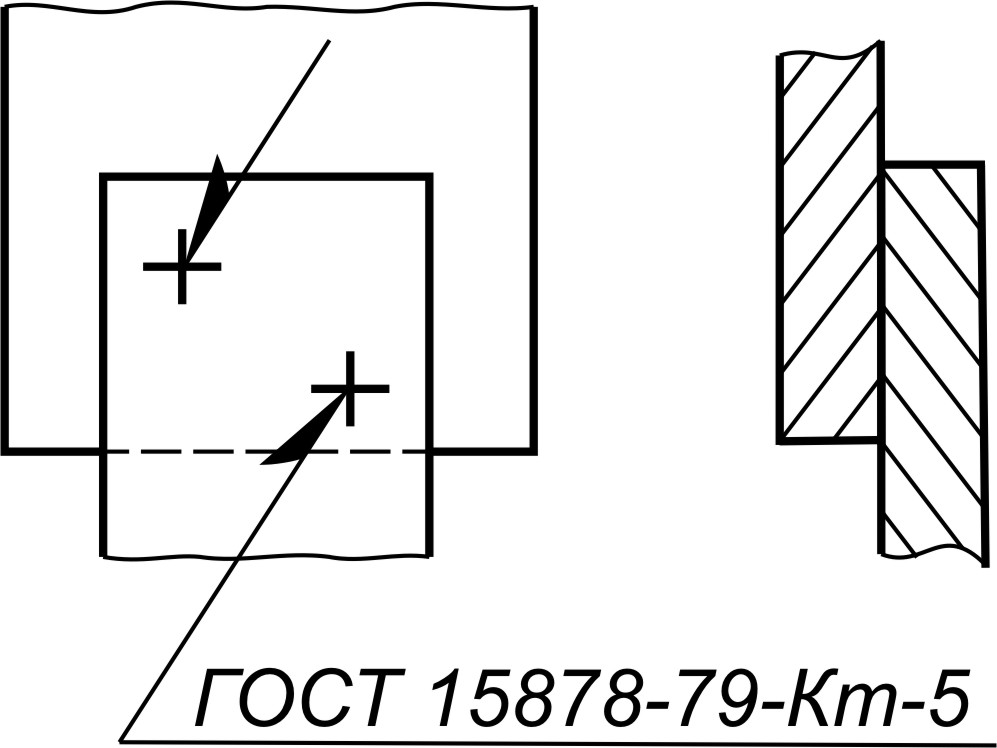
Сварные точки
Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.
Рисунок 4. Сварные точки на чертеже
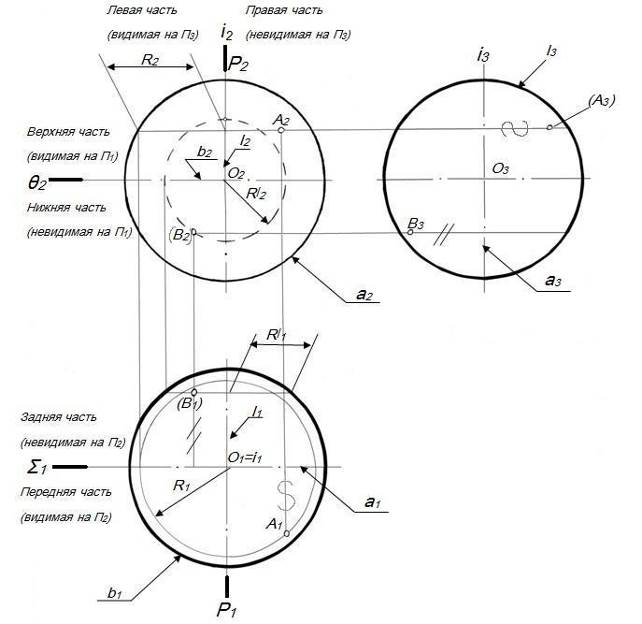
Трехкартинный чертеж точки
Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.
Рисунок 5. Трехкартинный чертеж точки
Конкурирующие точки на чертеже
Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.
Рисунок 6. Конкурирующие точки на чертеже
Что такое явная точка на чертеже
Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные – в реальной поверхности или точке пересечения рисок.
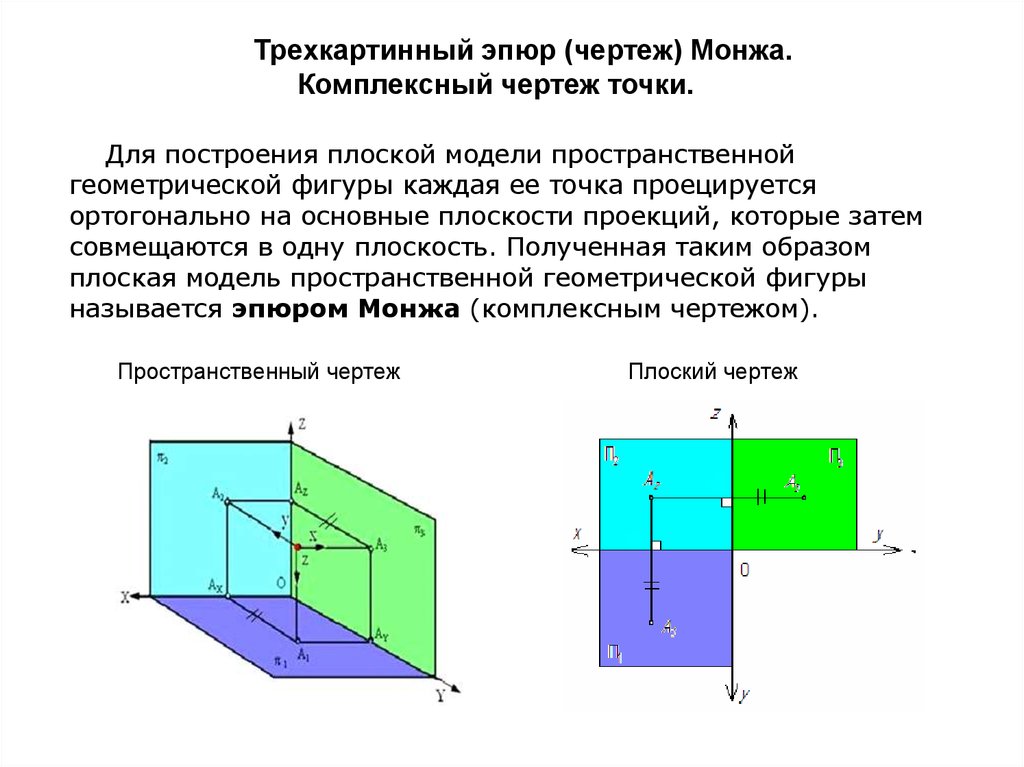
Как построить комплексный чертеж точки: инструкция
Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.
Построение комплексного чертежа точки А состоит следующих этапов:
- возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
- в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
- координаты точки описываются с помощью расстояния до плоскостей;
- для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
- третья плоскость вводится для построения профильной проекции.
Рисунок 7. Построение комплексного чертежа точки
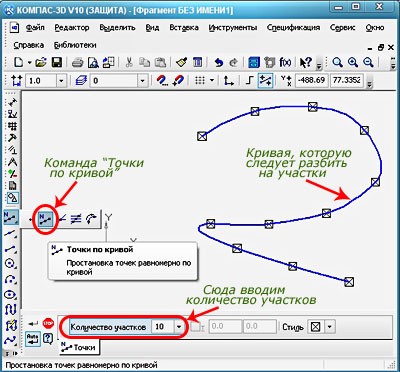
Как поставить точку на чертеже в Компасе
В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.
Рисунок 8. Как поставить точку в программе Компас
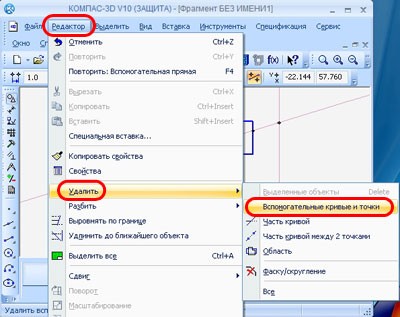
Как убрать точки на чертеже в Компасе
Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».
Рисунок 9. Как убрать точку в программе Компас
Ответы на вопросы
Как правильно показать невидимую сварную точку?
Невидимые сварные точки не имеют обозначения, в отличие от швов.
Как на чертеже показать характерные точки отрезка?
Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.
Чем отличается двухкартинный чертеж точки от трехкартинного?
Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.
Определение видимостиОпределение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.
Определение видимости рассмотрим на примерах: Определение видимости
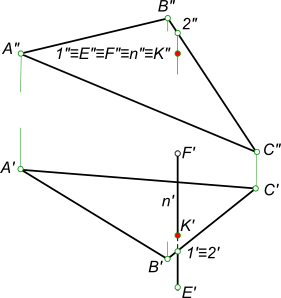
Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC – это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают. – имеется готовый эпюр пересечения прямой с плоскостью заданной следами Определение видимости
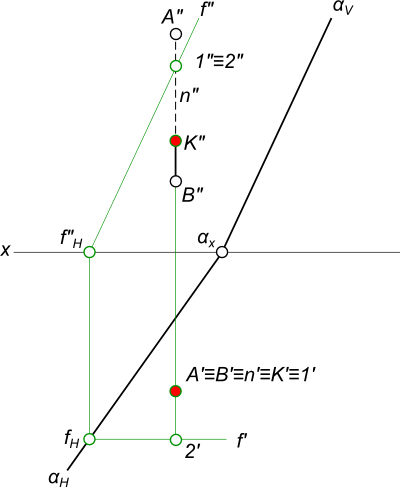
Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α – для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. + |
Как определить видимость на чертеже
В процессе создания чертежа инженер сталкивается с целым спектром проблем, умение решать которые является степенью его квалификации. Определение видимости на чертежах многосложных деталей есть одна из упомянутых проблем. Самый распространенный метод определения видимости на чертеже – метод конкурирующих точек.

Вам понадобится
- Изображения детали без определенной видимости по крайней мере в двух главных видах, захватывающих вид спереди, для этого лучше подойдут вид спереди и сверху, отмеченные ключевые точки на чертеже, в которых будет определяться видимость.
Инструкция
Найдите на чертеже точки, проекции которых на какой либо плоскости совпадают, не совпадая при этом на другой плоскости проекции. Такие точки называются конкурирующими и они будут использованы нами в качестве опорных точек при построении видимости, сообщая нам информацию о нахождении в пространстве тех объектов, к которым эти точки привязаны.
Через отмеченные вами ранее точки, предназначенные для определения видимости, проведите прямые таким образом, чтобы они были перпендикулярны одной из главных плоскостей проекции, при этом автоматически становясь параллельными другой плоскости проекции.
Отметьте точки пересечения прямых, проведенных вами в предыдущем шаге, с деталью. Эти точки будут конкурирующими, поскольку их проекции на одной плоскости будут совпадать, не совпадая при этом на другой плоскости. Если проекции точек совпадают на фронтальной плоскости (П1), то такое точки называются фронтально конкурирующими. Если проекции точек совпадают на горизонтальной плоскости (П2), то такие точки называются горизонтально-конкурирующими.
Определите видимость. Для фронтально конкурирующих точек видимость определяется на виде сверху. Та точка, горизонтальная проекция которой расположена ниже, то есть ближе к наблюдателю, будет видима на виде спереди. Соответственно другая точка, конкурирующая данной, будет невидима. Для горизонтально конкурирующих точек видимость определяется на виде спереди, при этом та точка будет видима, которая находится выше остальных, а все остальные, конкурирующие данной, будут невидимы.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.