Как найти невязки слау

Некоторые вычислительные особенности слау

Погрешности и
невязки

Для
оценки точности найденного решения
СЛАУ существует две общеупотребительной
меры погрешности:

1. вектор
   ошибок
   

где
точное решение

-найденное
решение

Мера абсолютно точная, только для того,
чтобы ею пользоваться нужно

Чтобы избежать трудностей, вводят другую
меру

1. вектор
   невязок
   

Невязка
– количественная мера несоответствия
между правыми и левыми частями системы
уравнений при подстановки в них
вычислительного решения.

Очевидно,
что равенство нулю вектора ошибок влечет
за собой равенство нулю вектора невязок.

Однако,
в общем случае из малости величины
невязок не следует малость ошибки. Т.е.
несмотря на то, что найденное решение
почти удовлетворяет уравнению, оно
может совсем не подходить в качестве
подлинного решения. Невязка полезна в
том смысле, что с ее помощью можно
осуществить контроль точности решения.
Т.к. использовать в качестве меры контроля
вектор ошибок не представляется возможным
в виду того, что неизвестно точное
решение.

Пример.
Рассмотрим систему

Предположим,
что мы провели вычисления (неважно каким
методом) и нашли решение

Если
вычислить невязки, то невязки будут
равны

Для
погрешность
10^-2, но точное решение

В
общем случае можно утверждать, что для
оценки величины невязки и погрешности
можно использовать следующие формулы:

Число
называется числом обусловленности
матрицы А и математически оно показывает,
насколько матрица системы А близка к
вырожденной или иными словами, числомера вырождения матрицы А, а именно, чем
выше,
тем ближе матрица к вырождению.

Обусловленность-
это внутреннее свойство матрицы СЛАУ.
Оно не связано с каким либо численным
методом. В общем случае, можно утверждать,
что матрица с большим числом обусловленности
дает большие ошибки при решении СЛАУ.

Математически
точно число обусловленности можно
вычислить.

Введем
число
;

Тогда
число обусловленности представляет
собой:

Тогда мы можем утверждать, что погрешность
решения:

Вычислительная
эффективность правила Крамера

Правило
Крамера широко применяется для нахождения
решения СЛУ

Если
сосчитать количество операций, которых
нам надо сделать

n	3	10	20
N	17	3.6*107	5*1019
t

Численные методы
решения СЛАУ

Все
численные методы решения СЛАУ принято
делить на два класса:

1. прямые

2. итерационные

Прямые
методы используют некоторые формулы
для вычисления неизвестных величин за
конечное число шагов вычислительного
процесса

Пример.
Метод обратной матрицы

Существенным
недостатком прямых методов является
необходимость хранения в памяти
компьютера всех n- квадратных элементов
матрицы системы, т.е прямые методы
никаким образом не учитывают разряженную
структуру матрицы в системы.

Кроме
этого применения прямых методов для
решения СЛАУ с большим числом переменных
приводит к значительному накоплению
вычислительных погрешностей.

К
широко известным методам относится
метод Гаусса, метод прогонки.

Итерационные
методы ( методы последовательных
приближений)-это методы, в которых с
помощью какого- либо алгоритма строится
цепочка приближенных решений

Каждый
цикл таких вычислений называется
итерацией.

Итерационные
алгоритмы сложнее прямых методов. Объем
необходимых вычислений при их использовании
заранее трудно определить, но они не
требуеют при работе с разряженными
матрицами хранение всех ее элементов.
Более того, зачастую в них используются
вычислительные формулы, задающие эти
примеры. Итерационный процесс устроен
таким образом, что вычислительные ошибки
от итерации к итерации не накапливаются.
Поэтому итерационный метод можно
использовать как для решения хорошо
обусловленных так и плохообусловленных
СЛАУ.

Примеры:
Метод простой итерации и метод Гаусса-
Зейделя

Метод исключения
Гаусса

Хорошо
известно, что алгоритм метода Гаусса
для решения СЛАУ состоит из двух основных
шагов.

1. На
   прямом ходе путем последовательного
   исключения переменных из уравнений
   системы, матрицу системы приводят к
   треугольному виду.

решение методом исключения дает
верхнетреугольную матрицу:

1. На
   обратном ходе вычисляется точное
   решение системы

подставляем в предыдущее уравнение и
получаем:

Метод
Гаусса применим эффективно лишь в том
случае, когда матрица системы хорошо
обусловлена, имеет низкое число
обусловленности.

Точность
вычисления значительно зависит от
способа нахождения ведущего элемента,
который мы используем, для исключения
переменных на прямом ходе.

Пример.Рассмотрим систему:

Возьмем
в качестве ведущего элемента

При
решении получим:

если округлить, то примерно получим,
что неправильно!

Теперь,
возьмем в качестве ведущего элемента
коэффициент перед
из второго уравнения, т.е 1.

Тогда,
если округлить, то получим правильное
решение

Правила
для выбора ведущего элемента:

1. выбор
   по столбцам

Рассматривается первый столбец.
Предполагается, что мы хотим исключить
.
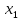
Находим в этом столбце максимальный
элемент, т.е.
Находим уравнение, где коэффициент присамый большой и переставляем это
уравнение на первое место и используем
коэффициент прив качестве ведущего элемента.

1. выбор
   по строке

Из первого уравнения находим переменную,
которую будем исключать. Ищем
и ищем соответственно,
которое соответствует этому максимальному
элементу. И ставимна первое место и исключаем его.

Эту методику можно обобщить на все
элементы

1. по
   всей матрице

Сканируем столбцы и строчки и ищем
.
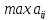
Находим,
и ставим этот элемент на первое место
.

Этот прием наиболее приемлем.

Метод прогонки

Метод
прогонки является частным случаем
метода Гаусса, который специально
предназначен для решения систем уравнений
с разряженной диагональной матрицей

1. Прямой
   ход состоит в том, что вычисляются
   коэффициенты

Сам процесс состоит в следующем.

1. Обратная
   прогонка соответствует вычислению
   переменных в обратном порядке, начиная
   с самого последнего x

зная
,
можно найти

Итерационные
методы

В общем случае схема итерационных
методов решения СЛАУ заключается в
следующем:

1. каким-
   либо посторонним способом нужно
   установить, какое- либо начальное
   решение
   

2. вычисляем
   правую часть:
   

3. находим
   невязку:
   

4. находим
   решение системы уравнений:
   ,–
   вектор поправок

5. 

6. из 5.
   пункта идем во 2.

Важным
вопросом является, когда нужно
остановиться!

В
качестве остановки используют какое-
либо векторное неравенство, которое
сравнивает решения, полученные на
предыдущей и последующей итерации.

Введем
норму:

Соседние файлы в папке ммм

• #
• #

  11.03.20169 б13Desktop__.ini

• #
• #
• #
• #
• #

Метод Гаусса с подсчетом невязки

Системы линейных уравнений

Системы n линейных уравнений с n неизвестными x₁, x₂, . x_n в общем случае принято записывать следующим образом:

где а_ij и b_i – произвольные константы. Число n неизвестных называется порядком системы.

Решением уравнения является такая совокупность значений переменных х₁, х₂,…, х_n , которая одновременно обращает все уравнения системы в тождество.

Необходимым и достаточным условием существования и единственности решения системы уравнений является линейная независимость уравнений. Или, более точно, неравенство нулю определителя, составленного из коэффициентов системы уравнений:

Эквивалентной (и весьма удобной. ) записью системы линейных уравнений является матричная запись

или сокращенно ,

в чем легко убедится, если воспользоваться правилами перемножения матриц: элемент, стоящий на пересечении i -й строки и j -го столбца матрицы-результата есть скалярное произведение i -й вектор-строки первой матрицы и j -го вектор-столбца второй матрицы.

Коэффициенты при неизвестных образуют квадратную матрицу размером n x n, (A) , переменные и свободные члены уравнений – векторы-столбцы длиной n (Х) и (В) , соответственно.

Решение системы уравнений есть вектор (X * ) , который обращает это матричное уравнение в тождество.

Для решения системы линейных уравнений применяются точные методы (прямые) в которых количество арифметических, необходимых для нахождения решения, операций точно определяется порядком системы и итерационные (приближенные) методы, в которых проводится пошаговое, итерационное уточнение решения.

Оценить близость какого-либо вектора (Х)_i к решению системы уравнений можно оценив близость вектора невязок , вычисляемого приведенным ниже образом, к нулевому вектору:

Для выражения меры близости в виде числа используется какая-либо норма вектора, например, Евклидова норма или длина вектора в n-мерном пространстве (другое определение – это корень квадратный из скалярного произведения вектора на себя):

Иногда используются другие векторные нормы: норма-максимум (равна наибольшей по абсолютной величине компоненте вектора)

или норма-сумма (равна сумме абсолютных величин компонентов вектора)

Обусловленность линейных алгебраических систем

Численное решение систем алгебраических уравнений является часто решаемой в рамках математического моделирования задачей. При этом как размерность задачи, так и характер матриц может существенно меняться. Вычисления, проводимые с определенной точностью, так же оказывают влияние на результат решения линейных систем. Кроме того, сами коэффициенты системы – матрица (А) и свободные члены – (В) могут быть представлены с определенной погрешностью.

Приведем такой пример:

Имеет, как нетрудно убедиться подстановкой, единственное решение x = 1, y = 1.

Предположим, что при подготовке системы к решению, правая часть первого уравнения была определена с небольшой абсолютной погрешностью в +0.01, то есть, правая часть первого из уравнений вместо 11 была взята равной 11,01.

Единственным решение этой системы уравнений уже будет вектор x=11,01 y=0.

Как нетрудно убедится, в этом случае погрешность определения значений переменных оказывается существенно больше, чем погрешность коэффициента. Задачи, в которых малое изменение исходных параметров кардинально сказывается на результате называются плохо обусловленными.

Рассмотрим в общем виде систему линейных уравнений, в которой вектор свободных членов (В) представлен с некоторой абсолютной погрешностью (ΔВ) .

Если вектор (X) является точным решением уравнения с “точным” вектором (В ) .

то при наличии погрешности в правой части (ΔВ) решение системы уравнений будет отличаться от (X) на некоторый вектор (ΔX) , что можно записать следующим образом:

, раскроем скобки в правой части

и учтем точное уравнение

, умножая обе части равенства на матрицу, обратную матрице коэффициентов

получим

т.е. абсолютная погрешность (ΔX) вычисления вектора решения (X) равна произведению матрицы, обратной матрице коэффициентов системы уравнений, на вектор абсолютной погрешности (ΔВ) .

Если перейти от матриц и векторов к соответствующим нормам, то получим, что норма вектора (ΔX) будет меньше либо равна произведению норм обратной матрицы и нормы вектора погрешности

Таким образом, если норма обратной матрицы будет велика, то абсолютная погрешность решения может быть существенно больше абсолютной погрешности правых частей уравнений системы.

Оценим, как будут при этом соотноситься относительная погрешность решения и относительной погрешностью коэффициентов. Для этого пронормируем два полученных ранее уравнения:

Перемножим отдельно левые и правые части неравенств, что, очевидно, не изменит знак неравенства и разделим обе части на и, окончательно получим:

Величина называется числом (мерой) обусловленности матрицы А . От этой величины зависит степень влияния погрешности коэффициентов системы уравнений на погрешность полученного решения. Если это число невелико, то относительная погрешность решения будет не сильно отличаться от относительной погрешности коэффициентов. Чем больше число обусловленности тем больше будет влияние погрешности коэффициентов на погрешность решения.

Аналогичный анализ можно провести и для случая наличия погрешности задания матрицы коэффициентов системы (ΔA) . И в этом случае, так же, возникает число обусловленности.

Для рассмотренного числового примера

и

Если взять, например, матричную норму-максимум,

, то получим

для матрицы (А) норму 1011, а для матрицы, обратной (А) – (А) -1 – 1101. Таким образом, число обусловленности оказывается равным более 1000000!

Прямые (точные) методы

Метод Гаусса и Гаусса-Жордана

Алгоритм решения заключается в приведении расширенной матрицы системы уравнений к треугольному виду (метод Гаусса) или псевдодиагональному виду (метод Гаусса-Жордана).

В данном методе (при не равенстве нулю определителя, составленного из коэффициентов системы) значения переменных определяются следующим образом

, i = 1, 2, …, n

Здесь в знаменателе стоит определитель матрицы коэффициентов системы. В числителе – определитель матрицы, полученной из матрицы коэффициентов путем замены i-го столбца на вектор-столбец свободных членов системы.

Для системы, записанной в общем виде:

Метод обращения матрицы

Решение системы уравнений, записанной в матричной форме, легко найти, если воспользоваться определением обратной матрицы:

где (1) – единичная диагональная матрица.

Умножим слева обе части уравнения на обратную матрицу коэффициентов системы (A) -1

Таким образом, для решения системы, необходимо обратить матрицу коэффициентов системы и умножить полученный результат на вектор-столбец свободных членов .

Несмотря на простоту записи, метод имеет достаточную вычислительную сложность, которая заключается в нахождении обратной матрицы .

Приближенные (итерационные) методы

Метод простых итераций, метод Зейделя

Данные методы рассмотрены на примере систем нелинейных уравнений.

Метод минимальных невязок

Для решения линейных систем уравнений можно применять и различные методы поиска экстремумов. Проблема решения системы уравнений заменяется эквивалентной задачей нахождения экстремума функции n переменных.

Одним из примеров является метод минимальных невязок. Вектор невязок определяется следующим образом.

Очевидно, что если на место вектора (Х) подставить вектор решения, то второе слагаемое окажется равным вектору свободных членов и вектор невязок становится нулевым.

Таким образом, минимизация компонентов вектора невязок эквивалентна задаче решения уравнений. Что бы знак невязок не влиял на результат, минимизируют сумму квадратов невязок (скалярное произведение вектора на себя):

Запишем итерационную формулу поиска решения в следующем виде

где индекс k обозначает номер итерационного шага, тау – константа, которую нам необходимо определить, Δ (k) (дельта) – вектор невязок на этом шаге.

Рассмотрим разность векторов невязок на двух последовательных шагах k и k+1

после подстановки имеем

Скалярное произведение этого вектора на себя имеет вид

Параметр тау можно выбрать таким образом, чтобы левая часть была минимальной. Условием экстремума является равенство нулю производной по тау правой части выражения

Окончательно, k-ый шаг метода выглядит следующим образом:

1. Задается начальное приближение (Х (k) )

2. Рассчитывается вектор невязок

3. Рассчитывается параметр тау. Для этого перемножается матрица коэффициентов и вектор невязок. Затем вычисляется его скалярный квадрат и произведение на матрицу невязок.

4. Рассчитывается новое приближение к вектору-решению

5. Проверяется один из критериев сходимости и, при необходимости, происходит переход к пункту 2.

Задачи, сводящиеся к решению систем линейных уравнений

Примеры решения задач, которые сводятся к нахождению корней системы линейных уравнений можно найти по следующей ссылке:

Невязка решения системы линейных уравнений это

Классы задач линейной алгебры

При численном решении большого круга задач в конечном итоге происходит их линеаризация, в связи с чем в соответствующих алгоритмах весьма широко используются методы линейной алгебры. В их числе:

• решение систем линейных алгебраических уравнений (СЛАУ);
• вычисление определителей матриц ;
• нахождение обратных матриц ;
• определение собственных значений и собственных векторов матриц

Постановка задачи решения СЛАУ: (1) , где – квадратная матрица коэффициентов размерности n, – вектор неизвестных, – вектор свободных коэффициентов. Иногда СЛАУ представляют в виде расширенной матрицы размерности n×(n+1), где в качестве последнего столбца фигурирует вектор свободных коэффициентов. В координатном представлении такая СЛАУ выглядит следующим образом:

(2)

Для решения СЛАУ применяют в основном два класса методов: прямые (выполняемые за заранее известное количество действий) и итерационные (обеспечивающие постепенную сходимость к корню уравнения, зависящую от многих факторов). Прямые методы обычно применяются для решения систем порядка n Если – решение существует и единственно. Если же определитель равен нулю, то тогда, если матрица вырождена (т.е. ее можно преобразовать к виду, когда как минимум одна строка коэффициентов – нули) решений бесконечное множество, иначе решения не существует.

Если не имеет элементов с большими по модулю значениями – решение устойчиво (см. пример к главе 1). Показателем плохо обусловленных систем является .

Алгоритм метода Гаусса

Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений. На примере первого уравнения системы (2) рассмотрим выражение для x₁:

.

Подставим выражение для x₁ во второе и все остальные уравнения системы:

.

Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. Таким образом, станут равны нулю все коэффициенты первого столбца, лежащие ниже главной диагонали. Затем аналогичная процедура проводится со второй строкой матрицы и нижележащими строками, при этом первая строка и первый столбец уже не изменяются. И так далее до тех пор, пока все коэффициенты, лежащие ниже главной диагонали, не будут равны нулю.

Общие формулы прямого хода:

, (3)

k = 1…n, j = 1…n+1. Звездочкой отмечены элементы k-й строки с измененными значениями, которые будут подставлены в следующую формулу. Для определенности будем считать первый индекс – по строкам, второй – по столбцам.

, (4)

i = k+1…n, j = 1… n+1, k фиксировано в уравнении (3). Для уменьшения количества действий достаточно изменять значения элементов, находящихся выше главной диагонали.

Второй этап решения СЛАУ методом Гаусса называется обратным ходом и состоит в последовательном определении x_k, начиная с x_n, так как для последнего решение фактически получено. Общая формула:

. (5)

Таким образом, вычисление корней происходит за 2/3 n 3 арифметических действий.

3. Выбор главного элемента.

Для уменьшения погрешности вычислений следует стремиться к тому, чтобы на главной диагонали матрицы стояли максимальные по модулю значения коэффициентов. Алгоритмически этого можно добиться, переставляя строки таким образом, чтобы на диагонали стоял наибольший по модулю элемент текущего столбца. Такая процедура называется выбором главного элемента и осуществляется всякий раз при переходе к новой строке в прямом цикле метода Гаусса.

4. Погрешность метода. Расчет невязок.

Точность результатов будет определяться только точностью выполнения арифметических операций при преобразовании элементов матрицы, т.е. ошибкой округления. Контроль правильности полученного решения осуществляется подстановкой полученных значений x₁… x_n в исходную систему уравнений и вычислением невязок, т.е. разностей между правыми и левыми частями уравнений:

, где k = 1…n. (6)

Специально отметим, что подставлять найденные значения следует в исходную (не преобразованную к верхнетреугольному виду) систему.

5. Преимущества и недостатки метода.

Преимущество метода в том, что он позволяет достичь результата за заранее известное и фиксированное число действий. Точность результатов будет определяться правильным выбором порядка коэффициентов в матрице и ее размерностью. Недостатком метода является резкое увеличение времени и погрешности вычислений с ростом n.

Итерационные методы решения систем линейных уравнений.

Простейшим итерационным методом решения СЛАУ является метод простой итерации. При этом система уравнений (1) преобразуется к виду (2) , а ее решение находится как предел последовательности (3) , где – номер итерации. Утверждается, что всякая система (2), эквивалентная (1), записывается в виде .

Теорема о достаточном условии сходимости метода простой итерации утверждает, что если норма матрицы ( ), то система уравнений (2) имеет единственное решение и итерационный процесс (3) сходится к решению со скоростью геометрической sпрогрессии.

Теорема о необходимом и достаточном условии сходимости метода простой итерации: Пусть система (2) имеет единственное решение. Итерационный процесс (3) сходится к решению системы (2) при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы по модулю меньше 1.

На практике для обеспечения сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами.

Представим СЛАУ в следующей форме, удовлетворяющей (3):

(4)

Зададим начальные приближения и вычислим правую часть (4), получим новые приближения , которые опять подставим в систему (4). Таким образом организуется итерационный процесс, который обрывается по условию , где – заданная погрешность.

К ускорению сходимости приводит использование приближения к решениям путем последовательного уточнения компонентов, причем k-я неизвестная находится из k-го уравнения. Такая модификация итерационного метода носит название метода Зейделя:

Критерий сходимости метода Зейделя: Пусть – вещественная симметричная положительно определенная матрица. Тогда метод Зейделя сходится.

Достоинствами метода простых итераций является простота программной реализации и более быстрый, по сравнению с линейными методами, поиск решения в матрицах большого размера. Недостатками являются сложный контроль условий сходимости и выбора начального приближения.

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ☞ ИНТЕРПОЛЯЦИЯ.

Метод наименьших квадратов

Пусть из физических соображений можно считать (предполагать), что величины $ x_<> $ и $ y_<> $ связаны линейной зависимостью вида $ y=kx+b $, а неизвестные коэффициенты $ k_<> $ и $ b_<> $ должны быть оценены экспериментально. Экспериментальные данные представляют собой $ m>1 $ точек на координатной плоскости $ (x_1,y_1), dots, (x_m,y_m) $. Если бы эти опыты производились без погрешностей, то подстановка данных в уравнение приводила бы нас к системе из $ m_<> $ линейных уравнений для двух неизвестных $ k_<> $ и $ b_<> $: $$ y_1=k,x_1+b, dots, y_m=k,x_m+b . $$ Из любой пары уравнений этой системы можно было бы однозначно определить коэффициенты $ k_<> $ и $ b_<> $.

Однако, в реальной жизни опытов без погрешностей не бывает

Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».

Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.

Будем предполагать, что величины $ x_<1>,dots,x_m $ известны точно, а им соответствующие $ y_1,dots,y_m $ — приближенно. Если $ m>2 $, то при любых различных $ x_ $ и $ x_j $ пара точек $ (x_,y_i) $ и $ (x_,y_j) $ определяет прямую. Но другая пара точек определяет другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.

Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k,x_i+b-y_i $, и выбирают прямую так, чтобы сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_ <0>$ уравнения этой прямой дают некоторое решение стоящей перед нами задачи, которое отнюдь не является решением системы линейных уравнений $$ k,x_1+b=y_1,dots, k,x_+b=y_m $$ (вообще говоря, несовместной).

Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость между величинами $ y_<> $ и $ x_<> $ полиномиальная: $$ y_1=f(x_1),dots , y_m=f(x_m), quad npu quad f(x)=a_0+a_1x+dots+a_x^ $$ Величина $ varepsilon_i=f(x_i)-y_i $ называется $ i_<> $-й невязкой 1) . Уравнения $$ left<begin a_0+a_1x_1+dots+a_x_1^&=&y_1, \ a_0+a_1x_2+dots+a_x_2^&=&y_2, \ dots & & dots \ a_0+a_1x_m+dots+a_x_m^&=&y_m end right. $$ называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).

Предположим что данные интерполяционной таблицы $$ begin x & x_1 & x_2 & dots & x_m \ hline y & y_1 & y_2 &dots & y_m end $$ не являются достоверными: величины $ x_<> $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_<> $ подвержены случайным (несистематическим) погрешностям.

Задача. Построить полином $ f_<>(x) $ такой, чтобы величина $$ sum_^m [f(x_j)-y_j]^2 $$ стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов 2) .

В случае $ deg f_<> =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_<> n $: $$S=left(begin 1 &1&1&ldots&1\ x_1 &x_2&x_3&ldots&x_\ vdots&& & &vdots\ x_1^ &x_2^&x_3^&ldots&x_m^ endright) cdot left(begin 1 &x_1&x_1^2&ldots&x_1^\ 1 &x_2&x_2^2&ldots&x_2^\ ldots&& & &ldots\ 1 &x_m&x_m^2&ldots&x_m^ endright)$$ $$det S = sum_<1le j_1 0 $. По теореме Крамера система нормальных уравнений имеет единственное решение.

Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы линейных уравнений. Этот результат приводится ☟ НИЖЕ. ♦

Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов $$ sigma=frac<1>sum_^m (f(x_j) -y_j)^2 $$ называется среднеквадратичным отклонением.

Показать, что линейный полином $ y=a_<0>+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_<>,y) $ прямую, проходящую через центроид

Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02 end $$

Решение. Имеем $$ s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$ $$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75, $$ $$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23, $$ $$ t_1 =0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 + $$ $$ +2.5 cdot 3.51 + 3 cdot 1.02=19.06 . $$ Решаем систему нормальных уравнений $$ left( begin 6 & 10.5 \ 10.5 & 22.75 end right) left( begin a_0 \ a_1 end right)= left( begin 9.23 \ 19.06 end right), $$ получаем уравнение прямой в виде $$ y= 0.375 + 0.665, x .$$

Вычислим и полиномы более высоких степеней. $$ f_2(x)=-1.568+3.579, x-0.833,x^2 , $$ $$ f_3(x)=2.217-5.942,x+5.475,x^2-1.201, x^3 , $$ $$ f_4(x)= -4.473+17.101,x-19.320,x^2+9.205, x^3-1.487,x^4 , $$ $$ f_5(x)= 16.390-71.235,x+111.233,x^2-77.620,x^3+25.067,x^4-3.0347, x^5 . $$

Среднеквадратичные отклонения: $$ begin deg & 1 & 2 & 3 & 4 & 5 \ hline sigma & 0.717 & 0.448 & 0.204 &0.086 & 0 end $$ ♦

Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.

Влияние систематических ошибок

Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02 end $$ имеет вид (охра) $$ y=0.175+0.779, x , . $$ Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид: $$ y=0.483+0.383, x , . $$ График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.

После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.

Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы. Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел 3) .

Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см. ☞ цитату). Как это сделать?

Псевдорешение системы линейных уравнений

Рассмотрим теперь обобщение задачи предыдущего пункта. В практических задачах часто бывает нужно найти решение, удовлетворяющее большому числу возможно противоречивых требований. Если такая задача сводится к системе линейных уравнений $$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&b_1\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_m endright. iff AX= <mathcal B>$$ при числе уравнений $ m_<> $ большем числа неизвестных $ n_<> $, то такая переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.

Псевдорешением системы $ AX= <mathcal B>$ называется столбец $ Xin mathbb R^n $, обеспечивающий минимум величины $$ sum_^m [a_x_1 +a_x_2+ldots+a_x_n-b_i]^2 . $$

Теорема. Существует псевдорешение системы

$$ AX= <mathcal B>$$ и оно является решением системы $$ left[A^<top>A right]X=A^ <top> <mathcal B> . $$ Это решение будет единственным тогда и только тогда, когда $ operatorname A =n $.

Система $ left[A^<top>A right]X=A^ <top> <mathcal B>$ называется нормальной системой по отношению к системе $ AX= <mathcal B>$. Формально она получается домножением системы $ AX= <mathcal B>$ слева на матрицу $ A^ <top>$. Заметим также, что если $ m=n_<> $ и $ det A ne 0 $, то псевдорешение системы совпадает с решением в традиционном смысле.

Доказательство ☞ ЗДЕСЬ.

Если нормальная система имеет бесконечное количество решений, то обычно в качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).

Пример. Найти псевдорешение системы

$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$

Решение. Имеем: $$A=left( begin 1 & 1 \ 1 & -1 \ 2 & 1 end right), operatorname A =2, <mathcal B>= left( begin 2 \ 0 \ 2 end right), A^<top>A= left( begin 6 & 2 \ 2 & 3 end right), A^ <top> <mathcal B>= left( begin 6 \ 4 end right). $$

Ответ. $ x_1=5/7, x_2 = 6/7 $.

Показать, что матрица $ A^<top>A $ всегда симметрична.

На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь попасть по монетке. Все промахиваются. Расстроенные, рыцари уходят в харчевню пропивать злосчастную монетку. Укажите максимально правдоподобное ее расположение, имея перед глазами зарубки: $$ begin 3, x &- 2, y&=& 6,\ x &-3,y&=&-3,\ 11,x& + 14,y&=& 154, \ 4,x&+y&=&48. end $$

Геометрическая интерпретация

Псевдообратная матрица

Пусть сначала матрица $ A_<> $ порядка $ mtimes n_<> $ — вещественная и $ m ge n_<> $ (число строк не меньше числа столбцов). Если $ operatorname (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_<> $ определяется как матрица $$ A^<+>=(A^<top>A)^ <-1>A^ <top> . $$ Эта матрица имеет порядок $ n times m_<> $. Матрица $ (A^<top>A)^ <-1>$ существует ввиду того факта, что при условии $ operatorname (A) = n $ будет выполнено $ det (A^ <top>A) > 0 $ (см. упражнение в пункте ☞ ТЕОРЕМА БИНЕ-КОШИ или же пункт ☞ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^ <+>cdot A = E_ $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_<> $. В случае $ m=n_<> $ псевдообратная матрица совпадает с обратной матрицей: $ A^<+>=A^ <-1>$.

Пример. Найти псевдообратную матрицу к матрице $$ A= left( begin 1 & 0 \ 0 & 1 \ 1 & 1 end right) . $$

Решение. $$ A^<top>= left( begin 1 & 0 & 1 \ 0 & 1 & 1 end right) Rightarrow A^ <top>cdot A = left( begin 2 & 1 \ 1 & 2 end right) Rightarrow $$ $$ Rightarrow (A^ <top>cdot A)^ <-1>= left( begin 2/3 & -1/3 \ -1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow quad A^ <+>= (A^ <top>cdot A)^ <-1>A^ <top>= left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 end right) . $$ При этом $$ A^ <+>cdot A = left( begin 1 & 0 \ 0 & 1 end right),quad A cdot A^ <+>= left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 \ 1/3 & 1/3 & 2/3 end right) , $$ т.е. матрица $ A^ <+>$ не будет правой обратной для матрицы $ A_<> $. ♦

Вычислить псевдообратную матрицу для $$ mathbf left( begin 1 & 0 \ 1 & 1 \ 1 & 1 end right) quad ; quad mathbf left( begin x_1 \ x_2 \ x_3 end right) . $$

Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений . Если $ A^ <+>$ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_<> $ находится по формуле $ X= A^ <+>mathcal B $ при любом столбце $ mathcal B_<> $. Верно и обратное: если $ E_<[1]>, E_<[2]>,dots, E_ <[m]>$ – столбцы единичной матрицы $ E_m $: $$ E_<[1]>=left( begin 1 \ 0 \ 0 \ vdots \ 0 end right), E_<[2]>=left( begin 0 \ 1 \ 0 \ vdots \ 0 end right),dots, E_<[m]>=left( begin 0 \ 0 \ 0 \ vdots \ 1 end right), $$ а псевдорешение системы уравнений $ AX=E_ <[j]>$ обозначить $ X_ $ (оно существует и единственно при условии $ operatorname (A) = n $), то $$ A^<+>=left[X_1,X_2,dots,X_m right] . $$

Теорема. Пусть $ A_<> $ вещественная матрица порядка $ mtimes n_<> $, $ m ge n_<> $ и $ operatorname (A) = n $. Тогда псевдообратная матрица $ A^ <+>$ является решением задачи минимизации

$$ min_> |AX-E_m|^2 $$ где минимум разыскивается по всем вещественным матрицам $ X_<> $ порядка $ ntimes m_<> $, а $ || cdot || $ означает евклидову норму матрицы (норму Фробениуса) : $$ |[h_]_|^2=sum_ h_^2 . $$ При сделанных предположениях решение задачи единственно.

С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_^<> $, у которой число строк меньше числа столбцов: $ m ☞ ЗДЕСЬ

Источники

[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

[spoiler title=”источники:”]

http://solidstate.karelia.ru/p/tutorial/meth_calc/files/07.shtml

http://vmath.ru/vf5/interpolation/mnk

[/spoiler]
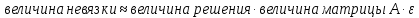
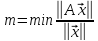
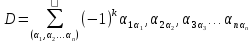
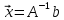
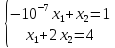
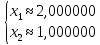