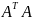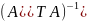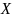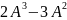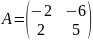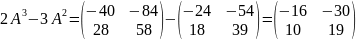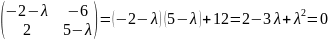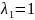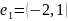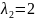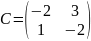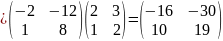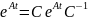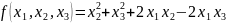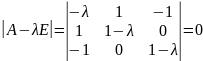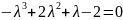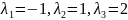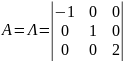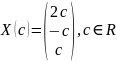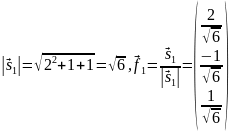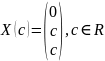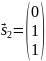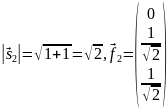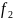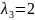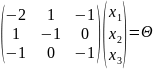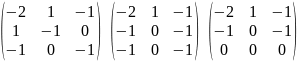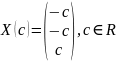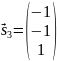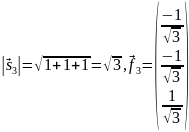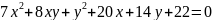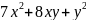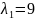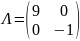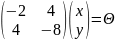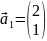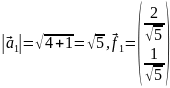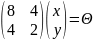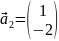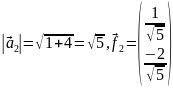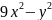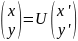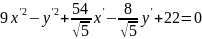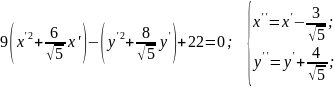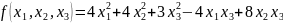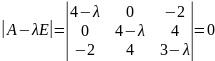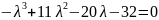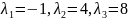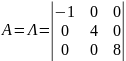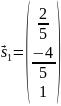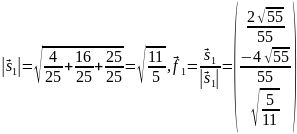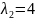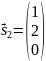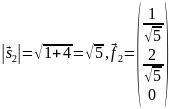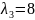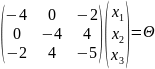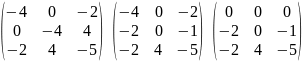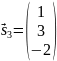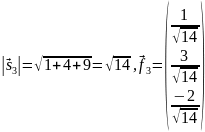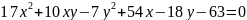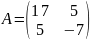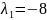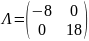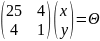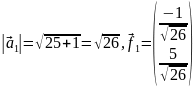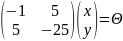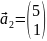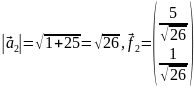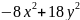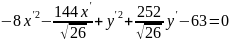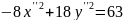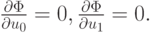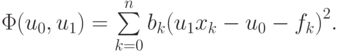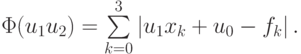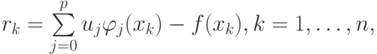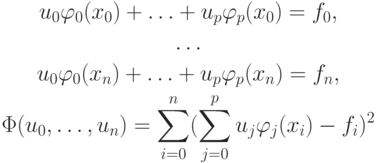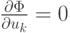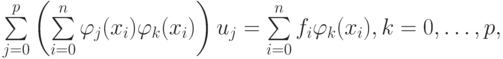Министерство
науки и высшего образования Российской
Федерации
К
алужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Московский
государственный технический университет
имени Н.Э. Баумана
(Национальный
Исследовательский Университет)»
(КФ
МГТУ им. Н.Э. Баумана)
|
ФАКУЛЬТЕТ |
М-КФ |
|
КАФЕДРА |
М10-КФ |
ДОМАШНЯЯ
РАБОТА №1
«____________________________________»
|
ДИСЦИПЛИНА: |
“Линейная |
|
Выполнил: |
_______________(Прудников
Подпись |
|
Проверил: |
_______________(Емельянов
Подпись |
|
Дата |
|
|
Результаты
-Балльная -Оценка |
|
Калуга,
2020 г.
Вариант
№21
Задание
№1
Решить
систему методом наименьших квадратов.
Найти сумму квадратов невязок.
Решение:
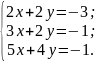
Разберем
данную неоднородную СЛАУ на три матрицы:
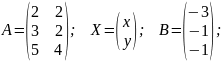
Приведем
запись данной нСЛАУ в форме матричного
уравнения:
AX=B
Домножим
получившееся уравнение на
и выразим матрицу X:
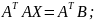
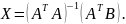
Найдем
матрицу
:
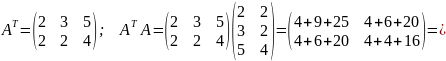
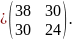
Теперь
найдём обратную матрицу
:
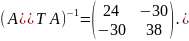
Найдём
матрицу
:

Зная
и
,
найдём матрицу
:
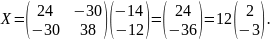
Из
получившейся матрицы мы видим, что х=2,
а у=-3.
Теперь найдём невязки, а затем найдём
квадрат суммы невязок Δ:
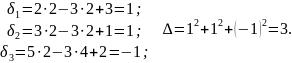
Задание
№2
Решить
выражение
двумя способами и найти
,
при
.
Решение:
-
Решим
уравнение классическим методом:
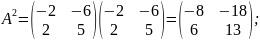
;
;
-
Теперь
решим методом приведения к диагональному
виду:
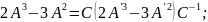
Решим
характеристическое уравнение:

;
Получившиеся
корни:

Матрицу
А
приведем к вертикальной матрице
.
-
Найдём
собственный вектор, если
:
Составим
систему:
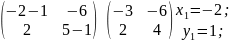
– первый
собственный вектор
-
Найдём
собственный вектор, если
:
Составим
систему:
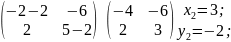
– второй
собственный вектор.
-
– матрица
перехода из собственных векторов -
Найдём
обратную матрицу матрице С:
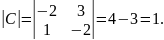
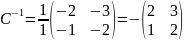
;
-
Чтобы
найтивоспользуемся следующей формулой:
-
;
-
.
Задание
№3
Приведите
квадратичную форму
к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
Решение:
-
-
Матрица
квадратичной формы в исходном
ортонормированном базисе имеет вид:
-

-
Найдем
собственные значения матрицы A. Для
этого решим характеристическое
уравнение:
.
Вычисляя
определитель получаем уравнение
.
Попробуем
найти корень среди делителей свободного
члена -2.
Проверяем на корни делители:-1, 1, 2, -2.
Подставляя в уравнение
,
убеждаемся, что это корни.
Из
этого следует, что в новом ортонормированном
базисе из собственных векторов матрица
квадратичной формы примет вид
.
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
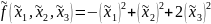
Решим
систему:
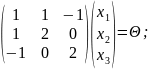
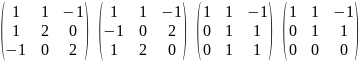
Ранг
матрицы равен 2
В
качестве базисного минора берем 1-й и
2-й столбцы. Переменные
,
– главные,
-свободная.
Пусть
равно c. Выпишем систему:
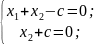
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
,
при с=1.
Нормируем
этот вектор:
.
Получили
первый вектор ортонормированного базиса
.
Решим
систему:

Ранг
матрицы равен 2.
В
качестве базисного минора берем 1-й и
2-й столбцы.
Переменные
и
– главные,
– свободная.
Пусть
равно с.
Выпишем систему:
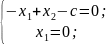
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
,
при с=1.
Нормируем
этот вектор:
.
Получили
второй вектор ортонормированного базиса
.
Решим
систему:
;
;
Ранг
матрицы равен 2.
В
качестве базисного минора берем 1-й и
2-й столбцы.
Переменные
и
– главные,
– свободная.
Пусть
равно с.
Выпишем систему:
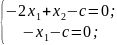
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
вектор
,
при с=1.
Нормируем
этот вектор:
– получили
третий вектор ортонормированного базиса
.
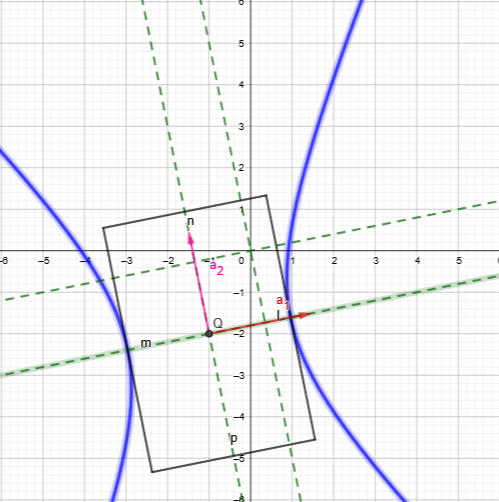
Задание
№4
Приведите уравнение
кривой
к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
Решение:
Запишем
матрицу квадратичной части кривой
.
Методом
ортогонального преобразования приведем
квадратичную форму
к каноническому виду.
-
Найдём
собственные значения матрицы А:
для этого решим характеристическое
уравнение
.
Получаем корни
и
.
матрица
квадратичной формы базиса f
-
Найдём
собственные векторы.-
Если
,
то
-
;
– первый
собственный вектор.
Сразу
нормируем этот вектор:
– первый
вектор ортонормированного базиса.
-
Если
,
то
;
– второй
собственный вектор.
Нормируем
этот вектор:
– второй
вектор ортонормированного базиса.
Получили
ортонормированный базис
,
в котором квадратичная форма имеет
канонический вид
.
Запишем
матрицу ортогонального преобразования
координат. Эта матрица связывает старые
координаты с новыми по закону
,
или
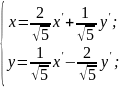
Изменение
базиса привело к линейной замене
переменных:
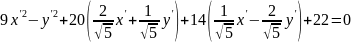
;
;
– уравнение
гиперболы

Задание
№3
Приведите
квадратичную форму
к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
Решение:
-
-
Матрица
квадратичной формы в исходном
ортонормированном базисе имеет вид:
-

-
Найдем
собственные значения матрицы A. Для
этого решим характеристическое
уравнение:
.
Вычисляя
определитель получаем уравнение
.
Попробуем
найти корень среди делителей свободного
члена -2.
Проверяем на корни делители:-1, 1, 2, -2, 4,
-4, 8, -8, 16, -16, 32, -32. Подставляя в уравнение
,
убеждаемся, что это корни.
Из
этого следует, что в новом ортонормированном
базисе из собственных векторов матрица
квадратичной формы примет вид
.
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
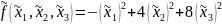
Решим
систему:
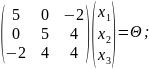

Ранг
матрицы равен 2
В
качестве базисного минора берем 1-й и
2-й столбцы. Переменные
,
– главные,
-свободная.
Пусть
равно c. Выпишем систему:
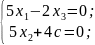
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
,
при с=1.
Нормируем
этот вектор:
.
Получили
первый вектор ортонормированного базиса
.
Решим
систему:
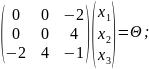
Ранг
матрицы равен 2.
В
качестве базисного минора берем 1-й и
2-й столбцы.
Переменные
и
– главные,
– свободная.
Пусть
равно с.
Выпишем систему:
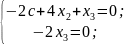
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
,
при с=1.
Нормируем
этот вектор:
.
Получили
второй вектор ортонормированного базиса
.
Решим
систему:
;
;
Ранг
матрицы равен 2.
В
качестве базисного минора берем 1-й и
2-й столбцы.
Переменные
и
– главные,
– свободная.
Пусть
равно с.
Выпишем систему:
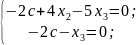
Тогда
получаем решение этой системы
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
вектор
,
при с=1.
Нормируем
этот вектор:
– получили
третий вектор ортонормированного базиса
.
Задание
№4
Приведите уравнение
кривой
к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
Решение:
Запишем
матрицу квадратичной части кривой
.
Методом
ортогонального преобразования приведем
квадратичную форму
к каноническому виду.
-
Найдём
собственные значения матрицы А:
для этого решим характеристическое
уравнение
.
Получаем корни
и
.
матрица
квадратичной формы базиса f
-
Найдём
собственные векторы.-
Если
,
то
-
;
– первый
собственный вектор.
Сразу
нормируем этот вектор:
– первый
вектор ортонормированного базиса.
-
Если
,
то
;
– второй
собственный вектор.
Нормируем
этот вектор:
– второй
вектор ортонормированного базиса.
Получили
ортонормированный базис
,
в котором квадратичная форма имеет
канонический вид
.
Запишем
матрицу ортогонального преобразования
координат. Эта матрица связывает старые
координаты с новыми по закону
,
или
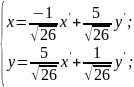
Изменение
базиса привело к линейной замене
переменных:
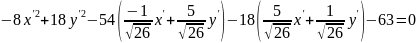
;
;
– уравнение
гиперболы
Соседние файлы в предмете Линейная алгебра
- #
- #
Аннотация: В лекции рассматриваются методы решения переопределенных систем уравнений. Обсуждается вопрос о выборе базиса на погрешность результата. Вкратце
описываются итерационные методы решения плохо обусловленных систем линейных
уравнений.
3.1. Пример использования метода наименьших квадратов (МНК)
Приведем простой пример получения переопределенной системы линейных уравнений. Такого рода задачи часто встречаются, например, при обработке результатов экспериментов.
Пусть f — линейная (или близкая к линейной) функция аргумента x: f(x) = u1x + u0. В точках xk известны значения функции f(xk). Тогда u0, u1 — коэффициенты, которые необходимо подобрать так, чтобы выполнялись условия u1xk + u0 = fk, k = 0,1,2,3,4, fk = f(xk).
Получим систему пяти уравнений относительно двух неизвестных. Это — переопределенная система. Она не имеет классического решения, так как в общем случае не существует прямой, проходящей через все 5 точек (это возможно только тогда, когда какие – либо три уравнения полученной системы линейными преобразованиями сводятся к двум другим — система линейно зависима).
Рассмотрим общий случай. Пусть коэффициенты {u0, u1} необходимо определить по результатам n + 1 измерения. Введем функцию, равную сумме квадратов невязок rk = u1xk + u0 – fk
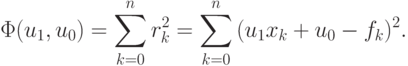 |
( 3.1) |
Примем за обобщенное решение переопределенной СЛАУ такие {u0,
u1} для которых 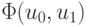
Выбор функции 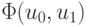

Если в качестве невязки выбрать rk = | u1xk + u0 – fk |,
то получим задачу линейного программирования на отыскании минимума функции
Получившийся таким образом функционал, вообще говоря, не дифференцируем. Для
решения задачи нельзя использовать метод наименьших квадратов.
Произвол имеется и в выборе базисных функций. Вообще говоря, можно было бы
записать невязку rk в виде
где 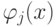
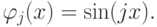
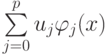
выбраны степенные функции 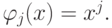
В случае выбора произвольной системы базисных функций переопределенная СЛАУ
и функционал 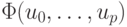
Отыщем обобщенное решение методом наименьших квадратов. Приравнивая все
частные производные по компонентам обобщенного решения к нулю
(условия минимума) и изменяя порядок
суммирования, получаем СЛАУ
Содержание
§
Вспомогательная страница к разделу
☞
ИНТЕРПОЛЯЦИЯ.
Все числа в настоящем разделе предполагаются вещественными.
Метод наименьших квадратов
Пусть из физических соображений можно считать (предполагать), что
величины $ x_{} $ и $ y_{} $ связаны линейной зависимостью вида $ y=kx+b $,
а неизвестные коэффициенты $ k_{} $ и $ b_{} $ должны быть оценены экспериментально.
Экспериментальные данные представляют собой $ m>1 $ точек на координатной
плоскости $ (x_1,y_1), dots, (x_m,y_m) $. Если бы эти опыты производились
без погрешностей, то подстановка данных в уравнение приводила бы нас к
системе из $ m_{} $ линейных уравнений для двух неизвестных $ k_{} $ и $ b_{} $:
$$
y_1=k,x_1+b, dots, y_m=k,x_m+b .
$$
Из любой пары уравнений этой системы можно было бы однозначно определить
коэффициенты $ k_{} $ и $ b_{} $.
Однако, в реальной жизни опытов без погрешностей
не бывает
Письмо в редакцию:
Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».
Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.
Будем предполагать, что величины $ x_{1},dots,x_m $
известны точно, а им соответствующие $ y_1,dots,y_m $ — приближенно.
Если $ m>2 $, то при любых различных $ x_{i} $ и $ x_j $ пара точек
$ (x_{i},y_i) $ и $ (x_{j},y_j) $ определяет прямую. Но другая пара точек определяет
другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.
Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k,x_i+b-y_i $, и выбирают прямую так, чтобы
сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_{0} $ уравнения этой прямой дают некоторое решение стоящей
перед нами задачи, которое отнюдь не является решением системы линейных
уравнений
$$ k,x_1+b=y_1,dots, k,x_{m}+b=y_m $$
(вообще говоря, несовместной).
Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость
между величинами $ y_{} $ и $ x_{} $ полиномиальная:
$$
y_1=f(x_1),dots , y_m=f(x_m), quad npu quad f(x)=a_0+a_1x+dots+a_{n-1}x^{n-1}
$$
Величина $ varepsilon_i=f(x_i)-y_i $ называется $ i_{} $-й невязкой1). Уравнения
$$
left{begin{array}{ccl}
a_0+a_1x_1+dots+a_{n-1}x_1^{n-1}&=&y_1, \
a_0+a_1x_2+dots+a_{n-1}x_2^{n-1}&=&y_2, \
dots & & dots \
a_0+a_1x_m+dots+a_{n-1}x_m^{n-1}&=&y_m
end{array}
right.
$$
называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).
Предположим что данные интерполяционной таблицы
$$
begin{array}{c|ccccc}
x & x_1 & x_2 & dots & x_m \ hline
y & y_1 & y_2 &dots & y_m
end{array}
$$
не являются достоверными: величины $ x_{} $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_{} $ подвержены случайным (несистематическим) погрешностям.
Задача. Построить полином $ f_{}(x) $ такой, чтобы величина
$$
sum_{j=1}^m [f(x_j)-y_j]^2
$$
стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов2).
В случае $ deg f_{} =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_{} < m-1 $, т.е. случай когда экспериментальных данных больше (обычно — много больше) чем значений параметров (коэффициентов полинома $ f_{} $), которые требуется определить.
Так, в случае $ deg f_{}=1 $ речь идет о построении прямой $ y=ax+b $ на плоскости $ (x,y) $, обеспечивающей
$$ min (varepsilon_1^2+varepsilon_2^2+dots + varepsilon_m^2) , . $$
Здесь $ varepsilon_j = a,x_j+b-y_j $.

Т
Теорема. Если $ mge n_{} $ и узлы интерполяции $ x_{1},dots,x_m $ все различны, то
существует единственный набор коэффициентов $ a_{0},dots,a_{n-1} $, обеспечивающий
минимальное значение для
$$
sum_{j=1}^m (a_0+a_1x_j+dots+a_{n-1}x_j^{n-1} -y_j)^2 .
$$
Этот набор определяется как решение системы нормальных уравнений
$$
underbrace{
left(begin{array}{llllll}
s_0 &s_1&s_2&ldots&s_{n-2}& s_{n-1}\
s_1 &s_2&s_3&ldots&s_{n-1}& s_{n}\
s_2 &s_3&s_4&ldots&s_{n}& s_{n+1}\
vdots& & & && vdots\
s_{n-1} &s_n&s_{n+1}&ldots &s_{2n-3}&s_{2n-2}
end{array}right)}_{displaystyle S_{ntimes n}}
left(begin{array}{l}
a_0 \ a_1 \ a_2 \ vdots \ a_{n-1} end{array} right)=
left(begin{array}{l}
t_0 \ t_1 \ t_2 \ vdots \ t_{n-1} end{array} right)
$$
при $ s_{k} = x_1^k+dots+x_m^k, t_{k} = x_1^ky_1+dots+x_m^k y_m $.
Если одно из значений $ x_{j} $ равно $ 0_{} $ , то полагаем $ 0^{0} = 1 $, так что $ s_{0}=m $
при любых $ {x_{1},dots, x_m} subset mathbb R $.
Доказательство. Рассмотрим сумму как полином от неопределенных
коэффициентов $ {a_{j}}_{j=0}^{n-1} $:
$$F(a_0,dots,a_{n-1})=
sum_{i=1}^m [f(x_i)-y_i]^2=
$$
$$
=sum_{i=1}^m [(a_0+a_1x_i+dots+a_{n-1}x_i^{n-1})-y_i]^2 .
$$
На основании теоремы из пункта ЭКСТРЕМУМЫ ПОЛИНОМА такая функция может принимать экстремальные значения только на вещественных решениях системы уравнений
$$
partial F / partial a_0=0, dots, partial F / partial a_{n-1}=0 .
$$
Распишем выражение для $ partial F / partial a_j $:
$$partial F / partial a_j =sum_{i=1}^m 2,[f(x_i)-y_i]
frac{partial (a_0+a_1x_i+dots+a_{n-1}x_i^{n-1})}{partial a_j}
$$
$$
=2, sum_{i=1}^m [f(x_i)-y_i] x_i^{j}=$$
$$=2, sum_{i=1}^m left[left(a_0x_i^{j}+a_1x_i^{j+1}+dots+a_{n-1}x_i^{j+n-1}
right)-y_ix_i^{j} right]=
$$
$$= 2left[a_0, sum_{i=1}^m x_i^{j}+a_1, sum_{i=1}^m x_i^{j+1}+
dots+a_{n-1}, sum_{i=1}^m x_i^{j+n-1}- sum_{i=1}^m y_ix_i^{j} right]=$$
$$=2 [a_0, s_j+a_1, s_{j+1}+dots+a_{n-1},s_{j+n-1}-t_j ] $$
Таким образом, условия $ left{partial F / partial a_j=0 right}_{j=0}^n $ можно переписать в виде
системы нормальных уравнений.
Покажем теперь, что матрица этой системы имеет ненулевой определитель.
Действительно, матрица $ S_{} $ — ганкелева. При $ m=n_{} $
$$S = left(begin{array}{ccccc}
1 &1&1&ldots&1\
x_1 &x_2&x_3&ldots&x_{n}\
vdots&& & &vdots\
x_1^{n-1} &x_2^{n-1}&x_3^{n-1}&ldots&x_n^{n-1}
end{array}right) cdot
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
ldots&& & &ldots\
1 &x_n&x_n^2&ldots&x_n^{n-1}
end{array}right) , .
$$
По теореме Бине-Коши вычисление определителя сводится к вычислению определителя Вандермонда:
$$
det S =prod_{1le j<kle n} (x_k-x_j)^2 .$$
Воспользуемся той же теоремой и для случая $ m>n $:
$$S=left(begin{array}{ccccc}
1 &1&1&ldots&1\
x_1 &x_2&x_3&ldots&x_{m}\
vdots&& & &vdots\
x_1^{n-1} &x_2^{n-1}&x_3^{n-1}&ldots&x_m^{n-1}
end{array}right) cdot
left(begin{array}{ccccc}
1 &x_1&x_1^2&ldots&x_1^{n-1}\
1 &x_2&x_2^2&ldots&x_2^{n-1}\
ldots&& & &ldots\
1 &x_m&x_m^2&ldots&x_m^{n-1}
end{array}right)$$
$$det S = sum_{1le j_1< j_2 <dots < j_n le m} left|begin{array}{cccc}
1 &1&ldots&1\
x_{j_1} &x_{j_2}&ldots&x_{j_n}\
vdots&& &vdots\
x_{j_1}^{n-1} &x_{j_2}^{n-1}&ldots&x_{j_n}^{n-1}
end{array}right| cdot
left|begin{array}{cccc}
1 &x_{j_1}&ldots&x_{j_1}^{n-1}\
1 &x_{j_2}&ldots&x_{j_2}^{n-1}\
ldots&& &ldots\
1 &x_{j_n}&ldots&x_{j_n}^{n-1}
end{array}right|=$$
$$=sum_{1le j_1< j_2 <dots < j_n le m} prod_{1le L < K le n} (x_{j_K}-x_{j_L})^2
.$$
Каждое слагаемое неотрицательно и отлично от нуля поскольку,
по предположению, все $ {x_j}_{j=1}^m $ различны. Поэтому $ det S >0 $.
По теореме Крамера система нормальных уравнений имеет единственное решение.
Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы
линейных уравнений. Этот результат приводится
☟
НИЖЕ.
♦
Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов
$$
sigma=frac{1}{m}sum_{j=1}^m (f(x_j) -y_j)^2
$$
называется среднеквадратичным отклонением.

?
Показать, что линейный полином $ y=a_{0}+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_{},y) $ прямую, проходящую через центроид
$$
(overline{x},overline{y}) = left(frac{x_1+x_2+ dots+x_m}{m},
frac{y_1+y_2+ dots+y_m}{m} right) .
$$
системы точек $ (x_{1},y_1),dots,(x_m,y_m) $.
П
Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02
end{array}
$$
Решение. Имеем
$$
s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$
$$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75,
$$
$$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23,
$$
$$
t_1
=0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 +
$$
$$
+2.5 cdot 3.51 + 3 cdot 1.02=19.06 .
$$
Решаем систему нормальных уравнений
$$
left(
begin{array}{cc}
6 & 10.5 \
10.5 & 22.75
end{array}
right)
left(
begin{array}{c}
a_0 \ a_1
end{array}
right)=
left(
begin{array}{c}
9.23 \ 19.06
end{array}
right),
$$
получаем уравнение прямой в виде
$$ y= 0.375 + 0.665, x .$$
Вычислим и полиномы более высоких степеней.
$$ f_2(x)=-1.568+3.579, x-0.833,x^2 , $$
$$ f_3(x)=2.217-5.942,x+5.475,x^2-1.201, x^3 , $$
$$ f_4(x)= -4.473+17.101,x-19.320,x^2+9.205, x^3-1.487,x^4 , $$
$$ f_5(x)= 16.390-71.235,x+111.233,x^2-77.620,x^3+25.067,x^4-3.0347, x^5 . $$
Среднеквадратичные отклонения:
$$
begin{array}{c|ccccc}
deg & 1 & 2 & 3 & 4 & 5 \ hline
sigma & 0.717 & 0.448 & 0.204 &0.086 & 0
end{array}
$$
♦
Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.
Влияние систематических ошибок
П
Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$
begin{array}{c|cccccc}
x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline
y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02
end{array}
$$
имеет вид (охра)
$$ y=0.175+0.779, x , . $$
Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид:
$$ y=0.483+0.383, x , . $$
График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.
После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.
Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы.
Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел3).
Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см.
☞
цитату). Как это сделать? — Ответ на этот вопрос постепенно излагается
☞
ЗДЕСЬ.
Псевдорешение системы линейных уравнений
Рассмотрим теперь обобщение задачи предыдущего пункта.
В практических задачах часто бывает нужно найти решение, удовлетворяющее
большому числу возможно противоречивых требований. Если такая задача
сводится к системе линейных уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&b_m
end{array}right.
iff
AX={mathcal B}
$$
при числе уравнений $ m_{} $ большем числа неизвестных $ n_{} $, то такая
переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого
компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.
Псевдорешением системы $ AX={mathcal B} $ называется столбец $ Xin mathbb R^n $, обеспечивающий минимум величины
$$
sum_{i=1}^m [a_{i1}x_1 +a_{i2}x_2+ldots+a_{in}x_n-b_i]^2 .
$$
Такому определению можно также соотнести
вероятностную интерпретацию. Пусть для определения неизвестных величин
$ x_{1},dots,x_n $ проводятся $ m_{} $ экспериментов, описываемых линейными
уравнениями:
$$
a_{i1}x_1 +a_{i2}x_2+ldots+a_{in}x_n =b_i quad npu quad iin {1,dots,m}
.
$$
При этом величины $ { a_{ij} }, i in {1,dots, m}, jin {1,dots, n} $ — известные постоянные, не подверженные
сопутствующим экспериментам (наблюдениям) погрешностям, а вот величины $ {b_{i}}_{i=1}^m $ этим
погрешностям подвержены. Формально каждое из равенств следует рассматривать как приближенное.
Понятно, что при таких обстоятельствах не имеет смысла гоняться за точным решением системы $ AX={mathcal B} $ (его может и не
существовать вовсе!). Искать следует приближенное решение, оптимальное
в некотором смысле. Оказывается, что именно выбор критерия в виде минимума квадратов разностей левых и правых частей уравнения
обеспечивает то, что псевдорешение дает максимально правдоподобные значения неизвестных величин $ x_1,dots,x_{n} $.
T
Теорема. Существует псевдорешение системы
$$
AX={mathcal B}
$$
и оно является решением системы
$$
left[A^{top}A right]X=A^{top} {mathcal B} .
$$
Это решение будет единственным тогда и только тогда, когда $ operatorname{rank} A =n $.
Система $ left[A^{top}A right]X=A^{top} {mathcal B} $ называется нормальной системой по отношению к системе $ AX={mathcal B} $. Формально она получается
домножением системы $ AX={mathcal B} $ слева на матрицу $ A^{top} $. Заметим также, что если $ m=n_{} $ и $ det A ne 0 $, то
псевдорешение системы совпадает с решением в традиционном смысле.
Доказательство
☞
ЗДЕСЬ.
Метод наименьших квадратов, рассмотренный в предыдущем пункте, является частным случаем задачи о псевдорешении системы линейных уравнений; в нём матрица $ A $ совпадает с матрицей Вандермонда.
Если нормальная система имеет бесконечное количество решений, то обычно в
качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).
П
Пример. Найти псевдорешение системы
$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$
Решение. Имеем:
$$A=left( begin{array}{rr}
1 & 1 \
1 & -1 \
2 & 1
end{array}
right),
operatorname{rank} A =2,
{mathcal B} =
left( begin{array}{r}
2 \ 0 \ 2
end{array}
right),
A^{top}A= left( begin{array}{rr}
6 & 2 \
2 & 3
end{array}
right),
A^{top} {mathcal B} =
left( begin{array}{r}
6 \ 4
end{array}
right).
$$
Ответ. $ x_1=5/7, x_2 = 6/7 $.
?
Показать, что матрица $ A^{top}A $ всегда симметрична.
?
На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь
попасть по монетке. Все промахиваются. Расстроенные,
рыцари уходят в харчевню пропивать злосчастную монетку. Укажите
максимально правдоподобное ее расположение, имея перед глазами зарубки:
$$
begin{array}{rrcr}
3, x &- 2, y&=& 6,\
x &-3,y&=&-3,\
11,x& + 14,y&=& 154, \
4,x&+y&=&48.
end{array}
$$
Геометрическая интерпретация
Псевдообратная матрица
Эта матрица определяется не только для квадратной матрицы.
Пусть сначала матрица $ A_{} $ порядка $ mtimes n_{} $ — вещественная и $ m ge n_{} $ (число строк не меньше числа столбцов).
Если $ operatorname{rank} (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_{} $ определяется как матрица
$$ A^{+}=(A^{top}A)^{-1} A^{top} . $$
Эта матрица имеет порядок $ n times m_{} $. Матрица $ (A^{top}A)^{-1} $ существует ввиду того факта, что при условии $ operatorname{rank} (A) = n $ будет выполнено $ det (A^{top} A) > 0 $ (см. упражнение в пункте
☞
ТЕОРЕМА БИНЕ-КОШИ или же пункт
☞
СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^{+} cdot A = E_{n} $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_{} $. В случае $ m=n_{} $ псевдообратная матрица совпадает с обратной матрицей: $ A^{+}=A^{-1} $.
П
Пример. Найти псевдообратную матрицу к матрице
$$ A= left( begin{array}{cc}
1 & 0 \
0 & 1 \
1 & 1
end{array}
right) .
$$
Решение.
$$
A^{top}= left( begin{array}{ccc}
1 & 0 & 1 \
0 & 1 & 1
end{array}
right) Rightarrow A^{top} cdot A =
left( begin{array}{cc}
2 & 1 \
1 & 2
end{array}
right) Rightarrow
$$
$$
Rightarrow
(A^{top} cdot A)^{-1} =
left( begin{array}{cc}
2/3 & -1/3 \
-1/3 & 2/3
end{array}
right)
Rightarrow
$$
$$
Rightarrow
quad A^{+} = (A^{top} cdot A)^{-1} A^{top} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3
end{array}
right) .
$$
При этом
$$
A^{+} cdot A =
left( begin{array}{cc}
1 & 0 \
0 & 1
end{array}
right),quad A cdot A^{+} =
left( begin{array}{rrr}
2/3 & -1/3 & 1/3 \
-1/3 & 2/3 & 1/3 \
1/3 & 1/3 & 2/3
end{array}
right) ,
$$
т.е. матрица $ A^{+} $ не будет правой обратной для матрицы $ A_{} $.
♦
?
Вычислить псевдообратную матрицу для
$$ mathbf{a)} left( begin{array}{cc}
1 & 0 \
1 & 1 \
1 & 1
end{array}
right) quad ; quad
mathbf{b)}
left( begin{array}{c}
x_1 \
x_2 \
x_3
end{array}
right)
.
$$
Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений. Если $ A^{+} $ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_{} $ находится по формуле $ X= A^{+} mathcal B $ при любом столбце $ mathcal B_{} $.
Верно и обратное: если
$ E_{[1]}, E_{[2]},dots, E_{[m]} $ – столбцы единичной матрицы $ E_m $:
$$
E_{[1]}=left(
begin{array}{c}
1 \ 0 \ 0 \ vdots \ 0
end{array}
right),
E_{[2]}=left(
begin{array}{c}
0 \ 1 \ 0 \ vdots \ 0
end{array}
right),dots,
E_{[m]}=left(
begin{array}{c}
0 \ 0 \ 0 \ vdots \ 1
end{array}
right),
$$
а псевдорешение системы уравнений $ AX=E_{[j]} $ обозначить $ X_{j} $ (оно существует и единственно при условии $ operatorname{rank} (A) = n $), то
$$ A^{+}=left[X_1,X_2,dots,X_m right] . $$
Т
Теорема. Пусть $ A_{} $ вещественная матрица порядка $ mtimes n_{} $, $ m ge n_{} $ и $ operatorname{rank} (A) = n $. Тогда псевдообратная матрица $ A^{+} $ является решением задачи минимизации
$$ min_{Xin mathbb R^{ntimes m}} |AX-E_m|^2 $$
где минимум разыскивается по всем вещественным матрицам $ X_{} $ порядка $ ntimes m_{} $, а $ || cdot || $ означает евклидову норму матрицы (норму Фробениуса) :
$$ |[h_{jk}]_{j,k}|^2=sum_{j,k} h_{jk}^2 . $$
При сделанных предположениях решение задачи единственно.
Образно говоря, если уж невозможно найти обратную матрицу для матрицы $ A_{mtimes n}^{} $, давайте найдем хотя бы такую матрицу $ X_{ntimes m} $, чтобы отклонение произведения $ Acdot X $ от единичной матрицы $ E_m $, вычисленное как квадрат евклидова расстояния между матрицами $ Acdot X $ и $ E_m $, было бы минимальным.
С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_{mtimes n}^{} $, у которой число строк меньше числа столбцов: $ m < n_{} $.
Будем искать эту матрицу как решение задачи минимизации
$$ min_{Yin mathbb R^{ntimes m}} |YA-E_n|^2 $$
где минимум разыскивается по всем вещественным матрицам $ Y_{} $ порядка $ ntimes m_{} $. Пусть $ operatorname{rank} (A) = m $, т.е. строки матрицы линейно независимы. Тогда псевдообратная к матрице $ A_{} $ определяется как матрица
$$ A^{+}= A^{top} (Acdot A^{top})^{-1} . $$
Очевидно, что в этом случае $ Acdot A^{+}=E_m $.
Задачи
Источники
[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234