Как найти неявное уравнение поверхности

Уравнение F(x,
у, z) = 0 называется
уравнением
данной поверхности в пространстве xyz,
если эта поверхность есть множество
точек этого пространства, координаты
которых удовлетворяют этому уравнению.

z=f(x,y)
– явное
уравнение
поверхности в пространстве xyz ( уравнение
графика функции f(x,y)).

F(x,y,z)=0
– неявное
уравнение поверхности в пространстве
xyz.

Вопрос
35. Уравнение
сферы

Уравнение сферы с
центром A (a; b; c) и
радиусом R имеет
вид:

(x – a)² + (y – b)² + (z – c)² = R².

Уравнение сферырадиуса r с центром
в начале координат:

Вопрос
36. Матрица,
ее элементы, обозначение, равенство
матриц

Матрицей
размера  называется
прямоугольная таблица, составленная
из  чисел
( строк,  столбцов). 

Числа a_i,j,
входящие в состав матрицы, называются
ее элементами. Здесь i —
номер строки матрицы, j —
номер столбца матрицы.

Обозначаются
матрицы

Равенство матриц

Две
матрицы равны, если эти матрицы имеют
одинаковые размеры, и все их соответствующие
элементы совпадают.

Вопрос
37. Матрица-строка,
матрица-столбец

Матрицей-строкойназывается матрица
размером 1хn, т.е. состоящая из одной
строки.

Матрицей-столбцомназывается матрица
размером mх1, состоящая из одного столбца.

Вопрос
38. Нулевая,
квадратная, треугольная, диагональная,
единичная матрицы

Матрица 0, все элементы которой равны
нулю, называется нулевой.

Матрица
размера nxn называетсяквадратной
матрицей n-го порядка. Элементы
а₁₁,а_22,…а_nn
квадратной матрицы n-го порядка
образуют её главную диагональ, а элементы
………….. – побочную диагональ.

Квадратная матрица называется треугольной,
если все элементы, расположенные, ниже
(или выше) главной диагонали равны нулю.

Квадратная матрица называется
диагональной, если все ее элементы,
не лежащие на главной диагонали, равны
нулю.

Диагональная матрица называется
единичной, если все элементы ее
главной диагонали равны единице.
Единичную матрицу обозначают буквой
Е.

Вопрос 39. Операции над матрицами

1. Сложение матриц – поэлементная операция

2. Вычитание матриц – поэлементная
операция

3. Произведение матрицы на
число – поэлементная операция

4. Транспонирование матрицы
А. Транспонированную матрицу обозначают
A^T или
A’

Вопрос 40. Определитель квадратной матрицы, треугольной матрицы, единичной матрицы, произведения матриц

Вопрос 41. Обратная матрица: определение, условие существования, формула для вычисления

Матрица
А^-1называется обратной (к) квадратной
матрице А, если АА^-1=А^-1А=Е

Для
того чтобы для матрицы А существовала
обратная матрица, необходимо и достаточно,
чтобы А была невырожденной.

Формула
для вычисления обратной матрицы

Вопрос 42. Решение матричных уравнений

С помощью обратной матрицы легко решается
линейное матричное уравнение вида АХ=В,
где А – невырожденная матрица порядка
n, В – матрица размера nxk, а Х – искомая
матрица. Умножая данное уравнение на
А^-1слева, получим:

А^-1(АХ)=А^-1В => (А^-1А)Х=А^-1В
=> ЕХ=А^-1В => Х=А^-1В

То что матрица Х действительно является
решением данного уравнения, легко
проверяется путем подстановки ее в
данное уравнение:

А(А^-1В)=( А^-1А)В=ЕВ=В,

а его единственность следует из
единственности обратной матрицы.

Аналогично, решение уравнения YA=B имеет
вид Y=BА^-1.

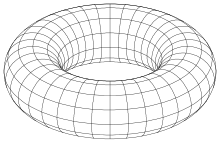
Неявная поверхность — это поверхность в евклидовом пространстве, определённая уравнением

Неявная поверхность является множеством нулей функции трёх переменных. Термин неявная здесь означает, что уравнение не решено относительно любой из переменных, x, y или z.

График функции обычно описывается уравнением и такое представление называется явным. Третьим важным способом описания поверхности является параметрическое представление —
, где координаты x, y и z точек поверхности представлены тремя функциями , зависящими от общих параметров . Обычно изменение представления поверхности осуществляется просто только в случае, если задано явное представление . Тогда другими двумя представлениями будут (неявное) и (параметрическое).

Примеры:

1. плоскость
2. сфера
3. тор
4. Поверхность рода 2: (см. рисунок).
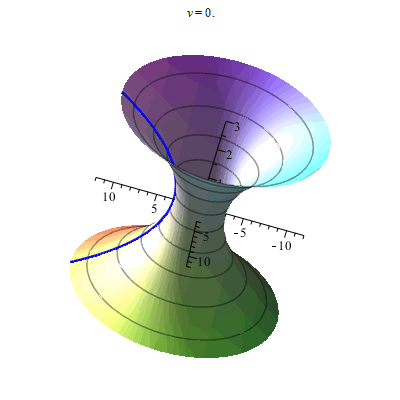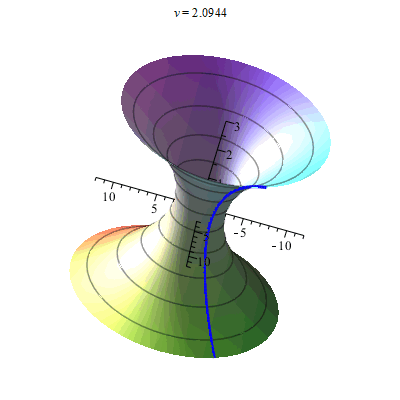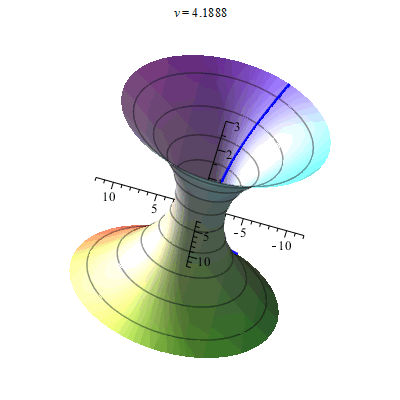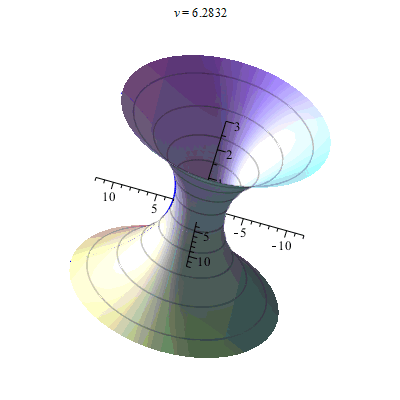
5. Поверхность вращения (см. рисунок рюмка).

Для плоскости, сферы и тора имеется простое параметрическое представление, что неверно для четвёртого примера.

Теорема о неявной функции описывает условия, при которых уравнение может быть решено (по меньшей мере неявно) относительно x, y или z. Но в общем случае явного решения может и не существовать. Эта теорема является ключевой для вычисления важных геометрических свойств поверхности, таких как касательные плоскости, нормали к поверхности, кривизны (см. ниже). Однако эти поверхности имеют существенный недостаток — их визуализация затруднительна.

Если является многочленом от x, y и z, поверхность называется алгебраической. Пример 5 не является алгебраической поверхностью.

Несмотря на трудность визуализации неявные поверхности дают относительно простые техники для их теоретической генерации (например, Поверхность Штайнера^[en]) и поверхности, интересные для практических целей (см. ниже).

Формулы[править | править код]

При следующих соглашениях неявная поверхность представлена уравнением , где функция удовлетворяет необходимым условиям дифференцируемости. Ниже будем обозначать частные производные функции как .

Касательная плоскость и нормальный вектор[править | править код]

Точка поверхности называется регулярной тогда и только тогда, когда градиент функции в точке не равен нулевому вектору , что означает

.

Если точка поверхности не регулярна, она называется особой (употребляется также термин сингулярная точка).

Уравнение касательной плоскости в регулярной точке

а уравнение нормального вектора

Нормальная кривизна[править | править код]

Чтобы сделать формулы проще, аргументы в формуле ниже опущены. Тогда

является нормальной кривизной поверхности в регулярной точке для единичного касательного вектора направления . является гессианом функции (матрицей вторых производных).

Доказательство этой формулы опирается (как и в случае неявной кривой) на теорему о неявной функции и формулу нормальной кривизны параметрической поверхности.

Приложения неявных поверхностей[править | править код]

Как и в случае неявных кривых легкой задачей является создание неявных поверхностей желаемой формы с помощью алгебраических операций (сложение, умножение) простых примитивов.

Эквипотенциальная поверхность двух точечных зарядов[править | править код]

Точечный заряд в точке образует потенциал в точке (физические константы опущены)

Эквипотенциальная поверхность для значения потенциала является неявной поверхностью , что есть сфера с центром в точке .

Потенциал четырёх точечных зарядов вычисляется пo формуле

На рисунке четыре заряда имеют величину 1 и расположены в точках
. Показанная поверхность является эквипотенциальной поверхностью (неявной поверхностью) .

Поверхность постоянного произведения расстояний[править | править код]

Овал Кассини можно определить как множество точек, для которых произведение расстояний от двух заданных точек постоянно (в отличие от эллипса, для которого постоянна сумма расстояний). Аналогично неявные поверхности могут быть определены как постоянное произведение расстояний от некоторых фиксированных точек.

На рисунке метаморфоз верхняя левая поверхность образуется по такому правилу. Эта поверхность является поверхностью уровня функции , где

Метаморфозы неявных поверхностей[править | править код]

Другой простой метод создания новых неявных поверхностей называется метаморфозом неявных поверхностей:

Для двух неявных поверхностей (на рисунке это поверхность постоянного произведения расстояний и тор) определяются новые поверхности с использованием параметра :

На рисунке представлены поверхности с величинами параметра .

Гладкая аппроксимация некоторых неявных поверхностей[править | править код]

-поверхности^[1] могут быть использованы для аппроксимирования любого гладкого и ограниченного объекта в , поверхность которого определяется многочленом, который равен произведению других многочленов. Другими словами, мы можем создать любой гладкий объект с единой алгебраической поверхностью. Обозначим многочлены как . Тогда аппроксимирующий объект определяется многочленом

^[1]

где определяет смешивающий параметр, контролирующий ошибку аппроксимации.

Аналогично гладкой аппроксимации неявных кривых уравнение

представляет для подходящих параметров гладкие аппроксимации трёх пересекающихся торов уравнениями

(На рисунке параметры равны )

Визуализация неявных поверхностей[править | править код]

Есть несколько алгоритмов рендеринга неявных поверхностей^[3], включая алгоритм «marching cubes»^[4]. Фактически, имеются две идеи визуализации неявных поверхностей — одна создаёт сеть многоугольников, которые затем отрисовываются (см. Триангуляризация поверхности^[en]), а вторая опирается на трассировку лучей, когда определяются точки пересечения лучей с поверхностью^[5].

См. также[править | править код]

• Неявная кривая

Примечания[править | править код]

Литература[править | править код]

• Adriano N. Raposo, Abel J.P. Gomes. Pi-surfaces: products of implicit surfaces towards constructive composition of 3D objects // Journal of WSCG. — 2019. — arXiv:1906.06751. (International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision)

• Jules Bloomenthal, Chandrajit Bajaj, Brian Wyvill. Introduction to Implicit Surfaces. — Morgan Kaufmann, 1997. — ISBN 978-1-55860-233-5.
• Ian Stephenson. Production Rendering: Design and Implementation. — Springer Science & Business Media, 2004. — ISBN 978-1-85233-821-3.
• Eric Haines, Tomas Akenine-Moller. Ray Tracing Gems. — Springer, 2019. — ISBN 978-1-4842-4427-2.
• Gomes A., Voiculescu I., Jorge J., Wyvill B., Galbraith C. Implicit Curves and Surfaces: Mathematics, Data Structures and Algorithms. — London: Springer-Verlag, 2009. — ISBN 978-1-84882-405-8.
• Thorpe J.A. Elementary Topics in Differential Geometry. — New York: Springer-Verlag, 1979. — (Undergraduate Texts in Mathematics). — ISBN 0-387-90357-7.
  • Торп Дж. Начальные главы дифференциальной геометрии. — «Мир», 1982. — (Современная математика. Вводные курсы).

Ссылки[править | править код]

• Sultanow: Implizite Flächen Архивная копия от 19 января 2021 на Wayback Machine
• Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN Архивная копия от 30 октября 2017 на Wayback Machine
• GEOMVIEW Архивная копия от 11 июля 2000 на Wayback Machine
• K3Dsurf: 3d surface generator Архивная копия от 10 ноября 2020 на Wayback Machine
• SURF: Visualisierung algebraischer Flächen Архивная копия от 8 марта 2021 на Wayback Machine

$ лежат в одной плоскости, определяемой векторами $vec_u$, $vec_v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
– $vec=$ — радиус-вектор произвольной точки касательной плоскости.
– $vec=$ — радиус вектор точки $P(u_0, v_0)$.
– Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac<varPhi_x>=displaystylefrac<varPhi_y>=displaystylefrac<varPhi_z>. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac<-1>. end

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac<pi><4>right)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec<2,1,-1>$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left<2x_0,-2y_0,0right>. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 5 = 0(x – 0) + 5(y – 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z – 1 = -3 /₁₆(x – 1) + 0(y – 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z – z₀ = f’_x(x₀,y₀,z₀)(x – x₀) + f’_y(x₀,y₀,z₀)(y – y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Уравнение кривой и поверхности

Определение. Пусть g – некоторая кривая на плоскости, а j(x, y) – функция двух переменных. Говорим, что уравнение

есть уравнение кривой g в неявном виде, если координаты любой точки MÎ g удовлетворяют (1), и обратно, каждая

пара (x, y) чисел, удовлетворяющих (1), задает точку M(x, y) на кривой.

Подчеркнем, что при составлении уравнений следствие обязательно надо проверять в обе стороны.

Пример 1. Уравнение

задает на плоскости пару прямых (см.чертеж). Координаты любой точки A(x, y)Î l₁ удовлетворяют (*), но нельзя

сказать, что (*) есть уравнение l₁ , поскольку есть еще точки, координаты которых удовлетворяют (*), но на l₁ эти точки не лежат.

С другой стороны, каждая точка, координаты которой удовлетворяют уравнению

x – 2 = 0, (**)

лежит на фигуре l₁U l₂ , но нельзя сказать что (**) задает эту фигуру, поскольку есть еще точки на l₁U l₂, координаты которых (**) не удовлетворяют.

Пример 2. Составим уравнение окружности g радиуса R с центром в точке O¢(a, b). Пусть M(x, y) – произвольная точка окружности g . Тогда

Обратно, если координаты точки M(x, y) удовлетворяют (2), то ½O¢M½= R, а значит, MÎg. Таким образом (2) и есть уравнение нашей окружности.

Если из уравнения (1) удается выразить одну координату через другую, то получим уравнение в явном виде:

Не всегда удается привести неявное уравнение кривой к явному виду. В каком случае это возможно гласит теорема о неявной функции, изучаемая в курсе математического анализа. Например, с уравнением окружности это сделать нельзя.

Предположим, что точка движется по кривой. Тогда ее координаты изменяются со временем:

x = j( t ),

При этом параметр t изменяется в определенных пределах: tÎI, где I – интервал числовой прямой. Говорим, что (4) есть параметрические уравнения кривой g, если точка M(x, y) лежит на кривой g тогда и только тогда, когда найдется такое tÎI, что будут выполнены оба равенства (4) одновременно. При этом, обязательно к системе (4) надо добавлять интервал изменения параметра. Физический смысл параметра в (4) не всегда время.

Пример 2. Параметрические уравнения окружности радиуса R с центром в начале координат имеют вид:

x = R·cos a ,

y = R·cos a , aÎR .

Не важно, что для одной и той же точки

может найтись несколько (или даже

бесконечно много) соответствующих ей

значений параметра. Это не запрещается.

Пример 3.Уравнения

x = t 2 ,

задают полукубическую параболу. Уравнения

x = e 2 t ,

тоже задают полукубическую параболу, но не всю, а только ее верхнюю половину. Для точки M, лежащей ниже оси, Ox не найдется такого t, для которого выполнено (***).

Определение. Пусть F – некоторая поверхность в пространстве, а F(x, y, z) – функция от трех переменных. Говорим, что

есть уравнение поверхности F в неявном виде, если координаты любой точки MÎF удовлетворяют (6), и обратно, каждая пара (x, y) чисел, удовлетворяющих (6), задает точку M(x, y, z) на поверхности.

Так же, как и для кривой, при составлении уравнения поверхности, необходимо проверять следствие в обе стороны.

Упражнение. Самостоятельно докажите, что сфера радиуса R с центром в точке O¢(a, b, с) задается уравнением

Если из уравнения (6) удается выразить одну переменную через две другие, то получим уравнение поверхности в явном виде: z = f (x, y). Вопрос, когда это возможно сделать, изучается в курсе математического анализа. Уравнение сферы невозможно переписать в явном виде.

Кривая в пространстве одним уравнением, как правило, не задается. Бывают исключительные случаи, типа уравнения x 2 + y 2 = 0, которое задает прямую – ось Oz. Кривая в пространстве обычно задается системой из двух уравнений

F₁(x, y, z) = 0,

Каждое из уравнений в отдельности задает поверхность. Если координаты

точки удовлетворяют системе, то она лежит на двух поверхностях одновременно, т.е. MÎF₁IF₂. Таким образом, система (8) задает линию пересечения двух поверхностей (хотя заметим, что не всегда это пересечение будет кривой). Аналогично, если мы хотим найти точки пересечения любых двух множеств, заданных своими уравнениями, мы должны объединить данные уравнения в одну систему.

Пример 4. Система уравнений

x 2 + y 2 + z 2 = R 2 .

задает окружность в плоскости Oxy. Первое уравнение системы задает сферу с центром в начале координат, а второе – плоскость Oxy. Их пересечение есть окружность g. Если подставить z = 0 в первое уравнение, то получим

Казалось бы, можно сказать, что это и есть уравнение окружности g. Но это не так. Уравнение (**** )

задает цилиндрическую поверхность (см. параграф «цилиндрические и конические поверхности»). Подставляя z = 0 в первое уравнение системы, нельзя отбрасывать при этом само уравнение z = 0.

Также кривая в пространстве может быть задана параметрическими уравнениями вида

x = j( t ),

где I – интервал числовой прямой. С параметрическими уравнениями поверхности мы встретимся в разделе «Дифференциальная геометрия».

Обозначим – радиус-вектор произвольной точки M(x, y, z) на кривой, т.е. вектор с координатами, составленными из неизвестных (x, y, z), а – вектор с координатами (j( t ), y( t ), s( t )). Тогда параметрические уравнения кривой можно переписать в виде одного векторного уравнения

[spoiler title=”источники:”]

http://math.semestr.ru/math/tangent-plane.php

http://lektsii.org/8-47911.html

[/spoiler]

Неявный поверхностный тор (R = 40, a = 15). Неявная поверхность рода 2. Неявная неявная -алгебраическая поверхность (рюмка).

В математике, неявная поверхность – это поверхность в евклидовом пространстве, определяемая уравнением

F (x, y, z) = 0. { displaystyle F (x, y, z) = 0.}

Неявная поверхность – это набор нулей функции трех переменных. Неявный означает, что уравнение не решается относительно x, y или z.

График функции обычно описывается уравнением z = f (x, y) { displaystyle z = f (x, y)}и называется явное представление. Третье важное описание поверхности – параметрическое: (x (s, t), y (s, t), z (s, t)) { displaystyle (x (s, t), y ( s, t), z (s, t))}, где x-, y- и z-координаты точек поверхности представлены тремя функциями x (s, t), y (s, t), z (s, t) { displaystyle x (s, t) ,, y (s, t) ,, z (s, t)}в зависимости от общих параметров s, t { displaystyle s, t}. Как правило, изменение представлений выполняется просто, только когда задано явное представление z = f (x, y) { displaystyle z = f (x, y)}: z – f (Икс, Y) знак равно 0 { Displaystyle ZF (Икс, Y) = 0}(неявно), (s, t, f (s, t)) { displaystyle (s, t, f (s, t))}(параметрический).

Примеры:

1. плоскость x + 2 y – 3 z + 1 = 0. { displaystyle x + 2y-3z + 1 = 0.}
2. сфера x 2 + y 2 + z 2 – 4 = 0. { displaystyle x ^ {2} + y ^ {2} + z ^ {2} -4 = 0.}
3. тор (Икс 2 + Y 2 + Z 2 + R 2 – a 2) 2-4 R 2 (x 2 + Y 2) = 0. { Displaystyle (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + y ^ {2}) = 0.}
4. Поверхность род 2: 2 y (y 2 – 3 x 2) (1 – z 2) + (x 2 + y 2) 2 – (9 z 2 – 1) (1 – z 2)) = 0 { displaystyle 2y (y ^ {2} -3x ^ {2}) (1-z ^ {2}) + (x ^ {2} + y ^ {2}) ^ {2} – (9z ^ {2} -1) (1-z ^ {2}) = 0}(см. Диаграмму).
5. Поверхность вращения x 2 + y 2 – (ln ⁡ (z + 3,2)) 2 – 0,02 = 0 { displaystyle x ^ {2} + y ^ {2} – ( ln (z + 3,2)) ^ {2} -0,02 = 0}(см. диаграмму рюмки).

Для плоскости, сферы и тора существуют простые параметрические представления. Это неверно для четвертого примера.

Теорема о неявной функции описывает условия, при которых уравнение F (x, y, z) = 0 { displaystyle F (x, y, z) = 0}может быть решено (по крайней мере неявно) относительно x, y или z. Но в целом решение не может быть явным. Эта теорема является ключом к вычислению основных геометрических характеристик поверхности: касательных плоскостей, нормалей поверхности, кривизны (см. Ниже). Но у них есть существенный недостаток: их сложно визуализировать.

Если F (x, y, z) { displaystyle F (x, y, z)}является полиномом от x, y и z, поверхность называется алгебраический. Пример 5 неалгебраический.

Несмотря на сложность визуализации, неявные поверхности предоставляют относительно простые методы создания теоретических (например, поверхность Штейнера ) и практически (см. Ниже) интересных поверхностей.

Содержание

• 1 Формулы
  • 1.1 Касательная плоскость и вектор нормали
  • 1.2 Нормальная кривизна
• 2 Применение неявных поверхностей
  • 2.1 Эквипотенциальная поверхность точечных зарядов
  • 2.2 Поверхность произведения постоянного расстояния
  • 2.3 Метаморфозы неявных поверхностей
  • 2.4 Гладкие аппроксимации нескольких неявных поверхностей
• 3 Визуализация неявных поверхностей
• 4 См. Также
• 5 Ссылки
• 6 Внешние ссылки

Формулы

На протяжении следующих рассмотрений неявная поверхность представляется уравнением F (x, y, z) = 0 { displaystyle F (x, y, z) = 0}где function F { displaystyle F}удовлетворяет необходимым условиям дифференцируемости. частные производные от F { displaystyle F}: F x, F y, F z, F xx,… { displaystyle F_ {x}, F_ {y}, F_ {z}, F_ {xx}, ldots}.

Касательная плоскость и вектор нормали

Точка поверхности (x 0, y 0, z 0) { displaystyle (x_ {0}, y_ {0}, z_ {0})}называется regularтогда и только тогда, когда gradient из F { displaystyle F}в (x 0, y 0, z 0) { displaystyle (x_ {0}, y_ {0}, z_ {0}) }не является нулевым вектором (0, 0, 0) { displaystyle (0,0,0)}, что означает

(F x (x 0 Y 0, Z 0), F Y (Икс 0, Y 0, Z 0), F Z (Икс 0, Y 0, Z 0)) ≠ (0, 0, 0) { Displaystyle (F_ {x} (x_ {0}, y_ {0}, z_ {0}), F_ {y} (x_ {0}, y_ {0}, z_ {0}), F_ {z} (x_ {0}, y_ { 0}, z_ {0})) neq (0,0,0)}.

Если точка поверхности (x 0, y 0, z 0) { displaystyle (x_ {0}, y_ { 0}, z_ {0})}не является регулярным, оно называется сингулярным .

Уравнение касательной плоскости в регулярной точке (x 0, y 0, z 0) { displaystyl e (x_ {0}, y_ {0}, z_ {0})}равно

F x (x 0, y 0, z 0) (x – x 0) + F y ( Икс 0, Y 0, Z 0) (Y – Y 0) + F Z (Икс 0, Y 0, Z 0) (Z – Z 0) = 0, { Displaystyle F_ {x} (x_ {0}, y_ {0}, z_ {0}) (x-x_ {0}) + F_ {y} (x_ {0}, y_ {0}, z_ {0}) (y-y_ {0}) + F_ { z} (x_ {0}, y_ {0}, z_ {0}) (z-z_ {0}) = 0,}

и вектор нормали равен

n (x 0, y 0, z 0) = (F x (x 0, y 0, z 0), F y (x 0, y 0, z 0), F z (x 0, y 0, z 0)) Т. { displaystyle mathbf {n} (x_ {0}, y_ {0}, z_ {0}) = (F_ {x} (x_ {0}, y_ {0}, z_ {0}), F_ {y } (x_ {0}, y_ {0}, z_ {0}), F_ {z} (x_ {0}, y_ {0}, z_ {0})) ^ {T}.}

Нормальная кривизна

Для упрощения формулы аргументы (x 0, y 0, z 0) { displaystyle (x_ {0}, y_ {0}, z_ {0})}опущены:

κ n = v ⊤ HF v ‖ grad ⁡ F ‖ { displaystyle kappa _ {n} = { frac { mathbf {v} ^ { top} H_ {F} mathbf {v}} { | operatorname {grad} F |}}}

– нормальная кривизна поверхности в регулярной точке для единичного касательного направления v { displaystyle mathbf {v }}. HF { displaystyle H_ {F}}– это матрица Гессе из F { displaystyle F}(матрица вторые производные).

Доказательство этой формулы опирается (как и в случае неявной кривой) на теорему о неявной функции и формулу для нормальной кривизны параметрической поверхности.

Применение неявных поверхностей

Как и в случае неявных кривых, легко создать неявные поверхности с желаемой формой, применяя алгебраические операции (сложение, умножение) к простым примитивам.

Эквипотенциальная поверхность 4 точечных зарядов

Эквипотенциальная поверхность точечных зарядов

Электрический потенциал точечного заряда qi { displaystyle q_ {i}}в точке pi = (xi, yi, zi) { displaystyle mathbf {p} _ {i} = (x_ {i}, y_ {i}, z_ {i})}генерируется в точка p = (x, y, z) { displaystyle mathbf {p} = (x, y, z)}потенциал (без физических констант)

F i (x, y, z) = qi ‖ p – pi ‖. { displaystyle F_ {i} (x, y, z) = { frac {q_ {i}} { | mathbf {p} – mathbf {p} _ {i} |}}.}

Эквипотенциальная поверхность для значения потенциала c { displaystyle c}– это неявная поверхность F i (x, y, z) – c = 0 { displaystyle F_ {i} (x, y, z) -c = 0}, который представляет собой сферу с центром в точке pi { displaystyle mathbf {p} _ {i}}.

Потенциал 4 { displaystyle 4}точечные заряды представлены как

F (x, y, z) = q 1 ‖ p – p 1 ‖ + q 2 ‖ p – p 2 ‖ + q 3 ‖ п – п 3 ‖ + д 4 ‖ п – п 4 ‖. { displaystyle F (x, y, z) = { frac {q_ {1}} { | mathbf {p} – mathbf {p} _ {1} |}} + { frac {q_ { 2}} { | mathbf {p} – mathbf {p} _ {2} |}} + { frac {q_ {3}} { | mathbf {p} – mathbf {p} _ {3} |}} + { frac {q_ {4}} { | mathbf {p} – mathbf {p} _ {4} |}}.}

Для изображения четыре заряда равны 1 и расположены в точках (± 1, ± 1, 0) { displaystyle ( pm 1, pm 1,0)}. Отображаемая поверхность – это эквипотенциальная поверхность (неявная поверхность) F (x, y, z) – 2,8 = 0 { displaystyle F (x, y, z) -2,8 = 0}.

Поверхность продукта с постоянным расстоянием

Овал Кассини можно определить как набор точек, для которого произведение расстояний до двух заданных точек является постоянным (в отличие от этого, для эллипса сумма постоянна). Подобным образом неявные поверхности могут быть определены как произведение постоянного расстояния до нескольких фиксированных точек.

В метаморфозах диаграммы верхняя левая поверхность генерируется по следующему правилу: При

F (x, y, z) = ((x – 1) 2 + y 2 + z 2 ⋅ (x + 1) 2 + Y 2 + Z 2 ⋅ Икс 2 + (Y – 1) 2 + Z 2 ⋅ Икс 2 + (Y + 1) 2 + Z 2) { Displaystyle { begin {align} F (x, y, z) = {} { Big (} { sqrt {(x-1) ^ {2} + y ^ {2} + z ^ {2}}} cdot { sqrt {(x + 1) ^ {2} + y ^ {2} + z ^ {2}}} \ qquad cdot { sqrt {x ^ {2} + (y-1) ^ {2} + z ^ {2} }} cdot { sqrt {x ^ {2} + (y + 1) ^ {2} + z ^ {2}}} { Big)} end {align}}}

произведение постоянного расстояния Отображается поверхность F (x, y, z) – 1.1 = 0 { displaystyle F (x, y, z) -1.1 = 0}.

Метаморфозы между двумя неявными поверхностями: тор и поверхность с постоянным произведением расстояния.

Метаморфозы неявных поверхностей

Еще один простой метод создания новых неявных поверхностей называется метаморфозами неявных поверхностей:

Для двух неявных поверхностей F 1 (x, y, z) = 0, F 2 (x, y, z) = 0 { displaystyle F_ {1} (x, y, z) = 0, F_ {2} (x, y, z) = 0}(на диаграмме: поверхность произведения с постоянным расстоянием и тор) новые поверхности определяются с помощью параметра проектирования μ ∈ [0, 1] { displaystyle mu in [0,1]}:

F (x, y, z) = μ F 1 (x, y, z) + (1 – μ) F 2 (x, y, z) знак равно 0 { Displaystyle F (x, y, z) = mu F_ {1} (x, y, z) + (1- mu) F_ {2} (x, y, z) = 0}

На схеме расчетный параметр последовательно равен μ = 0, 0,33, 0,66, 1 { displaystyle mu = 0, , 0,33, , 0,66, , 1}.

Аппроксимация трех торов (параллельная проекция ) POV-Ray изображение (центральная проекция) приближения трех торов.

Гладкие приближения семи ral неявные поверхности

Π { displaystyle Pi}-поверхности могут использоваться для аппроксимации любого заданного гладкого и ограниченного объекта в R 3 { displaystyle R ^ {3}}, поверхность которого определяется одним многочленом как произведение дополнительных многочленов. Другими словами, мы можем спроектировать любой гладкий объект с помощью единой алгебраической поверхности. Обозначим определяющие полиномы как fi ∈ R [x 1,…, xn] (i = 1,…, k) { displaystyle f_ {i} in mathbb {R} [x_ {1}, ldots, x_ {n}] (i = 1, ldots, k)}. Тогда аппроксимирующий объект определяется полиномом

F (x, y, z) = ∏ ifi (x, y, z) – r { displaystyle F (x, y, z) = prod _ {i } f_ {i} (x, y, z) -r}

где r ∈ R { displaystyle r in mathbb {R}}обозначает параметр смешивания, который управляет ошибка аппроксимации.

Аналогично гладкой аппроксимации с неявными кривыми уравнение

F (x, y, z) = F 1 (x, y, z) ⋅ F 2 (x, y, z) ⋅ F 3 (Икс, Y, Z) – р знак равно 0 { Displaystyle F (x, y, z) = F_ {1} (x, y, z) cdot F_ {2} (x, y, z) cdot F_ {3} (x, y, z) -r = 0}

представляет для подходящих параметров c { displaystyle c}гладкие аппроксимации трех пересекающихся торов уравнениями

F 1 = (x 2 + y 2 + z 2 + R 2 – a 2) 2-4 R 2 (x 2 + y 2) = 0, F 2 = (x 2 + y 2 + z 2 + R 2 – a 2) 2-4 R 2 (x 2 + z 2) = 0, F 3 = (x 2 + y 2 + z 2 + R 2 – a 2) 2-4 R 2 (y 2 + z 2) = 0. { displaystyle { begin {align} F_ {1} = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + y ^ {2}) = 0, \ [3pt] F_ {2} = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + z ^ {2}) = 0, \ [3pt] F_ {3} = ( x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (y ^ {2} + z ^ { 2}) = 0. end {align}}}

(На диаграмме параметры: R = 1, a = 0,2, r = 0,01. { Displaystyle R = 1, , a = 0,2, , r = 0,01.})

Изображение POV-Ray: ставка на метаморфозы сфера и поверхность произведения с постоянным расстоянием (6 точек).

Визуализация неявных поверхностей

Существуют различные алгоритмы рендеринга неявных поверхностей, включая алгоритм марширующих кубов. По сути, есть две идеи для визуализации неявной поверхности: одна создает сеть полигонов, которая визуализируется (см. триангуляция поверхности ), а вторая полагается на трассировку лучей, которая определяет точки пересечения лучей. с поверхностью.

См. Также

Ссылки

1. ^ Адриано Н. Рапосо; Абель Дж. П. Гомеш (2019). «Пи-поверхности: произведения неявных поверхностей на конструктивную композицию трехмерных объектов». WSCG 2019 27. Международная конференция в Центральной Европе по компьютерной графике, визуализации и компьютерному зрению. arXiv : 1906.06751. Cite имеет пустой неизвестный параметр: | 1 =()
2. ^Jules Bloomenthal; Chandrajit Bajaj; Brian Wyvill (15 августа 1997 г.) Введение в неявные поверхности. Морган Кауфманн. ISBN 978-1-55860-233-5.
3. ^Ян Стивенсон (1 декабря 2004 г.). Производственный рендеринг: проектирование и реализация. Springer Science Business Media. ISBN 978-1-85233-821-3.
4. ^Эрик Хейнс, Томас Акенин-Моллер: Рэй Tracing Gems, Springer, 2019, ISBN 978-1-4842-4427-2

• Gomes, A., Voiculescu, I., Jorge, J., Wyvill, B., Galbraith, C.: Неявные кривые и поверхности: математика, структуры данных и алгоритмы, 2009, Springer-Verlag London, ISBN 978-1-84882 -405-8
• Thorpe: Elementary Topics in Differential Geometry, Springer-Verlag, New York, 1979, ISBN 0-387-90357-7

Внешние ссылки