Как найти нижнюю сумму дарбу

Как найти нижнюю сумму дарбу

Интеграл Дарбу — один из способов обобщения интеграла Римана на любые ограниченные на отрезке функции. Различают верхний и нижний интеграл Дарбу. Интегралы Дарбу геометрически представляют собой верхнюю и нижнюю площадь под графиком.

Определение[править | править код]

Для определения интегралов Дарбу прежде необходимо ввести вспомогательное понятие сумм Дарбу.

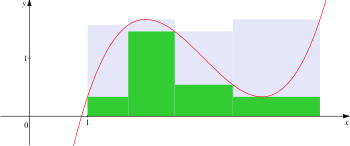
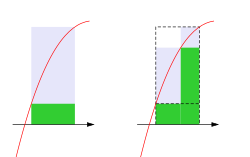
Нижняя (зеленая) и верхняя (серая) суммы Дарбу на 4 отрезках разбиения

Пусть на отрезке [a,b] определена функция вещественного переменного f.

Разбиением tau отрезка [a,b] будем называть конечное множество точек этого отрезка, включающего в себя точки a и b. [1] Для удобства дальнейших записей будем вводить обозначения. Точки разбиения tau обозначим за x_{i}, причём пронумеруем их в порядке возрастания (начиная с нуля):

{displaystyle tau =left{{{x}_{0},ldots {x}_{n}}right}, a={{x}_{0}}<{{x}_{1}}<ldots <{{x}_{n-1}}<{{x}_{n}}=b}.

Множество всех разбиений отрезка [a;b] обозначим за T.

Частичным отрезком разбиения Delta _{i} назовём отрезок {displaystyle [x_{i-1},x_{i}]}.

{displaystyle Delta _{i}=[x_{i-1},x_{i}]}

Длину частичного отрезка разбиения обозначим за Delta x_{i}.

{displaystyle Delta x_{i}=x_{i}-x_{i-1}}

Диаметром разбиения d назовём максимальную длину частичного отрезка разбиения Delta x_{i}.[2]

{displaystyle d=max Delta x_{i}}

Точные грани функции на частичных отрезках разбиения обозначим за m_i и M_{i}.

{displaystyle {{m}_{i}}=inf _{xin Delta _{i}}f(x)},
{displaystyle {{M}_{i}}=sup _{xin Delta _{i}}f(x)}.

Тогда, нижней суммой Дарбу {displaystyle s(f,tau )} функции f на разбиении tau называется

{displaystyle s(f,tau )=sum _{i=1}^{n}m_{i}Delta x_{i}}

Верхней суммой Дарбу {displaystyle S(f,tau )} называется

{displaystyle S(f,tau )=sum _{i=1}^{n}M_{i}Delta x_{i}}[3]

Тогда нижним интегралом Дарбу I_* называется

{displaystyle I_{*}=sup _{tau in T}s(f,tau )}

Верхним интегралом Дарбу I^* называется

{displaystyle I^{*}=inf _{tau in T}S(f,tau )}[4]

Альтернативные определения[править | править код]

Существуют также альтернативные определения интегралов Дарбу. Обычно они доказываются как свойства.

  • Нижний интеграл Дарбу есть предел нижних сумм Дарбу при стремлении диаметра разбиения к нулю, а верхний есть предел верхних.[5]
{displaystyle I_{*}=lim _{d(tau )to 0}s(f,tau )}
{displaystyle I^{*}=lim _{d(tau )to 0}S(f,tau )}
  • Нижний интеграл Дарбу есть нижний предел интегральных сумм при стремлении диаметра разбиения к нулю, а верхний есть верхний предел.[6]
{displaystyle I_{*}=varliminf _{d(tau )to 0}sigma (f,tau ,xi )}
{displaystyle I^{*}=varlimsup _{d(tau )to 0}sigma (f,tau ,xi )}

Свойства[править | править код]

Свойства сумм Дарбу[править | править код]

  • При любых произвольно взятых двух разбиениях одного и того же отрезка, нижняя сумма Дарбу на одном разбиении не превосходит верхней суммы Дарбу на другом разбиении.[7]
{displaystyle forall tau _{1},tau _{2}in Tquad s(f,tau _{1})leq S(f,tau _{2})}
  • Нижние суммы Дарбу ограничены сверху, а верхние — снизу.[4]

Поведение нижней (зеленая) и верхней (серая) сумм Дарбу на измельчении разбиения

  • При добавлении к имеющемуся разбиению новых точек нижняя сумма Дарбу никак не может уменьшиться, а верхняя никак не может увеличиться.[7]
{displaystyle {begin{aligned}s(f,tau ')geq s(f,tau )\S(f,tau ')leq S(f,tau )end{aligned}}quad tau '} — измельчение tau .
Более того, изменению этих сумм можно дать следующую оценку.
Пусть d — диаметр tau , измельчение {displaystyle tau '} — получено добавлением не более чем l точек к tau , M и m — точные грани функции f на отрезке [a;b]. Тогда
{displaystyle s(f,tau ')-s(f,tau )leq (M-m)ld}
{displaystyle S(f,tau )-S(f,tau ')leq (M-m)ld}[5]
{displaystyle s(f,tau )leq sigma (f,tau ,xi )leq S(f,tau )}[8]
{displaystyle s(f,tau )=inf _{xi in Xi }sigma (f,tau ,xi )},
{displaystyle S(f,tau )=sup _{xi in Xi }sigma (f,tau ,xi )}.

Свойства интегралов Дарбу[править | править код]

{displaystyle s(f,tau )leq I_{*}leq I^{*}leq S(f,tau )}[9]
  • Основная лемма Дарбу. Предел нижних сумм Дарбу при стремлении диаметра разбиения к нулю существует для любой ограниченной функции и равен нижнему интегралу Дарбу. Предел верхних сумм Дарбу при стремлении диаметра разбиения к нулю существует для любой ограниченной функции существует и равен верхнему интегралу Дарбу.[5]
{displaystyle exists lim _{d(tau )to 0}s(f,tau )} и {displaystyle I_{*}=lim _{d(tau )to 0}s(f,tau )}
{displaystyle exists lim _{d(tau )to 0}S(f,tau )} и {displaystyle I^{*}=lim _{d(tau )to 0}S(f,tau )}
Основная лемма Дарбу устанавливает эквивалентность первого и второго определения интегралов Дарбу.
f — интегрируема по Риману {displaystyle Leftrightarrow I_{*}=I^{*}}[10]

Вариации и обобщения[править | править код]

Кратный интеграл Дарбу[править | править код]

По аналогии с кратным интегралом Римана можно определить и кратный интеграл Дарбу. Пусть G — измеримое по Жордану множество, tau — его разбиение конечным числом измеримых по Жордану множеств. Обозначим множества этого разбиения за Delta _{i}.

{displaystyle tau =left{{{Delta }_{1},ldots {Delta }_{n}}right}}

За Delta x_{i} обозначим меру Жордана Delta _{i}.

Множество всех разбиений G будем обозначать T.

Диаметр разбиения d определим как максимум из диаметров множеств разбиения (диаметр множества разбиения — точная верхняя грань расстояний между его точками).

{displaystyle max _{i=1}^{n}sup _{x,yin Delta _{i}}|x-y|}

Точные грани функции на множествах разбиения обозначим за m_i и M_{i}.

{displaystyle {{m}_{i}}=inf _{xin Delta _{i}}f(x)},
{displaystyle {{M}_{i}}=sup _{xin Delta _{i}}f(x)}.

Тогда, нижней суммой Дарбу {displaystyle s(f,tau )} функции f на разбиении tau называется

{displaystyle s(f,tau )=sum _{i=1}^{n}m_{i}Delta x_{i}}

Верхней суммой Дарбу {displaystyle S(f,tau )} называется

{displaystyle S(f,tau )=sum _{i=1}^{n}M_{i}Delta x_{i}}[11]

Тогда нижним интегралом Дарбу I_* называется

{displaystyle I_{*}=sup _{tau in T}s(f,tau )}

Верхним интегралом Дарбу I^* называется

{displaystyle I^{*}=inf _{tau in T}S(f,tau )}[12]

Все вышеперечисленные свойства сумм Дарбу и интегралов Дарбу, а также альтернативные определения сохраняются.[13]

Примечания[править | править код]

  1. ↑ Ильин, 1985, с. 330.
  2. ↑ Ильин, 1985, с. 331.
  3. ↑ Архипов, 1999, с. 190.
  4. ↑ 1 2 Ильин, 1985, с. 337.
  5. ↑ 1 2 3 Ильин, 1985, с. 338.
  6. ↑ Архипов, 1999, с. 208.
  7. ↑ 1 2 3 Ильин, 1985, с. 336.
  8. ↑ Ильин, 1985, с. 335.
  9. ↑ 1 2 Архипов, 1999, с. 191.
  10. ↑ Кудрявцев, 2003, с. 553.
  11. ↑ Архипов, 1999, с. 559.
  12. ↑ Архипов, 1999, с. 548.
  13. ↑ Архипов, 1999, с. 550.

Литература[править | править код]

  • Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Начальный курс. — 2-е изд., перераб.. — М.: МГУ, 1985. — 662 с. с.
  • Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по математическому анализу: Учебник для университетов и пед. вузов. — М.: Высшая школа, 1999. — 695 с. с. — ISBN 5-06-003596-4.
  • Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. Дифференциальное и интегральное исчисления функций многих переменных. — М.: Дрофа, 2003. — 704 p.
Источник

Определение и условия существования определенного интеграла

разделов

от теории до практики

примеров

Примеры решения задач

видео

Примеры решения задач

  1. Задачи, приводящие к понятию определенного интеграла.

    Начать изучение

  2. Площадь криволинейной трапеции.

    Начать изучение

  3. Работа переменной силы.

    Начать изучение

  4. Понятие определенного интеграла.

    Начать изучение

  5. Необходимое условие интегрируемости функции.

    Начать изучение

  6. Суммы Дарбу и их свойства.

    Начать изучение

  7. Критерий интегрируемости функции.

    Начать изучение

  8. Классы интегрируемых функций.

    Начать изучение

Задачи, приводящие к понятию определенного интеграла.

Площадь криволинейной трапеции.

Пусть функция (f) непрерывна на отрезке (Delta = [a, b]) и неотрицательна, то есть (f(x) geq 0) при всех (x in Delta). Рассмотрим фигуру (G) (рис. 34.1), ограниченную отрезками прямых (x = a, x = b, y = 0) и графиком функции (y = f(x)), то есть
$$
G = {(x, y): a leq x leq b, 0 leq y leq f(x)}.nonumber
$$

Такую фигуру называют криволинейной трапецией, а отрезок (Delta) — ее основанием.

Рис. 34.1

Рис. 34.1

Разобьем отрезок (Delta) на (n) частей точками (x_{i}(i = overline{1, n-1})), где (x_{1} < x_{2} < ldots < x_{n-2} < x_{n-1}), и проведем через эти точки прямые, параллельные оси (Oy). Тогда фигура (G) разобьется на (n) частей, каждая из которых является криволинейной трапецией.

Обозначим (Delta x_{i} = x_{i}-x_{i-1}, x_{0} = a, x_{n} = b), и пусть  (xi_{i} in Delta_{i}), где (Delta_{i} = [x_{i-1}, x_{i}], i = overline{1, n}). Тогда сумма
$$
sigma = sum_{i=1}^{n}f(xi_{i})Delta x_{i},nonumber
$$
зависящая от разбиения отрезка (Delta) и выбора точек (xi_{i}), равна площади ступенчатой фигуры (рис. 34.1), составленной из (n) прямоугольников, причем основанием (i)-го прямоугольника служит отрезок (Delta_{i}), а длина его высоты равна (f(xi_{i})). Интуитивно ясно, что эта ступенчатая фигура будет мало отличаться от исходной фигуры (G) при достаточно мелком разбиении.

Будем увеличивать число точек разбиения так, чтобы наибольшая из длин отрезков (Delta_{i}) стремилась к нулю. Если при этом сумма (sigma) будет иметь предел (S), не зависящий ни от способа дробления отрезка (Delta), ни от выбора точек то естественно считать, что площадь фигуры (G) равна (S). Существование этого предела будет доказано ниже в разделе «Классы интегрируемых функций».

Пример 1.

Найти площадь фигуры, ограниченной параболой (y = x^{2}) и отрезками прямых (x = a), где (a > 0), и (y = 0) (рис. 34.2).

Решение.

Рис. 34.2
Рис. 34.1

(triangle) Пользуясь тем, что предел суммы (sigma) для непрерывной функции (f(x) = x^{2}) (см. раздел «Классы интегрируемых функций») не зависит от способа дробления отрезка (Delta = [0, a]) и выбора точек (xi_{i}) будем считать, что отрезок (Delta) разбит на (n) отрезков равной длины, а в качестве точки (xi_{i} (i = overline{1, n})) взят правый конец отрезка (Delta_{i}). Тогда (xi_{i} = x_{i} = displaystyle frac{a}{n}i, Delta x_{i} = frac{a}{n}, sigma = sum_{substack{i=1} }^{substack{n}}x_{i}^{2}Delta x_{i} = frac{a^{3}}{n^{3}}sum_{substack{i=1} }^{substack{n}}i^{2}).

Так как (displaystyle sum_{i=1}^{n}i^{2} = frac{n(n + 1)(2n + 1)}{6}) (доказательство представлено здесь), то (sigma =displaystyle frac{a^{3}}{3}left(1 + frac{1}{n}right)left(1 + frac{1}{2n}right)), откуда (displaystyle lim_{n rightarrow infty} sigma = frac{a^{3}}{3}). Поэтому искомая площадь  равна (displaystyle frac{a^{3}}{3}). (blacktriangle)

Заметим, что этот результат был получен еще Архимедом с помощью предельного перехода. Существует также простой способ нахождения предела для (sigma), основанный на формуле Ньютона Лейбница.

Работа переменной силы.

Пусть материальная точка движется вдоль числовой прямой (Ox) под действием силы (P), причем направление действия силы совпадает с направлением движения материальной точки. Предположим, что сила (P) задана как непрерывная функция от координаты (x) этой прямой, то есть (P = P(x)).

Найдем работу силы (P) при перемещении материальной точки от (x = a) до (x = b). Разобьем отрезок [(a, b)], как и в задаче о площади криволинейной трапеции, точками (x_{i}) и выберем  (xi_{i} in Delta_{i} (i = overline{1, n})). Тогда работа силы (P) на отрезке (Delta_{i}) приближенно равна (P(xi_{i})Delta x_{i}), а на отрезке [(a, b)] работу этой силы можно считать приближенно равной сумме (displaystyle sum_{i=1}^{n}P(xi_{i})Delta x_{i}). Предел этой суммы (при тех же условиях, что и в задаче о площади) естественно назвать работой переменной силы при перемещении материальной точки из точки (a) в точку (b).

В рассмотренных задачах речь идет о нахождении предела сумм вида (displaystyle sum_{i=1}^{n}f(xi_{i})Delta x_{i}), которые называют интегральными суммами. К вычислению предела таких сумм сводится решение многих важных задач из геометрии, физики, техники и других дисциплин. Поэтому вопросы, связанные с обоснованием предельного перехода описанного типа, заслуживают всестороннего изучения.

Понятие определенного интеграла.

Пусть функция одного переменного (f(x)) определена на отрезке [(a, b)] и пусть (x_{i} (i = overline{0, n})) — совокупность точек этого отрезка таких, что
$$
a = x_{0} < x_{1} < ldots < x_{i-1} < x_{i} < ldots < x_{n-1} < x_{n} = b.nonumber
$$

Назовем эту совокупность точек разбиением отрезка [(a, b)], обозначим разбиение (T = {x_{i}, i = overline{0, n}}), а отрезки (Delta_{i} = [x_{i-1}, x_{i}]), где (i = overline{1, n}), назовем отрезками разбиения (T).

Пусть (Delta x_{i} = x_{i}-x_{i-1}) — длина (i)-ro отрезка разбиения (T). Тогда число (l(T) = displaystyle max_{1leq i leq n}Delta x_{i}) назовем мелкостью разбиения (T) (или диаметром этого разбиения). Если (xi_{i} in Delta_{i}), то совокупность точек (xi_{i} (i = overline{1, n})) назовем выборкой и обозначим (xi = {xi_{i}, i = overline{1, n}}).

Сумму
$$
sigma_{T} = (xi, f) = sigma_{T}(xi) = sum_{substack{i=1} }^{substack{n}}f(xi_{i})Delta x_{i}.label{ref1}
$$
назовем интегральной суммой для функции (f) при заданном разбиении (T) и фиксированной выборке (xi).

Определение.

Число (J) называется определенным интегралом от функции (f) на отрезке [(a, b)] и обозначается (displaystyleint_{a}^{b}f(x)dx), если для любого (varepsilon > 0) существует такое число (delta = delta(varepsilon) > 0), что для любого разбиения (T), мелкость которого (l(T) < delta), и для любой выборки (xi) выполняется неравенство
$$
left|sum_{i=1}^{n}f(xi_{i})Delta x_{i}-Jright| < varepsilon.nonumber
$$

С помощью символов это определение можно записать так:
$$
left{ J = int_{a}^{b}f(x)dx right} Leftrightarrow forall varepsilon > 0 exists delta > 0: forall T : l(T) < delta(varepsilon) forall xi rightarrow |sigma_{T}(xi, f)-J| < varepsilon.label{ref2}
$$

Часто утверждение eqref{ref2} кратко записывают в виде (sigma_{T}(xi) rightarrow J) при (l(T) rightarrow 0) или (displaystyle lim_{l(T) rightarrow 0}sigma_{T}(xi) = J), имея в виду, что предел не зависит от выборки (xi).

Определение.

Если существует число (J), определяемое условиями eqref{ref2}, то функцию (f) называют интегрируемой (по Риману) на отрезке ([a, b]) и говорят, что существует интеграл от функции (f) на отрезке ([a, b]).

Необходимое условие интегрируемости функции.

Теорема 1.

Если функция (f(x)) интегрируема на отрезке [(a, b)], то она ограничена на этом отрезке.

Доказательство.

(circ) Пусть функция (f) интегрируема на отрезке [(a, b)]. Тогда существует число (J), удовлетворяющее условию eqref{ref2}. Полагая в eqref{ref2} (varepsilon = 1), получаем неравенство
$$
J-1 < sigma_{T}(xi, f) < J + 1.label{ref3}
$$
которое должно выполняться для любого разбиения (T) такого, что (l(T) < delta_{1} = delta(1)), и при любой выборке (xi).

Зафиксируем разбиение (T), удовлетворяющее условию (l(T) < delta_{1}), и предположим, что функция (f) не ограничена на отрезке ([a, b]). Тогда она не ограничена по крайней мере на одном из отрезков (Delta_{i}) разбиения (T). Без ограничения общности можно считать, что функция (f) не ограничена на отрезке (Delta_{1} = [x_{0}, x_{1}] = [a, x_{1}]).

Фиксируем точки (xi_{2}, ldots, xi_{n}), где (xi_{i} in Delta_{i}, i = overline{2, n}), и обозначим (A =displaystyle sum_{i=1}^{n}f(xi_{i})Delta x_{i}). Тогда (sigma_{T} = A + f(xi_{1})Delta x_{1}) и в силу eqref{ref3} получаем неравенства
$$
J-1 < f(xi_{1})Delta x_{1} + A < J + 1.label{ref4}
$$
которые должны выполняться для любого (xi_{1} in Delta_{1}).

Так как (Delta x_{1} > 0), то двойное неравенство eqref{ref4} равносильно неравенству
$$
frac{1}{Delta x_{1}}(J-1-A) < f(xi_{1}) < frac{1}{Delta x_{1}}(J + 1-A),nonumber
$$
из которого следует, что функция (f) ограничена на (Delta_{1}), что противоречит предположению о неограниченности функции (f) на отрезке (Delta_{1}).

Итак, предположение о неограниченности (f) на ([a, b]) приводит к противоречию. Теорема доказана. (bullet)

Замечание 1.

Ограниченность функции не является достаточным условием ее интегрируемости. Так, функция Дирихле
$$
D(x)=left{begin{array}{lc}1,&xin Q,\0,&xin J,end{array}right.nonumber
$$
не интегрируема на отрезке ([0,1]), хотя и ограничена.

(circ) Действительно, если выборки (xi) и (xi’) состоят соответственно из рациональных и иррациональных точек, то (sigma_{T}(xi) = 1), а (sigma_{T}(xi’) = 0) для любого разбиения (T) отрезка ([0,1]). Поэтому не существует предела интегральных сумм при (l(T) rightarrow 0). (bullet)

Суммы Дарбу и их свойства.

Пусть функция (f), определенная на отрезке ([a, b]), ограничена на этом отрезке и пусть (T = {x_{i}, i = overline{0, n}}) — разбиение отрезка ([a, b]), (Delta_{i} = [x_{i-1}, x_{i}], Delta x_{i} = x_{i}-x_{i-1} (i = overline{1, n})). Обозначим
$$
begin{array}{cc}M_{i} = displaystyle sup_{x in Delta_{i}}f(x),&displaystyle m_{i} = inf_{x in Delta_{i}}f(x),\displaystyle S_{T} = sum_{i=1}^{n}M_{i}Delta x_{i}&displaystyle s_{T} = sum_{i=1}^{n}m_{i}Delta x_{i}end{array}label{ref5}
$$

Назовем (S_{T}) и (s_{T}) соответственно верхней и нижней суммами Дарбу для функции (f) при заданном разбиении (T) отрезка ([a, b]). Заметим, что эти суммы не зависят от выборки (xi). Рассмотрим свойства сумм Дарбу.

Свойство 1.

Для любой выборки (xi) справедливы неравенства
$$
s_{T} leq sigma_{T}(xi) leq S_{T}.label{ref6}
$$

Доказательство.

(circ) Так как для любого (xi_{i} in Delta_{i}) выполняются неравенства
$$
m_{i} leq f(xi_{i}) leq M_{i},nonumber
$$
то
$$
m_{i}Delta x_{i} leq f(xi_{i})Delta x_{i} leq M_{i}Delta x_{i}.nonumber
$$
Складывая эти неравенства, получаем
$$
sum_{i=1}^{n}m_{i}Delta x_{i} leq sum_{i=1}^{n}f(xi_{i})Delta x_{i} leq sum_{i=1}^{n}M_{i}Delta x_{i}.label{ref7}
$$Согласно определению сумм Дарбу и интегральной суммы (sigma) утверждения eqref{ref7} и eqref{ref6} равносильны. (bullet)

Свойство 2.

Справедливы равенства
$$
S_{T} =  sup_{xi}sigma_{T}(xi).label{ref8}
$$
$$
s_{T} =  inf_{xi}sigma_{T}(xi).label{ref9}
$$

Доказательство.

(circ) Докажем утверждение eqref{ref8}. Согласно определению точной верхней грани нужно доказать, что выполняются следующие условия:
$$
forall xi rightarrow sigma_{T}(xi) leq S_{T},quad varepsilon > 0 exists xi’ : S_{T}-sigma_{T}(xi^{‘}) < varepsilonnonumber
$$Первое из этих условий выполняется в силу eqref{ref6}. Докажем второе условие.Так как (M_{i} =displaystyle sup_{x in Delta_{i}}f(x)), то по определению точной верхней грани
$$
forall varepsilon > 0 exists xi_{i}’ = xi_{i}'(varepsilon) in Delta_{i} : 0 leq M_{i}-f(xi_{i}’) < frac{varepsilon}{b-a}, i = overline{1, n}.nonumber
$$
Умножая (i)-е неравенство на (Delta x_{i}) и складывая все получаемые неравенства, находим
$$
0 leq S_{T}-sigma_{T}(xi’) < varepsilon,nonumber
$$
где (xi’ = {xi_{i}’, i = overline{1, n}}) — выборка. Итак, утверждение eqref{ref8} доказано. Аналогично доказывается, что справедливо и утверждение eqref{ref9}. (bullet)

Следующее свойство сумм Дарбу связано с еще одним понятием для разбиений. Назовем разбиение (T_{2}) продолжением (измельчением) разбиения (T_{1}), если каждая точка разбиения (T_{1}) является точкой разбиения (T_{2}). Иначе говоря, разбиение (T_{2}) либо совпадает с разбиением (T_{1}), либо получено из (T_{1}) добавлением по крайней мере одной новой точки.

Свойство 3.

Если разбиение (T_{2}) — продолжение разбиения (T_{1}), то
$$
s_{T_{1}} leq s_{T_{2}} leq S_{T_{1}} leq S_{T_{1}}.label{ref10}
$$
то есть при измельчении разбиения нижняя сумма Дарбу не уменьшается, а верхняя не увеличивается.

Доказательство.

(circ) Для доказательства неравенств eqref{ref10} достаточно рассмотреть случай, когда разбиение (T_{2}) получается из разбиения (T_{1}) добавлением только одной точки (x’ in (x_{i-1}, x_{i})). Пусть (Delta_{i}’) и (Delta_{i}″) — отрезки, на которые точка (x’) разбивает отрезок (Delta_{i}), a (lambda_{1}) и (lambda_{2}) — длины этих отрезков; тогда (Delta x_{i} = lambda_{1} + lambda_{2}). Обозначим (m_{i}’ =displaystyle inf_{x in Delta_{i}’}f(x), m_{i}″ = inf_{x in Delta_{i}″}f(x)). Очевидно, что (m_{i}’ geq m_{i}, m_{i}″geq m_{i}).

В суммах (s_{T_{2}}) и (s_{T_{1}}) равны все соответствующие слагаемые, за исключением тех, которые связаны с отрезком (Delta_{i}). Поэтому
$$
s_{T_{2}}-s_{T_{1}} = m_{i}’lambda_{1} + m_{i}″lambda_{2}-m_{i}(lambda_{1} + lambda_{2}),nonumber
$$
где (m_{i}^{‘} geq m_{i}, m_{i}^{″} geq m_{i}). Следовательно,
$$
s_{T_{2}}-s_{T_{1}} = (m_{i}’-m_{i})lambda_{1} + (m_{i}″-m_{i})lambda_{2} geq 0,nonumber
$$
то есть (s_{T_{2}} leq s_{T_{1}}).

Аналогично доказывается неравенство (S_{T_{2}} leq S_{T_{1}}). Отсюда, используя неравенство (s_{T_{2}} leq S_{T_{2}}) (см. eqref{ref6}), получаем цепочку неравенств eqref{ref10}. (bullet)

Свойство 4.

Для любых разбиений (T’) и (T″) справедливо неравенство
$$
s_{T’} leq S_{T″}.label{ref11}
$$

Доказательство.

(circ) Пусть разбиение (T) является продолжением как разбиения (T’), так и разбиения (T″) (в качестве (T) можно взять (T’) и добавить к нему те точки разбиения (T″), которые не входят в (T’)).Из неравенств eqref{ref10} при (T_{1} = T’, T_{2} = T) получаем
$$
s_{T’} leq s_{T} leq S_{T}nonumber
$$
Полагая в eqref{ref10} (T_{2} = T) и (T_{1} = T’). находим
$$
S_{T} leq S_{T″}.nonumber
$$
Объединяя полученные неравенства, имеем
$$
s_{T’} leq s_{T} leq S_{T} leq S_{T″},nonumber
$$
откуда следует неравенство eqref{ref11}. (bullet)

Свойство 5.

Существуют числа
$$
underline{J} = sup_{T}s_{T}, overline{J} = inf_{T}S_{T},nonumber
$$
удовлетворяющие для любых разбиений (T’) и (T″) отрезка ([a, b]) условию
$$
s_{T’} leq underline{J} leq overline{J} leq S_{T″}.label{ref12}
$$
Эти числа называют соответственно нижним и верхним интегралами Дарбу от функции (f) на отрезке ([a, b]).

Доказательство.

(circ) Из неравенства eqref{ref11} по теореме об отделимости числовых множеств следует, что существуют (underline{J} = sup s_{T}) и (overline{J} = inf S_{T}) (супремум и инфимум по всевозможным разбиениям отрезка ([a, b]) и для любых разбиений (T’) и (T″) выполняется неравенство eqref{ref12}. (bullet)

В заключение отметим, что все вышеперечисленные свойства справедливы для любой ограниченной на отрезке ([a, b]) функции.

Критерий интегрируемости функции.

Теорема 2.

Для того чтобы функция (f(x)), определенная на отрезке ([a, b]), была интегрируемой на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
$$
forall varepsilon > 0 exists delta_{varepsilon} > 0: forall T : l(T) < delta_{varepsilon} longrightarrow 0leq S_T-s_Tleq varepsilon.label{ref13}
$$

Доказательство.

(circ) Необходимость. Пусть функция (f) интегрируема на отрезке ([a, b]). Тогда она ограничена по теореме 1 и в силу определения интеграла
$$
exists J: forall varepsilon > 0 exists delta_{varepsilon} > 0: forall T : l(T) < delta_{varepsilon} forall xi longrightarrow J-frac{varepsilon}{3} < sigma_{T}(xi) < J + frac{varepsilon}{3}.nonumber
$$
Таким образом, при каждом разбиении (T) отрезка ([a, b]), мелкость которого удовлетворяет условию (l(T) < delta_{varepsilon}), неравенство
$$
J-frac{varepsilon}{3} < sigma_{T}(xi) < J + frac{varepsilon}{3}.label{ref14}
$$
выполняется при любой выборке (xi). Поэтому из левого неравенства eqref{ref14} и равенства eqref{ref9} следует, что
$$
J-frac{varepsilon}{3}leq inf_{substack{xi}}sigma_{T}(xi) = s_{T}.label{ref15}
$$
Аналогично из правого неравенства eqref{ref14} и равенства eqref{ref8} следует, что
$$
S_{T} = sup_{substack{xi}}sigma_{T}(xi) leq J + frac{varepsilon}{3},label{ref16}
$$

Из неравенств eqref{ref15}, eqref{ref6} и eqref{ref16} получаем цепочку неравенств
$$
J-frac{varepsilon}{3} leq s_{T} leq S_{T} leq J + frac{varepsilon}{3},nonumber
$$
откуда следует, что
$$
0 leq S_{T}-s_{T} leq frac{2varepsilon}{3} < varepsilon.nonumber
$$
Итак, интегрируемая на отрезке функция (f) удовлетворяет условию eqref{ref13}.

Достаточность. Пусть функция (f) ограничена на отрезке ([a, b]) и удовлетворяет условию eqref{ref13}. Докажем, что функция (f) интегрируема на отрезке ([a, b]), то есть
$$
exists J: forall varepsilon > 0 exists delta_{varepsilon} > 0: forall T : l(T) < delta_{varepsilon} forall xi longrightarrow left|sigma_{T}(xi)-Jright| < varepsilon.label{ref17}
$$

Воспользуемся свойством 5. Из неравенств eqref{ref12} следует, что
$$
0 leq overline{J}-underline{J} leq S_{T}-s_{T},nonumber
$$
откуда в силу eqref{ref13} получаем неравенство
$$
0 leq overline{J}-underline{J} leq S_{T}-s_{T} < varepsilon,nonumber
$$
справедливое для любого разбиения (T) такого, что (l(T) < delta_{varepsilon}). Так как числа (overline{J}) и (underline{J}) не зависят от (T), то отсюда следует, что
$$
overline{J} = underline{J}.
$$
Обозначим
$$
J = overline{J} = underline{J}label{ref18}
$$
и докажем, что число (J) есть интеграл от функции (f) на отрезке ([a, b]). Из eqref{ref12} и eqref{ref18} следует, что
$$
s_{T} leq J leq S_{T},label{ref19}
$$
а из eqref{ref19} и eqref{ref6} в силу eqref{ref13} получаем
$$
arrowvertsigma_{T}(xi)-Jarrowvert leq S_{T}-s_{T} < varepsilon.nonumber
$$
Это означает, что функция (f) интегрируема на отрезке ([a, b]), а число (J) есть интеграл от (f(x)) на ([a, b]). (bullet)

Следствие.

Если функция (f) интегрируема на отрезке ([a, b]), а число (J) — ее интеграл на этом отрезке, то
$$
J = sup s_{T} = inf S_{T}.nonumber
$$

Замечание 2.

Назовем колебанием функции (f) на отрезке (Delta_{i} = [x_{i-1}, x_{i}]) разбиения (T = {x_{i}, i = overline{0, n}}) число
$$
omega_{i}(f) = omega_{i} = M_{i}-m_{i},nonumber
$$
где (M_{i} = displaystyle sup_{x in Delta_{i}}f(x), m_{i} = inf_{x in Delta_{i}}f(x)). Тогда
$$
S_{T}-s_{T} = sum_{i=1}^{n}(M_{i}-m_{i})Delta x_{i} = sum_{i=1}^{n}omega_{i}Delta x_{i},nonumber
$$

Условие интегрируемости eqref{ref13} часто записывают в виде
$$
S_{T}-s_{T} = sum_{i=1}^{n}omega_{i}Delta x_{i} rightarrow 0.label{ref20}
$$
при (l(T) rightarrow 0).

Замечание 3.

При доказательстве свойств интеграла (§ 35, п. 1) будет использовано следующее равенство:
$$
omega_{i}(f) = sup_{x’, x″ in Delta_{i}} left|f(x^{″})-f(x^{‘})right|.label{ref21}
$$

(circ) Согласно определению точной верхней грани равенство eqref{ref21} означает, что выполняются следующие условия:
$$
|f(x″)-f(x’)| leq M_{i}-m_{i}.label{ref22}
$$
для любых (x’, x″ in Delta_{i}),
$$
forall varepsilon > 0 exists x_{i}’ in Delta_{i} exists x_{i}″ in Delta_{i}: M_{i}-m_{i}-varepsilon < |f(x_{varepsilon}″)-f(x_{varepsilon}’)|.label{ref23}
$$
Заметим, что формула eqref{ref21} справедлива, если (M_{i} = m_{i}), так как в этом случае (f(x) = M_{i} = m_{i}) для всех (x in Delta_{i}). Пусть (M_{i} > m_{i}), тогда для любых (x’, x″ in Delta_{i}) справедливы неравенства (m_{i} leq f(x’) leq M_{i}, m_{i} leq f(x″) leq M_{i}), откуда следует, что выполняется условие eqref{ref22}.

Для доказательства условия eqref{ref23} зададим произвольное число (varepsilon > 0), удовлетворяющее условию (varepsilon < M_{i}-m_{i}). В силу определения точных граней найдутся точки (x_{i}’ in Delta_{i}, x_{i}″ in Delta_{i}) такие, что
$$
f(x_{varepsilon}’) < m_{i} + frac{varepsilon}{2} < M_{i}-frac{varepsilon}{2} < f(x_{varepsilon}″),nonumber
$$
откуда следует, что выполняется условие eqref{ref23}. (bullet)

Замечание 4.

Можно доказать, что если для любого (varepsilon > 0) существует такое разбиение (tilde{T} = tilde{T}(varepsilon)), что (S_{tilde{T}}-s_{tilde{T}} < varepsilon), то найдется число (delta > 0) такое, что для любого разбиения (T), мелкость которого (l(T) < delta), выполняется неравенство (S_{T}-s_{T} < varepsilon). Поэтому критерий интегрируемости можно сформулировать так: для того чтобы ограниченная функция (f) была интегрируема по Риману на отрезке ([a, b]), необходимо и достаточно, чтобы для любого (varepsilon > 0) существовало такое разбиение (T) отрезка ([a, b]), что
$$
S_{T}-s_{T} < varepsilon.nonumber
$$

Классы интегрируемых функций.

Теорема 3.

Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.

Доказательство.

(circ) Пусть функция (f) непрерывна на отрезке ([a, b]). Тогда по теореме Кантора она равномерно непрерывна на этом отрезке, то есть
$$
forall varepsilon > 0 exists delta = delta_{varepsilon} > 0 forall x_{i}’, x_{i}″in [a, b]: |x’-x″| < delta rightarrow\ rightarrow |f(x″)-f(x’)| < frac{varepsilon}{b-a}.label{ref24}
$$

Докажем, что для функции (f) выполняется условие eqref{ref24}. Пусть (T = {x_{i}, i = overline{0, n}}) — произвольное разбиение отрезка ([a, b]) такое, что его мелкость (l(T) = displaystylemax_{1 leq i leq n}Delta x_{i}), где (Delta x_{i} = x_{i}-x_{i-1}). По теореме Вейерштрасса существуют точки (xi_{i}’,  xi_{i}″ in Delta_{i} = [x_{i-1}, x_{i}]) такие, что (f(xi_{i}’) = m_{i}, f(xi_{i}″ = M_{i})), где (m_{i} = displaystyleinf_{x in Delta_{i}}f(x), M_{i} = sup_{x in Delta_{i}}f(x), i = overline{1, n}). Поэтому из условия eqref{ref24} следует, (displaystyleomega_{i} = M_{i}-m_{i} = f(xi_{i}″)-f(xi_{i}’) < frac{varepsilon}{b-a}) так как (|xi_{i}″-xi_{i}’| leq Delta x_{i} leq l(T) < delta). Отсюда получаем
$$
sum_{i=1}^{n}omega_{i}Delta x_{i} < frac{varepsilon}{b-a} sum_{i=1}^{n}Delta x_{i} = frac{varepsilon}{b-a} (b-a) = varepsilon.nonumber
$$
Итак,
$$
forall varepsilon > 0 exists delta = delta_{varepsilon} > 0:quad forall T: l(T) < delta rightarrow S_{T}-s_{T} = sum_{i=1}^{n}omega_{i}Delta x_{i} < varepsilon,
$$
и по теореме 2 функция (f) интегрируема на отрезке ([a, b]). (bullet)

Пример 2.

Доказать, пользуясь определением интеграла и теоремой 3, что:

  1. $$
    intlimits_a^b dx = b-a,nonumber
    $$
  2. $$
    intlimits_a^b x dx = frac{b^{2}-a^{2}}{2}.nonumber
    $$

Решение.

(triangle) Функции (f(x) = 1) и (f(x) = x) непрерывны на отрезке и в силу теоремы 3 интегрируемы. Пусть (T = {x_{i}, i = overline{0, n}}) — произвольное разбиение отрезка ([a, b]).

  1. Если (f(x) = 1), то (sigma_{T}(xi) = displaystylesum_{i=1}^{n} 1 cdot Delta x_{i} = sum_{i=1}^{n}(x_{i}-x_{i-1}) = x_{n}-x_{0} = b-a), откуда (displaystylelim_{l(T) rightarrow 0} sigma_{T}(xi) = b-a), и поэтому (displaystyleintlimits_a^b dx = b-a).
  2. Пусть (displaystylexi_{i} = frac{x_{i} + x_{i-1}}{2}), тогда (xi_{i} in Delta_{i} = [x_{i-1}, x_{i}]) для (i = overline{1, n}), и, следовательно,
    $$
    sigma_{T}(xi) = sum_{i=1}^{n}xi_{i}Delta x_{i} = frac{1}{2} sum_{i=1}^{n}(x_{i} + x_{i-1})(x_{i}-x_{i-1}) = frac{1}{2} sum_{i=1}^{n}(x_{i}^{2}-x_{i-1}^{2}) = frac{1}{2}(b^{2}-a^{2})),nonumber
    $$
    откуда (displaystylelim_{l(T) rightarrow 0} sigma_{T}(xi) = (b^{2}-a^{2})).

    Так как функция (f(x) = x) интегрируема на отрезке ([a, b]), то из определения интеграла следует, что предел интегральной суммы не зависит от выбора точек (xi_{i}) на отрезках (Delta_{i}). Поэтому
    $$
    intlimits_a^b x dx = frac{b^{2}-a^{2}}{2}. blacktriangle nonumber
    $$

Теорема 4.

Если функция определена на отрезке и монотонна, то она интегрируема на этом отрезке.

Доказательство.

(circ) Пусть, например, функция (f) является возрастающей на отрезке ([a, b]); тогда для всех (x in [a, b]) выполняется условие
$$
f(a) leq f(x) leq f(b),nonumber
$$
и поэтому функция (f) ограничена на отрезке ([a, b]).

Рассмотрим произвольное разбиение (T = {x_{i}, i = overline{0, n}}) отрезка ([a, b]). Тогда (f(x_{i-1}) = m_{i}, f(x_{i}) = M_{i}), где (m_{i} = displaystyleinf_{x in Delta_{i}}f(x), M_{i} = sup_{x in Delta_{i}}f(x), Delta_{i} = [x_{i-1}, x_{i}]). Следовательно, получаем
$$
S_{T}-s_{T} = displaystylesum_{i=1}^{n}(M_{i}-m_{i})Delta_{i} = sum_{substack{i=1}}^{substack{n}}(f(x_{i})-f_{i-1})Delta_{i}nonumber
$$
откуда
$$
S_{T}-s_{T} leq l(T) sum_{i=1}^{n}(f(x_{i})-f(x_{i-1}) = l(T)(f(b)-f(a),nonumber
$$
так как
$$
f(x_{i})-f(x_{i-1}) > 0,quad Delta x_{i} leq max_{1 leq i leq n}Delta x_{i} = l(T).nonumber
$$

Отсюда имеем, что (S_{T}-s_{T} rightarrow 0) при (l(T) rightarrow 0). По теореме 2 функция (f) интегрируема на отрезке ([a, b]). (bullet)

Источник

Определение
верхней и нижней сумм. Пусть
f(x)
—ограниченная
на сегменте
[а,
b]
функция
и {Xk}—
произвольное разбиение этого сегмента.
Так как f(x)
ограничена
на сегменте [а,
b],
то
она ограничена и на любом частичном
сегменте [Xk-1,Xk],
а
поэтому у функции f(x)
существуют
точная нижняя грань mk
и
точная верхняя грань Mk
на
частичном сегменте
[Xk-1,
Xk]

Итак,
пусть

будем
называть соответственно верхней и
нижней суммами функции f(x) для данного
разбиения {Xk} сегмента [а, b].

Основные
свойства верхних и нижних сумм. Докажем
следу­ющие леммы.

Лемма
1.
Пусть—
интегральная
сумма, отвечающая данному разбиению
.
Тогда при любом выборе промежуточных
точек

всегда
справедливы неравенства
гдеs
и S
—
соответственно
нижняя и верхняя суммы, отвечающие тому
же разбиению.

Доказательство.
По определению чисел
и


заклю­чаем,
что

для
любого
из сегмента
.Умно­жая
написанные неравенства на
и
суммируя по всем k
от
1 до n,
получаем
требуемое утверждение леммы.

Лемма
2.
Пусть
—произвольное
фиксированное разбие­ние сегмента
[а, b],
—
произвольное
положительное число. Тогда можно выбрать
промежуточные точки
так,
чтобы интегральная сумма

и
верхняя сумма S
удовлетворяли неравенству
.
Промежуточные точки

можно выбрать и таким образом, чтобы
для интегральной суммы
и
ниж­ней суммыs
выполнялись неравенства
.

Доказательство.
Пусть
— фиксированное разбиение сегмента[а,
b]
и
.
Докажем сначала первое утверждение
лем­мы. Поскольку
,
то
для выбранного нами
найдется
точка

сегмента
такая,
что
.
Умножив
эти неравенства на
и
просуммировав по всем k
от
1 до n,
получим
.

Аналогично
в силу того, что
,
существует такая точка
,
что
.

Последние
неравенства после умножения на
и суммирования приводят к оценкам.
Лемма доказана.

Следствие.
Для любого фиксированного разбиения
справедливы следующие соотношения:,
где точные верхняя и нижняя грани берутся
по всевозможным промежуточным точкам.

Лемма
3. При
измельчении данного разбиения верхняя
сумма может только уменьшиться, а нижняя
сумма — только увеличиться.

Доказательство.
Пусть
—
данное разбиение, а разбиениеполучается
из него добавлением только одной новой
точки х. Общий случай сводится к данному.
Предположим, чтолежит внутри.
Тогда в выражении дляS
слагаемое

заменится на
,
где
.
Точная верхняя грань функции на части
сегмента не превосходит точной верхней
грани функции на всем сегменте. Поэтомуи.

Так
как все другие слагаемые в выражении
для верхней суммы сохранятся, то мы
доказали, что при добавлении точки
верхняя сумма может только уменьшиться.
Случай, когда к данному разбиению
добавляется несколько новых точек,
сводится, очевидно к рассмотренному.
Точно так же устанавливается, что при
измельчении данного разбиения нижняя
сумма может только увеличиться. Лемма
доказана.

Лемма
4. Для двух
произвольных и, вообще говоря, различных
разбиений сегмента [а, b]
нижняя сумма одного из этих разбиений
не превосходит верхней суммы другого
разбиения.

Доказательство.
Пусть
и— два произвольных разбиения сегмента
[a, b], a S’, s’, S”, s” — верхние и нижние
суммы этих разбиений соответственно.
Обозначим черезобъединение разбиенийи,
а через S и s верхнюю и нижнюю суммы
разбиения.
Заметим, чтоявляется
измельчением как разбиения,
так и разбиения.
Согласно утверждению леммы 3 справедливы
неравенства.

Кроме
того, в силу леммы 1 получим, что s <S.
Пользуясь свойством транзитивности
для числовых неравенств и используя
три подчеркнутых выше неравенства,
заключаем, что
.
Аналогично устанавливается, что.
Лемма доказана.Следствие.
Множество верхних сумм данной функции
f(x),. отвечающих всевозможным разбиениям
сегмента [а, b],
ограничено снизу. Множество нижних сумм
ограничено сверху.

Действительно,
любая верхняя сумма не меньше некоторой
фиксированной нижней суммы, следовательно,
множество верхних сумм ограничено
снизу. Аналогично проводятся рассуждения
для: нижних сумм. Также существуют точная
нижняя грань множества {S}
и точная верхняя грань множества {s}.

Определение
2.
Верхним
интегралом Дарбу
oт функции f(x) называется число I*, равное
точной нижней грани множества верхних
сумм {S} данной функции f(x) для всевозможных
разбиений сегмента [а, b]. Нижним интегралом
Дарбу от функции f(x) называется число
,
равное точной верхней грани множества
нижних сумм {s} данной функции f(x) для
всевозможных разбиений сегмента [а, b].

Лемма
5.
Нижний
интеграл Дарбу всегда не превосходит
верхнего интеграла Дарбу, т. е.
Доказательство.
Допустим противное, т. е. предположим,.
что
.
Тогда
.
Для указанного,
согласно определению числа,
найдется та­кое разбиение
сегмента
[а,
b],
что
для соответствующей верх­ней суммы
S‘
будет
выполнено неравенство
.
Точно так же можно указать такое разбиение
сегмента[а,
b],
что
для соответствующей нижней суммы s”
будет
выполнено неравен­ство
.
Вычтем второе неравенство из первого.
Полу­чим
.
Но
,
поэтому
,
т. е.
.
Получившееся
неравенство противоречит утверждению
леммы 4. Таким образом, доказываемое
утверждение справедливо, т. е.
.
Пусть,
a

произвольное
разбиение сегмента [a, b], d — диаметр
этого разбиения. Обозначим через
разбиение, полученное из разбиенияпутем добавления к немуl
произвольных новых точек. Пусть S и s —
верхняя и нижняя суммы разбиения
,
аS’
и s’ — верхняя и нижняя суммы разбиения
.
Справедливо следующее утверждение.Лемма
6.
Для разностей S—S’
и s’—s
выполняются следующие неравенства.

Доказательство.
Не ограничивая общности, мы можем
провести рассуждения лишь для случая,
когда к точкам разбиения
добавляется
только одна новая точка,
и доказать, что в этом случае справедливы
неравенства
.
Пусть вновь добавляемая точка
лежит внутри сегмента.
Тогда верхняя суммаS
будет отличаться от верхней суммы S’
только тем, что одно слагаемое

y
суммы S
заменится двумя слагаемыми

у суммы S’.
Все остальные слагаемые у верхних сумм
S
и S’
будут общими. Отсюда следует, что
.
Из последнего соотношения, учитывая,
что в силу свойств точных граней,
получим, что

Доказательство
оценки для нижних сумм аналогично. Лемма
доказана.

Определение
3.
Число A
называется пределом верхних сумм S
при стремлении к нулю диаметра разбиений
d,
если для любого положительного числа

можно
указать положительное число
такое, что при условии

выполняется неравенство
.
Для обозначения указанного предела
естественно употреблять символ.
Аналогично определяется пределB
нижних сумм S
при стремлении d
к нулю.

Основная
лемма Дарбу.
Верхний интеграл Дарбу
является пределом верхних суммS
при стремлении диаметра d
разбиений к нулю, т. е.
.
Аналогично
.
Доказательство.
Проведем доказательство первого
утверждения леммы. Заметим, что если
функция f
(x)
=c
= const,
то S
= c(b—d)=I*
для любого разбиения. Поэтому
.
Если f(x)
непостоянна, то
Фиксируем
произвольное положительное число.
По определению числасуществует такое разбиение,
что верхняя суммаS*
этого разбиения будет удовлетворять
условию
.
Обозначим черезl
число точек разбиения
,
не совпадающих с концами; сегмента [а,b].
Пусть
— произвольное разбиение сегмента [а,b],
диаметр которого удовлетворяет
неравенству
,
и пусть S — верхняя сумма этого разбиения.
Произведем измельчение разбиения,
добавив к нему отмеченные вышеl
точек разбиения
.
Полученное при этом разбиение обозначим
символом.
По лемме 6 верхняя сумма S’ этого последнего
разбиения) удовлетворяет условию

Но разбиение
можно рассматривать как измельчение
разбиения,
к которому добавляются точки разбиения,
не совпадающие с концами сегмента [а,b].
Поэтому в силу определенияи
леммы 3Выше
было показано, что,
поэтому.
Объединяя эти неравенства с установленными
выше неравенствами,
получаем, что,
если только d меньше указанного выше.
Следовательно,Для нижних
сумм
доказательство аналогично. Основная
лемма Дарбу доказана.

Необходимые и
достаточные условия интегрируемости.

Вспомогательная
теорема.
Для того чтобы ограниченная на сегменте
[а, b]
функция f(x)
была интегрируема на этом сегменте,
необходимо и достаточно, чтобы выполнялось
paвeнcтвo.

Доказательство.
Необходимость. Пусть функция f(х)
интегрируема по Риману на сегменте [а,
b].
Тогда существует предел I
ее интегральных сумм
при стремлении диаметраd
разбиений к нулю. По определению предела
интегральных сумм для любого
существует такое,
что для любого выбора промежуточных
точекразбиенияс
диаметром
выполняется
неравенство

.
Согласно лемме 2 для данного разбиения
можно так выбрать промежуточные точки
и
в каждом частичном сегменте,
что будут справедливы неравенства

.
Подчеркнем, что, кроме того, для данного
разбиения
одновременно
выполнены неравенства

.
Заметим
теперь, что

Отсюда,
учитывая, что модуль суммы четырех
величин не превосходит суммы их модулей,
получаем, что
.
Итак, для любогосуществует такое,
что для любого разбиенияc
диаметром.

справедливо неравенство
.
Поскольку для любого разбиения выполнены
неравенства
,
то из неравенства
вытекает,
что
,
а отсюда, в силу произвольностивытекает,
что

Достаточность.
Пусть
.
Согласно основной лемме Дарбу,
т. е. верхний интеграл является пределом
верхних сумм, а нижний интеграл —
пределом нижних сумм при стремлении
диаметраd
разбиений к нулю. Поэтому для любого
можно указать такое число,
что для любого разбиения с диаметромd<одновременно выполняются неравенства.
При любом, указанном разбиении любая
интегральная сумма
удовлетворяет
неравенствам
,
а значит, и неравенствам
.

Отсюда
(для любого разбиения с диаметромd,
меньшим
).

Таким
образом,
,
т. е. функция f(x)
интегрируема.

Основная
теорема.
Для того чтобы ограниченная на сегменте
[а, b]
функция f(x)
была интегрируемой на этом сегменте,
необходимо и достаточно, чтобы для
любого
нашлось такое разбиениесегмента
[а,b],
для которого
.

Доказательство.
Необходимость. Пусть функция /(х)
интегрируема на сегменте [а, b).
При доказательстве необходимости
вспомогательной теоремы установлено,
что для любого
существует
такое,
что для любого разбиения сегмента [а,b]
с диаметром d,
меньшим
,
справедливо неравенство
.
Необходимость доказана. Достаточность.
Дано, что для любого
существует такое разбиениесегмента [а,b],
что для соответствующих верхней и нижней
сумм выполнено соотношение
.
Тогда поскольку

то
.
Из этого неравенства и из произвольности
е заключаем, что
,
а по вспомогательной теореме получаем,
что функция f(x)
интегрируема. Теорема доказана.

Источник

Определенный интеграл и его свойства

Ранее мы рассматривали определенный интеграл как разность значений первообразной для подынтегральной функции. При этом предполагалось, что подынтегральная функция имеет первообразную на промежутке интегрирования.

В случае, когда первообразная выражается через элементарные функции, мы можем быть уверенными в ее существовании. Но если такого выражения нет, то вопрос о существовании первообразной остается открытым, и мы не знаем, существует ли соответствующий определенный интеграл.

Геометрические соображения подсказывают, что хотя, например, для функции y=e^{-x^2} нельзя выразить первообразную через элементарные функции, интеграл textstyle{intlimits_{a}^{b}e^{-x^2},dx} существует и равен площади фигуры, ограниченной осью абсцисс, графиком функции y=e^{-x^2} и прямыми x=a,~ x=b (рис. 6). Но при более строгом анализе выясняется, что само понятие площади нуждается в обосновании, а потому нельзя опираться на него, решая вопросы существования первообразной и определенного интеграла.

Геометрический смысл определённого интеграла

Докажем, что любая функция, непрерывная на отрезке [a,b] имеет на этом отрезке первообразную, и, следовательно, для нее существует определенный интеграл по этому отрезку. Для этого нам понадобится иной подход к понятию определенного интеграла, не опирающийся на предположение о существовании первообразной.

Далее выясним, что для многочисленных приложений наиболее целесообразен именно второй подход. Кроме того, мы увидим, что для широкого класса функций оба подхода приводят к одному и тому же результату.

Установим сначала некоторые свойства определенного интеграла, понимаемого как разность значений первообразной.

Оценки определенных интегралов

Теорема 1. Пусть функции y=f(x) ограничена на отрезке [a,b], а m=min_{xin[a,b]}f(x) и M=max_{xin[a,b]}f(x), соответственно, наименьшее и наибольшее значения функции y=f(x) на [a,b], причем на этом отрезке функция y=f(x) имеет первообразную. Тогда

m(b-a)leqslant intlimits_{a}^{b}f(x),dxleqslant M(b-a).

(1)

Доказательство. Пусть F(x) — одна из первообразных для функции y=f(x) на отрезке [a,b]. Тогда

intlimits_{a}^{b}f(x),dx=Bigl.{F(x)}Bigr|_{a}^{b}=F(b)-F(a).

По теореме Лагранжа F(b)-F(a)=F'(c)(b-a), где a&lt;c&lt;b. Ho F'(c)=f(c), значит, intlimits_{a}^{b}f(x),dx=f(c)(b-a).

По условию для всех значений x из отрезка [a,b] выполняется неравенство mleqslant f(x)leqslant M, поэтому mleqslant f(c)leqslant M и, следовательно,

m(b-a)leqslant f(c)(b-a)leqslant M(b-a), то есть m(b-a)leqslant intlimits_{a}^{b}f(x),dxleqslant M(b-a),

что и требовалось доказать.

Двойное неравенство (1) дает лишь весьма грубую оценку для значения определенного интеграла. Например, на отрезке [1;5] значения функции y=x^2 заключены между 1 и 25, а потому имеют место неравенства

4=1cdot(5-1)leqslant intlimits_{1}^{5}x^2,dxleqslant 25cdot(5-1)=100.

Чтобы получить более точную оценку, разбивают отрезок [a,b] на несколько частей точками a=x_0&lt;x_1&lt;ldots&lt;x_{n-1}&lt;x_n=b и к каждой части [x_k,x_{k+1}] применяют неравенство (1). Если на отрезке [x_k,x_{k+1}] выполняется неравенство m_kleqslant f(x)leqslant M_k, то

m_kcdotDelta x_kleqslant intlimits_{x_k}^{x_{k+1}} f(x),dxleqslant M_kcdot Delta x_k,,

где через Delta x_k обозначена разность (x_{k+1}-x_k), т. е. длина отрезка [x_k,x_{k+1}]. Записывая эти неравенства для всех значений k от 0 до n-1 и складывая их, получим:

sum_{k=0}^{n-1}(m_kcdotDelta x_k) leqslant sum_{k=0}^{n-1} intlimits_{x_k}^{x_{k+1}}f(x),dxleqslant sum_{k=0}^{n-1} (M_kcdot Delta x_k),

Но по аддитивному свойству определенного интеграла сумма интегралов по всем частям отрезка [a,b] равна интегралу по этому отрезку, т. е.

sum_{k=0}^{n-1} intlimits_{x_k}^{x_{k+1}}f(x),dx= intlimits_{a}^{b}f(x),dx,.

Значит,

sum_{k=0}^{n-1}(m_kcdotDelta x_k) leqslant sum_{k=0}^{n-1} intlimits_{a}^{b}f(x),dxleqslant sum_{k=0}^{n-1} (M_kcdot Delta x_k)

(2)

Например, если разбить отрезок [1;5] на 10 равных частей, каждая из которых имеет длину 0,4, то на частичном отрезке [1+0,!4k;,0,!4(k+1)] выполняется неравенство

(1+0,!4k)^2leqslant x^2leqslant bigl(1+0,!4(k+1)bigr)^2

Поэтому имеем:

0,!4sum_{k=0}^{9}(1+0,!4k)^2leqslant intlimits_{1}^{5}x^2,dxleqslant 0,!4sum_{k=0}^{9}bigl(1+0,!4(k+1)bigr)^2.

Вычисляя, получаем: 36,!64leqslant intlimits_{1}^{5} x^2,dxleqslant 46,!24. Эта оценка гораздо точнее полученной ранее 4leqslant intlimits_{1}^{5}x^2,dxleqslant100.

Чтобы получить еще более точную оценку интеграла, надо разбить отрезок [1;5] не на 10, а, скажем, на 100 или 1000 частей и сосчитать соответствующие суммы. Разумеется, данный интеграл проще вычислить с помощью первообразной:

intlimits_{1}^{5}x^2,dx= left.{frac{x^3}{3}}right|_{1}^{5}= frac{1}{3}(125-1)= frac{124}{3},.

Но если выражение для первообразной нам неизвестно, то неравенства (2) дают возможность оценить значение интеграла снизу и сверху.

Определенный интеграл как разделяющее число

Числа m_k и M_k, входящие в неравенство (2), могли выбираться произвольно, лишь бы на каждом из отрезков [x_k,x_{k+1}] выполнялось неравенство m_kleqslant f(x)leqslant M_k. Наиболее точная оценка интеграла при данном разбиении отрезка [a,b] получится, если взять M_k наименьшим, а m_k наибольшим из всех возможных значений. Это значит, что в качестве m_k надо взять точную нижнюю границу значений функции y=f(x) на отрезке [x_k,x_{k+1}], а в качестве M_k — точную верхнюю границу этих значений на том же отрезке:

m_k=inf_{xin[x_k,x_{k+1}]}f(x),qquad M_k=sup_{xin[x_k,x_{k+1}]}f(x).

(3)

Если y=f(x) — ограниченная функция на отрезке [a,b], то она ограничена и на каждом из отрезков [x_k,x_{k+1}], а потому для нее определены по равенствам (3) числа m_k и M_k,~ 0leqslant kleqslant n-1. При таком выборе чисел m_k и M_k суммы textstyle{sumlimits_{k=0}^{n-1}m_kDelta x_k} и textstyle{sumlimits_{k=0}^{n-1}M_kDelta x_k} называют, соответственно, нижней и верхней интегральными суммами Дарбу для функции y=-f(x) при данном разбиении P:

a=x_0&lt;x_1&lt;x_2&lt;ldots&lt;x_{n-1}&lt;x_n=b

отрезка [a,b]. Будем обозначать эти суммы соответственно s_{fP} и S_{fP}, а если функция y=f(x) фиксирована, то просто s_P и S_P.

Неравенство (2) означает, что если ограниченная на отрезке [a,b] функция y=f(x) имеет на этом отрезке первообразную, то определенный интеграл textstyle{intlimits_{a}^{b} f(x),dx} разделяет числовые множества {s_p} и {S_P}, состоящие соответственно из всех нижних и верхних сумм Дарбу для всевозможных разбиений P отрезка [a,b]. Вообще говоря, может случиться, что число, разделяющее эти два множества, не единственно. Но ниже мы увидим, что для наиболее важных классов функций (в частности, для непрерывных функций) оно единственно.

Это позволяет ввести новое определение для textstyle{intlimits_{a}^{b} f(x),dx}, не опирающееся на понятие первообразной, а использующее лишь суммы Дарбу.

Определение. Функция y=f(x), ограниченная на отрезке [a,b], называется интегрируемой на этом отрезке, если существует единственное число ell, разделяющее множества нижних и верхних сумм Дарбу, образованных для всевозможных разбиений отрезка [a,b]. Если функция y=f(x) интегрируема на отрезке [a,b], то единственное число, разделяющее эти множества, называют определенным интегралом этой функции по отрезку [a,b] и означают textstyle{intlimits_{a}^{b}f(x),dx}.

Мы определили интеграл textstyle{intlimits_{a}^{b} f(x),dx} для случая, когда a&lt;b. Если a&gt;b, то положим

intlimits_{a}^{b}f(x),dx= -intlimits_{b}^{a}f(x),dx,.

Это определение естественно, так как при изменении направления промежутка интегрирования все разности Delta x_k=x_{k+1}-x_k меняют знак, а тогда меняют знаки и суммы Дарбу и, тем самым, разделяющее их число, т.е. интеграл.

Так как при a=b все Delta x_k обращаются в нуль, то положим

intlimits_{b}^{a}f(x),dx=0.

Мы получили два определения понятия определенного интеграла: как разности значений первообразной и как разделяющего числа для сумм Дарбу. Эти определения в наиболее важных случаях приводят к одному и тому же результату:

Теорема 2. Если функция y=f(x) ограничена на отрезке [a,b] и имеет на нем первообразную y=F(x), причем существует единственное число, разделяющее нижние и верхние суммы Дарбу, то это число равно F(b)-F(a).

Доказательство. Мы доказали выше, что число F(a)-F(b) разделяет множества {s_P} и {S_P}. Так как по условию разделяющее число однозначно определено, то оно совпадает с F(b)-F(a).

Начиная с этого момента мы будем применять обозначение textstyle{intlimits_{a}^{b}f(x),dx} лишь для единственного числа, разделяющего множества {s_P} и {S_P}. Из доказанной теоремы следует, что при этом не возникает противоречия с тем пониманием этого обозначения, которым мы пользовались выше.

Свойства нижних и верхних сумм Дарбу

Для того чтобы данное ранее определение интеграла имело смысл, надо доказать, что множество верхних сумм Дарбу действительно расположено справа от множества нижних сумм Дарбу.

Лемма 1. Для каждого разбиения P соответствующая нижняя сумма Дарбу не превосходит верхней суммы Дарбу, s_Pleqslant S_P.

Доказательство. Рассмотрим некоторое разбиение P отрезка [a,b]:

a=x_0&lt;x_1&lt;x_2&lt;ldots&lt;x_k&lt;x_{k+1}&lt;ldots&lt;x_n=b

‘

Очевидно, что для любого k и для любого выбранного разбиения P выполняется неравенство s_Pleqslant S_P. Следовательно, m_kcdotDelta x_kleqslant M_kcdotDelta x_k, и потому

s_P= sum_{k=0}^{n-1}(m_kcdotDelta x_k)leqslant sum_{k=0}^{n-1}(M_kcdotDelta x_k)=S_P.

(4)

что и требовалось доказать.

Неравенство (4) справедливо лишь для фиксированного разбиения P. Поэтому пока еще нельзя утверждать, что нижняя сумма Дарбу одного разбиения не может превзойти верхнюю сумму Дарбу другого разбиения. Для доказательства этого утверждения нам понадобится следующая лемма:

Лемма 2. От добавления новой точки деления нижняя сумма Дарбу не может уменьшиться, а верхняя сумма не может увеличиться.

Доказательство. Выберем некоторое разбиение P отрезка [a,b] и добавим к нему новую точку деления {x^{ast}}. Обозначим новое разбиение P^{ast}. Разбиение P^{ast} является измельчением разбиения P, т.е. каждая точка разбиения P является, одновременно и точкой разбиения P^{ast}.

Пусть точка {x^{ast}} попала на отрезок [x_k,x_{k+1}]colon, x_k&lt;x^{ast}&lt; x_{k+1}. Рассмотрим два образовавшихся отрезка [x_k,x^{ast}] и [x^{ast};x^{x_{k+1}}] и обозначим соответствующие им точные нижние границы значений функции через m_{k}^{ast} и m_{k}^{astast}, а точные верхние границы через M_{k}^{ast} и M_{k}^{astast}.

Слагаемому m_k(x_{k+1}-m_{k}) первоначальной нижней суммы Дарбу в новой нижней сумме Дарбу соответствуют два слагаемых:

m_{k}^{ast}(x^{ast}-x_k)+ m_{k}^{astast}(x_{k+1}-x^{ast}).

При этом m_kleqslant m_{k}^{ast} и m_kleqslant m_{k}^{astast}, так как m_k — точная нижняя граница значений функции f(x) на всем отрезке [x_{k},m_{k+1}], а m_{k}^{ast} и m_{k}^{astast} лишь на его частях [x_{k},x^{ast}] и [x^{ast},x_{k+1}] соответственно.

Оценим снизу сумму полученных слагаемых:

begin{aligned} m_{k}^{ast}bigl(x^{ast}-x_{k}bigr)+ m_{k}^{astast}bigl(x_{k+1}-x^{ast}bigr) geqslant & ,,m_k bigl(x^{ast}-x_k)+m_k(x_{k+1}-x^{ast}bigr)=\ &=m_kbigl(x^{ast}-x_k+x_{k+1}-x^{ast}bigr)=\ &=m_kbigl(x_{k+1}-x_kbigr).end{aligned}

Так как остальные слагаемые и в старой и в новой нижних суммах Дарбу остались неизменными, то нижняя сумма Дарбу от добавления новой точки деления не уменьшилась, s_Pleqslant S_P.

Доказанное утверждение остается справедливым и при добавлении любого конечного числа точек к разбиению P.

Аналогично доказывается утверждение о верхней сумме Дарбу: S_{P^{ast}}leqslant S_{P}.

Перейдем к сравнению сумм Дарбу для любых двух разбиений.

Лемма 3. Ни одна нижняя сумма Дарбу не превосходит любой верхней суммы Дарбу (хотя бы отвечающей другому разбиению отрезка [a,b]).

Произвольное разбиение двух отрезков и третий отрезок, состоящий из всех точек первых двух разбиений

Доказательство. Рассмотрим два произвольных разбиения P_1 и P_2 отрезка [a,b] и образуем третье разбиение P_3, состоящее из всех точек разбиений P_1 и P_2. Таким образом, разбиение P_3 является измельчением как разбиения P_1, так и разбиения P_2 (рис. 7).

Обозначим нижние и верхние суммы Дарбу для этих разбиений соответственно s_1,~S_1.~s_2,~S_2 и докажем, что s_1leqslant S_2.

Так как P_3 — измельчение разбиения P_1, то s_1leqslant s_3. Далее, s_3leqslant S_3, поскольку суммы s_3 и S_3 соответствуют одному и тому же разбиению. Наконец, S_3leqslant S_2, так как P_3 является измельчением разбиения P_2.

Таким образом, s_1leqslant s_3leqslant S_3leqslant S_2, т.е. s_1leqslant S_2, что и требовалось доказать.

Из леммы 3 следует, что числовое множество X={s_P} нижних сумм Дарбу лежит левее числового множества Y={S_P} верхних сумм Дарбу.

В силу теоремы о существовании разделяющего числа для двух числовых множеств1, найдется хотя бы одно число /, разделяющее множества X и Y, т.е. такое, что для любого разбиения отрезка [a,b] выполняется двойное неравенство:

s_P= sum_{k=0}^{n-1}bigl(m_kcdotDelta x_kbigr) leqslant Ileqslant sum_{k=0}^{n-1}bigl(M_kcdotDelta x_kbigr)=S_P.

Если это число единственно, то textstyle{I= intlimits_{a}^{b} f(x),dx}.

Приведем пример, показывающий, что такое число I, вообще говоря, не является однозначно определенным. Напомним, что функцией Дирихле называют функцию y=D(x) на отрезке [0;1], определяемую равенствами:

D(x)= begin{cases}0,& text{if}~~ x~~text{is irrational number};\1,& text{if}~~ x~~ text{is rational number}.end{cases}

Какой бы отрезок [x_k,x_{k+1}] мы ни взяли, на нем найдутся и рациональные, и иррациональные точки, т.е. и точки, где D(x)=0, и точки, где D(x)=1. Поэтому для любого разбиения отрезка [0;1] все значения m_k равны нулю, а все значения M_k равны единице. Но тогда все нижние суммы Дарбу textstyle{sumlimits_{k=0}^{n-1}bigl(m_kcdotDelta x_kbigr)} равны нулю, а все верхние суммы Дарбу textstyle{sumlimits_{k=0}^{n-1}bigl(M_kcdotDelta x_kbigr)} равны единице,

так как sumlimits_{k=0}^{n-1}bigl(M_kcdotDelta x_kbigr)= sumlimits_{k=0}^{n-1}Delta x_k, а sumlimits_{k=0}^{n-1}Delta x_k — длина отрезка [0;1].

Итак, в рассматриваемом случае X={0},~Y={1} и любое число из промежутка [0;1] разделяет множества X и Y. Значит, функция Дирихле не является интегрируемой на отрезке [0;1].

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

From Wikipedia, the free encyclopedia

In the branch of mathematics known as real analysis, the Darboux integral is constructed using Darboux sums and is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal.[1] The definition of the Darboux integral has the advantage of being easier to apply in computations or proofs than that of the Riemann integral. Consequently, introductory textbooks on calculus and real analysis often develop Riemann integration using the Darboux integral, rather than the true Riemann integral.[2] Moreover, the definition is readily extended to defining Riemann–Stieltjes integration.[3] Darboux integrals are named after their inventor, Gaston Darboux (1842–1917).

Definition[edit]

The definition of the Darboux integral considers upper and lower (Darboux) integrals, which exist for any bounded real-valued function f on the interval {displaystyle [a,b].} The Darboux integral exists if and only if the upper and lower integrals are equal. The upper and lower integrals are in turn the infimum and supremum, respectively, of upper and lower (Darboux) sums which over- and underestimate, respectively, the “area under the curve.” In particular, for a given partition of the interval of integration, the upper and lower sums add together the areas of rectangular slices whose heights are the supremum and infimum, respectively, of f in each subinterval of the partition. These ideas are made precise below:

Darboux sums[edit]

Lower (green) and upper (green plus lavender) Darboux sums for four subintervals

A partition of an interval [a,b] is a finite sequence of values xi such that

{displaystyle a=x_{0}<x_{1}<cdots <x_{n}=b.}

Each interval [x_{i-1},x_{i}] is called a subinterval of the partition. Let {displaystyle f:[a,b]to mathbb {R} } be a bounded function, and let

{displaystyle P=(x_{0},ldots ,x_{n})}

be a partition of [a,b]. Let

begin{align} M_i = sup_{xin[x_{i-1},x_{i}]} f(x) , \ m_i = inf_{xin[x_{i-1},x_{i}]} f(x) . end{align}

The upper Darboux sum of f with respect to P is

U_{f, P} = sum_{i=1}^n (x_{i}-x_{i-1}) M_i . ,!

The lower Darboux sum of f with respect to P is

L_{f, P} = sum_{i=1}^n (x_{i}-x_{i-1}) m_i . ,!

The lower and upper Darboux sums are often called the lower and upper sums.

Darboux integrals[edit]

The upper Darboux integral of f is

U_f = inf{U_{f,P} colon P text{ is a partition of } [a,b]} . ,!

The lower Darboux integral of f is

L_f = sup{L_{f,P} colon P text{ is a partition of } [a,b]} . ,!

In some literature an integral symbol with an underline and overline represent the lower and upper Darboux integrals respectively.

{displaystyle {begin{aligned}L_{f}equiv {underline {int _{a}^{b}}}f(x),mathrm {d} x\[6pt]U_{f}equiv {overline {int _{a}^{b}}}f(x),mathrm {d} x,end{aligned}}}

and like Darboux sums they are sometimes simply called the lower and upper integrals.

If Uf = Lf, then we call the common value the Darboux integral.[4] We also say that f is Darboux-integrable or simply integrable and set

{displaystyle int _{a}^{b}{f(t),dt}=U_{f}=L_{f},}

An equivalent and sometimes useful criterion for the integrability of f is to show that for every ε > 0 there exists a partition Pε of [a, b] such that[5]

{displaystyle U_{f,P_{epsilon }}-L_{f,P_{epsilon }}<varepsilon .}

Properties[edit]

Examples[edit]

A Darboux-integrable function[edit]

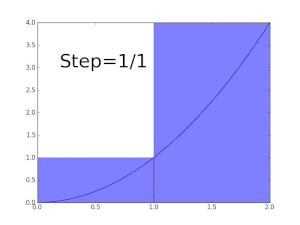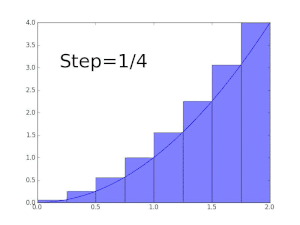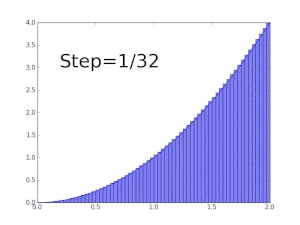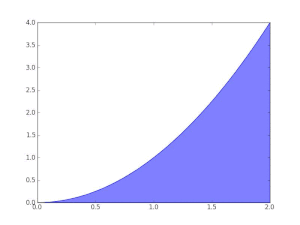
Suppose we want to show that the function f(x)=x is Darboux-integrable on the interval [0,1] and determine its value. To do this we partition [0,1] into n equally sized subintervals each of length 1/n. We denote a partition of n equally sized subintervals as P_{n}.

Now since f(x)=x is strictly increasing on [0,1], the infimum on any particular subinterval is given by its starting point. Likewise the supremum on any particular subinterval is given by its end point. The starting point of the k-th subinterval in P_{n} is {displaystyle (k-1)/n} and the end point is k/n. Thus the lower Darboux sum on a partition P_{n} is given by

{displaystyle {begin{aligned}L_{f,P_{n}}&=sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\&=sum _{k=1}^{n}{frac {k-1}{n}}cdot {frac {1}{n}}\&={frac {1}{n^{2}}}sum _{k=1}^{n}[k-1]\&={frac {1}{n^{2}}}left[{frac {(n-1)n}{2}}right]end{aligned}}}

similarly, the upper Darboux sum is given by

{displaystyle {begin{aligned}U_{f,P_{n}}&=sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\&=sum _{k=1}^{n}{frac {k}{n}}cdot {frac {1}{n}}\&={frac {1}{n^{2}}}sum _{k=1}^{n}k\&={frac {1}{n^{2}}}left[{frac {(n+1)n}{2}}right]end{aligned}}}

Since

{displaystyle U_{f,P_{n}}-L_{f,P_{n}}={frac {1}{n}}}

Thus for given any varepsilon >0, we have that any partition P_{n} with {displaystyle n>{frac {1}{varepsilon }}} satisfies

{displaystyle U_{f,P_{n}}-L_{f,P_{n}}<varepsilon }

which shows that f is Darboux integrable. To find the value of the integral note that

{displaystyle int _{0}^{1}f(x),dx=lim _{nto infty }U_{f,P_{n}}=lim _{nto infty }L_{f,P_{n}}={frac {1}{2}}}

Upper Darboux sum example

Darboux upper sums of the function y = x2

Lower Darboux sum example

Darboux lower sums of the function y = x2

A nonintegrable function[edit]

Suppose we have the Dirichlet function {displaystyle f:[0,1]to mathbb {R} } defined as

{displaystyle {begin{aligned}f(x)&={begin{cases}0&{text{if }}x{text{ is rational}}\1&{text{if }}x{text{ is irrational}}end{cases}}end{aligned}}}

Since the rational and irrational numbers are both dense subsets of mathbb {R} , it follows that f takes on the value of 0 and 1 on every subinterval of any partition. Thus for any partition P we have

{displaystyle {begin{aligned}L_{f,P}&=sum _{k=1}^{n}(x_{k}-x_{k-1})inf _{xin [x_{k-1},x_{k}]}f=0\U_{f,P}&=sum _{k=1}^{n}(x_{k}-x_{k-1})sup _{xin [x_{k-1},x_{k}]}f=1end{aligned}}}

from which we can see that the lower and upper Darboux integrals are unequal.

Refinement of a partition and relation to Riemann integration[edit]

When passing to a refinement, the lower sum increases and the upper sum decreases.

A refinement of the partition x_0, ldots, x_n is a partition y_0, ldots, y_m such that for all i = 0, …, n there is an integer r(i) such that

{displaystyle x_{i}=y_{r(i)}.}

In other words, to make a refinement, cut the subintervals into smaller pieces and do not remove any existing cuts.

If {displaystyle P'=(y_{0},ldots ,y_{m})} is a refinement of {displaystyle P=(x_{0},ldots ,x_{n}),} then

{displaystyle U_{f,P}geq U_{f,P'}}

and

{displaystyle L_{f,P}leq L_{f,P'}.}

If P1, P2 are two partitions of the same interval (one need not be a refinement of the other), then

{displaystyle L_{f,P_{1}}leq U_{f,P_{2}},}

and it follows that

{displaystyle L_{f}leq U_{f}.}

Riemann sums always lie between the corresponding lower and upper Darboux sums. Formally, if {displaystyle P=(x_{0},ldots ,x_{n})} and {displaystyle T=(t_{1},ldots ,t_{n})} together make a tagged partition

{displaystyle x_{0}leq t_{1}leq x_{1}leq cdots leq x_{n-1}leq t_{n}leq x_{n}}

(as in the definition of the Riemann integral), and if the Riemann sum of f is equal to R corresponding to P and T, then

{displaystyle L_{f,P}leq Rleq U_{f,P}.}

From the previous fact, Riemann integrals are at least as strong as Darboux integrals: if the Darboux integral exists, then the upper and lower Darboux sums corresponding to a sufficiently fine partition will be close to the value of the integral, so any Riemann sum over the same partition will also be close to the value of the integral. There is (see below) a tagged partition that comes arbitrarily close to the value of the upper Darboux integral or lower Darboux integral, and consequently, if the Riemann integral exists, then the Darboux integral must exist as well.

Details of finding the tags

For this proof, we shall use superscripts to index {displaystyle left{P^{(n)}right}} and variables related to it.

Let {displaystyle left{P^{(n)}right}} be a sequence of arbitrary partitions of [a,b] such that {displaystyle |P_{n}|to 0}, whose tags are to be determined.

By the definition of infimum, for
any epsilon >0, we can always find a {displaystyle t_{i}^{(n)}in left[x_{i}^{(n)},x_{i+1}^{(n)}right]}
such that {displaystyle inf _{xin left[x_{i}^{(n)},x_{i+1}^{(n)}right]}f(x)geq f(t_{i}^{(n)})-epsilon .}
Thus,

{displaystyle {begin{aligned}sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&leq &sum _{i=0}^{N^{(n)}-1}left(inf _{xin left[x_{i}^{(n)},x_{i+1}^{(n)}right]}f(x)+epsilon right)(x_{i+1}^{(n)}-x_{i}^{(n)})& \&=&sum _{i=0}^{N^{(n)}-1}inf _{xin left[x_{i}^{(n)},x_{i+1}^{(n)}right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+sum _{i=0}^{N-1}epsilon (x_{i+1}^{(n)}-x_{i}^{(n)})\&=&sum _{i=0}^{N^{(n)}-1}inf _{xin left[x_{i}^{(n)},x_{i+1}^{(n)}right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+epsilon (b-a).end{aligned}}}

Let {displaystyle epsilon =1/n(b-a)}, we have

{displaystyle {begin{aligned}sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})&leq &sum _{i=0}^{N^{(n)}-1}inf _{xin left[x_{i}^{(n)},x_{i+1}^{(n)}right]}f(x)(x_{i+1}^{(n)}-x_{i}^{(n)})+{frac {1}{n}}\&=&L_{f,P^{(n)}}+{frac {1}{n}}end{aligned}}}

Taking limits of both sides,

{displaystyle {begin{aligned}R_{f}=sum _{i=0}^{N^{(n)}-1}f(t_{i})(x_{i+1}^{(n)}-x_{i}^{(n)})leq lim _{nto infty }L_{f,P^{(n)}}+lim _{nto infty }{frac {1}{n}}=lim _{nto infty }L_{f,P^{(n)}}.end{aligned}}}

Similarly, (with a different sequences of tags)

{displaystyle {begin{aligned}R_{f}geq lim _{nto infty }U_{f,P^{(n)}}.end{aligned}}}

Thus, we have

{displaystyle R_{f}leq lim _{nto infty }L_{f,P^{(n)}}leq lim _{nto infty }U_{f,P^{(n)}}leq R_{f},}

which means that the Darboux integral exist and equals R_{f}.

See also[edit]

  • Regulated integral
  • Lebesgue integration
  • Minimum bounding rectangle

Notes[edit]

  1. ^ David J. Foulis; Mustafa A. Munem (1989). After Calculus: Analysis. Dellen Publishing Company. p. 396. ISBN 978-0-02-339130-9.
  2. ^ Spivak, M. (1994). Calculus (3rd. edition). Houston, TX: Publish Or Perish, Inc. pp. 253–255. ISBN 0-914098-89-6.
  3. ^ Rudin, W. (1976). Principles of Mathematical Analysis (3rd. edition). New York: McGraw-Hill. pp. 120–122. ISBN 007054235X.
  4. ^ Wolfram MathWorld
  5. ^ Spivak 2008, chapter 13.

References[edit]

  • “Darboux Integral”. Wolfram MathWorld. Retrieved 2013-01-08.
  • Darboux integral at Encyclopaedia of Mathematics
  • “Darboux sum”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
  • Spivak, Michael (2008), Calculus (4 ed.), Publish or Perish, ISBN 978-0914098911
  • “Equivalence of Darboux and Riemann integral”.[dead YouTube link]
Источник

Добавить комментарий