|
0 / 0 / 0 Регистрация: 15.04.2012 Сообщений: 2 |
|
|
1 |
|
[КуМир] Нерекурсивное для нахождения НОД четырёх натуральных чисел22.03.2015, 10:59. Показов 5307. Ответов 1
Составить программу для нахождения наибольшего общего делителя четырёх натуральных чисел. программа должна быть нерекурсивной. я сделала рекурсивно, не могу понять как переделать, чтоб она не зацикливалась. Код алг нач цел а, в, с, д цел НОД вывод 'Введите четыре натуральных числа: ' ввод а, в, с, д НОД:=Евклида (а, в) НОД:=Евклида (НОД, с) НОД:=Евклида (НОД, д) вывод НОД кон алг цел Евклида (цел а, в) дано а>0 и в>0 надо нач если а=1 или в=1 то знач:=1 иначе если а>в то знач:=Евклида (а-в, в) иначе если в>а то знач:= Евклида (а, в-а) иначе знач:=а все все все кон
0 |
|
841 / 604 / 211 Регистрация: 24.07.2013 Сообщений: 2,101 |
|
|
22.03.2015, 12:08 |
2 |
|
Алгоритм Евклида для нахождения НОД: Код алг цел НОД(цел a, цел b) нач цел k, l, m k := a l := b нц пока l <> 0 m := mod(k, l) k := l l := m кц знач := k кон
0 |
Конечно, вот пример программы на языке Кумир, реализующей алгоритм Евклида для вычисления наибольшего общего делителя (НОД) двух чисел:
Алгоритм Евклида для вычисления НОД(a, b):
1. Если b = 0, то вернуть a как результат (НОД(a, 0) = a)
2. Иначе, вычислить остаток от деления a на b, и присвоить его переменной r (r = a % b)
3. Вызвать рекурсивно алгоритм Евклида для пары (b, r), и вернуть полученный результат.Алгоритм Евклида на Кумире:
Модуль Математика
Ввод a, b: ЦелоеЧисло
Вывод "Введите два числа a и b: "
Ввод a, b
Вывод "НОД чисел ", a, " и ", b, " = ", НОД(a, b)
Конец
Эта программа использует рекурсивный подход алгоритма Евклида для нахождения НОД двух чисел. Пользователь вводит значения a и b, после чего программа вызывает функцию НОД(a, b), которая рекурсивно вычисляет НОД с помощью алгоритма Евклида и возвращает результат. Результат выводится на экран.

Программирование на алгоритмическом языке (7 класс)
- Введение
- Ветвления
- Сложные условия
- Циклы
- Циклы с переменной
- Графика
- Вспомогательные алгоритмы
- Анимация
- Случайные числа

Программирование на алгоритмическом языке
Тема 1. Введение

Алгоритм
Алгоритм – это четко определенный план решения задачи для исполнителя.
Свойства алгоритма
- дискретность : состоит из отдельных шагов (команд) понятность : должен включать только команды, известные исполнителю конечность : позволяет получить решение задачи за конечное число шагов определенность : при одинаковых исходных данных всегда выдает один и тот же результат массовость : может применяться при различных исходных данных
- дискретность : состоит из отдельных шагов (команд)
- понятность : должен включать только команды, известные исполнителю
- конечность : позволяет получить решение задачи за конечное число шагов
- определенность : при одинаковых исходных данных всегда выдает один и тот же результат
- массовость : может применяться при различных исходных данных

Программа
Программа – это
- алгоритм, записанный на каком-либо языке программирования набор команд для исполнителя
- алгоритм, записанный на каком-либо языке программирования
- набор команд для исполнителя
Команда – это описание действий, которые должен выполнить исполнитель.
- откуда взять исходные данные? что нужно с ними сделать?
- откуда взять исходные данные?
- что нужно с ними сделать?

Простейшая программа
название алгоритма
алг Первый
нач | начало алгоритма
кон | конец алгоритма
комментарии после | не обрабатываются
?
Что делает эта программа ?
5

5
Вывод текста на экран
алг Вывод на экран
нач
вывод “2+”
вывод “2=?” , нс
вывод “Ответ: 4”
кон
новая строка
Протокол :
2+2=?
Ответ: 4
5

Задания
«4»: Вывести на экран текст «лесенкой»
Вася
пошел
гулять
«5»: Вывести на экран рисунок из букв
Ж
ЖЖЖ
ЖЖЖЖЖ
ЖЖЖЖЖЖЖ
HH HH
ZZZZZ
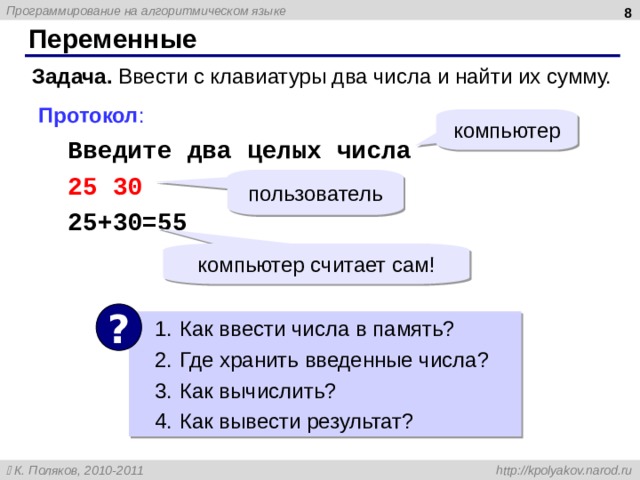
Переменные
Задача. Ввести с клавиатуры два числа и найти их сумму.
Протокол :
Введите два целых числа
25 30
25+30=55
компьютер
пользователь
компьютер считает сам!
?
- Как ввести числа в память?
- Где хранить введенные числа ?
- Как вычислить?
- Как вывести результат?
8
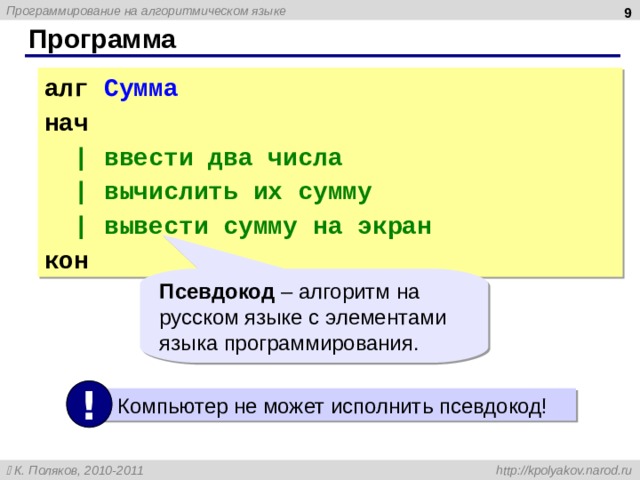
Программа
алг Сумма
нач
| ввести два числа
| вычислить их сумму
| вывести сумму на экран
кон
Псевдокод – алгоритм на русском языке с элементами языка программирования.
!
Компьютер не может исполнить псевдокод!
9
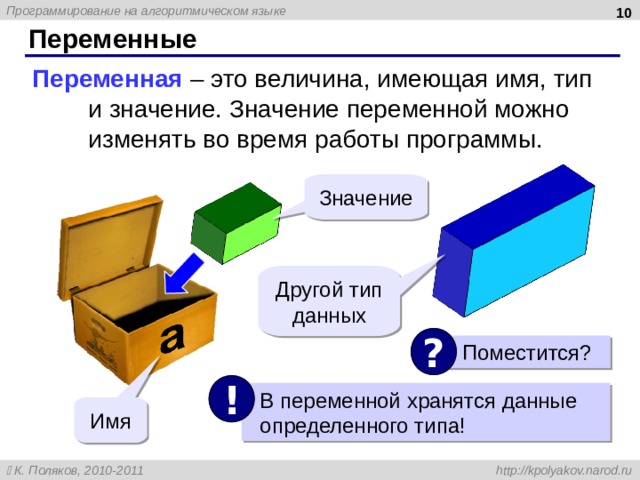
9
Переменные
Переменная – это величина, имеющая имя, тип и значение. Значение переменной можно изменять во время работы программы.
Значение
Другой тип данных
?
Поместится?
!
В переменной хранятся данные определенного типа!
Имя
10
![Имена переменных МОЖНО использовать латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _ латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _ заглавные и строчные буквы различаются имя не может начинаться с цифры Какие имена правильные? AXby R&B 4Wheel Вася “PesBarbos” TU154 [QuQu] _ABBA A+B](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img10.jpg)
Имена переменных
МОЖНО использовать
- латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _
- латинские буквы ( A-Z) , русские буквы (А-Я)
- цифры
- знак подчеркивания _
заглавные и строчные буквы различаются
имя не может начинаться с цифры
Какие имена правильные?
AXby R&B 4Wheel Вася “PesBarbos” TU154 [QuQu] _ABBA A+B
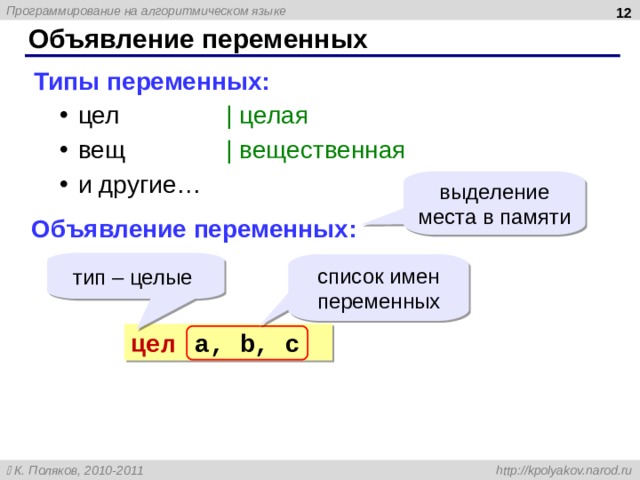
Объявление переменных
Типы переменных:
- цел | целая вещ | вещественная и другие…
- цел | целая
- вещ | вещественная
- и другие…
выделение места в памяти
Объявление переменных:
тип – целые
список имен переменных
цел a, b, c

Как записать значение в переменную?
Оператор присваивания
!
При записи нового значения старое стирается!
5
a := 5
Оператор – это команда языка программирова-ния (инструкция).
Оператор присваивания – это команда для записи нового значения в переменную.
13
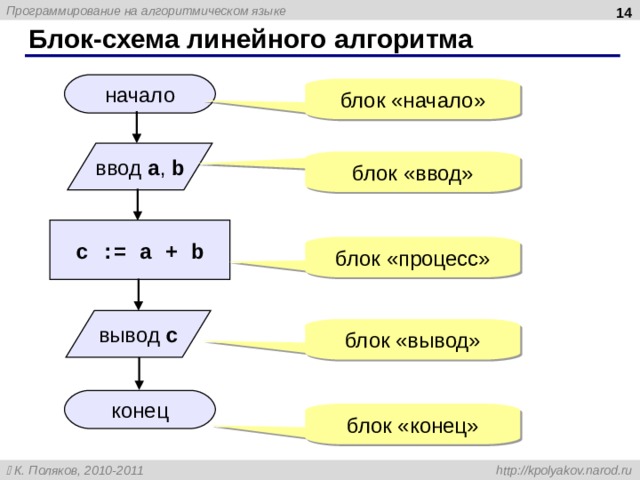
Блок-схема линейного алгоритма
начало
блок «начало»
ввод a , b
блок «ввод»
c := a + b
блок «процесс»
вывод c
блок «вывод»
конец
блок «конец»
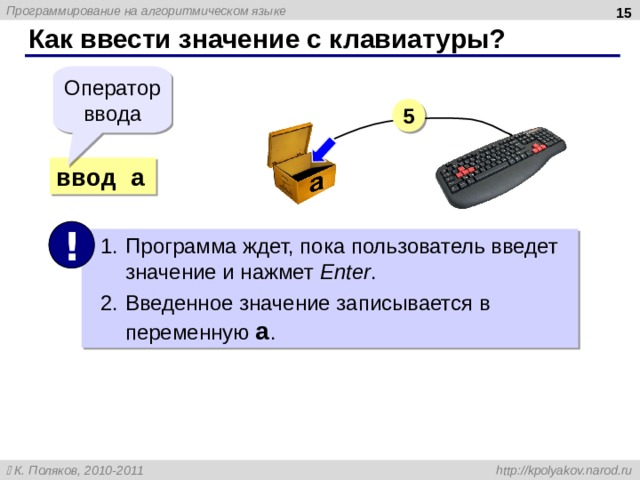
Как ввести значение с клавиатуры?
Оператор ввода
5
ввод a
!
- Программа ждет, пока пользователь введет значение и нажмет Enter .
- Введенное значение записывается в переменную a .
15

Ввод значений двух переменных
Ввод значений двух переменных .
ввод a, b
через пробел:
25 30
через запятую:
25,30
a
25
b
30
a
25
b
30
16
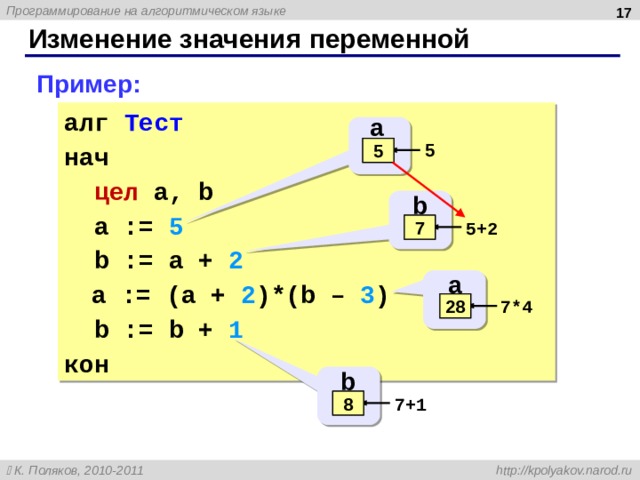
Изменение значения переменной
Пример:
алг Тест
нач
цел a, b
a := 5
b := a + 2
a := (a + 2 )*(b – 3 )
b := b + 1
кон
a
5
?
5
b
?
5+2
7
a
7*4
28
5
b
7
7+1
8

Арифметические операции
+ сложение – вычитание
* умножение / деление
- + сложение – вычитание * умножение / деление
цел a, b
- цел a, b
a := 7 * 3 – 4
a := a * 5
- a := 7 * 3 – 4 a := a * 5

Вывод данных
| вывод значения | переменной a
вывод a
| вывод значения | переменной a и переход | на новую строчку
вывод a , нс
| вывод текста
вывод ‘ Привет! ‘
вывод ‘ Ответ: ‘ , c
| вывод текста и значения переменной c
вывод a, ‘+’ , b, ‘=’ , c

Задача: сложение чисел
Задача. Ввести два целых числа и вывести на экран их сумму.
Простое решение:
алг Сумма
нач
цел a, b, c
ввод a, b
c := a + b
вывод c
кон
?
Что плохо?
20
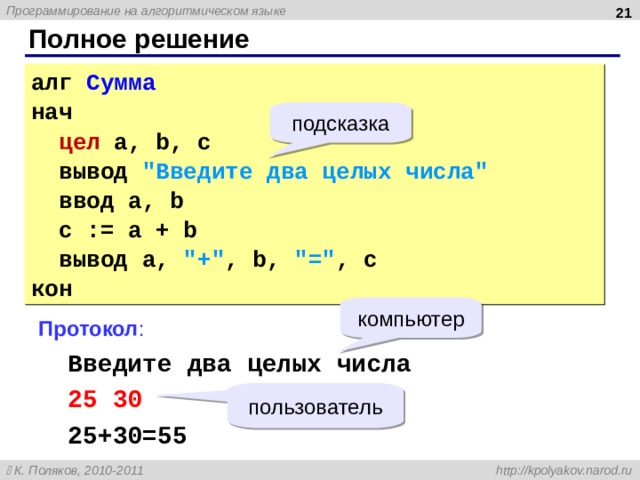
Полное решение
алг Сумма
нач
цел a, b, c
вывод “Введите два целых числа”
ввод a, b
c := a + b
вывод a, “+” , b, “=” , c
кон
подсказка
компьютер
Протокол :
Введите два целых числа
25 30
25+30=55
пользователь

Задания
«3»: Ввести три числа, найти их сумму.
Пример:
Введите три числа:
4 5 7
4+5+7=16
«4»: Ввести три числа, найти их сумму и произведение.
Пример:
Введите три числа:
4 5 7
4+5+7=16
4*5*7=140
Задания
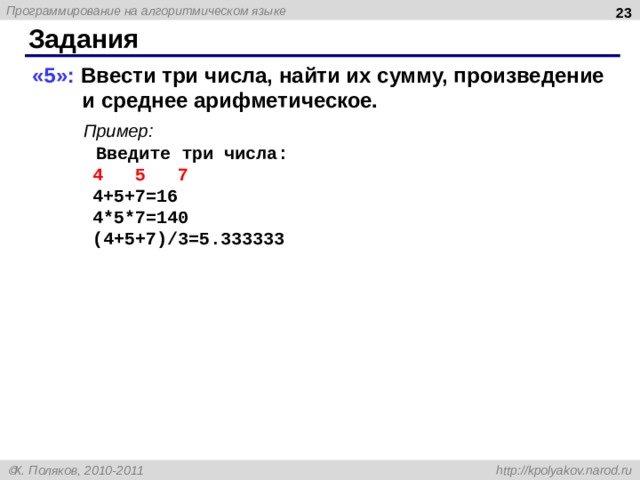
«5»: Ввести три числа, найти их сумму, произведение и среднее арифметическое.
Пример:
Введите три числа:
4 5 7
4+5+7=16
4*5*7=140
(4+5+7) / 3 =5.33 3333

Какие операторы неправильные?
алг Ошибки
нач
цел a, b
вещ x, y
a := 5
10 := x
y := 7 , 8
b := 2.5
x := 2 *(a + y)
a := b + x
кон
имя переменной должно быть слева от знака :=
целая и дробная часть отделяются точкой
нельзя записывать вещественное значение в целую переменную

Арифметические операции
+ сложение – вычитание
* умножение / деление
div деление нацело (остаток отбрасывается)
mod остаток от деления
- + сложение – вычитание * умножение / деление div деление нацело (остаток отбрасывается) mod остаток от деления
цел a, b
- цел a, b
a := 7 * 3 – 4 | 17
a := a * 5 | 85
b := div ( a, 10 ) | 8
a := mod (a, 10 ) | 5
- a := 7 * 3 – 4 | 17 a := a * 5 | 85 b := div ( a, 10 ) | 8 a := mod (a, 10 ) | 5

Порядок выполнения операций
- вычисление выражений в скобках умножение, деление, div , mod слева направо сложение и вычитание слева направо
- вычисление выражений в скобках
- умножение, деление, div , mod слева направо
- сложение и вычитание слева направо
1 2 4 5 3 6
- 1 2 4 5 3 6
z := ( 5 *a+c)/a*(b-c)/ b
- z := ( 5 *a+c)/a*(b-c)/ b
2 3 5 4 1 10 6 9 8 7
- 2 3 5 4 1 10 6 9 8 7
x:= ( 5 *c*c-d*(a+b))/((c+d)*(d- 2 *a))
- x:= ( 5 *c*c-d*(a+b))/((c+d)*(d- 2 *a))

Ручная прокрутка программы
алг Тест
нач
цел a, b
a := 5
b := a + 2
a := (a + 2 )*(b – 3 )
b := div (a, 5 )
a := mod (a,b)
a := a + 1
b := mod (a+ 14 , 7 )
кон
a
b
?
?
5
7
28
5
3
4
4

Команда «вывод»
цел a = 1, b = 3
вывод a, “+” , b, “=” , a+b
список вывода
- элементы разделяются запятыми элементы в кавычках – выводятся без изменений выражения (элементы без кавычек) вычисляются и выводится их результат
- элементы разделяются запятыми
- элементы в кавычках – выводятся без изменений
- выражения (элементы без кавычек) вычисляются и выводится их результат
?
Что будет выведено?
1+3=4
28
 ” , b, ” !” 4 3! цел a = 1, b = 3 вывод ” F( ” , b, ” ) = X( ” , a, ” )” F(3) = X(1) ” width=”640″
” , b, ” !” 4 3! цел a = 1, b = 3 вывод ” F( ” , b, ” ) = X( ” , a, ” )” F(3) = X(1) ” width=”640″
Что будет выведено?
цел a = 1, b = 3
вывод ” a +” , b, “= a+b ”
a +3= a+b
цел a = 1, b = 3
вывод a , “= F( ” , b, ” )”
1= F(3)
цел a = 1, b = 3
вывод ” a = F( ” , b, ” );”
a = F(3);
цел a = 1, b = 3
вывод a+b , ” ” , b, ” !”
4 3!
цел a = 1, b = 3
вывод ” F( ” , b, ” ) = X( ” , a, ” )”
F(3) = X(1)
 f( ” , b , ” ) ” f(1)f(3) цел a = 1, b = 3 вывод ” ” , b , ” ” 3 цел a = 1, b = 3 вывод a , ” + ” , b, ” =? ” 1+3 = ? ” width=”640″
f( ” , b , ” ) ” f(1)f(3) цел a = 1, b = 3 вывод ” ” , b , ” ” 3 цел a = 1, b = 3 вывод a , ” + ” , b, ” =? ” 1+3 = ? ” width=”640″
Как записать оператор «вывод»?
цел a = 1, b = 3
вывод ” X( ” , b, ” ) =” , a
X(3)=1
цел a = 1, b = 3
вывод a + b, ” = ” , a , ” + ” , b
4=1+ 3
цел a = 1, b = 3
вывод ” f( ” , a , ” )f( ” , b , ” ) ”
f(1)f(3)
цел a = 1, b = 3
вывод ” ” , b , ” ”
3
цел a = 1, b = 3
вывод a , ” + ” , b, ” =? ”
1+3 = ?

Программирование на алгоритмическом языке
Тема 2. Ветвления

Разветвляющиеся алгоритмы
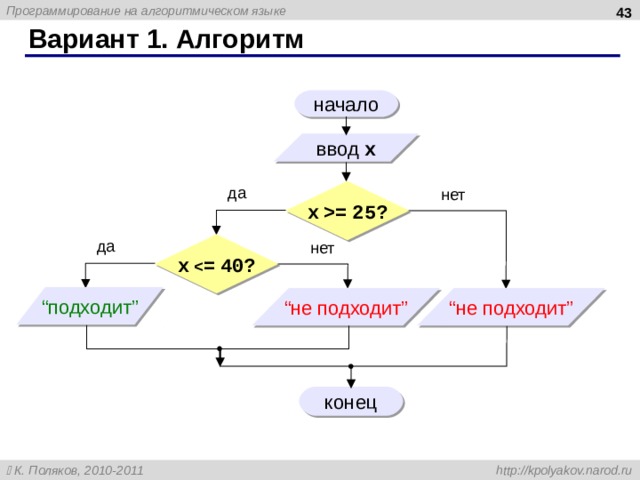
Задача. Ввести два целых числа и вывести на экран наибольшее из них.
Идея решения: надо вывести на экран первое число, если оно больше второго, или второе, если оно больше первого.
Особенность: действия исполнителя зависят от некоторых условий ( если … иначе … ).
Алгоритмы, в которых последовательность шагов зависит от выполнения некоторых условий, называются разветвляющимися.
 b? M:= a M:= b вывод M ? Если a = b? конец 33 ” width=”640″
b? M:= a M:= b вывод M ? Если a = b? конец 33 ” width=”640″
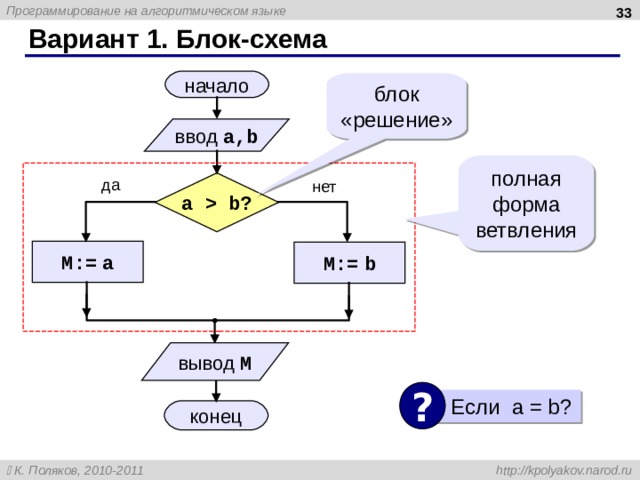
Вариант 1. Блок-схема
начало
блок «решение»
ввод a,b
полная форма ветвления
да
нет
a b?
M:= a
M:= b
вывод M
?
Если a = b?
конец
33
 b то иначе все вывод “Наибольшее число “, M кон полная форма условного оператора M:=a M:=b 33 ” width=”640″
b то иначе все вывод “Наибольшее число “, M кон полная форма условного оператора M:=a M:=b 33 ” width=”640″
33
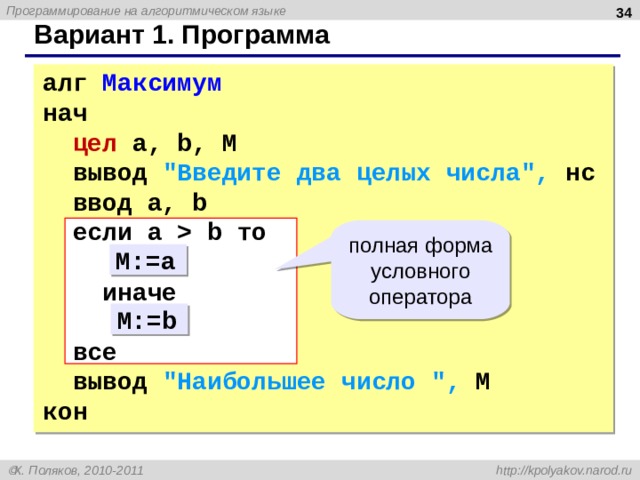
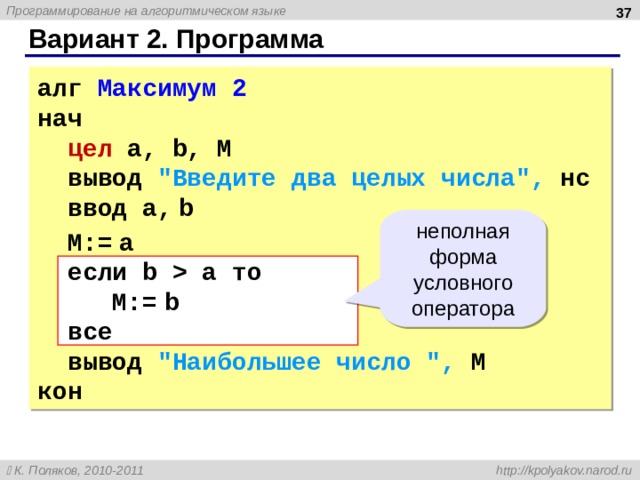
Вариант 1. Программа
алг Максимум нач цел a, b, M вывод “Введите два целых числа”, нс ввод a, b если a b то иначе все вывод “Наибольшее число “, M кон
полная форма условного оператора
M:=a
M:=b
33

33
Условный оператор
если условие то
| что делать, если условие верно
иначе
| что делать, если условие неверно
все
!
Вторая часть (иначе) может отсутствовать!
35
 a? M:= b вывод M конец ” width=”640″
a? M:= b вывод M конец ” width=”640″
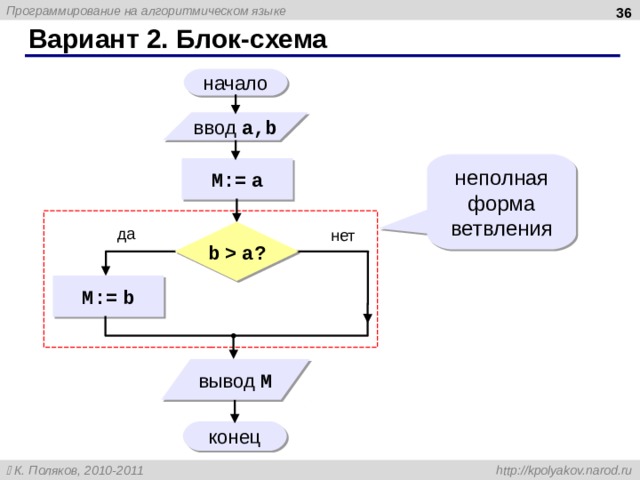
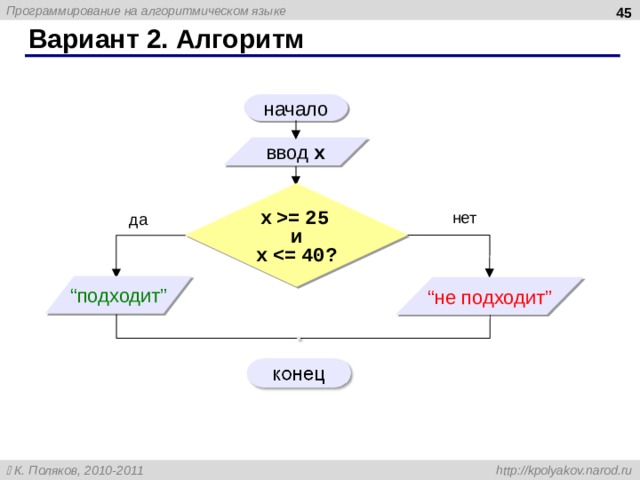
Вариант 2 . Блок-схема
начало
ввод a,b
неполная форма ветвления
M:= a
да
нет
b a?
M:= b
вывод M
конец
 a то M:= b все вывод “Наибольшее число “, M кон неполная форма условного оператора ” width=”640″
a то M:= b все вывод “Наибольшее число “, M кон неполная форма условного оператора ” width=”640″
Вариант 2. Программа
алг Максимум 2 нач цел a, b, M вывод “Введите два целых числа”, нс ввод a, b
M:= a если b a то M:= b все вывод “Наибольшее число “, M кон
неполная форма условного оператора
 b M:= a ” width=”640″
b M:= a ” width=”640″
Вариант 2б. Программа
алг Максимум 2 б нач цел a, b, M вывод “Введите два целых числа”, нс ввод a, b
M:= b если ??? то ??? все вывод “Наибольшее число “, M кон
a b
M:= a

Задания
« 3 »: Ввести два числа и вывести их в порядке возрастания.
Пример:
Введите два числа:
15 9
Ответ: 9 15
«4»: Ввести три числа и найти наибольшее из них.
Пример:
Введите три числа:
4 15 9
Наибольшее число 15

Задания
«5»: Ввести пять чисел и найти наибольшее из них.
Пример:
Введите пять чисел:
4 15 9 56 4
Наибольшее число 5 6

Программирование на алгоритмическом языке
Тема 3. Сложные условия

Сложные условия
Задача. Фирма набирает сотрудников от 25 до 40 лет включительно. Ввести возраст человека и определить, подходит ли он фирме (вывести ответ «подходит» или «не подходит» ) .
Особенность: надо проверить, выполняются ли два условия одновременно.
?
Можно ли решить известными методами ?
42
 = 25? да нет x “ подходит ” “ не подходит ” “ не подходит ” конец ” width=”640″
= 25? да нет x “ подходит ” “ не подходит ” “ не подходит ” конец ” width=”640″
42
Вариант 1. Алгоритм
начало
ввод x
да
нет
x = 25?
да
нет
x
“ подходит ”
“ не подходит ”
“ не подходит ”
конец
 = 25 то если x вывод “Подходит!” иначе вывод “Не подходит.” все иначе вывод “Не подходит.” все кон ” width=”640″
= 25 то если x вывод “Подходит!” иначе вывод “Не подходит.” все иначе вывод “Не подходит.” все кон ” width=”640″
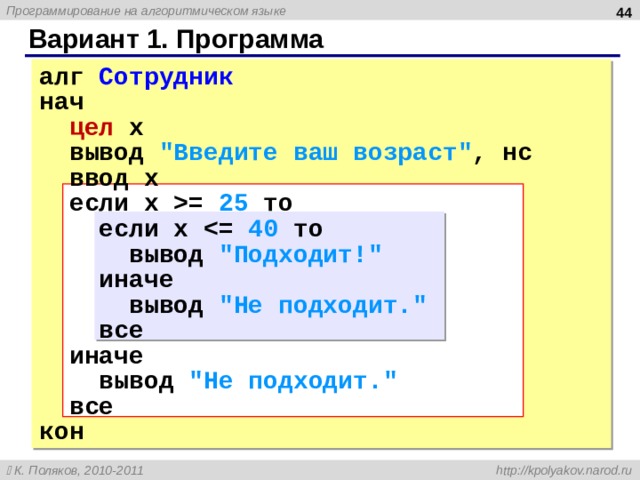
Вариант 1. Программа
алг Сотрудник
нач
цел x
вывод “Введите ваш возраст” , нс
ввод x
если x = 25 то
если x
вывод “Подходит!”
иначе
вывод “Не подходит.”
все
иначе
вывод “Не подходит.”
все
кон
 = 25 и x нет да “ подходит ” “ не подходит ” ” width=”640″
= 25 и x нет да “ подходит ” “ не подходит ” ” width=”640″
Вариант 2. Алгоритм
начало
ввод x
x = 25 и
x
нет
да
“ подходит ”
“ не подходит ”
 = 25 и x вывод “Подходит!” иначе вывод “Не подходит.” все кон сложное условие ” width=”640″
= 25 и x вывод “Подходит!” иначе вывод “Не подходит.” все кон сложное условие ” width=”640″
Вариант 2 . Программа
алг Сотрудник
нач
цел x
вывод “Введите ваш возраст” , нс
ввод x
если x = 25 и x
вывод “Подходит!”
иначе
вывод “Не подходит.”
все
кон
сложное условие
 = = Сложное условие – это условие, состоящее из нескольких простых условий (отношений), связанных с помощью логических операций : И – одновременное выполнение условий И – одновременное выполнение условий x = 25 И x x = 25 И x ИЛИ – выполнение хотя бы одного из условий ИЛИ – выполнение хотя бы одного из условий x ИЛИ x = 40 x ИЛИ x = 40 НЕ – отрицание, обратное условие НЕ – отрицание, обратное условие НЕ ( x 25 ) ??? НЕ ( x 25 ) ??? равно не равно x ” width=”640″
= = Сложное условие – это условие, состоящее из нескольких простых условий (отношений), связанных с помощью логических операций : И – одновременное выполнение условий И – одновременное выполнение условий x = 25 И x x = 25 И x ИЛИ – выполнение хотя бы одного из условий ИЛИ – выполнение хотя бы одного из условий x ИЛИ x = 40 x ИЛИ x = 40 НЕ – отрицание, обратное условие НЕ – отрицание, обратное условие НЕ ( x 25 ) ??? НЕ ( x 25 ) ??? равно не равно x ” width=”640″
Сложные условия
Простые условия (отношения)
= =
Сложное условие – это условие, состоящее из нескольких простых условий (отношений), связанных с помощью логических операций :
- И – одновременное выполнение условий
- И – одновременное выполнение условий
x = 25 И x
- x = 25 И x
- ИЛИ – выполнение хотя бы одного из условий
- ИЛИ – выполнение хотя бы одного из условий
x ИЛИ x = 40
- x ИЛИ x = 40
- НЕ – отрицание, обратное условие
- НЕ – отрицание, обратное условие
НЕ ( x 25 ) ???
- НЕ ( x 25 ) ???
равно
не равно
x
 =, =, И ИЛИ НЕ , =, =, И ИЛИ Пример 2 1 6 3 5 4 если не (a 2 ) или c 5 и b то … все если не (a 2 ) или c 5 и b то … все ” width=”640″
=, =, И ИЛИ НЕ , =, =, И ИЛИ Пример 2 1 6 3 5 4 если не (a 2 ) или c 5 и b то … все если не (a 2 ) или c 5 и b то … все ” width=”640″
Сложные условия
Порядок выполнения (приоритет = старшинство )
- выражения в скобках
- выражения в скобках
- НЕ , =, =, И ИЛИ
- НЕ
- , =, =,
- И
- ИЛИ
Пример
2 1 6 3 5 4
если не (a 2 ) или c 5 и b то
…
все
- если не (a 2 ) или c 5 и b то … все
 b) не (a b) a и b a c или b c a и b c a c и b d a и b a c или b c a и b c a c и b d не (a = b) или c = d не (a = b) или c = d a = b или не (c a c или b c или b a a = b или не (c a c или b c или b a Да Да Нет Нет Нет Да Да Да ” width=”640″
b) не (a b) a и b a c или b c a и b c a c и b d a и b a c или b c a и b c a c и b d не (a = b) или c = d не (a = b) или c = d a = b или не (c a c или b c или b a a = b или не (c a c или b c или b a Да Да Нет Нет Нет Да Да Да ” width=”640″
Сложные условия
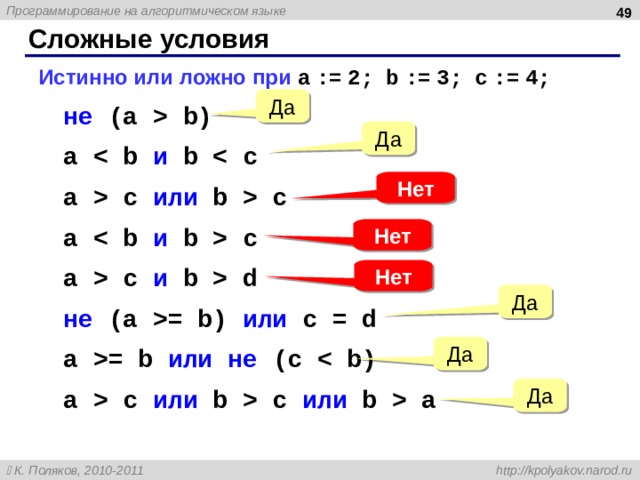
Истинно или ложно при a := 2; b := 3; c := 4;
не (a b)
- не (a b)
a и b
a c или b c
a и b c
a c и b d
- a и b a c или b c a и b c a c и b d
не (a = b) или c = d
- не (a = b) или c = d
a = b или не (c
a c или b c или b a
- a = b или не (c a c или b c или b a
Да
Да
Нет
Нет
Нет
Да
Да
Да
 10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10 x и x x и x 10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10 x нет таких 6 x 10 x все x x 6 ” width=”640″
10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10 x и x x и x 10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10 x нет таких 6 x 10 x все x x 6 ” width=”640″
Сложные условия
Для каких значений x истинны условия:
x и x
x и x 10
x 6 и x
x 6 и x 10
x или x
x или x 10
x 6 или x
x 6 или x 10
- x и x x и x 10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10
x
нет таких
6
x 10
x
все x
x 6

Задания
«3»: Ввести три числа и определить, верно ли, что они вводились в порядке возрастания.
Пример:
Введите три числа:
4 5 17
да
«4»: Ввести номер месяца и вывести название времени года.
Пример:
Введите номер месяца:
4
весна

Задания
«5»: Ввести возраст человека (от 1 до 150 лет) и вывести его вместе с последующим словом «год», «года» или «лет».
Пример:
Введите возраст: Введите возраст:
24 57
Вам 24 года Вам 57 лет

Программирование на алгоритмическом языке
Тема 4. Циклы

Циклы
Цикл – это многократное выполнение одинаковых действий.
- цикл с известным числом шагов цикл с неизвестным числом шагов (цикл с условием)
- цикл с известным числом шагов
- цикл с неизвестным числом шагов (цикл с условием)
Задача. Вывести на экран 5 раз слово «Привет».
Особенность: одинаковые действия выполняются 5 раз.
?
Можно ли решить известными методами ?
54
Циклы
алг Привет
нач
вывод “Привет” , нс
вывод “Привет” , нс
вывод “Привет” , нс
вывод “Привет” , нс
вывод “Привет” , нс
кон
?
Что плохо ?
55

Циклы
алг Привет
нач
нц 5 раз
вывод “Привет!” , нс
кц
кон
тело цикла
начало цикла
вывод “Привет!” , нс
конец цикла
?
Как выглядит блок-схема ?
56
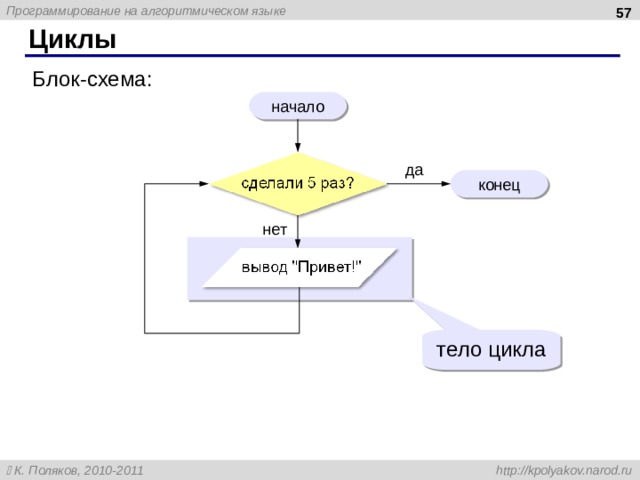
Циклы
Блок-схема:
начало
да
конец
нет
тело цикла

Число шагов – переменная
Задача: ввести количество повторения с клавиатуры.
алг Привет
нач
цел N
вывод “Сколько раз?” , нс
ввод N
нц N раз
вывод “Привет!” , нс
кц
кон

Задания
«3»: Ввести натуральное число и вывести в строчку все числа от 1 до этого числа.
Пример:
Введите натуральное число:
4
Ответ: 1 2 3 4
«4»: Ввести два целых числа, найти их произведение, не используя операцию умножения.
Пример:
Введите два числа:
4 15
4*15=60

Задания
«5»: Ввести натуральное число N и найти сумму всех чисел от 1 до N ( 1+2+3+…+ N ).
Пример:
Введите число слагаемых:
100
Сумма чисел от 1 до 100 равна 5050

Циклы
алг Привет
нач
нц 5 раз
вывод “Привет!” , нс
кц
кон
?
Как отсчитать ровно 5 раз ?
?
Как запоминать, сколько раз уже сделали ?
N := N + 1
61
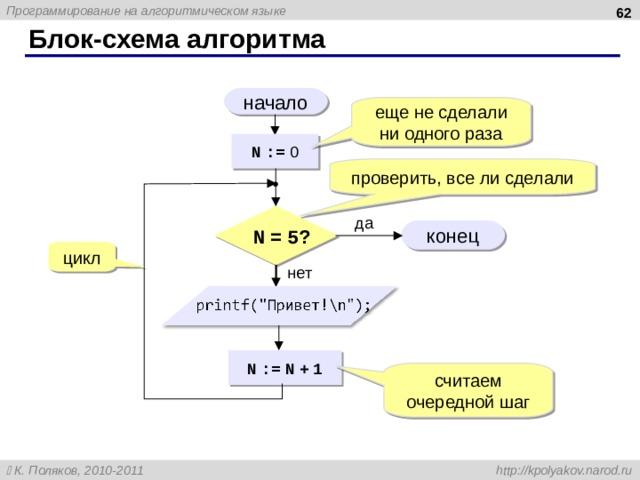
61
Блок-схема алгоритма
начало
еще не сделали ни одного раза
N := 0
проверить, все ли сделали
N = 5 ?
да
конец
цикл
нет
N := N + 1
считаем очередной шаг
61

Цикл с условием
алг Привет 2
нач
цел N
N:= 0
нц пока N 5
вывод “Привет!” , нс
N:= N + 1
кц
кон

Цикл с условием
Вместо знаков вопроса добавьте числа и операторы так, чтобы цикл выполнился ровно 5 раз:
алг Привет 3
нач
цел N
N: = 5
нц пока N ???
вывод “Привет!” , нс
???
кц
кон
0
N:= N – 1
Что получим?
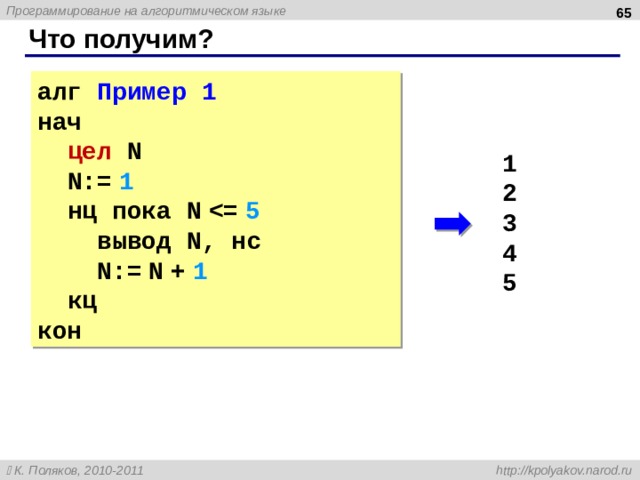
алг Пример 1
нач
цел N
N:= 1
нц пока N
вывод N , нс
N:= N + 1
кц
кон
1
2
3
4
5
Что получим?
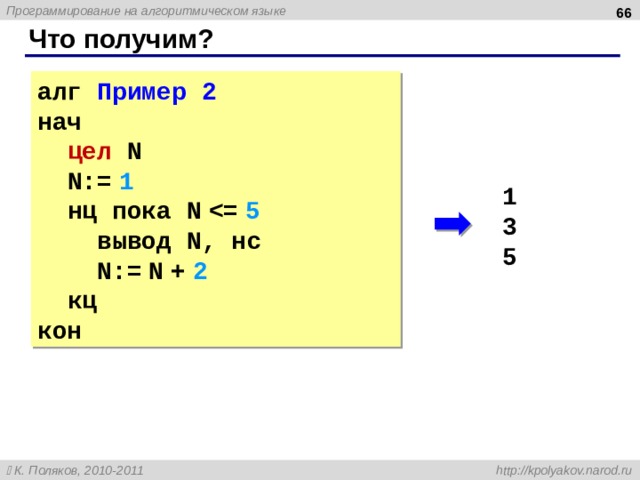
алг Пример 2
нач
цел N
N:= 1
нц пока N
вывод N , нс
N:= N + 2
кц
кон
1
3
5

Что получим?
алг Пример 3
нач
цел N
N:= 2
нц пока N 5
вывод N , нс
N:= N + 2
кц
кон
2
4
6
8
10
12
14
16
…
!
Условие цикла никогда не станет ложным – это зацикливание !
67
Что получим?
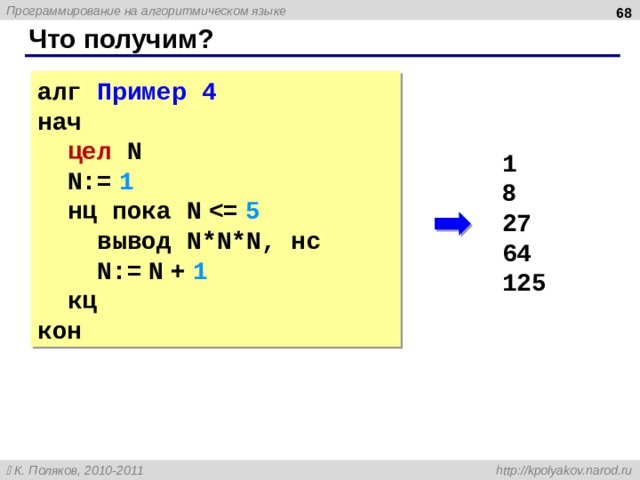
алг Пример 4
нач
цел N
N:= 1
нц пока N
вывод N * N*N , нс
N:= N + 1
кц
кон
1
8
27
64
125
 = 1 вывод N * N*N , нс N:= N – 1 кц кон 1 25 64 27 8 1 ” width=”640″
= 1 вывод N * N*N , нс N:= N – 1 кц кон 1 25 64 27 8 1 ” width=”640″
Что получим?
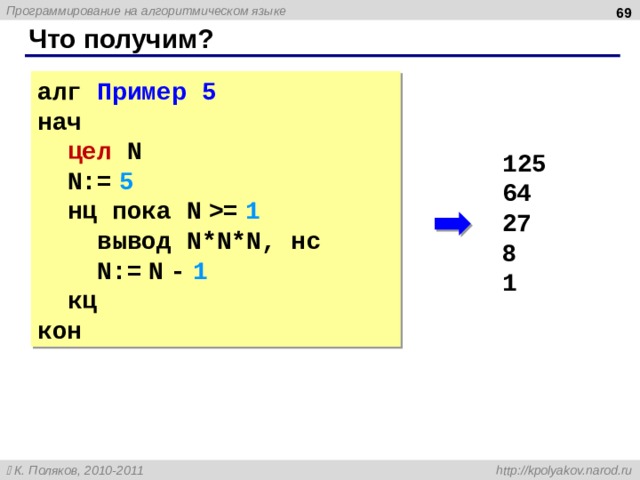
алг Пример 5
нач
цел N
N:= 5
нц пока N = 1
вывод N * N*N , нс
N:= N – 1
кц
кон
1 25
64
27
8
1

Задания
«3»: Ввести натуральное число вывести квадраты и кубы всех чисел от 1 до этого числа.
Пример:
Введите натуральное число:
3
1: 1 1
2: 4 8
3: 9 27
«4»: Ввести два целых числа a и b ( a ≤ b ) и вывести квадраты все чисел от a до b .
Пример:
Введите два числа:
4 5
4*4=16
5*5=25

Задания
«5»: Ввести два целых числа a и b ( a ≤ b ) и вывести сумму квадратов всех чисел от a до b .
Пример:
Введите два числа:
4 10
Сумма квадратов 371

Циклы с условием
Пример: Отпилить полено от бревна. Сколько раз надо сделать движения пилой?
Задача: Ввести целое число (
Идея решения: Отсекаем последовательно последнюю цифру, увеличиваем счетчик.
Проблема: Неизвестно, сколько шагов надо сделать.
Решение: Надо остановиться, когда n = 0 , т.е. надо делать «пока n 0 » .
n
123
count
12
0
1
1
0
2
3
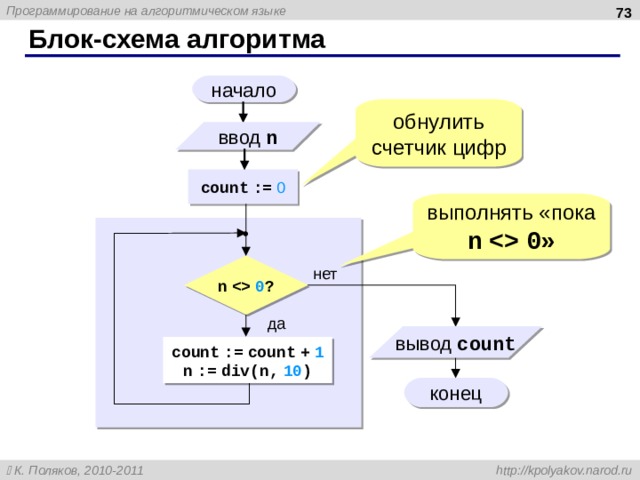
Блок-схема алгоритма
начало
обнулить счетчик цифр
ввод n
count := 0
выполнять «пока n 0 »
n 0 ?
нет
да
вывод count
count := count + 1
n := div(n, 10 )
конец

Программа
алг Число цифр
нач
цел n, count
вывод “Введите целое число” , нс
ввод n
count : = 0
вывод “В числе ” , n, ” нашли ” , c ount , ” цифр”
кон
, n1
; n1:= n
нц пока n 0
count:= count + 1
n:= div (n, 10 )
кц
n1,
?
Что плохо ?
74

Цикл с условием
Особенности:
- можно использовать сложные условия: можно записывать в одну строчку, разделяя команды точкой с запятой:
- можно использовать сложные условия:
- можно записывать в одну строчку, разделяя команды точкой с запятой:
нц пока a 5
a:= a + 5 ; b:= b – 2
кц
a 5
нц пока a
;
75
 b ; a:= a – b кц a:= 4 ; b:= 6 нц пока a ” width=”640″
b ; a:= a – b кц a:= 4 ; b:= 6 нц пока a ” width=”640″
Цикл с условием
Особенности:
- условие пересчитывается при каждом входе в цикл если условие на входе в цикл ложно, цикл не выполняется ни разу если условие никогда не станет ложным, программа зацикливается
- условие пересчитывается при каждом входе в цикл
- если условие на входе в цикл ложно, цикл не выполняется ни разу
- если условие никогда не станет ложным, программа зацикливается
a := 4 ; b := 6
нц пока a b ; a:= a – b кц
a:= 4 ; b:= 6
нц пока a
 b ; a:= a + 1 кц 1 раз b = -2 a:= 4 ; b:= 6 нц пока a зацикливание a:= 4 ; b:= 6 нц пока a ” width=”640″
b ; a:= a + 1 кц 1 раз b = -2 a:= 4 ; b:= 6 нц пока a зацикливание a:= 4 ; b:= 6 нц пока a ” width=”640″
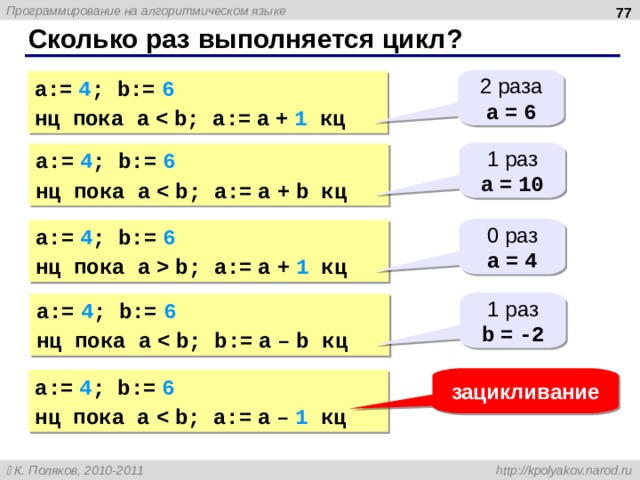
Сколько раз выполняется цикл ?
2 раза
a = 6
a:= 4 ; b:= 6
нц пока a
1 раз
a = 10
a:= 4 ; b:= 6
нц пока a
0 раз
a = 4
a:= 4 ; b:= 6
нц пока a b ; a:= a + 1 кц
1 раз
b = -2
a:= 4 ; b:= 6
нц пока a
зацикливание
a:= 4 ; b:= 6
нц пока a
Задания
«3»: Ввести целое число и определить, верно ли, что в нём ровно 3 цифры.
Пример:
Введите число: Введите число:
123 1234
Да. Нет.
«4»: Ввести целое число и найти сумму его цифр.
Пример:
Введите целое число:
1234
Сумма цифр числа 1234 равна 10.

Задания
«5»: Ввести целое число и определить, верно ли, что в его записи есть две одинаковые цифры , стоящие рядом .
Пример:
Введите целое число: Введите целое число:
1232 1224
Нет. Да.
«6»: Ввести целое число и определить, верно ли, что в его записи есть две одинаковые цифры , НЕ обязательно стоящие рядом.
Пример:
Введите целое число: Введите целое число:
1234 1242
Нет. Да.

Задания -2
«3»: Ввести целое число и определить, верно ли, что в нём ровно 1 цифра «9».
Пример:
Введите число: Введите число:
193 1994
Да. Нет.
«4»: Ввести целое число и определить, верно ли, что все его цифры четные.
Пример:
Введите число: Введите число:
2684 2994
Да. Нет.

Задания -2
«5»: Ввести целое число и определить, верно ли, что все его цифры расположены в порядке возрастания.
Пример:
Введите целое число: Введите целое число:
1238 1274
Да. Нет.
«6»: Ввести целое число и «перевернуть» его, так чтобы первая цифра стала последней и т.д.
Пример:
Введите целое число: Введите целое число:
1234 782
4321 287

Вычисление НОД
НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка.
Перебор:
- Записать в переменную k минимальное из двух чисел.
- Если a и b без остатка делятся на k , то стоп.
- Уменьшить k на 1.
- Перейти к шагу 2.
это цикл с условием!
?
Где будет НОД?
?
Почему алгоритм обязательно закончится?
82

Алгоритм Евклида
Надо : вычислить наибольший общий делитель (НОД) чисел a и b .
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.
НОД( a,b)= НОД( a-b, b)
= НОД( a, b-a)
Евклид
(365-300 до. н. э.)
Пример:
НОД (14 , 21 ) = НОД (14 , 21-14 ) = НОД (14 , 7 )
= НОД (7 , 7 ) = 7
много шагов при большой разнице чисел:
НОД (1998 , 2 ) = НОД (1996 , 2 ) = … = 2
 b? нет да b:=b-a a:=a-b ” width=”640″
b? нет да b:=b-a a:=a-b ” width=”640″
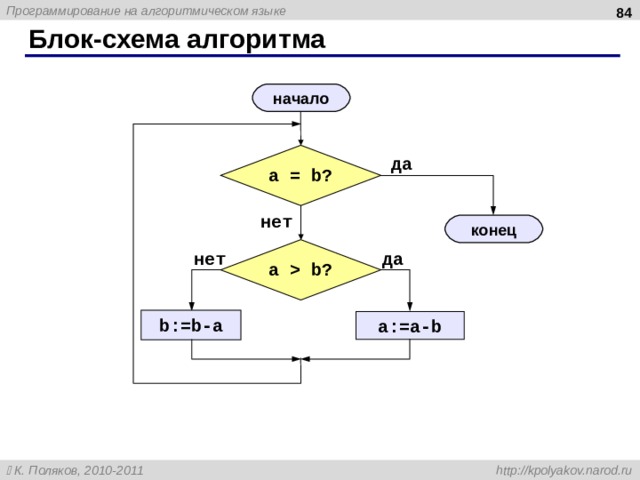
Блок-схема алгоритма
начало
a = b?
да
нет
конец
a b?
нет
да
b:=b-a
a:=a-b
 b то a:= a – b иначе b:= b – a все кц ? Где будет НОД? Как его вывести? ? Как вывести НОД в формате НОД(14,21) = 7? ? А без дополнительных переменных? 85 ” width=”640″
b то a:= a – b иначе b:= b – a все кц ? Где будет НОД? Как его вывести? ? Как вывести НОД в формате НОД(14,21) = 7? ? А без дополнительных переменных? 85 ” width=”640″
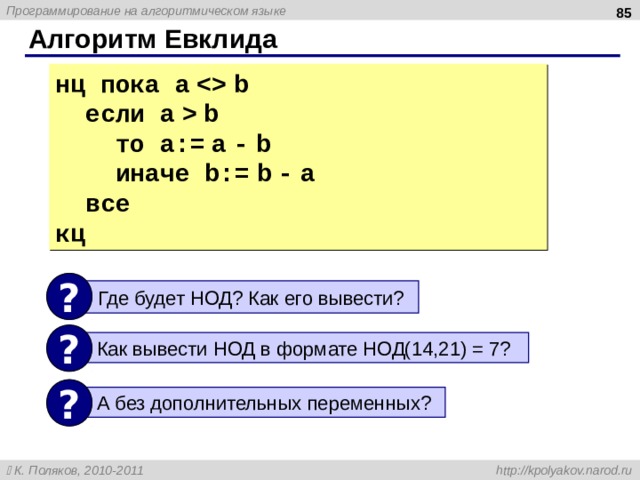
Алгоритм Евклида
нц пока a b
если a b
то a:= a – b
иначе b:= b – a
все
кц
?
Где будет НОД? Как его вывести?
?
Как вывести НОД в формате НОД(14,21) = 7?
?
А без дополнительных переменных?
85

Модифицированный алгоритм Евклида
Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД.
НОД( a,b)= НОД( mod (a,b), b)
= НОД( a, mod (b,a))
Пример:
НОД (14 , 21 ) = НОД (14 , 7 ) = НОД (0 , 7 ) = 7
Еще один вариант:
НОД( 2 · a,2 · b)= 2 · НОД( a, b)
НОД( 2 · a,b)= НОД( a, b) | при нечетном b
Алгоритм Евклида
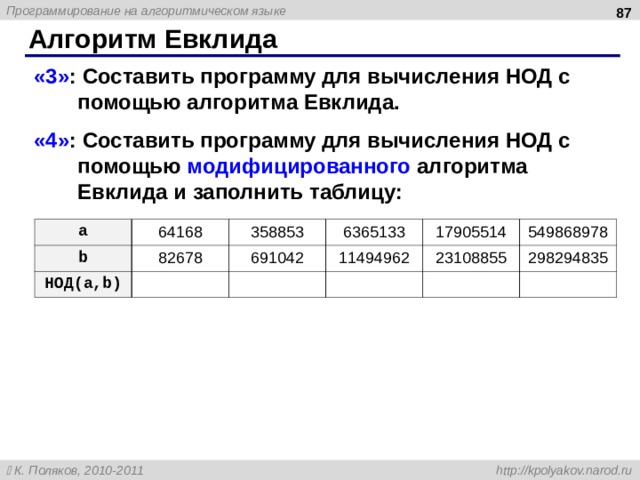
«3» : Составить программу для вычисления НОД с помощью алгоритма Евклида.
« 4 » : Составить программу для вычисления НОД с помощью модифицированного алгоритма Евклида и заполнить таблицу:
a
b
64168
НОД( a,b )
358853
82678
6365133
691042
11494962
17905514
23108855
549868978
298294835
Алгоритм Евклида
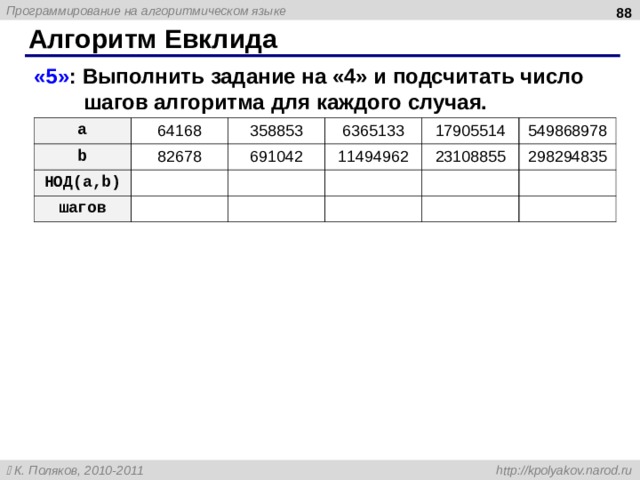
«5» : Выполнить задание на «4» и подсчитать число шагов алгоритма для каждого случая.
a
64168
b
82678
358853
НОД( a,b )
691042
шагов
6365133
11494962
17905514
23108855
549868978
298294835

Программирование на алгоритмическом языке
Тема 5. Циклы с переменной
Цикл с переменной
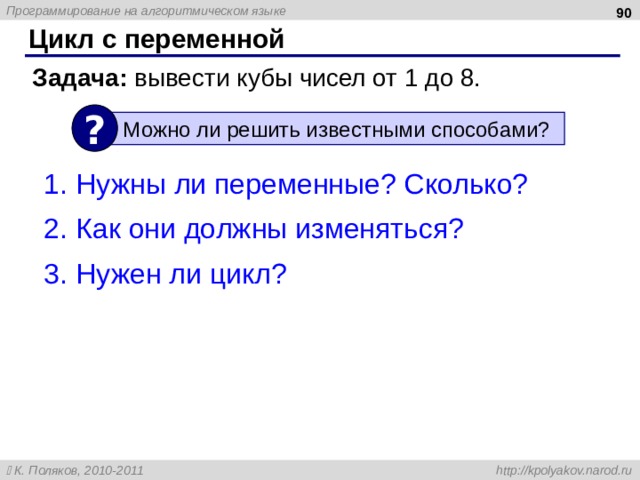
Задача: вывести кубы чисел от 1 до 8.
?
Можно ли решить известными способами ?
- Нужны ли переменные? Сколько?
- Как они должны изменяться?
- Нужен ли цикл?
90
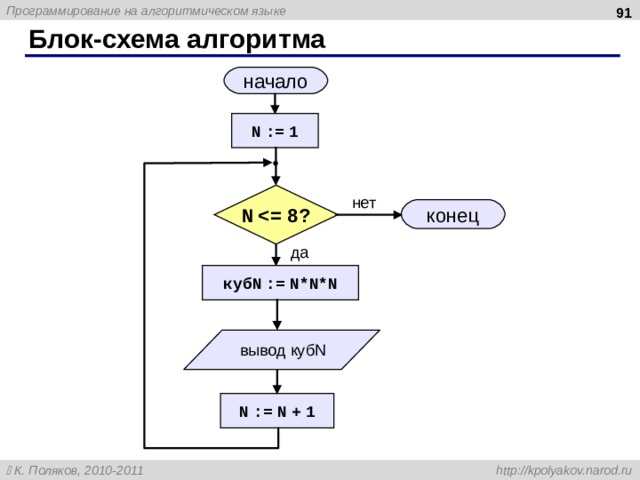
Блок-схема алгоритма
начало
N := 1
N
нет
конец
да
куб N := N*N*N
вывод куб N
N := N + 1
91

Цикл с переменной
Задача: вывести кубы натуральных чисел от 1 до 8.
алг Кубы
нач
цел N, куб N
N:= 1
нц пока N
куб N:= N*N*N
вывод куб N, нс
N:= N + 1
кц
кон
3 действия с N
N:= 1
N
N:= N + 1

Цикл с переменной
Задача: вывести кубы натуральных чисел от 1 до 8.
алг Кубы
нач
цел N, куб N
кон
для 1,2,3,…,8
нц для N от 1 до 8
куб N:= N*N*N
вывод куб N, нс
кц
?
Как обойтись без переменной куб N ?
93

Цикл с переменной
Задача: вывести кубы чётных чисел от 2 до 8.
алг Кубы
нач
цел N, куб N
кон
для 2,4,6,8
нц для N от 2 до 8 шаг 2
куб N:= N*N*N
вывод куб N, нс
кц
только целые !
94

Сколько раз выполняется цикл?
a := 1
нц для i от 1 до 3 ; a:=a+ 1 кц
a = 4
a := 1
нц для i от 3 до 1 ; a:=a+ 1 кц
a = 1
a = 1
a := 1
нц для i от 1 до 3 шаг -1 ; a:=a+ 1 кц
a = 4
a := 1
нц для i от 3 до 1 шаг -1 ; a:=a+ 1 кц
 0 и конечное значение начального, цикл не выполняется ни разу переменная цикла может быть только целой ( цел ) начальное и конечное значения и шаг – целые можно записывать в одну строчку, разделяя команды точкой с запятой: если шаг 0 и конечное значение если шаг начального, цикл не выполняется ни разу нц для n от 1 до 4 вывод n кц ; 96 ” width=”640″
0 и конечное значение начального, цикл не выполняется ни разу переменная цикла может быть только целой ( цел ) начальное и конечное значения и шаг – целые можно записывать в одну строчку, разделяя команды точкой с запятой: если шаг 0 и конечное значение если шаг начального, цикл не выполняется ни разу нц для n от 1 до 4 вывод n кц ; 96 ” width=”640″
Цикл с переменной
Особенности:
- переменная цикла может быть только целой ( цел ) начальное и конечное значения и шаг – целые можно записывать в одну строчку, разделяя команды точкой с запятой: если шаг 0 и конечное значение начального, цикл не выполняется ни разу
- переменная цикла может быть только целой ( цел )
- начальное и конечное значения и шаг – целые
- можно записывать в одну строчку, разделяя команды точкой с запятой:
- если шаг 0 и конечное значение
- если шаг начального, цикл не выполняется ни разу
нц для n от 1 до 4 вывод n кц
;
96
 = b | тело цикла i:= i – 1 кц нц для i от a до b шаг -1 | тело цикла кц Замена цикла для на пока возможна всегда . Замена пока на для возможна только тогда, когда можно заранее вычислить число шагов цикла. ” width=”640″
= b | тело цикла i:= i – 1 кц нц для i от a до b шаг -1 | тело цикла кц Замена цикла для на пока возможна всегда . Замена пока на для возможна только тогда, когда можно заранее вычислить число шагов цикла. ” width=”640″
Замена одного вида цикла на другой
i:= 1
нц пока i
| тело цикла
i:= i + 1
кц
нц для i от 1 до 10
| тело цикла
кц
i:= a
нц пока i = b
| тело цикла
i:= i – 1
кц
нц для i от a до b шаг -1
| тело цикла
кц
Замена цикла для на пока возможна всегда .
Замена пока на для возможна только тогда, когда можно заранее вычислить число шагов цикла.
Задания
«3»: Ввести натуральное число N и вывести числа от N до 1 (через одно) в порядке убывания.
Пример:
Введите натуральное число:
8
Ответ: 8 6 4 2
Задания
«4»: Ввести два целых числа a и b ( a ≤ b ) и вывести кубы всех чисел от a до b .
Пример:
Введите два числа:
4 6
4*4*4=64
5*5*5=125
6*6*6=216
«5»: Ввести целое число a и вывести сумму квадратов всех чисел от 1 до a с шагом 0.1 .
Пример:
Введите последнее число:
3
Сумма 91.7
1 2 + 1.1 2 + 1.2 2 + … + a 2

Задания-2
«4»: Ввести a и b и вывести квадраты и кубы чисел от a до b .
Пример:
Введите границы интервала:
4 6
4 : 16 64
5 : 25 125
6 : 36 216
«5»: Вывести квадраты и кубы 10 чисел следующей последовательности: 1, 2, 4, 7, 11, 16, …
Пример:
1: 1 1
2: 4 8
4: 16 64
…
46: 2116 97336

Программирование на алгоритмическом языке
Тема 6. Графика
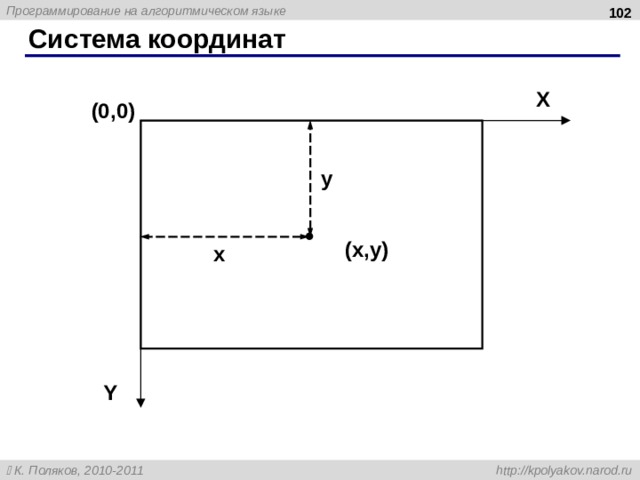
Система координат
X
(0,0)
y
( x , y )
x
Y
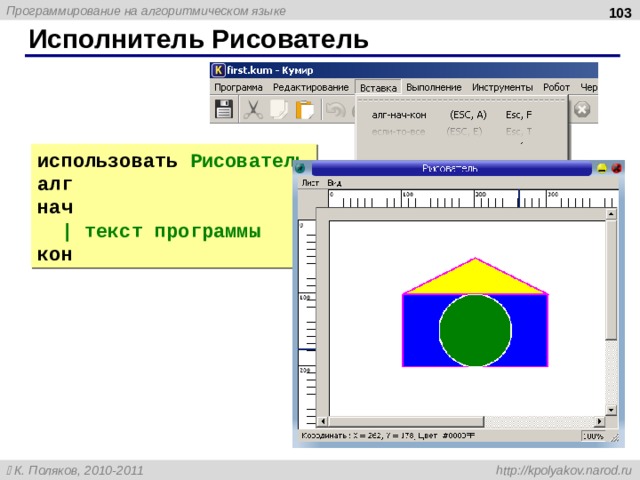
Исполнитель Рисователь
использовать Рисователь
алг
нач
| текст программы
кон

Линии
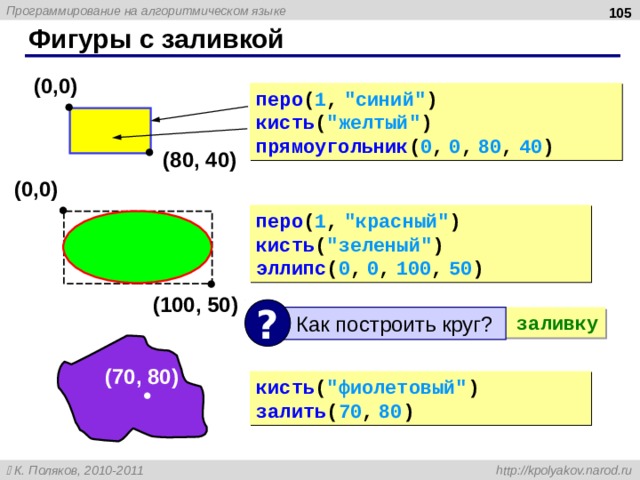
Цвет и толщина линий:
черный
белый
серый
фиолетовый
синий
голубой
зеленый
желтый
оранжевый
красный
толщина линии
перо ( 2 , “синий” )
(10, 15)
перо ( 1 , “зеленый” ) линия ( 10 , 1 5 , 90 , 80 )
(90, 80)
(5,5)
перо ( 1 , “красный“ )
в точку ( 5 , 5 )
линия в точку ( 50 , 5 )
линия в точку ( 70 , 50 )
линия в точку ( 30 , 80 )
линия в точку ( 5 , 60 )
(50,5)
(70, 50)
(5,60 )
(30,80)
104
104
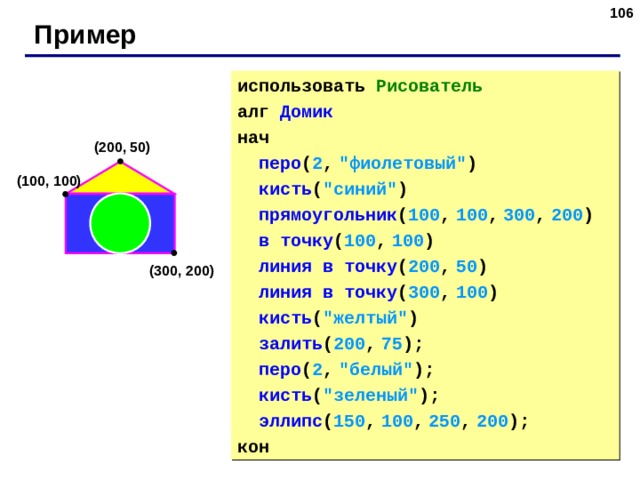
Фигуры с заливкой
(0,0)
перо ( 1 , “синий” )
кисть ( “желтый” )
прямоугольник ( 0 , 0 , 80 , 40 )
(80, 40)
(0,0)
перо ( 1 , “красный” )
кисть ( “зеленый” )
эллипс ( 0 , 0 , 100 , 50 )
(100, 50)
?
кисть ( “” ) ; | отменить заливку
Как построить круг?
(70, 80)
кисть ( “фиолетовый” )
залить ( 70 , 80 )
105
105
Пример
использовать Рисователь
алг Домик
нач
перо ( 2 , “фиолетовый” )
кисть ( “синий” )
прямоугольник ( 100 , 100 , 300 , 200 )
в точку ( 100 , 100 )
линия в точку ( 200 , 50 )
линия в точку ( 300 , 100 )
кисть ( “желтый” )
залить ( 200 , 75 );
перо ( 2 , “белый” );
кисть ( “зеленый” );
эллипс ( 150 , 100 , 250 , 200 );
кон
(200, 50)
(100, 100)
(300, 200)
105
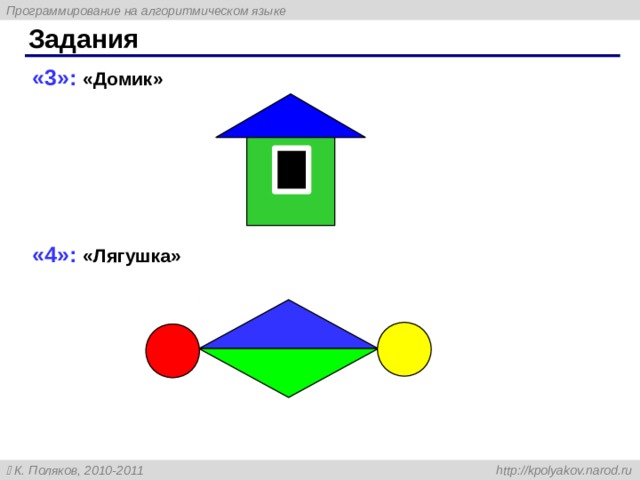
Задания
«3»: «Домик»
«4»: «Лягушка»
107
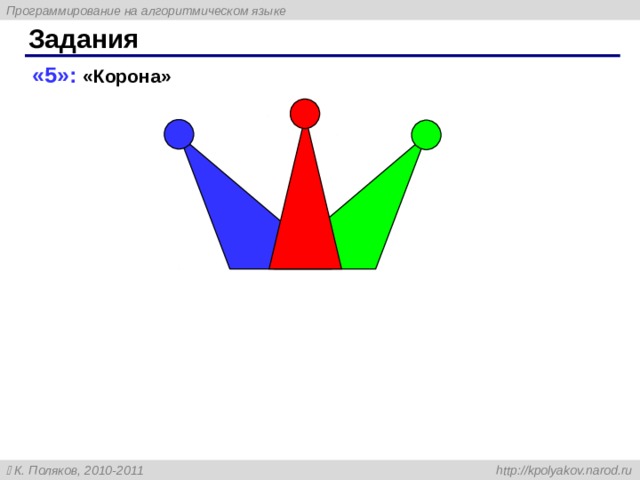
Задания
«5»: «Корона»
108
Штриховка
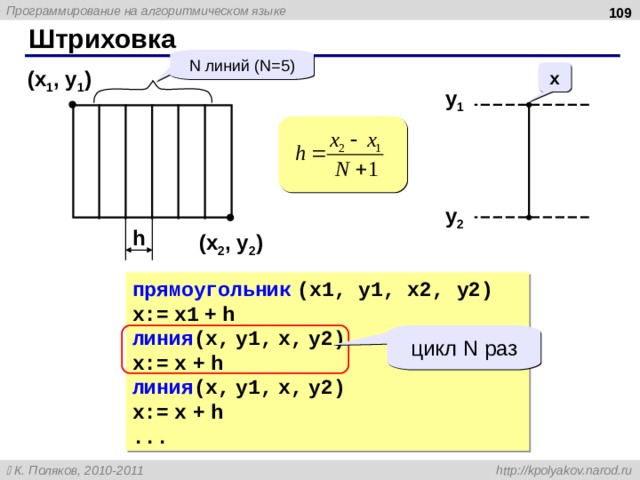
N линий ( N=5)
( x 1 , y 1 )
x
y 1
y 2
h
( x 2 , y 2 )
прямоугольник (x1, y1, x2, y2)
x:= x1 + h
линия (x, y1, x, y2)
x:= x + h
линия (x, y1, x, y2)
x:= x + h
…
цикл N раз

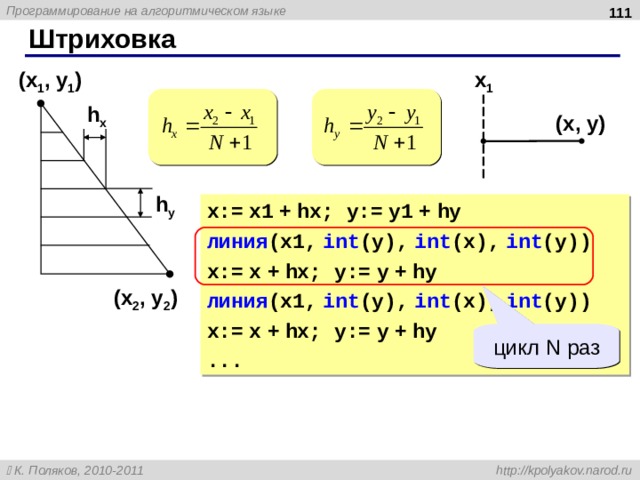
Штриховка (программа)
N
( x 1 , y 1 )
использовать Рисователь
алг Штриховка
нач
цел N = 5 | число линий
цел x1 = 100 , x2 = 300
цел y1 = 100 , y2 = 200
вещ h, x
h:=(x2 – x1)/(N + 1 )
прямоугольник ( x1, y1, x2, y2)
x:= x1 + h
нц N раз
линия ( int (x), y1, int (x), y2)
x:= x + h
кц
кон
вещ h, x
h
( x 2 , y 2 )
?
Почему?
целая часть
110
110
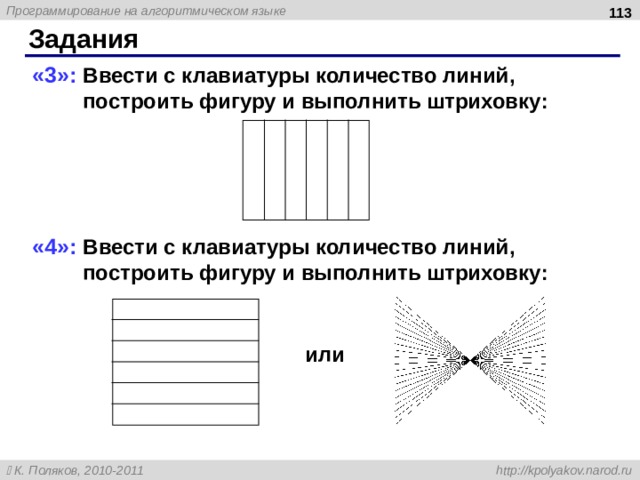
Штриховка
x 1
( x 1 , y 1 )
h x
( x , y )
h y
x:= x1 + hx ; y:= y1 + hy
линия (x1, int (y), int (x), int (y))
x:= x + hx; y:= y + hy
линия (x1, int (y), int (x), int (y))
x:= x + hx; y:= y + hy
…
( x 2 , y 2 )
цикл N раз
111

111
Штриховка
вещ hx, hy, x, y
hx:=(x2 – x1)/(N + 1 )
hy:=(y2 – y1)/(N + 1 )
в точку ( x1, y1)
линия в точку ( x1, y2)
линия в точку ( x2, y2)
линия в точку ( x1, y1)
x:= x1 + hx ; y:= y1 + hy
нц N раз
линия ( x1, int (y), int (x), int (y))
x:= x + hx
y:= y + hy
кц
( x 1 , y 1 )
h x
h y
( x 2 , y 2 )
Задания
« 3 »: Ввести с клавиатуры количество линий , построить фигуру и выполнить штриховку :
«4»: Ввести с клавиатуры количество линий , построить фигуру и выполнить штриховку :
или
113
113
Задания
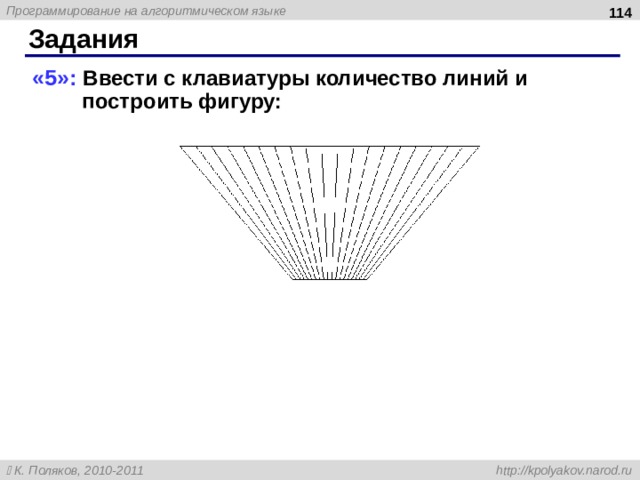
«5»: Ввести с клавиатуры количество линий и построить фигуру:

Программирование на алгоритмическом языке
Тема 7. Вспомогательные алгоритмы

Задача
?
Можно ли решить известными методами ?
Особенность: три похожие фигуры.
общее : размеры, угол поворота
отличия : координаты, цвет
- общее : размеры, угол поворота отличия : координаты, цвет
?
Сколько координат надо задать ?
116

С чего начать?
- найти похожие действия (три фигуры) найти общее (размеры, форма, угол поворота) и отличия (координаты, цвет) отличия = параметры алгоритма (доп. данные)
- найти похожие действия (три фигуры)
- найти общее (размеры, форма, угол поворота) и отличия (координаты, цвет)
- отличия = параметры алгоритма (доп. данные)
цепочка символов
использовать Рисователь
алг Тр ( цел x, y, лит цвет)
нач
в точку (x, y)
линия в точку (x, y- 60 )
линия в точку (x+ 100 , y)
линия в точку (x, y)
кисть (цвет)
залить (x+ 20 , y- 20 )
кон
( x , y -60)
параметры
60
( x , y )
100
( x +100, y )
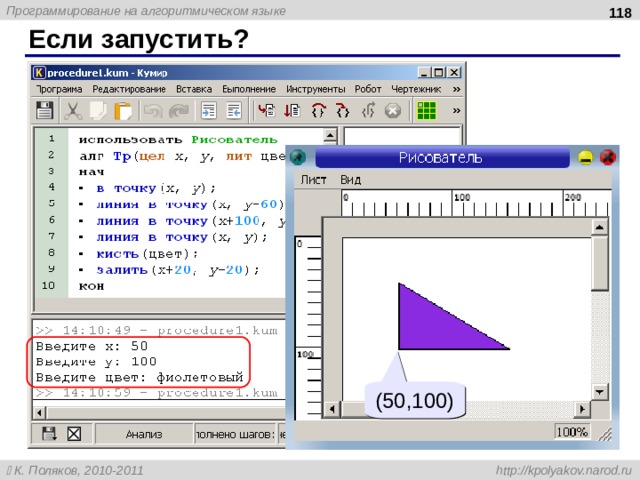
Если запустить?
(50,100)
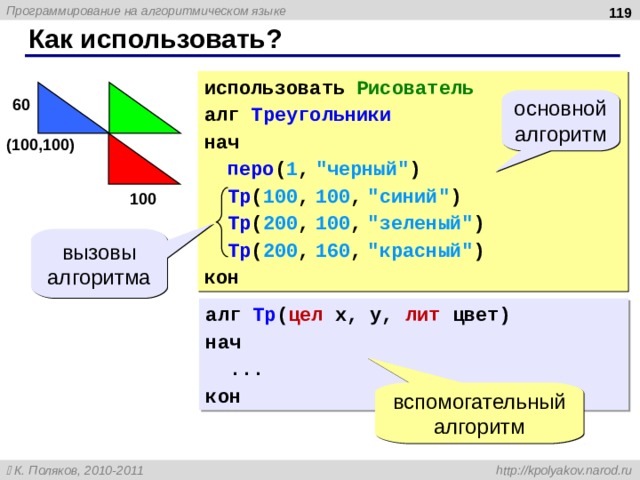
Как использовать?
использовать Рисователь
алг Треугольники
нач
перо ( 1 , “черный” )
Тр ( 100 , 100 , “синий” )
Тр ( 200 , 100 , “зеленый” )
Тр ( 200 , 160 , “красный” )
кон
основной
алгоритм
60
( 100 , 100 )
100
вызовы алгоритма
алг Тр ( цел x, y, лит цвет)
нач
…
кон
вспомогательный
алгоритм
119

Вспомогательные алгоритмы
- расположены ниже основного в заголовке перечисляются формальные параметры, они обозначаются именами для каждого параметра указывают тип однотипные параметры перечисляются через запятую при вызове в скобках указывают фактические параметры в том же порядке
- расположены ниже основного
- в заголовке перечисляются формальные параметры, они обозначаются именами
- для каждого параметра указывают тип
- однотипные параметры перечисляются через запятую
- при вызове в скобках указывают фактические параметры в том же порядке
алг Тр ( цел x, y, лит цвет)
Тр ( 200 , 100 , “зеленый” )
x
цвет
y
Задания
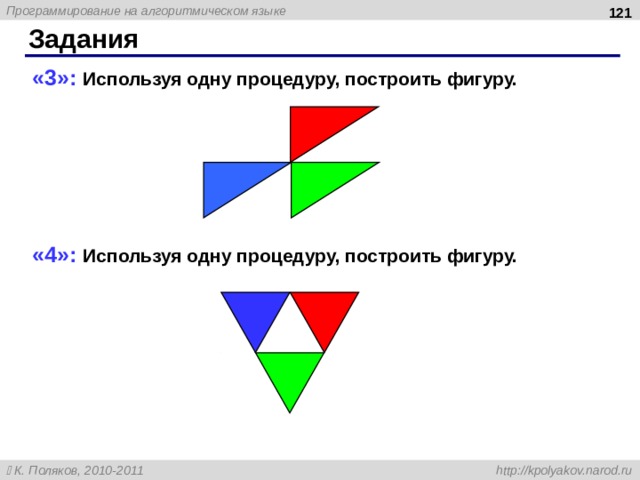
« 3 »: Используя одну процедуру, построить фигуру.
« 4 »: Используя одну процедуру, построить фигуру.
121
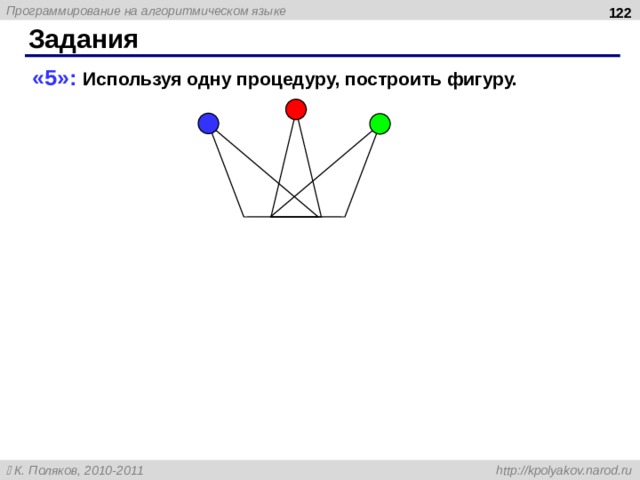
Задания
«5»: Используя одну процедуру, построить фигуру.
122

Рекурсивные объекты
Сказка о поп é и собаке:
Примеры:
У попа была собака, он ее любил.
Она съела кусок мяса, он ее убил.
В ямку закопал, надпись написал:
- У попа была собака, он ее любил. Она съела кусок мяса, он ее убил. В ямку закопал, надпись написал:
Сказка о поп é и собаке
- Сказка о поп é и собаке
Рисунок с рекурсией:
Факториал:
если
если
Рекурсивный объект – это объект, определяемый через один или несколько таких же объектов.
123
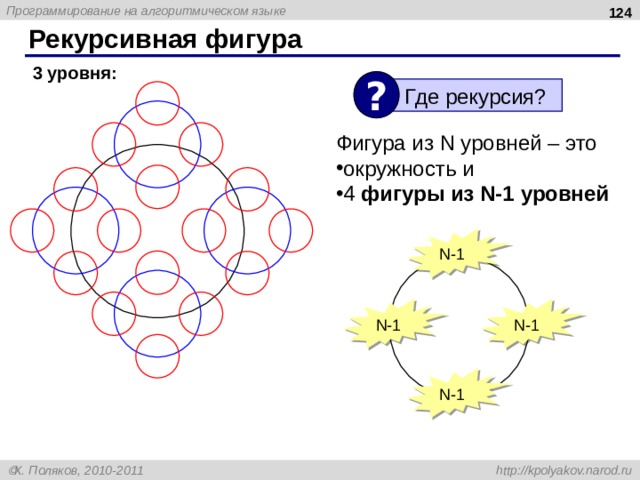
Рекурсивная фигура
3 уровня:
?
Где рекурсия?
Фигура из N уровней – это
- окружность и
- 4 фигуры из N-1 уровней
N-1
N-1
N-1
N-1

Рекурсивная фигура: алгоритм
центр
радиус
уровней
( x , y-R )
алг РекОк ( цел x, y, R, N )
нач
если N
окружность (x, y, R)
РекОк (x, y-R, div (R, 2 ), N – 1 )
РекОк (x+R, y, div (R, 2 ), N – 1 )
РекОк (x, y+R, div (R, 2 ), N – 1 )
РекОк (x-R, y, div (R, 2 ), N – 1 )
кон
( x , y )
( x+R , y )
окончание рекурсии
( x-R , y )
( x , y+R )
рекурсивные вызовы
Рекурсивный алгоритм – это алгоритм, который вызывает сам себя (с другими параметрами!).

Рекурсивная фигура: программа
использовать Рисователь
алг Рекурсия
нач
РекОк (200, 200, 100, 3)
кон
алг РекОк ( цел x, y, R, N )
нач
…
кон

Рекурсивные алгоритмы
- вызывают сами себя прямо … или через другой алгоритм: должно быть условие окончания рекурсии (иначе?) рекурсия может стать бесконечной все задачи могут быть решены без рекурсии, но… часто рекурсивные алгоритмы проще и понятнее как правило, алгоритмы без рекурсии работают быстрее и требуют меньше памяти
- вызывают сами себя прямо
- … или через другой алгоритм:
- должно быть условие окончания рекурсии (иначе?)
- рекурсия может стать бесконечной
- все задачи могут быть решены без рекурсии, но…
- часто рекурсивные алгоритмы проще и понятнее
- как правило, алгоритмы без рекурсии работают быстрее и требуют меньше памяти
A
прямая рекурсия
A
B
косвенная рекурсия
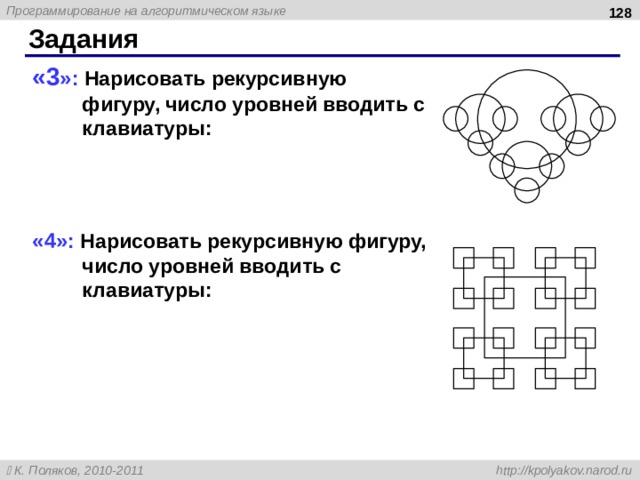
Задания
« 3 » : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
« 4 » : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
128

Задания
«5» : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
129

Программирование на алгоритмическом языке
Тема 8 . Анимация
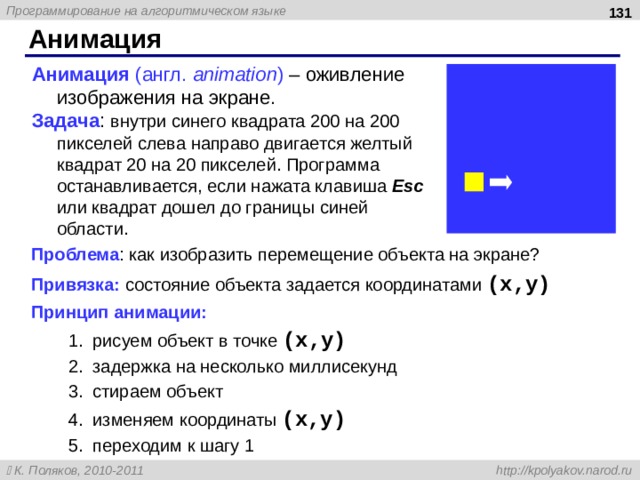
Анимация
Анимация (англ. animation ) – оживление изображения на экране.
Задача : внутри синего квадрата 200 на 200 пикселей слева направо двигается желтый квадрат 20 на 20 пикселей. Программа останавливается, если нажата клавиша Esc или квадрат дошел до границы синей области.
Проблема : как изобразить перемещение объекта на экране?
Привязка: состояние объекта задается координатами ( x,y)
Принцип анимации:
- рисуем объект в точке ( x,y) задержка на несколько миллисекунд стираем объект изменяем координаты ( x,y) переходим к шагу 1
- рисуем объект в точке ( x,y)
- задержка на несколько миллисекунд
- стираем объект
- изменяем координаты ( x,y)
- переходим к шагу 1
131

Процедура (рисование и стирание)
- одна процедура рисует и стирает стереть = рисовать цветом фона границу квадрата отключить
- одна процедура рисует и стирает
- стереть = рисовать цветом фона
- границу квадрата отключить
( x , y )
( x +20, y +20)
рисуем: цвет кисти – желтый
стираем: цвет кисти – синий
алг Фигура ( цел x, y, лит цвет)
нач
кисть (цвет)
прямоугольник (x,y,x+ 20 ,y+ 20 )
кон

Полная программа
использовать Рисователь
алг Анимация
нач
цел x, y | текущие координаты
кисть ( “синий” )
перо (1, “” ) | отключить контур
прямоугольник ( 0 , 0 , 200 , 200 ) | синий фон
x:= 0 ; y:= 100 | начальные координаты
кон
нц пока x
Фигура (x, y, “желтый” )
delay (50)
Фигура (x, y, “синий” )
x:= x + 5
кц
пока не дошли до границы
алг Фигура ( цел x, y, лит цвет)
нач
…
кон

Задания
«3»: Квадрат двигается справа налево:
«4»: Два квадрата двигаются в противоположных направлениях:
134
Задания
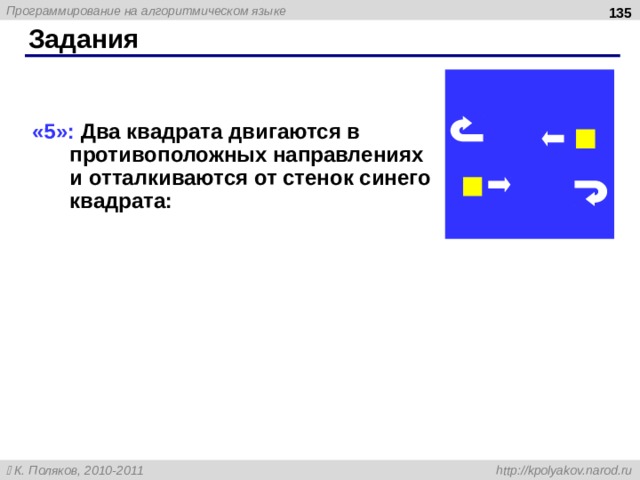
«5»: Два квадрата двигаются в противоположных направлениях и отталкиваются от стенок синего квадрата:

Управление клавишами
Задача : жёлтый квадрат внутри синего квадрата управляется клавишами-стрелками. Коды клавиш:
влево – 16777234 вверх – 16777235
вправо – 16777236 вниз – 16777237
Проблема : как изменять направление движения?
Решение :
ждать нажатия на клавишу, записать ее код в переменную c
c:= клав
выбор
при c = 16777234 : x:= x – 5 | влево
при c = 16777235 : y:= y – 5 | вверх
при c = 16777236 : x:= x + 5 | вправо
при c = 16777237 : y:= y + 5 | вниз
все
?
Когда стирать фигуру?
136
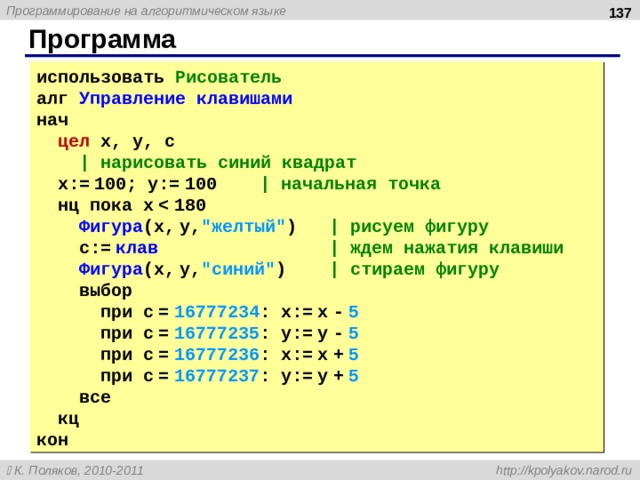
Программа
использовать Рисователь
алг Управление клавишами
нач
цел x, y, c
| нарисовать синий квадрат
x:= 100; y:= 100 | начальная точка
нц пока x
Фигура (x, y, “желтый” ) | рисуем фигуру
c:= клав | ждем нажатия клавиши
Фигура (x, y, “синий” ) | стираем фигуру
выбор
при c = 16777234 : x:= x – 5
при c = 16777235 : y:= y – 5
при c = 16777236 : x:= x + 5
при c = 16777237 : y:= y + 5
все
кц
кон
Задания
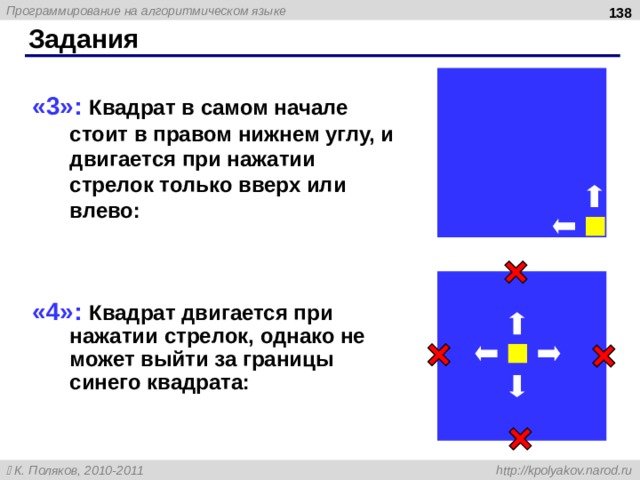
« 3 »: Квадрат в самом начале стоит в правом нижнем углу, и двигается при нажатии стрелок только вверх или влево:
«4»: Квадрат двигается при нажатии стрелок, однако не может выйти за границы синего квадрата:
138
Задания
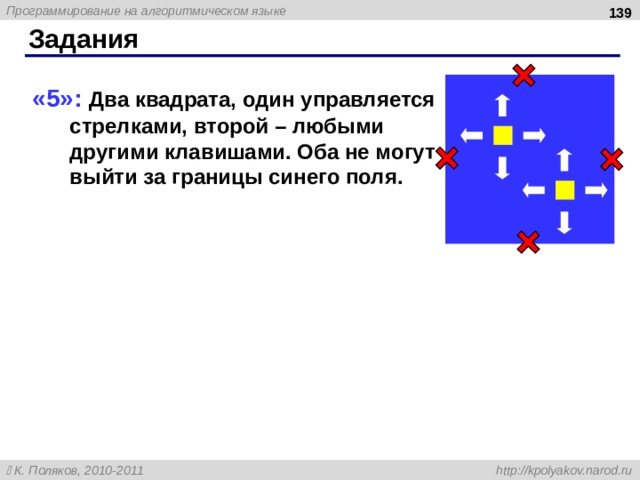
« 5 »: Два квадрата, один управляется стрелками, второй – любыми другими клавишами. Оба не могут выйти за границы синего поля.
139

Программирование на алгоритмическом языке
Тема 9 . Случайные числа

Случайность и ее моделирование
Случайно…
Случайный выбор:
- встретить друга на улице
- разбить тарелку
- найти 10 рублей
- выиграть в лотерею
- жеребьевка на соревнованиях
- выигравшие номера в лотерее
Как получить случайность?

142
Случайные числа на компьютере
Электронный генератор
- нужно специальное устройство
- нельзя воспроизвести результаты
Псевдослучайные числа – обладают свойствами случайных чисел, но каждое следующее число вычисляется по заданной формуле.
Метод середины квадрата (Дж. фон Нейман)
в квадрате
564321
- малый период (последовательность повторяется через 10 6 чисел)
458191
318458191041
209938992481
938992
142
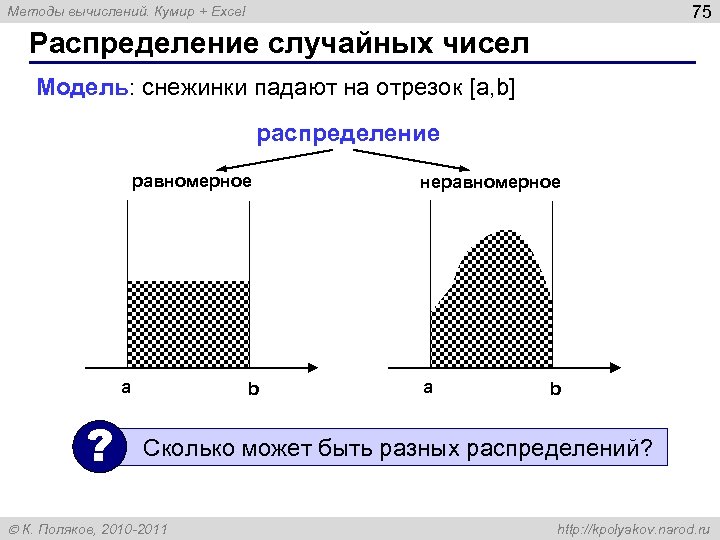
![143 Распределение случайных чисел Модель : снежинки падают на отрезок [a,b] распределение равномерное неравномерное a a b b ? Сколько может быть разных распределений ? 143](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img142.jpg)
143
Распределение случайных чисел
Модель : снежинки падают на отрезок [a,b]
распределение
равномерное
неравномерное
a
a
b
b
?
Сколько может быть разных распределений ?
143
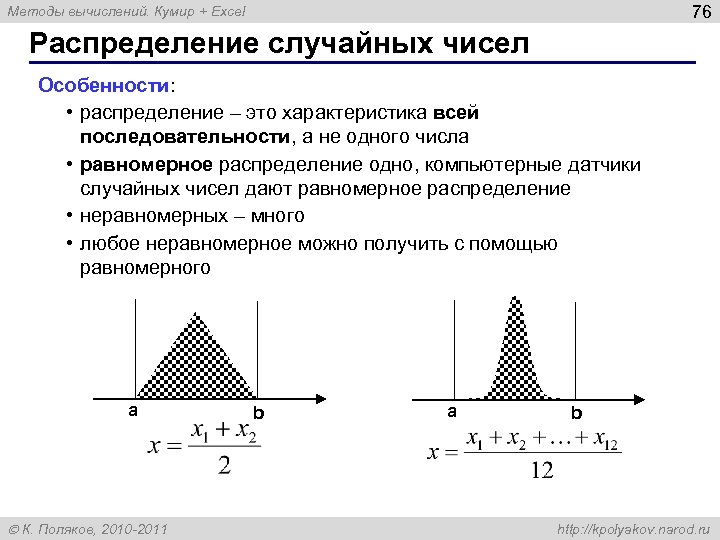
144
Распределение случайных чисел
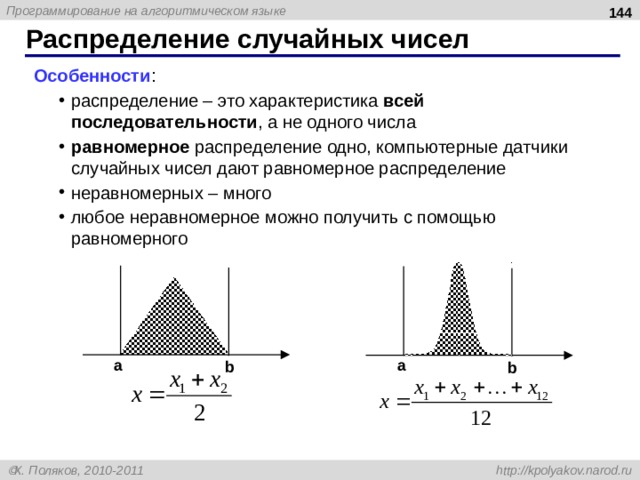
Особенности :
- распределение – это характеристика всей последовательности , а не одного числа равномерное распределение одно, компьютерные датчики случайных чисел дают равномерное распределение неравномерных – много любое неравномерное можно получить с помощью равномерного
- распределение – это характеристика всей последовательности , а не одного числа
- равномерное распределение одно, компьютерные датчики случайных чисел дают равномерное распределение
- неравномерных – много
- любое неравномерное можно получить с помощью равномерного
a
a
b
b
144
![Генератор случайных чисел Вещественные числа в интервале [0, 10 ) : вещ X, Y X:= r a nd ( 0 , 1 0 ) | интервал от 0 до 10 ( Y:= r a nd ( 0 , 1 0 ) | это уже другое число! англ. random – случайный Целые числа в интервале [0,10] : цел K , L K:= ira nd ( 0 , 1 0 ) | интервал от 0 до 10 ( L := ira nd ( 0 , 1 0 ) | это уже другое число! англ. i nteger – целый](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img144.jpg)
Генератор случайных чисел
Вещественные числа в интервале [0, 10 ) :
вещ X, Y
X:= r a nd ( 0 , 1 0 ) | интервал от 0 до 10 (
Y:= r a nd ( 0 , 1 0 ) | это уже другое число!
англ. random – случайный
Целые числа в интервале [0,10] :
цел K , L
K:= ira nd ( 0 , 1 0 ) | интервал от 0 до 10 (
L := ira nd ( 0 , 1 0 ) | это уже другое число!
англ. i nteger – целый
Случайные числа
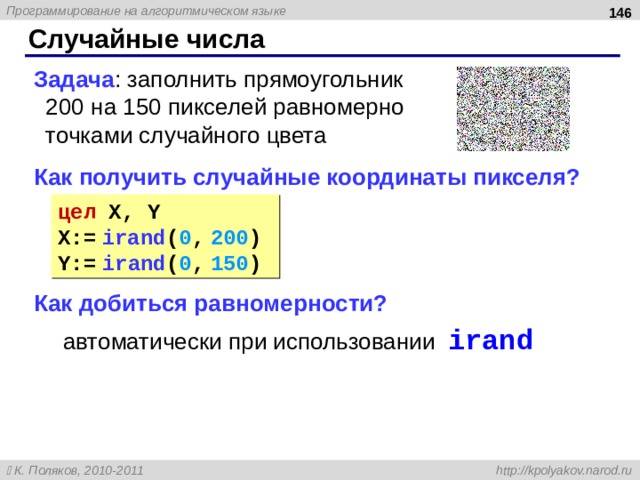
Задача : заполнить прямоугольник 200 на 150 пикселей равномерно точками случайного цвета
Как получить случайные координаты пикселя?
Как добиться равномерности?
автоматически при использовании irand
цел X, Y
X:= ira nd ( 0 , 200 )
Y:= ir a nd ( 0 , 1 5 0 )

Цвет пикселя на мониторе
!
Красный, зелёный и синий лучи создают почти такое же ощущение, как луч «смешанного» цвета!
red : R
green : G
blue : B
Вывод: цвет можно разложить на составляющие (каждая кодируется числом от 0 до 255).
Модель RGB :
R G B
RGB( 255 ,0, 255 )
RGB(0,0,0)
RGB( 255 , 255 , 255 )
RGB( 255 , 255 ,0)
RGB( 255 ,0,0)
RGB( 0 , 255 , 255 )
RGB(0, 255 ,0)
RGB(0,0, 255 )
RGB( 10 0, 10 0, 10 0)

Случайный цвет пикселя
Случайные составляющие цвета:
цел r , g, b
r:= ira nd ( 0 , 255 )
g:= ir a nd ( 0 , 255 )
b:= ir a nd ( 0 , 255 )
это разные числа!
Управление цветом пикселя:
случайный цвет
пиксель ( X , Y, RGB (r,g,b) )
встроенные функции Рисователя

Программа
использовать Рисователь
алг Случайные точки
нач
цел x, y, r, g, b
нц пока да
x:= irand ( 0 , 200 )
y:= irand ( 0 , 100 )
r:= irand ( 0 , 255 )
g:= irand ( 0 , 255 )
b:= irand ( 0 , 255 )
пиксель ( x,y, RGB (r,g,b))
кц
кон
это бесконечный цикл:
нц пока да
…
кц

Задания
«3»: Заполнить квадрат точками случайного цвета. размер квадрата ввести с клавиатуры:
Пример:
Введите размер квадрата:
150
«4»: Заполнить область точками случайного цвета:

Задания
«5»: Заполнить область точками случайного цвета:
или

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики высшей категории ,
ГОУ СОШ № 163, г. Санкт-Петербург
[email protected]

Методы вычислений (Кумир + Excel) 1. 2. 3. 4. 5. 6. Алгоритм Евклида Решение уравнений Оптимизация Восстановление зависимостей Статистика Моделирование К. Поляков, 2010 -2011

Методы вычислений Тема 1. Алгоритм Евклида К. Поляков, 2010 -2011

3 Методы вычислений. Кумир + Excel Вычисление НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка. Перебор: 1. Записать в переменную k минимальное из двух чисел. 2. Если a и b без остатка делятся на k, то стоп. 3. Уменьшить k на 1. 4. Перейти к шагу 2. это цикл с условием! Где ? НОД? будет ? Почему алгоритм обязательно закончится? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

4 Методы вычислений. Кумир + Excel Вычисление НОД (перебор) алг НОД нач цел a, b, k вывод “Введите два целых числа”, нс ввод a, b k: = imin(a, b) | минимальное из a и b нц пока mod(a, k)<>0 или mod(b, k)<>0 k: = k – 1 кц вывод “НОД(“, a, “, “, b, “)=”, k кон много операций для больших чисел К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

5 Методы вычислений. Кумир + Excel Алгоритм Евклида Надо: вычислить наибольший общий делитель (НОД) чисел a и b. Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД(a, b)= НОД(a-b, b) = НОД(a, b-a) Евклид (365 -300 до. н. э. ) Пример: НОД (14, 21) = НОД (14, 21 -14) = НОД (14, 7) = НОД (7, 7) = 7 много шагов при большой разнице чисел: НОД (1998, 2) = НОД (1996, 2) = … = 2 К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
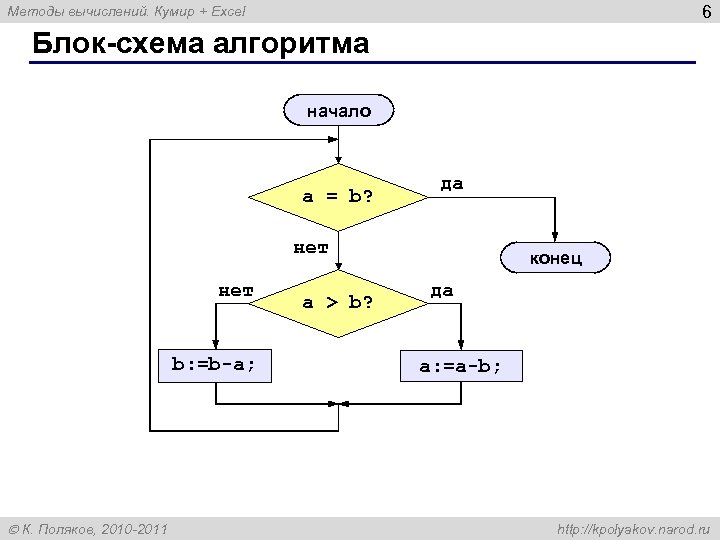
6 Методы вычислений. Кумир + Excel Блок-схема алгоритма начало a = b? да нет b: =b-a; К. Поляков, 2010 -2011 a > b? конец да a: =a-b; http: //kpolyakov. narod. ru

7 Методы вычислений. Кумир + Excel Алгоритм Евклида нц пока a <> b если a > b то a: = a – b иначе b: = b – a все кц ? ? ? Где будет НОД? Как его вывести? Как вывести НОД в формате НОД(14, 21) = 7? А без дополнительных переменных? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

8 Методы вычислений. Кумир + Excel Модифицированный алгоритм Евклида Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД(a, b)= НОД(mod(a, b) = НОД(a, mod(b, a)) Пример: НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7 Еще один вариант: НОД(2·a, 2·b)= 2·НОД(a, b) НОД(2·a, b)= НОД(a, b) | при нечетном b К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
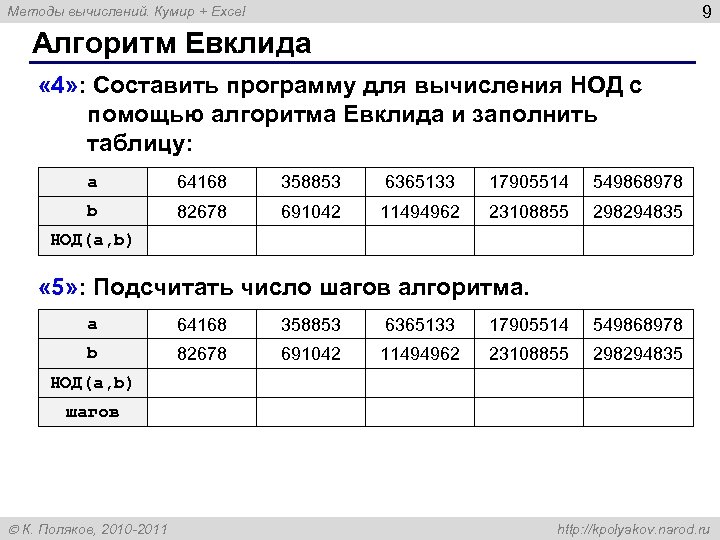
9 Методы вычислений. Кумир + Excel Алгоритм Евклида « 4» : Составить программу для вычисления НОД с помощью алгоритма Евклида и заполнить таблицу: a 64168 358853 6365133 17905514 549868978 b 82678 691042 11494962 23108855 298294835 НОД(a, b) « 5» : Подсчитать число шагов алгоритма. a 64168 358853 6365133 17905514 549868978 b 82678 691042 11494962 23108855 298294835 НОД(a, b) шагов К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

Методы вычислений Тема 2. Решение уравнений К. Поляков, 2010 -2011

11 Методы вычислений. Кумир + Excel Методы решения уравнений f (x) = 0 • Точные (аналитические) • Приближенные • графические y a x* b x • численные (методы последовательного приближения): 1) по графику найти интервал [a, b], в котором находится x* (или одно начальное приближение x 0) 2) по некоторому алгоритму уточнить решение, сужая интервал, в котором находится x* 3) повторять шаг 2, пока не достигнута требуемая точность: b–a< К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

12 Методы вычислений. Кумир + Excel Численные методы Применение: используются тогда, когда точное (аналитическое) решение неизвестно или очень трудоемко. • дают хотя бы какое-то решение • во многих случаях можно оценить ошибку и найти решение с заданной точностью • решение всегда приближенное, неточное К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
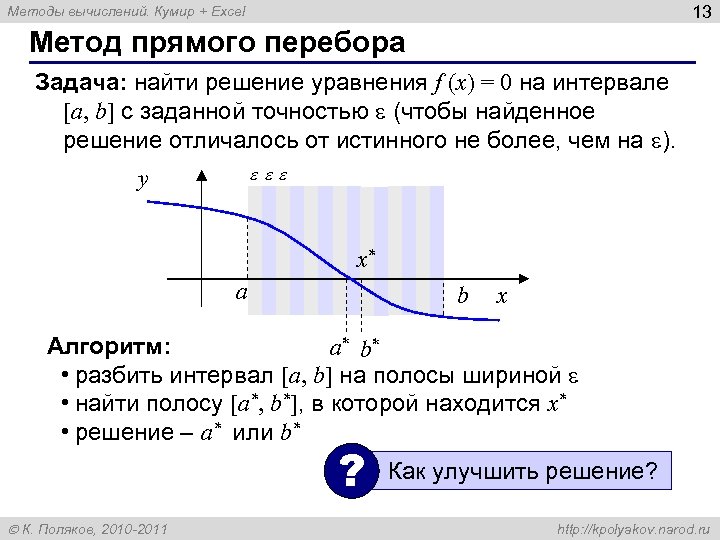
13 Методы вычислений. Кумир + Excel Метод прямого перебора Задача: найти решение уравнения f (x) = 0 на интервале [a, b] с заданной точностью (чтобы найденное решение отличалось от истинного не более, чем на ). y x* a b x Алгоритм: a* b* • разбить интервал [a, b] на полосы шириной • найти полосу [a*, b*], в которой находится x* • решение – a* или b* ? К. Поляков, 2010 -2011 Как улучшить решение? http: //kpolyakov. narod. ru
![14 Методы вычислений. Кумир + Excel Есть ли решение на [a, b]? есть решение 14 Методы вычислений. Кумир + Excel Есть ли решение на [a, b]? есть решение](https://present5.com/presentation/4b76c44bc63c24308d8c18a21719786d/image-14.jpg)
14 Методы вычислений. Кумир + Excel Есть ли решение на [a, b]? есть решение y y нет решения x* a ! y нет решения x* bx a b x x* x Если непрерывная функция f (x) имеет разные знаки на концах интервала [a, b], то в некоторой точке x внутри [a, b] она равна 0, то есть f (x) = 0! К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

15 Методы вычислений. Кумир + Excel Метод прямого перебора eps: = 0. 01 | точность решения x: = a нц пока f(x)*f(x+eps) > 0 x: =x+eps; | к следующему интервалу кц вывод “Решение: x=”, x ? Как повысить точность без лишних вычислений? ? К. Поляков, 2010 -2011 Что опасно? http: //kpolyakov. narod. ru

16 Методы вычислений. Кумир + Excel Метод прямого перебора алг Перебор нач вещ a, b, x, eps = 0. 01 a: = 0; b: = 3 x: = a нц пока f(x)*f(x+eps) > 0 x: = x + eps кц вывод “Решение: x=”, x кон алг вещ f(вещ x) нач знач: = 5*cos(x-1) кон ? К. Поляков, 2010 -2011 ? Что лишнее? Как найти все решения на [a, b]? http: //kpolyakov. narod. ru
17 Методы вычислений. Кумир + Excel Задания « 4» : Найти все решения уравнения на интервале [-5, 5] и вывести их на экран. « 5» : Сделать то же самое с помощью только одного цикла. ! К. Поляков, 2010 -2011 Запускать через Shift+F 9 (без вывода отладочной информации)! http: //kpolyakov. narod. ru
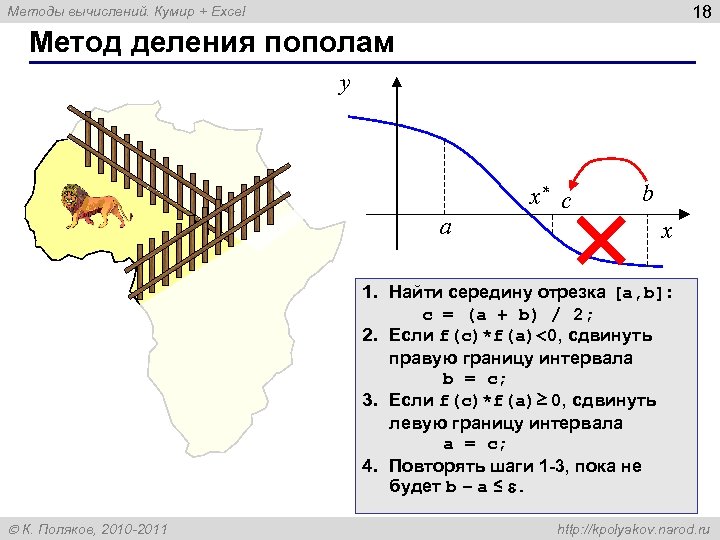
18 Методы вычислений. Кумир + Excel Метод деления пополам y a x* с b x 1. Найти середину отрезка [a, b]: c = (a + b) / 2; 2. Если f(c)*f(a)<0, сдвинуть правую границу интервала b = c; 3. Если f(c)*f(a)≥ 0, сдвинуть левую границу интервала a = c; 4. Повторять шаги 1 -3, пока не будет b – a ≤ . К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

19 Методы вычислений. Кумир + Excel Метод деления пополам • простота • можно получить решение с любой заданной точностью • нужно знать интервал [a, b] • на интервале [a, b] должно быть только одно решение • большое число шагов для достижения высокой точности • только для функций одной переменной К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

Методы вычислений. Кумир + Excel 20 Метод деления пополам нц пока b – a > eps c: = (a+b)/2 если f(a)*f(c) < 0 то b: = c иначе a: = c все кц вывод “Решение: x=”, (a+b)/2 К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

21 Методы вычислений. Кумир + Excel Задания « 4» : Найти все решения уравнения на интервале [-5, 5] методом деления пополам и вывести их на экран. « 5» : Сделать задачу на « 4» и сравнить число шагов цикла при использовании метода перебора и метода деления пополам. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

22 Методы вычислений. Кумир + Excel Методы вычислений Задача: найти все решения уравнения на интервале [-5, 5] ? Как решить «обычными» методами? Методы решения уравнений: • аналитические: решение в виде формулы • численные: приближенное решение, число 1) выбрать начальное приближение «рядом» с решением ? Как выбрать начальное приближение? 2) по некоторому алгоритму вычисляют первое приближение, затем – второе и т. д. 3) вычисления прекращают, когда значение меняется очень мало (метод сходится) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
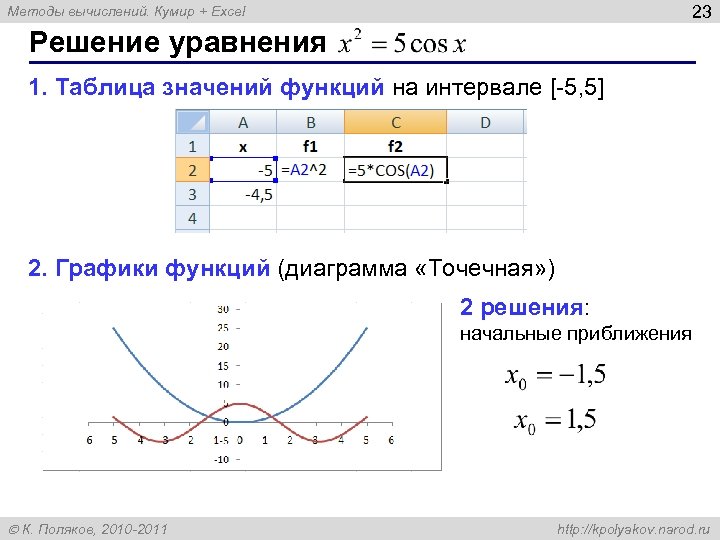
23 Методы вычислений. Кумир + Excel Решение уравнения 1. Таблица значений функций на интервале [-5, 5] 2. Графики функций (диаграмма «Точечная» ) 2 решения: начальные приближения К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
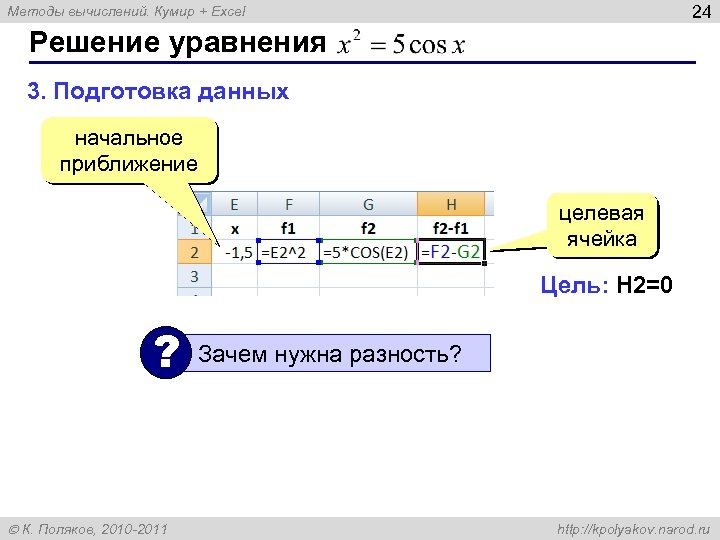
24 Методы вычислений. Кумир + Excel Решение уравнения 3. Подготовка данных начальное приближение целевая ячейка Цель: H 2=0 ? К. Поляков, 2010 -2011 Зачем нужна разность? http: //kpolyakov. narod. ru
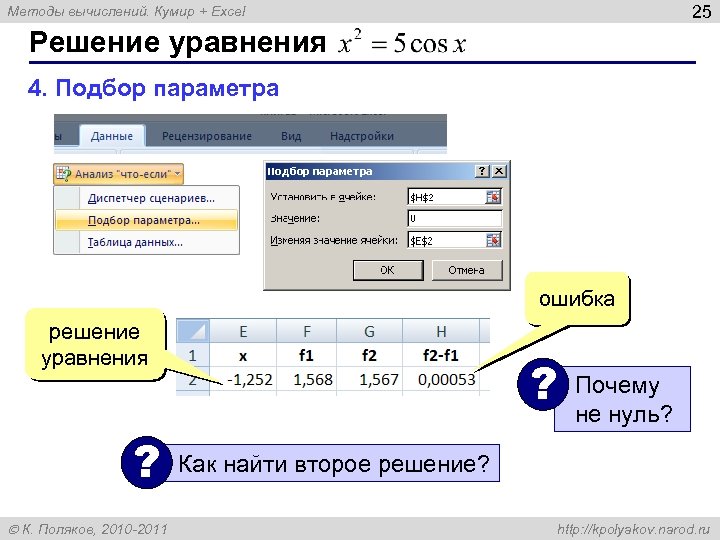
25 Методы вычислений. Кумир + Excel Решение уравнения 4. Подбор параметра ошибка решение уравнения ? К. Поляков, 2010 -2011 ? Почему не нуль? Как найти второе решение? http: //kpolyakov. narod. ru
26 Плавающее бревно На сколько погрузится бревно радиуса R, брошенное в воду, если плотность дерева ρд = 700 кг/м 3. Плотность воды ρв = 1000 кг/м 3? L H
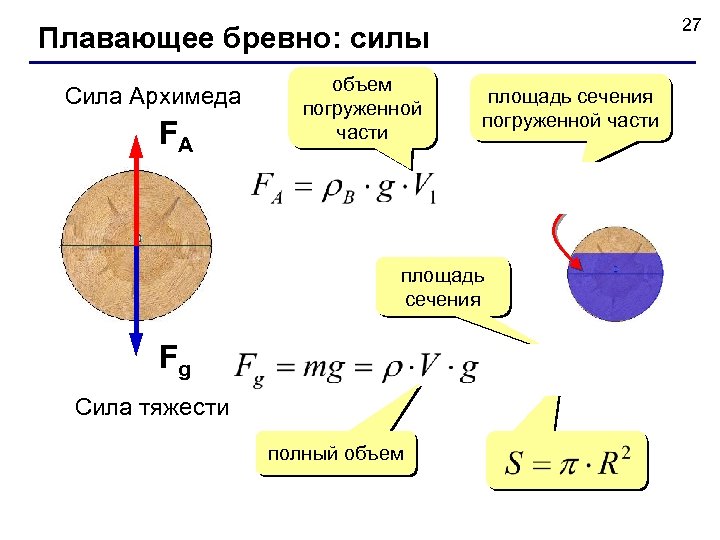
27 Плавающее бревно: силы Сила Архимеда FA объем погруженной части площадь сечения Fg Сила тяжести полный объем
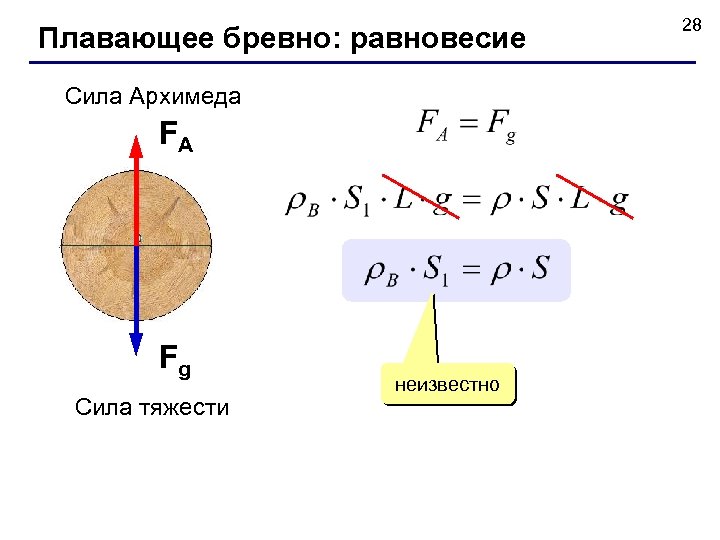
Плавающее бревно: равновесие Сила Архимеда FA Fg Сила тяжести неизвестно 28
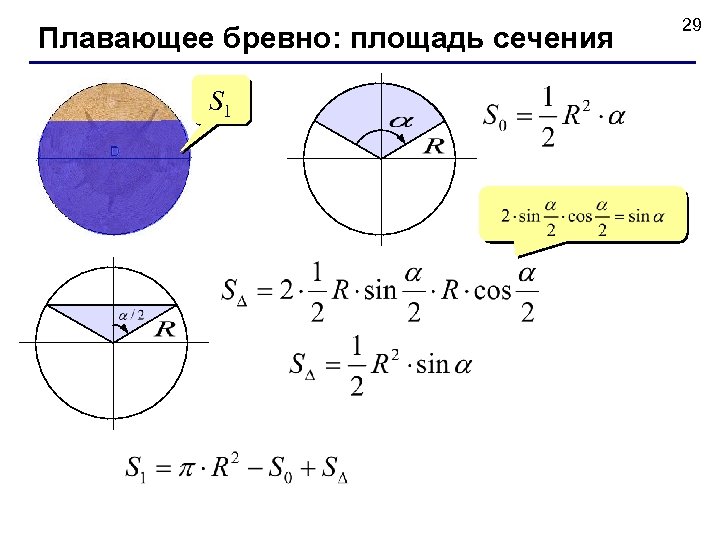
Плавающее бревно: площадь сечения S 1 29
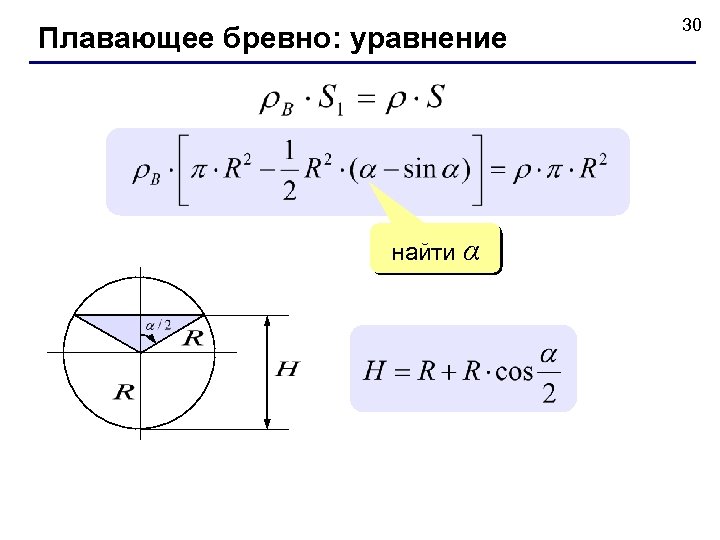
Плавающее бревно: уравнение найти α 30

Методы вычислений Тема 3. Оптимизация К. Поляков, 2010 -2011

32 Методы вычислений. Кумир + Excel Оптимизация – это поиск оптимального (наилучшего) варианта в заданных условиях. Оптимальное решение – такое, при котором некоторая заданная функция (целевая функция) достигает минимума или максимума. Постановка задачи: • целевая функция (расходы, потери, ошибки) (доходы, приобретения) • ограничения, которые делают задачу осмысленной Задача без ограничений: построить дом при минимальных затратах. Решение: не строить дом вообще. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
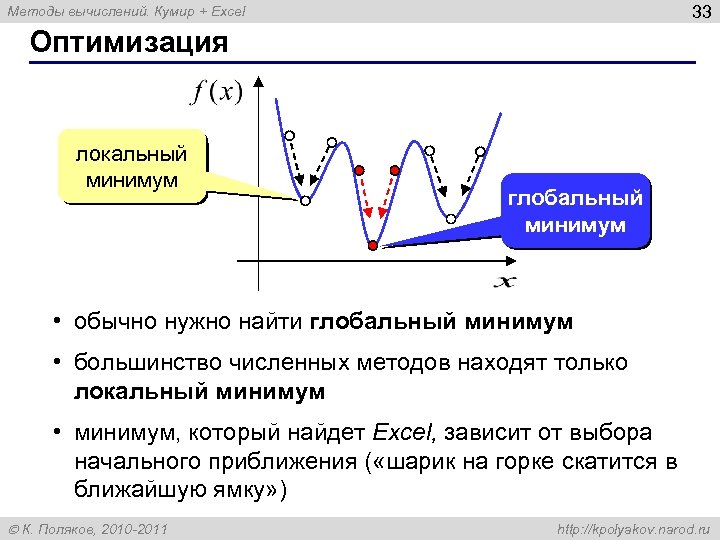
33 Методы вычислений. Кумир + Excel Оптимизация локальный минимум глобальный минимум • обычно нужно найти глобальный минимум • большинство численных методов находят только локальный минимум • минимум, который найдет Excel, зависит от выбора начального приближения ( «шарик на горке скатится в ближайшую ямку» ) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
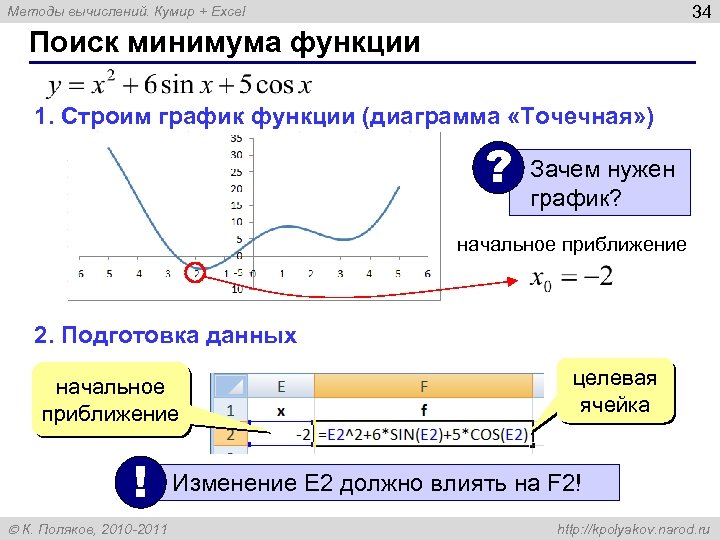
34 Методы вычислений. Кумир + Excel Поиск минимума функции 1. Строим график функции (диаграмма «Точечная» ) ? Зачем нужен график? начальное приближение 2. Подготовка данных начальное приближение ! К. Поляков, 2010 -2011 целевая ячейка Изменение E 2 должно влиять на F 2! http: //kpolyakov. narod. ru
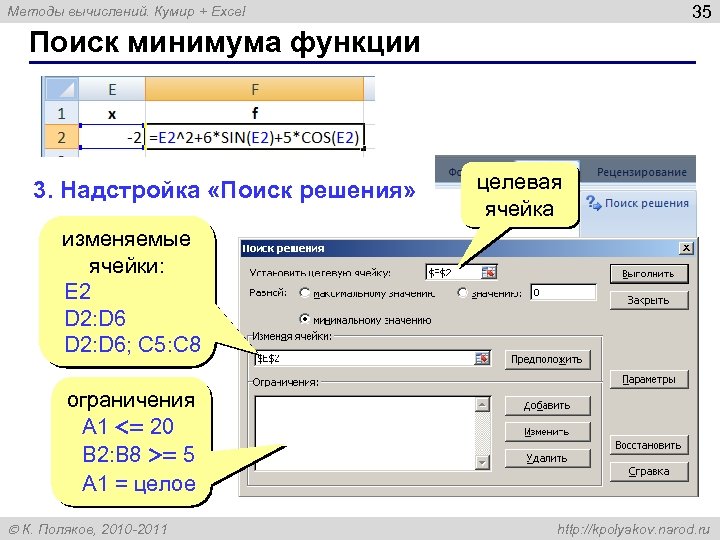
35 Методы вычислений. Кумир + Excel Поиск минимума функции 3. Надстройка «Поиск решения» целевая ячейка изменяемые ячейки: E 2 D 2: D 6; C 5: C 8 ограничения A 1 <= 20 B 2: B 8 >= 5 A 1 = целое К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
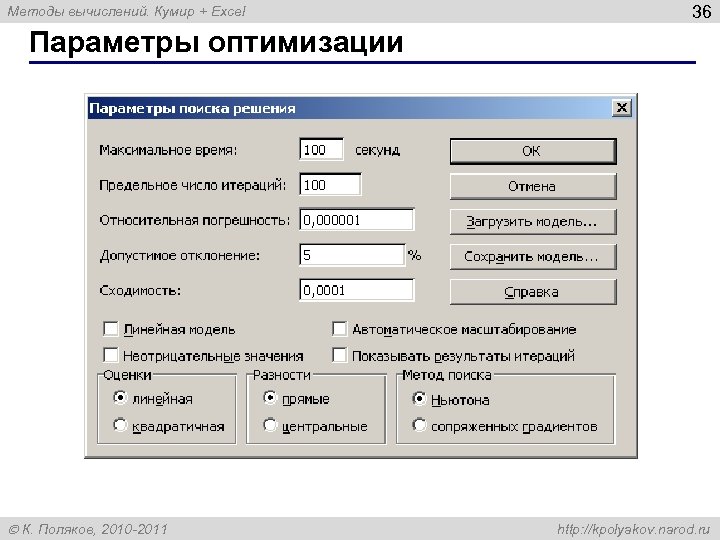
Методы вычислений. Кумир + Excel 36 Параметры оптимизации К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

37 Методы вычислений. Кумир + Excel Оптимизация ? Подбор параметра – это оптимизация? Надстройка «Поиск решения» позволяет: • искать минимум и максимум функции • использовать несколько изменяемых ячеек и диапазонов • вводить ограничения (<=, >=, целое, двоичное) ? Как влияет ограничение «A 1 -целое» на сложность решения задачи? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

Методы вычислений Тема 4. Восстановление зависимостей К. Поляков, 2010 -2011
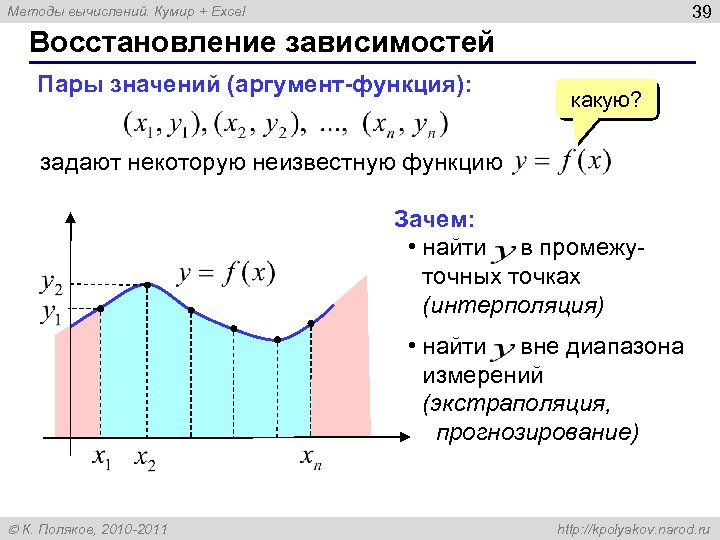
39 Методы вычислений. Кумир + Excel Восстановление зависимостей Пары значений (аргумент-функция): какую? задают некоторую неизвестную функцию Зачем: • найти в промежуточных точках (интерполяция) • найти вне диапазона измерений (экстраполяция, прогнозирование) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
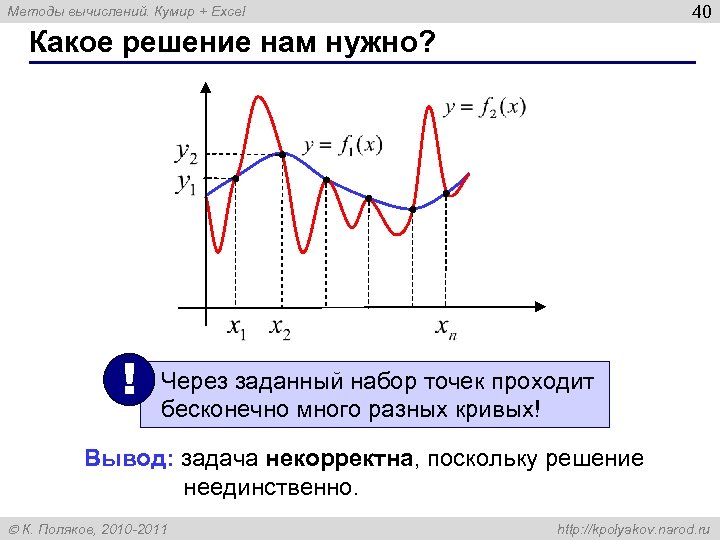
40 Методы вычислений. Кумир + Excel Какое решение нам нужно? ! Через заданный набор точек проходит бесконечно много разных кривых! Вывод: задача некорректна, поскольку решение неединственно. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
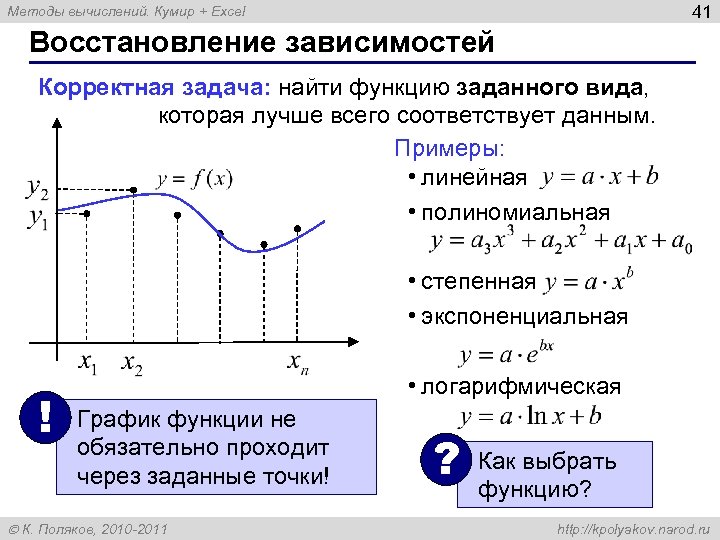
41 Методы вычислений. Кумир + Excel Восстановление зависимостей Корректная задача: найти функцию заданного вида, которая лучше всего соответствует данным. Примеры: • линейная • полиномиальная • степенная • экспоненциальная ! • логарифмическая График функции не обязательно проходит через заданные точки! К. Поляков, 2010 -2011 ? Как выбрать функцию? http: //kpolyakov. narod. ru
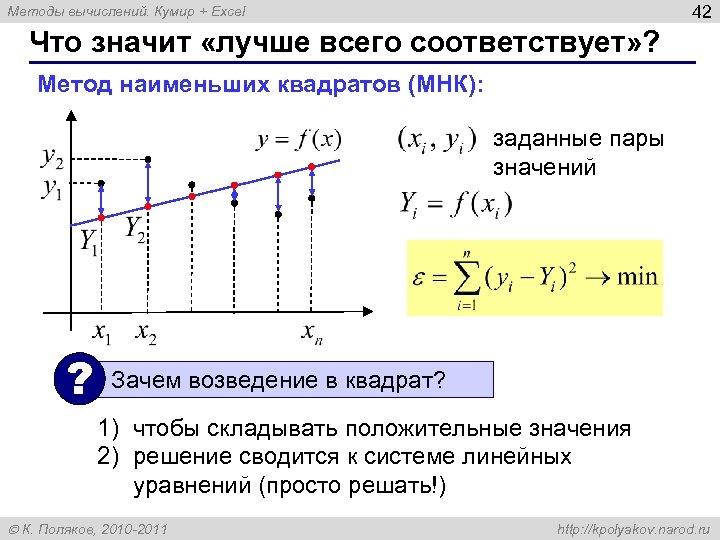
42 Методы вычислений. Кумир + Excel Что значит «лучше всего соответствует» ? Метод наименьших квадратов (МНК): заданные пары значений ? Зачем возведение в квадрат? 1) чтобы складывать положительные значения 2) решение сводится к системе линейных уравнений (просто решать!) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
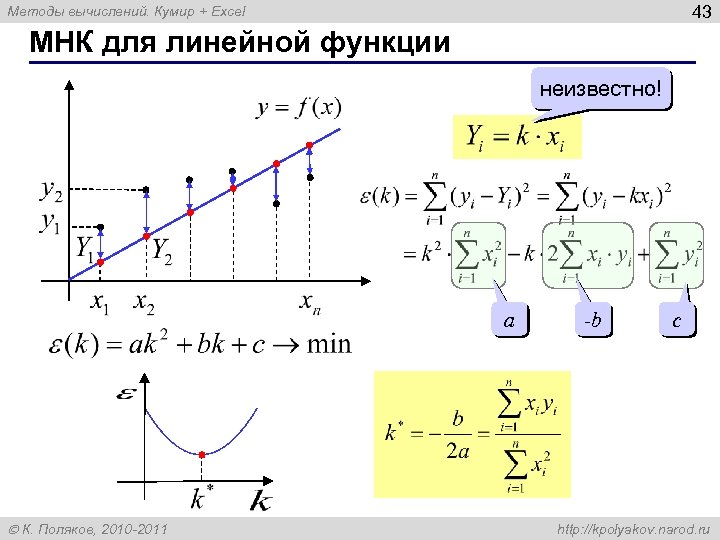
43 Методы вычислений. Кумир + Excel МНК для линейной функции неизвестно! a К. Поляков, 2010 -2011 -b c http: //kpolyakov. narod. ru
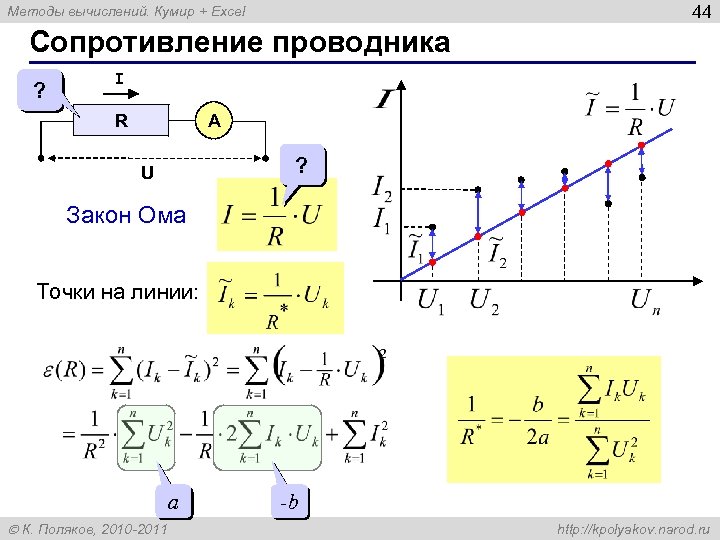
44 Методы вычислений. Кумир + Excel Сопротивление проводника ? I R A ? U Закон Ома Точки на линии: a К. Поляков, 2010 -2011 -b http: //kpolyakov. narod. ru

45 Методы вычислений. Кумир + Excel Обработка результатов эксперимента Задача. В файле mnk. txt записаны в столбик 10 пар чисел (напряжение, ток), полученные в результате эксперимента с одним резистором. Найти (приближенно) его сопротивление по методу наименьших квадратов. Этапы решения: 1. Прочитать данные из файла в массивы U и I. 2. Вычислить и . 3. Вычислить R*. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
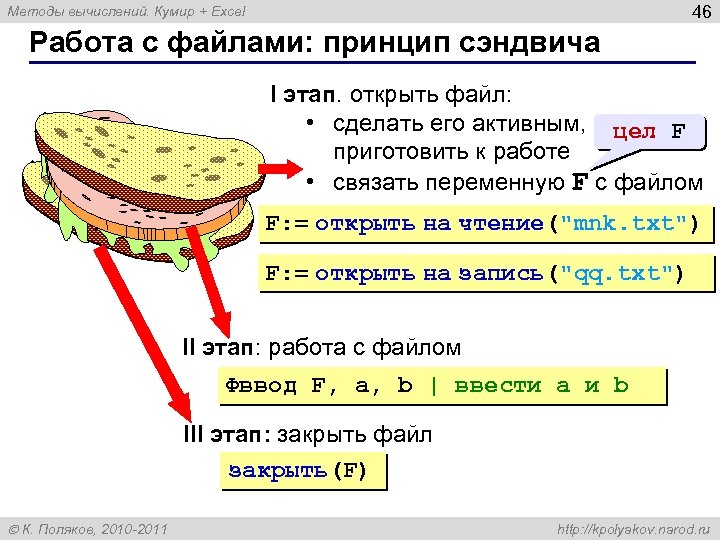
46 Методы вычислений. Кумир + Excel Работа с файлами: принцип сэндвича I этап. открыть файл: • сделать его активным, цел F приготовить к работе • связать переменную F с файлом F: = открыть на чтение(“mnk. txt”) F: = открыть на запись(“qq. txt”) II этап: работа с файлом Фввод F, a, b | ввести a и b III этап: закрыть файл закрыть(F) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

47 Методы вычислений. Кумир + Excel Обработка результатов эксперимента Чтение данных из файла: использовать Файлы П алг МНК цел k, F, N = 10 вещтаб U[1: N], I[1: N] F: = открыть на чтение(“mnk. txt”) нц для k от 1 до N Фввод F, U[k], I[k] вывод U[k], ” “, I[k], нс кц закрыть(F); кон К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

Методы вычислений. Кумир + Excel Обработка результатов эксперимента Вычисления: вещ UU UU: = 0; нц для k от 1 до 10 UU: = UU + U[k]*U[k]; кц ? ? К. Поляков, 2010 -2011 Как найти ? 48 Что вычисляем? ? Как найти R*? http: //kpolyakov. narod. ru

49 Методы вычислений. Кумир + Excel Задания « 4» : Используя метод наименьших квадратов, найти приближенное значение сопротивления по данным файла mnk. txt. « 5» : Сделать то же самое, предполагая, что в файле неизвестное количество пар значений, но не более 100. Цикл ввода должен выглядеть так: нц пока не конец файла(F) | читаем U[k] и I[k] | тут еще что-то надо сделать кц К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

50 Методы вычислений. Кумир + Excel Коэффициент достоверности (Excel) заданные пары значений – среднее значение Крайние случаи: • если график проходит через точки: • если считаем, что y не меняется и ! : Фактически – метод наименьших квадратов! К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
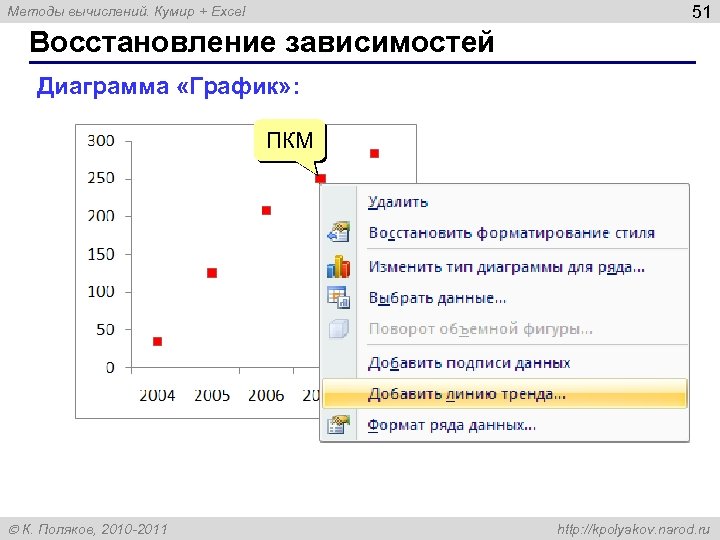
51 Методы вычислений. Кумир + Excel Восстановление зависимостей Диаграмма «График» : ПКМ К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
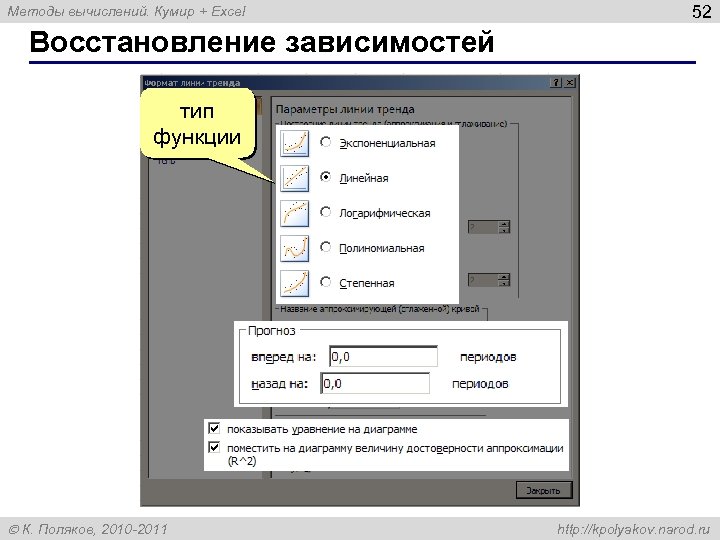
Методы вычислений. Кумир + Excel 52 Восстановление зависимостей тип функции К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
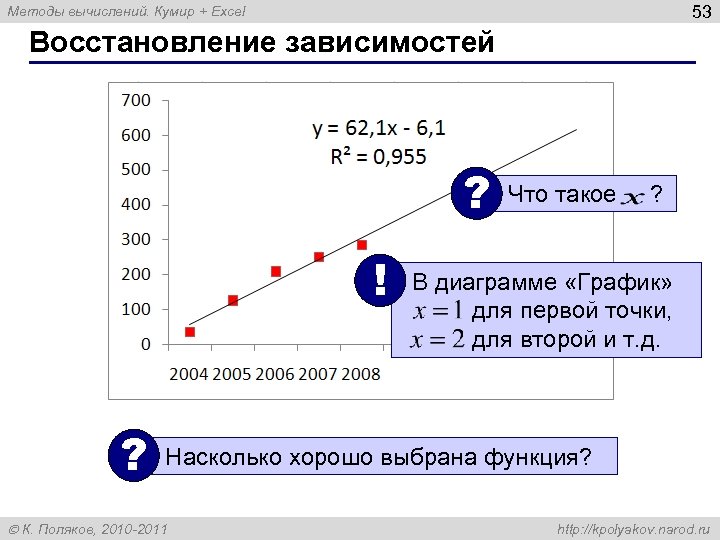
53 Методы вычислений. Кумир + Excel Восстановление зависимостей ? ! ? Что такое ? В диаграмме «График» для первой точки, для второй и т. д. Насколько хорошо выбрана функция? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

54 Методы вычислений. Кумир + Excel Восстановление зависимостей Сложные случаи (нестандартная функция): ? Что делать? Алгоритм: 1) выделить ячейки для хранения 2) построить ряд для тех же 3) построить на одной диаграмме ряды и 4) попытаться подобрать так, чтобы два графика были близки 5) вычислить в отдельной ячейке функции: СУММКВРАЗН – сумма квадратов разностей рядов ДИСПР – дисперсия 6) Поиск решения: К. Поляков, 2010 -2011 ! Это задача оптимизации! http: //kpolyakov. narod. ru

55 Методы вычислений Тема 5. Статистика К. Поляков, 2010 -2011

56 Методы вычислений. Кумир + Excel Ряд данных и его свойства Ряд данных – это упорядоченный набор значений Основные свойства (ряд A 1: A 20): • количество элементов =СЧЕТ(A 1: A 20) • количество элементов, удовлетворяющих некоторому условию: = СЧЕТЕСЛИ(A 1: A 20; “<5”) • минимальное значение =МИН(A 1: A 20) • максимальное значение =МАКС(A 1: A 20) • сумма элементов =СУММ(A 1: A 20) • среднее значение =СРЗНАЧ(A 1: A 20) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
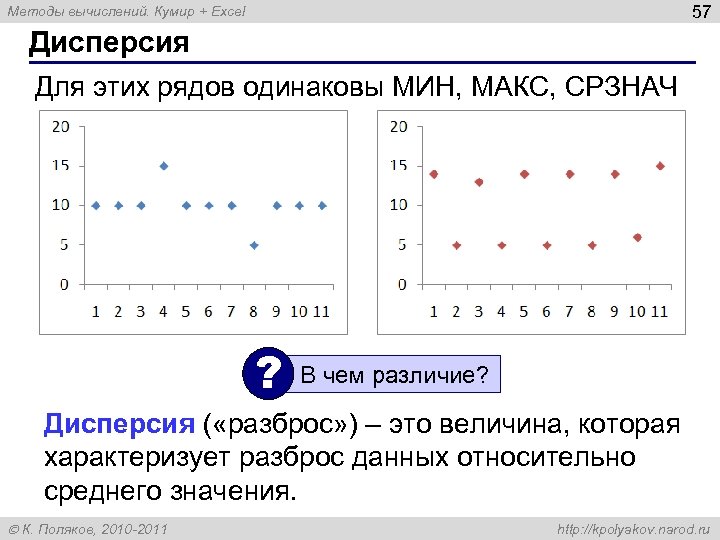
57 Методы вычислений. Кумир + Excel Дисперсия Для этих рядов одинаковы МИН, МАКС, СРЗНАЧ ? В чем различие? Дисперсия ( «разброс» ) – это величина, которая характеризует разброс данных относительно среднего значения. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
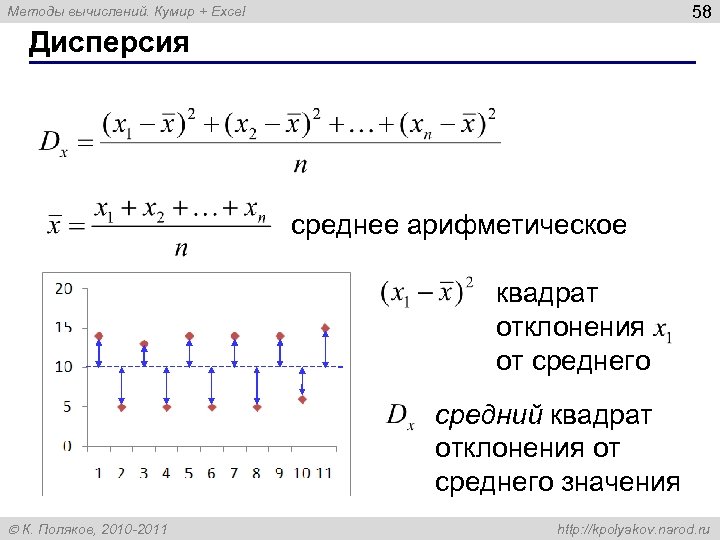
58 Методы вычислений. Кумир + Excel Дисперсия среднее арифметическое квадрат отклонения от среднего средний квадрат отклонения от среднего значения К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

59 Методы вычислений. Кумир + Excel Дисперсия и СКВО Стандартная функция =ДИСПР(A 1: A 20) Функции – Другие – Статистические Что неудобно: если измеряется в метрах, то – в м 2 ? В каких единицах измеряется? СКВО = среднеквадратическое отклонение =СТАНДОТКЛОНП(A 1: A 20) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
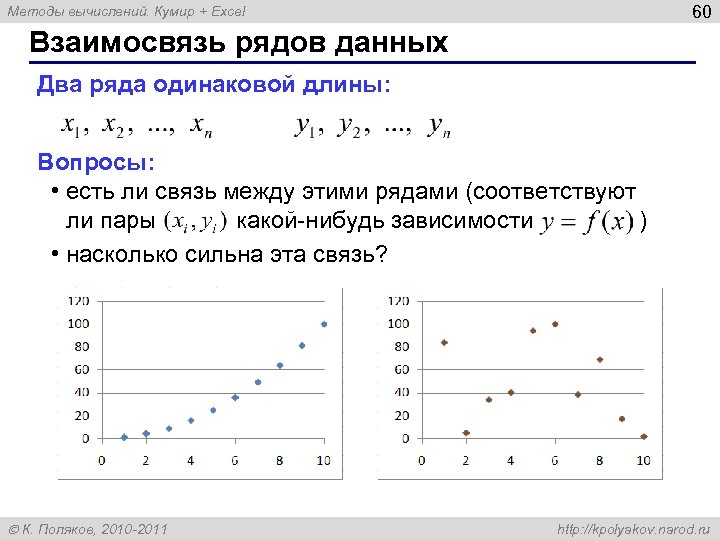
60 Методы вычислений. Кумир + Excel Взаимосвязь рядов данных Два ряда одинаковой длины: Вопросы: • есть ли связь между этими рядами (соответствуют ли пары какой-нибудь зависимости ) • насколько сильна эта связь? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

61 Методы вычислений. Кумир + Excel Взаимосвязь рядов данных Ковариация: ? Если и – один и тот же ряд? в среднем! Как понимать это число? увеличение приводит к увеличению • если увеличение приводит к уменьшению • если связь обнаружить не удалось • если Что плохо? • единицы измерения: если в метрах, в литрах, то – в м л • зависит от абсолютных значений и , поэтому ничего не говорит о том, насколько сильна связь К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

62 Методы вычислений. Кумир + Excel Взаимосвязь рядов данных Коэффициент корреляции: – СКВО рядов ? Какова размерность? и безразмерный! Как понимать это число? • если : увеличение приводит к увеличению • если : увеличение приводит к уменьшению • если : связь обнаружить не удалось =КОРРЕЛ(A 1: A 20; B 1: B 20) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

63 Методы вычислений. Кумир + Excel Взаимосвязь рядов данных Как понимать коэффициент корреляции? : очень слабая корреляция : слабая : средняя : сильная : очень сильная : линейная зависимость ? Если ! Метод для определения линейной зависимости! К. Поляков, 2010 -2011 , то связи нет? http: //kpolyakov. narod. ru

64 Методы вычислений Тема 6. Моделирование (по мотивам учебника А. Г. Гейна и др. , Информатика и ИКТ, 10 класс, М. : Просвещение, 2008) К. Поляков, 2010 -2011
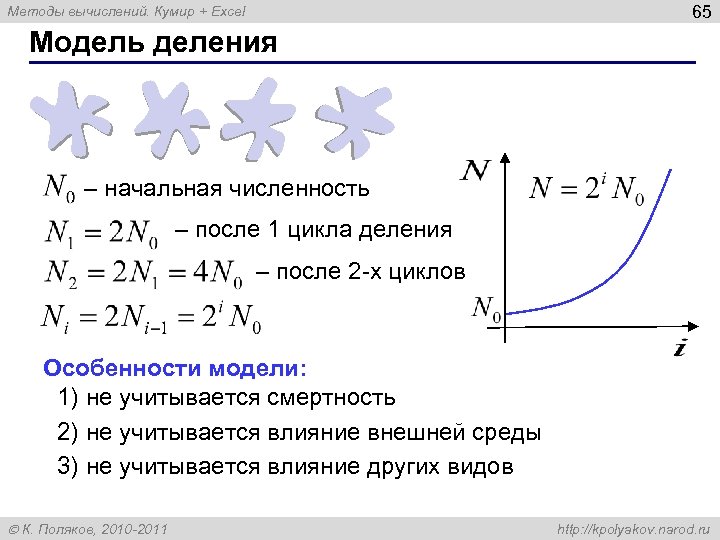
65 Методы вычислений. Кумир + Excel Модель деления – начальная численность – после 1 цикла деления – после 2 -х циклов Особенности модели: 1) не учитывается смертность 2) не учитывается влияние внешней среды 3) не учитывается влияние других видов К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
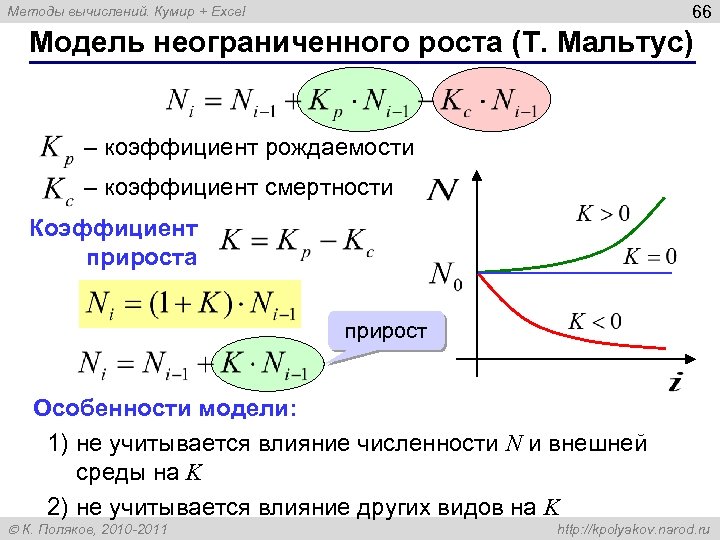
66 Методы вычислений. Кумир + Excel Модель неограниченного роста (T. Мальтус) – коэффициент рождаемости – коэффициент смертности Коэффициент прироста прирост Особенности модели: 1) не учитывается влияние численности N и внешней среды на K 2) не учитывается влияние других видов на K К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
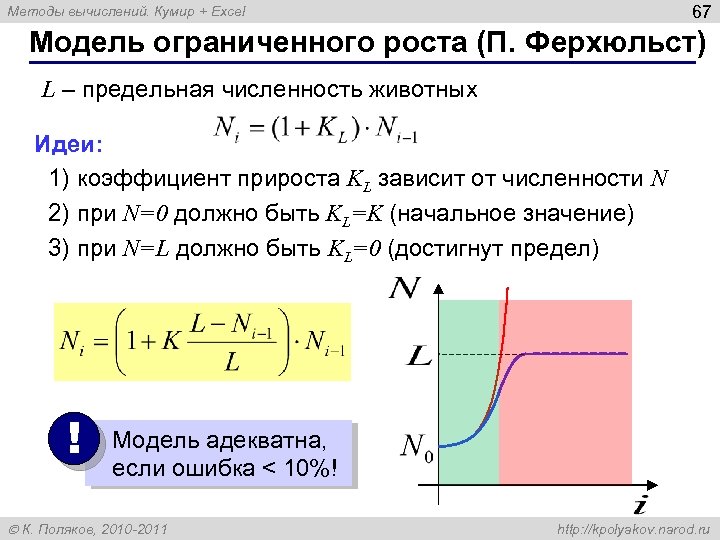
67 Методы вычислений. Кумир + Excel Модель ограниченного роста (П. Ферхюльст) L – предельная численность животных Идеи: 1) коэффициент прироста KL зависит от численности N 2) при N=0 должно быть KL=K (начальное значение) 3) при N=L должно быть KL=0 (достигнут предел) ! Модель адекватна, если ошибка < 10%! К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

68 Методы вычислений. Кумир + Excel Модель с отловом Примеры: рыбоводческое хозяйство, разведение пушных зверей и т. п. отлов ? Какая будет численность? , прирост = отлову ? Сколько можно отловить? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
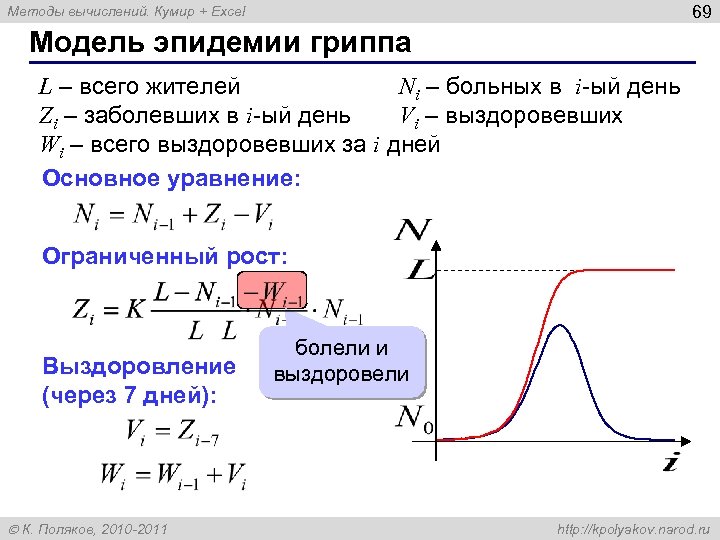
69 Методы вычислений. Кумир + Excel Модель эпидемии гриппа L – всего жителей Ni – больных в i-ый день Zi – заболевших в i-ый день Vi – выздоровевших Wi – всего выздоровевших за i дней Основное уравнение: Ограниченный рост: Выздоровление (через 7 дней): К. Поляков, 2010 -2011 болели и выздоровели http: //kpolyakov. narod. ru

70 Методы вычислений. Кумир + Excel Модель системы «хищник-жертва» Модель – не-система: караси щуки вымирают Модель – система: без еды 1) число встреч пропорционально Ni Zi 2) «эффект» пропорционален числу встреч численность уменьшается численность увеличивается К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
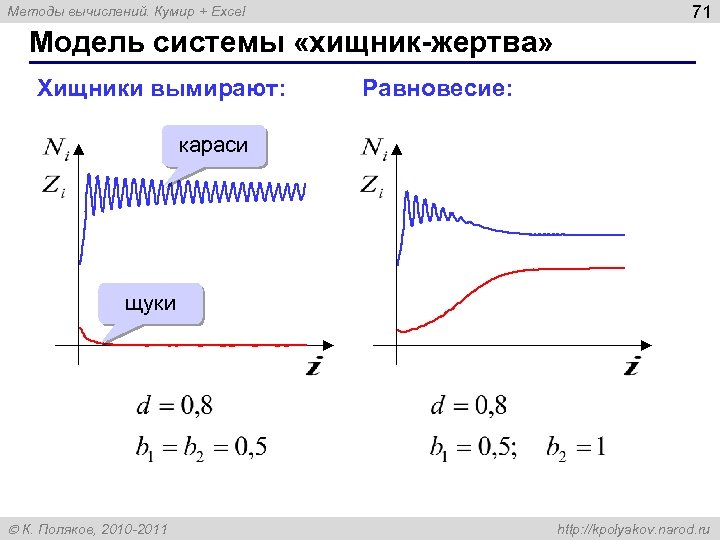
71 Методы вычислений. Кумир + Excel Модель системы «хищник-жертва» Хищники вымирают: Равновесие: караси щуки К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
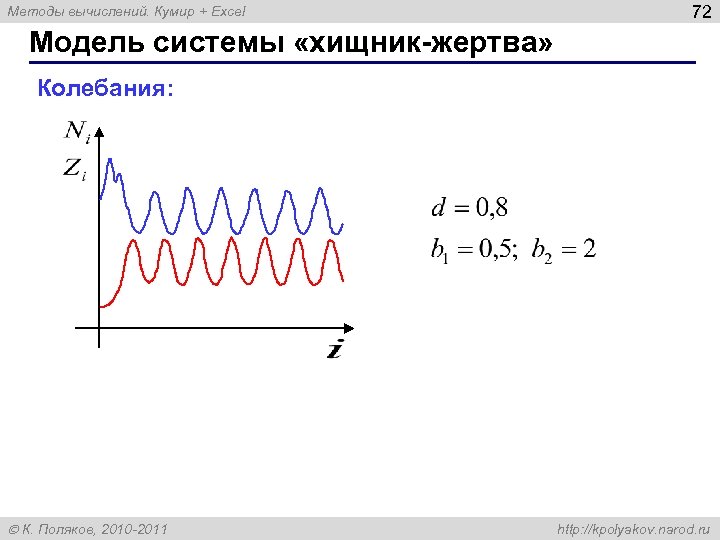
Методы вычислений. Кумир + Excel 72 Модель системы «хищник-жертва» Колебания: К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

73 Методы вычислений. Кумир + Excel Случайность и ее моделирование Случайно… 1) встретить друга на улице 2) разбить тарелку 3) найти 10 рублей 4) выиграть в лотерею Случайный выбор: 1) жеребьевка на соревнованиях 2) выигравшие номера в лотерее Как получить случайность? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

74 Методы вычислений. Кумир + Excel Случайные числа на компьютере Электронный генератор • нужно специальное устройство • нельзя воспроизвести результаты Псевдослучайные числа – обладают свойствами случайных чисел, но каждое следующее число вычисляется по заданной формуле. Метод середины квадрата (Дж. фон Нейман) 564321 458191 318458191041 в квадрате малый период • (последовательность повторяется через 106 чисел) 938992 209938992481 К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
75 Методы вычислений. Кумир + Excel Распределение случайных чисел Модель: снежинки падают на отрезок [a, b] распределение равномерное a ? b неравномерное a b Сколько может быть разных распределений? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
76 Методы вычислений. Кумир + Excel Распределение случайных чисел Особенности: • распределение – это характеристика всей последовательности, а не одного числа • равномерное распределение одно, компьютерные датчики случайных чисел дают равномерное распределение • неравномерных – много • любое неравномерное можно получить с помощью равномерного a К. Поляков, 2010 -2011 b a b http: //kpolyakov. narod. ru
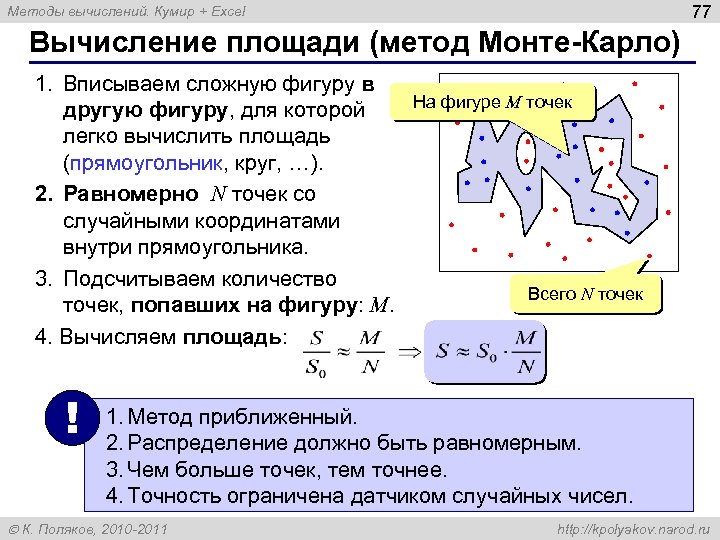
77 Методы вычислений. Кумир + Excel Вычисление площади (метод Монте-Карло) 1. Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …). 2. Равномерно N точек со случайными координатами внутри прямоугольника. 3. Подсчитываем количество точек, попавших на фигуру: M. 4. Вычисляем площадь: ! На фигуре M точек Всего N точек 1. Метод приближенный. 2. Распределение должно быть равномерным. 3. Чем больше точек, тем точнее. 4. Точность ограничена датчиком случайных чисел. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

78 Методы вычислений. Кумир + Excel Вычисление площади (x, y) Случайные координаты: x : = rand(0, R) y : = rand(0, R) Когда точка внутри круга? Программа: нц N раз | найти случайные координаты если x*x+y*y <= R*R то M : = M + 1 все кц S: = 4*R*R*M / N Как найти число ? ? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

79 Методы вычислений. Кумир + Excel Задания (метод Монте-Карло) « 4» : Вычислите площади кругов c радиусами R = 1, 2, 3, 4, 5. Используя электронные таблицы, найдите приближенную формулу для вычисления площади круга. « 5» : Вычислите объем шаров c радиусами R = 1, 2, 3, 4, 5. Используя электронные таблицы, найдите приближенную формулу для вычисления объема шара. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

80 Методы вычислений. Кумир + Excel Броуновское движение Случайное направление (в рад): alpha: = rand(0, 2*пи) Случайный шаг: h: = rand(0, h. Max) вещ пи = 3. 14159 Программа: нц пока да | найти случайное направление и шаг x: = x + h*cos(alpha) y: = y + h*sin(alpha) кц К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

81 Методы вычислений. Кумир + Excel Броуновское движение (программа) использовать Рисователь алг Броуновское движение нач вещ пи = 3. 14159, h, h. Max = 10, alpha вещ x = 200, y = 200 | начальные координаты перо(1, “синий”) в точку(int(x), int(y)) нц пока да | найти новые координаты линия в точку(int(x), int(y)) кц кон К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

82 Методы вычислений. Кумир + Excel Задания « 4» : Постройте траектории движения двух частиц в течение 200 шагов. Частицы должны двигаться одновременно. « 5» : Постройте траектории движения 10 частиц в течение 200 шагов. Частицы должны двигаться одновременно. Используйте массивы для хранения координат частиц. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

83 Методы вычислений. Кумир + Excel Системы массового обслуживания Примеры: 1) звонки на телефонной станции 2) вызовы «скорой помощи» 3) обслуживание клиентов в банке сколько линий? сколько бригад? сколько операторов? Особенности: 1) клиенты (запросы на обслуживание) поступают постоянно, но через случайные интервалы времени 2) время обслуживание каждого клиента – случайная величина ! Нужно знать характеристики (распределения) «случайностей» ! К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

84 Методы вычислений. Кумир + Excel Клиенты в банке Вход клиентов: 1) за 1 минуту – до Imax человек 2) равномерное распределение Обслуживание: 1) от Tmin до Tmax минут 2) равномерное распределение ? Сколько нужно касс, чтобы клиенты стояли в очереди не более М минут? К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

85 Методы вычислений. Кумир + Excel Клиенты в банке Число клиентов в помещении банка: было пришли ушли N : = N + in – out ! Допущение: клиенты распределены по кассам равномерно! Количество касс: K Средняя длина очереди: Q – длина очереди Время ожидания: Допустимая длина очереди: К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

86 Методы вычислений. Кумир + Excel Клиенты в банке Пришли за очередную минуту: in: = irand(0, in. Max) Случайное время обслуживания: T: = irand(Tmin, Tmax) ! Каждый оператор за эту минуту обслужит клиентов! Обслужены за очередную минуту и выходят: out: = int(K / T) К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

87 Методы вычислений. Кумир + Excel Клиенты в банке (программа) период моделирования L минут count: = 0 | счетчик плохих минут нц L раз in: = | случайное число входящих out: = | случайное число обслуженных N: = N + in – out если N/K > Qmax то count: = count + 1 все кц вывод count/L; ? Что выводится? К. Поляков, 2010 -2011 ? Как выбрать К? http: //kpolyakov. narod. ru

88 Методы вычислений. Кумир + Excel Клиенты в банке (исходные данные) in. Max : = 10 | max число входящих за 1 мин Tmin : = 1 | min время обслуживания Tmax : = 5 | max время обслуживания L : = 1000 | период моделирования в минутах M : = 10 | допустимое время ожидания Задача: найти минимальное K, при котором время ожидания в 90% случаев не больше M минут. К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru

89 Методы вычислений. Кумир + Excel Конец фильма ПОЛЯКОВ Константин Юрьевич д. т. н. , учитель информатики высшей категории, ГОУ СОШ № 163, г. Санкт-Петербург [email protected] ru К. Поляков, 2010 -2011 http: //kpolyakov. narod. ru
МБОУ «Школа-гимназия»
ПРОЕКТ
по информатике
на тему:
«Решение простейших математических задач
в системе программирования КуМир»
Выполняли
ученики 5 А класса:
Шипарёв Владислав,
Степанов Дмитрий
Руководитель:
учитель информатики,
Слащинина Е. В.
Ярцево,
2018
Паспорт проектной работы
|
Название проекта |
«Решение простейших математических задач в системе программирования «КуМир»» |
|
Руководитель проекта и консультант |
Слащинина Елена Владимировна |
|
Образовательная область |
Информатика |
|
Состав проектной группы |
Шипарёв Владислав, Степанов Дмитрий |
|
Тип проекта (информационный, исследовательский, ролевой, практико-ориентированный, творческий) |
информационный |
|
Заказчик проекта (гимназия, родители, учитель-предметник) |
МБОУ «Школа-гимназия» |
|
Цель проект |
|
|
Задачи проекта |
– изучить систему команд Кумира; – рассмотреть способы решения задач с использованием разных типов алгоритма (линейный, ветвление, циклический) – составить подборку задач по математике 5-6 класса, которые можно решить в системе Кумир, представить тексты всех задний в электронной форме. – решить задачи в системе программирования Кумир |
|
Предполагаемый продукт(ы) проекта |
Сборник задач с решением |
|
Этапы работы над проектом |
Подготовительный: – определение темы проекта; – уточнение цели и задач; – определение источников информации. Основной этап: – распределение обязанностей в группе – определение шагов действий для каждого участника группы – высказывание возможных путей разрешения спорных вопросов, обсуждения спорных вопросов; – поиск и сбор информации каждым участником проекта с помощью литературы, средств массовой информации, сети интернета, собственного опыта и исследования. Заключительный: – анализ полученной информации и её систематизации – подведение выводов; – изготовление буклетов и презентации как продуктов проекта; – защита проекта – обсуждение результатов работы |
|
Образовательные и культурно-просветительские учреждения, на базе которых выполнялся проект: база гимназии, библиотека, музей и др. |
МБОУ «Школа-гимназия» |
Содержание
- Введение ……………………………………………………………………………….. 4стр
- Основная часть
- Изучаем алгоритмы. Алгоритмы и исполнители ………………. 6стр
- Система программирования КуМир. Простые команды ……..7стр
- Величины в алгоритмах. Описание переменных …………………8стр
- Заключение ………………………………………………………………………………. 11стр
- Список литературных источников ……………………………………..12стр
- Приложение …………………………………………………………..13стр
Актуальность:
В наш информационный век профессия программиста является не только популярной, но и очень востребованной. Само название профессии происходит от слова «программа», оно здесь ключевое. Мы, как и многие современные школьники, тоже мечтаем быть программистами. Работа любого программиста начинается с написания первой простейшей программы. Создавать свои программы, и быть с компьютером на «ты», что может быть интереснее. Но так ли проста работа программиста, легко ли писать программы? Попробуем с этим разобраться.
Первая система программирования, с которой мы познакомились в этом учебном году, называется Кумир. С помощью исполнителя Чертёжник мы научились создавать рисунки в координатах. А затем решили научиться решать простейшие математические задачи из курса математики 5-6 класса.
Проблема: Можно ли простейшие алгебраические задачи решить средствами программирования?
Цель: научиться решать простейшие математические задачи в системе программирования Кумир; составить электронный сборник заданий для 5-6 класса.
Задачи:
- Изучить систему команд Кумира;
- Рассмотреть способы решения задач с использованием разных типов алгоритма (линейный, ветвление, циклический)
- Составить подборку задач по математике 5-6 класса, которые можно решить в системе Кумир, представить тексты всех задний в электронной форме.
- Решить задачи в системе программирования Кумир
Методы исследования: изучение теории по выбранной теме, анализ литературы, практическое применение.
Материалы и ресурсы: ватман, бумага формата А4, клей, карандаши.
Программные средства: веб-браузер, текстовый процессор OpenOfficeWritter, презентация.
Этапы работы над проектом
Подготовительный:
– определение темы проекта;
– уточнение цели и задач;
– определение источников информации.
Основной этап:
– распределение обязанностей в группе
– определение шагов действий для каждого участника группы
– высказывание возможных путей разрешения спорных вопросов, обсуждения спорных вопросов;
– поиск и сбор информации каждым участником проекта с помощью литературы, средств массовой информации, сети интернета, собственного опыта и исследования.
Заключительный:
– анализ полученной информации и её систематизации
– подведение выводов;
– защита проекта
-обсуждение результатов работы
Основная часть
Изучаем алгоритмы
Алгоритмы и исполнители
Все, что бы мы ни делали, имеет какую-то цель. Не всегда ее удается достигнуть, но для того чтобы это было возможно необходимо как следует сформулировать желаемый для себя результат, а потом продумать четкий план его достижения. Часто план сформулирован в виде предписаний или инструкций.
Алгоритм – понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую к достижению результата.
Исполнитель – тот объект или субъект, для управления которым составлен алгоритм.
Характеристики исполнителя:
- СКИ — система команд исполнителя – вся совокупность команд, которые исполнитель умеет выполнять.
- среда – обстановка, в которой функционирует исполнитель.
Свойства алгоритма:
- Понятность – алгоритм должен быть составлен только из команд, входящих в СКИ.
- Дискретность (детализация) – алгоритм разбивается на отдельные элементарные шаги, которые могут быть исполнены при помощи СКИ.
- Однозначность (определенность или детерминированность) – каждый шаг алгоритма имеет единственность толкования выполнения действия и порядка их выполнения.
- Результативность (конечность) – выполнение алгоритма должно приводить к результату за конечное число шагов.
- Массовость – возможность применения алгоритма к классу однотипных задач, различающихся исходными данными.
Определенная последовательность действий исполнителя всегда применяется к некоторым исходным данным. Например: для приготовления пирога нужны соответствующие продукты, для решения математической задачи – решение квадратного уравнения – нужны числовые данные (значения его коэффициентов). Необходимый и достаточный набор данных для решения поставленной задачи (получения искомого результата) называется полным набором данных.
Способы записи алгоритмов
На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке);
- графическая (изображения из графических символов блок-схемы);
- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
- программная (тексты на языках программирования).
Система программирования КуМир
КуМир (Комплект Учебных МИРов) – система программирования, предназначенная для поддержки начальных курсов информатики и программирования в средней и высшей школе.
Сайт: http://www.niisi.ru/kumir/ и http://lpm.org.ru/kumir2/
В системе КуМир используется школьный алгоритмический язык с русской лексикой и встроенными исполнителями Робот и Чертёжник.
При вводе программы КуМир осуществляет постоянный полный контроль ее правильности, сообщая на полях программы об всех обнаруженных ошибках.
При выполнении программы в пошаговом режиме КуМир выводит на поля результаты операций присваивания и значения логических выражений. Это позволяет ускорить процесс освоения азов программирования.
В простейшем случае программа на КуМире выглядит так:
алг Первый
нач
.
кон
После «алг» (алгоритм) пишется имя алгоритма, между «нач» (начало) и «кон» (конец) пишутся команды алгоритма. При написании автоматически создаются отступы вначале строки, это делает программу более наглядной, удалять или пытаться сделать отступ самим не надо.
Приведенный алгоритм «Первый» не будет ничего делать, т. к. между «нач» и «кон» у него нет команд.
Вот пример уже работоспособного алгоритма:
алг Площадь прямоугольника
нач
. вещ длина, ширина, площадь
. вывод “введите значения длины и ширины прямоугольника”
. ввод длина, ширина
. площадь := длина * ширина
. вывод “Площадь прямоугольника равна “, площадь
.кон
Его уже можно запустить на выполнение, он запросит у пользователя значения длины и ширины, вычислит и напечатает результат вычислений…
Простые команды
Эти команды используются практически во всех алгоритмах.
- команда описания переменных
- команда присваивания
- команды ввода-вывода
Величины в алгоритмах
Для запоминания информации в памяти используют величины.
Компьютер работает с информацией, хранящейся в его памяти. Отдельный информационный объект (число, символ, строка, таблица и пр.) называется величиной.
Величины в программировании, как и в математике, делятся на переменные и константы. Значение константы остается неизменной в течении всей работы программы, значение переменной величины может изменяться.
У каждой переменной есть имя, тип и текущее значение.
Прежде чем писать последовательность команд алгоритма, надо определить количество и тип переменных, участвующих в решении задачи.
Для этого из условия задачи выделить:
* что дано (например, сколько чисел и какие они: целые или вещественные)
* что требуется вывести как результат.
Придумывать имена переменным, как и самим алгоритмам, не обязательно, но желательно так, чтобы по ним было понятно назначение переменной в алгоритме. Имя – это последовательность слов, разделенных пробелами. Первое слово имени не должно начинаться с цифры. Ни одно из слов не должно быть ключевым словом (уже имеющим значение в АЯ, например: цел, кон и др.)
В именах можно использовать:
- буквы (русские и латинские, прописные и строчные)
- цифры
- два специальных знака: @ _
Примеры возможных имен: m, x2, площадь, погода на завтра, Ноябрь 7, Седьмое ноября, дом_57б.
Также будьте внимательны при использовании имен, одинаково выглядящих на русском языке и записанных латинскими буквами. Переменные “x” (икс) и “x” (хэ) – это разные переменные.
Типы переменных
Существуют три основных типа величин, с которыми работает компьютер: числовой, символьный и логический.
Тип величины определяет какие значения она может принимать и какие действия с ней можно выполнять. В зависимости от типа переменной в памяти компьютера будет выделена определенная область. В КуМире числовые типы бывают двух видов: целочисленные и вещественные.
Числовые типы
- цел – целые числа от -2147483647 до 2147483647
- вещ – действительные числа от -1.797693 × 10308 до 1.797693 × 10308
Текстовые типы
- сим – один любой символ
- лит – строка символов
Описание переменных
Для того чтобы компьютер мог работать с величиной, нужно указать тип и имя величины, например «цел n». Такое указание называется описанием величины.
алг
нач
цел а, б
вещ частное
…
кон
Команда присваивания
Для того чтобы запомнить или изменить значение величины есть специальная команда — команда присваивания, которая записывается в виде:
имя величины := выражение
Например:
частное := а/б
с:= div(а,б)
k:= sqrt(a)
Команда вывода
Позволяет выводить на экран текстовые сообщения, значения переменных и результаты выражений.
вывод “тексты”, имена величин, выражения, нс
Обратите внимание:
- текстовые сообщения берутся в кавычки;
- имена переменных и выражения перечисляются через запятую без кавычек;
- нс – команда перехода на новую строку
Команда ввода
Позволяет вводить с клавиатуры значения переменных перечисленных в этой команде
ввод а, б
Заключение
Вывод:
В ходе работы над проектом мы научились планировать свою деятельность и распределять обязанности в группе.
Выяснили, что такое алгоритм решения задачи, познакомились с системой программирования КуМир и изучили ее команды, составили свой сборник заданий, на основе учебников математики 5-6 класса и сопроводили его подробным решением каждой задачи.
Практическая значимость проекта: разработанный нами сборник заданий можно использовать на уроках информатики как дидактический материал, а также для самостоятельного изучения курса программирования в среде КуМир.
Литературные источники
- Сайт К. Полякова. Практикум по программированию в среде КумМир. URL: http://kpolyakov.spb.ru/school/kumir.htm
- Программирование в среде КуМир. URL: http://pskumir.blogspot.ru/
- Wiki. Изучаем алгоритмы. URL: https://wiki.lyc84.ru/index.php?
- Алгоритмизация в среде КуМир. URL: https://edusar.soiro.ru/course/view.php?id=475
- Практикум по программированию Д. Кириенко. URL: http://server.179.ru/wiki/?page=DenisKirienko/Kumir
Приложение
Решаем задачи и примеры
Сложение
алг сложение
нач
. цел а, б, сумма
. вывод “введите два целых числа”
. ввод а, б
. сумма:=а+б
. вывод “Сумма равна “, а,“+”,б,“=”,сумма
кон
Вычитание
алг вычитание
нач
. цел а, б, разность
. вывод “введите два целых числа”
. ввод а, б
. разность:=а-б
. вывод “Разность равна “, а,“-“,б,“=”,разность
кон
Умножение
алг умножение
нач
. цел а, б, произвидение
. вывод “введите два целых числа”
. ввод а, б
. произвидение:=а*б
. вывод “Произведение равно “, а,“*”,б,“=”,произвидение
кон
Деление
алг деление
нач
. вещ а, б, частное
. вывод “введите три числа”
. ввод а, б
. частное:=а/б
. вывод “Частное равно “, а,“/”,б,“=”,частное
кон
Периметр прямоугольника
алг Периметр прямоугольника
нач
. цел а, б, в, P |а-длина б-ширина в-2 P-периметр
. вывод “введите три целых числа а, б, в”
. ввод а, б, в
. P:=(а+б)*в
. вывод “Периметр равен “, ” (“, а, “+”, б, “)”, “*”, в, “=”, P
кон
Площадь прямоугольника
алг площадь прямоугольника
нач
. цел а, б, S
. ввод а, б
. S:=а*б
. вывод “площадь равна “, S
кон
Объём параллелепипеда
алг объем
нач
. цел a, b, h, V
. вывод “Введите три целых числа”
. ввод a, b, h
. V:=a*b*h
. вывод “Объём равен “, a,“*”,b,“*”,h,“=”,V
кон
Немного задач…
Скорость сближения
алг скорость сближения
нач
. вещ а, б, р, ч|
. вывод “введите три целых числа”
. ввод а, б, р
. ч:=р/(а+б)
. вывод “СКОРОСТЬ СБЛЖЕНИЕ =”, ч
кон
Нахождение скорости
алг задача
нач
. цел а, б, в, г | а-скорость лодки=6км/ч б-скорость лодки=9км/ч в-2 востолько раз больше скорость гидроцикла г-скорость гидроцикла=?
. вывод “введите три целых числа”
. ввод а, б, в
. г:=(а+б)*в
. вывод “скорость гидроцикла-“ , “(“, а, “+”, б, “)”, “*”, в, “=”, г
кон
Найти сумму n-го числа слагаемых
алг сумма
нач
. цел i,n |i – счетчик , n – число слагаемых
. вещ s | s -сумма
. вывод ‘введите число слагаемых n =’, нс
. s:=0
. ввод n
. нц n раз
. . вывод ‘введите слагаемое’,нс
. . ввод i
. . s:=s+i
. кц
. вывод ‘сумма ‘,n,‘-х слагаемых =’,s:0:2
кон
Найти произведение n-го числа множителей
алг произведение
нач
. цел i,n |i – счетчик , n – число множителей
. вещ p | p -произведение
. вывод ‘введите число множителей n =’, нс
. p:=1
. ввод n
. нц n раз
. . вывод ‘введите множитель’,нс
. . ввод i
. . p:=p*i
. кц
. вывод ‘произведение ‘,n,‘ множителей =’,p:0:2
кон
Сравнить а) два числа и вывести их в порядке возрастания;
алг сравнить два числа
нач
. цел a,b | a,b -числа
. вывод ‘введите два числа’, нс
. ввод a,b
. если a>b
. . то вывод ‘число ‘,a,‘ > числа ‘,b иначе
. . . вывод ‘число ‘,a,‘ < числа ‘,b
. все
кон
Сравнить б) три числа и вывести их в порядке возрастания;
алг сравнить три числа
нач
. цел a,b,c,m | a,b,c -числа, m – наибольшее число
. вывод ‘введите три числа’, нс
. ввод a,b,c
. если a>b
. . то
. . . если a>c
. . . . то
. . . . . m:=a
. . . . иначе m:=c
. . . все
. . иначе
. . . если b>c
. . . . то m:=b
. . . . иначе m:=c
. . . все
. все
. вывод ‘наибольшое число = ‘,m
кон
Представить двухзначное число в виде суммы разрядных слагаемых
алг сумма разрядных слагаемых
нач
. цел x,a,b| x – число, a,b – цифры числа
. вывод ‘введите число’, нс
. ввод x
. a:=div(x,10)
. b:= mod(x, 10)
. вывод x,‘=’,a,‘*10’,‘+’,b,‘*1’
кон
Представить трехзначное число в виде суммы разрядных слагаемых
алг сумма разрядных слагаемых
нач
. цел x,a,b,c| x – число, a,b – цифры числа
. вывод ‘введите число’, нс
. ввод x
. a:=div(x,100)
. b:= div(mod(x, 100),10)
. c:=mod(x,10)
. вывод x,‘=’,a,‘*100’,‘+’,b,‘*10’,‘+’,c,‘*1’
кон
Округлить число до тыс., сот., дес., до старшего разряда
алг округлить число
нач
. цел x,a,b,c,d| x – число, a,b,c,d – цифры числа
. вывод ‘введите число’, нс
. ввод x
. a:=div(x,1000)
. b:= mod(div(x, 100),10)
. c:=div(mod(x,100),10)
. d:=mod(x,10)
. если b>5 или b=5
. . то
. . . вывод x,‘~’,(a+1)*1000, ‘до тысяч’,нс
. . иначе
. . . вывод x,‘~’,a*1000, ‘до тысяч’,нс
. все
. если c>5 или c=5
. . то
. . . вывод x,‘~’,a*1000 +(b+1)*100,‘до сотен’,нс
. . иначе
. . . вывод x,‘~’,a*1000+b*100, ‘до сотен’,нс
. все
. если d>5 или d=5
. . то
. . . вывод x,‘~’,a*1000 +b*100+(c+1)*10, ‘до десятков’,нс
. . иначе
. . . вывод x,‘~’,a*1000+b*100+c*10, ‘до десятков’, нс
. все
. вывод x,‘~’,a*1000+b*100+c*10+d, ‘до единиц’, нс
кон
Сколько существует двузначных чисел, у которых
первая цифра больше второй.
алг двузначные числа
нач
. цел i,a,b,s| i – счетчик, a,b – цифры, s – сумма
. i:=10
. s:=0
. нц 90 раз
. . a:=div(i,10)
. . b:=mod(i,10)
. . если a>b
. . . то
. . . . s:=s+1
. . все
. . i:=i+1
. кц
. вывод s
кон
Найти сумму 1+2+3+4+5+ …+n-го числа слагаемых (с помощью цикла)
алг сумма n числа слагаемых
нач
. цел i,n,s| i – счетчик, n – число слагаемых, s – сумма
. вывод ‘введите число слагаемых n =’
. ввод n
. i:=1
. s:=0
. нц n раз
. . s:=s+i
. . i:=i+1
. кц
. вывод s
кон
Найти сумму 1+2+3+4+5+ …+n-го числа слагаемых (с помощью метода Гауса)
алг сумма n числа слагаемых
нач
. вещ i,n,s| i – счетчик, n – число слагаемых, s – сумма
. вывод ‘введите число слагаемых n =’
. ввод n
. s:=((1+n)*n)/2
. вывод s
кон
Найдите сумму: а) нечетных чисел 1+3+5+ …+n и б) четных чисел 2+4+6+.. +n(с помощью цикла)
алг сумма нечетных_четных слагаемых
нач
. цел i,n,s1,s2| i – счетчик, n – число слагаемых, s1 – сумма четных слагаемых, s2 – сумма нечетных слагаемых
. вывод ‘введите число слагаемых n =’
. ввод n
. i:=1
. s1:=0
. s2:=0
. нц n раз
. . если mod(i,2)=0
. . . то
. . . . s1:=s1+i
. . . иначе
. . . . s2:=s2+i
. . все
. . i:=i+1
. кц
. вывод ‘сумма четных слагаемых = ‘,s1, нс
. вывод ‘сумма нечетных слагаемых = ‘,s2, нс
.
кон
Найдите сумму: а) нечетных чисел 1+3+5+ …+n
(по формуле см. № 226 учебника 6 кл.)
алг сумма нечетных слагаемых
нач
. цел i,n,s2| i – счетчик, n – число слагаемых, s2 – сумма нечетных слагаемых
. вывод ‘введите число слагаемых n =’
. ввод n
. i:=1
. s2:=0
. нц n раз
. . если mod(i,2)<>0
. . . то
. . . . s2:=s2+1
. . все
. . i:=i+1
. кц
. вывод ‘сумма нечетных слагаемых = ‘,s2*s2, нс
.
Кон
Определить вид треугольника(если таковой существует): а) (остроугольный, прямоугольный, тупоугольный), если известные градусные меры всех его улов.
алг вид треугольника по углам
нач
. цел a,b,c| a,b,c – градусные меры всех углов треугольника
. вывод ‘введите величины углов треугольника a =,b=,c=’
. ввод a,b,c
. если a+b+c=180 и a<>0 и b<>0 и c<>0
. . то
. . . если a>90 или b>90 или c>90
. . . . то
. . . . . вывод ‘треугольник тупоугольный’
. . . . иначе
. . . . . если a=90 или b=90 или c=90
. . . . . . то
. . . . . . . вывод ‘треугольник прямоугольный’
. . . . . . иначе
. . . . . . . вывод ‘треугольник остроугольный’
. . . . . все
. . . все
. . иначе
. . . вывод‘треугольник не существует’
. все
кон
Определить вид треугольника(если таковой существует): б) (равнобедренный, равносторонний, разносторонний), если известны длины всех его сторон.
алг вид треугольника по сторонам
нач
. цел a,b,c| a,b,c – длины всех сторон треугольника
. вывод ‘введите длины сторон треугольника a =,b=,c=’
. ввод a,b,c
. если a<b+c и b<a+c и c<a+b
. . то
. . . если a=c=b
. . . . то
. . . . . вывод ‘треугольник равносторонний’
. . . . иначе
. . . . . если a=b или b=c или a=c
. . . . . . то
. . . . . . . вывод ‘треугольник равнобедренный’
. . . . . . иначе
. . . . . . . вывод ‘треугольник разносторонний’
. . . . . все
. . . все
. . иначе
. . . вывод‘треугольник не существует’
. все
кон
Найти НОД(а,в)
алг НОД
нач
. цел a,b,x,y| a,b – числа
. вывод ‘введите числа ‘
. ввод a,b
. x:=a
. y:=b
. нц пока a<>b
. . если a>b
. . . то a:=a–b
. . . иначе b:=b–a
. . все
. кц
. вывод‘НОД(‘,x,‘,’,y,‘)=’,a
кон

