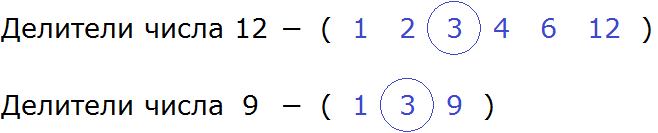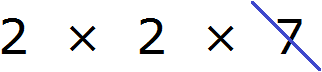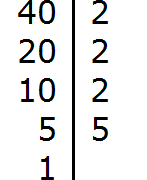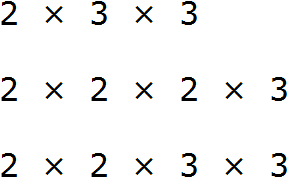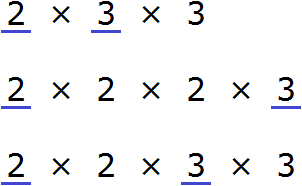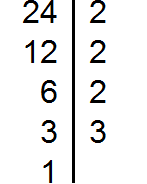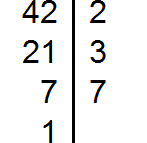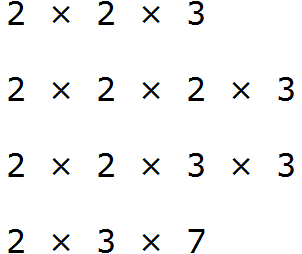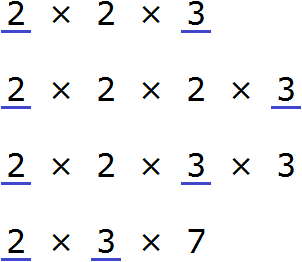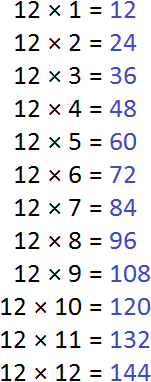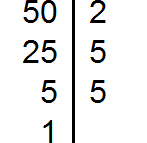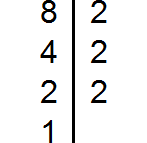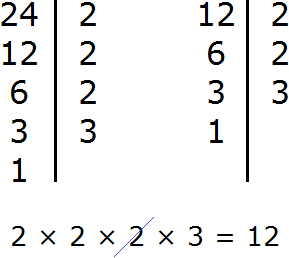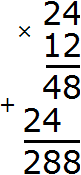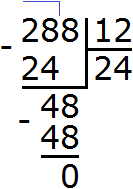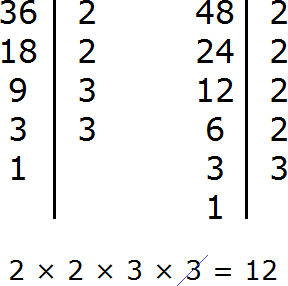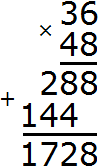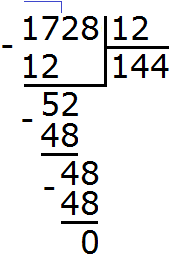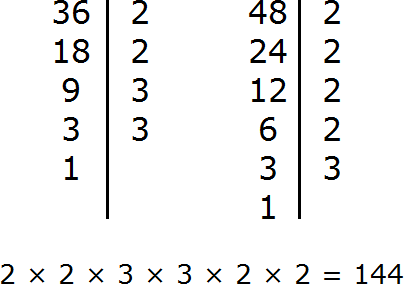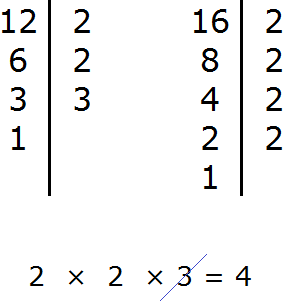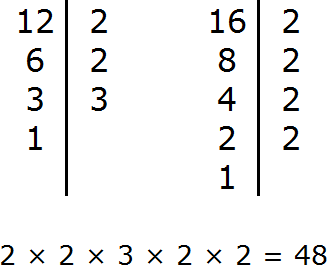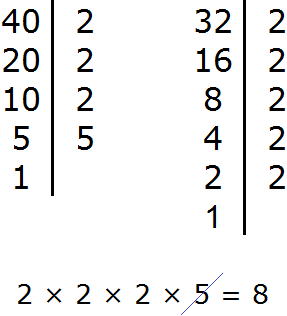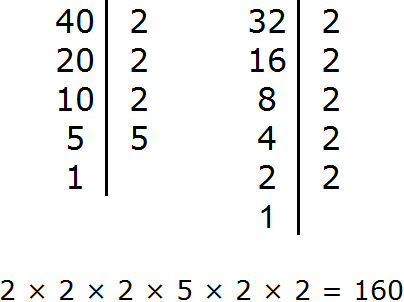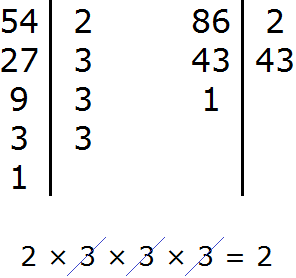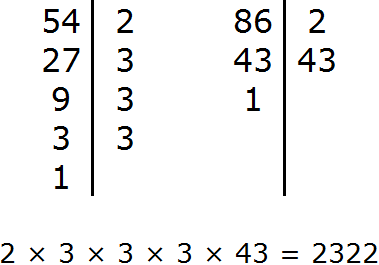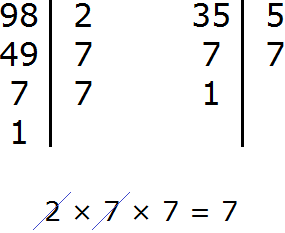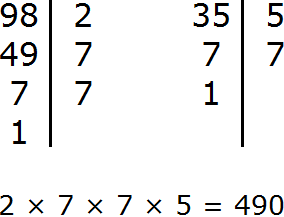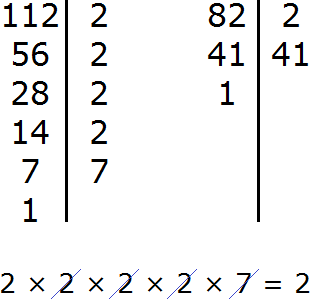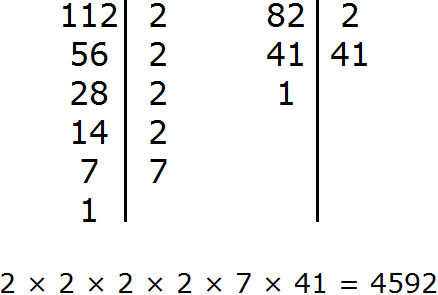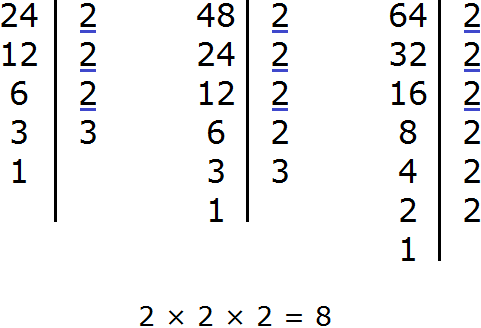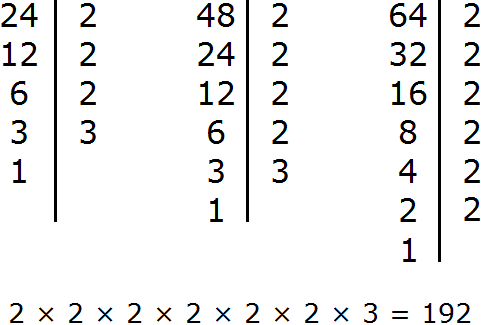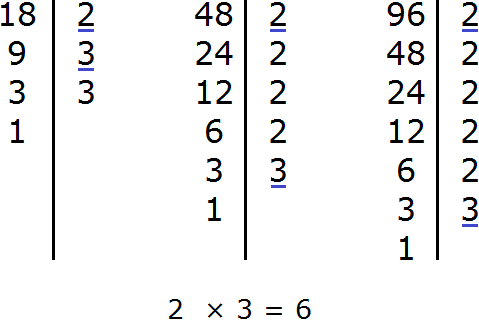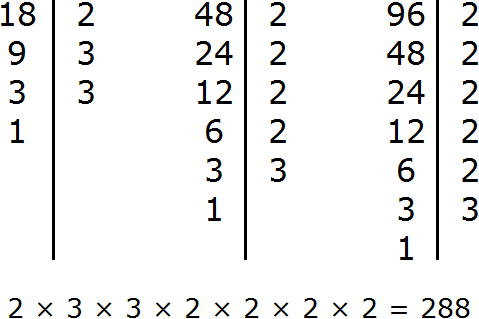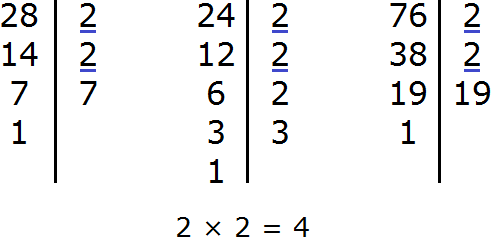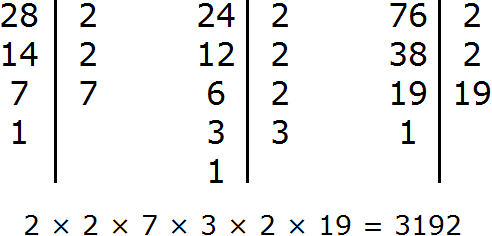Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.
Алгоритм Евклида для нахождения НОД
Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:
a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1
Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).
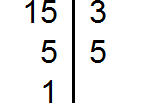
Найдите наибольший общий делитель чисел 64 и 48.
Решение
Введем обозначения: a=64, b=48.
На основе алгоритма Евклида проведем деление 64 на 48.
Получим 1 и остаток 16. Получается, что q1=1, r1=16.
Вторым шагом разделим 48 на 16, получим 3. То есть q2=3, а r2=0. Таким образом число 16 – это наибольший общий делитель для чисел из условия.
Ответ: НОД(64, 48)=16.
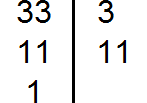
Чему равен НОД чисел 111 и 432?
Решение
Делим 432 на 111. Согласно алгоритму Евклида получаем цепочку равенств 432=111·3+99, 111=99·1+12, 99=12·8+3, 12=3·4.
Таким образом, наибольший общий делитель чисел 111 и 432 – это 3.
Ответ: НОД(111, 432)=3.
Найдите наибольший общий делитель чисел 661 и 113.
Решение
Проведем последовательно деление чисел и получим НОД(661, 113)=1. Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.
Ответ: НОД(661, 113)=1.
Нахождение НОД с помощью разложения чисел на простые множители
Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.
Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.
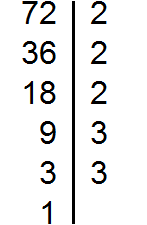
Найдите наибольший общий делитель чисел 72 и 96.
Решение
Найдем все простые множители чисел 72 и 96:
72361893122233
96482412631222223
Общими для двух чисел простые множители: 2, 2, 2 и 3. Это значит, что НОД(72, 96)=2·2·2·3=24.
Ответ: НОД(72, 96)=24.
Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.
Нахождение НОД трех и большего количества чисел
Независимо от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.
Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.
Решение
Введем обозначения: a1=78, a2=294, a3=570, a4=36.
Начнем с того, что найдем НОД чисел 78 и 294: d2=НОД(78, 294)=6.
Теперь приступим к нахождению d3=НОД(d2, a3)=НОД(6, 570). Согласно алгоритму Евклида 570=6·95. Это значит, что d3=НОД(6, 570)=6.
Найдем d4=НОД(d3, a4)=НОД(6, 36). 36 делится на 6 без остатка. Это позволяет нам получить d4=НОД(6, 36)=6.
d4=6, то есть, НОД(78, 294, 570, 36)=6.
Ответ: НОД(78, 294, 570, 36)=6.
А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.
Вычислите НОД чисел 78, 294, 570 и 36.
Решение
Произведем разложение данных чисел на простые множители: 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Для всех четырех чисел общими простыми множителями будут числа 2 и 3.
Получается, что НОД(78, 294, 570, 36)=2·3=6.
Ответ: НОД(78, 294, 570, 36)=6.
Нахождение НОД отрицательных чисел
Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.
Найдите НОД отрицательных целых чисел −231 и −140.
Решение
Для выполнения вычислений возьмем модули чисел, данных в условии. Это будут числа 231 и 140. Запишем это кратко: НОД(−231, −140)=НОД(231, 140). Теперь применим алгоритм Евклида для нахождения простых множителей двух чисел: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Получаем, что НОД(231, 140)=7.
А так как НОД(−231, −140)=НОД(231, 140), то НОД чисел −231 и −140 равен 7.
Ответ: НОД(−231, −140)=7.
Определите НОД трех чисел −585, 81 и −189.
Решение
Заменим отрицательные числа в приведенном перечне на их абсолютные величины, получим НОД(−585, 81, −189)=НОД(585, 81, 189). Затем разложим все данные числа на простые множители: 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.
Ответ: НОД(−585, 81, −189)=9.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: и
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
Раскладываем на множители число 40
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
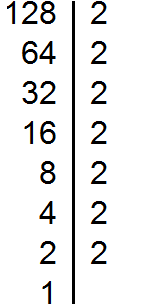
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
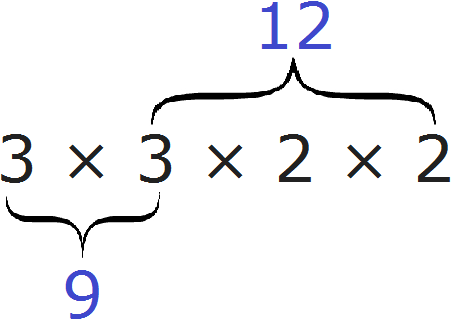
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
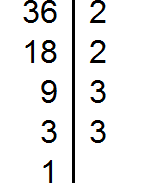
Разложим на множители число 24
Разложим на множители число 36
Получили три разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
Разложим на множители число 36
Разложим на множители число 42
Получили четыре разложения:
Теперь найдём и подчеркнём общие множители:
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
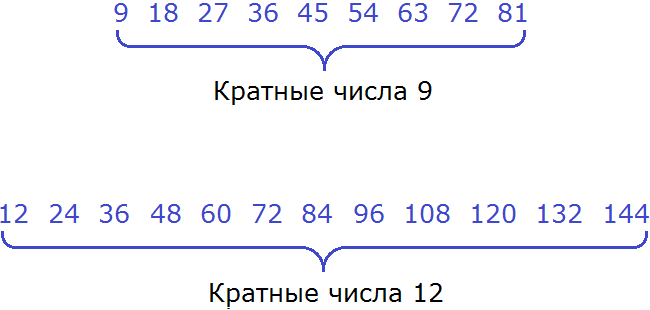
Теперь выпишем кратные обоих чисел:
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
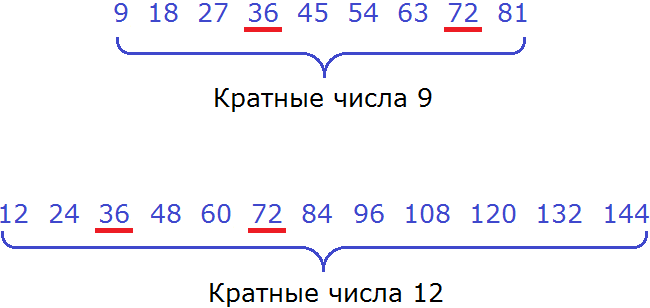
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
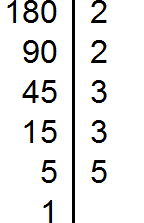
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
Разложим на множители число 180
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
Разложим на множители число 15
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
Разделим полученное число 288 на НОД чисел 24 и 12
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
Перемножим числа 36 и 48
Разделим 1728 на НОД чисел 36 и 48
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
Задание 2. Найдите НОК чисел 12 и 16
Решение:
Задание 3. Найдите НОД чисел 40 и 32
Решение:
Задание 4. Найдите НОК чисел 40 и 32
Решение:
Задание 5. Найдите НОД чисел 54 и 86
Решение:
Задание 6. Найдите НОК чисел 54 и 86
Решение:
Задание 7. Найдите НОД чисел 98 и 35
Решение:
Задание 8. Найдите НОК чисел 98 и 35
Решение:
Задание 9. Найдите НОД чисел 112 и 82
Решение:
Задание 10. Найдите НОК чисел 112 и 82
Решение:
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Калькулятор НОД и НОК
При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению. Вы можете найти НОД и НОК для двух, трех и четырех чисел
Выберите количество чисел для НОД и НОК
Наибольший общий делитель НОД
Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.
Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.
Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).
Свойства НОД
- Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.
Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15. - Если число a делится на b, то НОД(a, b) = b.
Например, число 20 делится на число 10, тогда НОД(20, 10) = 10. - При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.
Как найти наибольший общий делитель НОД
Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:
- Разложить числа на простые множители.
- Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
- Перемножить оставшиеся множители.
Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
58 – составное число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 – делится на простое число 2
12 : 2 = 6 – делится на простое число 2
6 : 2 = 3 – делится на простое число 2.
Завершаем деление, так как 3 простое числоРазложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
58 : 2 = 29 – делится на простое число 2.
Завершаем деление, так как 29 простое число - Выделим синим цветом и выпишем общие множители.
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
58 = 2 ⋅ 29
У чисел (24, 58) только один общий множитель – 2 и он и будет наибольшим общим делителем этих чиселОтвет: НОД (24, 58) = 2
Способ №2
- Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;
24 : 2 = 12;
24 : 3 = 8;
24 : 4 = 6;
24 : 6 = 4;
24 : 8 = 3;
24 : 12 = 2;
24 : 24 = 1;Для числа 58 выпишем все случаи, когда оно делится без остатка:
58 : 1 = 58;
58 : 2 = 29;
58 : 29 = 2;
58 : 58 = 1; - Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)
Общие делители чисел (24, 58): 1, 2
Ответ: НОД (24, 58) = 2
Наименьшее общее кратное НОК
Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.
Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).
Как найти наименьшее общее кратное НОК
Чтобы найти НОК двух, трех и более чисел необходимо:
- Разложить эти числа на простые множители.
- Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
- Умножить получившиеся множители.
Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
225 – составное число
30 – составное числоРазложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
225 : 3 = 75 – делится на простое число 3
75 : 3 = 25 – делится на простое число 3
25 : 5 = 5 – делится на простое число 5.
Завершаем деление, так как 5 простое числоРазложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
30 : 2 = 15 – делится на простое число 2
15 : 3 = 5 – делится на простое число 3.
Завершаем деление, так как 5 простое число - Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
225 = 3 ∙ 3 ∙ 5 ∙ 5
30 = 2 ∙ 3 ∙ 53) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450
Способ №2
- Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.
Выделим все кратные числа 225 зеленым цветом:
зеленым цветом:225 ∙ 1 = 225; 225 ∙ 2 = 450; 225 ∙ 3 = 675; 225 ∙ 4 = 900;
225 ∙ 5 = 1125; 225 ∙ 6 = 1350; 225 ∙ 7 = 1575; 225 ∙ 8 = 1800;
225 ∙ 9 = 2025; 225 ∙ 10 = 2250; 225 ∙ 11 = 2475; 225 ∙ 12 = 2700;
225 ∙ 13 = 2925; 225 ∙ 14 = 3150; 225 ∙ 15 = 3375; 225 ∙ 16 = 3600;
225 ∙ 17 = 3825; 225 ∙ 18 = 4050; 225 ∙ 19 = 4275; 225 ∙ 20 = 4500;
225 ∙ 21 = 4725; 225 ∙ 22 = 4950; 225 ∙ 23 = 5175; 225 ∙ 24 = 5400;
225 ∙ 25 = 5625; 225 ∙ 26 = 5850; 225 ∙ 27 = 6075; 225 ∙ 28 = 6300;
225 ∙ 29 = 6525; 225 ∙ 30 = 6750;Выделим все кратные числа 30 зеленым цветом:
30 ∙ 1 = 30; 30 ∙ 2 = 60; 30 ∙ 3 = 90; 30 ∙ 4 = 120;
30 ∙ 5 = 150; 30 ∙ 6 = 180; 30 ∙ 7 = 210; 30 ∙ 8 = 240;
30 ∙ 9 = 270; 30 ∙ 10 = 300; 30 ∙ 11 = 330; 30 ∙ 12 = 360;
30 ∙ 13 = 390; 30 ∙ 14 = 420; 30 ∙ 15 = 450; 30 ∙ 16 = 480;
30 ∙ 17 = 510; 30 ∙ 18 = 540; 30 ∙ 19 = 570; 30 ∙ 20 = 600;
30 ∙ 21 = 630; 30 ∙ 22 = 660; 30 ∙ 23 = 690; 30 ∙ 24 = 720;
30 ∙ 25 = 750; 30 ∙ 26 = 780; 30 ∙ 27 = 810; 30 ∙ 28 = 840;
30 ∙ 29 = 870; 30 ∙ 30 = 900; 30 ∙ 31 = 930; 30 ∙ 32 = 960;
30 ∙ 33 = 990; 30 ∙ 34 = 1020; 30 ∙ 35 = 1050; 30 ∙ 36 = 1080;
30 ∙ 37 = 1110; 30 ∙ 38 = 1140; 30 ∙ 39 = 1170; 30 ∙ 40 = 1200;
30 ∙ 41 = 1230; 30 ∙ 42 = 1260; 30 ∙ 43 = 1290; 30 ∙ 44 = 1320;
30 ∙ 45 = 1350; 30 ∙ 46 = 1380; 30 ∙ 47 = 1410; 30 ∙ 48 = 1440;
30 ∙ 49 = 1470; 30 ∙ 50 = 1500; 30 ∙ 51 = 1530; 30 ∙ 52 = 1560;
30 ∙ 53 = 1590; 30 ∙ 54 = 1620; 30 ∙ 55 = 1650; 30 ∙ 56 = 1680;
30 ∙ 57 = 1710; 30 ∙ 58 = 1740; 30 ∙ 59 = 1770; 30 ∙ 60 = 1800;
30 ∙ 61 = 1830; 30 ∙ 62 = 1860; 30 ∙ 63 = 1890; 30 ∙ 64 = 1920;
30 ∙ 65 = 1950; 30 ∙ 66 = 1980; 30 ∙ 67 = 2010; 30 ∙ 68 = 2040;
30 ∙ 69 = 2070; 30 ∙ 70 = 2100; 30 ∙ 71 = 2130; 30 ∙ 72 = 2160;
30 ∙ 73 = 2190; 30 ∙ 74 = 2220; 30 ∙ 75 = 2250; 30 ∙ 76 = 2280;
30 ∙ 77 = 2310; 30 ∙ 78 = 2340; 30 ∙ 79 = 2370; 30 ∙ 80 = 2400;
30 ∙ 81 = 2430; 30 ∙ 82 = 2460; 30 ∙ 83 = 2490; 30 ∙ 84 = 2520;
30 ∙ 85 = 2550; 30 ∙ 86 = 2580; 30 ∙ 87 = 2610; 30 ∙ 88 = 2640;
30 ∙ 89 = 2670; 30 ∙ 90 = 2700; 30 ∙ 91 = 2730; 30 ∙ 92 = 2760;
30 ∙ 93 = 2790; 30 ∙ 94 = 2820; 30 ∙ 95 = 2850; 30 ∙ 96 = 2880;
30 ∙ 97 = 2910; 30 ∙ 98 = 2940; 30 ∙ 99 = 2970; 30 ∙ 100 = 3000;
30 ∙ 101 = 3030; 30 ∙ 102 = 3060; 30 ∙ 103 = 3090; 30 ∙ 104 = 3120;
30 ∙ 105 = 3150; 30 ∙ 106 = 3180; 30 ∙ 107 = 3210; 30 ∙ 108 = 3240;
30 ∙ 109 = 3270; 30 ∙ 110 = 3300; 30 ∙ 111 = 3330; 30 ∙ 112 = 3360;
30 ∙ 113 = 3390; 30 ∙ 114 = 3420; 30 ∙ 115 = 3450; 30 ∙ 116 = 3480;
30 ∙ 117 = 3510; 30 ∙ 118 = 3540; 30 ∙ 119 = 3570; 30 ∙ 120 = 3600;
30 ∙ 121 = 3630; 30 ∙ 122 = 3660; 30 ∙ 123 = 3690; 30 ∙ 124 = 3720;
30 ∙ 125 = 3750; 30 ∙ 126 = 3780; 30 ∙ 127 = 3810; 30 ∙ 128 = 3840;
30 ∙ 129 = 3870; 30 ∙ 130 = 3900; 30 ∙ 131 = 3930; 30 ∙ 132 = 3960;
30 ∙ 133 = 3990; 30 ∙ 134 = 4020; 30 ∙ 135 = 4050; 30 ∙ 136 = 4080;
30 ∙ 137 = 4110; 30 ∙ 138 = 4140; 30 ∙ 139 = 4170; 30 ∙ 140 = 4200;
30 ∙ 141 = 4230; 30 ∙ 142 = 4260; 30 ∙ 143 = 4290; 30 ∙ 144 = 4320;
30 ∙ 145 = 4350; 30 ∙ 146 = 4380; 30 ∙ 147 = 4410; 30 ∙ 148 = 4440;
30 ∙ 149 = 4470; 30 ∙ 150 = 4500; 30 ∙ 151 = 4530; 30 ∙ 152 = 4560;
30 ∙ 153 = 4590; 30 ∙ 154 = 4620; 30 ∙ 155 = 4650; 30 ∙ 156 = 4680;
30 ∙ 157 = 4710; 30 ∙ 158 = 4740; 30 ∙ 159 = 4770; 30 ∙ 160 = 4800;
30 ∙ 161 = 4830; 30 ∙ 162 = 4860; 30 ∙ 163 = 4890; 30 ∙ 164 = 4920;
30 ∙ 165 = 4950; 30 ∙ 166 = 4980; 30 ∙ 167 = 5010; 30 ∙ 168 = 5040;
30 ∙ 169 = 5070; 30 ∙ 170 = 5100; 30 ∙ 171 = 5130; 30 ∙ 172 = 5160;
30 ∙ 173 = 5190; 30 ∙ 174 = 5220; 30 ∙ 175 = 5250; 30 ∙ 176 = 5280;
30 ∙ 177 = 5310; 30 ∙ 178 = 5340; 30 ∙ 179 = 5370; 30 ∙ 180 = 5400;
30 ∙ 181 = 5430; 30 ∙ 182 = 5460; 30 ∙ 183 = 5490; 30 ∙ 184 = 5520;
30 ∙ 185 = 5550; 30 ∙ 186 = 5580; 30 ∙ 187 = 5610; 30 ∙ 188 = 5640;
30 ∙ 189 = 5670; 30 ∙ 190 = 5700; 30 ∙ 191 = 5730; 30 ∙ 192 = 5760;
30 ∙ 193 = 5790; 30 ∙ 194 = 5820; 30 ∙ 195 = 5850; 30 ∙ 196 = 5880;
30 ∙ 197 = 5910; 30 ∙ 198 = 5940; 30 ∙ 199 = 5970; 30 ∙ 200 = 6000;
30 ∙ 201 = 6030; 30 ∙ 202 = 6060; 30 ∙ 203 = 6090; 30 ∙ 204 = 6120;
30 ∙ 205 = 6150; 30 ∙ 206 = 6180; 30 ∙ 207 = 6210; 30 ∙ 208 = 6240;
30 ∙ 209 = 6270; 30 ∙ 210 = 6300; 30 ∙ 211 = 6330; 30 ∙ 212 = 6360;
30 ∙ 213 = 6390; 30 ∙ 214 = 6420; 30 ∙ 215 = 6450; 30 ∙ 216 = 6480;
30 ∙ 217 = 6510; 30 ∙ 218 = 6540; 30 ∙ 219 = 6570; 30 ∙ 220 = 6600;
30 ∙ 221 = 6630; 30 ∙ 222 = 6660; 30 ∙ 223 = 6690; 30 ∙ 224 = 6720;
30 ∙ 225 = 6750; - Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).
Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750
Ответ: НОК (225 ; 30) = 450
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Нахождение НОД и НОК чисел
Онлайн-калькулятор “Нахождение НОД и НОК чисел“. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку “Вычислить” и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.
Выберите количество чисел, для которых требуется найти НОД и НОК:
2 числа
3 числа
4 числа
| Первое число | Второе число |
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6
Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144
Это следует знать!
Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7
В этом уроке мы поговорим о том как вычислять НОД и НОК. Дело в том, что элементарные арифметические вычисления должен уметь делать любой программист, так как алгоритм вычисления можно встретить во многих программах. Тем более вы их уже должны знать, если вы учились в школе 5 классе.
Наибольший общий делитель. НОД.
Для нахождения общего делителя вам нужно знать следующее:
Запомните: наибольший общий делитель (НОД) двух целых чисел – это наибольшее целое число, на которое делятся оба исходных числа без остатка. Однако одно из исходных чисел должно быть большее нуля.
Запомните: если у вас одно из двух чисел ноль, то НОД будет, то число что больше ноля.
Запомните: существует понятие взаимно-простых чисел, у которого нет общих делителей, кроме единицы. К примеру число 5 и 4, НОД этих чисел будет равен 1, так как если 5 разделить на 4 вы не получите целое число без остатка, следовательно НОД=1
Все остальные числа, у которых НОД больше 1, вычисляются по принципу бинарного алгоритма или с помощью алгоритма Евклида. В этой статье мы подробно разберем алгоритм Евклида, который еще называют взаимным вычитанием, поскольку НОД получается при последовательном вычитании меньшего из большего. Используем алгоритм Евклида в нашем примере НОД(12, 30). По алгоритму Евклида нам надо вычесть из большее меньшее, то есть из 30-12-12=6 В числе 30 у нас может поместиться число 12 только два раза, число 12 называют кратным, и остатком останется число 6. Теперь нам надо из числа 30 отнять кратное числа 6, которое у нас получилось, 30-6-6-6-6-6=5 НОД числа 12 и 30 будет равен 6. Так как нам надо найти именно наибольший делитель в нашем случаи 6 больше 5, следовательно НОД(12,30)=6. Как видите ничего сложного, теперь давайте составим блок схему.
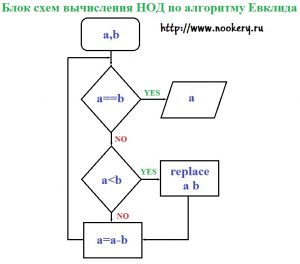
Блок-схема «Алгоритм Евклида»
рис.1
Если число a и b равно, НОД этих чисел будет любое из них, так как они могут делиться друг на друга. Если a и b не равны, мы их сравниваем a<b, если a меньше чем b то их надо поменять местами в a присвоить значение b, в b присвоить значение а и перейти к следующему вычислению описанного ниже. Если a больше чем b то, надо из а вычесть b, результат сохранить в a, и так до тех пор, пока а не станет равно b. Рассмотрим на примере.
Пример НОД(12,30).
- 12=30 | a==b; //в нашем случаи 12 не равно 30
- 12<30 | a<b;//производим сравнение на < >
- 30 12 | a==b; b==a; //меняем местами
- 30-12=18 | a=a-b;//производим вычитание
- 18=12| a==b;//равно ли а и b
- 18<12| a<b; //в нашем случае а >b
- 18-12=6|a=a-b; //производим вычитание
- 6=12|a==b; //в нашем случаи 6 не равно 12
- 6<12|a<b; //производим сравнение на < >
- 6 12| a==b; b==a; //меняем местами
- 12-6=6|a=a-b;//производим вычитание
- 6=6| a==b; //в нашем случаи 6 равно 6
- НОД(12,30)=6;
Наименьшее общее кратное(НОК).
НОК-это число которое из двух и более натуральных чисел является наименьшим натуральным числом, которое само делится нацело, и каждое из исходных чисел.
Самый простой и быстрый способ в плане реализации программного кода, это первоначально вычислить НОД двух чисел, затем произведение исходных двух целых чисел a и b разделить на НОД. Посмотрим на примере как это выглядет. Возьмем за пример все те же цифры 12 и 30 как мы помним наибольшее общее кратное равнялось 6. НОД=6 Следовательно по формуле НОК=a*b/НОД. НОК=12*30/6=60 Есть и другие варианты вычисления НОК к примеру каноническое разложение чисел. Рассмотрим пример, первоначально нам надо выяснить какое из чисел больше, потом мы раскладываем числа на кратные 12=2*2*3 , и число 30=2*3*5 Вычисляем произведение кратных чисел из числа 30, так как оно является наибольшим. В следующей операции, одинаковые цифры вычеркиваются, как это сделал я из большего меньшее, а оставшиеся кратные числа из 12 умножаются друг на друга, у нас осталось только число 2, которое умножается на произведение кратных чисел из 30, в результате вычисления вы и получите НОК. Выглядет это следующим образом НОК=2*3*5*2=60 Хорошо это можно представить в виде столбиков, как это можно видеть из рис. 2.

В целом ничего сложного, главное не запутаться, сейчас мы нарисуем блок схему наименьшего общего кратного (НОК).
Блок схема Наименьшего общего кратного (НОК)
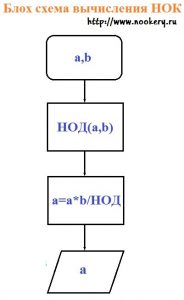
Алгоритм работы программы описан вначале, статьи о НОК.
Но как же быть если нам надо к примеру найти НОД трех и более натуральных чисел, или найти НОК трех или более натуральных чисел. Тут ничего сложного инструкцию по нахождению НОД из 3 чисел и НОК смотрим ниже.
НОД трех чисел:
- Сравниваем все числа К примеру a<b<c
- Начинаем вычисления с больших чисел к меньшим
- Вычисляем НОД по аналогии с двумя числами a и b
- Вычисляем по аналогии чисел НОД(a,b) и с Пример: НОД(a,b,c)=НОД((НОД(a,b)),с);
- НОД(12,30,60)
- 12<30<60
- НОД(60,30)=30
- НОД(30,12)=6
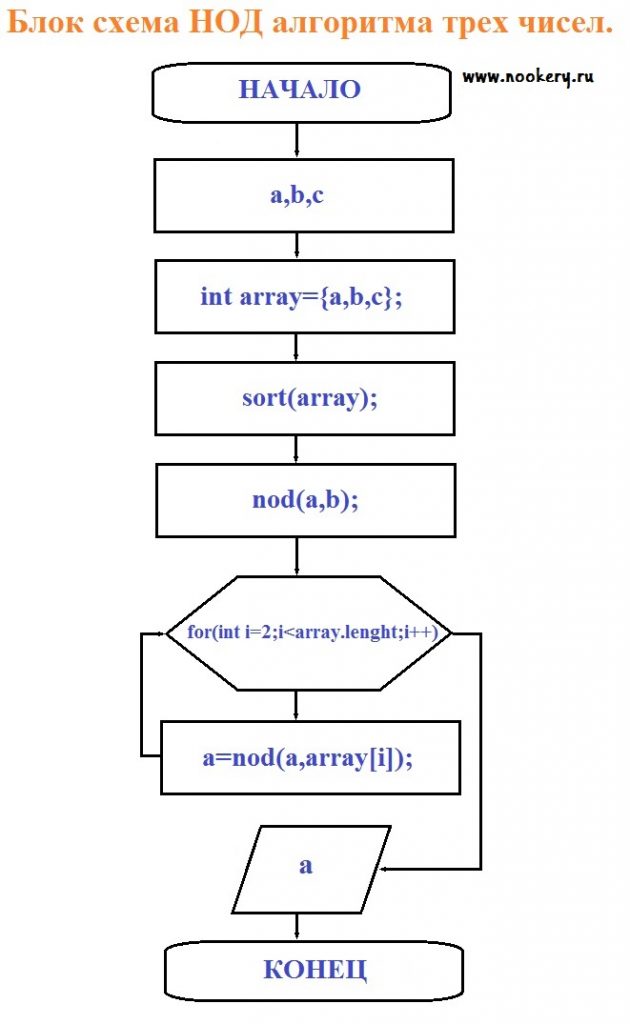
Точно так же производиться вычисления НОД из четырех чисел из пяти итд. По аналогии с НОД вычисляется и НОК с тремя и более числами. Приведу в пример НОД трех чисел блок схему алгоритма смотрите рис. 4.
Блок схема НОД алгоритма трех чисел, четырех чисел итд.
рис. 4
Разберем по подробнее работу программы блок схемы из рис. 4.
- У нас подается 3 числа, но их может быть сколько угодно.
- Их мы записываем в массив array.
- Выполняем метод sort(); Это мой метод он принимает массив чисел, делает сортировку по убыванию, пузырьковым методом, о нем вы можете прочитать из уроков о массивах.
- Выполняем метод nod(), который принимает первые два числа. Я создал метод по аналогии как написано выше в этой статье.
- В следующем блоке я помещаю в тело цикла метод nod(), который присваиваю возвращаемое число из метода nod() переменной a.
- Выводим результат.
- Завершаем работу программы.
Скачать калькулятор НОК и НОД .
Пока писал статью, написал программу НОК и НОД вычисления, которую можете скачать с сайта. Работа программы очень простая, достаточно в текстовое поле вписать цифры через пробел или запятую, нажать на кнопку вычислить или Enter и программа выведет результат. Программа написана на языке java. Может запускаться со всех систем.
рис 5.
Скачать калькулятор НОК и НОД .