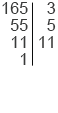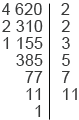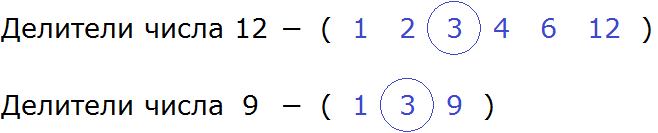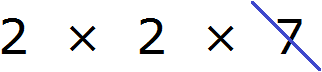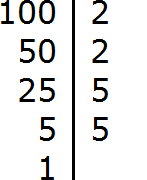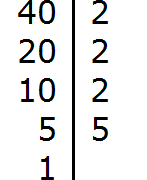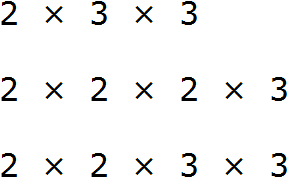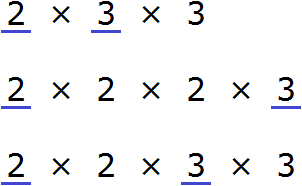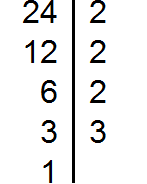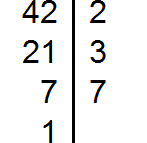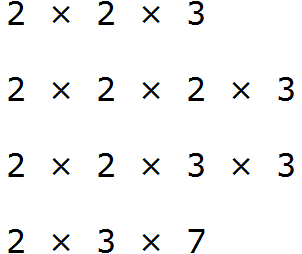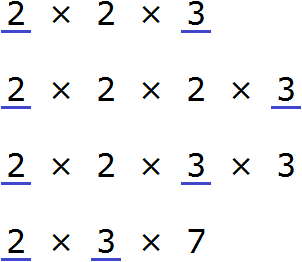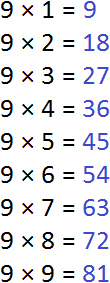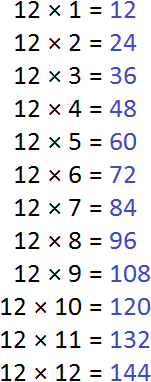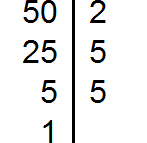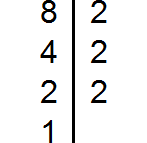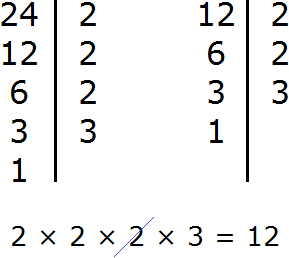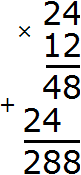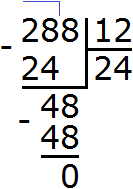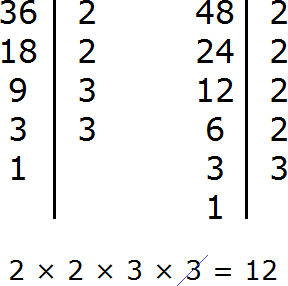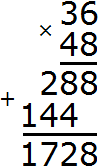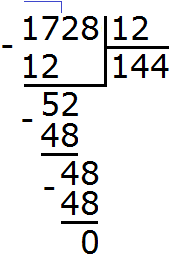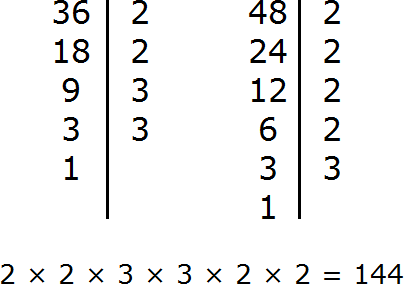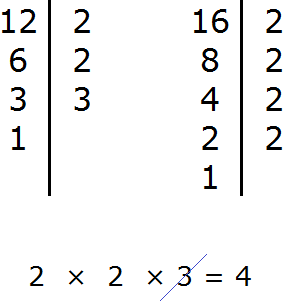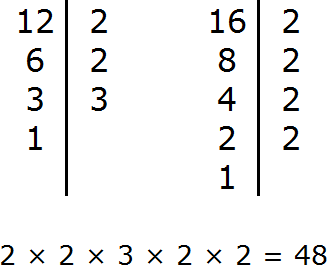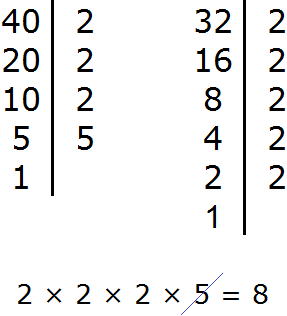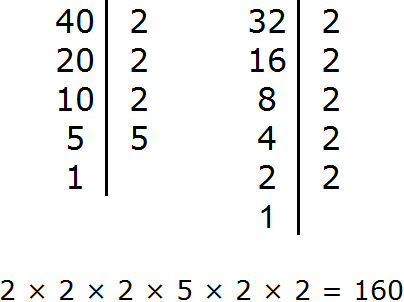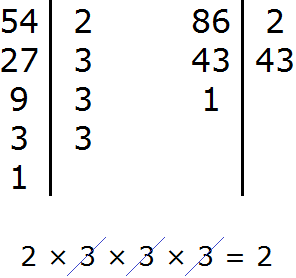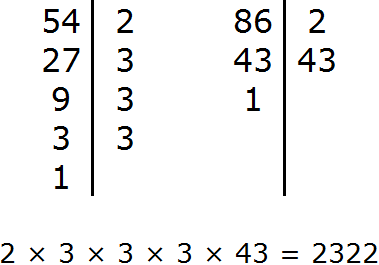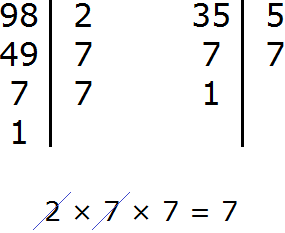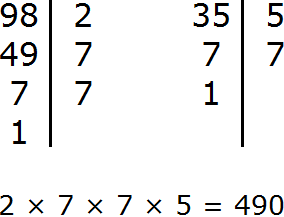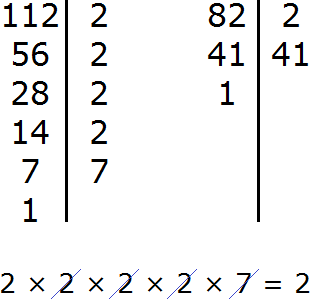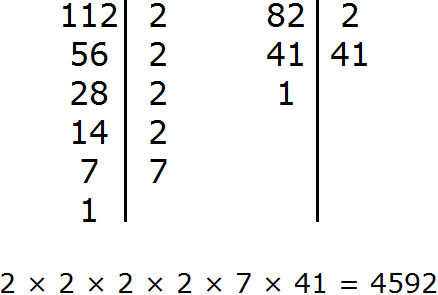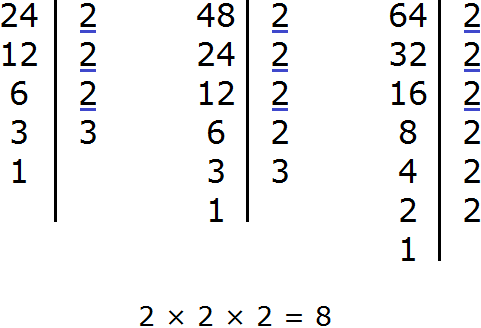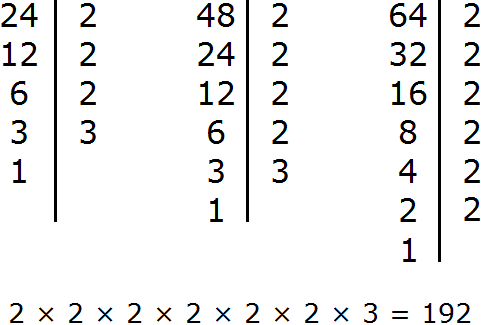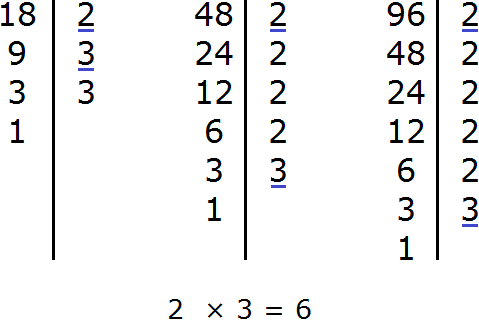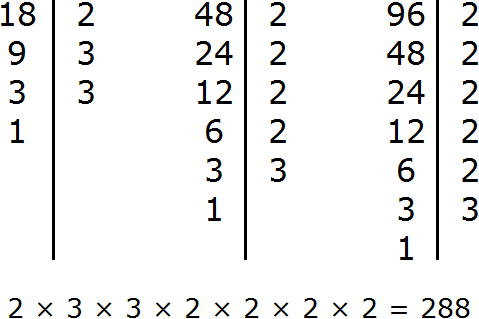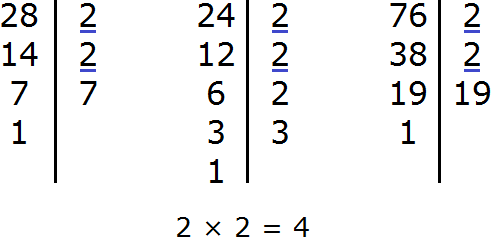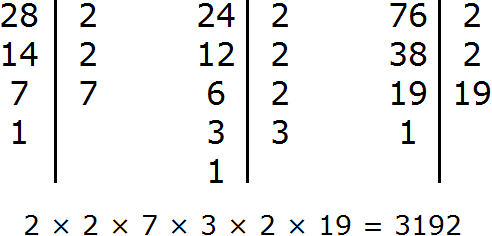Как найти нод гдз - Сайт, где вы сможете решить свои вопросы

Ответы к учебнику для 6 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Вопросы к параграфу

1. Какое число называют наибольшим общим делителем двух чисел?

Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое нацело делятся оба этих числа.

2. Как можно найти НОД двух натуральных чисел, используя их разложения на простые множители?

Чтобы найти наибольший общий делитель (НОД) надо:

Разложить оба числа на простые множители и записать их в виде произведения степеней.

Определить степени, основания которых являются одинаковыми в обоих произведениях.

Выбрать из каждой пары степеней с одинаковыми основаниями степень с меньшим показателем.

Перемножить выбранные степени.

Полученное число и будет НОД двух данных чисел.

Например найдём наибольший общий множитель для чисел 18 и 24, используя данное правило:

1. Разложим оба числа на простые множители и записать их в виде произведения степеней.

2. Определим степени, основания которых являются одинаковыми в обоих произведениях (соответствующие одинаковые основания степеней подчёркнуты линиями зелёного и фиолетового цвета).

3. Выберем из каждой пары степеней с одинаковыми основаниями степень с меньшим показателем.

4. Перемножить выбранные степени.

Значит набольший общий делитель чисел 18 и 24 равен 6.

Ответ: НОД (18, 24) = 6

3. Какие числа называют взаимно простыми?

Взаимно простые — это числа, у которых наибольший общий делитель равен 1.

4. Чему равен наибольший общий делитель двух чисел, одно из которых кратно другому?

Если одно из чисел кратно другому, то наибольшим общим делителем будет меньшее из этих чисел.

Решаем устно

1. Какие из чисел 1, 2, 3, 4, 5, 6, 10, 11, 14, 15, 17, 31, 32, 33 являются простыми, а какие — составными?

Простые числа:

1, 2, 3, 5, 11, 17, 31.

Составные числа:

4, 6, 10, 14, 15, 32, 33.

2. Назовите все простые значения х, при которых будет верным неравенство 40 < х < 50.

41, 43, 47, 49.

3. Назовите все составные значения у, при которых будет верным неравенство 15 < у < 25.

19, 18, 20, 21, 22, 24.

4. Какие одинаковые цифры надо поставить вместо звёздочек, чтобы было верным равенство 2,* + 4,* = 7,6?

Надо поставить цифры 8, так как 2,8 + 4,8 = 7,6.

5. Является ли данное разложение на множители разложением на простые множители:

1) 120 = 2 • 3 • 4 • 5

Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а число 4 — составное число.

2) 567 = 7 • 9

Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а число 9 — составное число.

3) 180 = 3 • 6 • 10

Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а числа 6 и 10 — составные.

6. Сколько всего делителей у числа а, если а = 3 • 5 • 19?

Делителями числа являются все возможные произведения его простых делителей, а также единицы:

1
3
3 • 5
3 • 19
3 • 5 • 19
5
5 • 19 = 95

Ответ: у этого числа всего 7 делителей.

Упражнения

138. Найдите наибольший общий делитель чисел:

139. Найдите наибольший общий делитель чисел:

140. Найдите наибольший общий делитель чисел а и b:

1) а = 2 • 2 • 3 • 5 • 7 • 19 и b = 2 • 3 • 3 • 7 • 11 • 13;

НОД(a, b) = 2 • 3 • 7 = 42

2) $a=2^{3}cdot 3^{2}cdot 7^{3}cdot 11^{2}cdot 19$ и $b=2^{2}cdot 3^{5}cdot 11^{2}cdot 19^{3}$

НОД(a, b) = 2² • 3² • 11² • 19 = 4 • 9 • 121 • 19 = 82 764

141. Найдите наибольший общий делитель чисел:

142. Найдите наибольший общий делитель чисел:

143. Среди данных пар чисел выберите пары взаимно простых чисел. Для пар чисел, не являющихся взаимно простыми, укажите наибольший общий делитель.

144. Составьте все пары взаимно простых чисел из чисел 12, 14, 33, 25.

Разложим числа на простые множители:

Взаимно простыми называются числа, у которых наибольший общий множитель равен 1. Значит взаимно простыми будут следующие пары чисел:

12 и 25;
14 и 33;
14 и 25;
33 и 25.

145. Составьте все пары взаимно простых чисел из чисел 15, 16, 21, 77.

Разложим числа на простые множители:

15 и 16;
15 и 77;
16 и 21;
16 и 77.

146. Запишите все правильные дроби со знаменателем 15, у которых числитель и знаменатель — взаимно простые числа.

$frac{1}{15}, frac{2}{15}, frac{4}{15}, frac{7}{15}, frac{8}{15}, frac{11}{15}, frac{13}{15}, frac{14}{15.}$

147. Запишите все неправильные дроби с числителем 16, у которых числитель и знаменатель — взаимно простые числа.

$frac{16}{1}, frac{16}{3}, frac{16}{5}, frac{16}{7}, frac{16}{9}, frac{16}{11}, frac{16}{13}, frac{16}{15}.$

148. Докажите, что:

1) числа 364 и 495 — взаимно простые

Числа 364 и 495 не имеют общих множителей, больших 1.

2) числа 380 и 399 не являются взаимно простыми

Числа 380 и 399 имеют общий множитель больший, чем 1. Это число 19. Значит они не являются взаимно простыми числами.

149. Докажите, что:

1) числа 945 и 572 — взаимно простые

Числа 945 и 572 не имеют общих множителей, больших 1.

2) числа 1 095 и 738 не являются взаимно простыми

Числа 1 095 и 738 имеют общий множитель больший, чем 1. Это число 3. Значит они не являются взаимно простыми числами.

150. Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.

Из цифр 2, 3, 4 можно записать двузначные числа (если цифры ы каждом различны):

23, 24,
32, 34,
42, 43.

Из них взаимно простыми будут пары чисел:

23 и 24;
23 и 32;
23 и 34;
23 и 42;
23 и 43;
43 и 24;
43 и 32;
43 и 34;
43 и 42.

Так как 223 и 43 — простые числа, а остальные числа чётные — значит между собой не могут быть взаимно простыми.

151. Напишите три нары составных чисел такие, что в парах числа являются взаимно простыми.

Например, такими числами могут быть:

16 и 25;
80 и 81;
28 и 333.

152. Между учениками 6 класса поделили поровну 155 тетрадей и 62 ручки. Сколько в этом классе учеников?

Разложим числа 155 и 62 на простые множители:

Наибольший общий делитель для этих чисел равен 31: НОД (155, 62) = 31.

Значит в классе 31 ученик.

Ответ: 31 ученик.

153. На автомобили погрузили 96 контейнеров с картофелем и 64 контейнера с капустой. Сколько было автомобилей, если известно, что их не меньше 20 и на всех автомобилях было одинаковое количество контейнеров с картофелем и одинаковое количество контейнеров с капустой?

1) Найдём все общие делители для чисел 96 и 64:

2) Значит общими делителями для чисел 96 и 64 могут быть числа:

3) Из чисел 2, 4, 8, 16 и 32 только число 32 > 20. Значит всего могло быть только 32 автомобиля.

Ответ: 32 автомобиля.

154. Между школьными библиотеками разделили 92 толковых и 138 орфографических словарей русского языка. Сколько было школ, если известно, что их не менее 25 и все школы получили одинаковые комплекты, состоящие из словарей двух видов?

1) Найдём все общие делители для чисел 92 и 138:

2) Значит общими делителями для чисел 92 и 138 могут быть числа:

2
23
2 • 23 = 46

3) Из чисел 2, 23 и 46 только число 46 > 25. Значит всего могло быть только 46 школ.

Ответ: 46 школ.

155. Для новогодних подарков приобрели 96 шоколадок, 72 апельсина и 84 банана. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все продукты? Сколько в отдельности шоколадок, апельсинов и бананов будет в каждом подарке?

1) Найдём наибольший общий делитель (НОД) для чисел 96, 72 и 84:

Значит наибольшее количество подарков, которые можно сформировать из всех продуктов, будет 12 штук.

2) Посчитаем, сколько шоколадок, апельсинов и бананов будет в каждом подарке:

96 : 12 = 8 (шт.) — шоколадок будет в каждом подарке.
72 : 12 = 6 (шт.) — апельсинов будет в каждом подарке.
84 : 12 = 7 (шт.) — бананов будет в каждом подарке.

Ответ: Всего получиться 12 подарков, в каждом подарке будет по: 8 шоколадок, 6 апельсинов и 7 бананов.

156. Из 156 жёлтых, 234 белых и 390 красных роз составляли букеты. Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?

Найдём наибольший общий делитель (НОД) для чисел 156, 234 и 390:

Значит наибольшее количество букетов, которые можно составить, если необходимо использовать все цветы — 78 штук.

Ответ: 78 букетов.

Упражнения для повторения

157. Используя цифры 2, 5 и 9 (цифры не могут повторяться), запишите трехзначное число, которое:

1) кратно 2

952 или 892 — чтобы число было кратно 2, на конце должна быть чётная цифра.

2) кратно 5

295 или 925 — чтобы число было кратно 5, а конце должна быть цифра 5 или 0, но среди заданных цифр нуля нет.

Можно ли с помощью этих цифр записать число, кратное 3

Чтобы число делилось на 3 надо, чтобы сумма его цифр делилась на 3.

2 + 5 + 9 = 7 + 9 = 16 — не делится на 3, значит ни одно трёхзначное число, составленное из этих цифр, не будет делится на 3.

158. Какую цифру можно поставить вместо звёздочки в записи 1*8, чтобы полученное число делилось нацело на 18?

Чтобы число делилось на 18 надо, чтобы число было чётным и сумма его цифр делилась на 9. Проверим последовательно все возможные варианты цифр на месте звёздочки:

если вместо звёздочки поставить 0, то получим чётное число 108, а 1 + 8 = 9 делится на 9 — значит на месте звёздочки может быть цифра 0;
если вместо звёздочки поставить 1, то получим чётное число 118, а 1 + 1 + 8 = 10 не делится на 9 — значит на месте звёздочки не может быть цифра 1;
если вместо звёздочки поставить 2, то получим чётное число 128, а 1 + 2 + 8 = 11 не делится на 9 — значит на месте звёздочки не может быть цифра 2;
если вместо звёздочки поставить 3, то получим чётное число 138, а 1 + 3 + 8 = 12 не делится на 9 — значит на месте звёздочки не может быть цифра 3;
если вместо звёздочки поставить 4, то получим чётное число 148, а 1 + 4 + 8 = 13 не делится на 9 — значит на месте звёздочки не может быть цифра 4;
если вместо звёздочки поставить 5, то получим чётное число 158, а 1 + 5 + 8 = 14 не делится на 9 — значит на месте звёздочки не может быть цифра 5;
если вместо звёздочки поставить 6, то получим чётное число 168, а 1 + 6 + 8 = 15 не делится на 9 — значит на месте звёздочки не может быть цифра 6;
если вместо звёздочки поставить 7, то получим чётное число 178, а 1 + 7 + 8 = 16 не делится на 9 — значит на месте звёздочки не может быть цифра 7;
если вместо звёздочки поставить 8, то получим чётное число 188, а 1 + 8+ 8 = 17 не делится на 9 — значит на месте звёздочки не может быть цифра 8;
если вместо звёздочки поставить 9, то получим чётное число 198, а 1 + 9 + 8 = 18 делится на 9 — значит на месте звёздочки может быть цифра 9.

Ответ: вместо звездочки можно поставить цифру 0 или 9.

159. Запишите число 19 в виде суммы трёх простых чисел.

19 = 3 + 5 + 11

160. Если к некоторому двузначному числу справа дописать нуль, то данное число увеличится на 432. Найдите это число.

Пусть х — искомое двузначное число, тогда 10х — число, которое получиться из искомого, если справа к нему дописать нуль. Мы знаем, что 10х на 432 больше, чем х. Можем составить уравнение:

Значит искомое число равно 48.

Ответ: 48.

161. Найдите числа, которых недостаёт в цепочке вычислений:

Составим уравнения и решим их:

Ответ: a = 0,05; b = 0,34; c = 0,04.

Составим уравнения и решим их:

Ответ: a = 1,5; x = 0,4; y = 0,05.

Задача от мудрой совы

162. Барон Мюнхгаузен рассказывал, что он разрезал арбуз на четыре части, а после того, как его съели, осталось пять корок. Может ли такое быть, если корки не ломать?

Да, это возможно. Для того, чтобы разрезать арбуз на 4 части, а потом получить 5 корок, надо:

вырезать сердцевину арбуза, например в виде цилиндра (на рисунке обозначено красными линиями), чтобы после того, как этот кусок будет съеден, осталось 2 корки — верхняя и нижняя;
разрезать оставшуюся часть арбуза ещё на 3 части (на рисунке линии разрезов обозначены синим).

Итого получиться:

4 куска — 1 центральный и 3 боковых
5 корок — верхняя, нижняя и 3 боковых.

Ответ: да, это возможно.

Ответы к учебнику для 6 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Источник

Главная
Справочники
Справочник по математике 5-9 класс
Обыкновенные дроби
Наибольший общий делитель

Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.

Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.

Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.

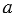
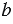
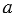
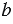
Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

Найдем НОД(240; 165).

240 = 222235 165 = 3511.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

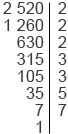
2 520 = 2223357 4 620 = 2235711.

Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 – дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520. Так же число 3 является множителем рассматриваемых чисел, а число 9 = 33 является только делителем числа 2520. Кроме чисел 4 и 3, общими делителями данных чисел являются числа 5 и 7.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Чтобы найти НОД нескольких натуральных чисел, надо:

разложить их на простые множители;
из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
найти произведение оставшихся множителей.

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2³3²5¹7¹

4 620 = 2²3¹5¹7¹11¹.

Тогда НОД мы можем найти по следующему правилу:

Определить степени, основания которых являются общими простыми делителями данных чисел.
Из каждой пары степеней с одинаковыми основаниями выбрать степень с меньшим показателем.
Перемножить выбранные степени. Полученное произведение является искомым наибольшим общим делителем.

Найдем НОД(2520; 4620):

Выписываем общие основания: 2, 3, 5, 7.
Выбираем наименьшие показатели данных степеней: 2², 3¹, 5¹, 7¹.
Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 2²3¹5¹7¹ = 420.

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

6 класс

Номер 142,
Мерзляк, Полонский, Якир, Учебник

Номер 163,
Мерзляк, Полонский, Якир, Учебник

Номер 171,
Мерзляк, Полонский, Якир, Учебник

Номер 239,
Мерзляк, Полонский, Якир, Учебник

Номер 247,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Задание 169,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 171,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1492,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

7 класс

Номер 351,
Мерзляк, Полонский, Якир, Учебник

Источник

Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.

Как найти НОД?

Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
выбрать одинаковые множители, входящие в оба разложения;
найти их произведение.

Примеры нахождения наибольшего общего делителя

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОД 12 и 8

1. Раскладываем 12 и 8 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2

3. Перемножаем эти множители и получаем: 2 · 2 = 4

Ответ: НОД (8; 12) = 2 · 2 = 4.

Пример 2: найти НОД 75 и 150

Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:

1. Раскладываем 75 и 150 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5

3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75

Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.

Частный случай или взаимно простые числа

Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:

Пример 3: найти НОД 9 и 5

1. Раскладываем 5 и 9 на простые множители:

Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.

Источник

Нахождение НОД и НОК чисел

Онлайн-калькулятор “Нахождение НОД и НОК чисел“. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку “Вычислить” и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.

Выберите количество чисел, для которых требуется найти НОД и НОК:

2 числа
3 числа
4 числа

Первое число	Второе число

Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6

Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144

Это следует знать!
Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7

Источник

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

12 : 3 = 4

9 : 3 = 3

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

2 × 3 = 6

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

28 : 4 = 7

16 : 4 = 4

НОД (28 и 16) = 4

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

100 : 20 = 5

40 : 20 = 2

НОД (100 и 40) = 20.

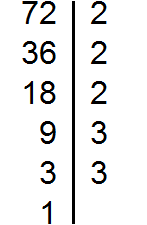
Пример 3. Найти НОД чисел 72 и 128

Раскладываем на множители число 72

Раскладываем на множители число 128

Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.

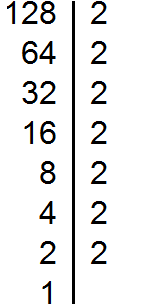
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

72 : 8 = 9

128 : 8 = 16

НОД (72 и 128) = 8

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

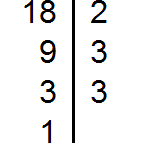
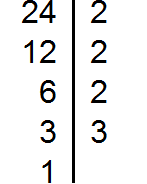
Например, найдём НОД для чисел 18, 24 и 36

Разложим на множители число 18

Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

18 : 6 = 3

24 : 6 = 4

36 : 6 = 6

НОД (18, 24 и 36) = 6

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

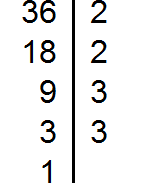
Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

12 : 6 = 2

24 : 6 = 4

36 : 6 = 6

42 : 6 = 7

НОД (12, 24 , 36 и 42) = 6

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

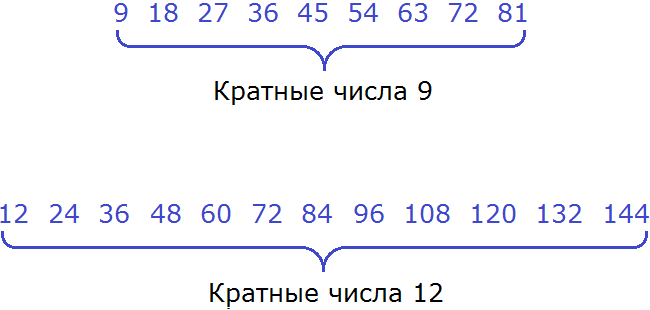
Теперь выпишем кратные обоих чисел:

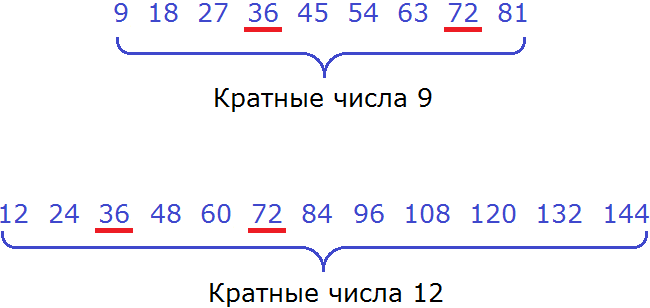
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

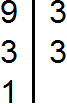
Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

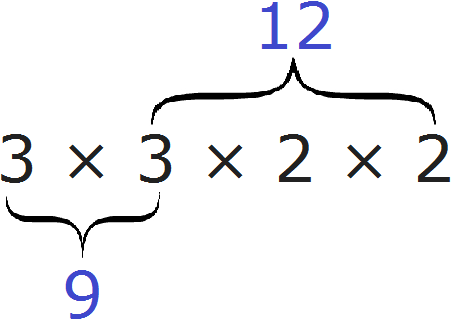
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12

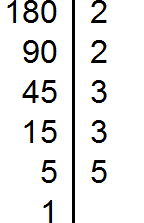
Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

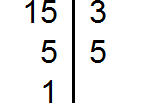
Разложим на множители число 15

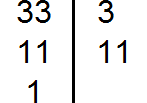
Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

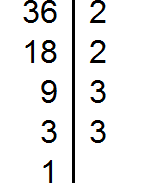
Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК (36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».