Для нахождения ${class{cyr}{НОД}}(a, b)$ можно поступить следующим естественным образом:
разложить оба числа по степеням простых чисел:
$a = 2^{alpha_1} cdot 3^{alpha_2} cdot ldots cdot p^{alpha_n}_n$,
$b = 2^{beta_1} cdot 3^{beta_2} cdot ldots cdot p^{beta_n}_n$,
($alpha_k$ и $beta_k$ могут быть равны нулю).
Тогда
${class{cyr}{НОД}}(a, b) =$ $2^{min(alpha_1, beta_1)} cdot 3^{min(alpha_2, beta_2)} cdot ldots cdot p^{min(alpha_n, beta_n)}_n.$
Например, для нахождения наибольшего общего делителя $2625$ и $8100$ получим:
$2625 = 2^0 cdot 3^1 cdot 5^3 cdot 7^1,$ $8100 = 2^2 cdot 3^4 cdot 5^2 cdot 7^0$,
значит
${class{cyr}{НОД}}(2625, 8100) =$ $2^0 cdot 3^1 cdot 5^2 cdot 7^0 = 75.$
Существенный недостаток этого способа в том, что разложить большое число на простые множители
не так просто, а точнее — не так быстро.
Евклид в 7 книге «Начал» описывает алгоритм нахождения «общей меры двух чисел». Алгоритм описан
геометрически, как нахождение общей меры двух отрезков. Он сводится к «последовательному отнятию» от большего
отрезка меньшего отрезка. Теперь этот алгоритм известен как алгоритм Евклида для нахождения
наибольшего общего делителя двух натуральных чисел.
Основная идея, на которой основан алгоритм, состоит в том, что НОД чисел $a$ и $b$ равен НОД
чисел $b$ и $a-b.$ Отсюда следуют, что если поделить $a$ на $b$ с остатком, т.е. представить в виде
$a = b cdot q + r$, то ${class{cyr}{НОД}}(a, b) = $ ${class{cyr}{НОД}}(b, r).$
Опишем красивую геометрическую интерпретацию алгоритма, интерактивная реализация которой предложена выше.
В прямоугольнике с длинами сторон $a$ и $b$ закрашиваем максимально возможный квадрат. В оставшемся
прямоугольнике снова закрашиваем максимально возможный квадрат. И так далее до тех пор, пока весь
исходный прямоугольник не будет закрашен. Длина стороны самого маленького квадрата и будет равна ${class{cyr}{НОД}}(a, b).$
Более подробно геометрическая интерпретация описана ниже, а параллельно приведено арифметическое описание алгоритма Евклида.
Онлайн калькулятор НОД и НОК двух чисел
Наибольший общий делитель (НОД)
НОД двух или более целых чисел — это наибольшее целое число, которое является делителем каждого из этих чисел.
Если натуральное число a делится на натуральное число bb, то bb называют делителем числа aa, а число aa называют кратным числа bb. aa и bb являются натуральными числами. Число gg называют общим делителем и для aa и для bb. Множество общих делителей чисел aa и bb конечно, так как ни один из этих делителей не может быть больше, чем aa. Значит, среди этих делителей есть наибольший, который называют наибольшим общим делителем чисел aa и bb и для его обозначения используют записи: НОД (a;b)(a;b) или D(a;b)(a;b)
Пример
Наибольший общий делитель (НОД) чисел 1818 и 2424 — это 66.
Как найти наибольший общий делитель (НОД)
Существует несколько способов нахождения наибольшего общего делителя (НОД) двух или более целых чисел:
- Алгоритм Евклида: НОД(a,b)=(a, b) = НОД (b,a(b, a mod b)b), где «mod» – это операция взятия остатка от деления большего числа на меньшее. Этот алгоритм можно продолжать до тех пор, пока одно из чисел не станет равно нулю. В этом случае НОД равен ненулевому числу.
Пример
НОД(18,24)=НОД(24,18)=НОД(18,6)=НОД(6,0)=6НОД(18, 24) = НОД(24, 18) = НОД(18, 6) = НОД(6, 0) = 6
- Разложение на простые множители: Найти все простые множители каждого из чисел и их степени. НОД будет равен произведению всех общих простых множителей в минимальной степени.
Пример
НОД(60,84)=22⋅31=12(60, 84) = 2^{2} cdot 3^{1} = 12, так как общие простые множители −2- 2 и 33, их минимальные степени −2- 2 и 11 соответственно.
- Таблица делителей: Составить таблицы всех делителей каждого числа и найти наибольшее общее число, которое является делителем обоих чисел. Этот метод не рекомендуется для больших чисел, так как он требует много времени и усилий.
Наименьшее общее кратное (НОК)
НОК двух или более целых чисел — это наименьшее число, которое делится на каждое из этих чисел без остатка.
Общими кратными чисел называются числа которые делятся на исходные без остатка. Например для чисел 2525 и 5050 общими кратными будут числа 50,100,150,20050,100,150,200 и т.д Наименьшее из общих кратных будет называться НОК и обозначается НОК(a;b)(a;b) или K(a;b).(a;b).
Пример
Наименьшее общее кратное чисел 88 и 1212 – это 2424. Т.е. НОК (8,12)=24(8, 12) = 24.
Как найти наименьшее общее кратное (НОК)
Чтобы найти НОК двух чисел, необходимо:
- Разложить числа на простые множители;
- Выписать множители, входящие в состав первого числа и добавить к ним множители, которые входят в состав второго и не ходят в состав первого;
- Найти произведение чисел, найденных на шаге 2. Полученное число и будет искомым наименьшим общим кратным.
Пример
Рассмотрим два числа: 88 и 1212. Найдем их НОКНОК:
- Разложим 88 и 1212 на простые множители: 8=23,12=22⋅38 = 2^3, 12 = 2^2 cdot 3.
- Выпишем все простые множители: 23⋅32^3 cdot 3.
- Для каждого простого множителя выберем наибольшую кратность: 232^3 и 33.
- Умножим выбранные простые множители между собой: 23⋅3=242^3 cdot 3 = 24.
Таким образом, НОК чисел 88 и 1212 равен 2424.
Свойства НОД и НОК
- Любое общее кратное чисел aa и bb делится на K(a;b)(a;b);
- Если a⋮bavdots b , то К(a;b)=a(a;b)=a;
- Если К(a;b)=k(a;b)=k и mm-натуральное число, то К(am;bm)=km(am;bm)=km. Если dd-общий делитель для aa и bb,то К(ad;bdfrac{a}{d};frac{b}{d})= kd frac{k}{d}
- Если a⋮cavdots c и b⋮cbvdots c ,то abcfrac{ab}{c} – общее кратное чисел aa и bb;
- Для любых натуральных чисел aa и bb выполняется равенство D(a;b)⋅К(a;b)=abD(a;b)cdot К(a;b)=ab;
- Любой общий делитель чисел aa и bb является делителем числа D(a;b)D(a;b).
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка.
Д(12) = {1,2,3,4,6,12}
Д(36) = {1,2,3,4,6,12,18,36}
Общий делитель двух данных чисел — это число, на которое делятся без остатка оба данных числа.
Рассмотрим на примере чисел 12 и 36. Общие делители этих чисел: 1, 2, 3, 4, 6 и 12, то есть на все эти числа оба наших числа делятся без остатка. Но математику из всех этих общих делителей интересует только наибольший – 12. Это число так и называют: наибольший общий делитель.
Наибольший общий делитель нескольких чисел (НОД) – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка.
И как вы заметили, если одно число делится без остатка на другое, то меньшее число и будет наибольшим общим делителем.
Если НОД чисел равен 1, такие числа называют взаимно простыми.
НОД (7; 9) = 1,
7 и 9 – взаимно простые числа.
Взаимно простые числа — это натуральные числа, которые имеют только один общий делитель — число 1.
Как найти наибольший общий делитель
Чтобы найти НОД двух или более натуральных чисел, нужно сначала разложить их на простые множители. Это удобно делать в столбик.
Пример 1. Найдем НОД чисел 28 и 10. Разложим их на простые множители.
28|2 10|2
14|2 5|5
7|7 1|
1|
28 = 2 · 2 · 7
10 = 2 · 5
Затем найдем общие множители. Мы видим, что число 2 – одинаковый простой множитель в обоих числах. Подчеркнем его. А поскольку больше повторяющихся чисел нет, это и будет наибольший общий делитель.
НОД(28;10) = 2
Пример 2. Найдем НОД чисел 28 и 36.
28|2 36|2
14|2 18|2
7|7 9|3
1| 3|3
1|
28 = 2 · 2 · 7
36 = 2 · 2 · 3 · 3
Общих множителей два: это 2 · 2. Чтобы найти НОД, нужно их перемножить.
НОД(28;36) = 2 · 2 = 4
То же самое при нахождении НОД трех и более чисел. Общий множитель находим во всех числах, а не только в паре.
Пример 3. Найдем НОД чисел 28, 36 и 48.
28|2 36|2 48|2
14|2 18|2 24|2
7|7 9|3 12|2
1| 3|3 6|2
1| 3|3
1|
28 = 2 · 2 · 7
36 = 2 · 2 · 3 · 3
48 = 2 · 2 · 2 · 2 · 3
НОД(28;36;48) = 2 · 2 = 4
Чтобы не путаться, можно подчеркивать общие множители только в одной строке (у одного числа), их и будем перемножать.
Таким образом у вас в голове должен сложиться алгоритм нахождения НОД:
1 – раскладываем числа на простые множители
2 – подчеркиваем одинаковые множители
3 – перемножаем их, не дублируя.
Потренируемся нахождению НОД на примерах
1. Найдите НОД(а;b), если а = 2 · 3 · 7 · 13; b = 3 · 3 · 3 · 13
У нас уже имеется разложение на простые множители, осталось лишь подчеркнуть общие и найти НОД.
а = 2 · 3 · 7 · 13
b = 3 · 3 · 3 · 13
НОД(а;b) = 3 · 13 = 39
2. Найдите НОД(96;72)
1) Разложим числа на простые множители:
96 = 2·2·2·2·2·3
72 = 2·2·2·3·3
2) Найдём общие множители введённых чисел: 2, 2, 2, 3
Наибольший общий делитель равен произведению найденных множителей:
НОД(96;72) = 2·2·2·3 = 24
3. Найдите НОД(840;1008;256)
1) Разложим числа на простые множители:
840 = 2·2·2·3·5·7
1008 = 2·2·2·2·3·3·7
256 = 2·2·2·2·2·2·2·2
2) Найдём общие множители введённых чисел: 2, 2, 2
Наибольший общий делитель равен произведению найденных множителей:
НОД(28;36;48) = 2·2·2 = 8
4. Найдите НОД(104;121). Являются ли эти числа взаимно простыми?
1) Разложим числа на простые множители:
104 = 2·2·2·13
121 = 11·11
2) Найдём общие множители введённых чисел: 1
НОД(104;121) = 1, значит это взаимно простые числа.
5. Докажите, что числа 102 и 119 не взаимно простые.
1) Разложим числа на простые множители:
102 = 2·3·17
119 = 7·17
2) Найдём общие множители введённых чисел: 17
НОД(102, 119) = 17 , значит числа не взаимно простые.
6. Чему будет равен НОД чисел а и b, если а кратно b?
а кратно b, значит а делится на b без остатка. Это означает, что число b и есть наибольший общий делитель.
Ответ: b.
7. Пример нахождения НОД чисел 50, 75 и 325.
1) Разложим числа 50, 75 и 325 на простые множители.
50= 2 ∙ 5 ∙ 5
75= 3 ∙ 5 ∙ 5
325= 5 ∙ 5 ∙ 13
2) Из множителей входящих в разложение одного из этих чисел, вычеркнем те, которые не входят в разложение других.
50= 2 ∙ 5 ∙ 5
75= 3 ∙ 5 ∙ 5
325= 5 ∙ 5 ∙13
3) Найдём произведение оставшихся множителей
5 ∙ 5 = 25
Ответ: НОД (50, 75 и 325) = 25
Задачи на нахождение НОД
Нахождение НОД используют при решении некоторых задач. Рассмотрим примеры задач.
Для учащихся 1 класса приготовили одинаковые подарки. Во всех подарках было 120 апельсинов, 280 шоколадок и 320 конфет. Сколько учащихся в 1 классе, если известно, что их больше 30?
Решение:
Так как для учащихся приготовили одинаковые подарки, то в них должно быть поровну апельсинов, шоколадок и конфет. Следовательно, количество учащихся равно общему делителю количества апельсинов, шоколадок и конфет.
Разложим числа 120, 280 и 320 на множители и найдем их наибольший общий делитель.
120 = 2 * 2 * 2 * 3 * 5;
280 = 2 * 2 * 2 * 5 * 7;
320 = 2 * 2 * 2 * 2 * 2 * 2 * 5.
НОД(120;280;320) = 2 * 2 * 2 * 5 = 40.
Поскольку все делители чисел 120, 280 и 320 кроме 40, меньше 30 (а по условию задачи в классе больше 30 учащихся), то число учащихся 40.
Ответ: в первом классе 40 учащихся.
Между учащимися 6 класс поровну разделили 84 мандарина и 56 апельсинов. Сколько учащихся в классе, если известно, что их более 25?
Разложим числа на простые множители:
84 = 2·2·3·7
56 = 2·2·2·7
НОД(84;56) = 2 · 2 · 7 = 28 (уч.)
Ответ: 28 учащихся в классе.
В гостиницу завезли 108 кроватей и 72 шкафа, которые поровну распределили по номерам. Сколько номеров в гостинице, если известно, что их больше 30?
108 = 2·2·3·3·3
72 = 2·2·2·3·3
НОД = 2·2·3·3 = 36 (н.)
Ответ: 36 номеров в гостинице.
Лист картона имеет форму прямоугольника, длина которого 48 см., а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа и сколько?
Решение:
1) S = a ∙ b – площадь прямоугольника.
S= 48 ∙ 40 = 1960 см² – площадь картона.
2) a – сторона квадрата
48 : a – число квадратов, которое можно уложить по длине картона.
40 : а – число квадратов, которое можно уложить по ширине картона.
3) НОД (40 и 48) = 8 (см) – сторона квадрата.
4) S = a² – площадь одного квадрата.
S = 8² = 64 (см²) – площадь одного квадрата.
5) 1960 : 64 = 30 (к.)
Ответ: 30 квадратов со стороной 8 см каждый.
Камин в комнате необходимо выложить отделочной плиткой в форме квадрата. Сколько плиток понадобится для камина размером 195 ͯ 156 см и каковы наибольшие размеры плитки?
Решение:
1) S = 196 ͯ 156 = 30420 (см ²) – S поверхности камина.
2) НОД (195 и 156) = 39 (см) – сторона плитки.
3) S = a² = 39² = 1521 (см ²) – площадь 1 плитки.
4) 30420 : = 20 (штук).
Ответ: 20 плиток размером 39 ͯ 39 (см).
Садовый участок размером 54 ͯ 48 м по периметру необходимо оградить забором, для этого через равные промежутки надо поставить бетонные столбы. Сколько столбов необходимо привезти для участка, и на каком максимальном расстоянии друг от друга будут стоять столбы?
Решение:
1) P = 2( a + b) – периметр участка.
P = 2(54 + 48) = 204 м.
2) НОД (54 и 48) = 6 (м) – расстояние между столбами.
3) 204 : 6 = 34 (с.)
Ответ: 34 столба, на расстоянии 6 м.
Из 210 бордовых, 126 белых, 294 красных роз собрали букеты, причём в каждом букете количество роз одного цвета поровну. Какое наибольшее количество букетов сделали из этих роз и сколько роз каждого цвета в одном букете?
Решение:
1) НОД ( 210, 126 и 294) = 42 (б.)
2) 210 : 42 = 5 (р.) – бордовых
3) 126 : 42 = 3 (р.) – белых
4) 294 : 42 = 7 (р.) – красных.
Ответ: 42 букета: 5 бордовых, 3 белых, 7 красных роз в каждом букете.
Таня и Маша купили одинаковое число почтовых наборов. Таня заплатила 90 руб., а Маша на 5 руб. больше. Сколько стоит один набор? Сколько наборов купила каждая?
Решение:
1) 90 + 5 = 95 (р.) – заплатила Маша.
2) НОД ( 90 и 95) = 5 (р.) – цена 1 набора.
3) 980 : 5 = 18 (н.) – купила Таня.
4) 95 : 5 = 19 (н.) – купила Маша.
Ответ: 5 рублей, 18 наборов, 19 наборов.
Заместитель директора Вера Александровна организует проведение дня здоровья. 424 человека повезут на стадион “Спартак” для проведения эстафет, а 477 человек – в плавательный бассейн с морской водой. Для перевозки нужно заказать автобусы. Перевозчик имеет автобусы с одинаковым количеством мест, все места должны быть заняты. Сколько автобусов надо заказать и сколько пассажиров будет в каждом автобусе?
1) НОД(424,477) = 53 (ч.) – в каждом автобусе,
2) 424 : 53 = 8 (ав.) – едут на стадион
3) 477 : 53 = 9 (ав.) – едут в бассейн
4) 8 + 9 = 17 (ав.) – всего
Ответ: 17 автобусов, 53 пассажира в каждом автобусе.
На празднике “Последнего звонка” выступающим первоклассникам принято дарить подарки. Ученики 11 “а” класса купили 58 конфет, ученики 11 “б” класс – 116 “чупа-чупсов”, а ученики 11 “в” класса – по одной мягкой игрушке. Сколько куплено мягких игрушек?
НОД (58;116) = 29
Ответ: куплено 29 мягких игрушек.
Друзья Алексей Николаевич и Борис Петрович решили заняться гостиничным бизнесом. Для своей гостиницы Алексей Николаевич завез 108 кроватей и 72 шкафа, а Борис Петрович – 128 кроватей и 64 шкафа. Кровати и шкафы распределяются по комнатам поровну. Сколько комнат в гостиницах каждого из друзей? У кого из них остановиться третьему другу Александру Ивановичу, если он отдыхает с семьей, состоящей вместе с ним из 8 человек?
1) НОД(108;72) = 36 (комн.) – у Алексея Николаевича;
2) 108:36=3 (кровати) – в номере;
3) НОД(128;64) = 32 (комн.) – у Бориса Петровича.
4) 128:32=4 (кровати) – в номере.
Ответ: Александру Ивановичу лучше остановиться у Бориса Петровича – 2 номера по 4 человека.
Калькулятор определения НОД и НОК
Для тех, кто уже отчаялся понять тему, НОД – калькулятор:
Если что-либо осталось для вас непонятным, задавайте вопросы в комментариях.
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Наибольший общий делитель
Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.
Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.
Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.
Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.
Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.
Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)
12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)
12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)
12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)
12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)
12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)
12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)
12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)
12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)
12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)
12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)
12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)
Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9
9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)
9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)
9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)
9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)
9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)
9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)
9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)
9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)
9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)
Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:
Выписав делители, можно сразу определить какой является наибольшим и общим.
Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3
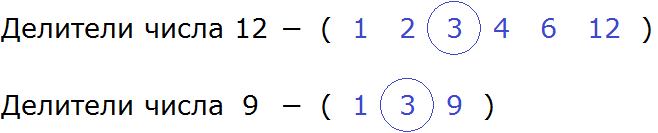
И число 12 и число 9 делятся на 3 без остатка:
12 : 3 = 4
9 : 3 = 3
Значит НОД (12 и 9) = 3
Второй способ нахождения НОД
Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий способ нахождения НОД
Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
В первую очередь, раскладываем числа 28 и 16 на простые множители:
Получили два разложения: 
и 
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:
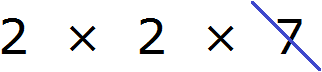
Теперь перемножаем оставшиеся множители и получаем НОД:
Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:
28 : 4 = 7
16 : 4 = 4
НОД (28 и 16) = 4
Пример 2. Найти НОД чисел 100 и 40
Раскладываем на множители число 100
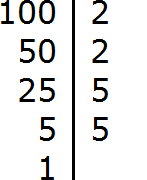
Раскладываем на множители число 40
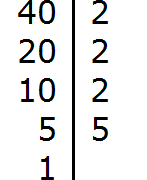
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения
Перемножим оставшиеся числа:
Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:
100 : 20 = 5
40 : 20 = 2
НОД (100 и 40) = 20.
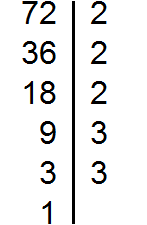
Пример 3. Найти НОД чисел 72 и 128
Раскладываем на множители число 72
Раскладываем на множители число 128
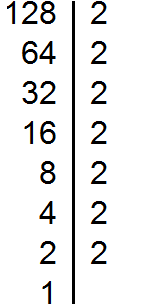Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:
Перемножим оставшиеся числа:
Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:
72 : 8 = 9
128 : 8 = 16
НОД (72 и 128) = 8
Нахождение НОД для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
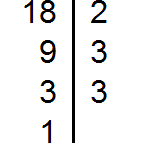
Разложим на множители число 24
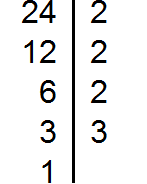
Разложим на множители число 36
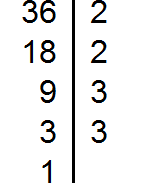
Получили три разложения:
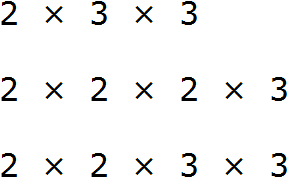
Теперь найдём и подчеркнём общие множители:
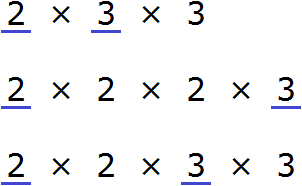
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
НОД (18, 24 и 36) = 6
Пример 2. Найти НОД для чисел 12, 24, 36 и 42
Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.
Разложим на множители число 12
Разложим на множители число 24
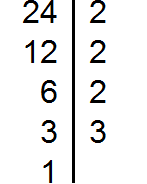
Разложим на множители число 36
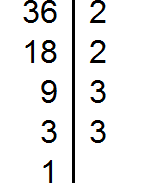
Разложим на множители число 42
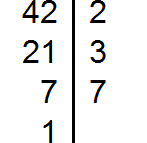
Получили четыре разложения:
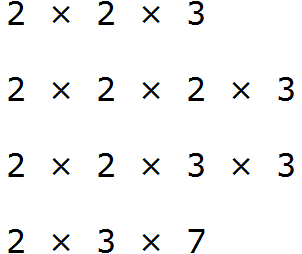
Теперь найдём и подчеркнём общие множители:
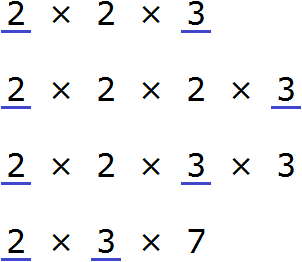
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:
2 × 3 = 6
Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
НОД (12, 24 , 36 и 42) = 6
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Итак, начнём. Кратные будем выделять синим цветом:
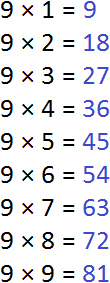
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:
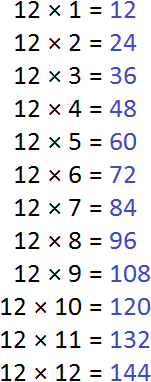
Теперь выпишем кратные обоих чисел:
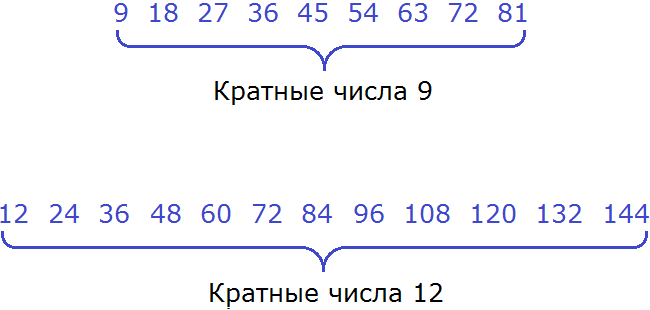
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:
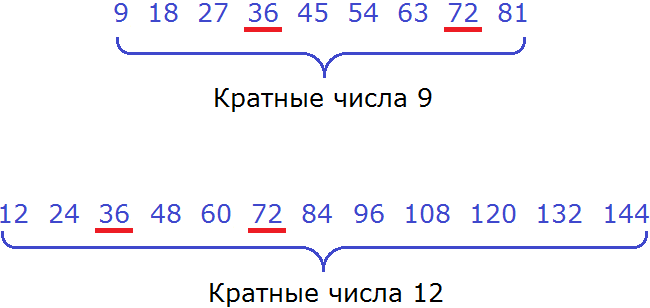
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.
Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
Второй способ нахождения НОК
Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Разложим на множители число 9
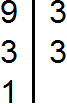
Разложим на множители число 12
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:
36 : 9 = 4
36 : 12 = 3
НОК (9 и 12) = 36
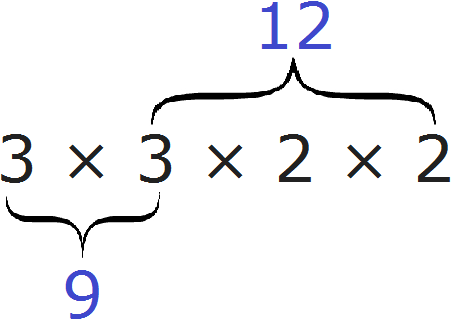
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.
Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Пример 2. Найти НОК чисел 50 и 180
Разложим на множители число 50
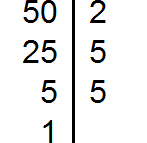
Разложим на множители число 180
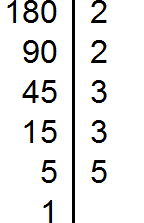
Выпишем первое разложение:
Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:
Теперь перемножаем эти множители:
Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:
900 : 50 = 18
900 : 180 = 5
НОК (50 и 180) = 900
Пример 3. Найти НОК чисел 8, 15 и 33
Разложим на множители число 8
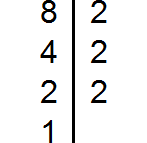
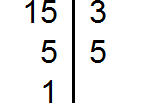
Разложим на множители число 15
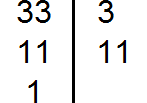
Разложим на множители число 33
Выпишем первое разложение:
Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Теперь перемножаем эти множители:
Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
НОК (8, 15 и 33) = 1320
Третий способ нахождения НОК
Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:
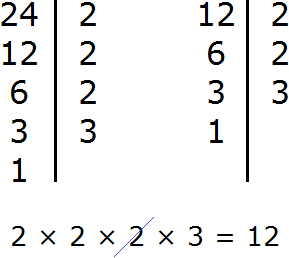
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.
Итак, перемножим числа 24 и 12
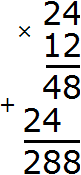
Разделим полученное число 288 на НОД чисел 24 и 12
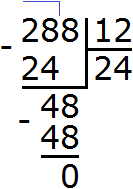
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24
НОК (24 и 12) = 24
Пример 2. Найти НОД и НОК чисел 36 и 48
Найдем НОД чисел 36 и 48
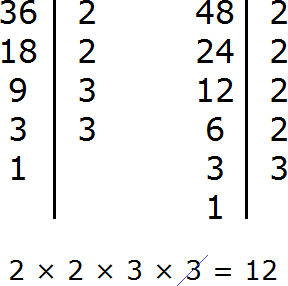
Перемножим числа 36 и 48
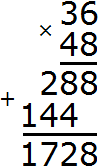
Разделим 1728 на НОД чисел 36 и 48
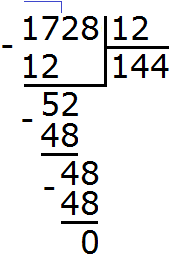
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144
НОК (36 и 48) = 144
Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144
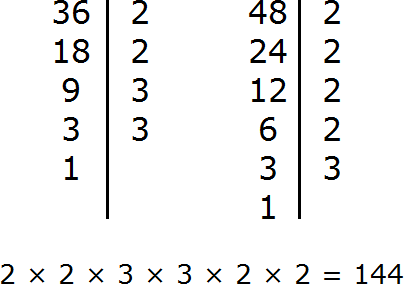
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».
Задания для самостоятельного решения
Задание 1. Найдите НОД чисел 12 и 16
Решение:
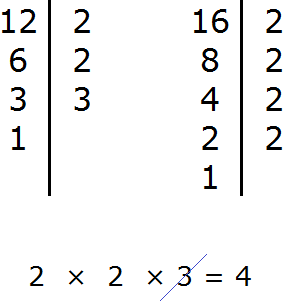
Задание 2. Найдите НОК чисел 12 и 16
Решение:
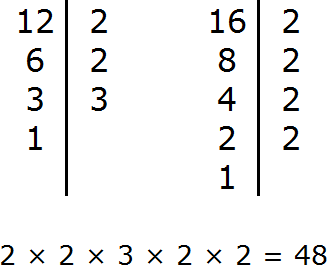
Задание 3. Найдите НОД чисел 40 и 32
Решение:
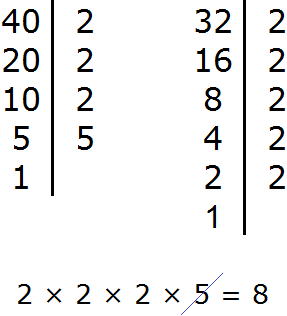
Задание 4. Найдите НОК чисел 40 и 32
Решение:
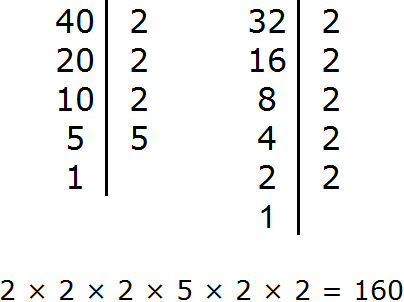
Задание 5. Найдите НОД чисел 54 и 86
Решение:
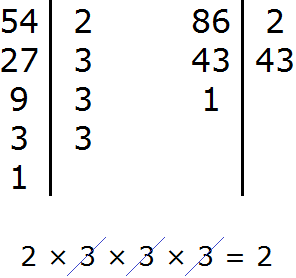
Задание 6. Найдите НОК чисел 54 и 86
Решение:
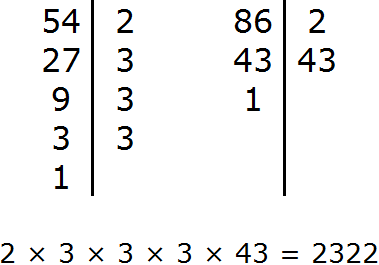
Задание 7. Найдите НОД чисел 98 и 35
Решение:
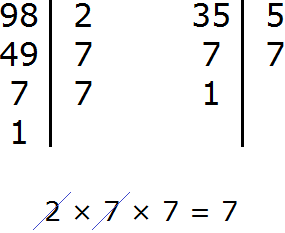
Задание 8. Найдите НОК чисел 98 и 35
Решение:
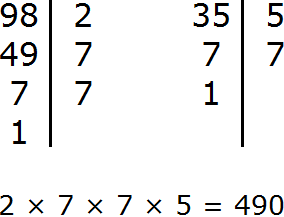
Задание 9. Найдите НОД чисел 112 и 82
Решение:
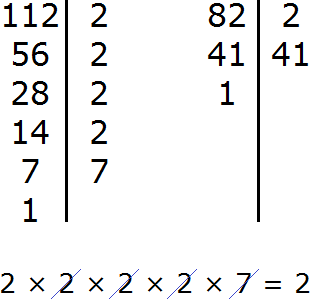
Задание 10. Найдите НОК чисел 112 и 82
Решение:
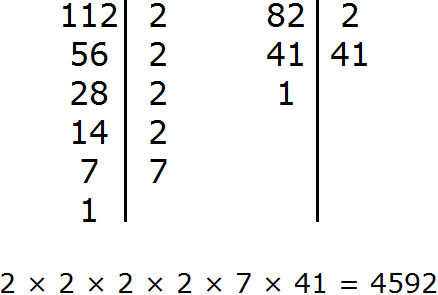
Задание 11. Найдите НОД чисел 24, 48, 64
Решение:
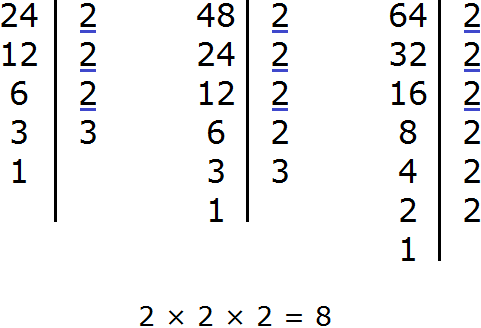
Задание 12. Найдите НОК чисел 24, 48, 64
Решение:
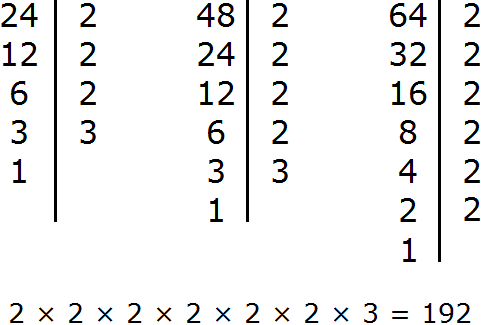
Задание 13. Найдите НОД чисел 18, 48, 96
Решение:
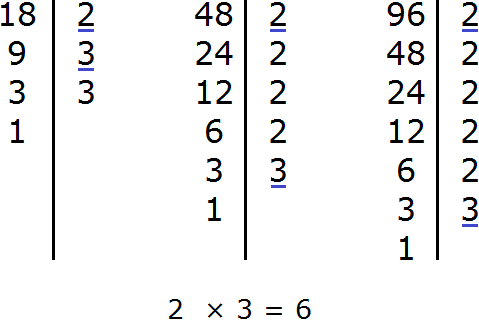
Задание 14. Найдите НОК чисел 18, 48, 96
Решение:
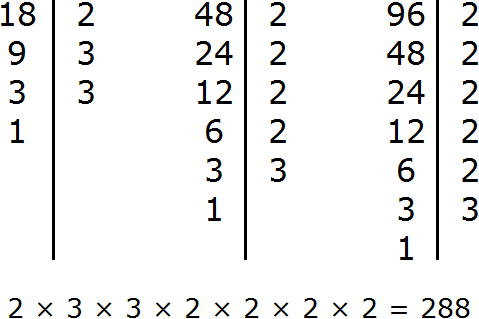
Задание 15. Найдите НОД чисел 28, 24, 76
Решение:
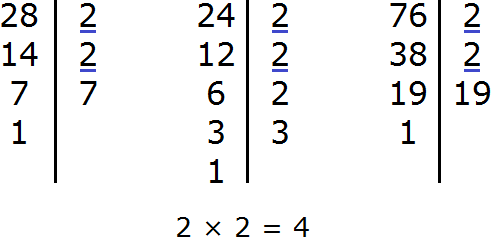
Задание 16. Найдите НОК чисел 28, 24, 76
Решение:
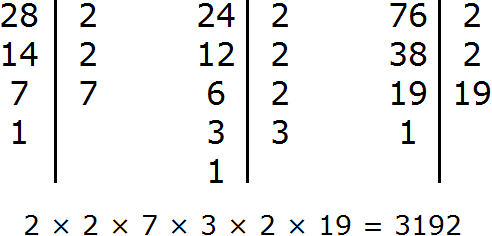
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Калькулятор НОД и НОК
При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению. Вы можете найти НОД и НОК для двух, трех и четырех чисел
Выберите количество чисел для НОД и НОК
Наибольший общий делитель НОД
Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.
Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.
Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).
Свойства НОД
- Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.
Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15. - Если число a делится на b, то НОД(a, b) = b.
Например, число 20 делится на число 10, тогда НОД(20, 10) = 10. - При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.
Как найти наибольший общий делитель НОД
Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:
- Разложить числа на простые множители.
- Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
- Перемножить оставшиеся множители.
Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
58 – составное число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 – делится на простое число 2
12 : 2 = 6 – делится на простое число 2
6 : 2 = 3 – делится на простое число 2.
Завершаем деление, так как 3 простое числоРазложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
58 : 2 = 29 – делится на простое число 2.
Завершаем деление, так как 29 простое число - Выделим синим цветом и выпишем общие множители.
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
58 = 2 ⋅ 29
У чисел (24, 58) только один общий множитель – 2 и он и будет наибольшим общим делителем этих чиселОтвет: НОД (24, 58) = 2
Способ №2
- Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;
24 : 2 = 12;
24 : 3 = 8;
24 : 4 = 6;
24 : 6 = 4;
24 : 8 = 3;
24 : 12 = 2;
24 : 24 = 1;Для числа 58 выпишем все случаи, когда оно делится без остатка:
58 : 1 = 58;
58 : 2 = 29;
58 : 29 = 2;
58 : 58 = 1; - Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)
Общие делители чисел (24, 58): 1, 2
Ответ: НОД (24, 58) = 2
Наименьшее общее кратное НОК
Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.
Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).
Как найти наименьшее общее кратное НОК
Чтобы найти НОК двух, трех и более чисел необходимо:
- Разложить эти числа на простые множители.
- Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
- Умножить получившиеся множители.
Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
225 – составное число
30 – составное числоРазложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
225 : 3 = 75 – делится на простое число 3
75 : 3 = 25 – делится на простое число 3
25 : 5 = 5 – делится на простое число 5.
Завершаем деление, так как 5 простое числоРазложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
30 : 2 = 15 – делится на простое число 2
15 : 3 = 5 – делится на простое число 3.
Завершаем деление, так как 5 простое число - Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
225 = 3 ∙ 3 ∙ 5 ∙ 5
30 = 2 ∙ 3 ∙ 53) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450
Способ №2
- Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.
Выделим все кратные числа 225 зеленым цветом:
зеленым цветом:225 ∙ 1 = 225; 225 ∙ 2 = 450; 225 ∙ 3 = 675; 225 ∙ 4 = 900;
225 ∙ 5 = 1125; 225 ∙ 6 = 1350; 225 ∙ 7 = 1575; 225 ∙ 8 = 1800;
225 ∙ 9 = 2025; 225 ∙ 10 = 2250; 225 ∙ 11 = 2475; 225 ∙ 12 = 2700;
225 ∙ 13 = 2925; 225 ∙ 14 = 3150; 225 ∙ 15 = 3375; 225 ∙ 16 = 3600;
225 ∙ 17 = 3825; 225 ∙ 18 = 4050; 225 ∙ 19 = 4275; 225 ∙ 20 = 4500;
225 ∙ 21 = 4725; 225 ∙ 22 = 4950; 225 ∙ 23 = 5175; 225 ∙ 24 = 5400;
225 ∙ 25 = 5625; 225 ∙ 26 = 5850; 225 ∙ 27 = 6075; 225 ∙ 28 = 6300;
225 ∙ 29 = 6525; 225 ∙ 30 = 6750;Выделим все кратные числа 30 зеленым цветом:
30 ∙ 1 = 30; 30 ∙ 2 = 60; 30 ∙ 3 = 90; 30 ∙ 4 = 120;
30 ∙ 5 = 150; 30 ∙ 6 = 180; 30 ∙ 7 = 210; 30 ∙ 8 = 240;
30 ∙ 9 = 270; 30 ∙ 10 = 300; 30 ∙ 11 = 330; 30 ∙ 12 = 360;
30 ∙ 13 = 390; 30 ∙ 14 = 420; 30 ∙ 15 = 450; 30 ∙ 16 = 480;
30 ∙ 17 = 510; 30 ∙ 18 = 540; 30 ∙ 19 = 570; 30 ∙ 20 = 600;
30 ∙ 21 = 630; 30 ∙ 22 = 660; 30 ∙ 23 = 690; 30 ∙ 24 = 720;
30 ∙ 25 = 750; 30 ∙ 26 = 780; 30 ∙ 27 = 810; 30 ∙ 28 = 840;
30 ∙ 29 = 870; 30 ∙ 30 = 900; 30 ∙ 31 = 930; 30 ∙ 32 = 960;
30 ∙ 33 = 990; 30 ∙ 34 = 1020; 30 ∙ 35 = 1050; 30 ∙ 36 = 1080;
30 ∙ 37 = 1110; 30 ∙ 38 = 1140; 30 ∙ 39 = 1170; 30 ∙ 40 = 1200;
30 ∙ 41 = 1230; 30 ∙ 42 = 1260; 30 ∙ 43 = 1290; 30 ∙ 44 = 1320;
30 ∙ 45 = 1350; 30 ∙ 46 = 1380; 30 ∙ 47 = 1410; 30 ∙ 48 = 1440;
30 ∙ 49 = 1470; 30 ∙ 50 = 1500; 30 ∙ 51 = 1530; 30 ∙ 52 = 1560;
30 ∙ 53 = 1590; 30 ∙ 54 = 1620; 30 ∙ 55 = 1650; 30 ∙ 56 = 1680;
30 ∙ 57 = 1710; 30 ∙ 58 = 1740; 30 ∙ 59 = 1770; 30 ∙ 60 = 1800;
30 ∙ 61 = 1830; 30 ∙ 62 = 1860; 30 ∙ 63 = 1890; 30 ∙ 64 = 1920;
30 ∙ 65 = 1950; 30 ∙ 66 = 1980; 30 ∙ 67 = 2010; 30 ∙ 68 = 2040;
30 ∙ 69 = 2070; 30 ∙ 70 = 2100; 30 ∙ 71 = 2130; 30 ∙ 72 = 2160;
30 ∙ 73 = 2190; 30 ∙ 74 = 2220; 30 ∙ 75 = 2250; 30 ∙ 76 = 2280;
30 ∙ 77 = 2310; 30 ∙ 78 = 2340; 30 ∙ 79 = 2370; 30 ∙ 80 = 2400;
30 ∙ 81 = 2430; 30 ∙ 82 = 2460; 30 ∙ 83 = 2490; 30 ∙ 84 = 2520;
30 ∙ 85 = 2550; 30 ∙ 86 = 2580; 30 ∙ 87 = 2610; 30 ∙ 88 = 2640;
30 ∙ 89 = 2670; 30 ∙ 90 = 2700; 30 ∙ 91 = 2730; 30 ∙ 92 = 2760;
30 ∙ 93 = 2790; 30 ∙ 94 = 2820; 30 ∙ 95 = 2850; 30 ∙ 96 = 2880;
30 ∙ 97 = 2910; 30 ∙ 98 = 2940; 30 ∙ 99 = 2970; 30 ∙ 100 = 3000;
30 ∙ 101 = 3030; 30 ∙ 102 = 3060; 30 ∙ 103 = 3090; 30 ∙ 104 = 3120;
30 ∙ 105 = 3150; 30 ∙ 106 = 3180; 30 ∙ 107 = 3210; 30 ∙ 108 = 3240;
30 ∙ 109 = 3270; 30 ∙ 110 = 3300; 30 ∙ 111 = 3330; 30 ∙ 112 = 3360;
30 ∙ 113 = 3390; 30 ∙ 114 = 3420; 30 ∙ 115 = 3450; 30 ∙ 116 = 3480;
30 ∙ 117 = 3510; 30 ∙ 118 = 3540; 30 ∙ 119 = 3570; 30 ∙ 120 = 3600;
30 ∙ 121 = 3630; 30 ∙ 122 = 3660; 30 ∙ 123 = 3690; 30 ∙ 124 = 3720;
30 ∙ 125 = 3750; 30 ∙ 126 = 3780; 30 ∙ 127 = 3810; 30 ∙ 128 = 3840;
30 ∙ 129 = 3870; 30 ∙ 130 = 3900; 30 ∙ 131 = 3930; 30 ∙ 132 = 3960;
30 ∙ 133 = 3990; 30 ∙ 134 = 4020; 30 ∙ 135 = 4050; 30 ∙ 136 = 4080;
30 ∙ 137 = 4110; 30 ∙ 138 = 4140; 30 ∙ 139 = 4170; 30 ∙ 140 = 4200;
30 ∙ 141 = 4230; 30 ∙ 142 = 4260; 30 ∙ 143 = 4290; 30 ∙ 144 = 4320;
30 ∙ 145 = 4350; 30 ∙ 146 = 4380; 30 ∙ 147 = 4410; 30 ∙ 148 = 4440;
30 ∙ 149 = 4470; 30 ∙ 150 = 4500; 30 ∙ 151 = 4530; 30 ∙ 152 = 4560;
30 ∙ 153 = 4590; 30 ∙ 154 = 4620; 30 ∙ 155 = 4650; 30 ∙ 156 = 4680;
30 ∙ 157 = 4710; 30 ∙ 158 = 4740; 30 ∙ 159 = 4770; 30 ∙ 160 = 4800;
30 ∙ 161 = 4830; 30 ∙ 162 = 4860; 30 ∙ 163 = 4890; 30 ∙ 164 = 4920;
30 ∙ 165 = 4950; 30 ∙ 166 = 4980; 30 ∙ 167 = 5010; 30 ∙ 168 = 5040;
30 ∙ 169 = 5070; 30 ∙ 170 = 5100; 30 ∙ 171 = 5130; 30 ∙ 172 = 5160;
30 ∙ 173 = 5190; 30 ∙ 174 = 5220; 30 ∙ 175 = 5250; 30 ∙ 176 = 5280;
30 ∙ 177 = 5310; 30 ∙ 178 = 5340; 30 ∙ 179 = 5370; 30 ∙ 180 = 5400;
30 ∙ 181 = 5430; 30 ∙ 182 = 5460; 30 ∙ 183 = 5490; 30 ∙ 184 = 5520;
30 ∙ 185 = 5550; 30 ∙ 186 = 5580; 30 ∙ 187 = 5610; 30 ∙ 188 = 5640;
30 ∙ 189 = 5670; 30 ∙ 190 = 5700; 30 ∙ 191 = 5730; 30 ∙ 192 = 5760;
30 ∙ 193 = 5790; 30 ∙ 194 = 5820; 30 ∙ 195 = 5850; 30 ∙ 196 = 5880;
30 ∙ 197 = 5910; 30 ∙ 198 = 5940; 30 ∙ 199 = 5970; 30 ∙ 200 = 6000;
30 ∙ 201 = 6030; 30 ∙ 202 = 6060; 30 ∙ 203 = 6090; 30 ∙ 204 = 6120;
30 ∙ 205 = 6150; 30 ∙ 206 = 6180; 30 ∙ 207 = 6210; 30 ∙ 208 = 6240;
30 ∙ 209 = 6270; 30 ∙ 210 = 6300; 30 ∙ 211 = 6330; 30 ∙ 212 = 6360;
30 ∙ 213 = 6390; 30 ∙ 214 = 6420; 30 ∙ 215 = 6450; 30 ∙ 216 = 6480;
30 ∙ 217 = 6510; 30 ∙ 218 = 6540; 30 ∙ 219 = 6570; 30 ∙ 220 = 6600;
30 ∙ 221 = 6630; 30 ∙ 222 = 6660; 30 ∙ 223 = 6690; 30 ∙ 224 = 6720;
30 ∙ 225 = 6750; - Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).
Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750
Ответ: НОК (225 ; 30) = 450
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
