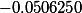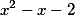О1)Общим делителем многочленов f(x)
и g(x)
называется такой d(x)
что, выполняются f(x)⋮d(x)
и g(x)⋮d(x).
О2)Наибольшим будет тот из общих
делителей степень которого больше.
Будем считать что, общий делитель d(x)
который делится на любой другой делитель
этих многочленов будет наибольшим
d(x)=(f(x),g(x))
очевидно что, общим делителем многочленов
будет и делитель вида:
с*d(x)=(с*f(x),с*g(x)),c=const
0.
НОД отыскивается с точностью до
постоянного множителя. Многочлены
отличающееся друг от друга постоянным
множителем называются ассоциированными.
НОД отыскивают с помощью алгоритма
Евклида который состоит в следующем: с
начал делят с остатком многочлен f(x)
на g(x) затем
g(x) на остаток
от первого деления затем
от первого деления на остаток
от второго деления и так далее до тех
пока не получится нулевой остаток при
этом получается цепочка равенств.
Последний не нулевой остаток и есть НОД
двух многочленов.
Пример 1:
В кольце R[x]
найти НОД двух многочленов:
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
||
|
|
|||
|
|
|||
|
|
|
|
|
||
|
|
|||
|
|
|||
|
|
.
На практике может возникнуть задача
отыскания нескольких многочленов:
НОД(f,g…q)=НОД(f,НОД(g,…НОД(t,q)…)).
Т1:НОД двух многочленов может быт
представлен в виде:
Где
из тогоже кольца что, и данные многочлены.
Доказательство:
Для нахождения НОД(f,g)
воспользуемся равенствами 1 алгоритма
Евклида:
подставляя это равенство во второе
равенство совокупности 1 можем выразить
остаток
.
действуя так и далее можно выразить
остаток
через f(x) и
g(x) а, также
последний остаток
.
Пример 2:
Из примера 1 запишем представление
остатков:
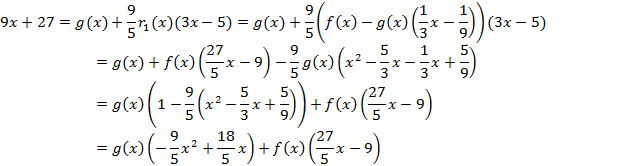
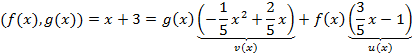
§ 8 Наименьшее общее кратное двух многочленов.
О1) Многочлен
называется общим кратным для
и
если
.
О2)Общее кратное f(x)
и g(x)
на которое делится любое общее кратное
этих многочленов называется наименьшим
общим кратным многочленов
и
и обозначается:
.
Т1:Для любых многочленов
существует наименьшее общее кратное
которое можно найти по формуле
Доказательство:
Пусть многочлен
некоторое произвольное общее кратное
многочленов f(x)
и g(x). Так
как М общее кратное то M(x)=f(x)p(x),
M(x)=g(x)q(x)
(f(x),g(x))=d(x),
тогда
g(x)⋮d(x)
Из этого равенства видно, что
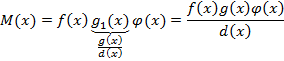
Получено выражение для произвольного
общего кратного многочленов f(x)
g(x) положив
в этом выражении 𝜑(x)=1
получим формулу для нахождения наименьшего
общего кратного.
Замечание:
[f,g]⋮f
[f,g]⋮g
M⋮[f,g]
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Исходный полином f(x) (его коэффициенты) |
| Делим на следующий полином / многочлен |
| Первый многочлен |
| Второй многочлен |
| Остатки от деления двух полиномов |
Рассматривается вычисление наибольшего общего делителя (НОД) двух многочленов. Принцип который используется, такой же как и для нахождения НОД обычных чисел.
Отличие нашего калькулятора в том, что
1. Он показывает промежуточные остатки при вычислении
2. Многочлены могут быть комплексными, то есть содержать мнимые числа.
Теории больше не будет, и сразу перейдем к примерам вычисления, и вы поймете, как это вычисляется.
Найти НОД двух многочленов
и
Сначала выбираем тот полином у которого степень выше и коэффицент при этой степени наибольший.
Делим один на другой f(x) на g(x). Можно делать это руками а можно воспользоваться калькулятором деления многочлена на многочлен.
Получаем остаток
Теперь делим уже g(x) на полученный остаток
получаем
Еще раз проделываем процедуру
получаем остаток
Если мы еще раз проведем такую же процедуру то получим в остатке ноль.
Закончили деление и смотрим на результат.
Предпоследнее значение от деления двух многочленов и есть значение НОД.
То есть наш ответ
Кто хочет получить результат в виде дроби то стоит обратить внимание на Непрерывные, цепные дроби онлайн которая нам это значение в виде дроби и окончательный красивый ответ есть
НОД двух функций
и
равен
Как же пользоватся ботом?
Выписыаем коэффициенты полиномов в строку разделяя их пробелом.
Получили
1 1 -4 0 5 это у нас первый полином
2 -1 -2 2 а это второй
Вводим их в соответсвующие поля и нажимаем рассчитать.
Смотрим результат
| Первый многочлен |
%20=%20x^{4}+(1)*x^{3}+(-4)*x^{2}+(5)) |
| Второй многочлен |
%20=%20(2)*x^{3}+(-1)*x^{2}+(-2)*x+(2)) |
| Остатки от деления двух полиномов |
То есть всё то что мы делали руками.
Замечание: Как видно, в остаток всегда “примешивается” какая то мелкая погрешность. Это надо учитывать, в окончательном оформлении своего решения.Но это не всегда так. Если коэффициенты при старших степенях полиномов на любом этапе вычислений равны единицы, то погрешность результата нулевая.
Попробуем найти НОД комплексных многочленов
Пишем любые коэффициенты с мнимыми значениями и получаем
| Первый многочлен |
%20=%20x^{6}+(1)*x^{5}+(i)*x^{4}+(i)*x^{3}+(i)) |
| Второй многочлен |
%20=%20x^{2}+(-i)*x+(i)) |
| Остатки от деления двух полиномов |
Еще один пример, с “нюансом”
| Первый многочлен |
%20=%20x^{6}+(-4)*x^{5}+(2)*x^{4}+(5)*x^{3}+(2)*x^{2}+(-4)*x+(-8)) |
| Второй многочлен |
%20=%20x^{5}+(-1)*x^{4}+(-1)*x^{3}+(1)*x^{2}+(-4)*x+(-4)) |
| Остатки от деления двух полиномов |
Смотрите!! НОД не равен )
И наш правильный ответ *x^{2}+(1008)*x+(2016))
Да, некоторые возразят “Ну, тут еще и думать надо..” Хотелось бы возразить, но не буду, так как согласен с ними что “Думать надо!”
Надеюсь, Ваши расчеты стали еще проще и быстрее!
2008-09 учебный год
Доцент Мартынова Т. А.
Изображение слайда
2
Слайд 2: МНОГОЧЛЕНЫ ОТ ОДНОЙ ПЕРЕМЕННОЙ
ЛЕКЦИЯ 3
Доцент Мартынова Т.А.
Изображение слайда
3
Слайд 3: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Пусть
– многочлен с коэффициентами из K.
Для любого c K положим
,
где выражение в правой части понимается как результат операций в кольце K.
Получаемый при этом элемент f(c) кольца K называется значением многочлена f ( x ) при x=c
(или в точке с по аналогии со случаем, когда с можно представлять как точку действительной оси).
Следовательно, многочлен f ( x ) определяет функцию f : K K.
Изображение слайда
4
Слайд 4: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Напомним, что мы дали формально-алгебраическое определение равенства двух многочленов, согласно которому два многочлена считаются равными, если их степени и соответствующие коэффициенты равны.
Ясно, что равные многочлены определяют одну и ту же функцию, т.е. если многочлены равны с алгебраической точки зрения, то они равны и с функциональной точки зрения.
Изображение слайда
5
Слайд 5: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Предположим, что два многочлена равны с функциональной точки зрения.
Обязательно ли они равны с алгебраической точки зрения?
Ответ на этот вопрос будет отрицательным для любого конечного кольца K = { c 1, c 2,…, c n }. Над таким кольцом одну и ту же функцию определяют два различных многочлена
f ( x )=( x – c 1 )( x – c 2 )…( x – c n )+ x и g ( x )= x.
Значит, если K – конечное кольцо, то алгебраическая и функциональная точки зрения на многочлен не совпадают.
Основная цель этого пункта доказать, что если K – бесконечная область целостности, то обе эти точки зрения на многочлен совпадают, т.е. различные с алгебраической точки зрения многочлены определяют различные функции.
Изображение слайда
6
Слайд 6: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
f(x)=(x-c)q(x)+r (1*)
Отметим сначала еще одно следствие теоремы о делении с остатком.
Следствие 2 (теорема Безу). Остаток от деления многочлена f(x) на двучлен x-c равен значению многочлена f(x) при x=c.
◘ Полагая x=c в равенстве (1*), получим f(c)=r. ◙
( Этьен Безу (1730–1783) – французский математик ).
Введем теперь понятие корня многочлена.
Определение 1. Элемент c кольца K называется корнем многочлена f ( x ), если f(c)=0.
Частным случаем теоремы Безу является
Следствие 3. Если элемент c кольца K является корнем многочлена, то остаток от деления многочлена f(x) на двучлен x-c равен 0. ◙
Изображение слайда
7
Слайд 7: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Из следствий 1 и 3 легко вытекает
Следствие 4 (характеристическое свойство корня). Элемент c кольца K является корнем многочлена f(x) тогда и только тогда, когда f(x) делится на двучлен x-c. ◙
Определение 2. Элемент c кольца K называется корнем многочлена f(x) кратности k, если f(x) делится на ( x-c ) k и не делится на ( x-c ) k +1. Корни кратности 1 называются простыми корнями.
Изображение слайда
8
Слайд 8: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
В дальнейшем полезной будет следующая
Т е о р е м а 2 (о числе корней). Число корней ( с учетом их кратности ) ненулевого многочлена f(x) над областью целостности K не превосходит его степени.
◘ Докажем это утверждение с помощью индукции по степени n многочлена f(x).
Многочлен нулевой степени вообще не имеет корней, так что для него теорема 2 справедлива.
Предположим теперь, что n> 0 и теорема 2 справедлива для всех многочленов степени n-1, и докажем её для любого многочлена f(x) степени n.
Если f(x) не имеет корней, то теорема 2 верна.
Изображение слайда
9
Слайд 9: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Пусть с – корень f ( x ) степени n.
По характеристическому свойству корня f ( x ) делится на x-c, т.е.
f(x)=(x-c)q(x), (4)
где q ( x ) – некоторый многочлен степени n-1, имеющий по предположению индукции не более n-1 корней.
Из равенства (4) видно, что любой корень многочлена q ( x ) является корнем многочлена f ( x ).
С другой стороны, поскольку K – целостное кольцо, любой отличный от с корень многочле – на f ( x ) является корнем многочлена q ( x ).
Отсюда следует, что f ( x ) имеет не более чем n корней. ◙
Изображение слайда
10
Слайд 10: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Т е о р е м а 3 (тождественности многочленов). Если K – бесконечная область целостности, то два многочлена f ( x ) и g ( x ) кольца K [ x ] равны между собой тогда и только тогда, когда они принимают равные значения при любом значении x из K.
Эта теорема показывает, что алгебраическая и функциональная точки зрения на многочлен над бесконечной областью целостности совпадают.
Доказательство теоремы 3 непосредственно будет вытекать из одной леммы, следствия из нее и очевидного факта, что равные многочлены определяют равные функции.
Изображение слайда
11
Слайд 11: 2. Корни многочлена. Алгебраическая и функциональная точки зрения на многочлен
Лемма 1. Пусть K – область целостности. Если многочлены f ( x ) и g ( x ), степени которых не превышают числа n, принимают равные значения для n + 1 различных элементов кольца K, то f ( x )= g ( x ).
◘ Пусть f ( c i ) = g ( c i ) ( i= 1,2,…, n, n+ 1). Предположим, что f ( x ) g ( x ) и рассмотрим многочлен h ( x )= f ( x )- g ( x ).
Он ненулевой, его степень не превосходит числа n и в тоже время он имеет n + 1 корней c 1, c 2,…, c n, c n+1, что противоречит теореме 2.
Следовательно, f ( x )= g ( x ). ◙
Из леммы 1 вытекает
Следствие 5. Если многочлены f ( x ) и g ( x ) принимают равные значения на некотором бесконечном подмно-жестве области целостности K, то f ( x )= g ( x ). ◙
Изображение слайда
12
Слайд 12: 3. Наибольший общий делитель многочленов
Основными задачами этого раздела являются рассмотрение вопросов:
Обоснование алгоритма нахождения НОД многочленов с помощью алгоритма Евклида. Нахождение линейного представления НОД многочленов.
Свойства взаимно простых многочленов.
НОК многочленов и его нахождение.
Изображение слайда
13
Слайд 13: 3. Наибольший общий делитель многочленов
В этом разделе будем рассматривать многочлены над произвольным полем P.
Определение 1. Наибольшим общим делителем ( НОД) многочленов
f 1 ( x ), f 2 ( x ), …, f m ( x ) из кольца P [ x ]
называется многочлен d ( x ), обладающий следующими свойствами:
1) каждый из многочленов f 1 ( x ), f 2 ( x ), …, f m ( x ) делится на d ( x ), т.е. d ( x ) является их общим делителем;
2) d ( x ) делится на любой общий делитель многочленов f 1 ( x ), f 2 ( x ), …, f m ( x ).
Обозначение: НОД ( f 1 ( x ), f 2 ( x ), …, f m ( x )).
Изображение слайда
14
Слайд 14: 3. Наибольший общий делитель многочленов
Понятно, что в случае существования НОД определяется с точностью до множителя нулевой степени (любые два НОДа должны делиться друг на друга);
нормированный НОД определяется однозначно.
НОД двух многочленов f ( x ) и h ( x ) может быть найден при помощи алгоритма Евклида.
Прежде всего, ясно, что если,
то НОД ( f ( x ), h ( x ) ) = h ( x ).
Изображение слайда
15
Слайд 15: 3. Наибольший общий делитель многочленов
Пусть.
Делим с остатком многочлен f(x) на многочлен h ( x ),
затем многочлен h ( x ) – на остаток от первого деления,
затем остаток от первого деления – на остаток от второго деления и т.д.,
пока не получится нулевой остаток (последнее неизбежно, так как степени остатков строго убывают).
Изображение слайда
16
Слайд 16: 3. Наибольший общий делитель многочленов
Это дает следующую цепочку равенств:
(E)
Изображение слайда
17
Слайд 17: 3. Наибольший общий делитель многочленов
(Е)
Из которых получаем доказательство следующего утверждения.
Т е о р е м а 3. Для любых многочленов f(x) и h ( x ) из P [ x ] существует их НОД( f ( x ), h ( x )), причем если
, то он совпадает с последним неравным нулю остатком в равенствах ( E ) Евклида, т.е.
НОД( f ( x ), h ( x ))= r k ( x ). ◙
Изображение слайда
18
Слайд 18: 3. Наибольший общий делитель многочленов
(Е)
НОД( f ( x ), h ( x ))= r k ( x ).
◘ Покажем сначала, что многочлен r k ( x ) является общим делителем многочленов f(x) и h ( x ).
Учитывая последнее равенство в (Е), из предпоследнего равенства получим, что,
из третьего снизу равенства в (Е) имеем и т.д.
Поднимаясь снизу вверх по равенствам (Е) через конечное число шагов получим, что и..
Таким образом, условие 1) определения 1 для многочлена r k ( x ) выполнено.
Изображение слайда
19
Слайд 19: 3. Наибольший общий делитель многочленов
(Е)
НОД( f ( x ), h ( x ))= r k ( x ).
Пусть теперь d ( x ) – любой общий делитель многочленов f(x) и h ( x ).
Из первого равенства системы (Е) легко получаем, что ;
из второго – ; из третьего – и т.д.
Спускаясь по равенствам (Е), через конечное число шагов получим, что.
Таким образом, и условие 2) определения 1 для многочлена r k ( x ) выполнено.
Итак, НОД( f ( x ), h ( x ))= r k ( x ). ◙
Изображение слайда
20
Слайд 20: 3. Наибольший общий делитель многочленов
Пример 3. В кольце многочленов с действительными коэффициентами найдем НОД многочленов
и.
◘ Делим f(x) на h ( x ) с остатком:
Изображение слайда
21
Слайд 21: 3. Наибольший общий делитель многочленов
Поскольку НОД находится с точностью до константы, для удобства можно разделить полученный остаток на -3 и выполнять деление многочлена h ( x ) на r 1 (x) : (-3), что не скажется на результате.
Однако, имея в виду дальнейшее линейное представление НОД, мы не будем делать этого и все вычисления будем производить точно.
Изображение слайда
22
Слайд 22: 3. Наибольший общий делитель многочленов
Выполним деление h ( x ) на r 1 (x) :
Изображение слайда
23
Слайд 23: 3. Наибольший общий делитель многочленов
Выполним деление r 1 (x) на r 2 (x) :
Поскольку остаток r 2 ( x ) = 0 равен нулю, то НОД ( f(x),h(x) )= x +1. ◙
Изображение слайда
24
Слайд 24: 3. Наибольший общий делитель многочленов
НОД нескольких многочленов f 1 ( x ), f 2 ( x ),…, f m ( x ) может быть найден индуктивным способом на основании следующей формулы:
.
Таким образом, для того чтобы найти наибольший общий делитель многочленов f 1 ( x ), f 2 ( x ),…, f m ( x ), следует в соответствии с этой формулой найти сначала
d 1 ( x )=НОД( f 1 ( x ), f 2 ( x )), затем
d 2 ( x )=НОД( d 1 ( x ), f 3 ( x )) и т.д.;
и, наконец, найти многочлен
d m -1 ( x )=НОД( d m-2 ( x ), f m ( x )),
который и будет искомым наибольшим делителем.
Изображение слайда
25
Слайд 25: 4. Линейное представление НОД многочленов
Т е о р е м а 4 (о линейном представлении НОД): Если d(x) = НОД ( f(x),h(x) ), где f(x) и h(x) – многочлены из кольца P [ x ], то в P [ x ] существуют такие многочлены u(x) и v(x), что
f(x)u(x) + h(x)v(x)=d(x). (5)
◘ Для доказательства этого утверждения достаточно выразить НОД ( f(x),h(x) )= d(x)=r k (x) из предпоследнего равенства системы (Е), затем заменить в нем r k -1 (x) выражением его из предшествующего равенства и т.д. Продолжая этот процесс, поднимаемся по равенствам Евклида снизу вверх до тех пор, пока не исключим все остатки и получим выражение вида (5). ◙
Изображение слайда
26
Слайд 26: 4. Линейное представление НОД многочленов
f(x)u(x) + h(x)v(x)=d(x). (5)
◘ Действительно из (Е)
Имеем НОД ( f(x),h(x) )= d(x)= r k (x) = r k -2 (x) – r k -1 (x) q k -1 (x) = = r k -3 (x)(-1) + r k -2 (x)(1+q k -1 (x) q k – 2 (x) ) = … = = f(x)u(x)+h(x)v(x).
Изображение слайда
27
Слайд 27: 4. Линейное представление НОД многочленов
f(x)u(x) + h(x)v(x)=d(x). (5)
Пример 4. Проиллюстрируем теорему 4, опираясь на вычисления примера 3.
Запишем равенства (Е) для выполненных там делений, при этом будем использовать пока буквенные обозначения:
Выражая r 2 (x) из последнего равенства (напомним, что в примере 3 НОД ( f(x),h(x) ) = r 2 (x) ) и подставляя в него выражение из первого равенства, получим
Изображение слайда
28
Слайд 28: 4. Линейное представление НОД многочленов
f(x)u(x) + h(x)v(x)=d(x). (5)
или f(x)u(x) + h(x)v(x)=d(x), где,
и d(x)=x+1.
Таким образом,
,
где и,
искомое линейное представление
НОД ( f(x),h(x) ) = x +1. ◙
Изображение слайда
29
Слайд 29: 4. Линейное представление НОД многочленов
Определение 3. Многочлены f(x) и h(x) из кольца P [ x ] называются взаимно простыми, если их НОД равен некоторому элементу с из поля P.
Поскольку НОД многочленов определяется с точностью до множителей нулевой степени, то можно считать, что для взаимно простых многочленов f(x) и h(x) их НОД равен 1.
Отметим два следствия из теоремы 4.
Следствие 5. Многочлены f(x) и h(x) взаимно просты тогда и только тогда, когда в кольце P [ x ] существуют такие многочлены u(x) и v (x), что
f(x)u(x) + h(x)v(x)=1. (6)
Изображение слайда
30
Слайд 30: 4. Линейное представление НОД многочленов
Следствие 5. Многочлены и взаимно просты тогда и только тогда, когда в кольце P [ x ] существуют такие многочлены u(x) и v(x), что
f(x)u(x) + h(x)v(x)=1. (6)
◘ Пусть f(x) и h(x) взаимно просты, т.е. НОД ( f(x),h(x) ) = 1. Тогда равенство (6) вытекает непосредственно из теоремы 4.
Обратно, пусть равенство (6) выполняется и d(x) – общий делитель многочленов f(x) и h(x).
Тогда из равенства (6) получаем, что.
Это означает, что d(x) P.
Следовательно, f(x) и h(x) – взаимно простые многочлены. ◙
Изображение слайда
31
Слайд 31: 4. Линейное представление НОД многочленов
Следствие 6. Если f(x) и h(x) – многочлены из кольца P [ x ], d(x) = НОД ( f(x),h(x) ), то многочлены
и взаимно просты.
◘ В самом деле, по теореме 4 справедливо равенство
(5).
Поделив его на d(x), получим равенство
,
из которого вытекает взаимная простота многочленов f 1 (x) и h 1 (x). ◙
Изображение слайда
32
Слайд 32: Свойства взаимно простых многочленов
Отметим еще три свойства взаимно простых многочленов.
1°. Если многочлен f ( x ) взаимно прост с многочленами g ( x ) и h ( x ), то он взаимно прост и с их произведением g ( x ) h ( x ).
◘ Ввиду взаимной простоты многочленов f ( x ) и g ( x ) по следствию 5 для них существует представление вида
f ( x ) u ( x ) + g ( x ) v ( x ) = 1.
Умножая это равенство на h ( x ) получим равенство
f ( x ) ( u ( x ) h ( x )) + ( g ( x ) h ( x )) v ( x ) = h ( x ). (7)
Предположим, что НОД( f ( x ), g ( x ) h ( x ))= d ( x ). Из равенства (7) вытекает, что d ( x ) – общий делитель многочленов f ( x ) и h ( x ). Но многочлены f ( x ) и h ( x ) взаимно простые и поэтому d ( x )=1.
Таким образом, многочлен f ( x ) взаимно прост с произведением g ( x ) h ( x ). ◙
Изображение слайда
33
Слайд 33: Свойства взаимно простых многочленов
2°. Если произведение f ( x ) g ( x ) делится на многочлен h ( x ) и многочлены g ( x ) и h ( x ) взаимно просты, то многочлен f ( x ) делится на h ( x ).
◘ Из взаимной простоты многочленов g ( x ) и h ( x ) по следствию 5 следует существование многочленов u ( x ) и v ( x ) со свойством
g ( x ) u ( x ) + h ( x ) v ( x ) = 1.
Умножая это равенство на f ( x ), получим равенство
( f ( x ) g ( x )) u ( x ) + h ( x ) ( f ( x ) v ( x )) = f ( x ).
Из последнего равенства легко вытекает делимость f ( x ) на h ( x ). ◙
Изображение слайда
34
Слайд 34: Свойства взаимно простых многочленов
3°. Если многочлен f ( x ) делится на многочлены g ( x ) и h(x), которые взаимно просты между собой, то f ( x ) делится и на их произведение g ( x ) h ( x ).
◘ Пусть f ( x ) делится на g ( x ) и h ( x ).
Тогда f ( x )= g ( x ) s ( x ) и g ( x ) s ( x ) делится на h ( x ).
Отсюда, ввиду взаимной просты многочленов g ( x ) и h ( x ), по свойству 2° получаем, что s ( x ) делится на h ( x ), т.е. s ( x )= h ( x ) t ( x ) для некоторого многочлена t ( x ).
Подставляя найденное выражение для s ( x ) в равенство f ( x )= g ( x ) s ( x ) окончательно получим f ( x )=( g ( x ) h ( x )) t ( x ). ◙
Изображение слайда
35
Слайд 35: 4. Наименьшее общее кратное многочленов
Определение 4. Наименьшим общим кратным многочленов f 1 ( x ), f 2 ( x ), …, f m ( x ) из кольца P [ x ] называется многочлен k(x), обладающий следующими свойствами:
1) k(x) делится на каждый из многочленов f 1 ( x ), f 2 ( x ), …, f m ( x ), т.е. является их общим кратным;
2) любое общее кратное многочленов делится на k(x).
Обозначение: НОК( f 1 ( x ), f 2 ( x ), …, f m ( x ) ).
Изображение слайда
36
Слайд 36: 4. Наименьшее общее кратное многочленов
Понятно, что, в случае существования, НОК определяется с точностью до множителя нулевой степени (любые два НОК должны делиться друг на друга); нормированное НОК определяется однозначно.
Т е о р е м а 5 (о НОК двух многочленов). Любое общее кратное многочленов f ( x ) и h ( x ) имеет вид
, где t(x) P [ x ]. (8)
При этом
. ( 9 )
Изображение слайда
37
Слайд 37: 4. Наименьшее общее кратное многочленов
◘ Пусть
d ( x )=НОД( f ( x ), h ( x )), и.
Используя эти обозначения, перепишем равенство
(8)
в виде
.
Отсюда видно, что любой многочлен вида (8) является общим кратным многочленов f ( x ) и h ( x ).
Изображение слайда
38
Слайд 38: 4. Наименьшее общее кратное многочленов
Пусть теперь k ( x ) – общее кратное многочленов f ( x ) и h ( x ). Покажем, что оно имеет вид
(8).
По условию k ( x ) делится на f ( x ) и поэтому k ( x )= f ( x ) q ( x ). С другой стороны, поскольку, то, и, следовательно,.
Так как по следствию 6 многочлены f 1 ( x ) и h 1 ( x ) взаимно просты, отсюда и из свойства 2° взаимно простых многочленов получаем, что, т.е. q ( x )= h 1 ( x ) t ( x ). Но тогда имеем
.
Таким образом, любое общее кратное k ( x ) многочленов f ( x ) и h ( x ) имеет вид (8) и первое утверждение теоремы 5 доказано.
Изображение слайда
39
Слайд 39: 4. Наименьшее общее кратное многочленов
Докажем равенство
(9).
В самом деле, из равенства
(8)
следует, что многочлен есть общее кратное многочленов f ( x ) и h ( x ) и, что любое общее кратное f ( x ) и h ( x ) на него делится.
Таким образом,
. ◙
Изображение слайда
40
Слайд 40: 4. Наименьшее общее кратное многочленов
Т е о р е м а 5 (о НОК двух многочленов). Любое общее кратное многочленов многочленов f ( x ) и h ( x ) имеет вид
, где t(x) P [ x ]. (8)
При этом
. ( 9 )
Из теоремы 5 вытекает
Следствие 7. Наименьшее общее кратное двух взаимно простых многочленов равно их произведению. ◙
Изображение слайда
41
Слайд 41: 4. Наименьшее общее кратное многочленов
Пример 5. В кольце многочленов R [ x ] с действительными коэффициентами найдем НОК многочленов
и.
Согласно вычислениям примера 1 НОД ( f(x),h(x) = x+ 1. По формуле ( 8 ) имеем
.
Поделив сначала многочлен на двучлен x+1, получим многочлен.
Теперь =
= =.
Изображение слайда
42
Слайд 42: 4. Наименьшее общее кратное многочленов
НОК нескольких многочленов f 1 ( x ), f 2 ( x ), …, f m ( x ) может быть найден индуктивным способом на основании следующей формулы:
.
Таким образом, для нахождения НОК ( f 1 ( x ), f 2 ( x ), …, f m ( x ) ) следует в соответствии с этой формулой найти сначала k 1 ( x )=НО K ( f 1 ( x ), f 2 ( x )), затем k 2 ( x )=НОК( k 1 ( x ), f 3 ( x )) и т.д.; и, наконец, многочлен k m -1 ( x )=НОК( k m-2 ( x ), f m ( x )), который и будет искомым НОК.
Изображение слайда
43
Последний слайд презентации: АЛГЕБРА (3-й семестр)
Изображение слайда
%20=%20x^{5}+x^{4}-4*x^{3}+5*x)
%20=%202*x^{3}-x^{2}-2*x+2)
*x^{2}+(0.5)*x+(3.5))
*x+(1.1358024691358))