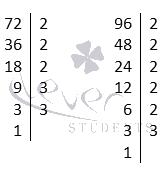Как найти нод с помощью разложения

Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.

Алгоритм Евклида для нахождения НОД

Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».

Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:

a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1

Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).

Нахождение НОД с помощью разложения чисел на простые множители

Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.

Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.

Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.

Нахождение НОД трех и большего количества чисел

Независимо  от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.

А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.

Нахождение НОД отрицательных чисел

Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.

Нахождение нод с помощью разложения чисел на простые множители

Рассмотрим
еще один способ нахождения НОД. Наибольший
общий делитель может быть найден
по разложениям
чисел на простые множители. Сформулируем
правило: НОД
двух целых положительных чисел a и b равен
произведению всех общих простых
множителей, находящихся в разложениях
чисел a и b на
простые множители.

Приведем
пример для пояснения правила нахождения
НОД. Пусть нам известны разложения
чисел 220 и 600 на
простые множители, они имеют
вид 220=2·2·5·11 и 600=2·2·2·3·5·5.
Общими простыми множителями, участвующими
в разложении чисел 220 и 600,
являются 2, 2 и5.
Следовательно, НОД(220,
600)=2·2·5=20.

Таким
образом, если разложить числа a и b на
простые множители и найти произведение
всех их общих множителей, то этим будет
найден наибольший общий делитель
чисел a и b.

Рассмотрим
пример нахождения НОД по озвученному
правилу.

Пример.

Найдите
наибольший общий делитель чисел 72 и 96.

Решение.

Разложим
на простые множители числа 72 и 96:

То
есть, 72=2·2·2·3·3 и 96=2·2·2·2·2·3.
Общими простыми множителями
являются 2, 2, 2и 3.
Таким образом, НОД(72,
96)=2·2·2·3=24.

Ответ:

НОД(72,
96)=24.

В
заключение этого пункта заметим, что
справедливость приведенного правила
нахождения НОД следует из свойства
наибольшего общего делителя, которое
утверждает, чтоНОД(m·a₁,
m·b₁)=m·НОД(a₁,
b₁),
где m –
любое целое положительное число.

К
началу страницы

Нахождение нод трех и большего количества чисел

Нахождение
наибольшего общего делителя трех и
большего количества чисел может быть
сведено к последовательному нахождению
НОД двух чисел. Мы об этом упоминали,
при изучении свойств НОД. Там мы
сформулировали и доказали теорему:
наибольший общий делитель нескольких
чисел a₁,
a₂,
…, a_k равен
числу d_k,
которое находится при последовательном
вычислении НОД(a₁,
a₂)=d₂, НОД(d₂,
a₃)=d₃, НОД(d₃,
a₄)=d₄,
…,НОД(d_k-1,
a_k)=d_k.

Давайте
разберемся, как выглядит процесс
нахождения НОД нескольких чисел,
рассмотрев решение примера.

Пример.

Найдите
наибольший общий делитель четырех
чисел 78, 294, 570 и 36.

Решение.

В
этом примере a₁=78, a₂=294, a₃=570, a₄=36.

Сначала
по алгоритму Евклида определим наибольший
общий делитель d₂ двух
первых чисел 78 и 294.
При делении получаем
равенства 294=78·3+60; 78=60·1+18;60=18·3+6 и 18=6·3.
Таким образом, d₂=НОД(78,
294)=6.

Теперь
вычислим d₃=НОД(d₂,
a₃)=НОД(6,
570).
Опять применим алгоритм Евклида:570=6·95,
следовательно, d₃=НОД(6,
570)=6.

Осталось
вычислить d₄=НОД(d₃,
a₄)=НОД(6,
36).
Так как 36 делится
на 6,
тоd₄=НОД(6,
36)=6.

Таким
образом, наибольший общий делитель
четырех данных чисел равен d₄=6,
то есть,НОД(78,
294, 570, 36)=6.

Ответ:

НОД(78,
294, 570, 36)=6.

Разложение
чисел на простые множители также
позволяет вычислять НОД трех и большего
количества чисел. В этом случае наибольший
общий делитель находится как произведение
всех общих простых множителей данных
чисел.

Пример.

Вычислите
НОД чисел из предыдущего примера,
используя их разложения на простые
множители.

Решение.

Разложим
числа 78, 294, 570 и 36 на
простые множители,
получаем 78=2·3·13,294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Общими простыми множителями всех данных
четырех чисел являются числа 2 и 3.
Следовательно, НОД(78,
294, 570, 36)=2·3=6.

Ответ:

НОД(78,
294, 570, 36)=6.

К
началу страницы

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.

Как найти НОД?

Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

1. разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
2. выбрать одинаковые множители, входящие в оба разложения;
3. найти их произведение.

Примеры нахождения наибольшего общего делителя

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОД 12 и 8

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2

3. Перемножаем эти множители и получаем: 2 · 2 = 4

Ответ: НОД (8; 12) = 2 · 2 = 4.

Пример 2: найти НОД 75 и 150

Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5

3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75

Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.

Частный случай или взаимно простые числа

Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:

Пример 3: найти НОД 9 и 5

Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.

#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳

Цикл статей “Дроби”

Первая часть Вторая часть Третья часть

Четвертая часть Пятая часть Шестая часть Седьмая часть Восьмая часть

Здравствуйте, уважаемые читатели!

Предлагаю рассмотреть ещё один способ нахождения Наибольшего Общего Делителя (НОД) двух чисел, известный под названием «АЛГОРИТМ ЕВКЛИДА», использование которого в случаях многозначных чисел часто оказывается значительно рациональнее традиционного способа с разложением чисел на простые множители.

Для начала опишем последовательность шагов алгоритма.

На первом шаге необходимо провести деление бОльшего числа на мЕньшее. Если деление удалось, т.е. остаток оказался равен нулю, то меньшее число и будет Наибольшим Общим Делителем этих двух чисел. В случае ненулевого остатка необходимо продолжить выполнение алгоритма.

На втором шаге необходимо разделить мЕньшее из двух данных чисел (первый делитель) на полученный в первом делении остаток. Если при этом делении получится нулевой остаток, то НОД двух данных чисел равен остатку от деления на первом шаге или, что то же, делителю на втором шаге. В случае ненулевого остатка следует продолжить выполнение алгоритма.

На третьем шаге следует разделить предыдущий делитель (остаток от предпоследнего деления) на остаток, полученный на предыдущем шаге. В случае получения нулевого остатка НОД будет равен остатку, полученному на предыдущем шаге или, что тоже, последнему делителю. В случае получения ненулевого остатка повторять действия на этом шаге вплоть до получения нулевого остатка — в этом случае последний ненулевой остаток или, что то же, последний делитель и будет Наибольшим Общим Делителем.

Замечу, что описание Алгоритма Евклида для нахождения НОД двух натуральных чисел значительно «объёмнее» его исполнения. Найдём, например, НОД (1729; 2584) сначала с использованием традиционного метода с разложением чисел на простые множители, а затем с помощью алгоритма Евклида.

Чтобы реально оценить преимущество алгоритма Евклида, рекомендую самостоятельно проделать разложение этих чисел на простые множители и все остальные операции по нахождению НОД данных чисел этим способом.

А теперь используем алгоритм:

ОТВЕТ: НОД (1729; 2584) = 19.

В заключение отмечу, что алгоритм Евклида тем эффективнее (в сравнении с традиционным), чем больше числа, НОД которых следует найти.

Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.

Читайте наш канал в телеграм – по этой ссылке

Другие статьи автора:

Цикл статей “Дроби”

1 статья 2 статья 3 статья 4 статья 5 статья 6 статья

7 статья 8 статья 9 статья [Текущая]

Как найти НОД

• Нахождение путём разложения на множители
• Алгоритм Евклида

Рассмотрим два способа нахождения наибольшего общего делителя.

Нахождение путём разложения на множители

Первый способ заключается в нахождении наибольшего общего делителя путём разложения данных чисел на простые множители.

Чтобы найти НОД нескольких чисел, достаточно, разложить их на простые множители и перемножить между собой те из них, которые являются общими для всех данных чисел.

Алгоритм Евклида

Второй способ (иначе его называют способом Евклида) заключается в нахождении НОД путём последовательного деления.

Сначала мы рассмотрим этот способ в применении только к двум данным числам, а затем разберёмся в том, как его применять к трём и более числам.

Если большее из двух данных чисел делится на меньшее, то число, которое меньше и будет их наибольшим общим делителем.

В остальных случаях, чтобы найти наибольший общий делитель двух чисел используется следующий порядок действий:

1. Из двух данных чисел большее число делят на меньшее.
2. Затем, меньшее число делят на остаток, получившийся от деления большего числа на меньшее.
3. Далее, первый остаток делят на второй остаток, который получился от деления меньшего числа на первый остаток.
4. Второй остаток делят на третий, который получился от деления первого остатка на второй и т. д.
5. Таким образом деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель как раз и будет наибольшим общим делителем.

Чтобы найти наибольший общий делитель трёх и более данных чисел, используем следующий порядок действий:

1. Сперва находим наибольший общий делитель любых двух чисел из нескольких данных.
2. Затем находим НОД найденного делителя и какого-нибудь третьего данного числа.
3. Затем находим НОД последнего найденного делителя и четвёртого данного числа и так далее.