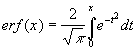Как найти ноль функции маткад

Математические
встроенные функции

Нахождение
нулей функции. Встроенная функция root

Решение
блоков. Функции Find и Minerr

Интерполяция
функций

Оператор
вычисления производной

Оператор
вычисления определенного интеграла

Пример:
нахождение точек экстремума функции и
длины кривой

Преобразования
Фурье

Статистическая
обработка данных

Математические
встроенные функции

• Вычисление
  значений функции Бесселя I-го и II-го
  рода целого индекса.

• Интеграл
  ошибок.

• Г-функция
  Эйлера.

• Нормированная
  функция распределения нормальной
  случайной величины.

Бесселевы функции

Функции Бесселя относятся к классу так
называемых специальных функций,
используемых в частности при решении
задач математической физики. В MathCADе
реализовано вычисление значений функций
Бесселя I-го и II-го рода целого индекса.

Бесселевы функции 1-го рода: J0(x),
J1(x), Jn(n,x),

где x- вещественное
число,n- целое
число,n>1.

.

Бесселевы функции 2-го рода: Y0(x),
Y1(x), Yn(n,x),

где x-
положительное вещественное число,n- целое число,n>1.

Замечание: Cм. Справочник по специальным
функциям /Под ред. М.Абрамовица, И.Стиган.
М.:Наука, 1979.

Специальные статистические функции

Данная версия системы содержит три
специальные функции, связанные в первую
очередь с расчетами в области математической
статистики.

erf(x)- интеграл
ошибок

Г(x)- Г-функция
Эйлера

cnorm(x)-
нормированная функция распределения
нормальной случайной величины

Нахождение нулей функции. Встроенная функция root

• Встроенная
  функция нахождения нулей функции.

• Изменение
  точности вычислений.

Нулем функции одной независимой
переменной называется такое значение
ее аргумента, при котором значение
функции равно нулю, т.е. нуль функции
f(x)- это корень
уравненияf(x)=0.

Для поиска нулей функции, а также корней
уравнения применяется встроенная
функция root. Формат функции:

root(выражение,имя_переменной)

Чтобы найти нуль функции (или корень
уравнения):

1) задайте начальное предполагаемое
значение неизвестного,

2) используйте функцию root для решения.

Например, организовать поиск корня
уравнения x3+x+1=0можно следующим образом:

x:=0.5
zeroval:=root(x3+x+1,x)

Замечание: В MathCADе решение уравнения
ищется приближенно методом секущих.
Находится действительный или комплексный
корень в соответствии с типом начального
приближения. Условием прекращения
вычислений является
(TOL
встроенная переменная, ее значение по
умолчанию 0.001,xn- значение функцииroot,
f(xn)
– значение выражения). При этом
необходимое для начала итераций по
методу секущих кромеx0
еще одно приближениеx1определяется по формулеx1=x0+h,
где h= TOL, еслиx0
= 0, иначеh =x0 TOL. Другим
условием прекращения вычислений является
превышение определенного количества
итераций, при этом выдается диагностическое
сообщение’not
converging’. Изменить точность вычисления
можно, задав новое определение встроенной
переменной TOL.

Сообщение “not
converging” (нет сходимости) может
появиться по следующим причинам:

1) функция не имеет нулей;

2) нули функции значительно удалены от
указанного начального приближения;

3) между начальным приближением и нулями
есть локальный минимум или максимум;

4) нарушается непрерывность выражения
на промежутке между начальным приближением
и нулем.

Лучший способ установить причину ошибки
– построить график функции. Если функция
имеет несколько нулей, укажите различные
к ним начальные приближения.

Соседние файлы в папке Пособие по MathCAD

• #
• #
• #
• #
• #

Желтыми прямоугольниками выделены вычисления, в которых требуется участие пользователя.

Красными прямоугольниками выделены комментарии к пунктам, в которых требуется участие пользователя.

Зелеными прямоугольниками выделены пункты и комментарии к ним, в которых система работает автоматически, т.е. без участия пользователя.

Шаблон исследования функции одной переменной

Шаблон№1. Исследовать функцию

1. Задаем функцию // пользователь выбирает функцию сам

2. Строим первоначальный график заданной функции

// выводит автоматически

3. Находим область определения функции

Определим четность функции

функция ни нечетная, ни четная

// Пользователь сам составляет уравнение или неравенство (возможно систему) для нахождения области определения функции. Система решит его сама. После чего, получив точки, пользователь делает вывод. Если область определения принадлежит множеству действительных чисел, то надо лишь это указать, не решая никаких уравнений.

4. Найдем нули функции

Точка пересечения с осью Oy

точка пересечения с осью Ox

// Пользователю только надо сделать вывод о четности функции

// В некоторых случаях требует участия пользователя

5. Найдем пределы функции

6. Найдем точки экстремума. Для этого найдем сперва производную функции

Приравняем производную к нулю:

являются критическими точками

Найдем точки экстремума

Точка минимума

Точка максимума

Определим промежутки возрастания и убывания функции

График функции убывает на промежутке:

// Требует участия пользователя для анализа точек и составления промежутков монотонности

График функции возрастает на промежутке:

// пользователь должен заменить функцию на свою

Наибольшее значение

Наименьшее значение

// В скобках надо заменить значения на те, которые получились при нахождении точек экстремума

7. Найдем вторую производную

Точек перегиба нет

// Вывод делает пользователь

G (x) всюду отрицательно, значит точек перегиба нет, и график функции выпуклый кверху на всей области определения

8. Построим график функции

Шаблон исследования функции двух переменных

Шаблон №2. Исследовать функцию двух переменных:

1. Задаем функцию

// Пользователь сам выбирает функцию

2. Построим первоначальный график функции

// выводит автоматически

3. Находим область определения функции

// Для функции двух переменных система MathCAD может решать только функции с областью определения R. Для разрывных функции график не строит

4. Найдем точки пересечения с осями координат

Точка пересечения в начале координат

5. Строим линии уровня

// автоматически

6. Определяем повторный предел заданной функции

7. Находим частные производные

Проводим повторное дифференцирование

8. Определяем стационарные точки

Приравниваем частные производные первого порядка к нулю

стационарные точки. Получаем точку с координатами

// Пользователь сам делает вывод

9. Найдем точки локального экстремума

// Иногда требует участия пользователя

// Пользователь сам должен сделать вывод

т. к. Д>0, то в точке М функция имеет экстремум

A >0, C>0 значит точка М -точка локального минимума

10. Находим глобальный экстремум функции

// Заменить значения в скобках на ваши координаты точки М

11. Строим график функции

// автоматически