Как для всех функций. Если исследовать с помощью производной, то полезна формула $%|x|^’=frac{x}{|x|}.$%
$$а)y=|x-3|-1$$
$$б)y=4-|x+2| $$
$$в)y=x^{-2}$$
$% a) y=0Leftrightarrow |x-3|-1=0 Leftrightarrow |x-3|=1 Leftrightarrow (x-3=1 $% или $%x-3=-1) Leftrightarrow (x=4 $% или $%x=2).$%Нули функции $%2$% и $%4.$%
$% y>0Leftrightarrow |x-3|-1>0 Leftrightarrow |x-3|>1 Leftrightarrow (x-3>1 $% или $%x-3<-1) Leftrightarrow (x>4 $% или $%x<2).$% Сохраняет положителный знак во множестве $%(-infty;2)cup (4;infty).$%
$%y<0Leftrightarrow |x-3|-1<0 Leftrightarrow |x-3|<1 Leftrightarrow -1<x-3<1Leftrightarrow 2<x<4$%. Сохраняет отрицательный знак во множестве $%(2;4).$%
Возрастает в промежутке $%[3;infty).$% убывает в промежутке $%(-infty;3]$%
b)По аналогии можете исследовать сами. Возрастает в $%(-infty;-2],$%убывает в промежутке $%[-2;infty).$%
с) Не имеет нулей, принимает только положительные значения. Возрастает в $%(-infty;0),$%убывает в промежутке $%(0;infty).$%.Графики первих двух вы посмотрите у @Anatoliy. А график третьего сейчас покажу
«Построение графика квадратной функции, содержащей модуль»
Тема: “Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х2— 6x + 3.)
Цель.
- Исследовать расположение графика функции на
координатной плоскости в зависимости от модуля. - Развить навыки построения графика функции,
содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1. Построить график
функции у = х2 — 6х + 3. Найти нули функции.
Решение.
1. Направление “ветвей” параболы: если а = 1, а >
0, то “ветви” параболы направлены вверх.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3,
у(3) = 9 – 18 + 3 = — 6, А(3; -6).
3. Уравнение оси симметрии: х = 3.
4. Нули функции: у(х) = 0, х2 — 6х + 3 = 0, D = 36 — 4·3 =
36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2
= 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Рис.1.
Алгоритм построения графика квадратной
функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных
функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
Рис. 2.
2.у = |х| + 1. График функции на рисунке 3.
Рис.3.
3. у = |х + 1|. График функции рисунке 4.
Рис.4.
Вывод.
1. График функции у = |х| + 1 получается из графика
функции у = |х| параллельным переносом на вектор
{0;1}.
2. График функции у = |х + 1| получается из графика
функции у = |х| параллельным переносом на вектор
{-1;0}.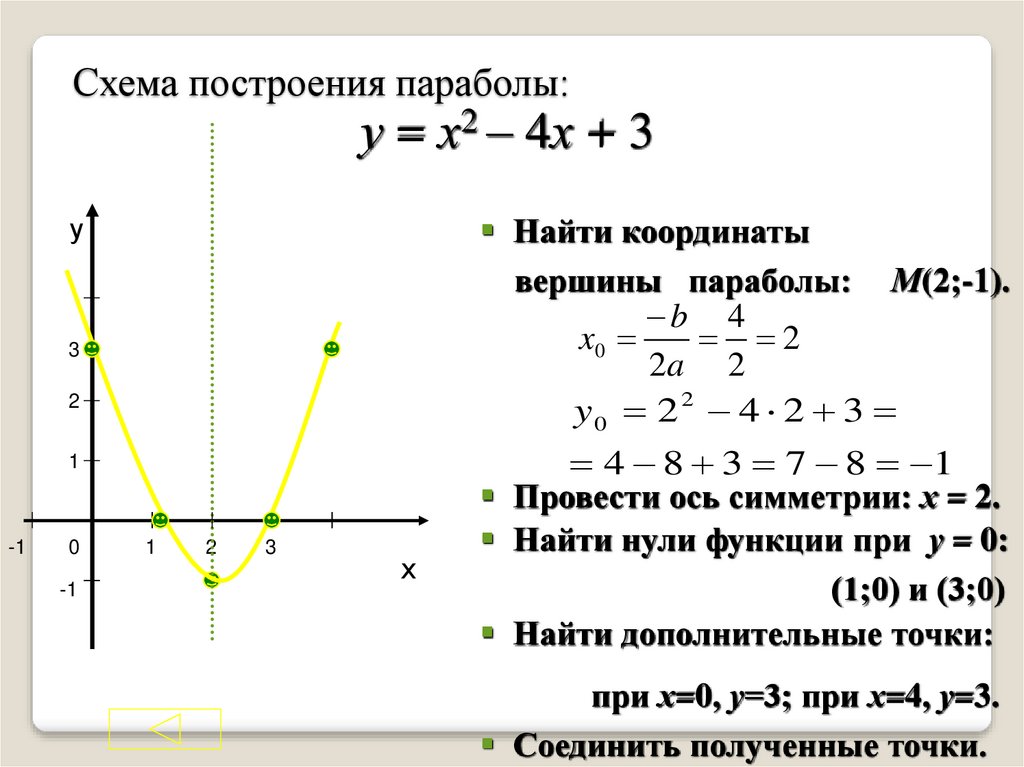
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в
группах.
Группа 1. Построить графики функций:
а) у = х2 — 6|x| + 3,
б) у = |х2 — 6х + 3|.
Решение.
а)
1.Построить график функции у = х2-6х+3.
2. Отобразить его симметрично относительно оси
Оу.
График на рисунке 5.
Рис.5.
б) 1. Построить график функции у = х2 — 6х + 3.
2. Отобразить его симметрично относительно оси
Ох.
График функции на рисунке 6.
Рис. 6.
Вывод.
1. График функции у = f(|x|) получается из графика
функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика
функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x2 — 6|x| + 3|;
б) y = |x2 — 6x + 3| — 3.
Решение.
а)
1. График функции у = х2 + 6x + 3 отображаем
относительно оси Оу, получается график функции у
= х2 — 6|x| + 3.
2. Полученный график отображаем симметрично
относительно оси Ох.
График функции на рисунке 7.
Рис.7.
Вывод.
График функции y = |f (|x|)| получается из графика
функции у = f(х), последовательным отображением
относительно осей координат.
б)
1. График функции у = х2 — 6х + 3 отображаем
относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Рис.8.
Вывод. График функции у = |f(x)| + a
получается из графика функции у = |f(x)|
параллельным переносом на вектор {0,a}.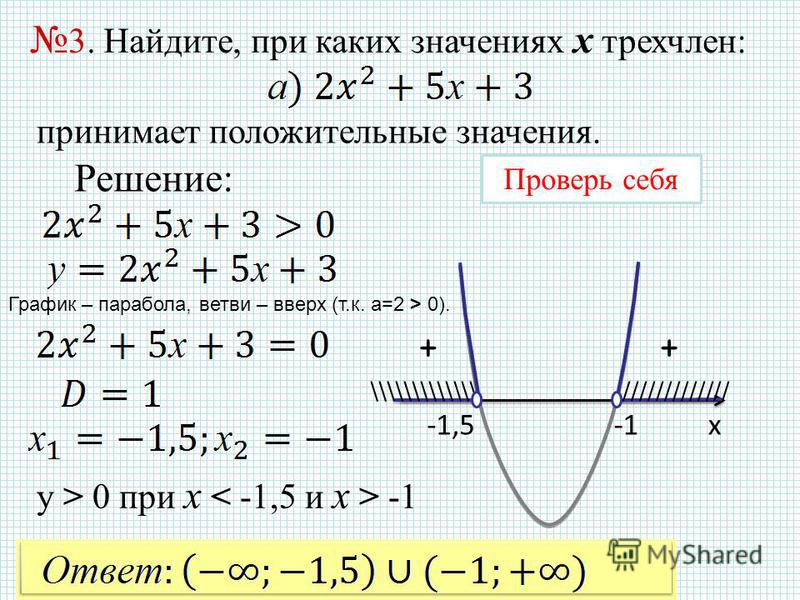
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х2 + 6x + 3 при х < 0
для точек у(0) = 3, у( — 1) = — 4.
График функции на рисунке 9.
Рис.9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х2 + 6х + 3 при х 6.
1. Направление “ветвей” параболы: а = — 1, а < 0,
“ветви” параболы направлены вниз.
2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2,
А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х2 — 6х + 3 при х = 7
у(7) = 10.
График на рис.10.
Рис.10.
Вывод. При решении данной группы
уравнений необходимо рассматривать нули
модулей, содержащихся в каждом из уравнений.
Затем строить график функции на каждом из
полученных промежутков.
(При построении графиков данных функций каждая
группа исследовала влияние модуля на вид графика
функции и сделала соответствующие заключения.)
Получили сводную таблицу для графиков функций,
содержащих модуль.
Таблица построения графиков
функций, содержащих модуль.
| Вид функции | Способ построения графика функции |
| 1. у = f(|x|)
2. у = |f(x)| 3. у = |f(|x|)| 4. у = |f(x)| + a |
1. Отобразить график функции у = f(x) симметрично относительно оси Оу. 2. Отобразить 3. Последовательно отобразить график функции у = 4. Параллельный перенос перенос графика функции |
Группа 4.
Построить график функции:
а) у = х2 — 5x + |x — 3|;
б) у = |x2 — 5x| + x — 3.
Решение.
а) у = х2 — 5х + |х — 3|, переходим к
совокупности систем:
Строим график функции у = х2 -6х + 3 при х 3,
затем график функции у = х2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
Рис.11.
б) у = |х2 — 5х| + х — 3, переходим к
совокупности систем:
Строим каждый график на соответствующем
интервале.
График функции на рисунке 12.
Рис.12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на
вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х2 — 5х + |x — 3||,
б) у= ||x2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно
оси Ох.
Рис.13.
Рис. 14.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0.
Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Рис.15.
Вывод. Два модуля в предложенных
уравнениях существенно усложнили построение
общего графика, состоящего из трех отдельных
графиков.
Учащиеся записывали выступления каждой из
групп, записывали выводы, участвовали в
самостоятельной работе.
3. Задание на дом.
Построить графики функций с различным
расположением модуля:
1. у = х2 + 4х + 2;
2. у = — х2 + 6х — 4.
4. Рефлексивно – оценочный этап.
1.Оценки за урок складываются из отметок:
а) за работу в группе;
б) за самостоятельную работу.
2. Какой момент был наиболее интересен на уроке?
3. Трудное ли домашнее задание?
Урок окончен.
Новые нули дзета-функции / Хабр
Астрологи объявили на хабре неделю профанных доказательств великих теорем.
- Теорема о четырёх красках.
- Теорема Ферма.
- Перед вами «доказательство гипотезы Римана».
Сначала я хотел тоже, оформить статью по приколу, что типа автор полностью уверен, что всё доказал, где мои деньги, но у меня, похоже, нет такого запаса самоиронии. Так что, обманываться вам придётся сознательно.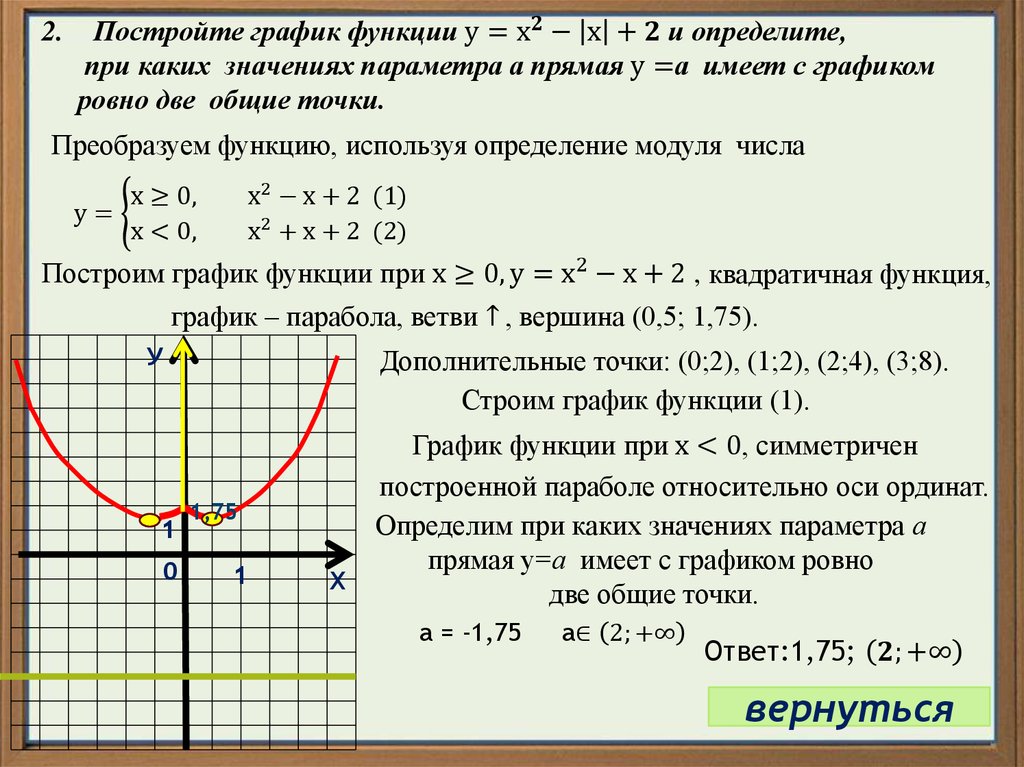
А ещё, статья же для плюсов пишется, а не для минусов. Так что, вспоминаем о существовании юмора и продолжаем читать.
Итак, сначала по-быстрому (и не по-настоящему) докажем потрясающее очень хорошо сбалансированное равенство
Для любого .
С детского сада всем известно, что сумма геометрической прогрессии равна
А сейчас полезно узнать, что существует такая особенная функция
На графике она похоже на синус, только без колебаний. Другими словами, нечётная.
Значит
Доказали. (Даже похоже получилось)
Если , то
Эту сумму можно разделить на одну единицу и две суммы единиц, тогда получится, что сумма единиц будет минус одной второй
Вот и дзета-функция от нуля тоже минус одна вторая.
Только, знак не так однозначен, ведь можно поделить и так:
Или даже вот так:
В общем, половинная сумма известна, а вот её знак уже подозрительно шатается.
Вот так забудешь поставить где надо различный знак и всё — сумма уже не нулевая, всё доказательство насмарку. Такое чувство, что при равенство может быть немножечко не очень верное.
Ладно, при нуле, может, и нет. Но при остальных значениях точно ноль. Поэтому даже верен интеграл
— Если не равен нулю.
На этом, кстати, работает преобразование Фурье — интеграл имеет не нулевое значение только если частотная составляющая и колебательный множитель в показателе экспоненты под интегралом гасят друг друга в ноль.
Да, всё понятно… При нуле и не должно работать. А так работает всегда. (Честно-честно)
Теперь надо вспомнить про дзета-функцию.
И про гамма функцию
Для дзеты можно повторить за гаммой и оставить аргумент в правой части уменьшенным на единицу
И тогда, если эти две функции перемножить
После замены переменной
Магия суммы геометрической прогрессии приведёт вот к такому простенькому интегралу:
Который на самом деле выглядит вот так
Да, это интеграл нашей знакомой функции, только второе и третье слагаемое в обычной ситуации дают нулевой вклад.
Но у нас гипотеза Римана, реальная часть меньше единицы. А так как там ещё единица отнимается, так и вообще степень становится меньше нуля. Особый случай, второе слагаемое вдруг обретает свою важную роль и начинает активно балансировать всё, чтобы не улетело в бесконечность. А третье слагаемое как-то теряется.
После замены переменных наша дзета-функция выглядит как приготовленная для разделки жареная курочка:
Да, перед нами обратное преобразование Фурье, а поиск нулей — это всего лишь поиск выпадающих частот. При частоты выпадают одна за другой, как на параде. А вот при других значениях — надо разбираться.
Ах да, надо ещё с тривиальными нулями что-то порешать. А то они внаглую идут только по чётным целым отрицательным числам, а у нас дробь из отрицательных целых зануляет и те и другие. Не сходится.
Но сам Риман сразу при открытии этой функции сказал: да [разве нужны нам]ер эти нули, вместе с полюсом.
Берём, умножаем на всё что под руку попадётся.
Получается Кси-функция, в которой нет тривиальных нулей, и даже если менять на , то получится то же самое — добавилась симметрия вокруг оси. А все остальные нули остались.
Убрали. Но! Нам же это только мешает! До этого сигму можно было в любую сторону шатать, вдруг на ноль попадёшь, а теперь надо обязательно, чтобы если слева ноль то и справа ноль. Это как два раза подряд выиграть в лотерею. Но математики же оптимисты! Шансы существуют. Это как выиграть один раз, но в дважды крутой лотерее.
Так что, составим соответствующее равенство, верное при таких нулях.
Ничего особенного, одинаковые выражения справа и слева, только знак у сигмы поменялся. Доказанная симметрия — она сразу и у знак переключает. А вот так — только у сигмы, без , выполнить равенство слабо?
«Новые» нули функции именно это и обязаны делать.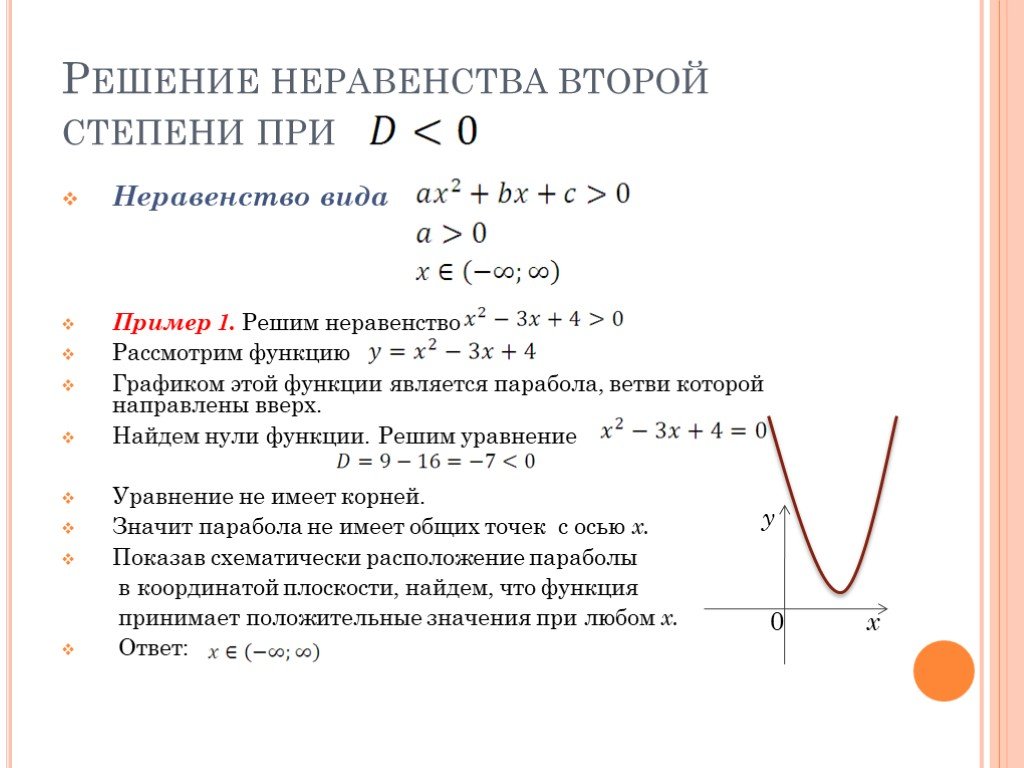
Конечно, если интеграл ноль, без разницы, что там за конечный множитель перед ним. Но и убирать этот множитель не надо, он должен помочь найти такое место, ведь прежде чем обнулиться функция должна потихонечку симметричненько уронить логарифм своего значения.
Смотря на это равенство, можно начать сомневаться, что и осевые нули бывают. Но нет — доказано, на оси нулей столько, что забирай — не закончатся. А вот то что не при любом такое бывает — уже намекает на ограничения.
А ещё, может ли выполняться это равенство при не нулевых значениях интеграла? Мнимая часть точно должна быть нулевой, ведь она меняет знак. А реальная? Ну вот, даже прямое уравнение и то с подвохом — при нулевом выполняется с любой сигмой. И такие линии выполнения равенства есть и при комплексных значениях, они изогнутые. Если оставшаяся реальная часть на такой линии обнулится, то это именно то что мы ищем. Такие линии даже напрямую чередуются с нулями: на графике значений кси-функции около оси она то пересекает линию нулевых мнимых значений, то пересекает линию нулевых действительных значений.
График с выделением линий нулевых мнимых значений кси-функции, пересечения не совпадают, а чередуются с нулями дзета-функции.
Будет, конечно прикол, если «новый» ноль окажется не на этой линии. Он, конечно, может быть на линии, но я же не проверял, что только на ней. У кси-функции линии нулевой реальной части и линии нулевой мнимой части чередуются, но ещё по оси идёт линия нулевой мнимой части. Так что, если пересечения отходящих в сторону от оси линий не будет, новых нулей не ожидается.
***
Немного объясню прикол с нулевой суммой из начала статьи, а то может быть не понятно. Дело в том, что сумма всех натуральных степеней одного числа сходится только если число меньше единицы. Для комплексных чисел сравнение превращается из больше/меньше в направление изменения фазы — меня до сих пор удивляет, почему для математиков было открытием, что кроме вперёд/назад можно ходить и вправо/влево, и ещё разворачиваться в любом направлении. А больше/меньше определять можно отдельно для реальных или мнимых частей, или модуля.
Для схождения модуль числа должен быть меньше единицы. Если число равно единице, то для суммы слагаемые аналогичны нулевой степени натурального основания, и сходиться такая сумма из бесконечности единиц точно не будет. А если модуль больше единицы, то тем более.
Если модуль равен единице, но фаза отличается, то сумма превращается в постоянное кружение вокруг одной точки, и вопрос спорный — эта точка как-то относится к тому, что должно получиться, или нет? А если добавить такое кружение с противоположной фазой, и значит, в другую сторону? Общее значение будет реальным и равным единице — за счёт того, что первый шаг — в котором фаза ещё не проявлена — дублируется. Но имеет ли такая сумма отношение к понятию суммы, и можно ли расширить нулевое значения сложения этих сумм для всех комплексных степеней? Условно, очень условно. Если говорить точно, то нет. Но если в аналитическом смысле, то совсем же другое дело.
Только, аналитика тоже может быть неожиданной. Например. Преобразование Фурье можно было бы считать суммой из двух различных преобразований Лапласа.
Преобразование Лапласа — это интеграл, в котором множитель состоит из натурального основания в степени минус параметра — как преобразование Фурье, только без мнимого множителя, и с уменьшенным вдвое диапазоном интегрирования. Для комплексной функции колебания с одной частотой преобразование будет давать
На есть ограничения, при их нарушении интеграл не сходится. Если посмотреть, как будет выглядеть результат, если объединить отрицательный и положительный диапазон, чтобы было похоже на преобразование Фурье, то получится
Вот так. Оказывается, такие манипуляции не учитывают, что частота может совпадать с параметром, и не всегда будет давать ноль. Иногда это может быть дельта-функцией.
Кроме того, ограничение на преобразование Лапласа определяют только одно из этих двух слагаемых — это максимум, другое при тех же параметрах не сходится. Так что, это тоже условно. Но условность интересная. Преобразование Фурье-то здесь равно дельта-функции не условно.
Различие у нас уже встречалось, когда нечётность «особенной» функции упрощалась.
И слева что-то, что при нуле не рассчитывается, и справа претендент на дельта-функцию. Кругом подвох.
Второе слагаемое в особенной функции, конечно, подозрительное. С другой стороны, именно это слагаемое балансирует интеграл при определении нетривиальных нулей дзета-функции. И здесь, похоже, тоже балансирует.
Так что же за этим всем стоит? Если порассуждать: первое слагаемое понятное, второе слагаемое подозрительное, третье слагаемое не участвует в интеграле. И возникает по этому поводу такая мысль. А что, если существует и четвёртое слагаемое, только оно на столько странное, что даже не проявляется? Или, наоборот, всё доказательство сводится к тому, что такого слагаемого нет? Как доказать, что чего-то нет, если его нет? А, ну да, у нас тут гипотеза Римана, был бы наглядный пример.
Рассмотрим подробнее преобразование Фурье.
Если задать функцию затухающего колебания
То преобразование Лапласа с ней справится.
А вот преобразование Фурье как интеграл по всему диапазону — разойдётся.
Если ограничить диапазон интегрирования, точнее, обнулить функцию для , то
Результаты аналогичны. Аналитически, что полный диапазон, что закрытый диапазон, должны давать ноль. А здесь, промежуточный вариант, даёт какое-то не нулевое распределение.
— Ещё один промежуточный вариант, симметричный.
Если сложить то что получится при изменение знака у :
Если при этом сменить знак фазы, то всё упрощается как надо:
Преобразование Фурье двух встречных экспонент давало бы ноль, если бы знак не влиял на сходимость.
Эта статья ничем не заканчивается. Пойду чай попью.
С++ — Не удается модифицировать ноль?
спросил
11 лет, 3 месяца назад
Изменено
1 год, 8 месяцев назад
Просмотрено
70 тысяч раз
Почему X % 0 является недопустимым выражением?
Я всегда думал, что X % 0 должно равняться X. Поскольку вы не можете делить на ноль, не должен ли ответ, естественно, быть остатком, X (все, что осталось)?
- С++
- по модулю
- делить на ноль
7
Стандарт C++ (2003) говорит в §5.6/4,
[…] Если второй операнд / или % равен нулю, поведение undefined ; […]
То есть следующие выражения вызывают неопределенное поведение (UB):
X / 0; //УБ Х % 0; //УБ
Обратите внимание, что -5 % 2 НЕ равно -(5% 2) (как, кажется, предлагает Петар в своем комментарии к своему ответу).
Это определяется реализацией. В спецификации указано (§5.6/4),
.
[…] Если оба операнда неотрицательны, то и остаток неотрицательный; , если нет, знак остатка определяется реализацией .
6
Этот ответ не для математика. Этот ответ пытается дать мотивацию (за счет математической точности).
Математики: См. здесь.
Программисты: Помните, что деление на 0 равно undefined . Таким образом, mod , основанный на делении, также является неопределенным .
Представляет деление на положительные X и D ; состоит из целой части и дробной части:
(X / D) = целое число + дробная часть
= пол (X / D) + (X % D) / D
Переставив, вы получите:
(Х % Д) = Д * (Х / Д) - Д * этаж (Х / Д)
Замена 0 на D :
(X % 0) = 0 * (X / 0) - 0 * этаж (X / 0)
С момента деления на 0 равно undefined :
(X % 0) = 0 * undefined - 0 * floor(undefined)
= не определено - не определено
= не определено
2
X % D по определению число 0 <= R < D , такое, что существует Q , так что
X = D*Q + R
Итак, если D = 0 , такого числа не может существовать (поскольку 0 <= R < 0 )
4
Я думаю, потому что, чтобы получить остаток от X % 0 , вам нужно сначала вычислить X / 0 , что дает бесконечность, а попытка вычислить остаток от бесконечности на самом деле невозможна.
Однако лучшим решением в соответствии с вашими мыслями было бы сделать что-то вроде этого
REMAIN = Y ? Х % Г : Х
Другой способ, который может быть концептуально простым для понимания проблемы:
На данный момент игнорируя проблему знака аргумента, a % b можно легко переписать как a - ((a / b) * b) . Выражение a / b не определено, если b равно нулю, поэтому в этом случае общее выражение должно быть таким же.
В конце концов, модуль — это фактически операция деления, так что если a / b не определено, вполне разумно ожидать, что a % b также будет.
X % Y дает результат в целочисленном диапазоне [ 0, Y ) . X % 0 должен был бы дать результат больше или равный нулю и меньше нуля.
2
вы можете избежать случая «деления на 0» (A%B) для его типа float identity mod(a,b) for float(B)=b=0.
0 , который не определен или определен по-разному между любыми двумя реализациями , чтобы избежать логических ошибок (жестких сбоев) в пользу арифметических ошибок…
путем вычисления mod([a*b],[b])==b*(a-этаж(a))
INSTREAD OF
вычисления mod([a],[b])
где [a*b]==ваша ось X с течением времени
[b] == максимум кривой качания (который никогда не будет достигнут) == первая производная функции качания
https://www.shadertoy.com/view/MslfW8
Я полагаю, потому что для получения остаток от X % 0, вам нужно сначала вычислить X / 0, что дает бесконечность, и попытка вычислить остаток от бесконечности на самом деле невозможна.
Однако лучшим решением в соответствии с вашими мыслями было бы сделать что-то вроде этого,
ans = Y ? Х % Г : Х
Кроме того, в документах C++ написано, что X % 0 или X / 0 приводит к неопределенному значению.
Как компьютеры делят:
Начните с делимого и вычитайте делитель, пока результат не станет меньше делителя.
Количество вычитаний — это результат, а то, что у вас осталось, — это остаток. Например, чтобы разделить 10 и 3:
10 - 3 = 7 7 - 3 = 4 4 - 3 = 1
Так
10/3 = 3 10 % 3 = 1
Чтобы разделить 1 и 0:
1 / 0 1 - 0 = 1 1 - 0 = 1 1 - 0 = 1 ...
So
1/0 = Бесконечность (технически даже бесконечность слишком мала, но ее легко классифицировать как таковую) 1 % 0 = NaN
Если ничего не мешает, ЦП будет продолжать выполнять это до тех пор, пока не перегрузится и не вернет абсолютно случайный результат. Итак, на уровне процессора есть инструкция, что если делитель равен 0, вернуть NaN или Infinity (в зависимости от вашей платформы).
Это никогда не закончится, поэтому остаток не определен (для компьютеров это NaN ).
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
элементарная теория чисел – Полиномы, индуцирующие нулевую функцию по модулю $n$ 9{ underline k} = x(x-1)cdots(x-k+1)$.
{underline p} = (n/p) x(x-1)cdots(x-p+1)$. Возможны и другие многочлены степени $p$. 9p – x$ по модулю $p$.
Какой унитарный многочлен наименьшей степени индуцирует нулевую функцию по модулю $n$?
Для этого нам нужно $c_d = 1$, где $d$ — степень полинома, которая должна быть кратна $n / gcd(n, d!)$, поэтому $n / gcd(n , d!)$ должно быть равно $1$, или, другими словами, $gcd(n, d!) = n$, что означает, что $n$ делит $d!$. Это называется функцией Кемпнера. Таким образом, мы можем принять $c_d = 1$, а все остальные $c_k$ равны $0$.
Это дает следующую таблицу для примеров в вопросе: 9r$ унитарный многочлен наименьшей степени, индуцирующий нулевую функцию по модулю $n$?
Поскольку «монический полином наименьшей степени» не уникален (см. примеры чуть выше), уместно спросить, когда степени совпадают. Для этого $r + lambda(n)$ должна быть функцией Кемпнера от $n$ (назовем ее $K(n)$), то есть наименьшим $k$ таким, что $n$ делит $k! $.
Как решать уравнения с модулем: основные правила
30 декабря 2016
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
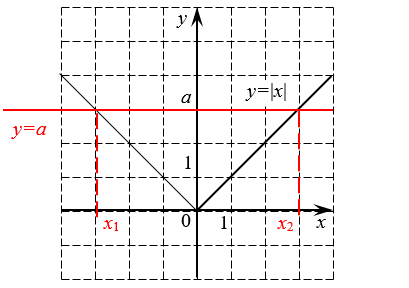
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
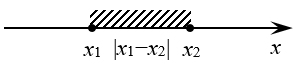
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft( x right) right|=a]
Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
или:
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
[2x+1=5Rightarrow 2x=4Rightarrow x=2]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :
[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft( x right) right|=gleft( x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
[x-{{x}^{3}}ge 0]
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left( x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
[x-1=pm left( {{x}^{2}}-3x+2 right)]
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]
[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
[5-3x=5-3x]
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
[xin left( -infty ;frac{5}{3} right)]
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
[3x-5=0Rightarrow left| 3x-5 right|=0]
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
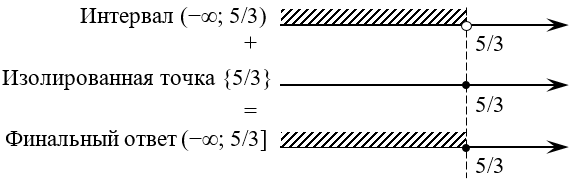
Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Смотрите также:
- Простейшие уравнения с модулем
- Уравнение с двумя модулями
- Сложные выражения с дробями. Порядок действий
- Сводный тест по задачам B15 (2 вариант)
- Как решать биквадратное уравнение
- B4: счетчики на электричество
План урока:
Модуль числа
Решение уравнений с модулем
Уравнения с параметрами
Модуль числа
Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:
|9| = |– 9| = 9
|674| = |– 674| = 674
|2,536| = |– 2,536| = 2,536
Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:
Именно такое определение обычно и применяется в математике.
Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:
Также модуль возникает при извлечении квадратного корня из четной степени числа:
В частности, если n = 1, получим формулу:
Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:
Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:
В результате получилась «галочка».
Пример. Постройте график ф-ции у = |х2 – 4х + 3|
Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х2 – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:
Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х2 – 4х + 3|, надо перевернуть эту часть графика:
Решение уравнений с модулем
Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид
|у(х)| = b
где b – какое-то число, а у(х) – произвольная ф-ция.
Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.
Пример. Найдите корни ур-ния
|125x10 + 97x4– 12,56х3 + 52х2 + 1001х – 1234| = – 15
Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.
Ответ: корни отсутствуют.
Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.
Пример. Решите ур-ние
|13х – 52| = 0
Решение.
Ясно, что подмодульное выр-ние равно нулю:
13х – 52 = 0
13х = 52
х = 4
Ответ: 4.
Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:
|b| = b
|– b| = b
То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.
Пример. Решите ур-ние
|х| = 10
Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.
Ответ: 10; (– 10).
Пример. Решите ур-ние
|10х + 5| = 7
Решение. Исходное ур-ние разбивается на два других ур-ния:
10х + 5 = 7 или 10х + 5 = – 7
10х = 2 или 10х = – 12
х = 0,2 или х = – 1,2
Ответ: 0,2; (– 1,2).
Пример. Найдите корни ур-ния
|x2– 2х – 4| = 4
Решение. Снова заменим исходное равенство на два других:
x2– 2х – 4 = 4 или x2– 2х – 4 = – 4
Имеем два квадратных ур-ния. Решим каждое из них:
x2– 2х – 4 = 4
x2– 2х – 8 = 0
D = b2– 4ас = (– 2)2 – 4•1•(– 8) = 4 + 32 = 36
х1 = (2 – 6)/2 = – 2
х2 = (2 + 6)/2 = 4
Нашли корни (– 2) и 4. Решаем второе ур-ние:
x2– 2х – 4 = – 4
x2– 2х = 0
х(х – 2) = 0
х = 0 или х – 2 = 0
х = 0 или х = 2
Получили ещё два корня: 0 и 2.
Ответ: – 2, 4, 0, 2
Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:
|у(х)| = |g(x)|
Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.
Пример. Решите ур-ние
|x2 + 2x– 1| = |х + 1|
Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:
x2 + 2x– 1 = х + 1 или x2 + 2x– 1 = – (х + 1)
х2 + х – 2 = 0 или х2 + 3х = 0
Решим 1-ое ур-ние:
х2 + х – 2 = 0
D = b2– 4ас = 12 – 4•1•(– 2) = 1 + 8 = 9
х1 = (1 – 3)/2 = – 1
х2 = (1 + 3)/2 = 2
Теперь переходим ко 2-омуур-нию:
х2 + 3х = 0
х(х + 3) = 0
х = 0 или х + 3 = 0
х = 0 или х = – 3
Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.
Ответ:(– 1), (– 2), 2, 0.
Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.
Пример. Найдите решение уравнения, содержащего модуль:
|х2 + 3,5х – 20| = 4,5х
Решение. Рассмотрим два отдельных равенства:
х2 + 3,5х – 20 = 4,5х илих2 + 3,5х – 20 = – 4,5х
х2 – х – 20 = 0 или х2 + 8х – 20 = 0
Решим каждое из полученных квадратных ур-ний.
х2 – х – 20 = 0
D = b2– 4ас = 12 – 4•1•(– 20) = 1 + 80 = 81
х1 = (1 – 9)/2 = – 4
х2 = (1 + 9)/2 = 5
х2 + 8х – 20 = 0
D = b2– 4ас = 82 – 4•1•(– 20) = 64 + 80 = 144
х3 = (– 8 – 12)/2 = – 10
х4 = (– 8 + 12)/2 = 2
Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:
4,5х ≥ 0
Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.
Ответ: 2 и 5
Мы рассмотрели три случая, когда ур-ние имеет вид:
- у(х) = b (b– это некоторая константа)
- |у(х)| = |g(x)|
- |у(х)| = g(x)
Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.
Пример. Найдите корни ур-ния
|x + 1| + |x– 4| = 6
Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:
Если отметить обе точки на прямой, то они образуют на ней 3 интервала:
Исследуем ур-ние на каждом из полученных промежутков.
Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что
|x + 1| = – (х + 1) = – х – 1
|x– 4| = – (х – 4) = – х + 4
Тогда ур-ние примет вид
|x + 1| + |x– 4| = 6
– х – 1 – х + 4 = 6
–2х = 3
х = – 1,5
Это значение удовлетворяет условию х <– 1, поэтому корень верный.
Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:
|x + 1| = х + 1
|x– 4| = – (х – 4) = – х + 4
Ур-ние примет вид:
|x + 1| + |x– 4| = 6
x + 1 – x+ 4 = 6
5 = 6
Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.
При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому
|x + 1| = х + 1
|x– 4| = х – 4
Исходное ур-ние будет выглядеть так
|x + 1| + |x– 4| = 6
х + 1 + х – 4 = 6
2х = 9
х = 4,5
Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.
Уравнения с параметрами
Изучим ур-ния:
5х = 10
5х = 15
5х = 20
Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.
Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:
5х = v
Решением таких ур-ний будет дробь v/5.
Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.
Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде
ах + b= 0
где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):
ах2 + bx + c = 0
Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.
Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.
Пример. Решите ур-ние
х2 – 2ах = 0
и найдите его корни при значении параметра а, равном 3.
Решение. Вынесем множитель х за скобки:
х2 – 2ах = 0
х(х – 2а) = 0
х = 0 или х – 2а = 0
х = 0 или х = 2а
Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:
при а = 3х = 2•3 = 6
Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.
Пример. Решите ур-ние
р2х – 3рх = р2 – 9
Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:
рх(р – 3) = (р – 3)(р + 3)
Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.
Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во
0•х•(0 – 3) = (0 – 3) (3 – 0)
0 = – 9
Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.
Если р – 3 = 0, то есть р = 3, получится следующее
3•х•0 = 0•(3 + 3)
0 = 0
Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.
Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим
В этом случае ур-ние имеет единственный корень.
Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.
Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.
Пример. Сколько корней имеет ур-ние
|х2 – 6х + 5| = b
при различных значениях параметра b.
Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х2 – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:
х2 – 6х + 5 = 0
D = b2– 4ас = (– 6)2 – 4•1•5 = 36 + 20 = 16
х1 = (6 – 4)/2 = 1
х2 = (6 + 4)/2 = 5
Итак, нули ф-ции – это точки 1 и 5. Найдем координату х0 вершины параболы по формуле:
х0 = –b/2a = 6/2 = 3
Подставив х0 в квадратичную ф-цию найдем координату у0 вершины параболы:
32 – 6•3 + 5 = 9 – 18 + 5 = – 4
Теперь построим квадратичную ф-цию:
Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:
Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:
При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.
При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.
Если 0 <b< 4, то прямая пересекает график в 4 точках.
При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.
Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.
Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.
Пример. При каком а ур-ние
х4 – (а + 2)х2 + 3а – 3 = 0
имеет ровно 4 корня?
Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х2:
у2 – (а + 2)у + 3а – 3 = 0 (1)
Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у1 и у2. Тогда, проводя обратную замену х2 = у1 и х2 = у2, мы получим два разных квадратных ур-ния, корни которых будут равны
Если же хоть один из двух корней, например, у1, окажется равным нулю, то величины
Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у1 будет отрицательным числом, то ур-ние
х2 = у1
вовсе не будет иметь решений, и тогда останется не более 2 корней.
Итак, решим ур-ние (1):
у2 – (а + 2)у + 3а – 3 = 0
D = b2– 4ас = (– (а + 2))2 – 4•1•(3а – 3) = (а + 2)2 – 12 а + 12 =
= а2 + 4а + 4 – 12а + 12 = а2 – 8а + 16 = а2 – 2•4•а + 42 = (а – 4)2
Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)2 положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.
Извлечем корень из дискриминанта:
Корни ур-ния (1) можно вычислить по формулам:
И у1, и у2 должны быть положительными величинами, однако у1 меньше, чем у2 (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:
Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство
|а – 4| = а – 4
Тогда имеем
а + 2 – (а – 4) > 0
6> 0
Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.
Если а < 4, то справедливо соотношение
|а – 4| = – (а – 4)
Тогда получится следующее:
а + 2 – |а – 4|> 0
а + 2 – (– (а – 4)) > 0
а + 2 + а – 4 > 0
2а > 2
а > 1
Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение
а > 4
можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).
Ответ: а∊(1; 4)∪(4; + ∞).
Пример. При каких параметрах а у ур-ния
х2 – 2(а + 1)х + а2 + 2а – 3 = 0
существует два корня, которые принадлежат интервалу (– 5; 5)?
Решение. Данное ур-ние является квадратным. Найдем его дискриминант:
D = b2– 4ас = (– 2(а + 1))2 – 4•1•( а2 + 2а – 3) = 4(а2 + 2а + 1) – 4(а2 + 2а – 3) =
= 4(а2 + 2а + 1 – а2– 2а + 3) = 4•4 = 16
Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам
Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х1) был больше – 5, больший (это х2) – меньше – 5:
Значит, должны выполняться два нер-ва
х1>– 5и х2<5
а – 1 >– 5 и а + 3 < 5
а >– 4 и а < 2
Эти два нер-ва выполняются, если а∊(– 4; 2)
Ответ: (– 4; 2)
Здравствуйте, дорогие читатели, подписчики и гости канала. В этом выпуске рассмотрим построение графика функции с модулем сводящегося к построению кусочно-заданной функции.
Решение
Найдем значение х, при котором выражение под модулем равно нулю.
Тогда при раскрытии модуля, получаем кусочно-заданную функцию
1) Найдем координаты вершины параболы и дополнительные точки для построения графика функции при первом условии:
2) Найдем координаты вершины параболы и дополнительные точки для построения графика функции при втором условии:
3) Построим график функции и ответим на вопрос, при каких значениях m, прямая у=m имеет с графиком ровно три общие точки:
Проведем на графике две прямые у=m, которые параллельны оси абсцисс. Первая прямая совпадает с осью Ох, т.е. m=0, вторая проходит через общую точку соединения двух частей графика m=0,25
Ответ m=0, m=0,25
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
