Как найти номер булевой функции

Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики)^[1] от n аргументов — в дискретной математике — отображение Bⁿ → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n, обозначающее количество аргументов, называется арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n-я прямая степень) Bⁿ называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P₂, а от n аргументов — P₂(n). Переменные, принимающие значения из булева множества, называются булевыми переменными^[2]. Булевы функции названы по фамилии математика Джорджа Буля.

При работе с булевыми функциями происходит полное абстрагирование от того содержательного смысла, какой предполагается в алгебре высказываний^[2]. Тем не менее между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если^[3]:

• установить взаимно-однозначное соответствие между булевыми и пропозициональными переменными;
• установить связь между булевыми функциями и логическими связками;
• оставить приоритет операций без изменений.

Основные сведения[править | править код]

Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2ⁿ. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 2⁽²ⁿ⁾. Поэтому в этом разделе рассматриваются только простейшие и важнейшие булевы функции.

Практически все булевы функции низших арностей (0, 1, 2 и 3) получили исторически сложившиеся имена. Если значение функции не зависит от одной из переменных (то есть, по сути, для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная, не играя никакого «значения», называется фиктивной.

Таблицы истинности[править | править код]

Булева функция задаётся конечным набором значений, что позволяет представить её в виде таблицы истинности, например^[4]:

x1	x2	…	xn−1	xn	f(x1, x2, …, xn)
0	0	…	0	0	0
0	0	…	0	1	0
0	0	…	1	0	1
0	0	…	1	1	0
1	1	…	0	0	1
1	1	…	0	1	0
1	1	…	1	0	0
1	1	…	1	1	0

Нульарные функции[править | править код]

При n = 0 количество булевых функций сводится к двум 2²⁰ = 2¹ = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
Таблица значений и названий нульарных булевых функций:

	Значение	Обозначение	Название
	0	F0,0 = 0	тождественный ноль
	1	F0,1 = 1	тождественная единица, тавтология

Унарные функции[править | править код]

При n = 1 число булевых функций равно 2²¹ = 2² = 4. Определение этих функций содержится в следующей таблице.

Таблица значений и названий булевых функций от одной переменной:

x0=x	1	0	Обозначение	Название
0	0	0	F1,0 = 0	тождественный ноль
1	0	1	F1,1 = x = ¬x = x’ = NOT(x)	отрицание, логическое «НЕТ», «НЕ», «НИ», инвертор, SWAP (обмен)
2	1	0	F1,2 = x	тождественная функция, логическое “ДА”, повторитель
3	1	1	F1,3 = 1	тождественная единица, тавтология

Бинарные функции[править | править код]

При n = 2 число булевых функций равно 2²² = 2⁴ = 16.

Таблица значений и названий булевых функций от двух переменных (в зависимости от области применения, функции имеют разные словесные названия, но один и тот же номер):

x0=x	1	0	1	0	Обозначение функции	Название функции
x1=y	1	1	0	0
0	0	0	0	0	F2,0 = 0	тождественный ноль
1	0	0	0	1	F2,1 = x ↓ y = x NOR y = NOR(x,y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x,y) = NOT(MAX(X,Y))	стрелка Пи́рса – “↓” (кинжал Куайна – “†”), функция Ве́бба – “°”[5], НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, инверсия максимума
2	0	0	1	0	F2,2 = x > y = x GT y = GT(x,y) = x → y = x y	функция сравнения “первый операнд больше второго операнда”, инверсия прямой импликации, коимпликация[6]
3	0	0	1	1	F2,3 = y = y’ = ¬y = NOT2(x,y) = НЕ2(x,y)	отрицание (негация, инверсия) второго операнда
4	0	1	0	0	F2,4 = x < y = x LT y = LT(x,y) = x ← y = x y	функция сравнения “первый операнд меньше второго операнда”, инверсия обратной импликации, обратная коимпликация[6]
5	0	1	0	1	F2,5 = x = x’ = ¬x = NOT1(x,y) = НЕ1(x,y)	отрицание (негация, инверсия) первого операнда
6	0	1	1	0	F2,6 = x >< y = x <> y = x NE y = NE(x, y) = x ⊕ y = x XOR y = XOR(x,y) = XMAX(x,y) = x XMAX y	функция сравнения “операнды не равны”, сложение по модулю 2, исключающее «или», сумма Жегалкина[7], исключающий max
7	0	1	1	1	F2,7 = x | y = x NAND y = NAND(x,y) = x НЕ-И y = НЕ-И(x,y) = NOT(MIN(X,Y))	штрих Ше́ффера, пунктир Чулкова[8], НЕ-И, 2И-НЕ, антиконъюнкция, инверсия минимума
8	1	0	0	0	F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x,y) = x И y = И(x,y) = min(x,y)	конъюнкция, 2И, минимум
9	1	0	0	1	F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x,y)	функция сравнения “операнды равны”, эквивалентность
10	1	0	1	0	F2,10 = YES1(x,y) = ДА1(x,y) = x	первый операнд
11	1	0	1	1	F2,11 = x ≥ y = x >= y = x GE y = GE(x,y) = x ← y = x ⊂ y	функция сравнения “первый операнд не меньше второго операнда”, обратная импликация (от второго аргумента к первому)
12	1	1	0	0	F2,12 = YES2(x,y) = ДА2(x,y) = y	второй операнд
13	1	1	0	1	F2,13 = x ≤ y = x <= y = x LE y = LE(x,y) = x → y = x ⊃ y	функция сравнения “первый операнд не больше второго операнда”, прямая (материальная) импликация (от первого аргумента ко второму)
14	1	1	1	0	F2,14 = x ∨ y = x + y = x OR y = OR(x,y) = x ИЛИ y = ИЛИ(x,y) = max(x,y)	дизъюнкция, 2ИЛИ, максимум
15	1	1	1	1	F2,15 = 1	тождественная единица, тавтология

При двух аргументах префиксная, инфиксная и постфиксная записи, по экономичности, почти одинаковы.

Некоторые функции, имеющие смысл в цифровой технике, например функции сравнения, минимум и максимум, не имеют смысла в логике, так как в логике, в общем случае, логические значения TRUE и FALSE не имеют жёсткой привязки к числовым значениям (например в TurboBasic’е, для упрощения некоторых вычислений, TRUE = -1, а FALSE = 0) и невозможно определить, что больше TRUE или FALSE, импликации же и др. имеют смысл и в цифровой технике и в логике.

Тернарные функции[править | править код]

При n = 3 число булевых функций равно 2⁽²³⁾ = 2⁸ = 256. Некоторые из них определены в следующей таблице:
Таблица значений и названий некоторых булевых функций от трёх переменных, имеющих собственное название:

x0=x	1	0	1	0	1	0	1	0	Обозначения	Названия
x1=y	1	1	0	0	1	1	0	0
x2=z	1	1	1	1	0	0	0	0
1	0	0	0	0	0	0	0	1	F3,1 = x↓y↓z = ↓(x,y,z) = Webb2(x,y,z) = NOR(x,y,z)	3ИЛИ-НЕ, функция Вебба, стрелка Пирса, кинжал Куайна – “†”
23	0	0	0	1	0	1	1	1	F3,23 = = ≥2(x,y,z)	Переключатель по большинству с инверсией, 3ППБ-НЕ, мажоритарный клапан с инверсией
31	0	0	0	1	1	1	1	1	F3,31 = x OR (y AND z) = Gi,j = Gi,j-1 OR (Pi,j-1 AND Gi-1,j-1)	Оператор Valency-2 (валентность=2) в параллельно префиксных сумматорах
126	0	1	1	1	1	1	1	0	F3,126 = (x≠y≠z) = [≠(x,y,z)] = NE(x,y,z)	Неравенство
127	0	1	1	1	1	1	1	1	F3,127 = x|y|z = |(x,y,z) = NAND(x,y,z)	3И-НЕ, штрих Шеффера
128	1	0	0	0	0	0	0	0	F3,128 = x&y&z = &(x,y,z) = (x AND y AND z) = AND(x,y,z) = (x И y И z) = И(x,y,z) = min(x,y,z)	3И, минимум
129	1	0	0	0	0	0	0	1	F3,129 = (x=y=z) = [=(x,y,z)] = EQV(x,y,z)	Равенство
150	1	0	0	1	0	1	1	0	F3,150 = x⊕y⊕z = x⊕2y⊕2z = ⊕2(x,y,z)	Тернарное сложение по модулю 2
184	1	0	1	1	1	0	0	0	F3,184 =	Условная дизъюнкция
216	1	1	0	1	1	0	0	0	F3,216 = f1	Разряд займа при тернарном вычитании
232	1	1	1	0	1	0	0	0	F3,232 = f2 = [>=2(x,y,z)] = ≥2(x,y,z) = (x И y) ИЛИ (y И z) ИЛИ (z И x)	Разряд переноса при тернарном сложении, переключатель по большинству, 3ППБ, мажоритарный клапан
254	1	1	1	1	1	1	1	0	F3,254 = (x+y+z) = +(x,y,z) = (x OR y OR z) = OR(x,y,z) = (x ИЛИ y ИЛИ z) = ИЛИ(x,y,z) = max(x,y,z)	ИЛИ, максимум

При трёх и более аргументах префиксная (и постфиксная) запись экономичнее инфиксной записи.
Обычный вид записи функций — префиксный (перед операндами). При инфиксной (между операндами) записи функций функции называются операторами, а аргументы функции — операндами.

Полные системы булевых функций[править | править код]

Суперпозиция и замкнутые классы функций[править | править код]

Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:

0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		0

Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.

В качестве простейших примеров замкнутых классов булевых функций можно назвать множество , состоящее из одной тождественной функции, или множество , все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы и , мы с помощью суперпозиции сможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество всех возможных булевых функций тоже является замкнутым.

Тождественность и двойственность[править | править код]

Две булевы функции тождественны друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. Тождественность функций f и g можно записать, например, так:

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

(дистрибутивность конъюнкции и дизъюнкции)

Функция называется двойственной функции , если . Легко показать, что в этом равенстве f и g можно поменять местами, то есть функции f и g двойственны друг другу. Из простейших функций двойственны друг другу константы 0 и 1, а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Полнота системы, критерий Поста[править | править код]

Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством .

Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:

Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с , целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом, критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию.
Пост доказал, что множество замкнутых классов булевых функций — счётное множество.

Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.

Представление булевых функций[править | править код]

Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее, чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция может быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбранной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?
• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
  • В частности: существует ли способ приведения произвольной формулы к эквивалентной ей канонической форме такой, что две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Дизъюнктивная нормальная форма (ДНФ)[править | править код]

Простой конъюнкцией или конъюнктом называется конъюнкция некоторого конечного набора переменных или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций.
Элементарная конъюнкция

• правильная, если каждая переменная входит в неё не более одного раза (включая отрицание);
• полная, если каждая переменная (или её отрицание) входит в неё ровно 1 раз;
• монотонная, если она не содержит отрицаний переменных.

Например   — является ДНФ.

Совершенной дизъюнктивной нормальной формой или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: .

Легко убедиться, что каждой булевой функции соответствует некоторая ДНФ, а функции, отличной от тождественного нуля — даже СДНФ. Для этого достаточно в таблице истинности этой функции найти все булевы векторы, на которых её значение равно 1, и для каждого такого вектора построить конъюнкцию , где . Дизъюнкция этих конъюнкций является СДНФ исходной функции, поскольку на всех булевых векторах её значения совпадают со значениями исходной функции. Например, для импликации результатом является , что можно упростить до .

Конъюнктивная нормальная форма (КНФ)[править | править код]

Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.

Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».

КНФ может быть преобразована к эквивалентной ей ДНФ путём раскрытия скобок по правилу:

которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило

выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать описанным выше способом, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.

Алгебраическая нормальная форма (АНФ или полином Жегалкина)[править | править код]

Алгебраическая нормальная форма (общепринятое название в зарубежной литературе) или полином Жегалкина (название, используемое в отечественной литературе) — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции («И», AND), а в качестве сложения — сложение по модулю 2 (исключающее «ИЛИ», XOR). Для получения полинома Жегалкина следует выполнить следующие действия:

1. Получить СДНФ функции
2. Все ИЛИ заменить на Исключающее ИЛИ
3. Во всех термах заменить элементы с отрицанием на конструкцию: («элемент» «исключающее ИЛИ» 1)
4. Раскрыть скобки по правилам алгебры Жегалкина и привести попарно одинаковые термы

Классификация булевых функций[править | править код]

• По количеству n входных операндов, от которых зависит значение на выходе функции, различают нульарные (n = 0), унарные (n = 1), бинарные (n = 2), тернарные (n = 3) булевы функции и функции от большего числа операндов.

• По количеству единиц и нулей в таблице истинности отличают узкий класс сбалансированных булевых функций (также называемых уравновешенными или равновероятностными, поскольку при равновероятных случайных значениях на входе или при переборе всех комбинаций по таблице истинности вероятность получения на выходе значения 1 равна 1/2) от более широкого класса несбалансированных булевых функций (так же называемых неуравновешенными, поскольку вероятность получения на выходе значения 1 отлична от 1/2). Сбалансированные булевы функции в основном используются в криптографии.

• По зависимости значения функции от перестановки её входных битов различают симметричные булевы функции (значение которых зависит только от количества единиц на входе) и несимметричные булевы функции (значение которых так же зависит от перестановки её входных бит).

• По значению функции на противоположных друг другу наборах значений аргументов отличают самодвойственные функции (значение которых инвертируется при инвертировании значения всех входов) от остальных булевых функций, не обладающих таким свойством. Нижняя часть таблицы истинности для самодвойственных функций является зеркальным отражением инвертированной верхней части (если расположить входные комбинации в таблице истинности в естественном порядке).

• По алгебраической степени нелинейности отличают линейные булевы функции (АНФ которых сводится к линейной сумме по модулю 2 входных значений) и нелинейные булевы функции (АНФ которых содержит хотя бы одну нелинейную операцию конъюнкции входных значений). Примерами линейных функций являются: сложение по модулю 2 (исключающее «ИЛИ», XOR), эквивалентность, а также все булевы функции, АНФ которых содержит лишь линейные операции сложения по модулю 2 без конъюнкций. Примерами нелинейных функций являются: конъюнкция («И», AND), штрих Шеффера («НЕ-И», NAND), стрелка Пирса («НЕ-ИЛИ», NOR), а также все булевы функции, АНФ которых содержит хотя бы одну нелинейную операцию конъюнкции.

Существенные и фиктивные переменные[править | править код]

Переменная булевой функции называется существенной, если для булевой функции существует два набора значений её аргументов, различающиеся лишь значением этой переменной и значения булевой функции на них различаются. Если значения этой функции на них совпадают, то переменная называется фиктивной. Переменная является существенной тогда и только тогда, когда она входит в совершенную ДНФ булевой функции или она входит в полином Жегалкина булевой функции.

Две булевы функции называются равными, если множества их существенных переменных равны и на любых двух равных наборах значений существенных переменных значения функций совпадают.^[9]

См. также[править | править код]

• Булева алгебра
• Битовые операции
• Комбинационная логика
• Секвенциальная логика
• Троичная логика
• Троичные функции
• Логические элементы

Литература[править | править код]

• Алексеев В. Б. (лектор), Поспелов А.Д. (составитель). Дискретная математика (курс лекций, II семестр). — М.: Изд. отд. фак. Вычислит. математики и кибернетики МГУ им. М. В. Ломоносова, 2002. — 44 с.
• Быкова С. В., Буркатовская Ю. Б. Булевы функции: учебное пособие для студентов высших учебных заведений, обучающихся по специальности ВПО 010501 «Прикладная математика и информатика». — Томск: Томский гос. ун-т, 2010. — 190 с.
• Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике. — М.: ФИЗМАТЛИТ, 2009.
• Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стереотип.. — М.: Издательский центр «Академия», 2008. — 448 с.
• Кузнецов О. П. Дискретная математика для инженера. — СПб.: Лань, 2007. — 394 с.
• Учебные пособия кафедры математической кибернетики ВМиК МГУ (на сайте кафедры математической кибернетики МГУ ВМК).
• Ложкин С.А. Лекции по основам кибернетики : учеб. пособие по курсам «Основы кибернетики» и «Структур. реализация дискрет. функций». — М.: Изд. отд. фак. Вычислит. математики и кибернетики МГУ им. М. В. Ломоносова, 2004. — 254 с.
• Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2001. — 126 с.
• Самофалов К. Г., Романкевич А. М., Валуйский В. Н., Каневский Ю. С., Пиневич М. М. Прикладная теория цифровых автоматов. — Киев: Вища Школа, 1987. — С. 183—189. — 375 с.
• Яблонский С. В. Введение в дискретную математику. — М.: Высш. шк., 2006. — 384 с.

Ссылки[править | править код]

Когда меня учили делать архитектуру микропроцессоров мы изучали булевую логику, там по картам Карно мы упрощали преобразование логической функции в электрическую схему на тригерах (элементах неили). Прошло очень много времени, я постарел и мало что помню. Но эту легкотню я знаю как сделать.

Смотри F(x,y,z) булевая = может иметь значения 1 или 0 (правда или ложь), аргументы тоже булевые x,y,z=1 или 0.
Таблицы обычно рисуют для функций двух переменных а у тебя их три, похоже на тензор. и как же превратить его в таблицу? Легко. Сделаем две таблицы. Или можно сделать кубик, объемную таблицу.

1) х =0 рисуй таблицу 2 на 2. По вертикали над таблицей y (0,1), по горизонтали над таблицей z(0,1). в таблице F.
Потом вторую таблицу х =1. у и z так само.
И значения функции посчитай и впиши туда.

2 вариант) чуть сложнее. нужно будет рисовать кубик 2 на 2 на 2. Над перпендикулярными тремя ребрами x,y,z 0,1 внутри маленьких кубиков значения F.

3 вариант) косая табличка. Рисуй таблицу 2 на 2. и каждую клетку подели по диагонали параллельными отрезками. (так чтобы направления диагоналей совпадали) Можно например про горизонтали x 0 1, по вертикале y 0, 1, по диагонали z 0, 1 Теперь в эти треугольнички впиши F. Например под диагональю F(x.y.0), а над нею F(x.y.1)

Определение:

Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики, англ. Boolean function) от переменных — отображение , где — булево множество.

Элементы булева множества и обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Элементы декартова произведения называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается , а от n переменных — . Булевы функции названы так по фамилии математика Джорджа Буля.

Основные сведения

Определение:

А́рность (англ. arity) функции — количество ее аргументов.

Каждая булева функция арности полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины . Число таких векторов равно . Поскольку на каждом векторе булева функция может принимать значение либо , либо , то количество всех n-арных булевых функций равно . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:

Таблица истинности

Практически все булевы функции малых арностей ( и ) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной (англ. dummy variable).

Нульарные функции

При количество булевых функций равно , первая из них тождественно равна , а вторая . Их называют булевыми константами — тождественный нуль и тождественная единица.

Унарные функции

При число булевых функций равно .

Таблица значений булевых функций от одной переменной:

Функции от одной переменной
0
1
Сохраняет 0	✓	✓
Сохраняет 1		✓		✓
Самодвойственная		✓	✓
Монотонная	✓	✓		✓
Линейная	✓	✓	✓	✓

Названия булевых функций от одной переменной:

Обозначение	Название
	тождественный ноль, тождественная ложь, тождественное “НЕТ”
	тождественная функция, логическое “ДА”, “YES”(англ.)
	отрицание, логическое “НЕТ”, “НЕ”, “НИ”, “NOT”(англ.), “NO”(англ.)
	тождественная единица, тождественная истина, тождественное “ДА”, тавтология

Бинарные функции

При число булевых функций равно .

Таблица значений булевых функций от двух переменных:

Функции от двух переменных:
x	y
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Сохраняет 0	✓	✓	✓	✓	✓	✓	✓	✓
Сохраняет 1		✓		✓		✓		✓		✓		✓		✓		✓
Самодвойственная				✓		✓					✓		✓
Монотонная	✓	✓		✓		✓		✓								✓
Линейная	✓			✓		✓	✓			✓	✓		✓			✓

Названия булевых функций от двух переменных:

Обозначение	Другие обозначения	Название
		тождественный ноль, тождественная ложь, тождественное “НЕТ”
	И И	2И, конъюнкция
		больше, инверсия прямой импликации
	ДА1	первый операнд
		меньше, инверсия обратной импликации
	ДА2	второй операнд
		сложение по модулю 2, не равно, ксор, исключающее «или»
	ИЛИ ИЛИ	2ИЛИ, дизъюнкция
	ИЛИ-НЕ ИЛИ-НЕ	НЕ-2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса
		равенство, эквивалентность
	НЕ2	отрицание (негация, инверсия) второго операнда
		больше или равно, обратная импликация (от второго аргумента к первому)
	НЕ1	отрицание (негация, инверсия) первого операнда
		меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму)
	И-НЕ И-НЕ	НЕ-2И, 2И-НЕ, антиконъюнкция, Штрих Шеффера
		тождественная единица, тождественная истина, тождественное “ДА”, тавтология

Тернарные функции

При число булевых функций равно . Некоторые из них определены в следующей таблице:

Таблица истинности некоторых тернарных функций
0	0	0	1	1	0	1	0	1	0	0	0	0	0
0	0	1	0	1	1	1	0	0	1	0	0	0	1
0	1	0	0	1	1	1	0	0	1	0	0	0	1
0	1	1	0	0	1	1	0	0	0	1	1	1	1
1	0	0	0	1	1	1	0	0	1	0	1	0	1
1	0	1	0	0	1	1	0	0	0	1	0	1	1
1	1	0	0	0	1	1	0	0	0	1	1	1	1
1	1	1	0	0	0	0	1	1	1	1	1	1	1

Названия булевых функций трех переменных:

Обозначения	Другие обозначения	Названия
		3-ИЛИ-НЕ, функция Вебба, функция Даггера, стрелка Пирса
		Переключатель по большинству с инверсией, 3-ППБ-НЕ, мажоритарный клапан с инверсией
		Неравенство
		3-И-НЕ, штрих Шеффера
	И И И	3-И, минимум
		Равенство
		Тернарное сложение по модулю 2
	И ИЛИ И ИЛИ И	переключатель по большинству, 3-ППБ, мажоритарный клапан
		Разряд займа при тернарном вычитании
		Разряд переноса при тернарном сложении
	ИЛИ ИЛИ ИЛИ	3-ИЛИ, максимум

Представление функции формулой

Определение:

Если выбрать некоторый набор булевых функций , то с использованием выбранных функций можно записать некоторые другие булевы функции. Такая запись булевой функции называется формулой (англ. formula).

Например, если , то функция представляется в виде

Тождественность и двойственность

Определение:

Две булевы функции тождественны (англ. identical) друг другу, если на любых одинаковых наборах аргументов они принимают равные значения.

Тождественность функций f и g можно записать, например, так:

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

(дистрибутивность конъюнкции и дизъюнкции)

Определение:

Функция называется двойственной (англ. duality) функции , если .

Легко показать, что в этом равенстве и можно поменять местами, то есть функции и двойственны друг другу. Из простейших функций двойственны друг другу константы и , а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Суперпозиции

Определение:

Суперпозиция функций, композиция функций (англ. function composition) — функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных.

Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.

Пусть нам дан некоторый набор булевых функций . Получить новую функцию, являющеюся композицией функций из , мы можем следующими способами:

• Подстановкой одной функции в качестве некоторого аргумента для другой;
• Отождествлением аргументов функций.

Полнота системы, критерий Поста

Определение:

Замыкание множества функций (англ. сlosure) — подмножество всех булевых функций, что любую из этих функций можно выразить через функции исходного множества.

Определение:

Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций.

Американский математик Эмиль Пост ^[1] сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:

• функции, сохраняющие константу и ,
• самодвойственныые функции ,
• монотонные функции ,
• линейные функции .

Набор булевых функций является полным тогда и только тогда, когда он не содержится полностью ни в одном из классов , иными словами, когда в нем имеется хотя бы одна функция, не сохраняющая ноль, хотя бы одна функция, не сохраняющая один, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.

Представление булевых функций

Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?
• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Дизъюнктивная нормальная форма (ДНФ)

Основная статья: ДНФ

Определение:

Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов.

Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.

Примеры ДНФ:

.

.

Конъюнктивная нормальная форма (КНФ)

Основная статья: КНФ

Определение:

Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.

Пример КНФ:

Полином Жегалкина

Определение:

Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или.

Полином Жегалкина имеет следующий вид:

С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: , который, в свою очередь, по теореме Поста является полным.

Примеры:

Тождественные функции. Выражение функций друг через друга

Определение:

Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения.

Приведение тождественной функции есть выражение булевой функции через другие.

Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.

Пример:

Выразим следующие функции через систему функций .

Подстановка одной функции в другую

Определение:

Подстановкой (англ. substitution) функции в функцию называется замена -того аргумента функции значением функции :

Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.

При подстановке функции вместо -того аргумента функции , результирующая функция будет принимать аргументы, которые можно разделить на следующие блоки:

1.	— аргументы функции до подставленного значения функции
2.	— используются как аргументы для вычисления значения функции
3.	— аргументы функции после подставленного значения функции

Пример:

Исходные функции: — подстановка функции вместо второго аргумента функции . В данном примере при помощи подстановки мы получили функцию .

Отождествление переменных

Определение:

Отождествлением переменных (англ. identification of variables) называется подстановка -того аргумента функции вместо -того аргумента:

Таким образом, при отождествлении переменных мы получаем функцию с количеством аргументов .

Пример:

— исходная функция — функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию — проектор единственного аргумента.

Схемы из функциональных элементов

Определение:

Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе , в котором: 1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса .

Отождествление переменных осуществляется при помощи ветвления проводников.

Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.

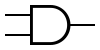
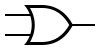
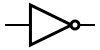
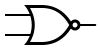
Некоторые логические элементы:

И	ИЛИ	НЕ	Штрих Шеффера	Стрелка Пирса

Стандартный базис

Определение:

Стандартный базис — система булевых функций:

Если рассматривать множество бинарных булевых функций , то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания:

Функции являются отрицаниями функций соответственно.

Тождественность функций можно доказать с помощью таблицы истинности.

Пример:

Выразим через стандартный базис обратную импликацию .

Полнота стандартного базиса

Утверждение:

Данное утверждение – следствие теоремы об СДНФ. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше.

Замечание:

По закону де Моргана:

Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:

(конъюнктивный базис Буля)

(дизъюнктивный базис Буля)

Теоремы о числе функций в базисе

Теорема:

Максимально возможное число булевых функций в безызбыточном базисе — четыре.

Доказательство:

Рассмотрим произвольный безызбыточный базис . Тогда по теореме Поста содержит следующие функции (не обязательно различные): , где — классы Поста. Значит, так как — безызбыточный базис, а система — полная, то Рассмотрим . Возможны два случая: 1. , тогда также не сохраняет единицу и немонотонная, т.е. . Значит, . 2. , тогда несамодвойственная, т.е. . Значит, .

Теорема:

Для любого числа найдётся базис , что .

Доказательство:

Приведём примеры базисов для каждого : ; ; ; ; Докажем, что последняя система является базисом: ; ; ; (доказывается с помощью таблицы истинности).

См. также

• Специальные формы КНФ
• Сокращенная и минимальная ДНФ
• Пороговая функция
• Cумматор
• Полные системы функций. Теорема Поста о полной системе функций

Примечания

Источники информации

• Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретной математике. — М.: Наука, 1969.
• Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. — М.: «Энергия», 1980. — 344 с.
• Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.
• Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1986.
• Алексеев В. Б. Дискретная математика (курс лекций, II семестр). Сост. А. Д. Поспелов
• Быкова С. В., Буркатовская Ю. Б., Булевы функции, учебно-методический комплекс, Томск, 2006
• Учебные пособия кафедры математической кибернетики ВМиК МГУ
• Булева функция — Википедия
• http://psi-logic.narod.ru/bool/bool.htm

4 БУЛЕВЫ ФУНКЦИИ
И ПРЕОБРАЗОВАНИЯ

4.1 Цель занятия

Ознакомление на
практических примерах с основными
понятиями булевой алгебры. Изучение
способов задания булевых функций. Анализ
формул и тождеств, которые определяют
свойства операций булевой алгебры.
Изучение и использование методов
доказательства тождеств булевой алгебры.

4.2 Методические
указания по организации самостоятельной
работы студентов

4.2.1 При подготовке
к практическому занятию необходимо
повторить лекционный материал,
теоретический материал, представленный
в пункте 4.2.2 настоящих методических
указаний, соответствующие разделы
литературы [1-10] по следующим вопросам:

• булевы
  переменные и функции (основные понятия);

• область определения
  и область значений булевой функции;

• способы задания
  булевых функций;

• реализация булевых
  функций формулами;

• принцип двойственности
  в булевой алгебре;

• булевы алгебры,
  законы и тождества булевой алгебры.

Подготовка и
выполнение практического занятия
проводится в два этапа. Первый этап
связан с изучением на практических
примерах следующих основных понятий и
определений булевой алгебры: булевы
переменные; булевы функции; интерпретация
булевой функции; n-мерный
булев куб; область определения булевой
функции; таблица истинности (соответствия)
булевой функции; отрицание, конъюнкция,
дизъюнкция, эквиваленция, импликация,
стрелка Пирса, штрих Шеффера; булева
формула; суперпозиция булевых функций;
инфиксная
запись формул; эквивалентные формулы;
двойственная функция; самодвойственная
функция; принцип двойственнойсти;
двухэлементная булева алгебра; алгебра
логики.

При выполнении
первого этапа обучаемый должен предложить
и записать индивидуальный пример для
каждого из рассмотренных выше понятий
и определений.

Второй этап
выполнения практического занятия связан
с решением практических заданий,
представленных в подразделе 4.3 на основе
предложенных типовых примеров (см.
раздел 4.4).

4.2.2 Основные
теоретические положения по изучаемой
теме.

4.2.2.1 Основные
понятия и определения.
Булевы
переменные и функции.

Рассмотрим основные
понятия и определения алгебры логики.

Пусть задано
двухэлементное множество

и двоичные переменные, принимающие
значения из

.
Элементы

часто обозначают 0 и 1, однако они не
являются числами в обычном смысле.
Наиболее распространенная интерпретация
двоичных переменных – логическая: «нет»
– «да», «истинно» (и) – «ложно» (или),
«false»
– «true».
Будем считать, что

,
рассматривая 0 и 1 как формальные символы,
не имеющие арифметического смысла.

Определение.

Переменные, которые
могут принимать значения только из
множества

,
называются булевыми
или логическими
переменными.
Элемент 1
называется единичным
элементом,
или единицей;
элемент 0
называется нулевым
элементом,
или нулем.
Сами значения 0
и
1
называются булевыми
константами.

Пример.

Булевыми переменными,
которые способны принимать лишь два
различных значения, характеризуются
объекты с двумя возможными состояниями
(наличие или отсутствие у объекта
определенного признака, низкое или
высокое напряжение, истинное или ложное
высказывание).

Пример.

В языках
программирования для работы с такими
переменными, как правило, вводится
специальный логический тип (например,
в языках Pascal
и Java

boolean,
в


bool).
Переменная этого типа принимает два
значения «false»
и «true».

Отношения между
булевыми переменными представляются
булевыми
функциями,
которые подобно числовым функциям могут
зависеть от одной, двух и, вообще,

переменных (аргументов).

Определение.
Функция вида

,
аргументы

и значения

которой принадлежат множеству

,
называется

-местной
булевой
(переключательной,
логической)
функцией.

Важнейшая особенность
булевых функций состоит в том, что они,
как и их аргументы, принимают свои
значения из двухэлементного множества

,
т.е. характеризуются одним из двух
возможных состояний.

Пример.

В вычислительной
технике булевы функции применяются для
описания алгоритмов, средств вычислительной
техники – дискретных устройств.
Дискретные устройства предназначаются
для преобразования дискретной информации,
разлагающейся на элементарные единицы
– биты. Биты в устройствах реализуются
сигналами, которые описываются двоичными
переменными – булевыми.

Определение.

Совокупность
конкретных значений аргументов булевой
функции называется кортежем,
двоичным
словом (
-словом)
или булевым
набором длины

и обозначается как

.
Для булевой функции

конкретное (индивидуальное) значение
булевого набора

называется также интерпретацией
булевой функции
f.

Пример. Для
булевой функции

кортежами являются следующие совокупности
конкретных значений аргументов:

,

,

,

;
для булевой функции

кортежами являются:

,

,

,

и т.д.

Определение.

Множество всех
двоичных слов, обозначаемое как

,
называется n-мерным
булевым кубом
и содержит

элементов-слов, т.е.

.

Пример.

В множество двоичных
слов для булевой функции

входит

слова: (0) и (1); в множество двоичных слов
для булевой функции

входит

слов:

,

,

,

,

,

,

,

.

Определение.

Областью
определения булевой функции
от

-переменных
служит множество слов длины

,
которые представляют собой всевозможные
наборы из

двоичных цифр и их общее количество
равно

.

Определение.

Функция, зависящая
от

аргументов, является полностью
определенной,
если указаны её значения для всех наборов
(кортежей, слов) значений элементов.

Пример.

Булева функция от
двух элементов является полностью
определенной, если указаны её значения
для каждого из четырех возможных наборов
(
),
функция трех аргументов – на 8 (
)
наборах также будет полностью определенной.

Теорема. Число
всех функций, зависящих от

переменных

,
равно

.

Действительно,
булева функция

аргументов определена на

наборах, на которых она может принимать
«0» или «1» из общего количества

.
Поэтому в соответствие каждой булевой
функции можно поставить

-разрядное
двоичное число. Но количество различных

-разрядных
чисел равно

,
а следовательно и количество различных
булевых функций равно

.

Пример. От
двух аргументов

существует 16 булевых функций, т.е.

;
от трех – 256 (
),
от четырех – 65536 функций (
).

4.2.2.3 Способы задания булевых функций.

Существует четыре
способа задания булевой функции:

• вербальный
  (словесный);

• табличный (с
  помощью таблицы истинности);

• порядковым номером,
  который имеет функция;

• аналитический (в
  виде формулы).

Задание булевых
функций при помощи таблиц.
Булевы функции можно задавать с помощью
таблиц, подобных таблицам сложения и
умножения одноразрядных чисел. В левой
части такой таблицы перечисляются все

наборов значений переменных (булевых
наборов длины

),
а в правой части − значения функций на
этих наборах. Этот способ задания
универсален, т.е. пригоден для любой
функции, однако громоздок, поэтому
применяется для задания функции
небольшого числа переменных.

Определение.

Таблицы, в которых
каждой интерпретации (то есть набору
аргументов) функции поставлено в
соответствие её значение, называются
таблицами
истинности (соответствия)
булевой функции.

В таблице истинности
каждой переменной

и значению самой функции

соответствует по одному столбцу, а
каждой интерпретации 
по одной строке. Интерпретации расположены
в определенном порядке − лексикографическом,
который совпадает с порядком возрастания
наборов, рассматриваемых как двоичные
числа.

Пример.

Таблица истинности
функции

может иметь следующий вид (таблица 4.1).

Таблица 4.1 – Пример
таблицы истинности функции

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

В столбцах 1, 2, 3
даны все возможные кортежи значений
трех аргументов, т.е. сочетание нулевых
и единичных значений трех аргументов.
В столбце 4 – значения функции

.

Рассмотрим булевы
функции, которые зависят от одной и двух
переменных.

Булевы функции,
которые зависят от одной переменной,
приведены в таблице 4.2 (их количество
равно

).

Таблица 4.2 
Таблица истинности для булевых
функций одной переменной

0	0	0	1	1
1	0	1	0	1

Две функции

и

представляют собой функции-константы:

• 

   является
  абсолютно ложной (константа нуля);

• 

   является
  абсолютно истинной (константа единицы).

Функция

(функция повторения аргумента) повторяет
значения переменной

и поэтому просто совпадает с ней. Функция

,
называемая отрицанием
или инверсией
(

читается «не

»),
является единственной нетривиальной
функцией. Она равна 1, когда аргумент
принимает значение 0, и равна 0 при
аргументе 1.

Всевозможные
булевы функции двух переменных

представлены в таблице 4.3 (их количество
равно

).

Таблица 4.3 
Таблица истинности для булевых функций
двух переменных

0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

В таблице 4.4
приведена характеристика булевых
функций двух переменных.

Таблица 4.4 
Характеристика булевых функций
двух переменных

Функция	Обозначения (другие обозначения)	Названия	Чтение
	0	Константа 0 (тождественный нуль, всегда ложно)	Константа 0 (Любое 0)
	( ) (AND, И)	Конъюнкция (произведение, пересечение, логическое «и»)	и (и и ). Истинна тогда, когда истинны обе переменные
	( ) (>)	Отрицание импликации (запрет)	, но не
		Повторение (утверждение) первого аргумента	Как
	( )	Отрицание обратной импликации	Не , но
		Повторение второго аргумента	Как
	( )	Сумма по модулю 2 (неравнозначность, антиэквивалетность)	не как (или или ). Истинна, когда истинны или , или в отдельности
	( ) (OR, ИЛИ)	Дизъюнкция (логическая сумма, логическое «или»)	или ( или хотя бы ). Истинна тогда, когда истинны или , или , или обе переменные
	( )	Стрелка Пирса (функция Вебба, отрицание дизъюнкции)	Не и не . Истинна только тогда, когда и ложны
	( ) (Eqv)	Эквиваленция (равнозначность, эквивалентность)	как ( , если, и только если )
	( )	Отрицание (инверсия) второго аргумента	Не
	( )	Обратная импликация (обратное разделение с запретом)	Если , то ( или не )
	( )	Отрицание (инверсия) первого аргумента	Не
	( ) (Imp)	Импликация (следование, селекция)	Если , то (не или ). Ложна тогда и только тогда, когда истинна и ложна
	( )	Штрих Шеффера (отрицание конъюнкции, несовместимость, логическое «не-и»)	Не или не . Ложна только тогда, когда и истинны
	1	Константа 1 (тождественная единица, всегда истинно)	Константа 1 (Любое 1)

Шесть из приведенных
функций не зависят от

или

(или от обоих вместе). Это две константы
(

и

),
повторения (
,

)
и отрицания (

и

),
являющиеся функциями одной переменной
(

или

.)
Из остальных десяти функций две (

и

)
отличаются от соответствующих им (

и

)
лишь порядком расположения элементов
и поэтому не являются самостоятельными.
Поэтому из 16 функций двух переменных
только восемь являются оригинальными
(
).

В математической
логике часто употребляются так называемые
элементарные функции, которые играют
такую же важную роль, как, например,

или

в математическом анализе. Элементарные
логические функции – это одноместные
и двухместные логические функции.

Примеры элементарных
функций одной переменной приведены в
таблице 4.2.

Примеры элементарных
функций двух переменных представлены
в таблицах 3.3 и 3.4, это: отрицание

(
);
дизъюнкция

;
конъюнкция

;
импликация

;
эквивалентность

;
сумма по модулю 2

;
штрих Шеффера

;
стрелка Пирса

.

Булевы функции
можно рассматривать как логические
операции над величинами, принимающими
два значения – 0 и 1. Основными в двузначной
логике являются три функции:

• отрицание (функция

  ,
  принимающая значения 1, когда
  
  ,
  и значение 0, когда
  
  );

• дизъюнкция (функция
  
  ,
  принимающая значение 0 тогда и только
  тогда, когда оба аргумента имеют значение
  0);

• конъюнкция (функция
  
  ,
  принимающая значение 1 тогда и только
  тогда, когда оба аргумента имеют значение
  1).

Задание булевой
функции порядковым номером.
Каждой функции присваивается порядковый
номер в виде натурального числа, двоичный
код которого представляет собой столбец
значений функции в таблице истинности.
Младшим разрядом считается самая нижняя
строка (значение функции на интерпретации

,
а старшим 
самая верхняя (значение функции на
интерпретации

).
Указанный порядковый номер функции,
как двоичный, так и десятичный, полностью
определяет булеву функцию.

Часто для упрощения
записи булевой функции вместо полного
перечисления интерпретаций используют
только двоичные значения наборов, для
которых функция принимает единичные
значения. Такую форму записи называют
числовой.

Пример.

Найдем порядковый
номер функции

,
которая задана таблицей истинности
(см. табл. 3.1). Для этого переведем двоичное
число

в десятичную систему счисления:

Кортеж значений
аргументов (интерпретацию) также можно
рассматривать как запись целого
положительного числа в двоичной системе
счисления. Первая интерпретация в
таблице истинности называется нулевой,
последняя – единичной (номер интерпретации

,
где

– количество аргументов функции).

Определение.

Десятичный
эквивалент двоичного представления
интерпретации называется номером
интерпретации (кортежа).

Пример.

Шестой интерпретацией
является

,
т.е.

.

Пример.

Пусть функция

принимает единичные значения на
интерпретациях 1, 4, 7. Тогда, используя
числовую форму записи, функция будет
иметь вид:

,
что означает, что функция принимает
единичные значения на наборах 1, 4 и 7.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Булевы функции и алгебра логики. Двойственность булевых функций

Компьютерная дискретная математика
Булевы функции и алгебра логики.
Двойственность булевых функций
Лекции 4-5
Н.В. Белоус
Факультет компьютерных наук
Кафедра ПО ЭВМ, ХНУРЭ
ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021-446, e-mail: [email protected]
900igr.net

2. Тема 1 Булевы функции и алгебра логики

3. Булевы переменные и функции

Переменные, которые могут принимать значения
только из множества B={0,1}, называются логическими
или булевыми переменными. Сами значения 0 и 1
булевых
переменных
называются
булевыми
константами.
3

4. Булевы переменные и функции

Функция вида y=f(x1,x2,…,xn), аргументы и значения
которой заданы на множестве B, называется nместной булевой функцией. Такие функции также
называют логическими или переключательными
функциями.
4

5. Основные определения

Кортеж (x1,x2,…,xn) конкретных значений булевых
переменных называется двоичным словом (n-словом)
или булевым набором длины n.
Для булевой функции y=f(x1,x2,…,xn) конкретное
(индивидуальное) значение булевого набора (x1,x2,…,xn)
называется также интерпретацией булевой функции f.
Множество всех двоичных слов, обозначаемое через
Bn, образует область определения булевой функций и
называется n-мерным булевым кубом и содержит 2n
элементов-слов: |Bn|=2n.
Каждому двоичному слову соответствует одно из
двух возможных значений (0 или 1), таким образом,
область значений представляет собой кортеж длиной 2n,
состоящий из 1 и 0.
5

6. Способы задания булевых функций

I. Таблицы истинности
Таблицы, в которых каждой интерпретации
функции поставлено в соответствие ее значение,
называются таблицами истинности булевой
функции.
В таблице истинности каждой переменной и
значению самой функции соответствует по одному
столбцу, а каждой интерпретации — по одной строке.
Количество строк в таблице соответствует количеству
различных интерпретаций функции.
6

7. Булевы функции одной переменной

x
0
1
2
3
0
0
0
1
1
1
0
1
0
1
1. 0 0 — функция константа 0,
2. 1 = x — функция повторения аргумента,
3. 2 = x — функция инверсии или отрицания аргумента,
4. 3 1 — функция константа 1.
7

8. Булевы функции двух переменных

x
0
0
1
1
y
0
1
0
1
f0
0
0
0
0
f1
0
0
0
1
f2
0
0
1
0
f3
0
0
1
1
f4
0
1
0
0
f5
0
1
0
1
f6
0
1
1
0
f7
0
1
1
1
f8
1
0
0
0
f9
1
0
0
1
f10
1
0
1
0
f11
1
0
1
1
f12
1
1
0
0
f13
1
1
0
1
f14
1
1
1
0
f15
1
1
1
1
8

9. Булевы функции двух переменных

Функ- Обозция начение
Название
Другие
обоз-я
Прочтение
f0(x,y)
0
константа 0
константа 0
f1(x,y)
x y
конъюнкция (логическое «и»)
·, &, &&,*, И,
, AND, min
xиy
f2(x,y)
x y
отрицание импликации
>
x и не y
f3(x,y)
x
повторение первого аргумента
как x
f4(x,y)
x y
отрицание обратной импликации
f5(x,y)
Y
повторение второго аргумента
f6(x,y)
x y
исключающее «или»
(сумма по модулю 2)
, < >, > <,
f7(x,y)
x y
дизъюнкция
(логическое «или»)
OR, ИЛИ,
+, max
<
не x и y
как y
x не как y
!=, XOR
x или у
9

10. Булевы функции двух переменных

Функция
Обозначение
Название
Другие
обоз-я
Прочтение
f8(x,y)
x y
отрицание дизъюнкции
(стрелка Пирса)
f9(x,y)
x y
эквивалентность
f10(x,y)
отрицание второго аргумента
y
не y
f11(x,y)
y
x y
обратная импликация
x, если y
(x или не y)
f12(x,y)
x
отрицание первого аргумента
x
не x
если x, то y
(не x или y)
не x и не y
x y
, , Eqv, =
f13(x,y)
x y
импликация
, , Imp
f14(x,y)
x|y
отрицание конъюнкции
(штрих Шеффера)
x y
f15(x,y)
1
константа 1
x как y
не x или не y
константа 1
10

11. Способы задания булевых функций

II. Номера булевых функций и интерпретаций
Каждой функции присваивается порядковый номер
в виде натурального числа, двоичный код которого
представляет собой столбец значений функции в
таблице истинности.
Младшим разрядом считается самая нижняя строка
(значение функции на интерпретации (1,1,…,1)), а
старшим — самая верхняя (значение функции на
интерпретации (0,0,…,0)).
11

12. Способы задания булевых функций

Каждой
интерпретации
булевой
функции
присваивается свой номер – значение двоичного кода,
который представляет собой интерпретация.
Интерпретации, записанной в верхней строке
таблицы истинности, присваивается номер 0, затем
следует интерпретация номер 1 и т.д.
В
самой
нижней
строке
расположена
интерпретация с номером 2n–1, где n — количество
переменных, от которых зависит булева функция.
12

13. Пример

Найти
порядковый
номер
функции
f(x,y),
принимающей следующие значения: f(0,0)=1, f(0,1)=1,
f(1,0)=0, f(1,1)=1.
x
0
0
1
1
y f(x,y)
0 1
1 1
0 0
1 1
Двоичный код, соответствующий
значению этой функции – 1101.
11012 = 1 23 + 1 22 + 0 21 + 1 20 =
=8+4+0+1=1310
Таким образом
f13(x,y) = (1101)2
13

14. Пример

Построить таблицу истинности для функции f198
198 | 2
0 | 99 | 2
1 | 49 | 2
1 | 24 | 2
0 | 12 | 2
0 |6 | 2
0 |3 | 2
1 |1
x
0
0
0
0
1
1
1
1
y
0
0
1
1
0
0
1
1
z f (x,y,z)
0
1
1
1
0
0
1
0
0
0
1
1
0
1
1
0
Пример заполнения таблицы истинности
14

15. Способы задания булевых функций

III. Задание булевых функций с помощью формул
Формула – это выражение, задающее некоторую
функцию в виде суперпозиции других функций.
Суперпозицией называется прием получения новых
функций путем подстановки значений одних функций
вместо значений аргументов других функций.
15

16. Пример

Рассмотрим формулу булевой алгебры, задающую
некоторую функцию f(x,y,z)
f ( x, y,z ) ( x y ) z
Эта формула содержит функции:
g(x1) – отрицание,
s(x1,x2) – конъюнкция,
l(x1,x2) – дизъюнкция.
Представим данную формулу в виде суперпозиции
указанных функций следующим образом:
f (x,y,z) = l(s(x,g(y)),z)
16

17. Приоритет выполнения операций

Если в формуле отсутствуют скобки, то
операции
выполняются
в
следующей
последовательности:
1. Отрицание.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность
Пример
Убрать все возможные скобки
–
~
(( x y ) z ) ( x y ) x y z x y
Расставить скобки с учетом приоритета операций
(((
xx
x yy
y))
y (y(yz y ~
z zx~z)
))x~ ~
xy(x
xy
y yy )
17

18. Эквивалентные формулы

Формулы, представляющие одну и ту же функцию,
называются эквивалентными или равносильными.
18

19. Законы и тождества алгебры логики

1) Коммутативность конъюнкции и дизъюнкции
x y = y x
Доказательство
x y = y x
Доказательство
2) Ассоциативность конъюнкции и дизъюнкции
x (y z)= (x y) z
Доказательство
x (y z)=(x y) z
Доказательство
3) Дистрибутивность конъюнкции и дизъюнкции
относительно друг друга
x (y z) = (x y) (x z)
Доказательство
x (y z) = (x y) (x z)
Доказательство
19

20. Законы и тождества алгебры логики

4) Идемпотентность конъюнкции и дизъюнкции
x x = x
x x = x
5) Закон исключенного третьего
Доказательство
x x 1
6) Закон противоречия
Доказательство
x x 0
8) Закон элиминации
x (x y) = x
Доказательство
x (x y) = x
Доказательство
20

21. Законы и тождества алгебры логики

7) Тождества с константами.
x 0 = x
x 1 = x
x 1 = 1
x 0 = 0
9) Закон двойного отрицания.
x x
10) Законы де Моргана.
x y x y
x y x y
Доказательство
Доказательство
21

22. Тема 2 Двойственность булевых функций

23. Двойственные булевы функции

Функция f*(x1,…,xn) называется двойственной к
функции f(x1,…,xn), если
f ( x1 ,…, xn ) f ( x1 ,…, xn )
*
Пример
Найти двойственные функции
( x y )* x y x y
( x y )* x y x y
( x )* x x
(0)* 0 1
(1)* 1 0
Пример построения двойственной функции
23

24. Самодвойственные булевы функции

Функция, равная своей двойственной, называется
самодвойственной.
f = f*
x y
f(x,y)
f*(x,y)
x y f(x,y)=f*(x,y)
0 0 f(0,0)
f (1,1)
0 1 f(0,1)
f (1,0)
0 0 f(0,0)= f (1,1)
0 1 f(0,1)= f (1,0)
1 0 f(1,0)
f (0,1)
1 0 f(1,0)= f (0,1)
1 1 f(1,1)
f (0,0)
1 1 f(1,1)= f (0,0)
24

25.

Пример
Является ли функция f(x,y,z) самодвойственной?
f(x,y,z) —
x y z f (x,y,z) f* (x,y,z)
0 0 0
0
0
0 0 1
1
1
0 1 0
0
1
0 1 1
1
1
1 0 0
0
0
1 0 1
0
1
1 1 0
0
0
1 1 1
1
1
несамодвойственная
25

26. Принцип двойственности

Пусть функция F заданна суперпозицией
функций f0,…,fn, где n N. Функцию F*,
двойственную F, можно получить, заменив в формуле
F функции f0,…,fn на двойственные им f0*,…,fn*.
26

27.

Правило получения двойственных формул
Для того чтобы получить двойственную формулу
булевой алгебры необходимо заменить в ней все
конъюнкции на дизъюнкции, дизъюнкции на
конъюнкции, 0 на 1, 1 на 0, и использовать скобки, где
необходимо, чтобы порядок выполнения операций
остался прежним.
27

28.

Правило получения двойственных формул
Пример
Найти функцию, двойственную функции
f ( x, y,z ) x y y z x z
Решение
f * ( x , y , z ) ( x y y z x z )*
( x y ) ( y z ) ( x z ) ( y x z ) ( x z )
y x y z x z x x z z
x y y z x z x z
x y y z x z f ( x, y,z )
28

29.

Правило получения двойственных формул
Если функции равны, то и двойственные им функции
также равны.
Пусть f1 и f2 – некоторые функции, заданные
формулами. Тогда если
f1 = f2 ,
то
f1* = f2*
29