Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: (2; 4; 6; 8; 10…) А правило «первое число равно (3), а каждое следующее число в два раза больше предыдущего» формирует последовательность: (3; 6; 12; 24; 48….)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами
(или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности (3; 6; 12; 24; 48…) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность (3; 6; 12; 24; 48…) обозначить как (a_n), то можно записать, что (a_1=3), (a_2=6), (a_3=12), (a_4=24) и так далее.
Иными словами, для последовательности (a_n={ 3;: 6; :12; : 24; : 48; : 96; : 192; : 384…}).
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
… |
|
обозначение элемента |
(a_1) |
(a_2) |
(a_3) |
(a_4) |
(a_5) |
(a_6) |
(a_7) |
(a_8) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
(96) |
(192) |
(384) |
… |
Отметим, что членами последовательности необязательно должны быть различные числа. Она может состоять из одних и тех же чисел, например, выглядеть вот так: (1; : 1; : 1; : 1…) .
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
– I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Пример: Напишите первые пять членов последовательности квадратов натуральных чисел.
Решение: Натуральными называют числа, возникающие естественным образом при счете количества предметов, то есть: (1; : 2; : 3; : 4; : 5) и т.д. Нашу же последовательность формируют квадраты этих чисел, то есть (1^2;: 2^2; : 3^2; : 4^2; : 5^2…) . Таким образом, имеем ответ: (1; : 4; : 9; : 16; : 25…)
Ответ: (1; : 4; : 9; : 16; : 25…)
Отметим, что последовательности в начале статьи заданы именно словесным способом.
– II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: (b_n=frac{n-1}{n^2}). Вычислите первые пять членов этой последовательности.
Решение: Вычислим (b_1). Это первый член последовательности, то есть его порядковый номер (n) равен единице. Тогда его значение равно (b_1=frac{1-1}{1^2} =frac{0}{1}=0).
У второго члена (n=2), то есть его значение равно (b_2=frac{2-1}{2^2} =frac{1}{4}).
Третий ((n=3)): (b_3=frac{3-1}{3^2} =frac{2}{9}).
Четвертый ((n=4)): (b_4=frac{4-1}{4^2} =frac{3}{16}).
Пятый ((n=5)): (b_5=frac{5-1}{5^2} =frac{4}{25}) .
Готово. Можно писать ответ.
Ответ: (b_n= {0; : frac{1}{4}; : frac{2}{9}; : frac{3}{16}; : frac{4}{25}…}).
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: (a_n=8+5n-n^2). Вычислите (a_9).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер (n=9). Подставляем в формулу: (a_9=8+5·9-9^2=8+45-81=-28).
Ответ: (a_9=-28).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: (c_1=4), (c_{n+1}=c_n+3). Вычислите первые пять членов этой последовательности.
Решение: Первый член нам известен: (c_1=4).
Второй мы получим, подставив в формулу вместо (n) единицу: (c_{1+1}=c_1+3)
(c_2=c_1+3=4+3=7)
Третий ((n=2)): (c_{2+1}=c_2+3 )
(c_3=c_2+3=7+3=10).
Четвертый ((n=3)): (c_{3+1}=c_3+3)
(c_4=c_3+3=10+3=13).
Пятый ((n=4)): (c_{4+1}=c_4+3)
(c_5=c_4+3=13+3=16).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
Ответ: (c_n={4; : 7; : 10; : 13; : 16…}).
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула (c_{n+1}=c_n+3) требовала именно этого. В ней (c_n) – это предыдущий элемент, а (c_{n+1}) – следующий за ним (ведь его номер на единицу больше).
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента (z_1=2;) (z_2=5). Так же известна формула следующего элемента (z_{n+2}=3z_{n+1}-z_n). Вычислите значения третьего, четвертого и пятого членов.
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
|
Последовательность на данный момент: |
Вычисления: |
||||||||||||
|
Так как формула дана для элемента с номером (n+2), то чтобы найти (z_3) нужно подставлять вместо (n) единицу:
|
||||||||||||
|
Теперь найдем (z_4), подставив вместо (n) двойку: (z_{2+2}=3z_{2+1}-z_2) (z_4=3z_3-z_2=3·13-5=34) |
||||||||||||
|
Наконец вычисляем (z_5), подставляя вместо (n) тройку: (z_{3+2}=3z_{3+1}-z_3) (z_5=3z_4-z_3=3·34-13=89) |
||||||||||||
|
Готово. Можно писать ответ. |
Ответ: (c_3=13); (c_4=34); (c_5=89).
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности (a_n=n^2-n):
а) (1) б) (3) в) (6) г) (10) ?
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
(a_1=1^2-1=0) – мимо.
(a_2=2^2-2=2) – тоже не то.
(a_3=3^2-3=6) – есть!
Нужный элемент найден.
Ответ: (6).
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
-
Подставляют заданное число в формулу (n) -го члена вместо (a_n);
-
Решая полученное уравнение, находят неизвестное (n);
-
Если (n) – натуральное, то данное число – член последовательности.
Пример: Выяснить, является ли число (3) членом последовательности (a_n=)(frac{51+2n}{n+4}) ?
Решение:
|
(a_n=)(frac{51+2n}{n+4}) |
Если число (3) – член последовательности, то значит при некотором значении (n), формула (frac{51+2n}{n+4}) должна дать нам тройку. Найдем это (n) по алгоритму выше. |
|
(3=)(frac{51+2n}{n+4}) |
Решаем это уравнение. Умножаем левую и правую части на знаменатель ((n+4)). |
|
(3cdot (n+4)=51+2n) |
Получилось линейное уравнение. Раскрываем скобки слева. |
|
(3n+12=51+2n) |
Собираем неизвестные слева, числа справа… |
|
(3n-2n=51-12) |
…и приводим подобные слагаемые. |
|
(n=39) |
Готово. Найденное значение – это то число, которое надо подставить вместо (n) в формулу (frac{51+2n}{n+4}), чтоб получилось тройка (можете проверить это сами). Значит (39)-ый член последовательности равен трем. |
Ответ: Да, число (3) является элементом данной последовательности.
Смотри также:
Арифметическая прогрессия
Геометрическая прогрессия
Рассмотрим последовательность. -19,2; -17,4; -15,6; -13,8;…
Заметим, что каждый член, начиная со второго, получается из предыдущего прибавлением числа 1,8.
Рассмотрим последовательность, в которой первый член равен 5, а каждый следующий получается из предыдущего прибавлением числа -2
5; 3; 1; -1; -3;…
Мы получили две арифметические прогрессии.
Рассмотрим ещё одну последовательность. Выпишем в порядке убывания дроби с числителем один и чётными знаменателями.
1/2; 1/4; 1/6; 1/8; …
Для любого натурального числа n можно указать соответствующее ему число в этой последовательности, оно равно 1/2n.
На сотом месте стоит число 1/200.
Числа, образующие последовательность, называются членами последовательности.
Их обозначают буквами с индексами, указывающими номер члена, а первое – первый член последовательности, а второе – второй член последовательности, а пятое – пятый член последовательности, а энное – n-й член последовательности, то есть член последовательности с номером n.
Мы рассмотрели последовательности, в которых бесконечно много членов. Они называются бесконечными.
Выпишем все двузначные числа, делящиеся на 20. Принято говорить, что они кратны 20-ти. Таких чисел всего 4, они образуют конечную последовательность.
Чтобы найти последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Последовательность нечётных натуральных чисел задаётся формулой а энное равно два эн плюс 1.
Последовательность дробей задаётся формулой бэ энное равно единице, делённой на два эн.
Эти формулы позволяют найти любой член последовательности по его номеру и называются формулами n-го члена
Найдём первые члены последовательности , заданной формулой n-го члена це энное равно минус единице в степени эн, делённой на 3.
Найдём первые члены последовательности , заданной формулой n-го члена бэ энное равно семи.
Ещё один способ задания последовательности – рекуррентный. Задаётся первый член и формула, выражающая каждый следующий член через предыдущий. Можно задать первые несколько членов и формулу, задающую каждый член последовательности, начиная с некоторого, через предыдущие. Такая формула называется рекуррентной – от латинского слова recurro, что значит возвращаться
Зададим первые два члена последовательности и рекуррентную формулу.
Найдём несколько членов последовательности.
Эта последовательность описана в трудах итальянского математика Леонардо из Пизы, известного под именем Леонардо Фибоначчи. Члены последовательности называют числами Фибоначчи.
Повторение. Числовая функция
Пусть ![]() – числовое множество.
– числовое множество.
Числовой функцией
называется закон, по которому каждому элементу из
сопоставляется единственное число.
Множество ![]() – это область определения.
– это область определения.
Числовая последовательность
Числовая последовательность – это числовая функция (
), которая определена на множестве натуральных чисел (
).
Областью определения является множество натуральных чисел (![]() ).
).
Обозначают члены последовательности так:
![]() ;
; ![]() ;
; ![]() ;…;
;…; ![]()
Числовая последовательность – это частный случай функции. Как и любая функция, последовательность может задаваться различными способами.
Способы задания числовой последовательности:
1. Аналитический (при помощи формулы)
2. Словесный
3. Рекуррентный
Аналитический способ задания числовой последовательности
Последовательность задана аналитически, если указана формула для вычисления ее -го члена.
![]() , где
, где ![]()
Рассмотрим примеры:
1. ![]() ,
,
Это аналитическое задание последовательности чисел: ![]() ;
; ![]() ;
; ![]() ;…;
;…; ![]() ;… Указав конкретное значение
;… Указав конкретное значение ![]() , нетрудно найти член последовательности с соответствующим номером.
, нетрудно найти член последовательности с соответствующим номером.
Построим график данной последовательности. Согласно определению графика функции, графиком данной последовательности является множество всех точек ![]() , где
, где ![]() (см. Рис. 1). Все эти точки лежат на правой ветви гиперболы
(см. Рис. 1). Все эти точки лежат на правой ветви гиперболы ![]() .
.

Рис. 1. График числовой последовательности ![]()
Функция ![]() при
при ![]() убывает, следовательно, числовая последовательность
убывает, следовательно, числовая последовательность ![]() также убывает.
также убывает.
2. ![]()
Выпишем несколько членов данной числовой последовательности:
![]() ;
; ![]() ;
; ![]() ;…
;…
График данной последовательности – это множество точек с координатами ![]() , где
, где ![]() (см. Рис. 2). Все эти точки лежат на ломаной
(см. Рис. 2). Все эти точки лежат на ломаной ![]() .
.

Рис. 2. График числовой последовательности ![]()
Числовая последовательность ![]() убывает при
убывает при ![]() , возрастает при
, возрастает при ![]() .
.
Словесный способ задания числовой последовательности
Словесный способ задания числовой последовательности используется, когда правило задания последовательности описано словами, не указывая формулы.
Пример
Дано: ![]() – это -я цифра после запятой в десятичной записи числа
– это -я цифра после запятой в десятичной записи числа ![]() .
.
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;…
;…
Рекуррентный способ задания числовой последовательности
Последовательность задана рекуррентно, если указано правило, по которому -й член вычисляется по предыдущим членам.
Пример
![]() ;
; ![]() ;
; ![]() , где
, где ![]()
В данном примере задана возможность получения любого -го члена последовательности:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;…
;…
Задача 1
В числовой последовательности ![]() ;
; ![]() ;
; ![]() , где
, где ![]() найти 7 член.
найти 7 член.
Решение
Для того чтобы найти 7 член данной последовательности, необходимо знать 5 и 6 член. В предыдущем примере мы нашли 3, 4 и 5 член, следовательно, можно найти 6, а далее и 7 член.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Ответ: ![]() .
.
Задача 2
Дано:
![]()
Найти: ![]()
Решение
Подставляем ![]() в формулу для -го члена последовательности
в формулу для -го члена последовательности ![]() :
:
![]()
Ответ: ![]() .
.
Задача 3
Дано:
![]()
Найти: является ли число ![]() некоторым членом заданной последовательности?
некоторым членом заданной последовательности?
Решение
Приравниваем формулу для -го члена последовательности ![]() к числу
к числу ![]() , получим уравнение относительно
, получим уравнение относительно ![]() . Если
. Если ![]() будет натуральным числом, то число
будет натуральным числом, то число ![]() является членом заданной последовательности.
является членом заданной последовательности.
![]()
![]()
![]()
![]()
Следовательно: ![]()
Ответ: число ![]() является 5 членом заданной последовательности.
является 5 членом заданной последовательности.
Задача 4
Укажите формулу общего члена последовательности, которая задана несколькими членами: 1; 4; 9; 16; 25.
Решение
Запишем каждый член последовательности в следующем виде:
![]()
![]()
![]()
![]()
![]()
Видно, что члены последовательности представляют собой квадраты последовательных натуральных чисел. Таким образом, делаем вывод, что:
![]() , где
, где ![]()
Ответ:![]() , где
, где ![]() .
.
Список литературы
1. Виленкин Н.Я., Сурвило Г.С. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков, К.И. Алгебра для 9 класса с углубл. изуч. математики. – М.: Мнемозина, 2003.
3. Мордкович А.Г. Алгебра 9 класс, учебник для общеобразовательных учреждений. – М.: Мнемозина, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт hijos.ru (Источник)
3. Интернет-сайт Hellper.ru (Источник)
4. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Упражнения 1, 7 (в-е), 8, (глава 11,§1 стр. 219) – Виленкин Н.Я., Сурвило Г.С. Алгебра 9 кл. (Источник)
2. Найти 15 член последовательности, заданной формулой -го члена: ![]() ,
, ![]()
3. Последовательность задана при помощи рекуррентного соотношения ![]() ,
, ![]() ,
, ![]() . Выписать несколько первых членов этой последовательности.
. Выписать несколько первых членов этой последовательности.
4. Проверить, являются ли числа ![]() и
и ![]() членами последовательности
членами последовательности ![]()
Содержание:
- Основные понятия и определения
- Задание последовательности формулой ее общего члена
- Рекуррентный способ задания последовательности
Основные понятия и определения
Определение
Последовательностью называется функция, которая переводит множество
натуральных
чисел $N$ в некоторое множество
$X$ :
$left{x_{n}right}=left{x_{n}right}_{n=1}^{infty}=left{x_{1} ; x_{2} ; ldots ; x_{n} ; ldotsright}, x_{i} in N$
Элемент $x_{1}$ называется первым членом
последовательности, $x_{2}$ – вторым, … ,
$x_{n}$ –
$n$-ым или общим членом последовательности.
Пример
Задание. Для последовательности $x_{n}={-1 ; 2 ; 5 ; 8 ;-3 ; 0 ; ldots}$
определить, чему равен третий член $x_{3}$
Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для
заданной последовательности имеем, что $x_{3}=5$
Ответ. $x_{3}=5$
Задание последовательности формулой ее общего члена
Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член
последовательности, зная его номер.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти формулу общего члена последовательности
$x_{n}={6 ; 20 ; 56 ; 144 ; 352 ; ldots}$
Решение. Запишем каждый член последовательности в следующем виде:
$n=1 : x_{1}=6=2 cdot 3=2^{1} cdot 3=2^{1} cdot(2 cdot 1+1)$
$n=2 : x_{2}=20=4 cdot 5=2^{2} cdot 5=2^{2} cdot(2 cdot 2+1)$
$n=3 : x_{3}=56=8 cdot 7=2^{3} cdot 7=2^{3} cdot(2 cdot 3+1)$
Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на
последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.
Таким образом, делаем вывод, что
$x_{n}=2^{n} cdot(2 n+1)$
Ответ. Формула общего члена: $x_{n}=2^{n} cdot(2 n+1)$
Пример
Задание. Найти 15 член последовательности, заданной формулой
$n$-го члена:
$x_{n}=frac{(-1)^{n}}{n}, n in N$
Решение. Для того чтобы найти $x_{15}$ ,
подставим в формулу общего члена значение $n=15$ . Получим:
$x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$
Ответ. $x_{15}=frac{(-1)^{15}}{15}=-frac{1}{15}$
Пример
Задание. Проверить, являются ли числа
$a=6$ и
$b=1$ членами последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$
Решение. Число $a=6$ является
членом последовательности $left{x_{n}right}, n in N$ , если существует
такой номер $n_{0} in N$ , что
$x_{n_{0}}=a=6$ :
$6=x_{n o}=frac{n_{0}^{2}+11}{n_{0}+1} Rightarrow frac{n_{0}^{2}+11}{n_{0}+1}=6 Rightarrow$
$Rightarrow n_{0}^{2}-6 n_{0}+5=0 Rightarrow=left{begin{array}{l}{n_{0}=1} \ {n_{0}=5}end{array}right.$
Таким образом, число $a=6$ является первым и
пятым членами заданной последовательности.
Проверим теперь, является ли число $b=1$ членом указанной
последовательности $left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$ . Рассуждая аналогично,
как и для $a=6$ , получаем:
$frac{n_{0}^{2}+11}{n_{0}+1}=1 Rightarrow n_{0}^{2}-n_{0}+10=0 Rightarrow D=1-40=-39 lt 0$
Таким образом, уравнение $n_{0}^{2}-n_{0}+10=0$ не имеет
решение в натуральных числах, а значит, $b=1$ не
является членом последовательности $left{x_{n}right}$
Ответ. Число $a=6$ является
первым и пятым членами заданной последовательности, а
$b=1$ не является членом последовательности
$left{x_{n}right}=left{frac{n^{2}+11}{n+1}right}$
Рекуррентный способ задания последовательности
Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения.
В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому
правилу. Например, известен первый член $x_{1}$
последовательности и известно, что $x_{n+1}=fleft(x_{n}right)$ , то
есть $x_{2}=fleft(x_{1}right), x_{3}=fleft(x_{2}right)$ и так далее до нужного члена.
Пример
Примером рекуррентно заданной последовательности является последовательность чисел
Фибоначчи – 1, 1, 2, 3, 5, 8, 13, … , в которой каждое последующее число, начиная с третьего, является суммой
двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:
$x_{n+2}=x_{n+1}+x_{n}, n in N, x_{1}=x_{2}=1$
Пример
Задание. Последовательность $left{x_{n}right}$
задана при помощи рекуррентного соотношения $x_{n+2}=frac{1}{2}left(x_{n+1}+x_{n}right), x_{1}=2, x_{2}=4$ .
Выписать несколько первых членов этой последовательности.
Решение. Найдем третий член заданной последовательности:
$x_{3}=frac{1}{2}left(x_{2}+x_{1}right)=frac{4+2}{2}=frac{6}{2}=3$
Аналогично находим далее, что
$x_{4}=frac{1}{2}left(x_{3}+x_{2}right)=frac{3+4}{2}=frac{7}{2}=3,5$
$x_{5}=frac{1}{2}left(x_{4}+x_{3}right)=frac{3+3,5}{2}=frac{6,5}{2}=3,25$
и так далее.
При рекуррентном задании последовательностей, получаются очень громоздкими выкладки, так как, чтобы найти элементы с
большими номерами, необходимо найти все предыдущие члены указанной последовательности, например, для
нахождения $x_{500}$ надо найти все предыдущие 499 членов.
Читать дальше: ограниченные последовательности.
Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией 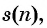

Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 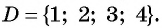 В таком случае говорят, что рассматривается функция натурального аргумента, или числовая последовательность.
В таком случае говорят, что рассматривается функция натурального аргумента, или числовая последовательность.
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 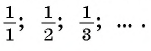 На
На 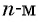 месте запишется число
месте запишется число 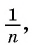 которое является
которое является 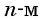 членом данной последовательности.
членом данной последовательности.
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 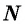 натуральных чисел, т. е. зависимость, при которой каждому натуральному числу ставится в соответствие единственное действительное число.
натуральных чисел, т. е. зависимость, при которой каждому натуральному числу ставится в соответствие единственное действительное число.
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 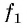 — первый член последовательности,
— первый член последовательности, 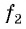 — второй член последовательности,
— второй член последовательности, 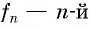 член последовательности. Последовательность с
член последовательности. Последовательность с 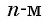 членом
членом 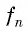 обозначается
обозначается 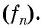 Для обозначения последовательности можно использовать любую букву латинского алфавита. Например, последовательность
Для обозначения последовательности можно использовать любую букву латинского алфавита. Например, последовательность 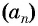 имеет вид
имеет вид 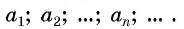
Если 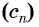 — последовательность нечетных натуральных чисел
— последовательность нечетных натуральных чисел 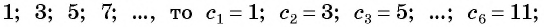
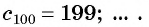
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 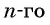 члена. Например, последовательность четных натуральных чисел можно задать с помощью формулы
члена. Например, последовательность четных натуральных чисел можно задать с помощью формулы 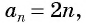 а последовательность чисел, обратных натуральным числам, задается формулой
а последовательность чисел, обратных натуральным числам, задается формулой 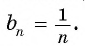
С помощью формулы 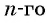 члена можно найти любой член последовательности.
члена можно найти любой член последовательности.
Например, пусть последовательность 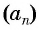 задана формулой
задана формулой 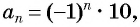 тогда
тогда
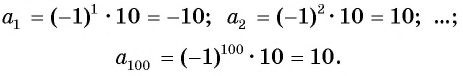
Чтобы найти некоторый член последовательности с помощью формулы 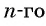 члена, нужно вместо п подставить в формулу натуральное число, равное номеру искомого члена (индексу в его обозначении).
члена, нужно вместо п подставить в формулу натуральное число, равное номеру искомого члена (индексу в его обозначении).
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 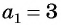 и
и 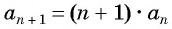 определяют бесконечную последовательность:
определяют бесконечную последовательность: 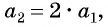 т. е.
т. е. 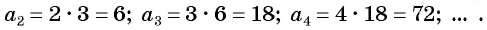
Пример №1
Найдите несколько членов последовательности 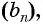 где
где 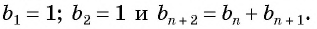
Решение:
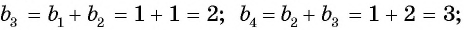
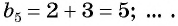
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 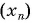 задана формулой
задана формулой 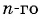 члена
члена 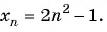 Найдите:
Найдите: 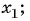
Решение:
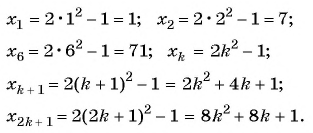
Пример №3
Последовательность задана формулой 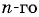 члена
члена 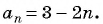 Является ли членом этой последовательности число:
Является ли членом этой последовательности число:
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 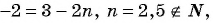 значит, число -2 не является членом последовательности;
значит, число -2 не является членом последовательности;
б) 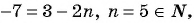 значит, число -7 является членом последовательности с номером 5.
значит, число -7 является членом последовательности с номером 5.
Пример №4
Для каких членов последовательности 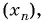 заданной формулой
заданной формулой 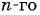 члена
члена 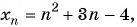 выполняется неравенство
выполняется неравенство 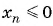 ?
?
Решение:
Подставим в неравенство 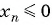 выражение для
выражение для 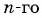 члена, получим
члена, получим 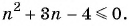 Решение полученного квадратного неравенства есть отрезок [-4; 1], выберем из этого отрезка только натуральные числа, получим
Решение полученного квадратного неравенства есть отрезок [-4; 1], выберем из этого отрезка только натуральные числа, получим 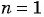 . Значит, данное неравенство выполняется только для первого члена последовательности.
. Значит, данное неравенство выполняется только для первого члена последовательности.
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 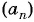 , если
, если 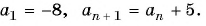
Решение:
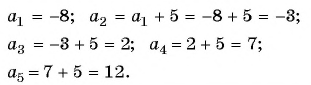
Пример №6
Запишите несколько первых членов последовательности 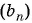 , если
, если 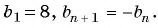
Задайте эту последовательность формулой 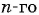 члена.
члена.
Решение:
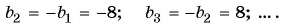
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 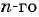 члена имеет вид
члена имеет вид 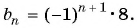
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С – 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С – 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С – 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
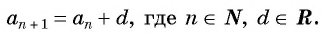
Число 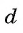 называется разностью арифметической прогрессии.
называется разностью арифметической прогрессии.
Из равенства 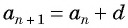 следует, что
следует, что 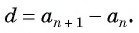
Чтобы задать арифметическую прогрессию 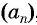 , достаточно задать ее первый член
, достаточно задать ее первый член 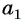 и разность
и разность 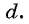
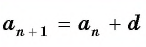
Например, если  то получится арифметическая прогрессия 3; 7; 11; 15; … .
то получится арифметическая прогрессия 3; 7; 11; 15; … .
Если 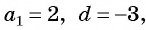 то арифметическая прогрессия имеет вид 2; -1; -4; -7; -10; … .
то арифметическая прогрессия имеет вид 2; -1; -4; -7; -10; … .
Если 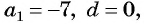 то все члены арифметической прогрессии равны между собой: -7; -7; -7; -7; … .
то все члены арифметической прогрессии равны между собой: -7; -7; -7; -7; … .
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 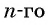 члена арифметической прогрессии
члена арифметической прогрессии
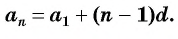
Выведем эту формулу. Если 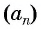 — арифметическая прогрессия с разностью
— арифметическая прогрессия с разностью 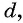 то, используя определение, получим верные равенства:
то, используя определение, получим верные равенства:
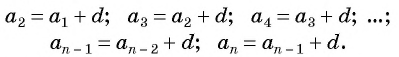
Сложим эти равенства:
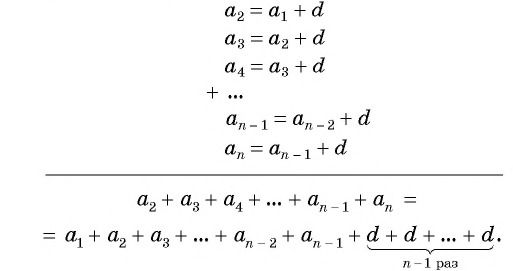
После упрощения получим:
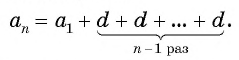
Так как число слагаемых 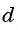 равно
равно 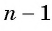 , то равенство примет вид
, то равенство примет вид
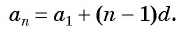
Получили формулу
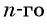 члена арифметической прогрессии
члена арифметической прогрессии 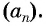
Формула 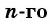 члена арифметической прогрессии
члена арифметической прогрессии 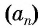 позволяет вычислить любой член прогрессии, зная ее первый член
позволяет вычислить любой член прогрессии, зная ее первый член 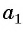 , номер члена
, номер члена 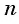 и разность прогрессии
и разность прогрессии 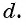
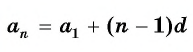
Пример №7
Последовательность 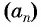 — арифметическая прогрессия,
— арифметическая прогрессия, 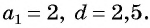 Найдите 100-й член прогрессии.
Найдите 100-й член прогрессии.
Решение:
По формуле 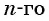 члена получим:
члена получим:
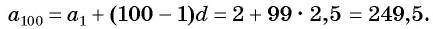
Ответ: 249,5.
Пример №8
Последовательность 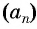 — арифметическая прогрессия,
— арифметическая прогрессия, 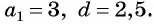 Является ли членом этой прогрессии число: а) 168; б) 201?
Является ли членом этой прогрессии число: а) 168; б) 201?
Решение:
а) По условию 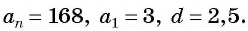 Подставим эти значения в формулу
Подставим эти значения в формулу 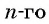 члена
члена 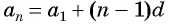 и получим уравнение
и получим уравнение 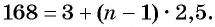 Решив его, получим, что
Решив его, получим, что 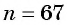 — корень уравнения. Так как 67 — натуральное число, то число 168 является членом этой прогрессии с номером 67.
— корень уравнения. Так как 67 — натуральное число, то число 168 является членом этой прогрессии с номером 67.
б) Подставим значения 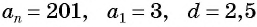 в формулу
в формулу 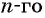 члена
члена 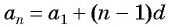 и получим уравнение
и получим уравнение 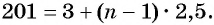 Решим его:
Решим его: 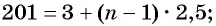
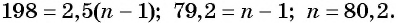 Так как корень уравнения 80,2 — не натуральное число, то число 201 не является членом этой прогрессии.
Так как корень уравнения 80,2 — не натуральное число, то число 201 не является членом этой прогрессии.
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 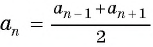 при
при 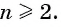
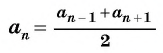 при
при 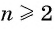
Доказательство. В арифметической прогрессии 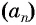 для члена
для члена 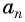 запишем по формуле
запишем по формуле 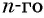 члена предыдущий и последующий члены, т. е.
члена предыдущий и последующий члены, т. е. 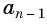 и
и 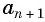 :
:
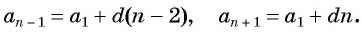
Найдем их среднее арифметическое:
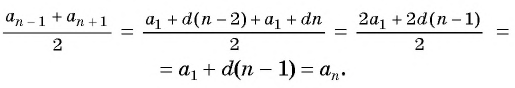
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности  каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, т. е.
каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, т. е. 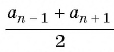 . Тогда
. Тогда 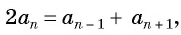 ,
,
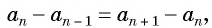 значит, разность каждого ее члена с предыдущим членом есть одно и то же число. Обозначим его
значит, разность каждого ее члена с предыдущим членом есть одно и то же число. Обозначим его 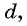 получим
получим 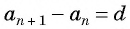 при любом натуральном
при любом натуральном 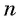 , следовательно,
, следовательно, 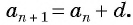 Значит, по определению последовательность
Значит, по определению последовательность 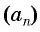 — арифметическая прогрессия.
— арифметическая прогрессия.
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов: 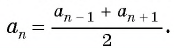
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
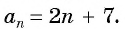
Решение:
Запишем для 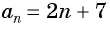 предыдущий и последующий члены последовательности:
предыдущий и последующий члены последовательности:
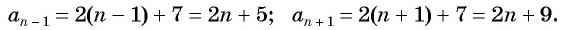
Найдем среднее арифметическое этих членов: 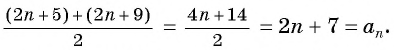
По характеристическому свойству арифметической прогрессии последовательность 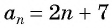 является арифметической прогрессией.
является арифметической прогрессией.
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 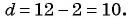 Тогда каждый следующий член последовательности равен предыдущему, сложенному с числом 10: 2; 12; 22; 32; 42;….
Тогда каждый следующий член последовательности равен предыдущему, сложенному с числом 10: 2; 12; 22; 32; 42;….
Пример №11
Известны члены арифметической прогрессии: 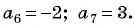 Найдите разность этой прогрессии.
Найдите разность этой прогрессии.
Решение:
Найдем разность арифметической прогрессии:
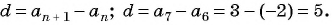
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 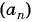 — арифметическая прогрессия. Найдите двадцатый член прогрессии, если
— арифметическая прогрессия. Найдите двадцатый член прогрессии, если 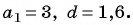
Решение:
По формуле 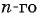 члена арифметической прогрессии
члена арифметической прогрессии 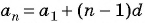 получим:
получим: 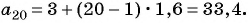
Пример №13
Запишите формулу 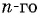 члена для арифметической прогрессии -15,5; -14,9; -14,3; … и найдите ее двадцатый член.
члена для арифметической прогрессии -15,5; -14,9; -14,3; … и найдите ее двадцатый член.
Решение:
По условию 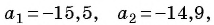 тогда
тогда 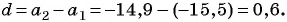 Запишем формулу
Запишем формулу 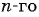 члена данной арифметической прогрессии, подставив в формулу
члена данной арифметической прогрессии, подставив в формулу 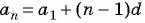 значения для
значения для 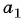 и
и 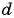 :
:
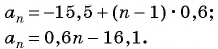
Подставим 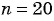 в формулу
в формулу 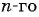 члена данной арифметической прогрессии и найдем ее двадцатый член:
члена данной арифметической прогрессии и найдем ее двадцатый член: 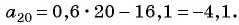
Пример №14
В арифметической прогрессии 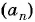 известно, что
известно, что 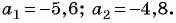 Число 16 является членом этой прогрессии. Найдите его номер.
Число 16 является членом этой прогрессии. Найдите его номер.
Решение:
Так как 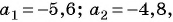 то
то 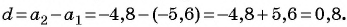 По условию
По условию 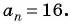 Воспользуемся формулой
Воспользуемся формулой 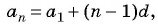 тогда
тогда
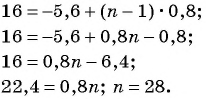
Пример №15
В арифметической прогрессии 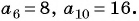 Найдите разность прогрессии и ее первый член.
Найдите разность прогрессии и ее первый член.
Решение:
По условию 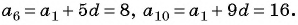
Решим систему уравнений
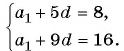
Вычтем из второго уравнения первое, получим 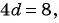 откуда
откуда 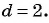 Подставим
Подставим 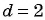 в первое уравнение системы, получим
в первое уравнение системы, получим 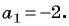
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 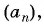 если
если 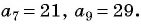
Решение:
По характеристическому свойству арифметической прогрессии 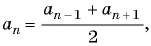 т. е.
т. е. 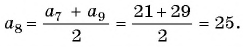
Пример №17
При каком значении 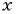 последовательность
последовательность 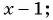
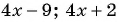 является арифметической прогрессией?
является арифметической прогрессией?
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
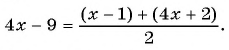
Решим полученное уравнение:
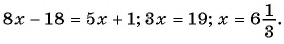
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии  у которой
у которой 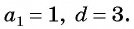
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 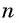 первых членов арифметической прогрессии:
первых членов арифметической прогрессии: 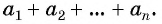
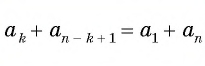
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е. 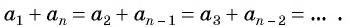
В общем виде: 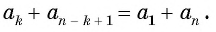
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 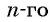 члена:
члена: 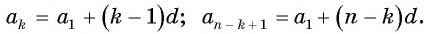
Тогда получим:
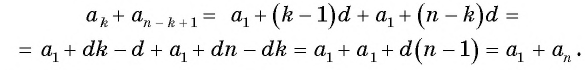
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 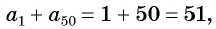 то и
то и 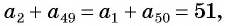 и
и 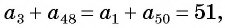 и
и 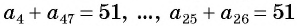 (рис. 94), то искомая сумма равна
(рис. 94), то искомая сумма равна 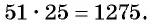
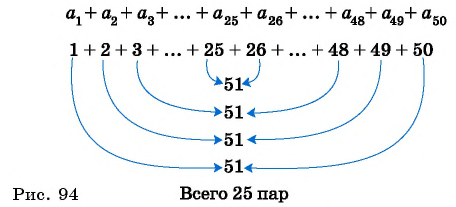
Выведем формулу суммы 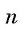 первых членов арифметической прогрессии.
первых членов арифметической прогрессии.
Обозначим 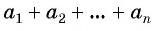 через
через 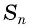 и запишем эту сумму дважды: с первого члена до
и запишем эту сумму дважды: с первого члена до 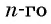 и с
и с 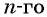 члена до первого:
члена до первого:
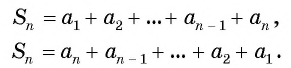
Сложим эти два равенства и получим:
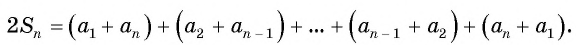
По свойству 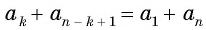 заменим каждую сумму в скобках на
заменим каждую сумму в скобках на 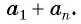
Число всех таких пар сумм равно 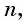 значит, удвоенная искомая сумма равна:
значит, удвоенная искомая сумма равна:
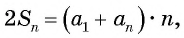 т. е.
т. е. 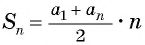 — формула суммы
— формула суммы 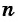 первых членов арифметической прогрессии.
первых членов арифметической прогрессии.
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 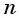 первых членов арифметической прогрессии можно записать и в другом виде. Для этого по формуле
первых членов арифметической прогрессии можно записать и в другом виде. Для этого по формуле 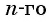 члена арифметической прогрессии выразим
члена арифметической прогрессии выразим 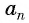 через
через 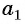 и
и 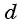 и получим:
и получим:
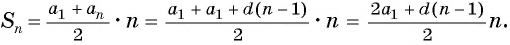
Если известен первый член прогрессии и разность, то удобно использовать формулу 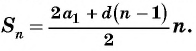
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 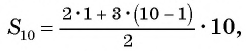
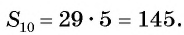 Каждый из друзей выучил по 145 новых слов.
Каждый из друзей выучил по 145 новых слов.

Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 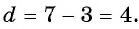 Применим формулу суммы
Применим формулу суммы
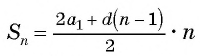
для и получим:
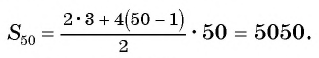
Ответ: 5050.
Пример №19
В арифметической прогрессии 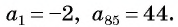 Найдите сумму 85 первых членов арифметической прогрессии.
Найдите сумму 85 первых членов арифметической прогрессии.
Решение:
Применим формулу суммы 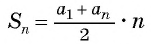 и получим:
и получим: 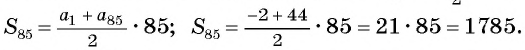
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
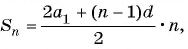
так как 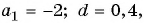 то
то 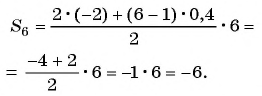
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 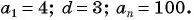 По формуле
По формуле 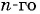 члена арифметической прогрессии
члена арифметической прогрессии 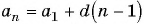 найдем количество членов этой прогрессии:
найдем количество членов этой прогрессии: 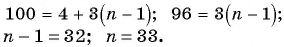
Воспользуемся формулой суммы 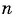 первых членов арифметической прогрессии
первых членов арифметической прогрессии 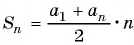 п и найдем искомую сумму:
п и найдем искомую сумму: 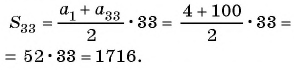
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 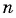 первых членов арифметической прогрессии
первых членов арифметической прогрессии 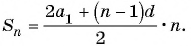 Так как
Так как 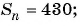
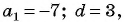 ,то составим и решим уравнение:
,то составим и решим уравнение:
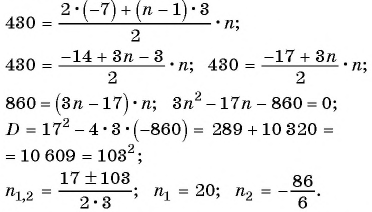
Так как 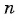 — натуральное число, то
— натуральное число, то 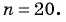
Пример №23
В арифметической прогрессии 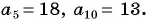 Найдите сумму членов этой прогрессии с четвертого по семнадцатый включительно.
Найдите сумму членов этой прогрессии с четвертого по семнадцатый включительно.
Решение:
Найдем 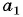 и
и 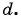 Поскольку
Поскольку 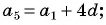
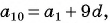 то составим систему уравнений
то составим систему уравнений
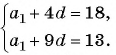
Решим полученную систему способом сложения:
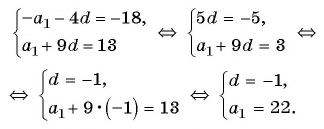
Тогда 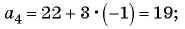
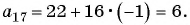
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 – 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна: 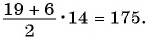
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 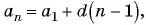
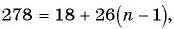 откуда
откуда 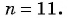
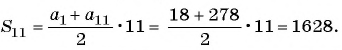
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 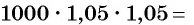
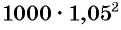 (р.), через три года —
(р.), через три года — 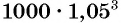 (р.) и т. д. Получим числовую последовательность:
(р.) и т. д. Получим числовую последовательность: 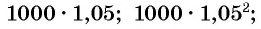
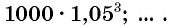
Через шесть лет сумма будет равна 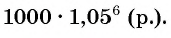
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
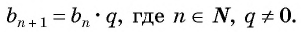
Число 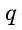 называется знаменателем геометрической прогрессии.
называется знаменателем геометрической прогрессии.
Из равенства 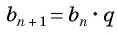 следует, что
следует, что 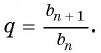
Чтобы задать геометрическую прогрессию 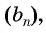 достаточно задать ее первый член
достаточно задать ее первый член 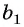 , и знаменатель
, и знаменатель 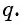
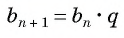
Например, если 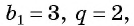 то получится геометрическая прогрессия 3; 6; 12; 24; … .
то получится геометрическая прогрессия 3; 6; 12; 24; … .
Если 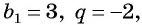 то получится геометрическая прогрессия, знаки членов у которой чередуются, так как знаменатель прогрессии является отрицательным числом: 3; -6; 12; -24; … .
то получится геометрическая прогрессия, знаки членов у которой чередуются, так как знаменатель прогрессии является отрицательным числом: 3; -6; 12; -24; … .
Если 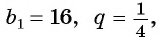 то геометрическая прогрессия имеет
то геометрическая прогрессия имеет
вид 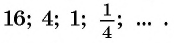
Если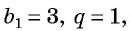 то все члены геометрической прогрессии равны между собой: 3; 3; 3; 3; … .
то все члены геометрической прогрессии равны между собой: 3; 3; 3; 3; … .
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 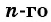 члена геометрической прогрессии
члена геометрической прогрессии
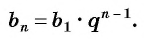
Выведем эту формулу. Если 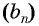 — геометрическая прогрессия и
— геометрическая прогрессия и 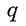 — ее знаменатель, то по определению верны равенства:
— ее знаменатель, то по определению верны равенства:
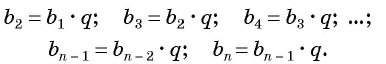
Перемножим эти равенства между собой:
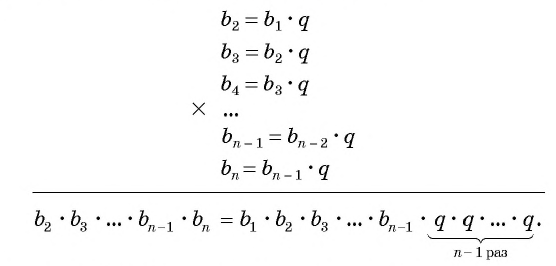
Разделим обе части равенства на произведение 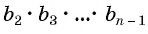 и получим
и получим 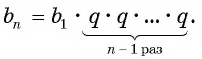
Так как число множителей 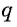 равно
равно 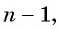 то равенство примет вид
то равенство примет вид
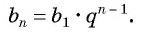
Получили формулу 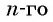 члена геометрической прогрессии.
члена геометрической прогрессии.
Формула 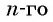 члена геометрической прогрессии
члена геометрической прогрессии 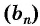 позволяет вычислить любой член прогрессии, зная ее первый член, номер члена и знаменатель прогрессии.
позволяет вычислить любой член прогрессии, зная ее первый член, номер члена и знаменатель прогрессии.
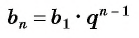
Пример №25
Последовательность 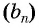 — геометрическая прогрессия,
— геометрическая прогрессия, 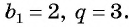 Найдите 8-й член прогрессии.
Найдите 8-й член прогрессии.
Решение:
По формуле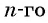 члена получим:
члена получим:
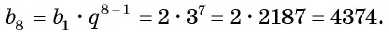
Ответ: 4374.
Пример №26
Последовательность 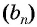 — геометрическая прогрессия,
— геометрическая прогрессия, 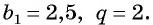 Является ли число 320 членом этой прогрессии?
Является ли число 320 членом этой прогрессии?
Решение:
По условию 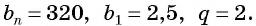 Подставим эти значения в формулу
Подставим эти значения в формулу 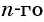 члена
члена 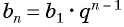 и получим уравнение
и получим уравнение 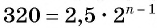
Решим это уравнение: 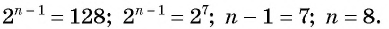
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 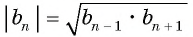 при
при 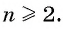
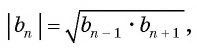
или 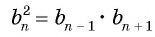 при
при 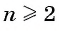
Доказательство:
В геометрической прогрессии 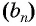 для члена
для члена 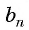 запишем по формуле
запишем по формуле 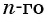 члена предыдущий и последующий (соседние) члены, т. е.
члена предыдущий и последующий (соседние) члены, т. е. 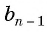 и
и 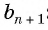 :
:
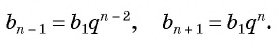
Найдем среднее пропорциональное (среднее геометрическое) соседних с 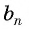 членов геометрической прогрессии. Для этого перемножим равенства
членов геометрической прогрессии. Для этого перемножим равенства 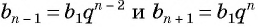 и получим:
и получим:
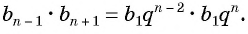
Выполним преобразования в правой части равенства:
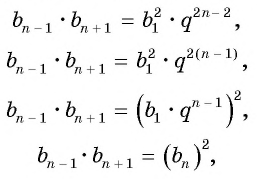
откуда получим, что
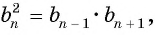 или
или 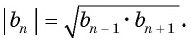
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности  модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов, т. е.
модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов, т. е. 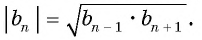 .
.
Тогда 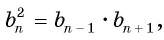 значит,
значит, 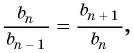 т. е. частное от деления каждого члена последовательности на предшествующий ему член есть одно и то же число, отличное от нуля. Обозначим его
т. е. частное от деления каждого члена последовательности на предшествующий ему член есть одно и то же число, отличное от нуля. Обозначим его 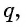 получим
получим 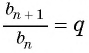 при любом натуральном
при любом натуральном 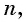 следовательно,
следовательно, 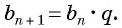 Значит, по определению последовательность
Значит, по определению последовательность 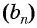 — геометрическая прогрессия.
— геометрическая прогрессия.
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
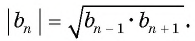
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой 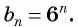
Решение:
Запишем для 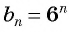 предыдущий и последующий члены последовательности:
предыдущий и последующий члены последовательности:
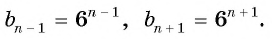
Найдем среднее пропорциональное этих членов:
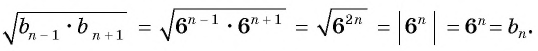
По характеристическому свойству геометрической прогрессии последовательность 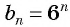 является геометрической прогрессией.
является геометрической прогрессией.
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 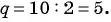 Тогда каждый следующий член равен предыдущему, умноженному на число 5: 2; 10; 50; 250; 1250; 6250; ….
Тогда каждый следующий член равен предыдущему, умноженному на число 5: 2; 10; 50; 250; 1250; 6250; ….
Пример №29
Известны члены геометрической прогрессии: 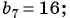
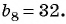
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то 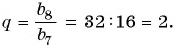
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 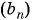 — геометрическая прогрессия. Найдите пятый член этой прогрессии, если
— геометрическая прогрессия. Найдите пятый член этой прогрессии, если 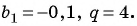
Решение:
По формуле 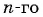 члена геометрической прогрессии
члена геометрической прогрессии 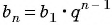 получим:
получим:
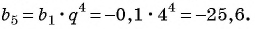
Пример №31
Запишите формулу 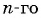 члена для геометрической прогрессии -216; 36; -6; … и найдите ее седьмой член.
члена для геометрической прогрессии -216; 36; -6; … и найдите ее седьмой член.
Решение:
По условию 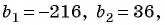 тогда
тогда 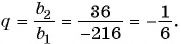 Запишем формулу
Запишем формулу 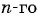 члена данной геометрической прогрессии, подставив в формулу
члена данной геометрической прогрессии, подставив в формулу 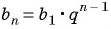 значения для
значения для 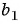 и
и 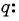
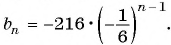
Подставим 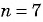 в формулу
в формулу 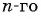 члена данной геометрической прогрессии и найдем ее седьмой член:
члена данной геометрической прогрессии и найдем ее седьмой член:
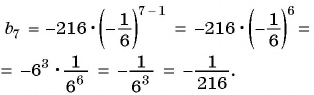
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
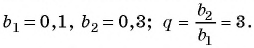
Известно, что 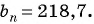 По формуле
По формуле 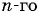 члена геометрической прогрессии
члена геометрической прогрессии 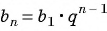 получим:
получим:
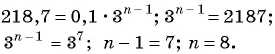
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 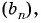 если
если 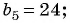
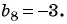
Решение:
По условию 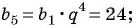
Составим систему уравнений
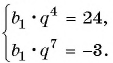
Разделим второе уравнение на первое и получим: 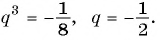
Подставим это значение 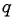 в первое уравнение системы и получим
в первое уравнение системы и получим 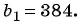
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 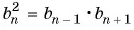 и получим
и получим 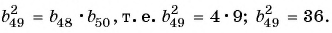 Тогда
Тогда 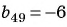 или
или 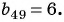
Пример №35
При каком значении 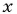 последовательность
последовательность 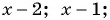
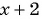 является геометрической прогрессией?
является геометрической прогрессией?
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
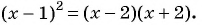
Решим полученное уравнение: 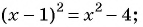
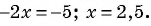
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).

Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 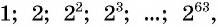 т. е.
т. е. 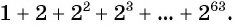
Выведем формулу, по которой можно находить сумму 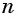 первых членов геометрической прогрессии.
первых членов геометрической прогрессии.
Обозначим сумму 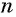 первых членов геометрической прогрессии
первых членов геометрической прогрессии 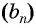 через
через 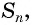 тогда:
тогда:
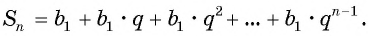
Умножим обе части этого равенства на знаменатель прогрессии 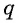 и получим:
и получим:
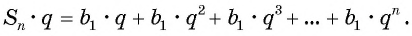
Вычтем из второго равенства первое и получим:
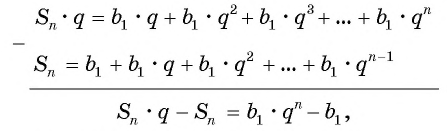
т. e. 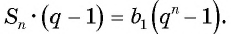 Выразим из этого равенства
Выразим из этого равенства 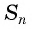 при
при 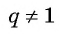 и получим формулу суммы
и получим формулу суммы 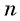 первых членов геометрической прогрессии
первых членов геометрической прогрессии 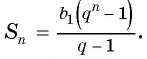
Если 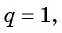 то все члены прогрессии равны первому члену, и сумму
то все члены прогрессии равны первому члену, и сумму 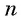 первых прогрессии членов такой геометрической прогрессии можно найти по формуле
первых прогрессии членов такой геометрической прогрессии можно найти по формуле 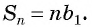
Формула суммы n первых членов геометрической прогрессии:
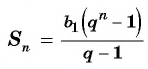
Вычислим по формуле суммы 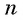 первых членов геометрической прогрессии число зерен, которое запросил в награду мудрец, т. е. сумму
первых членов геометрической прогрессии число зерен, которое запросил в награду мудрец, т. е. сумму
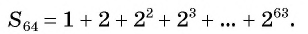
Первый член геометрической прогрессии 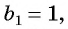 знаменатель
знаменатель 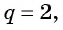 количество членов прогрессии равно 64.
количество членов прогрессии равно 64.
Тогда 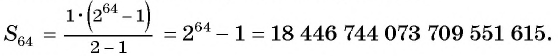
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 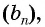 в которой
в которой 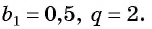
Решение:
Применим формулу суммы 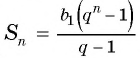 для
для
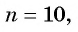 получим
получим 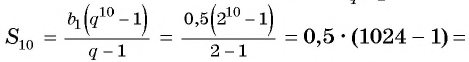
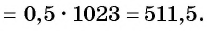
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 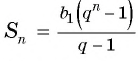 значения
значения 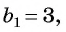
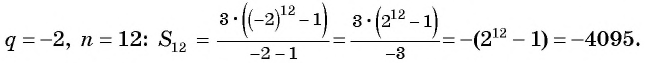
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 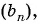 если
если
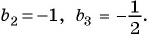
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
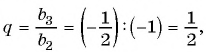 тогда
тогда 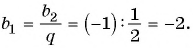
По формуле 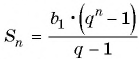 найдем
найдем
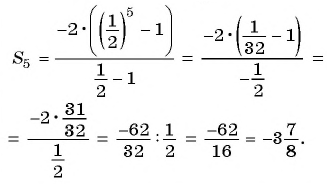
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если 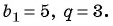
Решение:
Подставим в формулу 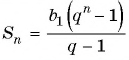 значения
значения 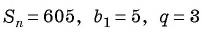 и найдем
и найдем 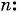
Пример №40
В геометрической прогрессии 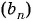 известно, что
известно, что  Найдите
Найдите 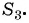
Решение:
Найдем знаменатель прогрессии:
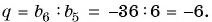
Подставим в формулу 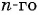 члена геометрической прогрессии
члена геометрической прогрессии 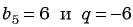 и найдем первый член прогрессии:
и найдем первый член прогрессии:
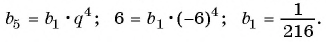
По формуле 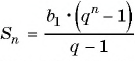 найдем сумму трех первых членов геометрической прогрессии:
найдем сумму трех первых членов геометрической прогрессии: 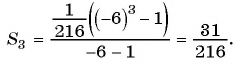
Пример №41
В геометрической прогрессии  известно, что
известно, что 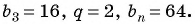 Найдите сумму п первых членов этой прогрессии.
Найдите сумму п первых членов этой прогрессии.
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 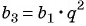 найдем первый член прогрессии:
найдем первый член прогрессии: 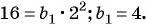 Воспользуемся формулой
Воспользуемся формулой 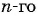 члена геометрической прогрессии
члена геометрической прогрессии 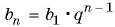 и найдем
и найдем 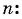
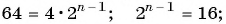
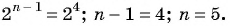
По формуле суммы 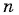 первых членов геометрической прогрессии найдем
первых членов геометрической прогрессии найдем 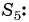
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 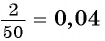 — конечная десятичная дробь. Бесконечная периодическая десятичная дробь получается в случае, когда деление «не заканчивается», например
— конечная десятичная дробь. Бесконечная периодическая десятичная дробь получается в случае, когда деление «не заканчивается», например 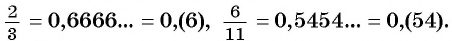
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 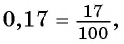
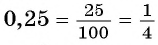 ит. п.).
ит. п.).
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
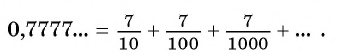
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 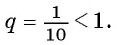 Такие геометрические прогрессии называются бесконечно убывающими геометрическими прогрессиями.
Такие геометрические прогрессии называются бесконечно убывающими геометрическими прогрессиями.
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель 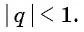
Например, геометрическая прогрессия 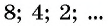 является бесконечно убывающей геометрической прогрессий, так как
является бесконечно убывающей геометрической прогрессий, так как 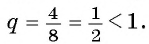
Геометрическая прогрессия 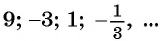 также является бесконечно убывающей геометрической прогрессией, поскольку
также является бесконечно убывающей геометрической прогрессией, поскольку 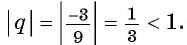
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 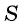 и находят по формуле
и находят по формуле
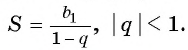
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 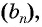 у которой
у которой 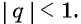 Сумма
Сумма 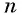 первых членов данной прогрессии
первых членов данной прогрессии 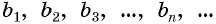 вычисляется по формуле
вычисляется по формуле 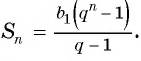 Запишем эту формулу в виде
Запишем эту формулу в виде
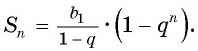
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 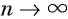 ). Поскольку
). Поскольку 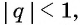 то при неограниченном увеличении числа
то при неограниченном увеличении числа 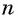 степень
степень 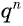 стремится к нулю, а значение разности
стремится к нулю, а значение разности 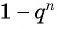 стремится к единице. Значит, при неограниченном увеличении числа
стремится к единице. Значит, при неограниченном увеличении числа 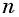 сумма
сумма 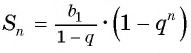 стремится к числу
стремится к числу 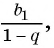 что можно записать в виде
что можно записать в виде 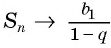 при
при 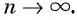
Число 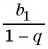 называют суммой бесконечно убывающей геометрической прогрессии
называют суммой бесконечно убывающей геометрической прогрессии 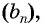 у которой
у которой 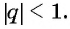 Таким образом,
Таким образом,
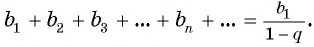
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 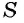 и получим формулу:
и получим формулу: 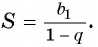
Вычислим по этой формуле сумму разрядных слагаемых:
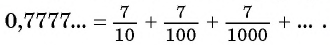
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 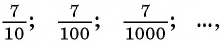 первый член которой равен
первый член которой равен 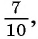
а знаменатель равен 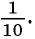
Сумма бесконечно убывающей геометрической прогрессии:
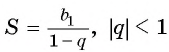
Так как 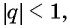 то можем найти сумму этой бесконечной прогрессии. Подставим
то можем найти сумму этой бесконечной прогрессии. Подставим 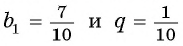 в формулу
в формулу 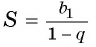 и получим:
и получим: 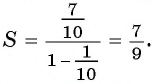
Значит, 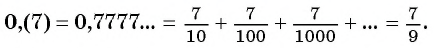
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 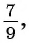 , т. е.
, т. е. 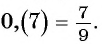
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
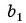 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии 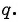
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
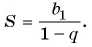
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число 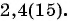
(1) 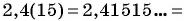
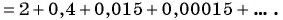
(2) 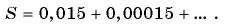
(3) 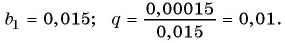
(4) 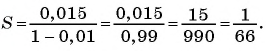
(5) 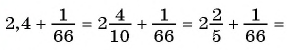
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 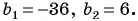 Является ли эта прогрессия бесконечно убывающей геометрической прогрессией?
Является ли эта прогрессия бесконечно убывающей геометрической прогрессией?
Решение:
Найдем знаменатель прогрессии: 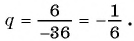 Так как
Так как 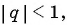 то данная прогрессия является бесконечно убывающей геометрической прогрессией.
то данная прогрессия является бесконечно убывающей геометрической прогрессией.
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а) 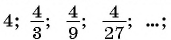
б) 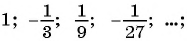
в) 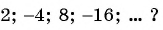
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 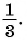 Так как
Так как 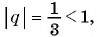 то прогрессия является бесконечно убывающей геометрической прогрессией.
то прогрессия является бесконечно убывающей геометрической прогрессией.
б) Поскольку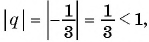 , то прогрессия является бесконечно убывающей геометрической прогрессией.
, то прогрессия является бесконечно убывающей геометрической прогрессией.
в) Знаменатель прогрессии 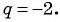 Так-как
Так-как 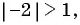 то прогрессия не является бесконечно убывающей геометрической прогрессией.
то прогрессия не является бесконечно убывающей геометрической прогрессией.
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 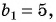
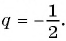
Решение:
По формуле 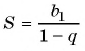 получим:
получим: 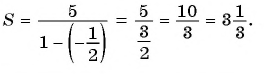
Пример №45
В бесконечно убывающей геометрической прогрессии 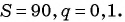 Найдите первый член этой прогрессии.
Найдите первый член этой прогрессии.
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 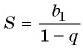 подставим
подставим 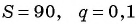 и получим
и получим 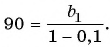 Решим полученное уравнение:
Решим полученное уравнение:
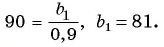
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1) 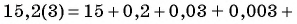
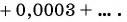
(2) 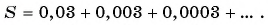
(3) 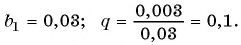
(4) 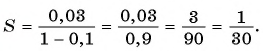
(5) 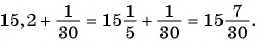
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
