Примеры решения задач
Пример 1. Генератор постоянного тока параллельного возбуждении имеет номинальную
мощность P
2
=10 кВт; номинальное напряжение U = 230 В; частоту вращения n =1450 об/мин;
сопротивление обмоток цепи обмотки возбуждения R
В
=150 Ом; сопротивление обмоток
якоря R
Я
= 0,3 Ом; КПД в номинальном режиме η = 86,5 %. Падением напряжения в
щеточном контакте пренебречь.
Определить: ток генератора, ток в цепи возбуждения, ток в цепи якоря, ЭДС якоря, электро–
магнитный момент, электромагнитная мощность, мощность приводного двигателя.
Генератор работает при номинальной нагрузке.
Решение:
Ток генератора:
Ток в обмотке возбуждения: I
В
=
Ток в цепи якоря: I
Я
= I + I
В
= 43,5 +1,5 = 45А.
ЭДС якоря: E =U + I
Я
R
Я
= 230 + 45 0,3 = 243,5 В.
Электромагнитная мощность: P
эм
= E I
Я
= 243,5 45 =10957 Вт .
Электромагнитный момент: M
эм
= 9,55
Мощность приводного двигателя: P
1
=
Пример 2. В генераторе постоянного тока независимого возбуждения с номинальным
напряжением U = 440 В установился ток I = 64 А при частоте якоря n = 2800 об/мин. В новом
режиме работы нагрузка и магнитный поток не изменились, но частота якоря стала
n* = 740 об/мин.
Определить напряжение и ток в генераторе в новом режиме.
Решение:
В генераторе независимого возбуждения ток генератора равен току якоря, т.е. I = I
Я
.
В номинальном режиме:
Напряжение на нагрузке U = I R
Н
.
ЭДС якоря E =U + I R
Я
= I R
Н
+ I R
Я
, с другой стороны E = С
Е
п Ф.
Получили: I R
Н
+ I R
Я
= С
Е
п Ф.
В новом режиме, соответственно:
E* =U* + I* R
Я
= I* Rн + I* R
Я
= С
Е
п* Ф.
Возьмем отношение, полученных уравнений и получим:
I*=
A и
U* =
B
Пример 3. В электродвигателе постоянного тока с параллельным возбуждением, имеющим
номинальные данные: мощность на валу P
2
=130 кВт ; напряжение U = 220 В; ток,
потребляемый из сети I = 640 А; частоту вращения n = 600 об/мин; сопротивление цепи
обмотки возбуждения R
В
= 43 Ом; сопротивление обмотки якоря R
Я
= 0,007 Ом.
Определить номинальные суммарные и электрические потери в обмотках.
Решение:
Ток в обмотке возбуждения: I
В
=
Ток в цепи якоря: I
Я
= I − I
В
= 640-5,116 = 634,884 A.
Электрические потери мощности
в цепи якоря: ΔP
эл
Я
= I
Я
2
R
Я
= 634,884
2
0,007 = 2821,544 Вт;
в обмотке возбуждения:
ΔP
эл B
= I
B
2
R
B
=U I
B
= 220 5,116=1125,52 Вт .
Суммарные потери мощности:
ΣΔP = ΔP
эл B
+ ΔP
эл Я
=1125,52 + 2821,544 = 3947,064 Вт .
Расчетные формулы параметров машин постоянного тока
В таблице 1 представлены расчетные формулы для определения основных параметров машин постоянного тока.
В данной таблице собраны все формулы, которые касаются расчета параметров машин постоянного тока.
Таблица 1 — Расчетные формулы для определения основных параметров машин постоянного тока
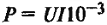
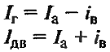
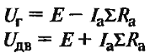
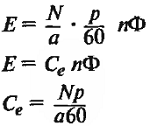
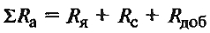
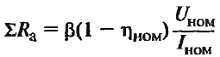
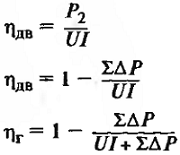
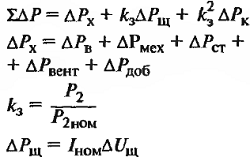
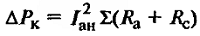
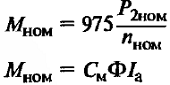
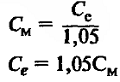
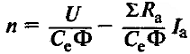
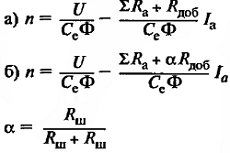
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Мощность, кВт | N – число проводников обмотки якоря; а – число пар параллельных ветвей в обмотке якоря; р – число пар полюсов; n – скорость вращения, об/мин. |
|
| Сопротивление якорной цепи, Ом | Ф – магнитный поток пары полюсов, вебер; Rя, Rс, Rдоб. – сопротивления обмотки якоря, последовательной обмотки возбуждения и добавочных полюсов, Ом |
|
| Ориентировочной значение сопротивления цепи якоря, Ом | Значение коэффициента β двигателей различного типа возбуждения: для независимого и параллельного возбуждения β=0,5; для смешанного β=0,6; для последовательного β=0,75; |
|
| КПД двигателя и генератора | ∆Рх – потери холостого хода машины или постоянные потер, кВт; ∆Рв – потери на возбуждение, кВт; ∆Рмех. – механические потери на трение в подшипниках и о коллектор, кВт; ∆Рст. – магнитные потери в стали якоря, кВт; ∆Рвент. – вентиляционные потери, кВт; ∆Рдоб. – добавочные потери. В некомпенсированных машинах ∆Рдоб. = 1%Рном, в компенсированных 0,5%, кВт; kз – коэффициент загрузки; ∆Uщ = 2 В для графитных щеток; ∆Uщ = 0,6 В для металлографитных; |
|
| Переменные потери | См – конструктивная постоянная момента; Ф – магнитный поток, вебер; |
|
| Расчетные коэффициенты для двигателя параллельного возбуждения | а) искусственная скоростная характеристика при введении добавочного сопротивления Rдоб. последовательно в цепь якоря; б) искусственная скоростная характеристика двигателя при шунтировании якоря двигателя сопротивлением Rш; α – коэффициент шунтирования. |
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Поделиться в социальных сетях
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «PayPal» .
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.

В данной статье будет рассматриваться пример расчета реактивной мощности асинхронного.

Для питания потребителей постоянного тока, требуется выбрать внешнюю аккумуляторную батарею, для.

В данной статье будет рассматриваться изменение напряжения (потеря напряжения) при пуске асинхронного.
В данном примере требуется выбрать сечение проводов (по нагреву, по току и по потере напряжения) для.

Требуется определить потери активной и реактивной мощности в автотрансформаторе типа АТДЦТН-125000/220/110.
Отправляя сообщение, Вы разрешаете сбор и обработку персональных данных.
Политика конфиденциальности.
Источник
Мощность постоянного тока
 Мощность – это работа, произведенная за единицу времени. Электрическая мощность равна произведению тока на напряжение: P=U∙I. Отсюда можно вывести другие формулы для мощности:
Мощность – это работа, произведенная за единицу времени. Электрическая мощность равна произведению тока на напряжение: P=U∙I. Отсюда можно вывести другие формулы для мощности:
Единицу измерения мощности получим, подставив в формулу единицы измерения напряжения и тока:
Единица измерения электрической мощности, равная 1 ВА, называется ватом (Вт). Название вольт-ампер (ВА) используется в технике переменного тока, но только для измерения полной и реактивной мощности.
Единицы измерения электрической и механической мощности связаны следующими соотношениями:
1 Вт =1/9,81 кГ•м/сек ≈1/10 кГ•м/сек;
Если не учитывать неизбежных потерь энергии, то двигатель мощностью 1 кВт может перекачивать каждую секунду 102 л воды на высоту 1 м или 10,2 л воды на высоту 10 м.
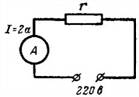
1. Нагревательный элемент электрической печи на мощность 500 Вт и напряжение 220 В выполнен из проволоки высокого сопротивления. Рассчитать сопротивление элемента и ток, который через него проходит (рис. 1).
Ток найдем по формуле электрической мощности P=U∙I,
откуда I=P/U=(500 Bm)/(220 B)=2,27 A.
Сопротивление рассчитывается по другой формуле мощности: P=U^2/r,
откуда r=U^2/P=(220^2)/500=48400/500=96,8 Ом.
2. Какое сопротивление должна иметь спираль (рис. 2) плитки при токе 3 А и мощности 500 Вт?
Для этого случая применим другую формулу мощности: P=U∙I=r∙I∙I=r∙I^2;
отсюда r=P/I^2 =500/3^2 =500/9=55,5 Ом.
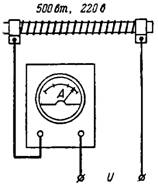
3. Какая мощность превращается в тепло при сопротивлении r=100 Ом, которое подключено к сети напряжением U=220 В (рис. 3)?
4. В схеме на рис. 4 амперметр показывает ток I=2 А. Подсчитать сопротивление потребителя и электрическую мощность, расходуемую в сопротивлении r=100 Ом при включении его в сеть напряжением U=220 В.
P=U∙I=220∙2=440 Вт, или P=U^2/r=220^2/110=48400/110=440 Вт.
5. На лампе указано лишь ее номинальное напряжение 24 В. Для определения остальных данных лампы соберем схему, показанную на рис. 5. Отрегулируем реостатом ток так, чтобы вольтметр, подключенный к зажимам лампы, показывал напряжение Uл=24 В. Амперметр при этом показывает ток I=1,46 А. Какие мощность и сопротивление имеет лампа и какие потери напряжения и мощности возникают на реостате?
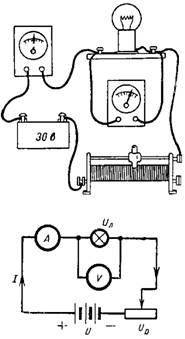
Мощность лампы P=Uл∙I=24∙1,46=35 Вт.
Ее сопротивление rл=Uл/I=24/1,46=16,4 Ом.
Падение напряжения на реостате Uр=U-Uл=30-24=6 В.
Потери мощности в реостате Pр=Uр∙I=6∙1,46=8,76 Вт.
6. На щитке электрической печи указаны ее номинальные данные (P=10 кВт; U=220 В).
Определить, какое сопротивление представляет собой печь и какой ток проходит через нее при работе P=U∙I=U^2/r;
r=U^2/P=220^2/10000=48400/10000=4,84 Ом; I=P/U=10000/220=45,45 А.

7. Каково напряжение U на зажимах генератора, если при токе 110 А его мощность равна 12 кВт (рис. 7)?
Так как P=U∙I, то U=P/I=12000/110=109 В.
8. На схеме на рис. 8 показана работа электромагнитной токовой защиты. При определенном токе электромагнит ЭМ, который удерживается пружиной П, притянет якорь, разомкнет контакт К и разорвет цепь тока. В нашем примере токовая защита разрывает токовую цепь при токе I≥2 А. Сколько ламп по 25 Вт может быть одновременно включено при напряжении сети U=220 В, чтобы ограничитель не сработал?
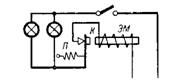
Защита срабатывает при I=2 А, т. е. при мощности P=U∙I=220∙2=440 Вт.
Разделив общую мощность одной лампы, получим: 440/25=17,6.
Одновременно могут гореть 17 ламп.
9. Электрическая печь имеет три нагревательных элемента на мощность 500 Вт и напряжение 220 В, соединенных параллельно.
Каковы общее сопротивление, ток и мощность при работе печи (рис.91)?
Общая мощность печи P=3∙500 Вт =1,5 кВт.
Результирующий ток I=P/U=1500/220=6,82 А.
Результирующее сопротивление r=U/I=220/6,82=32,2 Ом.
Ток одного элемента I1=500/220=2,27 А.
Сопротивление одного элемента: r1=220/2,27=96,9 Ом.
10. Подсчитать сопротивление и ток потребителя, если ваттметр показывает мощность 75 Вт при напряжении сети U=220 В (рис.10).
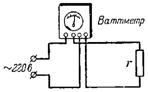
Так как P=U^2/r, то r=U^2/P=48400/75=645,3 Ом.
11. Плотина имеет перепад уровней воды h=4 м. Каждую секунду через трубопровод на турбину попадает 51 л воды. Какая механическая мощность превращается в генераторе в электрическую, если не учитывать потерь (рис. 11)?
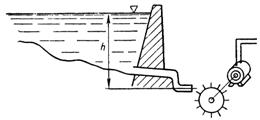
Механическая мощность Pм=Q∙h=51 кГ/сек ∙4 м =204 кГ•м/сек.
Отсюда электрическая мощность Pэ=Pм:102=204:102=2 кВт.
12. Какую мощность должен иметь двигатель насоса, перекачивающего каждую секунду 25,5 л воды с глубины 5 м в резервуар, расположенный на высоте З м? Потери не учитываются (рис. 12).
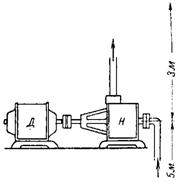
Общая высота подъема воды h=5+3=8 м.
Механическая мощность двигателя Pм=Q∙h=25,5∙8=204 кГ•м/сек.
Электрическая мощность Pэ=Pм:102=204:102=2 кВт.
13. Гидроэлектростанция получает из водохранилища на одну турбину каждую секунду 4 м3 воды. Разница между уровнями воды в водохранилище и турбине h=20 м. Определить мощность одной турбины без учета потерь (рис. 13).
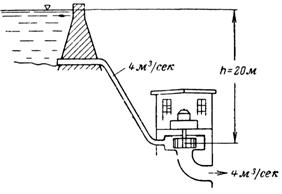
Механическая мощность протекающей воды Pм=Q∙h=4∙20=80 т/сек•м; Pм=80000 кГ•м/сек.
Электрическая мощность одной турбины Pэ=Pм:102=80000:102=784 кВт.
14. У двигателя постоянного тока с параллельным возбуждением обмотка якоря и обмотка возбуждения соединены параллельно. Обмотка якоря имеет сопротивление r=0,1 Ом, а ток якоря I=20 А. Обмотка возбуждения имеет сопротивление rв=25 Ом, а ток возбуждения равен Iв=1,2 А. Какая мощность теряется в обеих обмотках двигателя (рис. 14)?
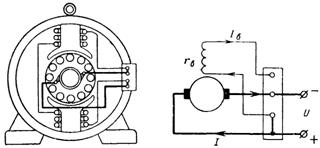
Потери мощности в обмотке якоря P=r∙I^2=0,1∙20^2=40 Вт.
Потери мощности в обмотке возбуждения
Общие потери в обмотках двигателя P+Pв=40+36=76 Вт.
15. Электроплитка на напряжение 220 В имеет четыре переключаемые ступени нагрева, что достигается путем различных включений двух нагревательных элементов с сопротивлениями r1 и r2, как это показано на рис. 15.
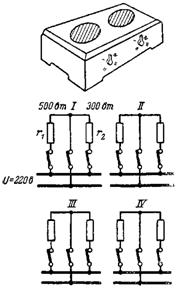
Определить сопротивления r1 и r2, если первый нагревательный элемент имеет мощность 500 Вт, а второй 300 Вт.
Так как мощность, выделяемая в сопротивлении, выражается формулой P=U∙I=U^2/r, то сопротивление первого нагревательного элемента
а второго нагревательного элемента r2=U^2/P2 =220^2/300=48400/300=161,3 Ом.
В положении ступени IV сопротивления соединяются последовательно. Мощность электроплитки в этом положении равна:
P3=U^2/(r1+r2 )=220^2/(96,8+161,3)=48400/258,1=187,5 Вт.
В положении ступени I нагревательные элементы соединены параллельно и результирующее сопротивление равно: r=(r1∙r2)/(r1+r2)=(96,8∙161,3)/(96,8+161,3)=60,4 Ом.
Мощность плитки в положении ступени I: P1=U^2/r=48400/60,4=800 Вт.
Эту же мощность получим, сложив мощности отдельных нагревательных элементов.
16. Лампа с вольфрамовой нитью рассчитана на мощность 40 Вт и напряжение 220 В. Какие сопротивление и ток имеет лампа в холодном состоянии и при рабочей температуре 2500 °С?
Отсюда сопротивление нити лампы в горячем состоянии rt=U^2/P=220^2/40=1210 Ом.
Сопротивление холодной нити (при 20 °С) определим по формуле rt=r∙(1+α∙∆t),
откуда r=rt/(1+α∙∆t)=1210/(1+0,004∙(2500-20) )=1210/10,92=118 Ом.
Через нить лампы в горячем состоянии проходит ток I=P/U=40/220=0,18 А.
Ток при включении равен: I=U/r=220/118=1,86 А.
При включении ток примерно в 10 раз больше, чем ток горячей лампы.
17. Каковы потери напряжения и мощности в медном контактном проводе электрифицированной железной дороги (рис. 16)?
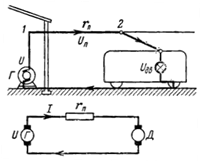
Провод имеет сечение 95 мм2. Двигатель электропоезда потребляет ток 300 А на расстоянии 1,5 км от источника тока.
Потеря (падение) напряжения в линии между точками 1 и 2 Uп=I∙rп.
Сопротивление контактного провода rп=(ρ∙l)/S=0,0178∙1500/95=0,281 Ом.
Падение напряжения в контактном проводе Uп=300∙0,281=84,3 В.
Напряжение Uд на зажимах двигателя Д будет на 84,3 В меньше, чем напряжение U на зажимах источника Г.
Падение напряжения в контактном проводе во время движения электропоезда меняется. Чем дальше электропоезд удаляется от источника тока, тем длиннее линия, а значит, больше ее сопротивление и падение напряжения в ней. Ток по рельсам возвращается к заземленному источнику Г. Сопротивление рельсов и земли практически равно нулю.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
6.1. Расчет генератора постоянного тока с параллельным возбуждением
Для
расчета генератора постоянного тока
с параллельным
возбуждением необходимо:
усвоить
устройство и принцип действия
электрических машин постоянного
тока; знать формулы,
выражающие взаимосвязь между
электрическими величинами, характеризующими
данный тип электрической машины.
–
отчетливо представлять связь между
напряжением U
на зажимах машины, ЭДС Е
и падением напряжения IR
в
обмотке якоря генератора и двигателя.
Для
генератора Е
=U+
IЯ·
∑R,
для
двигателя U
= Е + IЯ·
∑R
В этих
формулах ∑R=
RЯ+
RДП
+
RКО
+
RС
+
RЩ
– сумма сопротивлений всех участков
цепи якоря: RЯ
– обмотки якоря;
RДП
– обмотки добавочных полюсов; RКО
– компенсационной обмотки;
RЩ
– переходного щеточного контакта;
RС
– последовательной
обмотки возбуждения.
При
отсутствии в машине (это зависит от её
типа и предложенной задачи) каких-либо
из указанных обмоток в формулу,
определяющую ∑R,
не входят соответствующие слагаемые.
Полезный
вращающий момент М
на валу двигателя определяется по
формуле
M
=![]() Н·м,
Н·м,
где
Р2
–
полезная механическая мощность,
Вт.
n
– об/мин.
– частота вращения вала двигателя.
Пример
Генератор
постоянного тока с параллельным
возбуждением работает в номинальном
режиме.
Его технические
данные:
РНОМ
=16000Вт – номинальная мощность;
Uном
=230 В – номинальное напряжение;
RЯ=0,13
Ом – сопротивление обмотки якоря;
RВ=164
Ом – сопротивление обмотки возбуждения;
ηНОМ
= 90,1
%
номинальный коэффициент полезного
действия.
Определить:
Iном
– ток нагрузки, I
B
– ток возбуждения,
I
Я
–
ток якоря,
РЯ
–
потери мощности в якоре,
РВ
–
потери мощности в обмотке возбуждения,
РЩ
– потери мощности в щеточном контакте,
РХ
=
РСТ
+РМЕХ
– потери холостого хода, состоящие из
потерь в стали и механических потерь.
РДОБ
–
добавочные потери,
∑P
–
суммарные потери мощности,
Е
– ЭДС генератора.
Решение
I.
Ток нагрузки
Iном
= Рном
/
Uном
=16000 Вт / 230 В = 69,6 А
2.
Ток возбуждения IB
=
U
H
0M
/
R
B
= 230 В / I64
Ом = 1,4 А.
3.
Ток якоря
Iя
=
Iном
+ Iв
=69,6
А + 1,4 А = 71 А
4.
Потери мощности в обмотке якоря
Ря
=
I2я
·
Rя
=712
А2
·0,13 Ом = 655
Вт.
5.
Потери мощности в обмотке возбуждения
РВ
= I2В
·
RВ
=1,42
А2
·
164 Ом
= 321 Вт.
6.
Потери мощности в щеточном контакте
Рщ
=
∆ UЩ
·
Iя=2
В • 71 А= 1428 Вт.
Здесь
∆ UЩ
= 2 В –
падение
напряжения на электрографитированных
щетках.
7.
Добавочные потери мощности РДОБ
=
0,01·РНОМ
= 0,01 • 16000 Вт = 160 Вт.
8.
Мощность,
потребляемая генератором от первичного
двигателя
Р1
=
Рном
/ ηНОМ
=
16000 Вт / 0,901 = 17758 Вт
9.
Суммарные потери мощности в генераторе
∑Р
= Р1
–
Рном
= 17758 Вт –16000 Вт = 1758 Вт
10.
Потери холостого хода, состоящие из
потерь в стали и механических потерь
Рх
= ∑Р –
(РЯ+
РВ
+
РЩ+
РДОБ)
=
1758 Вт – (655+321+142+160) Вт = 480 Вт
11.
ЭДС генератора, без учета потерь в
щеточном контакте
Е =
U+
IЯ
·
Rя
= 230 В + 71 А · 0,13 Ом = 239,23 В
С
учетом потерь в щеточном контакте
Е =U+
IЯ
· (Rя
+ Rщ)=
U
+(Iя
· Rя
+∆ UЩ)
=230 В+(71 0,13
Ом +2 В) = 241,23 В
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ПРАКТИЧЕСКАЯ РАБОТА №11
«Расчет параметров генераторов постоянного тока»
ЦЕЛЬ РАБОТЫ: рассчитать ток генератора в
номинальном режиме, ЭДС генератора, номинальное изменение напряжения, ток в
обмотке возбуждения, ток в цепи якоря при номинальной нагрузке.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
В процессе работы генератора постоянного тока в обмотке якоря индуцируется ЭДС ![]() . При
. При
подключении к генератору нагрузки в цепи якоря возникает ток, а на выводах генератора устанавливается напряжение, определяемое уравнением напряжений для цепи якоря генератора:
![]() . (11.1)
. (11.1)
Здесь
![]() (11.2)
(11.2)
—
сумма сопротивлений всех участков цепи якоря: обмотки
якоря ![]() , обмотки добавочных полюсов
, обмотки добавочных полюсов ![]() , компенсационной
, компенсационной
обмотки ![]() , последовательной обмотки
, последовательной обмотки
возбуждения ![]() и переходного щеточного контакта
и переходного щеточного контакта ![]() .
.
При отсутствии в машине
каких-либо из указанных обмоток в (11.2) не входят
соответствующие слагаемые.
Якорь генератора приводится во вращение
приводным двигателем, который создает на валу генератора вращающий момент ![]() . Если генератор работает в режиме х.х.
. Если генератор работает в режиме х.х. ![]() , то
, то
для вращения его якоря нужен
сравнительно небольшой момент холостого
хода ![]() . Этот момент обусловлен тормозными моментами, возникающими в генераторе при его работе в режиме х.х.: моментами от сил трения и вихревых токов в якоре.
. Этот момент обусловлен тормозными моментами, возникающими в генераторе при его работе в режиме х.х.: моментами от сил трения и вихревых токов в якоре.
При неизменной частоте
вращения ![]() вращающий момент приводного двигателя
вращающий момент приводного двигателя ![]() уравновешивается суммой противодействующих моментов: моментом
уравновешивается суммой противодействующих моментов: моментом
х.х. ![]() и электромагнитным моментом М, т.
и электромагнитным моментом М, т.
е.
![]() . (11.3)
. (11.3)
Выражение (11.3) — уравнение
моментов для генератора при ![]() . Умножив члены уравнения (11.3) на угловую
. Умножив члены уравнения (11.3) на угловую
скорость вращения якоря ![]() , получим уравнение мощностей:
, получим уравнение мощностей:
![]() , (11.4)
, (11.4)
где ![]() — подводимая от
— подводимая от
приводного двигателя к генератору мощность (механическая); ![]() — мощность х.х., т. е. мощность, подводимая к
— мощность х.х., т. е. мощность, подводимая к
генератору в режиме х.х. (при отключенной нагрузке); ![]() — электромагнитная мощность генератора.
— электромагнитная мощность генератора.
Механическая мощность,
развиваемая приводным
двигателем ![]() , преобразуется в генераторе в полезную электрическую мощность
, преобразуется в генераторе в полезную электрическую мощность ![]() , передаваемую нагрузке, и мощность, затрачиваемую на покрытие потерь
, передаваемую нагрузке, и мощность, затрачиваемую на покрытие потерь![]() .
.
Так как генераторы обычно
работают при неизменной частоте вращения, то их характеристики рассматривают при условии ![]() . Рассмотрим основные характеристики генераторов постоянного тока.
. Рассмотрим основные характеристики генераторов постоянного тока.
Характеристика холостого
хода — зависимость
напряжения на выходе
генератора в режиме х.х. ![]() от тока возбуждения
от тока возбуждения ![]() :
:
![]() при
при ![]() и
и ![]() .
.
Нагрузочная характеристика
— зависимость напряжения на выходе генератора U при работе с нагрузкой от тока возбуждения ![]() :
:
![]() при
при ![]() и
и ![]() .
.
Внешняя характеристика — зависимость напряжения на выходе генератора U
от тока нагрузки ![]() :
:
![]() при
при ![]() и
и ![]() ,
,
где ![]() —
—
регулировочное сопротивление в цепи обмотки возбуждения.
Регулировочная
характеристика —
зависимость тока возбуждения ![]() от тока нагрузки
от тока нагрузки ![]() при неизменном напряжении на выходе генератора:
при неизменном напряжении на выходе генератора:
![]() при
при ![]() и
и ![]() .
.
Вид
перечисленных характеристик определяет рабочие свойства генераторов
постоянного тока.
При
оценке свойств генераторов постоянного тока используется понятие номинального
изменения напряжения на выходе генератора при сбросе нагрузки: ![]() (11.5)
(11.5)
Обычно для генератора независимого возбуждения ![]() .
.
Характеристика ![]() показывает, как следует менять
показывает, как следует менять
ток в цепи возбуждения, чтобы при изменениях нагрузки генератора напряжение на
его выводах оставалось неизменным, равным номинальному. При этом частота вращения сохраняется постоянной ![]() .
.
При работе
генератора без нагрузки в цепи возбуждения устанавливают ток ![]() , при котором напряжение на
, при котором напряжение на
выводах генератора становится равным номинальному.
В генераторе
постоянного тока независимого возбуждения ток в обмотке возбуждения
определяется по формуле: Iв= Uном /rв. (11.6)
Ток в цепи якоря при номинальной нагрузке: Iаном= Iном+ Iв. (11.7)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1.
Решить
задачу №1. Генератор постоянного тока независимого возбуждения мощностью Рном
и напряжением Uном имеет
сопротивление обмоток в цепи якоря, приведенное к рабочей температуре, Σr ; в
генераторе применены электрографитированные щетки марки ЭГ (∆Uщ
=
2,5 В). Определить номинальное изменение напряжения при сбросе нагрузки.
Значения параметров приведены в табл. 11.1.
Таблица 11.1
|
Параметр |
Варианты |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
Рном |
20 |
45 |
15 |
90 |
80 |
30 |
18 |
|
Uном, |
230 |
460 |
230 |
460 |
460 |
230 |
230 |
|
Σr, |
0,12 |
0,22 |
0,15 |
0,12 |
0,11 |
0,08 |
0,13 |
Решение:
– определить ток в номинальном режиме Iаном;
– определить ЭДС генератора Ea,
выразив его из уравнения
напряжений (10.18) ;
–определить
номинальное изменение напряжения при сбросе нагрузки ∆Uном.
2.
Решить
задачу №2. Генератор постоянного тока параллельного возбуждения имеет
номинальные данные: мощность Рном, напряжение Uном, частота
вращения nном,
сопротивление обмоток в цепи якоря, приведенное к рабочей температуре, Σr, падение
напряжения в щеточном контакте пары щеток ∆Uщ
= 2 В, сопротивление цепи обмотки возбуждения
rв, КПД в
номинальном режиме ηном, ток генератора Iном, ток в
цепи возбуждения Iв, ток в
цепи якоря Iаном, ЭДС
якоря Еаном, электромагнитная
мощность Рзм, электромагнитный момент при номинальной нагрузке Мном,
мощность приводного двигателя Р1ном.
Значения перечисленных параметров
приведены в табл. 11.2. Требуется определить значения параметров, не указанных
в таблице.
Таблица 11.2
|
Параметр |
Варианты |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Рном , кВт |
10 |
— |
— |
18 |
45 |
|
Uном, В |
230 |
230 |
460 |
230 |
— |
|
nном , об/мин |
1450 |
— |
— |
1500 |
1000 |
|
Σr , Ом |
0,3 |
0,15 |
— |
— |
— |
|
rв , Ом |
150 |
100 |
— |
— |
92 |
|
ηном , % |
86,5 |
— |
88 |
— |
88 |
|
Iном , А |
— |
87 |
— |
— |
97,8 |
|
Iв ,А |
— |
— |
4 |
— |
— |
|
Iаном ,А |
— |
— |
— |
75 |
— |
|
Еа, В |
— |
— |
480 |
240 |
477 |
|
Рзм.ном, |
— |
— |
55 |
— |
— |
|
Мном, Н•м |
— |
280 |
525 |
— |
— |
|
Р1ном , кВт |
— |
23 |
— |
21 |
— |
3.
Оформить отчет по практической работе.
4.
Ответить на контрольные вопросы.
5.
Сделать вывод о проделанной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что происходит в цепи якоря при подключении
к генератору нагрузки?
2. Чем якорь генератора приводится во вращение и что происходи на валу в
этот момент?
3. Во что в генераторе преобразуется механическая мощность, развиваемая приводным двигателем?
4. Что такое регулировочная характеристика?
5. Что такое нагрузочная характеристика?
Подборка по базе: 2.4 Практическая работа Структурно-ф ункциональное описание.doc, контрольная работа 3.docx, практическая работа 3.docx, Курсовая работа на отправку1.docx, Практическая работа.docx, Практическая работа НТТз-20.doc, Контрольная работа сказки.docx, М.Н. Лукьянов_Лабораторная работа 1.docx, Курсовая работа_Скобцов ПФБ-3-014.docx, ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО АСТРОНОМИИ.docx
ПРАКТИЧЕСКАЯ РАБОТА
«РАСЧЕТ ПАРАМЕТРОВ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА»
Генератор постоянного тока имеет: номинальную мощность P2; номинальное напряжение U; частоту вращения n; номинальный ток генератора I; ток в цепи возбуждения IВ; ток в цепи якоря IЯ; сопротивление обмоток цепи обмотки возбуждения RВ; сопротивление в цепи якоря RЯ , приведенное к рабочей температуре; ЭДС якоря E; электромагнитный момент при номинальной нагрузке Mэм ; электромагнитная мощность Pэм ; мощность приводного двигателя P1; КПД в номинальном режиме η.
Определить: для выбранного варианта значения параметров генератора постоянного тока, не указанные в таблицах 1, 2.
Таблица 1
Параметры генератора
| № | P2
кВт |
U
В |
n
об/мин |
I
А |
IВ
А |
IЯ
А |
RВ ,
Ом |
RЯ
Ом |
| 1 | 24 | 230 | 1450 | – | – | – | 150 | 0,3 |
| 2 | – | 110 | 3000 | – | – | 17 | Нет | 0,55 |
| 3 | – | 220 | 1000 | 15,6 | Нет | – | Нет | 1 |
| 4 | – | 230 | – | 87 | – | – | 100 | 0,15 |
| 5 | – | 110 | 2000 | 25 | – | – | Нет | – |
| 6 | – | 220 | 630 | 80 | Нет | – | Нет | 0,144 |
| 7 | – | 460 | – | – | 4 | – | – | – |
| 8 | – | 110 | 3000 | 95 | – | – | Нет | – |
| 9 | – | 220 | 630 | – | Нет | 80 | Нет | 0,144 |
| 10 | 18 | 230 | 1500 | – | – | 80 | – | – |
| 11 | – | 110 | 3000 | – | – | 21,5 | Нет | – |
| 12 | 220 | 460 | – | Нет | 405 | 5,5 | 0,008 | |
| 13 | 45 | – | 1000 | 97,8 | – | – | 92 | – |
| 14 | – | 110 | 4000 | 260 | – | – | Нет | – |
| 15 | – | 220 | 1000 | – | Нет | 16 | 0,8 | 0,9 |
| 16 | – | 110 | 3600 | – | 1,8 | 34 | – | – |
| 17 | – | 110 | 4000 | – | – | 15 | Нет | – |
| 18 | – | 220 | 1000 | 15,6 | Нет | – | Нет | 1 |
| 19 | – | 230 | – | 90 | – | – | 90 | 0,2 |
| 20 | – | 110 | 3000 | – | – | 170 | Нет | – |
| 21 | – | 220 | 630 | – | Нет | 175 | 4,6 | – |
| 22 | 20 | 230 | 1450 | – | – | 92,5 | – | – |
| 23 | – | 110 | 3000 | 95 | – | – | Нет | – |
| 24 | – | 220 | 460 | 405 | Нет | – | Нет | 0,009 |
| 25 | – | 110 | 3000 | – | 1,5 | 12 | – | – |
Таблица 2
Параметры генератора
| № | EВ | Mэм Н·м | Pэм кВт | P1 кВт | η% | Способ возбуждения |
| 1 | – | 171 | – | – | 90 | параллельное |
| 2 | – | – | – | – | 89 | последовательное |
| 3 | – | – | – | – | 87 | независимое |
| 4 | – | 280 | – | 23 | – | параллельное |
| 5 | – | 15 | – | – | 82 | последовательное |
| 6 | – | – | 18,52 | – | 87 | независимое |
| 7 | 480 | 525 | 55 | – | 88 | параллельное |
| 8 | – | 37,5 | – | – | 85 | последовательное |
| 9 | – | – | – | – | 86 | независимое |
| 10 | 240 | – | – | 21 | – | параллельное |
| 11 | – | 7,8 | – | – | 89 | последовательное |
| 12 | – | – | – | – | 85 | независимое |
| 13 | 477 | – | – | – | 88 | параллельное |
| 14 | – | 72 | – | – | 88 | последовательное |
| 15 | – | – | – | – | 85 | независимое |
| 16 | – | 10,5 | – | – | 85 | параллельное |
| 17 | – | 4,5 | – | – | 80 | последовательное |
| 18 | – | – | – | – | 88 | независимое |
| 19 | – | 280 | – | 25 | – | параллельное |
| 20 | – | 62 | – | – | 90 | последовательное |
| 21 | – | – | 42,52 | – | 82 | независимое |
| 22 | 235 | – | – | 23 | – | параллельное |
| 23 | – | 35 | – | – | 89 | последовательное |
| 24 | – | – | – | – | 80 | независимое |
| 25 | – | – | 1,4 | – | 75 | параллельное |
Примеры решения задач
Пример 1. Генератор постоянного тока параллельного возбуждении имеет номинальную мощность P2 =10 кВт; номинальное напряжение U = 230 В; частоту вращения n =1450 об/мин; сопротивление обмоток цепи обмотки возбуждения RВ =150 Ом; сопротивление обмоток
якоря RЯ = 0,3 Ом; КПД в номинальном режиме η = 86,5 %. Падением напряжения в щеточном контакте пренебречь.
Определить: ток генератора, ток в цепи возбуждения, ток в цепи якоря, ЭДС якоря, электро-
магнитный момент, электромагнитная мощность, мощность приводного двигателя. Генератор работает при номинальной нагрузке.
Решение:
Ток генератора: 
Ток в обмотке возбуждения: IВ =
Ток в цепи якоря: IЯ = I + IВ = 43,5 +1,5 = 45А.
ЭДС якоря: E =U + IЯ ⋅ RЯ = 230 + 45 ⋅ 0,3 = 243,5 В.
Электромагнитная мощность: Pэм = E ⋅ IЯ = 243,5⋅ 45 =10957 Вт .
Электромагнитный момент: M эм= 9,55
Мощность приводного двигателя: P1=
Пример 2. В генераторе постоянного тока независимого возбуждения с номинальным напряжением U = 440 В установился ток I = 64 А при частоте якоря n = 2800 об/мин. В новом режиме работы нагрузка и магнитный поток не изменились, но частота якоря стала
n* = 740 об/мин.
Определить напряжение и ток в генераторе в новом режиме.
Решение:
В генераторе независимого возбуждения ток генератора равен току якоря, т.е. I = IЯ .
В номинальном режиме:
Напряжение на нагрузке U = I ⋅ RН .
ЭДС якоря E =U + I ⋅ RЯ = I ⋅ RН + I ⋅ RЯ , с другой стороны E = СЕ ⋅ п ⋅Ф.
Получили: I ⋅ RН + I ⋅ RЯ = СЕ ⋅ п ⋅Ф.
В новом режиме, соответственно:
E* =U* + I* ⋅ RЯ= I* ⋅ Rн+ I* ⋅ RЯ= СЕ⋅ п* ⋅ Ф.
Возьмем отношение, полученных уравнений и получим:
I*= A и
A и
U* = B
B
Пример 3. В электродвигателе постоянного тока с параллельным возбуждением, имеющим номинальные данные: мощность на валу P2=130 кВт ; напряжение U = 220 В; ток, потребляемый из сети I = 640 А; частоту вращения n = 600 об/мин; сопротивление цепи обмотки возбуждения RВ= 43 Ом; сопротивление обмотки якоря RЯ= 0,007 Ом.
Определить номинальные суммарные и электрические потери в обмотках.
Решение:
Ток в обмотке возбуждения: IВ =
Ток в цепи якоря: IЯ= I − IВ = 640-5,116 = 634,884 A.
Электрические потери мощности
в цепи якоря: ΔPэл Я= IЯ2⋅ RЯ= 634,8842 ⋅ 0,007 = 2821,544 Вт;
в обмотке возбуждения:
ΔPэл B = IB2 ⋅ RB =U⋅ IB = 220 ⋅5,116=1125,52 Вт .
Суммарные потери мощности:
ΣΔP = ΔPэл B + ΔPэл Я =1125,52 + 2821,544 = 3947,064 Вт .
Пример 4. Двигатель постоянного тока последовательного возбуждения включен в сеть с напряжением U = 220 В при номинальном вращающем моменте M =101,7 Н⋅м развивает частоту вращения якоря n = 750 об/мин. КПД двигателя η = 75 %; сопротивление цепи обмотки возбуждения RВ = 0,197 Ом; сопротивление обмотки якоря RЯ = 0,443 Ом. Пуск двигателя осуществляется при пусковом реостате R пуск =1,17 Ом. Пусковой ток приводит к увеличению магнитного потока в 1,2 раза.
Определить номинальные мощность на валу, электромагнитную и потребляемую мощности; суммарные потери в двигателе; пусковой ток и пусковой момент.
Решение:
Мощность на валу: P2= M 
Потребляемая мощность: P1= 10644,4 Вт
10644,4 Вт
Суммарные потери: ΣΔP = P1– P2=10644,4 − 7983,45 = 2660,95 Вт.
Т.к. двигатель с последовательным возбуждением, тогда ток якоря находим:
IЯ= IВ =I =
ЭДС якоря: E =U − I ⋅ (RЯ + RВ ) = 220 − (0,443 + 0,197) ⋅ 48,38 =189,04 В.
Электромагнитная мощность: Pэм = E⋅ I=189,04 ⋅ 48,38 = 9145,6 Вт .
Пусковой ток:  пуск =
пуск =
Номинальный момент: М = CМ ⋅Ф⋅ I =101,7 ,
пусковой момент: М пуск = CМ ⋅Фпуск ⋅ Iпуск = CМ ⋅1,2⋅Ф⋅ Iпуск .
Возьмем отношение, полученных уравнений и получим:
М пуск =
Кратность
пускового тока: 
пускового момента:  = 3
= 3
