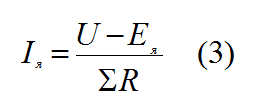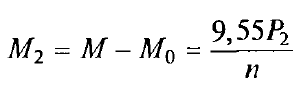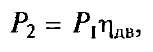Как найти номинальный момент двигателя постоянного тока

Вращающий
момент двигателя постоянного тока
создается взаимодействием магнитного
потока индуктора Ф с
током якоряI_я.
При числе параллельных ветвей обмотки
якоря 2а сила
тока в каждой из них будет равна По
формуле вращающий
момент, создаваемый каждым стержнем
обмотки

где D –
диаметр
якоря
и l –
активная
длина
стержня
в м.
Полный электромагнитный вращающий
момент двигателя в ньютонометрах
получим, помножив т на
число стержней, в обмотке N:

Обозначив
полюсное деление через τ,
можем
написать:

и
окончательно

где
постоянный коэффициент 

Вращающий
момент двигателя постоянного тока
пропорционален произведению магнитного
потока индуктора на ток якоря.

Механическая
мощность на валу двигателя, согласно
равенству ,
выразится формулой

47
Основной характеристикой для оценки
электромеханических свойств
электродвигателя является механическая
характеристика, представляющая собой
зависимость n=f(М) или =
f(М). Иногда используется так называемая
скоростная характеристика, представляющая
собой зависимость n=f(I). или=
f(I). 

Рис.
2. Механические характеристики двигателя
постоянного тока при различных
сопротивлениях цепи якоря (а) и напряжениях
(б)

Изменяя
сопротивление реостата в цепи якоря
можно получить при номинальной нагрузке
различные угловые скорости электродвигателя
на искусственных характеристиках — ω1,
ω2,
ω3

48 Пуск двигателей постоянного тока

Двигатели
постоянного тока пускаются в ход с
помощью пускового реостата, ограничивающего
пусковой ток. Из уравнения электрического
равновесия 

Так
как в момент пуска n =
0, то E =
с Ф n =
0 и, следовательно

Сопротивление
якоря R_я очень
мало (десятые, а то и сотые доли ома) и
потому пусковой ток якоря I_яn получается
очень большим, во много раз превышающим
номинальный. Чтобы ограничить пусковой
ток, на время пуска последовательно с
якорем включается пусковой реостат R_n.

В
этом случае

Величина
сопротивления R_n выбирается
по допустимому пусковому току якоря,
обычно

По
мере разгона двигателя пусковой реостат
ступень за ступенью выводится.
Металлические проволочные пусковые
реостаты входят в комплект поставки
двигателя. При пуске двигателя
параллельная обмотка возбуждения
включается на полное напряжение, то
есть регулировочный реостат R_peг в
цепи параллельной обмотки выводится
полностью, пуск осуществляется при
максимальном потоке Ф, что увеличивает
пусковой момент и облегчает запуск.
Реверсирование —
изменение
направления
вращения
двигателя
—
производится
путем
изменения
направления действия вращающего
момента. Для этого требуется изменить
направление магнитного потока двигателя
постоянного тока, т. е. переключить
обмотку возбуждения или якорь, при этом
в якоре будет протекать ток другого
направления. При переключении и цепи
возбуждения, и якоря направление
вращения останется прежним.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Электродвигатель постоянного тока

Основные параметры электродвигателя постоянного тока

Постоянная момента

,

• где M — момент электродвигателя, Нм,
• – постоянная момента, Н∙м/А,
• I — сила тока, А

Постоянная ЭДС

Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.

Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]

,

• где — электродвижущая сила, В,
• – постоянная ЭДС, В∙с/рад,
• — угловая частота, рад/с

Постоянные момента и ЭДС в точности равны между собой K_T = K_E. Постоянные K_T и K_E равны друг другу, если они определены в единой системе едениц.

Постоянная электродвигателя

Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя K_м. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.

,

Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.

Жесткость механической характеристики двигателя

,

• где — жесткость механической характеристики электродвигателя постоянного тока

Напряжение электродвигателя

Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):

,

Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:

Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции K_TK_E/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.

Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].

Мощность электродвигателя постоянного тока

Упрощенная модель электродвигателя выглядит следующим образом:

• где I – сила тока, А
• U — напряжение, В,
• M — момент электродвигателя, Н∙м
• R — сопротивление токопроводящих элементов, Ом,
• L — индуктивность, Гн,

• P_эл — электрическая мощность (подведенная), Вт
• P_мех — механическая мощность (полезная), Вт
• P_теп — тепловые потери, Вт
• P_инд — мощность затрачиваемая на заряд катушки индуктивности, Вт
• P_тр — потери на трение, Вт

Механическая постоянная времени

Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.

,

• где — механическая постоянная времени, с

Источник

Момент двигателя постоянного тока

Если обмотку возбуждения и якорь двигателя подключить к сети постоянного тока напряжением U то, возникает электромагнитный вращающий момент М_эм. Полезный вращающий момент М на валу двигателя меньше электромагнитного на значение противодействующего момента, создаваемого в машине силами трения и равного моменту М_х в режиме х.х., т. е. М = М_эм—М_х.

Пусковой момент двигателя должен быть больше статического тормозного М_т в состоянии покоя ротора, иначе якорь двигателя не начнет вращаться. В установившемся режиме (при n = соnst) имеет место равновесие вращающего М и тормозного М_т моментов:

Из механики известно, что механическая мощность двигателя может быть выражена через вращающий момент и угловую скорость

Следовательно, полезный вращающий момент двигателя М (Н • м), выраженный через полезную мощность Р (кВт) и частоту вращения n (об/мин),

Обсудим некоторые важные вопросы пуска и работы двигателей постоянного тока. Из уравнения электрического состояния двигателя следует, что

В рабочем режиме ток якоря I_я ограничивается э. д. с. E, если n приблезительно равно n_ном. В момент пуска п = 0, э. д. с. Е = 0 и пусковой ток I_п = U/R_яв 10—30 раз больше номинального. Поэтому прямой пуск двигателя, т. е. непосредственное включение якоря на напряжение сети, недопустимо. Чтобы ограничить большой пусковой ток якоря, перед пуском последовательно с якорем включается пусковой реостат R_п с небольшим сопротивлением. В этом случае при Е = О

После пуска и разгона наступает установившийся режим работы двигателя, при котором тормозной момент на валу Мт будет уравновешиваться моментом, развиваемым двигателем М_эм, т. е. М_эм == М_т(при n = соnst.)

Электродвигатели постоянного тока могут восстанавливать нарушенный изменением тормозного момента установившийся режим работы, т. е. могут развивать вращающий момент М, равный новому значению тормозного момента М_т при соответственно новой частоте вращения n’.

Действительно, если тормозной момент нагрузки М_т окажется больше вращающего момента двигателя М_эм, то частота вращения якоря уменьшится. При постоянных напряжении U и потоке Ф это вызовет уменьшение э. д. с. Е якоря, увеличение тока якоря и вращающего момента до наступления равновесия, при котором М_эм = М_т и n’ n’. Таким образом, двигатели постоянного тока обладают свойством саморегулирования — могут развивать вращающий момент, равный тормозному.

Регулирование частоты

Частота вращения якоря двигателя постоянного тока определяется на основании уравнения электрического состояния U = Е + R_яI_япосле подстановки в него э. д. с. Е = сФn:

(13)

Падение напряжения в якоре R_яI_я небольшое: при номинальной нагрузке оно не превышает 0,03 — 0,07 U_ном.

Таким образом, частота вращения двигателя постоянного тока прямо пропорциональна приложенному напряжению сети и обратно пропорциональна магнитному потоку статора. Из уравнения (13) следует, что регулировать частоту вращения двигателя можно двумя способами: изменяя поток статора Ф или напряжение U подводимое к двигателю. Регулирование частоты вращения изменением магнитного поля машины осуществляется с помощью регулировочного реостата в цепи возбуждения двигателя. Изменение подводимого к двигателю напряжения производится регулированием напряжения источника.

Можно ввести дополнительный реостат в цепь якоря. В этом случае пусковой реостат заменяется пускорегулирующимR_пр Такой реостат выполняет функции как пускового реостата, так и регулировочного. Уравнение (13) при этом имеет вид

(14)

Отсюда следует, что регулирование частоты вращения двигателя можно осуществить, изменяя напряжение сети, сопротивление пускорегулирующего реостата или поток статора.

Реверсирование двигателей. Из уравнения вращающего момента двигателя М_эм = kФI_я вытекает, что реверсирование, т. е. изменение направления вращения якоря, может быть осуществлено изменением направления тока в обмотке возбуждения (потока Ф) или тока якоря.

Для реверсирования двигателя «на ходу» изменяют направление тока якоря (переключением якорных выводов), а обмотку возбуждения не переключают, так как она обладает большой индуктивностью и разрыв ее цепи с током недопустим. Реверсирование отключенного двигателя осуществляется и изменением направления тока в обмотке возбуждения (переключением ее выводов).[4]

Источник

Как рассчитать номинальный момент двигателя постоянного тока

Главное меню

Судовые двигатели

Работа электропривода характеризуется в первую очередь механической характеристикой двигателя ? = f (М) или n = f (М). Для двигателя постоянного тока также часто исполь­зуют электромеханические характеристики ? = f (I­ _я ) или n = f ( I _я ), где ?, n, I _я , М — соответственно угловая скорость, частота вращения, сила тока якоря и вращающий момент двига­теля. Механические характеристики можно рассчитывать как в абсолютных, так и в относительных единицах. Для двигателей постоянного тока наибольшее распространение получил расчет характеристик в относительных единицах.

При расчетах в относительных единицах за базисные величины принимают номинальные данные двигателя I _я , М _ном , U _ном , n _ном . Иногда в качестве базисных принимают величины, отличающиеся от номинальных (например, момент статической нагрузки). Вели­чины, выражаемые в относительных единицах, в дальнейшем будут обозначены знаком.

Сопротивления главной цепи в относительных единицах опре­деляют в долях номинального сопротивления.. Под номинальным понимают такое сопротивление цепи якоря, которое при непо­движном якоре и номинальном расчетном напряжении U _ном обусловливает номинальную силу тока в якоре:

Сопротивление цепи якоря складывается из внутреннего и внешнего сопротивлений. Значения внутреннего сопротивления обмоток двигателей серий ДП и Д в долях номинального при ПВ = 25 % приведены в табл. 2.23. В графе r _я * указано сопроти­вление якоря и дополнительных полюсов двигателей, а в графе r’ _n * — сопротивление обмотки двигателей последовательного воз­буждения. Сопротивление стабилизирующих обмоток двигателей параллельного возбуждения настолько мало, что им можно пре­небречь. При расчете типовых характеристик для группы двига­телей сопротивление обмоток следует определять как среднее арифметическое значений, приведенных в соответствующих стро­ках табл. 2.23.

Расчет механических характеристик двигателей в относитель­ных единицах приведен ниже и является универсальным. Этот метод расчета пригоден для различных способов возбуждения и соединения обмоток.

Схема включения двигателя изображена на рис. 2.12, на кото­ром показаны три варианта (1, 2, 3) включения обмоток после­довательного возбуждения. Сила тока в этих обмотках обозна­чена через I _п1 , I _п2 , I _п3 . Обмотка параллельного возбуждения в общем случае получает питание от независимого источника с напряжением U _в .

При расчете механических характеристик, как правило, используют известные схему включения обмотки последова­тельного возбуждения, сопро­тивления последовательной и шунтирующей цепей R _п и R _ш , напряжение источника пита­ния цепи якоря (главной цепи) U _г , МДС обмотки параллель­ного возбуждения и соотно­шение между МДС обмоток последовательного и параллельного возбуждения при номиналь­ной нагрузке. Напряжение U _г может иметь независимое от на­грузки значение U _г — const (сеть постоянного тока). При приме­нении вращающихся или статических преобразователей энергии задают внешнюю характеристику этих преобразователей U _г = f (I) (I — сила тока нагрузки).

МДС главных полюсов двигателя обусловлена суммарным действием электрического тока в обмотках возбуждения, рас­положенных на этих полюсах. Поскольку номинальная МДС, принятая за базисную, складывается из МДС обмотки параллель­ного возбуждения и МДС обмотки последовательного возбуждения или стабилизирующей обмотки, то можно принять, что МДС обмотки параллельного возбуждения в относительных единицах будет составлять 0,5 для двигателей серий ДП и Д смешанного возбуждения и 0,9 для двигателей серий ДП и Д параллельного возбуждения. На долю обмотки последовательного возбуждения или стабилизирующей обмотки будет приходиться остальная часть МДС. Учитывая, что эта часть соответствует МДС при протека­нии номинального тока, для любой силы тока МДС обмотки после­довательного возбуждения можно выразить следующими форму­лами:

для двигателей серий ДП и Д смешанного возбуждения,

где I* _п — сила тока, протекающего по обмотке последовательного возбуждения;

для двигателей параллельного возбуждения со стабилизиру­ющей обмоткой серий ДП и Д

Полная МДС главных полюсов выражается в виде алгебраиче­ской суммы МДС обмоток последовательного и параллельного возбуждения:

В некоторых случаях для реализации повышенных (понижен­ных) частот вращения двигателей МДС обмотки параллельного возбуждения берут меньше (больше) номинальной.

Общий метод расчета механической характеристики двигате­лей постоянного тока в рассматриваемой схеме (см. рис. 2.12) включения заключается в нахождении зависимостей F* = f (I _я * ) и I _п * = f (I _я *) и последующем переходе к зависимости n* = f (М*).

Зависимость силы тока в последовательной обмотке от силы тока якоря двигателя устанавливают по одному из следующих уравнений:

каждое из которых справедливо при наличии обмотки последова­тельного возбуждения только в одной цепи.

Соответственно зависимость ЭДС от силы тока якоря определяют по одной из следующих зависимостей:

Частоту вращения п при заданной силе тока якоря находят по формуле n = Е/Ф _{с E} , где Ф — магнитный поток двигателя; с _Е — коэффициент пропорциональности напряжения.

Для получения уравнений в относительных единицах введем следующие базисные величины: n _б = n _ном ; I _б = I _ном ; Е _б = U _ном ; Ф _б = Ф _ном ; R _б = R _ном . Используя соотношения

Тогда формулу для определения частоты вращения в относи­тельных единицах запишем так:

так как в относительных единицах Ф* = (Е/п)*.

Магнитный поток Ф* для соответствующей силы тока якоря при известной МДС главных полюсов (F* = F* _пар + F* _п ) опреде­ляют по универсальным нагрузочным характеристикам. Нагру­зочной характеристикой называют зависимость (Е/n)* = f (F*) при постоянной силе тока якоря I* _я . Так как вид нагрузочных характеристик зависит от силы тока якоря, то они изображаются в виде семейства кривых, построенных при различных значе­ниях I _я . Характеристика при I _я = 0 является кривой намагни­чивания двигателя.

На рис. 2.13 показаны универсальные характеристики двига­телей серий ДП и Д. Характеристики изображены в относитель­ных единицах. За базисные величины приняты номинальная МДС главных полюсов двигателя при ПВ = 25 % и номинальный магнитный поток Ф главных полюсов при протекании по якорю двигателя тока номинальной силы при ПВ — 25 % в направле­нии, соответствующем двигательному режиму. Типовые нагрузоч­ные характеристики соответствуют действительным нагрузоч­ным характеристикам конкретных двигателей серий ДП и Д, отличаясь от характеристик, полученных на основе опыта, на 2—3 %.

Электромагнитный момент двигателя (в Н?м)

где c _M — коэффициент момента.

Вращающий момент на валу двигателя отличается от электро­магнитного на величину, определяемую механическими потерями и потерями в железе якоря. Таким образом, вращающий момент на валу двигателя может быть представлен в следующем виде:

где ?Р — потери мощности на трение; ?Р _ст — потери мощности в стали; k _M — коэффициент пропорциональности моментов.

Параметр ?M* = k _M * (?P* + ?Р* _ст )/n* определяют по кривым, выражающим зависимость ?M* = f (Е/n)* при различ­ных постоянных значениях частоты вращения n*. Такие кривые, построенные в относительных единицах, показаны на рис. 2.14.

Пользуясь этими кривыми, нетрудно найти момент ?М* при раз­личных магнитных потоках главных полюсов и частотах враще­ния. Коэффициент момента с _M можно определить, исходя из того, что при базисных силе тока, магнитном потоке и частоте вращения вращающий момент на валу двигателя также должен быть равен базисному (номинальному). Следовательно, пользуясь выражением (2.39), можно написать, что при М _дв = М _б = М _ном т. е.

Определив по рис. 2.14, что для (Е/n)* = 1 и n* = 1 ?М* = 0,03, найдем

Окончательно формула для определения вращающих моментов на валу имеет вид

Источник

В этой статье описаны основные формулы, величины и их обозначения которые относятся ко всем двигателям постоянного тока.

В результате взаимодействия I_я тока якоря в проводнике L обмотки якоря с внешним магнитным полем возникает электромагнитная сила создающая электромагнитный момент М который приводит якорь во вращение с частотой n.

Противо ЭДС двигателя E_я

При вращении якоря пазовый проводник пресекает линии поля возбуждения с магнитной индукцией B и в соответствии с явлением электромагнитной индукции в проводнике наводится ЭДС E_я направленная навстречу I_я. Поэтому эта ЭДС называется противо ЭДС  и она прямо пропорциональна Ф магнитному потоку и частоте вращения n.

E_я = С_е * Ф * n (1)

C_e — постоянный коэффициент определяемой конструкцией двигателя.

Применив второй закон Кирхгофа получаем уравнение напряжения двигателя.

U = E_я + I_я * ∑R (2)

где ∑R — суммарное сопротивления обмотки якоря включающая сопротивление :

• обмотки якоря
• добавочных полюсов
• обмотки возбуждения (для двигателей с последовательным возбуждением)

Ток якоря I_я

Выразим из формулы 2 ток якоря.

 

Частота вращения якоря

Из формул 1 и 2 выведем формулу для частоты вращения якоря.

Электромагнитная мощность двигателя

P_эм = Е_я I_я (5)

Электромагнитный момент

 где: ω = 2*π*f — угловая скорость вращения якоря, C_м — постоянный коэффициент двигателя (включает в себя конструктивные особенности данного двигателя)

Момент на валу двигателя, т.е. полезный момент, где М₀ момент холостого хода;

Р₂ — полезная мощность двигателя

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.