Как найти норма математика – Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 июня 2021 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. норма.

Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Определение[править | править код]

Норма вектора[править | править код]

Норма в векторном пространстве $V$ над полем вещественных или комплексных чисел — это функционал ${displaystyle pcolon Vto mathbb {R_{+}} }$ , обладающий следующими свойствами:

$p(x)=0Rightarrow x=0_{V};$
$forall x,yin V,p(x+y)leqslant p(x)+p(y)$ (неравенство треугольника);
${displaystyle forall alpha in mathbb {C} ,forall xin V,p(alpha ,x)=|alpha |p(x).}$

Эти условия являются аксиомами нормы.

Векторное пространство с нормой называется нормированным пространством, а условия (1—3) — также аксиомами нормированного пространства.

Из аксиом нормы очевидным образом вытекает свойство неотрицательности нормы:

$forall xin V,p(x)geqslant 0$ .

Действительно, из третьего свойства следует: $p(0_{V})=p(0cdot 0_{V})=0cdot p(0_{V})=0$ , а из свойства 2 — $forall xin Vcolon 0=p(0_{V})=p(x-x)leqslant p(x)+p(-x)=2p(x)$ .

Чаще всего норму обозначают в виде: $|cdot |$ . В частности, $|x|$ — это норма элемента $x$ векторного пространства $mathbb {R}$ .

Вектор с единичной нормой ${displaystyle left(|x|=1right)}$ называется единичным или нормированным.

Любой ненулевой вектор $x$ можно нормировать, то есть разделить его на свою норму: вектор ${frac {x}{|x|}}$ имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.

Норма матрицы[править | править код]

Нормой матрицы $A$ называется вещественное число $|A|$ , удовлетворяющее первым трём из следующих условий:

$|A|geqslant 0$ , причём $|A|=0$ только при $A=0$ ;
$|alpha A|=|alpha |cdot |A|$ , где $alpha in mathbb{R}$ ;
$|A+B|leqslant |A|+|B|$ ;
$|AB|leqslant |A|cdot |B|$ .

Если выполняется также и четвёртое свойство, норма называется субмультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы субмультипликативны.

Матричная норма $|cdot |_{{ab}}$ из $K^{{mtimes n}}$ называется согласованной с векторной нормой $|cdot |_{{a}}$ из $K^n$ и векторной нормой $|cdot |_{{b}}$ из $K^{m}$ если справедливо:

$|Ax|_{b}leqslant |A|_{{ab}}|x|_{a}$

для всех $Ain K^{{mtimes n}},xin K^{n}$ .

Норма оператора[править | править код]

Норма оператора $A$ — число, которое определяется так:

$|A|=sup _{{|x|=1}}|Ax|$ ,

где $A$ — оператор, действующий из нормированного пространства $L$ в нормированное пространство $K$ .

Это определение эквивалентно следующему:

$|A|=sup _{{xneq 0}}{frac {|Ax|}{|x|}}$

Свойства операторных норм:

$|A|geqslant 0$ , причём $|A|=0$ только при $A=0$ ;
$|alpha A|=|alpha |cdot |A|$ , где $alpha in {mathbb {R}}$ ;
$|A+B|leqslant |A|+|B|$ ;
$|AB|leqslant |A|cdot |B|$ .

В конечномерном случае, оператору в некотором базисе соответствует матрица — матрица оператора. Если норма на пространстве(пространствах), где действует оператор, допускает одно из стандартных выражений в базисе, то свойства нормы оператора повторяют аналогичные свойства нормы матрицы.

Свойства нормы[править | править код]

${displaystyle |x|-|y| leqslant |xpm y|leqslant |x|+|y|}$
${displaystyle {{bigl (}|x|-|y|{bigr )}}^{2}leqslant {|xpm y|}^{2}leqslant {{bigr (}|x|+|y|{bigl )}}^{2}}$
${frac {|x|^{2}+|y|^{2}-|x-y|^{2}}{2|x||y|}}in [-1,1]$ [косинус угла]
$|0_{V}|=|x-x|=|0x|=0cdot |x|=0$
$0=|x-x|leqslant |x|+|-x|=2|x|Rightarrow |x|geqslant 0$

Эквивалентность норм[править | править код]

Примеры[править | править код]

Линейные нормированные пространства[править | править код]

Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму

$|x|={sqrt {langle x,xrangle }},quad xin X.$

где $pgeqslant 1$ (обычно подразумевается, что это натуральное число).
В частности:

Нормы функций в $C[0,1]$ — пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:

«L0 норма»[править | править код]

Особым случаем является $ell _{0}$ (L0-«норма»), определяемая как количество ненулевых элементов вектора. Строго говоря, это не является нормой, так как не выполняется третья аксиома нормы. В основном таким видом «нормы» пользуются в задачах разреженного кодирования, в частности в Compressive sensing, где нужно найти наиболее разреженное представление вектора (с наибольшим количеством нулей), то есть с наименьшей $ell _{0}$ -нормой. С помощью этой «нормы» может быть определенно расстояние Хэмминга.

Некоторые виды матричных норм[править | править код]

Порожденные нормы $|A|_{{p}}=sup _{{|x|_{{p}}=1}}|Ax|_{{p}}$ :

Здесь $A^{dagger }$ — сопряжённая к $A$ матрица, ${mathrm {Tr}}$ — след матрицы.

Связанные понятия[править | править код]

Топология пространства и норма[править | править код]

Норма задаёт на пространстве метрику (в смысле — функцию расстояния метрического пространства), порождая таким образом метрическое пространство, а значит топологию, базой которой являются всевозможные открытые шары, то есть множества вида $B(x,r)={ycolon |x-y|<r}$ . Понятия сходимости, определённой на языке теоретико-множественной топологии в такой топологии и определённой на языке нормы, при этом совпадают.

См. также[править | править код]

Полунорма
Метрика
Скалярное произведение

Примечания[править | править код]

↑ М. Вербицкий. Начальный курс топологии. Задачи и теоремы. — Litres, 2018-12-20. — С. 163-164. — 346 с.

Источник

Норма (модуль, длина) вектора

В пространстве V каждому вектору x∈V ставим в соответствие некоторое неотрицательное число 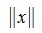так, чтобы для произвольных векторов x,y ∈V и произвольного скаляра λ выполнялись следующие условия:

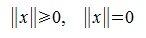тогда и только тогда, когда x=0.
.
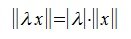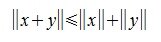(неравенство треугольника).

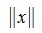называется нормой (длиной, модулем) вектора x∈V .

Примеры норм в линейных пространствах

1. max-норма, или m – норма:

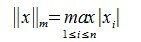
2. l-норма:

l-норма

3. Евклидова норма:

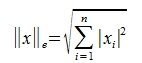
е-норма

Пример вычисления нормы (длины, модуля) вектора

Вычислим нормы вектора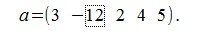

1. m-норма:

2. l-норма: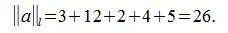

3. Евклидова норма:

Источник

Вычисление нормы и чисел обусловленности матрицы

1
норма матрицы представляет из себя
максимальное из чисел, полученных при
сложении всех элементов каждого столбца,
взятых по модулю. Не путайте со сложением
матриц!

Р
ассмотрим
на примере: пусть дана матрица размера
3х2. В первом столбце стоят элементы: 8,
3, 8. Все элементы положительные. Найдем
их сумму: 8+3+8=19. В втором столбце стоят
элементы: 8, -2, -8. Два элемента – отрицательные,
поэтому при сложении этих чисел,
необходимо подставлять модуль этих
чисел (т.е. без знаков “минус”).
Найдем их сумму: 8+2+8=18. Максимальное из
этих двух чисел – это 19. Значит первая
норма матрицы равна 19.

2
норма матрицы представляет из себя
квадратный корень из суммы квадратов
всех элементов матрицы. А это значит мы
возводим в квадрат все элементы матрицы,
затем складываем полученные значения
и из результата извлекаем квадратный
корень.

В
нашем случае, 2 норма матрицы получилась
равна квадратному корню из 269. На схеме,
я приближенно извлекла квадратный
корень из 269 и в результате получила
приблизительно около 16,401. Хотя более
правильно не извлекать корень.

3
норма матрицы представляет из себя
максимальное из чисел, полученных при
сложении всех элементов каждой строки,
взятых по модулю.

нашем примере: в первой строке стоят
элементы: 8, 8. Все элементы положительные.
Найдем их сумму: 8+8=16. В второй строке
стоят элементы: 3, -2. Один из элементов
отрицательный, поэтому при сложении
этих чисел, необходимо подставлять
модуль этого числа. Найдем их сумму:
3+2=5. В третьей строке стоят элементы 8,
и -8. Один из элементов отрицательный,
поэтому при сложении этих чисел,
необходимо подставлять модуль этого
числа. Найдем их сумму: 8+8=16. Максимальное
из этих трех чисел – это 16. Значит третья
норма матрицы равна 16.

Число
обусловленности квадратной матрицы A
определяется, как

k(A)
= ||A||·||A -1||

Число
обусловленности имеет следующее
значение: если машинная точность, с
которой совершаются все операции с
вещественными числами, равна ε, то при
решении системы линейных уравнений Ax
= b результат будет получен с относительной
погрешностью порядка ε·k(A). Хотя число
обусловленности матрицы зависит от
выбора нормы, если матрица хорошо
обусловлена, то её число обусловленности
будет мало при любом выборе нормы, а
если она плохо обусловлена, то её число
обусловленности будет велико при любом
выборе нормы. Таким образом, обычно
норму выбирают исходя из соображений
удобства. На практике наиболее широко
используют 1-норму, 2-норму и ∞-норму,
задающиеся формулами:

В
Matlab
используется следующие функции поиска
нормы:

Пусть
А —матрица. Тогда n=norm(A) эквивалентно
п=погп(А,2) и возвращает вторую норму, т.
е. самое большое сингулярное число А.
Функция n=norm(A, 1) возвращает первую норму,
т. е. самую большую из сумм абсолютных
значений элементов матрицы по столбцам.
Норма неопределенности n=norm(A, inf) возвращает
самую большую из сумм абсолютных значений
элементов матрицы по рядам. Норма
Фробениуса
(Frobenius) norm(A, ‘fro’) = sqrt(sum(diag(A’A))).

Пример:

»
A=[2,3,1;1,9,4;2,6,7]

A
=

2
3 1

1
9 4

2
6 7

»
norm(A,1)

ans
=

Числа
обусловленности матрицы определяют
чувствительность решения системы
линейных уравнений к погрешностям
исходных данных. Следующие функции
позволяют найти числа обусловленности
матриц.

cond(X)
— возвращает число обусловленности,
основанное на второй норме, то есть
отношение самого большого сингулярного
числа X к самому малому. Значение cond(X),
близкое к 1, указывает на хорошо
обусловленную матрицу;

с
= cond(X,p) — возвращает число обусловленности
матрицы, основанное на р-норме:
norm(X,p)*norm(inv(X),p), где р определяет способ
расчета:

р=1
— число обусловленности матрицы,
основанное на первой норме;

р=2
— число обусловленности матрицы,
основанное на второй норме;

p=
‘fro’ — число обусловленности матрицы,
основанное на норме Фробе-ниуса
(Frobenius);

р=’inf’
— число обусловленности матрицы,
основанное на норме неопределенности.

с
= cond(X) — возвращает число обусловленности
матрицы, основанное на второй норме.

Пример:

»
d=cond(hilb(4))

d
=

1.5514е+004

condeig(A)
— возвращает вектор чисел обусловленности
для собственных значений А. Эти числа
обусловленности — обратные величины
косинусов углов между левыми и правыми
собственными векторами;

[V.D.s]
= condeig(A) — эквивалентно
[V,D] = eig(A): s = condeig(A);.

Большие
числа обусловленности означают, что
матрица А близка к матрице с кратными
собственными значениями.

Пример:

»
d=condeig(rand(4))

d
=

1.0766

1.2298

1.5862

1.7540

rcond(A)
— возвращает обратную величину
обусловленности матрицы А по первой
норме, используя оценивающий обусловленность
метод LAPACK. Если А — хорошо обусловленная
матрица, то rcond(A) около 1.00, если плохо
обусловленная, то около 0.00. По сравнению
с cond функция rcond реализует более
эффективный в плане затрат машинного
времени, но менее достоверный метод
оценки обусловленности матрицы.

Пример:

»
s=rcond(hilb(4))

s
=

4.6461е-005

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

У этого термина существуют и другие значения, см. норма.

Норма — понятие, обобщающее абсолютную величину (модуль) числа, а также длину вектора на случай элементов (векторов) линейного пространства.

Норма в векторном линейном пространстве ${displaystyle L}$ над полем вещественных или комплексных чисел есть функция ${displaystyle p:Lto mathbb {R} }$ , удовлетворяющая следующим условиям:

${displaystyle p(x)geq 0}$ , причём ${displaystyle ~p(x)=0}$ только при ${displaystyle ~x=0}$ ;
${displaystyle p(x+y)leq p(x)+p(y)}$ для всех ${displaystyle x,yin L}$ (неравенство треугольника);
${displaystyle ~p(alpha x)=|alpha |p(x)}$ для каждого скаляра ${displaystyle ~alpha }$ .

Норма ${displaystyle ~x}$ обычно обозначается ${displaystyle |x|}$ . Линейное пространство с нормой называется нормированным пространством.

Примеры норм в линейных пространствах

Топология пространства и норма

Норма задаёт на пространстве топологию, базой которой являются всевозможные открытые шары, то есть множества вида ${displaystyle B(x,epsilon )={ymid |x-y|<epsilon }}$ . Понятия сходимости, определённой на языке теоретико-множественной топологии в такой топологии и определённой на языке нормы, при этом совпадают.

Эквивалентность норм

Две нормы ${displaystyle p}$ и ${displaystyle q}$ на пространстве ${displaystyle L}$ называются эквивалентными, если существует две положительные константы ${displaystyle C_{1}}$ и ${displaystyle C_{2}}$ такие, что для любого ${displaystyle xin L}$ выполняется ${displaystyle C_{1}p(x)leq q(x)leq C_{2}p(x)}$ . Эквивалентные нормы задают на пространстве одинаковую топологию. В конечномерном пространстве все нормы эквивалентны.

Операторная норма

Норма оператора ${displaystyle A}$ – число, которое определяется, как:

${displaystyle |A|=sup _{|x|=1}|Ax|}$ .

где ${displaystyle A}$ — оператор, действующий из нормированного пространства ${displaystyle L}$ в нормированное пространство ${displaystyle K}$ .

Свойства операторных норм:

${displaystyle |A|geq 0}$ , причём ${displaystyle |A|=0}$ только при ${displaystyle A=0}$ ;
${displaystyle |alpha A|=|alpha |cdot |A|}$ ;
${displaystyle |A+B|leq |A|+|B|}$ ;
${displaystyle |AB|leq |A|cdot |B|}$ .

Матричная норма

Нормой матрицы ${displaystyle A}$ называется действительное число ${displaystyle |A|}$ , удовлетворяющее первым трём из следующих условий:

${displaystyle |A|geq 0}$ , причём ${displaystyle |A|=0}$ только при ${displaystyle A=0}$ ;
${displaystyle |alpha A|=|alpha |cdot |A|}$ ;
${displaystyle |A+B|leq |A|+|B|}$ ;
${displaystyle |AB|leq |A|cdot |B|}$ .

Если выполняется также и четвёртое свойство, норма называется мультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы мультипликативны. Немультипликативные нормы для матриц являются простыми нормами, заданными в линейных пространствах матриц.

Виды матричных норм

m-норма: ${displaystyle |A|_{m}=max _{i}sum _{j}|a_{ij}|}$
l-норма: ${displaystyle |A|_{l}=max _{j}sum _{i}|a_{ij}|}$
Евклидова норма: ${displaystyle |A|_{E}={sqrt {sum _{i,j}|a_{ij}|^{2}}}}$
Сингулярная норма (подчинена евклидовой норме векторов): ${displaystyle |A|_{2}=max _{i}sigma _{i}(A)}$

ca:Norma (matemàtiques)
da:Norm (matematik)
he:נורמה (מתמטיקה)
nl:Norm (wiskunde)
pl:Norma (matematyka)
sv:Norm (matematik)
ur:امثولہ (ریاضی)

Источник

Численные методы линейной алгебры

Основные положения численного анализа

Классическим средством изучения математических моделей и исследований на их основе свойств реальных объектов являются аналитические методы, позволяющие получать точные решения в виде математических формул. Эти методы дают наиболее полную информацию о решении задачи, и они до настоящего времени не утратили своего значения. Однако, к сожалению, класс задач, для которого они могут использоваться, весьма ограничен. Поэтому решение, как правило, осуществляется численными методами.

Численные методы — это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям. Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой. Численные методы, в отличие от аналитических, дают не общие, а частные решения. При этом требуется выполнить достаточное количество арифметических и логических действий над числовыми и логическими массивами.

В численном анализе используются два класса численных методов:

1. Прямые методы, позволяющие найти решение за определенное число операций.

2. Итерационные методы, основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию.

Решения, получаемые численными методами, в силу их приближенности содержат некоторые погрешности. Рассмотрим их источники и типы.

Один из типов погрешностей обусловлен неадекватностью выбранной математической модели исходной физической. Эта неадекватность в большей или меньшей степени присуща всем приближенно решаемым задачам. Данная погрешность является неустранимой. Неточность (неопределенность) задания исходных данных приводит также к неустранимым погрешностям.

Если мы устраним неопределенность в исходных данных и найдем решение с помощью какого-либо численного метода, то получим результат, не в точности соответствующий исходным данным в силу погрешности численного метода. В компьютере все числа представляются в конечном виде, и поэтому при использовании вычислительного алгоритма реализуются ошибки арифметических и других операций над числами, а также ошибки округления.

Дадим некоторые понятия из теории погрешностей вычислительных действий над приближенными величинами.

Пусть [math]x[/math] — точное, но, как правило, неизвестное значение некоторой величины, а [math]widehat{x}[/math] — ее известное приближенное значение.

Абсолютной погрешностью приближения [math]widehat{x}[/math] называется разность [math]Delta=bigl|x-widehat{x}bigr|[/math] (в общем случае [math]Deltawidehat{x}[/math] имеет размерность величины [math]x[/math]).

Относительная погрешность приближения [math]widehat{x}[/math] обозначается [math]delta[/math] и выражается отношением [math]delta= frac{Deltawidehat{x}}{|widehat{x}|}[/math] ([math]delta[/math] — безразмерная величина, [math]widehat{x}ne0[/math]). Часто величина [math]delta[/math] вычисляется в процентах, и тогда она умножается на сто.

Так как величина [math]x[/math], как правило, неизвестна, а погрешность необходимо определять, то в рассмотрение вводится предельная абсолютная погрешность [math]Delta(widehat{x}):[/math]

[math]Deltawidehat{x}= |x-widehat{x}|leqslant Delta(widehat{x}).[/math]

Раскрывая в этом неравенстве модуль, получаем соотношение, задающее отрезок, которому принадлежит точное значение: [math]widehat{x}-Delta(widehat{x}) leqslant xleqslant Delta(widehat{x})[/math]. Таким образом, величина [math]x[/math] находится в ∆-окрестности (дельта-окрестности), определяемой величинами [math]widehat{x}[/math] и [math]Delta(widehat{x})[/math].

Предельная относительная погрешность приближения [math]widehat{x}[/math] определяется отношением [math]delta(widehat{x})= frac{Delta(widehat{x})}{|widehat{x}|}[/math].

Такие погрешности оцениваются при рассмотрении численных методов. Эти оценки могут производиться до выполнения вычислений (априорные оценки) и после них (апостериорные оценки).

Как правило, численный алгоритм решения задачи завершается, если погрешность меньше заданной заранее величины.

Норма матриц: понятие, определение, примеры

При решении многих практических задач необходимо как-то “измерять” матрицы, чтобы говорить, что одна матрица больше другой. Правило, по которому матрице (в частности, матрице-столбцу) ставится в соответствие некоторое неотрицательное число, имеющее смысл меры, определяет понятие норма матрицы.

Нормой матрицы-столбца [math]x=begin{pmatrix}x_1\vdots\x_nend{pmatrix}[/math] называется функция [math]|x|[/math], удовлетворяющая следующим аксиомам:

1. [math]|x|geqslant0[/math] для любого столбца [math]x[/math], причем [math]|x|=0[/math] в том и только в том случае, если [math]x[/math] — нулевой столбец;

3. [math]|x+y|leqslant|x|+|y|[/math] для любых двух столбцов [math]x[/math] и [math]y[/math] размеров [math](ntimes1)[/math].

Аксиома 3 называется неравенством треугольника.

Примером нормы матрицы-столбца может быть семейство норм

[math]|x|= Biggl(sum_{i=1}^{n}|x_i|^pBiggr)^{1/p},[/math]

где при любом целом положительном [math]p[/math] определяется функция, удовлетворяющая условиям 1-3.

Приведем часто используемые нормы матриц-столбцов.

1. [math]|x|_1=max_{iinmathbb{N}}|x_i|[/math] — максимум среди модулей элементов столбца;

2. [math]textstyle{|x|_2=sumlimits_{i=1}^{n}|x_i|}[/math] — сумма модулей элементов столбца;

3. [math]textstyle{|x|_3=sqrt{sumlimits_{i=1}^{n}x_i^2}}[/math] — квадратный корень из суммы квадратов элементов.

Последняя норма называется евклидовой, так как совпадает с модулем столбца (длиной вектора), т.е. [math]|x|_3=|x|=sqrt{x^Tx}[/math].

Замечания 10.1

1. Можно показать, что справедливы следующие соотношения

[math]|x|_2geqslant|x|_3geqslant|x|_1[/math], а также [math]sqrt{n}cdot|x|_3geqslant|x|_2,~ sqrt{n}cdot|x|_1geqslant|x|_3[/math].

2. Норма может быть использована при анализе сходимости последовательностей матриц-столбцов.

Последовательность матриц-столбцов [math]bigl{x^{(1)},x^{(2)},ldots,x^{(k)},ldotsbigr}[/math] сходится к столбцу [math]x_{ast}[/math], если [math]lim_{kto+infty}x_i^{(k)}=x_{ast i}[/math], для всех [math]i=1,2,ldots,n[/math]. Для того чтобы последовательность [math]bigl{x^{(1)},x^{(2)}, ldots,x^{(k)},ldotsbigr}[/math] сходилась к столбцу х., необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|x^{(k)}-x_{ast}bigr|=0[/math].

3. Для определения псевдорешений систем линейных алгебраических уравнений ранее использовалась евклидова норма [math]|x|_3[/math].

4. Нормы позволяют оценить скорость сходимости последовательностей. Рассмотрим последовательность [math]bigl{x^{(k)}bigr}[/math], сходящуюся к [math]x_{ast}[/math]. Предположим, что все ее элементы различны и ни один из них не совпадает с [math]x_{ast}[/math]. Наиболее эффективный способ оценивания скорости сходимости состоит в сопоставлении расстояния [math]bigl|x^{(k+1)}-x_{ast}bigr|[/math] между [math]x^{(k+1)}[/math] и [math]x_{ast}[/math] с расстоянием [math]bigl|x^{(k)}-x_{ast}bigr|[/math] между [math]x^{(k)}[/math] и [math]x_{ast}[/math].

Последовательность [math]bigl{x^{(k)}bigr}[/math] называется сходящейся с порядком [math]{p}[/math], если [math]{p}[/math] — максимальное число, для которого

[math]0leqslant lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p} < +infty.[/math]

Поскольку величина [math]{p}[/math] определяется предельными свойствами [math]bigl{x^{(k)}bigr}[/math], она называется асимптотической скоростью сходимости.

Если последовательность [math]bigl{x^{(k)}bigr}[/math] — сходящаяся с порядком [math]{p}[/math], то число

[math]c=lim_{kto+infty} frac{|x^{(k+1)}-x_{ast}|}{|x^{(k)}-x_{ast}|^p},.[/math]

называется асимптотическим параметром ошибки. Если [math]p=1,~ c<1[/math], то сходимость линейная, если [math]p=2[/math] — квадратичная, если [math]p=3[/math] — кубическая и т.д. Если [math]p>1[/math] или [math]p=1,~c=0[/math], то сходимость сверхлинейная. Линейная сходимость является синонимом сходимости со скоростью геометрической профессии. Сверхлинейная сходимость является более быстрой, чем определяемая любой геометрической прогрессией.

Пример 10.1. Вычислить нормы матрицы-столбца [math]x=begin{pmatrix} 1&-2&3&-4 end{pmatrix}^T[/math].

Решение.

[math]begin{aligned} mathsf{1)}~, |x|_1&= max_{iinmathbb{N}}|x_i|= maxbigl{|1|,|-2|,|3|,|-4|bigr}=4,;\[5pt] mathsf{2)}~, |x|_2&= sum_{i=1}^{4}|x_i|= |1|+|-2|+|3|+|-4|=10,;\[5pt] mathsf{3)}~, |x|_3&= sqrt{sum_{i=1}^{4}x_i^2}= sqrt{1^2+(-2)^2+3^2+(-4)^2}=sqrt{30},. end{aligned}[/math]

Заметим, что свойство [math]|x|_2geqslant|x|_3geqslant|x|_1[/math], очевидно, выполняется.

Пусть [math]A[/math] — произвольная матрица размеров [math](mtimes n)[/math].

Нормой матрицы [math]A[/math] называется функция [math]|A|[/math], удовлетворяющая следующим аксиомам:

1) [math]|A|geqslant0[/math] для любой матрицы [math]A[/math], причем [math]|A|=0[/math] в том и только в том случае, если [math]A[/math] — нулевая матрица;

3) [math]|A+B|leqslant|A|+|B|[/math] для любых двух матриц [math]A[/math] и [math]B[/math] размеров [math](mtimes n)[/math] (неравенство треугольника);

Матричные нормы удобно определять через нормы матриц-столбцов. Для этого, задавшись какой-нибудь нормой для матриц-столбцов, рассматриваются значения [math]|Ax|[/math] при всевозможных х, удовлетворяющих условию [math]|x|=1[/math]. Максимальное из этих значений, которое найдется всегда, берется в качестве нормы матрицы [math]Acolon, |A|= max_{|x|=1}|Ax|[/math]. Такую матричную норму называют индуцированной.

Заметим, что в качестве определения индуцированной матричной нормы часто используется выражение [math]|A|=sup_{xne0}frac{|Ax|}{|x|}[/math], характеризующее максимальную величину, на которую преобразование, описываемое матрицей [math]A[/math], может растянуть любой ненулевой вектор в заданной норме.

Наиболее употребительными являются следующие формулы для вычисления значений норм матриц с действительными элементами.

1) [math]textstyle{|A|_1= maxlimits_{1leqslant ileqslant m}sumlimits_{j=1}^{n}|a_{ij}|}[/math] — максимум суммы модулей элементов в строке;

2) [math]textstyle{|A|_2= maxlimits_{1leqslant jleqslant n}sumlimits_{i=1}^{m}|a_{ij}|}[/math] максимум суммы модулей элементов в столбце;

3) [math]|A|_3=sqrt{lambda_{max}(A^TA)}[/math] — квадратный корень из максимального собственного значения [math]lambda_i[/math] матрицы [math]A^TA[/math];

4) [math]textstyle{|A|_4= sqrt{sumlimits_{i=1}^{m} sumlimits_{j=1}^{n} a_{ij}^2}}[/math] — квадратный корень из суммы квадратов элементов.

Заметим, что вычисление нормы [math]|A|_3= sqrt{lambda_{max}(A^TA)}[/math] связано с весьма трудоемкими операциями. Поскольку справедливо неравенство

[math]|A|_3=sqrt{lambda_{max}(A^TA)} leqslant |A|_4= sqrt{sumlimits_{i=1}^{m} sum_{j=1}^{n} a_{ij}^2},[/math]

то норма [math]|A|_4[/math] часто используется в оценках вместо [math]|A|_3[/math]. Норма [math]|A|_4[/math] возникает, если матрице [math]A[/math] поставить в соответствие “длинный столбец”:

[math]begin{pmatrix}a_{11},a_{21},ldots, a_{m1},a_{12},a_{22},ldots, a_{m2},ldots,a_{nn} end{pmatrix}^T[/math] и применить норму [math]|x|_3[/math].

Пример 10.2. Вычислить нормы матриц [math]A=begin{pmatrix}1&-2&3\ 4&5&-6\ -7&8&9 end{pmatrix}!,~ B=begin{pmatrix}1&0&0\ 0&1&0\ 0&0&1 end{pmatrix}[/math].

Решение. а)

[math]begin{aligned}|A|_1&= maxbigl{|1|+|-2|+|3|;, |4|+|5|+|-6|;, |-7|+|8|+|9|bigr}= max{6;,15;,24}=24;\[5pt] |A|_2&= maxbigl{|1|+|4|+|-7|;, |-2|+|5|+|8|;, |3|+|-6|+|9|bigr}= max{12;15;18}=18;\[5pt] |A|_4&= sqrt{1^2+(-2)^2+3^2+4^2+5^2+(-6)^2+(-7)^2+8^2+9^2}=\[2pt] &=sqrt{1+4+9+16+25+36+49+64+81}= sqrt{285};end{aligned}[/math]

б) [math]|B|_1=|B|_2=1,,~ |B|_4=sqrt{1+1+1}=sqrt{3}[/math].

Норма матриц может быть использована при анализе сходимости различных численных процедур. Пусть имеется последовательность матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] размеров [math]mtimes n[/math]. Матрица [math]A[/math] называется пределом последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math], если [math]lim_{kto+infty}a_{ij}^{(k)}=a_{ij}[/math] для всех [math]i=1,ldots,m[/math] и [math]j=1,ldots,n[/math]. Это обозначается [math]lim_{kto+infty}A^{(k)}=A[/math].

Для сходимости последовательности матриц [math]bigl{A^{(1)},ldots,A^{(k)},ldotsbigr}[/math] к матрице [math]A[/math] необходимо и достаточно, чтобы [math]lim_{kto+infty}bigl|A^{(k)}-Abigr|=0[/math]. При этом последовательность, составленная из норм матриц [math]A^{(k)}[/math], сходится к норме матрицы [math]A[/math], т.е. [math]lim_{kto+infty} bigl|A^{(k)}bigr|=|A|[/math].

Отметим некоторые свойства предела матриц. Если [math]lim_{kto +infty}A^{(k)}=A,~ lim_{kto+infty}B^{(k)}=B[/math], то:

[math]begin{array}{ll}mathsf{1)}~ limlimits_{kto+infty}bigl[A^{(k)}pm B^{(k)}bigr]=Apm B;&qquad mathsf{2)}~ limlimits_{kto+infty}bigl[A^{(k)}cdot B^{(k)}bigr]=Acdot B;\\[-5pt] mathsf{3)}~ limlimits_{kto+infty}bigl[A^{(k)}bigr]^{-1}=A^{-1};&qquad mathsf{4)}~ limlimits_{kto+infty}bigl[CA^{(k)}bigr]=CA,~ limlimits_{kto+infty}bigl[A^{(k)}Dbigr]=AD.end{array}[/math]

где считается, что все операции определены.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определение[править | править код]

Норма вектора[править | править код]

Норма матрицы[править | править код]

Норма оператора[править | править код]

Свойства нормы[править | править код]

Эквивалентность норм[править | править код]

Примеры[править | править код]

Линейные нормированные пространства[править | править код]

«L0 норма»[править | править код]

Некоторые виды матричных норм[править | править код]

Связанные понятия[править | править код]

Топология пространства и норма[править | править код]

См. также[править | править код]

Примечания[править | править код]

Норма (модуль, длина) вектора

Примеры норм в линейных пространствах

Пример вычисления нормы (длины, модуля) вектора

Вычисление нормы и чисел обусловленности матрицы

Топология пространства и норма

Эквивалентность норм

Операторная норма

Матричная норма

Виды матричных норм

Численные методы линейной алгебры

Основные положения численного анализа

Норма матриц: понятие, определение, примеры

Вам также может понравиться

Как найти девушку по своему вкусу

Как найти температуру охладителя

Как найти закладки в телефоне самсунг а51

Добавить комментарий Отменить ответ