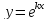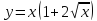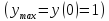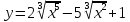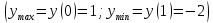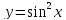Как найти нормаль к линии

Норма́ль в геометрии — обобщение понятия перпендикуляра к прямой или плоскости на произвольные гладкие кривые и поверхности.

Нормаль к кривой в заданной её точке — прямая, перпендикулярная к касательной прямой в указанной точке кривой. Плоская гладкая кривая имеет в каждой точке единственную нормаль, расположенную в той же плоскости. Пространственная кривая в каждой своей точке имеет бесконечное множество нормалей, формирующих так называемую нормальную плоскость. Две из этих нормалей выделяются особо: нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью, а нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью^[1].

Нормаль к поверхности в заданной её точке — прямая, перпендикулярная к касательной плоскости в указанной точке поверхности. Нормаль для гладкой поверхности определяется однозначно^[1].

Понятие нормали может быть легко распространено на многомерные многообразия. Кроме геометрии, нормали широко используются в геометрической оптике, механике, при создании трёхмерной компьютерной графики, в теории потенциала и в других естественных науках^[2].

Вектор нормали[править | править код]

Вектор нормали (или орт нормали) к поверхности в данной точке — единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Аналогично определяются векторы нормали к пространственной кривой в данной точке; среди них, соответственно сказанному выше, выбирают два, ортогональных друг к другу: вектор главной нормали и вектор бинормали.

Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным полем векторов нормали. В противном случае поверхность называют односторонней или неориентируемой. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.

Примерами односторонних и, следовательно, неориентируемых поверхностей являются бутылка Клейна или лист Мёбиуса.

Нормаль к пространственной кривой[править | править код]

Пусть — векторное уравнение кривой. Тогда направление главной нормали может быть получено как двойное векторное произведение: В случае естественной параметризации кривой (её длиной дуги) орт главной нормали^[3] равен .

Векторное уравнение бинормали в точке имеет вид:

Уравнение нормальной плоскости^[3] в точке :

Нормаль к плоской кривой[править | править код]

Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке имеет следующий вид.

Способ задания плоской кривой	Уравнение кривой	Уравнение нормали
Параметрическое задание
Явное задание
Неявное задание

Нормаль к поверхности[править | править код]

В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности (см. статью Поверхность). Примером точки поверхности, где нормаль не определена, является вершина конуса — в ней не существует касательной плоскости.

Координаты орта нормали для разных способов задания поверхности приведены в таблице:

	Координаты нормали в точке поверхности
параметрическое задание:
неявное задание:
явное задание:

Здесь . Все производные берутся в точке . Из формул видно, что в случае неявного задания направление нормали к функции совпадает с направлением её градиента.

Сечение поверхности плоскостью, содержащей нормаль поверхности в заданной точке, образует некоторую кривую, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).

Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол . Тогда кривизна кривой связана с кривизной нормального сечения (с той же касательной) формулой Мёнье^[4]:

Кривизна нормального сечения в заданной точке зависит от направления этого сечения; если кривизна не постоянна, то максимум и минимум достигаются в двух взаимно перпендикулярных направлениях, называемых главными направлениями. На сфере, на торцах эллипсоида и т. п. кривизна постоянна, и все направления — главные^[5].

Примечания[править | править код]

Литература[править | править код]

• Нормаль // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
• Погорелов А. И. Дифференциальная геометрия. — 6-е изд. — М.: Наука, 1974. — 176 с.
• Рашевский П. К. Курс дифференциальной геометрии. — 4-е изд. — М.: ГИТТЛ, 1956.

Ссылки[править | править код]

• Нормаль // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Рассмотрим
кривую, уравнение которой имеет вид

Уравнение
касательной к данной кривой в точке
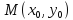имеет вид:

(34)

Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.

Уравнение
нормали к данной кривой в точке
имеет вид:

(35)

_{Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.}

_{Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.}

Пример
17

Написать
уравнения касательной и нормали к кривой
в точке, абсцисса которой равна.

Решение:

Найдем
значение функции в точке
:

Найдем
производную заданной функции в точке

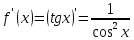
Уравнение
касательной найдем по формуле (34):

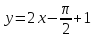
Уравнение
нормали найдем по формуле (35):

Ответ:
Уравнение
касательной :

Уравнение
нормали :.

Пример
18

Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса

в
точке
,
для которой.

Решение:

Найдем
как производную функции, заданной
параметрически по формуле (10):

Найдем
координаты точки касания
:
и значение производной в точке касания
:

Уравнение
касательной найдем по формуле (34):

Найдем
координаты
точкипересечения
касательной с осью:

Длина
касательной равна длине отрезка
:

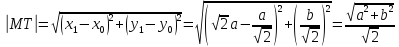
Согласно
определению, подкасательная
равна

Где
угол
– угол между касательной и осью. Поэтому,– угловой коэффициент касательной,
равный

Таким
образом, подкасательная
равна

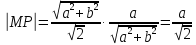
Уравнение
нормали найдем по формуле (35):

Найдем
координатыточкипересечения нормали с осью:

Длина
нормали равна длине отрезка
:

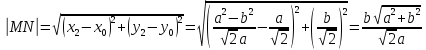
Согласно
определению, поднормаль
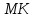равна

Где
угол
– угол между нормалью и осью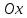. Поэтому,– угловой коэффициент нормали, равный

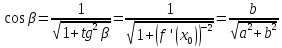
Поэтому,
поднормаль
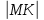равна:

Ответ:
Уравнение
касательной :

Уравнение
нормали :

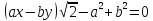
Длина
касательной
;
подкасательная;

Длина
нормали
; поднормаль

Задания
7. Написать
уравнения касательной и нормали:

1. К параболе в точке, абсцисса которой

.

2.
К окружности
в точках пересечения её с осью абсцисс

.

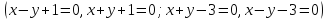3.
К циклоиде
в точке, для которой

.

4.
В каких точках кривой
касательная параллельна:

а)
оси Оx; б) прямой

.

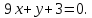
10.
Промежутки монотонности функции.
Экстремумы функции.

Условие
монотонности функции:

Для
того, чтобы дифференцируемая на
функцияне возрастала, необходимо и достаточно,
чтобы во всех точках, принадлежащих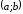ее производная была неположительна .

(36)

Для
того, чтобы дифференцируемая на
функция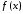не убывала, необходимо и достаточно,
чтобы во всех точках, принадлежащихее производная была неотрицательна.

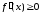(37)

Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции

Пример
19

Найти
промежутки монотонности функции
.

Решение:

Найдем
производную функции
.

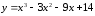Найдем
промежутки знакопостоянства полученной
производной. Для этого

разложим полученный
квадратный трехчлен на множители:

.

Исследуем
знак полученного выражения, используя
метод интервалов.

Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на
и убывает на.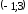

Ответ:
Заданная
функция
возрастает на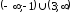и убывает на.

_{Определение}
Функция
имеет в точкелокальный
максимум (минимум),
если существует такая окрестность
точки
,
что для всех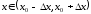выполняется условие

().

Локальный
минимум или максимум функции
называетсялокальным
экстремумом.

Необходимое
условие существования экстремума.

Пусть
функция
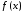определена в некоторой окрестности
точки.
Если функцияимеет
в точке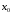экстремумом, то производная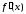в точкелибо равна нулю, либо не существует.

Точка
называетсякритической
точкой
функции
,
если производнаяв точкелибо равна нулю, либо не существует.

Достаточные
условия наличия экстремума в критической
точке
.

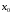Пусть
точка
является критической.

Первое
достаточное условие экстремума:

Пусть
функция
непрерывна в некоторой окрестноститочкии дифференцируема в каждой точке.

Точка
является локальным максимумом, если
при переходе через

производная
функции меняет знак с плюса на минус.

Точка
является локальным минимумом, если при
переходе через

производная
функции меняет знак с минуса на плюс.

Пример
20

Найти
экстремумы функции
.

Решение:

Найдем
производную заданной функции

Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:

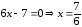
Исследуем
знак производной, используя метод
интервалов.

Из
рисунка видно, что при переходе через
точку
производная меняет знак с плюса на
минус. Следовательно, в точке–
локальный максимум.

При
переходе через точку
производная меняет знак с минуса на
плюс.

Следовательно,
в точке
–
локальный минимум.

При
переходе через точку
производная не меняет знак. Следовательно,
критическая точкане является экстремумом заданной
функции.

Ответ:
–
локальный максимум,
–
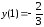локальный минимум.

Второе
достаточное условие экстремума:

Если
первые
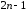производные функциив точке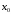равны нулю, а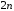-ная
производная функциив точкеотлична от нуля, то точкаявляется экстремумом функции,
причем,

если

,
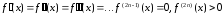(38)

то
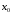-локальный
минимум

если

,
(39)

то
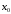-локальный
максимум.

Пример
21

Найти
экстремумы функции, пользуясь второй
производной
.

Решение:

ОДЗ:
.

Найдем
первую производную заданной функции

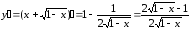
Найдем
критические точки функции:

Точку
мы не рассматриваем, так как функция
определена только в левой окрестности.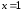

Найдем
вторую производную

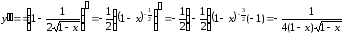
Находим

Таким
образом, на основании (39) делаем вывод
о том, что при
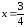
– локальный максимум.

Ответ:
–
локальный максимум.

Задания
8.

Исследовать
на возростание и убывание функции:

1.	2.	3.
4.	5.	6.

Исследовать
на экстремумы функции:

7.
8.
9.
	10.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Найдем производную, дифференцируя функцию $ y(x) $ по переменной $ x $:

$$ (x^2)’_x+ (2xy^2)’_x + (3y^4)’_x = (6)’_x $$

Учитывая, что $ y^2 $ и $ y^4 $ сложные функции продолжаем:

$$ 2x + 2y^2 + 4xyy’ + 12y^3 y’ = 0 $$

Выражаем $ y’ $ из полученного уравнения:

$$ 4xyy’ + 12y^3 y’ = -2x – 2y^2 $$

Выносим $ y’ $ за скобки:

$$ y'(4xy + 12y^3) = -2x – 2y^2 $$

Делим обе части уравнения на выражение $ 4xy+12y^3 $:

$$ y’ = -frac{2x+2y^2}{4xy + 12y^3} = -frac{x+y^2}{2xy+6y^3} $$

Теперь вычисляем значение $ y’ $:

$$ y’ = -frac{1 + (-1)^2}{2cdot 1 cdot (-1) + 6cdot (-1)^3} = -frac{2}{-8} = frac{1}{4} $$

Зная, что $ y’ = frac{1}{4} $ и $ y(x_0) = y(1) = -1 $ составляем уравнения касательной и нормали к кривой в точке $ M(1;-1) $.

Получаем уравнение касательной:

$$ y – (-1) = frac{1}{4} (x – 1) $$

Записываем в красивой форме:

$$ y = frac{1}{4} x – frac{3}{4} $$

Получаем уравнение нормали:

$$ y – (-1) = -frac{1}{frac{1}{4}} (x – 1) $$

Раскрываем скобки и записываем в красивой форме, полученное уравнение:

$$ y+1 = -4(x-1) $$

$$ y = -4x + 3 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$

Итак, искомый тангенс:

$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$

Ответ. $operatorname{tg} phi=frac{1}{7}$

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами.  Для начала ознакомимся с понятием вектора прямой.

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

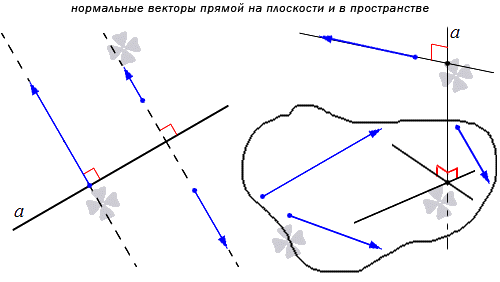
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1.  Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·j→, t∈R, t≠0.

Прямоугольная система Oxyz имеет нормальный вектор i→, относящийся к прямой Оz. Вектор j→ также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный Оz, считается нормальным для Oz.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат Оху выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Если дано уравнение  в отрезках вида xa+yb=1 или уравнение с угловым коэффициентом y=k·x+b, тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Если прямая определена каноническим уравнением прямой на плоскости x-x1ax=y-y1ay или параметрическим x=x1+ax·λy=y1+ay·λ, тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a→=(ax, ay). Возможность нахождения координат нормального вектора n→ возможно, благодаря условию перпендикулярности векторов n→ и a→.

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔ay·x-ax·y+ax·y1-ay·x1x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔ay·x-ax·y+ax·y1-ay·x1=0

Для решения можно выбирать любой удобный способ.

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат Охуz.

Когда прямая задается при помощи уравнений пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, тогда нормальный вектор плоскости относится к A2x+B2y+C2z+D2=0 и A2x+B2y+C2z+D2=0, тогда получаем запись векторов  в виде n1→=(A1, B1, C1) и n2→=(A2, B2, C2).

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x-x1ax=y-y1ay=z-z1az или параметрического, имеющего вид x=x1+ax·λy=y1+ay·λz=z1+az·λ, отсюда ax, ay и az считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a→=(ax, ay, az). Отсюда следует, что нахождение координат нормального  с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a→=(ax, ay, az).