Касательная плоскость и нормаль к поверхности
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0).
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Решение онлайн
- Видеоинструкция
Правила ввода функций:
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
z – z0 = f’x(x0,y0)(x – x0) + f’y(x0,y0)(y – y0)
Вектор ![]() называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
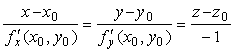
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)
По условию задачи x0 = 0, y0 = 1, тогда z0 = 5
Найдем частные производные функции z = x^3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f’x(x,y) = (x3+5•y)’y = 5
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
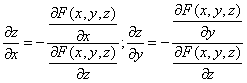
Для нашей функции:
![]()
Тогда:
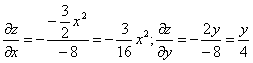
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример. Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
fy’ (x, y) = (y/x + xy – 5x3)’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z= y/x + xy – 5x3
![]()
z0 = 2/(-1) + (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2) ![]() z – 1= –15x – 15 – 2y +4
z – 1= –15x – 15 – 2y +4 ![]() 15x + 2y + z + 10 = 0.
15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0: ![]() .
.
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: ![]() .
.
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z – z0 = f’x(x0,y0,z0)(x – x0) + f’y(x0,y0,z0)(y – y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x2+3•x•y•+y2)’x = 2•x+3•y3
f’x(x,y) = (x2+3•x•y•+y2)’y = 9•x•y2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение
Уравнение нормали онлайн
Уравнение нормали
к графику функции
в точке
,
при условии, что
имеет вид:
Уравнение нормали онлайн
Переменная функции:
Точка в которой необходимо найти нормаль:
Написать уравнение нормали к функцииfxx34x7в точкеx00
Установить калькулятор на свой сайт
Другие полезные разделы:
Решение производных онлайн
Основные правила дифференцирования
Параметрическая производная онлайн
Оставить свой комментарий:
Найти касательную и нормаль онлайн
Здесь можно онлайн найти уравнение касательной и нормали к графику функции в заданной точке, построить график этой функции, касательную и нормальную линию.
Найти касательную к кривой, заданной уравнением на плоскости в заданной точке:
tangent to x e^-x^2 at x=1/3
Найти нормаль к кривой, заданной уравнением на плоскости в заданной точке:
normal line to y=sin(2x)+2cos(x) at x=pi/4
Похожие публикации
2019-11-02 • Просмотров [ 21632 ]
|
Порядок вывода комментариев:
Dmitry Tumanov 2022-05-04 0 №2 (X^3+2)/(x^3-2)
Dmitry Tumanov 2022-05-04 0 №1 33 |
Новые сообщения
Новое в библиотеке
Лучшее на сайте
![]()
Анекдоты и фразы
“Зевнул перед зеркалом. Вызвал рекурсию… “

На поверхности S, заданной уравнением `x^2-y^2-z^2=-1` задана точка M(1;1;1). Вектор (A,B,C)-вектор нормали к поверхности S в точке M.
Известна одна из координат нормали C=4, найдите A=
Для решения данной задачи в поля A или B или C нужно вписать известную координату вектора в данном примере C=4 в остальных двух ячейках
впишите n , в ответе будут расчитаны 3 координаты, вам необходимо выбрать нужную координату и вписать в ответ.
Пример ввода функции:
`x^2-y^2-z^2=-1` M(1;1;1) –>> S=x**2-y**2-z**2=-1 ->> `M_x=1`,`M_y=1`,`M_z=1`
`x^2-3y^2+2z^2=9` M(1;0;2) –>> S=x**2-3*y**2+2*z**2=9 ->> `M_x=1`,`M_y=0`,`M_z=2`
Для решения задач необходима регистрация


Калькулятор онлайн.
Составить уравнение плоскости
Этот калькулятор онлайн составляет (находит) уравнение плоскости по трем точкам, лежащим на плоскости или по нормали и одной точке лежащей на плоскости.
Онлайн калькулятор для нахождения уравнения плоскости не просто даёт ответ задачи, он приводит подробное
решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Общее уравнение плоскости
Пусть заданы:
прямоугольная система координат Oxyz,
произвольная плоскость ( pi );
точка ( M_0(x_0;y_0;z_0) in pi );
вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости ( pi ) (смотри рисунок).

Рассмотрим произвольную точку М(х; у; z). Точка М лежит на плоскости ( pi ) тогда и только тогда, когда векторы
( vec{M_0M} ) и ( vec{N} ) взаимно перпендикулярны. Так как координаты вектора ( vec{M_0M} )
равны ( x-x_0, ; y-y_0, ; z-z_0 ) , то в силу условия перпендикулярности двух векторов (скалярное произведение
должно быть равно нулю) получаем, что точка М (х; у; z) лежит на плоскости ( pi ) тогда и только тогда, когда
( A(x-x_0)+B(y-y_0)+C(z-z_0)=0 tag{1} )
Это и есть искомое уравнение плоскости ( pi ), так как ему удовлетворяют координаты х; у; z любой точки М, лежащей на плоскости ( pi ),
и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.
Раскрывая скобки, приведем уравнение (1) к виду
( Ax+By+Cz+(-Ax_0-By_0-Cz_0)=0 )
Далее, обозначая число ( -Ax_0-By_0-Cz_0 ) через ( D ), получаем
( Ax +By+Cz+D=0 tag{2} )
Уравнение (2) называется общим уравнением плоскости. Таким образом, плоскость является поверхностью первого порядка, так как
определяется уравнением первой степени.
Верно и обратное: всякое уравнение первой степени вида (2) определяет в заданной прямоугольной системе координат плоскость.
Действительно, пусть заданы прямоугольная система координат Oxyz и уравнение ( Ax+By+Cz+D=0 ) с произвольными коэффициентами
А, В, С и D, причем из коэффициентов А, В и С хотя бы один отличен от нуля. Данное уравнение заведомо имеет хотя бы одно решение
( x_0, ; y_0, ; z_0 ) ( если, например, ( C neq 0 ), то, взяв произвольные х0, и y0, из уравнения получим:
( z_0 = -frac{A}{C}x_0 – frac{B}{C}y_0-frac{D}{C} ) ).
Таким образом, существует хотя бы одна точка M0(x0; y0; z0), координаты которой
удовлетворяют уравнению, т.е. Ax0+By0+Cz0+D=0. Вычитая это числовое равенство из уравнения
Ax+By+Cz+D=0, получаем уравнение
A(x-x0) + B(y-y0) + C(z-z0) + D=0,
эквивалентное данному. Полученное уравнение (а стало быть, и уравнение Ax+By+Cz+D=0 ) совпадает с уравнением (1) и, значит, определяет
плоскость ( pi ), проходящую через точку M0(x0 и перпендикулярную вектору ( vec{N}(A;B;C) ).
Вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости, называется нормальным вектором или нормалью этой плоскости.
Теорема
Если два уравнения ( A_1x+B_1y+C_1z+D_1=0 ) и ( A_2x+B_2y+C_2z+D_2=0 ) определяют одну и ту же плоскость, то их коэффициенты
пропорциональны, т.е.
$$ frac{A_2}{A_1} = frac{B_2}{B_1} = frac{C_2}{C_1} = frac{D_2}{D_1} $$
Угол между двумя плоскостями
Рассмотрим две плоскости ( pi_1 ), и ( pi_2 ), заданные соответственно уравнениями
( A_1x+B_1y+C_1z+D_1=0, ;; A_2x+B_2y+C_2z+D_2=0 )
При любом расположении плоскостей ( pi_1 ), и ( pi_2 ) в пространстве один из углов ( varphi )
между ними равен углу между их нормалями ( vec{N_1}(A_1;B_1;C_1) ) и ( vec{N_2}(A_2;B_2;C_2) ) и вычисляется по
следующей формуле:
$$ cos varphi = frac{ vec{N_1} cdot vec{N_2}}{ |vec{N_1}| |vec{N_2}| } =
frac{A_1 A_2 + B_1 B_2 + C_1 C_2}{sqrt{A_1^2 + B_1^2 + C_1^2} ; sqrt{A_2^2 + B_2^2 + C_2^2} } tag{3} $$
Второй угол равен ( 180^circ -cos varphi )
Условие параллельности плоскостей
Если плоскости ( pi_1 ) и ( pi_2 ) параллельны, то коллинеарны их нормали ( vec{N_1} ) и
( vec{N_2} ), и наоборот. Но тогда
$$ frac{A_1}{A_2} = frac{B_1}{B_2} = frac{C_1}{C_2} tag{4} $$
Условие (4) является условием параллельности плоскостей ( pi_1 ) и ( pi_2 )
Условие перпендикулярности плоскостей
Если плоскости ( pi_1 ) и ( pi_2 ) взаимно перпендикулярны, то их нормали ( vec{N_1} ) и
( vec{N_2} ) также перпендикулярны, и наоборот. Поэтому из формулы (3) непосредственно получаем условие
перпендикулярности плоскостей ( pi_1 ) и ( pi_2 ):
( A_1 A_2 + B_1 B_2 + C_1 C_2 = 0 )
