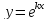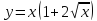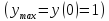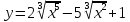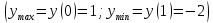VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x”(t_0) & y”(t_0) & z”(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Окружность. Форма и положение.
Окружность – это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.
Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности – это радиусы.
Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.
Всякая хорда (AD), прочерченная через центр – диаметр.
Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.
Какая-нибудь часть окружности (напр. EmF ) называется дугой.
О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.
Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.
Часть плоскости, ограниченная окружностью, именуют кругом.
Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.
Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги, заключенные между параллельными хордами, равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема. Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой.
Из предыдущего следует, что окружность есть кривая линия.
2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности.
Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
Как найти нормаль окружности
Предположим, что функция (y = fleft( x right)) определена на интервале (left( right)) и непрерывна в точке ( in left( right).) В этой точке (точка (M) на рисунке (1)) функция имеет значение ( = fleft( <> right).)
Пусть независимая переменная в точке () получает приращение (Delta x.) Соответствующее приращение функции (Delta y) выражается формулой [Delta y = fleft( <+ Delta x> right) – fleft( <> right).] На рисунке (1) точка () имеет координаты (left( <+ Delta x, + Delta y> right).) Построим секущую (M.) Ее уравнение имеет вид [y – = kleft( > right),] где (k) − угловой коэффициент, зависящий от приращения (Delta x) и равный [k = kleft( <Delta x>right) = frac<<Delta y>><<Delta x>>.] При уменьшении (Delta x) точка () стремится к точке (M:) ( to M.) В пределе (Delta x to 0) расстояние между точками (M) и () стремится к нулю. Это следует из непрерывности функции (fleft( x right)) в точке (:) [ <limlimits_<Delta x to 0>Delta y = 0,>;; <Rightarrow limlimits_<Delta x to 0>left| > right| > = <limlimits_<Delta x to 0>sqrt <<<left( <Delta x>right)>^2> + <<left( <Delta y>right)>^2>> = 0.> ] Предельное положение секущей (M) как раз и представляет собой касательную прямую к графику функции (y = fleft( x right)) в точке (M.)
Возможны два вида касательных − наклонные и вертикальные .
Определение (1) .
Если существует конечный предел (limlimits_ <Delta x to 0>kleft( <Delta x>right) = ,) то прямая, имеющая уравнение [y – = kleft( > right),] называется наклонной касательной к графику функции (y = fleft( x right)) в точке (left( <,> right).)
Определение 2 .
Если предельное значение (k) при (Delta x to 0) является бесконечным: (limlimits_ <Delta x to 0>kleft( <Delta x>right) = pm infty,) то прямая, имеющая уравнение [x = ,] называется вертикальной касательной к графику функции (y = fleft( x right)) в точке (left( <,> right).)
Важно отметить, что [ <= limlimits_ <Delta x to 0>kleft( <Delta x>right) > = <limlimits_<Delta x to 0>frac<<Delta y>><<Delta x>> > = > right),> ] то есть угловой коэффициент касательной равен значению производной функции (fleft( <> right)) в точке касания (.) Поэтому уравнение наклонной касательной можно записать в таком виде: [ = f’left( <> right)left( > right);;text<или>>;; > right)left( > right) + fleft( <> right).> ] Поскольку угловой коэффициент прямой равен тангенсу угла наклона (alpha,) который прямая образует с положительным направлением оси абсцисс, то справедливо следующее тройное равенство: [k = tan alpha = f’left( <> right).]
Прямая, перпендикулярная касательной и проходящая через точку касания (left( <,> right),) называется нормалью к графику функции (y = fleft( x right)) в этой точке (рисунок (2)).
Из геометрии известно, что произведение угловых коэффициентов перпендикулярных прямых равно (-1.) Поэтому, зная уравнение касательной в точке (left( <,> right):) [y – = f’left( <> right)left( > right),] можно сразу записать уравнение нормали в виде [y – = – frac<1><> right)>>left( > right).]
Предположим, что кривая задана полярным уравнением (r = fleft( theta right),) выражающим зависимость длины радиуса-вектора (r) от полярного угла (theta.) В декартовых координатах такая кривая будет описываться системой уравнений [left< begin x = rcos theta = fleft( theta right)cos theta \ y = rsin theta = fleft( theta right)sintheta end right..] Таким образом, мы записали уравнение кривой в параметрической форме, где роль параметра играет угол (theta.) Далее легко получить выражение для углового коэффициента касательной, проведенной к кривой в точке (left( <,> right):) [ >><<>> > = <frac<<<<left( right)>^prime >>> <<<<left( right)>^prime >>> > = <frac<<sin theta + rcos theta >><<costheta – rsin theta >>.> ] В результате уравнения касательной и нормали будут записываться в следующем виде: [ = frac<<>><<>>left( > right)>;;; <(text<касательная>),> ] [ = -frac<<>><<>>left( > right)>;;; <(text<нормаль>).> ] Исследование кривой можно провести непосредственно в полярных координатах без перехода к декартовой системе. В таком случае наклон касательной удобно определять не углом (theta) с полярной осью (т.е. с положительным направлением оси абсцисс), а углом (beta) с прямой, содержащей радиус-вектор (r) (рисунок (3)).
Тангенс угла (beta) вычисляется по формуле [tan beta = frac<<>>.] Угол, образованный нормалью с продолженным радиусом-вектором, равен (beta + largefrac<pi ><2>normalsize.) По формуле приведения получаем: [ <tan left( <beta + frac<pi ><2>> right) > = < – cot beta = – frac<1><<tan beta >> > = < – frac<<>>.> ]
[spoiler title=”источники:”]
http://www.calc.ru/Okruzhnost-Forma-I-Polozheniye.html
http://www.math24.ru/%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F-%D0%BA%D0%B0%D1%81%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B9-%D0%B8-%D0%BD%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D0%B8.html
[/spoiler]
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given three integers a, b, c representing coefficients of the equation x2 + y2 + ax + by + c = 0 of a circle, the task is to find the equation of the normal to the circle from a given point (x1, y1).
Note: Normal is a line perpendicular to the tangent at the point of contact between the tangent and the curve.

Examples:
Input: a = 4, b = 6, c = 5, x1 = 12, y1 = 14
Output: y = 1.1x + 0.8Input: a = 6, b = 12, c = 5, x1 = 9, y1 = 3
Output: y = -0.5x + 7.5
Approach: Follow the steps below to solve the problem:
- The normal to a circle passes through the center of the circle.
- Therefore, find the coordinates of the center of the circle (g, f), where g = a/2 and f = b/2.
- Since the center of the circle and the point where the normal is drawn lie on the normal, calculate the slope of the normal (m) as m = (y1 – f) / (x1 – g).
- Hence, the equation of the normal is y – y1 = m * (x – x1).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double normal_slope(double a, double b,
double x1, double y1)
{
double g = a / 2;
double f = b / 2;
if (g - x1 == 0)
return (-1);
double slope = (f - y1) / (g - x1);
if (slope == 0)
return (-2);
return slope;
}
void normal_equation(double a, double b,
double x1, double y1)
{
double slope = normal_slope(a, b, x1, y1);
if (slope == -1) {
cout << "x = " << x1;
}
if (slope == -2) {
cout << "y = " << y1;
}
if (slope != -1 && slope != -2) {
x1 *= -slope;
x1 += y1;
if (x1 > 0)
cout << "y = " << slope
<< "x + " << x1;
else
cout << "y = " << slope
<< "x " << x1;
}
}
int main()
{
int a = 4, b = 6, c = 5;
int x1 = 12, y1 = 14;
normal_equation(a, b, x1, y1);
return 0;
}
Java
import java.util.*;
class GFG{
static double normal_slope(double a, double b,
double x1, double y1)
{
double g = a / 2;
double f = b / 2;
if (g - x1 == 0)
return (-1);
double slope = (f - y1) / (g - x1);
if (slope == 0)
return (-2);
return slope;
}
static void normal_equation(double a, double b,
double x1, double y1)
{
double slope = normal_slope(a, b, x1, y1);
if (slope == -1)
{
System.out.print("x = " + x1);
}
if (slope == -2)
{
System.out.print("y = " + y1);
}
if (slope != -1 && slope != -2)
{
x1 *= -slope;
x1 += y1;
if (x1 > 0)
System.out.print("y = " + slope +
"x + " + x1);
else
System.out.print("y = " + slope +
"x " + x1);
}
}
public static void main(String[] args)
{
int a = 4, b = 6;
int x1 = 12, y1 = 14;
normal_equation(a, b, x1, y1);
}
}
Python3
def normal_slope(a, b, x1, y1):
g = a / 2
f = b / 2
if (g - x1 == 0):
return (-1)
slope = (f - y1) / (g - x1)
if (slope == 0):
return (-2)
return slope
def normal_equation(a, b, x1, y1):
slope = normal_slope(a, b, x1, y1)
if (slope == -1) :
print("x = ", x1)
if (slope == -2) :
print("y = ", y1)
if (slope != -1 and slope != -2):
x1 *= -slope
x1 += y1
if (x1 > 0) :
print("y = ", slope, "x + ", x1)
else :
print("y = ", slope, "x ", x1)
a = 4
b = 6
c = 5
x1 = 12
y1 = 14
normal_equation(a, b, x1, y1)
C#
using System;
class GFG{
static double normal_slope(double a, double b,
double x1, double y1)
{
double g = a / 2;
double f = b / 2;
if (g - x1 == 0)
return (-1);
double slope = (f - y1) / (g - x1);
if (slope == 0)
return (-2);
return slope;
}
static void normal_equation(double a, double b,
double x1, double y1)
{
double slope = normal_slope(a, b, x1, y1);
if (slope == -1)
{
Console.WriteLine( "x = " + x1);
}
if (slope == -2)
{
Console.WriteLine("y = " + y1);
}
if (slope != -1 && slope != -2)
{
x1 *= -slope;
x1 += y1;
if (x1 > 0)
Console.WriteLine("y = " + slope +
"x +" + Math.Round(x1, 2));
else
Console.WriteLine("y = " + slope +
"x " + Math.Round(x1, 2));
}
}
public static void Main(String []args)
{
int a = 4, b = 6;
int x1 = 12, y1 = 14;
normal_equation(a, b, x1, y1);
}
}
Javascript
<script>
function normal_slope( a, b, x1, y1)
{
var g = a / 2;
var f = b / 2;
if (g - x1 == 0)
return (-1);
var slope = (f - y1) / (g - x1);
if (slope == 0)
return (-2);
return slope;
}
function normal_equation( a, b, x1, y1)
{
var slope = normal_slope(a, b, x1, y1);
if (slope == -1) {
document.write("x = " + x1);
}
if (slope == -2) {
document.write("y = " + y1);
}
if (slope != -1 && slope != -2) {
x1 *= -slope;
x1 += y1;
if (x1 > 0)
document.write(
"y = " + slope + "x + " + x1.toFixed(1)
);
else
document.write(
"y = " + slope+ "x " + x1.toFixed(1)
);
}
}
var a = 4, b = 6, c = 5;
var x1 = 12, y1 = 14;
normal_equation(a, b, x1, y1);
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
Last Updated :
20 Oct, 2022
Like Article
Save Article
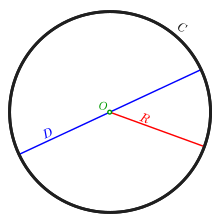
Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Построение окружности циркулем
Практическое построение окружности возможно с помощью циркуля.
Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква 
Хорды, дуги и касательные[править | править код]
Хорды и дуги[править | править код]
-
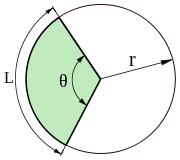
Секторы круга
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: 
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.
Взаимное расположение прямой и окружности[править | править код]

Если расстояние от центра окружности до прямой равно радиусу, то прямая и окружность имеют одну точку пересечения, которая называется точкой касания. Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведённому в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности[5].
Если расстояние от центра окружности до прямой меньше радиуса, то прямая пересекает окружность в двух точках и называется секущей.
Если расстояние от центра окружности до прямой больше радиусу, то окружность и прямая не имеют точек пересечения.
Углы[править | править код]
-
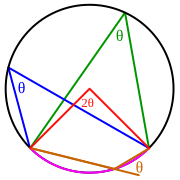
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
-

К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Вписанный угол — угол, вершина которого принадлежит окружности, а стороны пересекают эту окружность. Говорят, что центральный или вписанный углы опираются на дугу, высекаемую на окружности их лучами, или же на хорду, стягивающую эту дугу.
Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.
Из определения радиана следует, что длина 





Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.
Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.
Свойства вписанных углов:
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
- Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Другие свойства:
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
- Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.
Свойства[править | править код]

Формулы[править | править код]
Если радиус круга равен 1, то его окружность равна 2π.
Длина окружности:
Радиус окружности:
Диаметр окружности:
Площадь круга радиуса R:
Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:
Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:
История[править | править код]
Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.
Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.
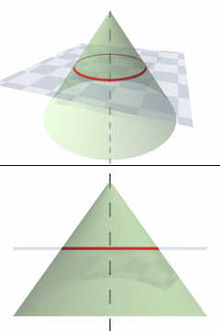
Окружность получается как сечение конуса плоскостью, перпендикулярной его оси
Аналитическая геометрия окружностей[править | править код]
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.
Декартовы координаты[править | править код]

Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Общее уравнение окружности записывается как:
или
где
Точка 

Уравнение окружности радиуса 
Уравнение окружности, проходящей через точки 
Тогда в явном виде координаты центра окружности определяются по формулам:
Окружность также можно описать с помощью параметрического уравнения:
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
Если центр окружности совпадает с началом координат, функции принимают вид:
Полярные координаты[править | править код]
Окружность радиуса 

Если полярные координаты центра окружности 
Если же центр является началом координат, то уравнение будет иметь вид
Комплексная плоскость[править | править код]
На комплексной плоскости окружность задаётся формулой:
или в параметрическом виде
Окружности в пространстве[править | править код]
В пространстве окружность радиуса 

плоскостью
,
где 
Например, при 
Касательные и нормали[править | править код]
Уравнение касательной к окружности в точке 
Уравнение нормали в той же точке можно записать как
Концентрические окружности[править | править код]

Концентрические окружности
Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:
являются концентрическими в том и только в том случае, когда 

Дополнительные сведения[править | править код]
Определение треугольников для одной окружности[править | править код]

- Треугольник ABC называется вписанным в окружность (A,B,C), если все три его вершины A, B и C лежат на этой окружности. При этом окружность называется описанной окружностью треугольника ABC (См. Описанная окружность).
- Касательная к окружности, проведённая через любую вершину вписанного в неё треугольника, антипараллельна стороне треугольника, противоположной данной вершине.
- Треугольник ABC называется описанным около окружности (A’,B’,C’), если все три его стороны AB, BC и CA касаются этой окружности в некоторых точках соответственно C’ , A’ и B’ . При этом окружность называется вписанной окружностью треугольника ABC (См. Вписанная окружность).
- Треугольник ABC называется внеописанным для окружности (A’,B’,C’), если все 3 его стороны AB, BC и CA касаются этой окружности в некоторых точках соответственно C’ , A’ и B’ , а именно: одной из 2 сторон касается непосредственно, а также продолжений 2 других сторон за пределы треугольника. При этом окружность называется вневписанной окружностью треугольника ABC (См. Вневписанная окружность).
Варианты определения окружности[править | править код]
- Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом (Определение через угол, опирающийся на диаметр окружности).
- Окружность с хордой AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под постоянным углом с одной стороны, равным вписанному углу дуги AB, и под другим постоянным углом с другой стороны, равным 180 градусов минус вписанный угол дуги AB, указанный выше (Определение через вписанный угол).
- Фигура состоящая из таких точек
что отношение длин отрезков AX и BX постоянно:
является окружностью (Определение через окружность Аполлония).
- Фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками, также является окружностью (Определение через теорему Пифагора для произвольного прямоугольного треугольника, вписанного в окружность, с гипотенузой, являющейся диаметром окружности).
- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку E внутри неё провести любые хорды AB, CD, GF и т. д., тогда справедливы равенства:
(см. рис.). Равенства всегда будут выполняться независимо от выбора точки E и направлений проведённых через неё хорд (Определение через пересекающиеся хорды).

- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку M вне её провести две касательные до точек их касания с окружностью, например, A и B, тогда их длины всегда будут равны:
. Равенство всегда будет выполняться независимо от выбора точки M (Определение через равные касательные).
- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Отношение длины любой её хорды к синусу любого её вписанного угла, опирающегося на эту хорду, есть величина постоянная, равная диаметру этой окружности (Определение через теорему синусов).
- Окружность — это частный случай эллипса, у которого расстояние между фокусами равно нулю (Определение через вырожденный эллипс).
- Окружность есть Синусоидальная спираль при
.
Связанные определения для двух окружностей[править | править код]
- Две окружности, имеющие общий центр, называются концентрическими.
- Две окружности, имеющие лишь одну общую точку, называются касающимися внешним образом, если их круги не имеют других общих точек, и внутренним образом, если их круги лежат один внутри другого.
- Две окружности, имеющие две общие точки, называются пересекающимися. Их круги (ими ограниченные) пересекаются по области, называемой двойным круговым сегментом.
- Углом между двумя пересекающимися (или касающимися) окружностями называется угол между их касательными, проведёнными в общей точке пересечения (или касания).
- Также углом между двумя пересекающимися (или касающимися) окружностями можно считать угол между их радиусами (диаметрами), проведёнными в общей точке пересечения (или касания).
- Поскольку для любой окружности её радиус (или диаметр) и касательная, проведённые через любую точку окружности, взаимно перпендикулярны, то радиус (или диаметр) можно считать нормалью к окружности, построенной в данной её точке. Следовательно, два типа углов, определённых в двух предыдущих двух пунктах, всегда будут равны между собой, как углы со взаимно перпендикулярными сторонами.
- Радикальная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведённых к двум данным окружностям из любой точки M данного геометрического места точек.
Определения углов для двух окружностей[править | править код]
- Угол между двумя пересекающимися окружностями — угол между касательными к окружностям в точке пересечения этих окружностей. Оба угла между двумя пересекающимися окружностями равны.
- Угол между двумя непересекающимися окружностями — угол между двумя общими касательными к двум окружностям, образуемый в точке пересечения этих двух касательных. Точка пересечения этих двух касательных должна лежать между двумя окружностями, а не со стороны одной из них (этот угол не рассматривается). Оба вертикальных угла между двумя непересекающимися окружностями равны.
Ортогональность (перпендикулярность)[править | править код]

Две окружности, пересекающиеся под прямым углом, называются ортогональными (перпендикулярными). Две окружности, заданные уравнениями:
являются ортогональными тогда и только тогда, когда выполняется условие:
Другими словами, две пересекающиеся в точках A и B окружности с центрами O и O’ называются ортогональными, если являются прямыми углы OAO’ или OBO’ . Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведённые в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведённые в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведённому в точку касания. Обычно угол между кривыми — это угол между их касательными, проведёнными в точке их пересечения.
Связанные определения для трёх окружностей[править | править код]
- Три окружности называются взаимно касающимися (пресекающимися), если любые две из них касаются (пресекаются) друг друга.
- В геометрии радикальный центр трёх окружностей — это точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данные окружности ортогонально.
Лемма Архимеда[править | править код]
Лемма Архимеда. Если окружность вписана в сегмент окружности, стягиваемый хордой 




Лемма Архимеда играет важную роль при построении изоциркулярного преобразования.
Доказательство
Пусть 


















Теорема Декарта для радиусов четырёх попарно касающихся окружностей[править | править код]
Теорема Декарта утверждает, что радиусы любых четырёх взаимно касающихся окружностей удовлетворяют некоторому квадратному уравнению.
Их иногда называют окружностями Содди.
Движение по окружности[править | править код]
Многомерное обобщение[править | править код]
Обобщённую окружность можно определить для любой математической структуры, где задано понятие расстояния. В частности, обобщением для многомерного евклидова пространства является гиперсфера; в трёхмерном пространстве это обычная сфера. В сферической геометрии важную роль играют окружности на сфере, центр которых совпадает с центром сферы («большие круги»).
В культуре и мистике[править | править код]
Окружность, наряду с близкими понятиями круга, кольца и сферы, с глубокой древности считалась божественным символом высшего совершенства, символом красоты и равенства. Античные астрономы были убеждены, что небесные светила размещены на вращающихся сферах и, таким образом, движутся по окружностям. Рыцари короля Артура сидели за круглым столом, что подчёркивало их равноправие[7].
В египетской мифологии бог-творец Хнум вылепил людей на гончарном круге. В Книге Притчей Соломоновых говорится, что при сотворении мира Бог «проводил круговую черту по лицу бездны» (Прит. 8:27). Для защиты от «нечистой силы» полагалось очертить вокруг себя окружность (магический круг). На изображениях христианских святых их лица окружены круглым нимбом. Преисподняя во многих религиях состоит из концентрических кругов, что символизирует безысходность. В Стоунхендже и других кромлехах камни расставлены по окружности[7][8].
В различных мистических доктринах окружность часто символизирует бесконечность и цикличность существования (уроборос, Сансара), равновесие (инь/ян), стабильность и др.[9]. Похожий смысл усматривается в идиомах и поговорках многих народов, например: «круглый год», «круг общения», «порочный круг», «круговая порука» и т. п. Вероятно, широко распространённый обычай обмениваться кольцами между женихом и невестой символизирует вечность чувств, устойчивость семьи[8][10].
Окружность используется в графике многих символов, например, в знаке пацифизма, символе охраны авторского права (©) и т. д.
См. также[править | править код]
- Глоссарий планиметрии: О
- Вневписанная окружность
- Вписанная и вневписанные в треугольник окружности
- Вписанные и описанные фигуры для треугольника
- Вписанная окружность
- Категория:Окружности — основные понятия и теоремы для окружностей
- Описанная окружность
- Циклоида
- 360° (значения)
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1984, с. 15—16.
- ↑ Элементарная математика, 1976, с. 408—409.
- ↑ 1 2 3 Элементарная математика, 1976, с. 410—411.
- ↑ Элементарная математика, 1976, с. 409—410.
- ↑ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Геометрия. 7—9 классы: учебник для общеобразовательных учреждений. — 19-е изд. — М.: Просвещение, 2009. — С. 167. — 384 с. — ISBN 978-5-09-021136-9.
- ↑ Элементарная математика, 1976, с. 510.
- ↑ 1 2 Яковлева Т. С., Деменок С. Л. Структуры и символы (Абстракция – эмпирический факт). — СПб.: Страта, 2020. — С. 65—69. — 232 с. — (Просто). — ISBN 978-5-907314-11-5.
- ↑ 1 2 Круг Архивная копия от 5 августа 2021 на Wayback Machine.
- ↑ Abdullahi, Yahya (October 29, 2019), The Circle from East to West, in Charnier, Jean-François, The Louvre Abu Dhabi: A World Vision of Art, Rizzoli International Publications, Incorporated, ISBN 9782370741004.
- ↑ Круг. Дата обращения: 17 марта 2022. Архивировано 24 января 2022 года.
Литература[править | править код]
- Атанасян Л. С., Бутузов В. Ф.. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М.: Вита-Пресс, 2003.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70.
- Маркушевич А. И. Замечательные кривые, выпуск 4. — М.: Гостехиздат, 1952. — 32 с. Архивная копия от 14 сентября 2008 на Wayback Machine
- Окружность // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
Ссылки[править | править код]
- Окружность Архивная копия от 8 мая 2017 на Wayback Machine на www.univer.omsk.su.
- Круг и окружность Архивная копия от 17 марта 2017 на Wayback Machine на сайте Метмат (методика преподавания математики).
Рассмотрим
кривую, уравнение которой имеет вид

Уравнение
касательной к данной кривой в точке
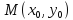 имеет вид:
имеет вид:
 (34)
(34)
Нормалью
к кривой в данной точке называется
прямая, проходящая через данную точку,
перпендикулярную к касательной в этой
точке.
Уравнение
нормали к данной кривой в точке
 имеет вид:
имеет вид:
 (35)
(35)
Длина
отрезка касательной, заключенного между
точкой касания и осью абсцисс называется
длиной
касательной,
проекция этого отрезка на ось абсцисс
называется подкасательной.
Длина
отрезка нормали, заключенного между
точкой касания и осью абсцисс называется
длиной
нормали,проекция
этого отрезка на ось абсцисс называется
поднормалью.
Пример
17
Написать
уравнения касательной и нормали к кривой
 в точке, абсцисса которой равна
в точке, абсцисса которой равна .
.
Решение:
Найдем
значение функции в точке
 :
:

Найдем
производную заданной функции в точке

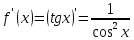

Уравнение
касательной найдем по формуле (34):

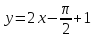
Уравнение
нормали найдем по формуле (35):


Ответ:
Уравнение
касательной :
Уравнение
нормали : .
.
Пример
18
Написать
уравнения касательной и нормали, длины
касательной и подкасательной, длины
нормали и поднормали для эллипса

в
точке
 ,
,
для которой .
.
Решение:
Найдем
 как производную функции, заданной
как производную функции, заданной
параметрически по формуле (10):



Найдем
координаты точки касания
 :
:
и значение производной в точке касания
 :
:



Уравнение
касательной найдем по формуле (34):

Найдем
координаты
 точки
точки пересечения
пересечения
касательной с осью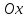 :
:

Длина
касательной равна длине отрезка
 :
:
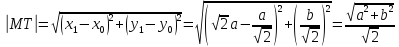
Согласно
определению, подкасательная
 равна
равна

Где
угол
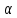 – угол между касательной и осью
– угол между касательной и осью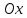 . Поэтому,
. Поэтому, – угловой коэффициент касательной,
– угловой коэффициент касательной,
равный

Таким
образом, подкасательная
 равна
равна
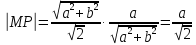
Уравнение
нормали найдем по формуле (35):

Найдем
координаты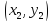 точки
точки пересечения нормали с осью
пересечения нормали с осью :
:

Длина
нормали равна длине отрезка
 :
:
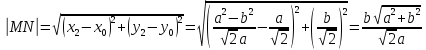
Согласно
определению, поднормаль
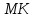 равна
равна

Где
угол
 – угол между нормалью и осью
– угол между нормалью и осью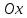 . Поэтому,
. Поэтому, – угловой коэффициент нормали, равный
– угловой коэффициент нормали, равный
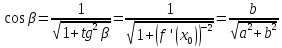
Поэтому,
поднормаль
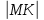 равна:
равна:

Ответ:
Уравнение
касательной :

Уравнение
нормали :
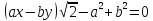
Длина
касательной
 ;
;
подкасательная ;
;
Длина
нормали
 ; поднормаль
; поднормаль
Задания
7. Написать
уравнения касательной и нормали:
1. К параболе в точке, абсцисса которой
 .
.
2.
К окружности
 в точках пересечения её с осью абсцисс
в точках пересечения её с осью абсцисс
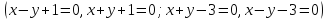 .
.
3.
К циклоиде
 в точке, для которой
в точке, для которой
 .
.
4.
В каких точках кривой
 касательная параллельна:
касательная параллельна:
а)
оси Оx; б) прямой
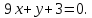
 .
.
10.
Промежутки монотонности функции.
Экстремумы функции.
Условие
монотонности функции:
Для
того, чтобы дифференцируемая на
 функция
функция не возрастала, необходимо и достаточно,
не возрастала, необходимо и достаточно,
чтобы во всех точках, принадлежащих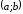 ее производная была неположительна .
ее производная была неположительна .
 (36)
(36)
Для
того, чтобы дифференцируемая на
 функция
функция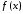 не убывала, необходимо и достаточно,
не убывала, необходимо и достаточно,
чтобы во всех точках, принадлежащих ее производная была неотрицательна.
ее производная была неотрицательна.
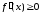 (37)
(37)
Промежутки,
на которых производная функции сохраняет
определенный знак, называются промежутками
монотонности
функции

Пример
19
Найти
промежутки монотонности функции
 .
.
Решение:
Найдем
производную функции
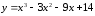 .
.

Найдем
промежутки знакопостоянства полученной
производной. Для этого
разложим полученный
квадратный трехчлен на множители:
 .
.
Исследуем
знак полученного выражения, используя
метод интервалов.

Таким
образом, получаем согласно (36), (37),что
заданная функция возрастает на
 и убывает на
и убывает на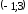 .
.
Ответ:
Заданная
функция
 возрастает на
возрастает на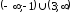 и убывает на
и убывает на .
.
Определение
Функция
 имеет в точке
имеет в точке локальный
локальный
максимум (минимум),
если существует такая окрестность
точки

 ,
,
что для всех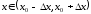 выполняется условие
выполняется условие
( ).
).
Локальный
минимум или максимум функции
 называетсялокальным
называетсялокальным
экстремумом.
Необходимое
условие существования экстремума.
Пусть
функция
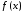 определена в некоторой окрестности
определена в некоторой окрестности
точки .
.
Если функция имеет
имеет
в точке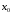 экстремумом, то производная
экстремумом, то производная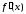 в точке
в точке либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Точка
 называетсякритической
называетсякритической
точкой
функции
 ,
,
если производная в точке
в точке либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Достаточные
условия наличия экстремума в критической
точке
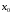 .
.
Пусть
точка
 является критической.
является критической.
Первое
достаточное условие экстремума:
Пусть
функция
 непрерывна в некоторой окрестности
непрерывна в некоторой окрестности точки
точки и дифференцируема в каждой точке
и дифференцируема в каждой точке .
.
Точка
 является локальным максимумом, если
является локальным максимумом, если
при переходе через
производная
функции меняет знак с плюса на минус.
Точка
 является локальным минимумом, если при
является локальным минимумом, если при
переходе через
производная
функции меняет знак с минуса на плюс.
Пример
20
Найти
экстремумы функции
 .
.
Решение:
Найдем
производную заданной функции

Приравнивая
в полученной производной к нулю числитель
и знаменатель, найдем критические точки:

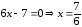
Исследуем
знак производной, используя метод
интервалов.


Из
рисунка видно, что при переходе через
точку
 производная меняет знак с плюса на
производная меняет знак с плюса на
минус. Следовательно, в точке –
–
локальный максимум.
При
переходе через точку
 производная меняет знак с минуса на
производная меняет знак с минуса на
плюс.
Следовательно,
в точке
 –
–
локальный минимум.
При
переходе через точку
 производная не меняет знак. Следовательно,
производная не меняет знак. Следовательно,
критическая точка не является экстремумом заданной
не является экстремумом заданной
функции.
Ответ:
 –
–
локальный максимум,
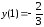 –
–
локальный минимум.
Второе
достаточное условие экстремума:
Если
первые
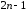 производные функции
производные функции в точке
в точке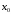 равны нулю, а
равны нулю, а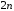 -ная
-ная
производная функции в точке
в точке отлична от нуля, то точка
отлична от нуля, то точка является экстремумом функции
является экстремумом функции ,
,
причем,
если
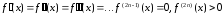 ,
,
(38)
то
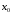 -локальный
-локальный
минимум
если
 ,
,
(39)
то
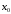 -локальный
-локальный
максимум.
Пример
21
Найти
экстремумы функции, пользуясь второй
производной
 .
.
Решение:
ОДЗ:
 .
.
Найдем
первую производную заданной функции
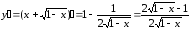
Найдем
критические точки функции:

Точку
 мы не рассматриваем, так как функция
мы не рассматриваем, так как функция
определена только в левой окрестности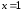 .
.
Найдем
вторую производную
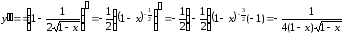
Находим

Таким
образом, на основании (39) делаем вывод
о том, что при
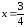
 – локальный максимум.
– локальный максимум.
Ответ:
 –
–
локальный максимум.
Задания
8.
Исследовать
на возростание и убывание функции:
|
1. |
2. |
3. |
|
4. |
5. |
6. |
Исследовать
на экстремумы функции:
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мастер
(1171),
закрыт
13 лет назад
” />
Дополнен 14 лет назад

Дополнен 14 лет назад
Нужно построить линию пересечения поверхностей методом концентрических сфер. Не могу определить Rmin
BeardMax
Просветленный
(26657)
14 лет назад
Нормаль к дуге окружности всегда проходит через ее центр.
Сначала найди центр окружности. Для этого из двух произвольных точек на дуге (например A и B) проведи окружности радиусом 140. Точка их пересечения С и есть центр окружности дуги АВ.
Прямая СО нормальна к дуге АВ.
Отрезок ОD и есть искомый Rmin.
























![{begin{cases}x=x_{0}+{dfrac {R}{{sqrt {a^{2}+c^{2}}}}}cdot !left(ccdot cos t-{dfrac {acdot bcdot sin t}{{sqrt {a^{2}+b^{2}+c^{2}}}}}right)!,\[10pt]y=y_{0}+{dfrac {Rcdot {sqrt {a^{2}+c^{2}}}}{{sqrt {a^{2}+b^{2}+c^{2}}}}}cdot sin t,\[10pt]z=z_{0}-{dfrac {R}{{sqrt {a^{2}+c^{2}}}}}cdot !left(acdot cos t+{dfrac {bcdot ccdot sin t}{{sqrt {a^{2}+b^{2}+c^{2}}}}}right)!,end{cases}}tin [0;2pi ).](https://wikimedia.org/api/rest_v1/media/math/render/svg/c12fa86cb1797c21874c93d0344e32228f0acf62)