Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Уравнение касательной плоскости и нормали к поверхности
Как найти?
Постановка задачи
Найти уравнение касательной плоскости и нормали к поверхности $ F(x,y,z) = 0 $ в точке $ M(x_0,y_0,z_0) $
План решения
Уравнение касательной плоскости к поверхности записывается следующем образом:
$$ F’_x bigg |_M (x-x_0) + F’_y bigg |_M (y-y_0) + F’_z bigg |_M (z-z_0) = 0 $$
Уравнение нормали к поверхности составляется по формуле:
$$ frac{x-x_0}{F’_x Big |_M} = frac{y-y_0}{F’_y Big |_M} = frac{z-z_0}{F’_z Big |_M} $$
- Находим частные производные $ F’_x, F’_y, F’_z $ в точке $ M(x_0,y_0,z_0) $
- Подставляем найденные значения производных в формулы для составления уравнений
ЗАМЕЧАНИЕ
Если в условии задачи задана точка $ M (x_0,y_0) $ с двумя координатами, то необходимо дополнительно вычислить координату $ z_0 $ из уравнения $ F(x_0,y_0,z_0) = 0 $, подставив в него известные координаты $ x_0 $ и $ y_0 $.
Примеры решений
| Пример 1 |
| Найти уравнение касательной плоскости и нормали к поверхности $ z = x^2 + y^2 $ в точке $ M(1,-2,5) $ |
| Решение |
|
Переносим $ z $ в правую часть и записываем поверхность в виде: $$ F(x,y,z) = x^2 + y^2 – z $$ Находим частные производные первого порядка функции $ F(x,y,z) $: $$ F’_x = 2x $$ $$ F’_y = 2y $$ $$ F’_z = -1 $$ Вычисляем значения полученных производных в точке $ M(1,-2,5) $: $$ F’_x Big |_M = F’_x(1,-2,5) = 2 cdot 1 = 2 $$ $$ F’_y Big |_M = F’_y (1,-2,5) = 2 cdot (-2) = -4 $$ $$ F’_z Big |_M = F’_z (1,-2,5) = -1 $$ Подставляем полученные данные в формулу касательной плоскости: $$ 2(x-1) + (-4)(y+2) + (-1)(z-5) = 0 $$ Раскрываем скобки и записываем окончательное уравнение плоскости: $$ 2x – 4y – z – 5 = 0 $$ Теперь запишем уравнение нормали к поверхности с помощью второй формулы: $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ 2x – 4y – z – 5 = 0 $$ $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$ |
| Пример 2 |
| Составить уравнение касательной плоскости и нормали к поверхности $ z = e^{xcos y} $ в точке $ M(1,pi, frac{1}{e}) $ |
| Решение |
|
Записываем поверхность в виде: $$ F = e^{xcos y} – z $$ Находим частные производные от функции $ F(x,y,z) $: $$ F’_x = e^{xcos y} cdot (xcos y)’_x = cos y e^{xcos y} $$ $$ F’_y = e^{xcos y} cdot (xcos y)’_y = -xsin y e^{xcos y} $$ $$ F’_z = -1 $$ Вычисляем значения производных в точке $ M(1,pi,frac{1}{e}) $: $$ F’_x Big |_M = F’_x (1,pi,frac{1}{e}) = cos pi cdot e^{1 cdot cos pi} = -1 cdot e^{(-1)} = -e^{-1} $$ $$ F’_y Big |_M = F’_y (1,pi, frac{1}{e}) = -1 cdot sin pi cdot e^{1 cdot cos pi} = -1 cdot 0 cdot e^1 = 0 $$ $$ F’_z Big |_M = -1 $$ Подставляем в первую формулу касательной плоскости полученные ранее неизвестные данные: $$ -e^{-1}(x-1) + 0 cdot (y-pi) + (-1) cdot (z-frac{1}{e}) = 0 $$ Раскрываем скобки: $$ -xfrac{1}{e} + frac{1}{e} – z + frac{1}{e} = 0 $$ Домножаем обе части уравнения на $ -e $ и получаем окончательное уравнение плоскости: $$ x + ez – 2 = 0 $$ Используя вторую формулу находим уравнение нормали к поверхности: $$ frac{x-1}{-e^{-1}} = frac{y-pi}{0} = frac{z-e^{-1}}{-1} $$ Умножим уравнение на дробь $ frac{1}{-e} $: $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$ |
| Ответ |
| $$ x + ez – 2 = 0 $$ $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$ |
Касательная плоскость и нормаль к поверхности
Пусть M0(x0;
y0;
z0)
– фиксированная точка на поверхности,
заданной функцией z
= f(x;
y)
или уравнением F(x;
y;
z)
= 0.
Касательной
плоскостью к
поверхности в точке M0
называется плоскость, в которой
расположены касательные к всевозможным
кривым, проведенным на поверхности
через точку M0.
Нормалью называется
прямая, проходящая через точку M0
перпендикулярно касательной плоскости.
Из
определений следует, что нормальный
вектор касательной плоскости
и направляющий вектор нормали совпадают.
Если поверхность
задана уравнением z
= f(x;
y),
то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
к данной поверхности имеет вид
![]() (1)
(1)
а
канонические
уравнения нормали,
проведенной через точку M0(x0;
y0;
z0)
поверхности, имеют вид
![]()
(2)
В случае, когда
уравнение гладкой поверхности задано
в неявном виде: F(x;
y;
z)
= 0 и F(x0;
y0;
z0)
= 0, то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
имеет вид
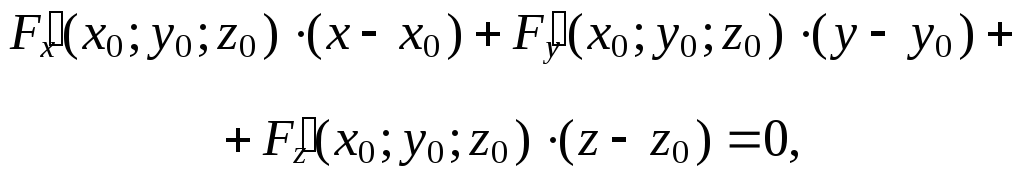
(3)
а уравнение
нормали
![]() (4)
(4)
Пример 15.Найти уравнение касательной плоскости
и уравнения нормали к поверхности![]() в точкеM0(1; 2;
в точкеM0(1; 2;
–1).
Решение
Вычисляем значения
частных производных в точке M0(1;
2; –1)
![]()
![]()
![]()
Подставляя их в
уравнения (3) и (4), получаем соответственно
уравнение касательной плоскости:
![]() канонические уравнения нормали:
канонические уравнения нормали:![]()
Тест 11. Уравнение
касательной плоскости к поверхности
![]() в точкеP0(2;
в точкеP0(2;
–3; 2) имеет следующий вид:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Производная по направлению. Градиент
Частные производные
![]() и
и![]() представляют собой производные от
представляют собой производные от
функцииz
= f(x;
y)
по двум частным направлениям осей Ox
и Oy
(рисунок 43).
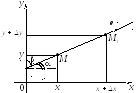
Рисунок 43
Пусть функция z
= f(x;
y)
определена в некоторой окрестности
точки М(х;
у),
![]() – некоторое направление, задаваемое
– некоторое направление, задаваемое
единичным вектором![]() где
где![]() ибо
ибо![]() (или
(или![]() );cos ,
);cos ,
cos
– косинусы углов, образуемых вектором
е
с осями координат и называемые
направляющими
косинусами.
При перемещении
в данном направлении
![]() точкиM(x;
точкиM(x;
y)
в точку M1(x
+ x;
y
+ y)
функция z
получит приращение
![]() z
z
= f(x
+ x;
y
+
+ y)
– f(x;
y),
называемое приращением
функции
![]() в данном направлении
в данном направлении![]()
Если
![]() то, очевидно, что
то, очевидно, что![]()
![]() следовательно,
следовательно,![]()
Производной
![]() по направлению
по направлению![]()
функции двух переменных
z
= f(x;
y)
называется предел отношения приращения
функции в этом направлении к величине
перемещения
![]() при стремлении последней к нулю, т. е.
при стремлении последней к нулю, т. е.
![]()
Производная
![]() характеризует
характеризует
скорость
изменения функции в направлении
![]()
Формула для
производной функции z
= f(x;
y)
по
направлению
имеет вид
![]()
Пример 16.
Дана
функция z
= x2
+ y2,
в точке M(1;
1) направление составляет с осью Ox
угол
![]() Найти производную функции по указанному
Найти производную функции по указанному
направлению в этой точке.
Решение
Так как
![]() то угол
то угол![]() По формуле производной функции по
По формуле производной функции по
направлению получим
![]()
В точке M(1;
1) получаем:
![]()
Градиентом grad
z
функции z
= f(x;
y)
называется вектор с координатами
![]()
Рассмотрим скалярное
произведение векторов
![]() и единичного вектора
и единичного вектора![]()
Получим
![]()
Итак, производная
по направлению
есть скалярное произведение градиента
grad
z
и единичного вектора, задающего
направление
![]()
Градиент функции
grad
z
в данной точке характеризует направление
максимальной скорости изменения функции
в этой точке.
Пример 17.
Найти
градиент функции
![]() в точкеM(0;
в точкеM(0;
1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:
$$
begin{equation}
F_{x}^{‘}(M_0)cdot(x-x_0)+F_{y}^{‘}(M_0)cdot(y-y_0)+F_{z}^{‘}(M_0)cdot(z-z_0)=0
end{equation}
$$
Уравнение нормали имеет вид:
$$
begin{equation}
frac{x-x_0}{F_{x}^{‘}(M_0)}=frac{y-y_0}{F_{y}^{‘}(M_0)}=frac{z-z_0}{F_{z}^{‘}(M_0)}
end{equation}
$$
Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:
$$
begin{equation}
f_{x}^{‘}(x_0,y_0)cdot(x-x_0)+f_{y}^{‘}(x_0,y_0)cdot(y-y_0)-(z-z_0)=0
end{equation}
$$
Уравнение нормали в случае явного задания поверхности таково:
$$
begin{equation}
frac{x-x_0}{f_{x}^{‘}(x_0,y_0)}=frac{y-y_0}{f_{y}^{‘}(x_0,y_0)}=frac{z-z_0}{-1}
end{equation}
$$
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.
Решение
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:
$$
z_0=3x_{0}^{2}y_{0}^{4}-6x_0y_{0}^{3}+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20.
$$
Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_{x}^{‘}$ и $z_{y}^{‘}$:
$$
z_{x}^{‘}=6xy^4-6y^3+5;\
z_{y}^{‘}=12x^2y^3-18xy^2-4.
$$
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:
$$
z_{x}^{‘} left(x_0, y_0right)=6x_0y_{0}^{4}-6y_{0}^{3}+5=-12-6+5=-13;\
z_{y}^{‘}left(x_0, y_0right)=12x_{0}^{2}y_{0}^{3}-18x_0y_{0}^{2}-4=48-(-36)-4=80.
$$
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:
$$
-13cdot(x-(-2))+80cdot(y-1)-(z-20)=0;\
-13x+80y-z-86=0.
$$
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:
$$
frac{x-(-2)}{-13}=frac{y-1}{80}=frac{z-20}{-1}; frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}.
$$
Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}$.
Пример №2
Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt{x^2+y^2}-2xy-39$ в точке $M_0(3;-4;z_0)$.
Решение
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
$$
z_0=5sqrt{x_{0}^{2}+y_{0}^{2}}-2x_0y_0-39=5sqrt{25}+24-39=10.
$$
Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_{x}^{‘}$ и $z_{y}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:
$$
z_{x}^{‘}=frac{10x}{sqrt{x^2+y^2}}-2y; z_{x}^{‘} left(x_0, y_0right)=frac{10cdot 3}{sqrt{3^2+(-4)^2}}-2cdot(-4)=11;\
z_{y}^{‘}=frac{10y}{sqrt{x^2+y^2}}-2x; z_{y}^{‘} left(x_0, y_0right)=frac{10cdot (-4)}{sqrt{3^2+(-4)^2}}-2cdot 3=-10.\
$$
Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_{x}^{‘} left(x_0, y_0right)=11$, $z_{y}^{‘} left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:
$$
11cdot(x-3)+(-10)cdot(y-(-4))-(z-10)=0; 11x-10y-z-63=0; \
frac{x-3}{11}=frac{y-(-4)}{-10}=frac{z-10}{-1}; frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}.
$$
Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}$.
Пример №3
Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.
Решение
Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:
$$
3xy^2z+5xy+z^2-10xz+2y-1=0.
$$
$$F(x,y,z)=3xy^2z+5xy+z^2-10xz+2y-1$$
Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.
Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:
$$
3x_0y_{0}^{2}z_0+5x_0y_0+z_{0}^{2}-10x_0z_0+2y_0-1=36-10+9-30-4-1=0.
$$
Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$:
begin{aligned}
& F_{x}^{‘}=3y^2z+5y-10z;\
& F_{y}^{‘}=6xyz+5x+2; \
& F_{z}^{‘}=3xy^2+2z-10x. end{aligned}
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:
begin{aligned}
& F_{x}^{‘}(M_0)=3y_{0}^{2}z_0+5y_0-10z_0=-4;\
& F_{y}^{‘}(M_0)=6x_0y_0z_0+5x_0+2=-29; \
& F_{z}^{‘}(M_0)=3x_0y_{0}^{2}+2z_0-10x_0=8. end{aligned}
Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_{x}^{‘} left(M_0right)=-4$, $F_{y}^{‘} left(M_0right)=-29$ и $F_{z}^{‘} left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
$$
-4cdot(x-1)-29cdot(y-(-2))+8(z-3)=0; -4x-29y+8z-78=0.\
frac{x-1}{-4}=frac{y-(-2)}{-29}=frac{z-3}{8}; frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}.
$$
Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}$.
Пример №4
Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.
Решение
Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
$$
z_{0}^{3}+4x_0y_0z_0=-3x_{0}^{2}+5y_0+7;\
z_{0}^{3}=-15+7; z_{0}^{3}=-8; z_0=-2.
$$
Перенесём все слагаемые в левую часть равенства:
$$
z^3+4xyz+3x^2-5y-7=0.
$$
Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:
begin{aligned}
& F_{x}^{‘}=4yz+6x; ; F_{x}^{‘}(M_0)=4y_0z_0+6x_0=-24;\
& F_{y}^{‘}=4xz-5; ; F_{y}^{‘}(M_0)=4x_0z_0-5=-5;\
& F_{z}^{‘}=3z^2+4xy; ; F_{z}^{‘}(M_0)=3z_{0}^{2}+4x_0y_0=12.
end{aligned}
Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_{x}^{‘} left(M_0right)=-24$, $F_{y}^{‘} left(M_0right)=-5$ и $F_{z}^{‘} left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
$$
-24cdot(x-0)-5cdot(y-(-3))+12(z-(-2))=0; -24x-5y+12z+9=0.\
frac{x-0}{-24}=frac{y-(-3)}{-5}=frac{z-(-2)}{12}; frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}.
$$
Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}$.
Касательная плоскость и нормаль к поверхности
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0).
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Решение онлайн
- Видеоинструкция
Правила ввода функций:
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
z – z0 = f’x(x0,y0)(x – x0) + f’y(x0,y0)(y – y0)
Вектор ![]() называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
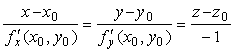
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)
По условию задачи x0 = 0, y0 = 1, тогда z0 = 5
Найдем частные производные функции z = x^3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f’x(x,y) = (x3+5•y)’y = 5
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
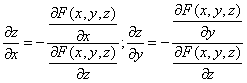
Для нашей функции:
![]()
Тогда:
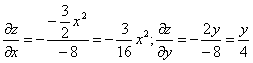
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример. Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
fy’ (x, y) = (y/x + xy – 5x3)’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z= y/x + xy – 5x3
![]()
z0 = 2/(-1) + (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2) ![]() z – 1= –15x – 15 – 2y +4
z – 1= –15x – 15 – 2y +4 ![]() 15x + 2y + z + 10 = 0.
15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0: ![]() .
.
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: ![]() .
.
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z – z0 = f’x(x0,y0,z0)(x – x0) + f’y(x0,y0,z0)(y – y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x2+3•x•y•+y2)’x = 2•x+3•y3
f’x(x,y) = (x2+3•x•y•+y2)’y = 9•x•y2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение
Норма́ль в геометрии — обобщение понятия перпендикуляра к прямой или плоскости на произвольные гладкие кривые и поверхности.

В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.
Нормаль к кривой в заданной её точке — прямая, перпендикулярная к касательной прямой в указанной точке кривой. Плоская гладкая кривая имеет в каждой точке единственную нормаль, расположенную в той же плоскости. Пространственная кривая в каждой своей точке имеет бесконечное множество нормалей, формирующих так называемую нормальную плоскость. Две из этих нормалей выделяются особо: нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью, а нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью[1].
Нормаль к поверхности в заданной её точке — прямая, перпендикулярная к касательной плоскости в указанной точке поверхности. Нормаль для гладкой поверхности определяется однозначно[1].
Понятие нормали может быть легко распространено на многомерные многообразия. Кроме геометрии, нормали широко используются в геометрической оптике, механике, при создании трёхмерной компьютерной графики, в теории потенциала и в других естественных науках[2].
Вектор нормали[править | править код]

Векторы нормали в точках поверхности
Вектор нормали (или орт нормали) к поверхности в данной точке — единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Аналогично определяются векторы нормали к пространственной кривой в данной точке; среди них, соответственно сказанному выше, выбирают два, ортогональных друг к другу: вектор главной нормали и вектор бинормали.
Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным полем векторов нормали. В противном случае поверхность называют односторонней или неориентируемой. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.
Примерами односторонних и, следовательно, неориентируемых поверхностей являются бутылка Клейна или лист Мёбиуса.
Нормаль к пространственной кривой[править | править код]
Пусть 
![{displaystyle [[mathbf {r} ', mathbf {r} ''], mathbf {r} '].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ee7697e2619ae6eceeffeda8525c1fd2068d8ea)

Векторное уравнение бинормали в точке 
Уравнение нормальной плоскости[3] в точке 
Нормаль к плоской кривой[править | править код]
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке 
| Способ задания плоской кривой |
Уравнение кривой | Уравнение нормали |
|---|---|---|
| Параметрическое задание |  |

|
| Явное задание |  |

|
| Неявное задание |  |

|
Нормаль к поверхности[править | править код]
В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности (см. статью Поверхность). Примером точки поверхности, где нормаль не определена, является вершина конуса — в ней не существует касательной плоскости.
Координаты орта нормали для разных способов задания поверхности приведены в таблице:
| Координаты нормали в точке поверхности | |
|---|---|
параметрическое задание: 
|

|
неявное задание: 
|

|
явное задание: 
|

|
Здесь 


Сечение поверхности плоскостью, содержащей нормаль поверхности в заданной точке, образует некоторую кривую, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).
Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол 


Кривизна 
Примечания[править | править код]
- ↑ 1 2 Математическая энциклопедия, 1982, с. 1049—1050.
- ↑ Нормаль // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 416. — 847 с.
- ↑ 1 2 Рашевский, 1956, с. 146.
- ↑ Погорелов, 1974, с. 125—126.
- ↑ Погорелов, 1974, с. 132—133.
Литература[править | править код]
- Нормаль // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Погорелов А. И. Дифференциальная геометрия. — 6-е изд. — М.: Наука, 1974. — 176 с.
- Рашевский П. К. Курс дифференциальной геометрии. — 4-е изд. — М.: ГИТТЛ, 1956.
Ссылки[править | править код]
- Нормаль // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
![{boldsymbol {r}}(lambda )={boldsymbol {r}}(t_{0})+lambda [{boldsymbol {r}}'(t_{0}),~{boldsymbol {r}}''(t_{0})].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b484d034092a7ddfd4f6cea0efa4b3f9f0cac69f)


