Как найти нормаль прямой на плоскости

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами.  Для начала ознакомимся с понятием вектора прямой.

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

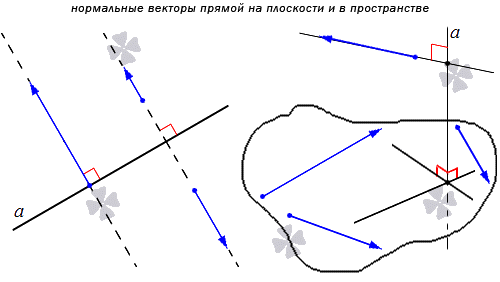
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1.  Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·j→, t∈R, t≠0.

Прямоугольная система Oxyz имеет нормальный вектор i→, относящийся к прямой Оz. Вектор j→ также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный Оz, считается нормальным для Oz.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат Оху выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Если дано уравнение  в отрезках вида xa+yb=1 или уравнение с угловым коэффициентом y=k·x+b, тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Если прямая определена каноническим уравнением прямой на плоскости x-x1ax=y-y1ay или параметрическим x=x1+ax·λy=y1+ay·λ, тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a→=(ax, ay). Возможность нахождения координат нормального вектора n→ возможно, благодаря условию перпендикулярности векторов n→ и a→.

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔ay·x-ax·y+ax·y1-ay·x1x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔ay·x-ax·y+ax·y1-ay·x1=0

Для решения можно выбирать любой удобный способ.

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат Охуz.

Когда прямая задается при помощи уравнений пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, тогда нормальный вектор плоскости относится к A2x+B2y+C2z+D2=0 и A2x+B2y+C2z+D2=0, тогда получаем запись векторов  в виде n1→=(A1, B1, C1) и n2→=(A2, B2, C2).

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x-x1ax=y-y1ay=z-z1az или параметрического, имеющего вид x=x1+ax·λy=y1+ay·λz=z1+az·λ, отсюда ax, ay и az считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a→=(ax, ay, az). Отсюда следует, что нахождение координат нормального  с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a→=(ax, ay, az).

В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.

Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.

Можно выразить уравнение прямой и другим способом:

$y = kx + b$.

Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ – в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.

Нормальное уравнение прямой можно выразить и в тригонометрическом виде:

$x cdot cos{alpha} + y cdot sin{alpha} – p = 0$

где $alpha$ – угол между прямой и осью абсцисс, а $p$ – расстояние от начала координат до рассматриваемой прямой.

Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:

1. когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
2. когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
3. когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
4. для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.

Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.

Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:

$y – y_0 = k cdot (x – x_0)$

Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой – самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.

Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.

Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как

$n_1 cdot (x – x_n) + n_2 cdot (y – y_0) = 0$

Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат

$Ax + By + C = 0$,

то нормальный вектор описывается формулой:

$bar{n}(A; B)$.

При этом говорят, что координаты нормального вектора “снимаются” с уравнения прямой.

Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:

$frac{x – x_0}{p_1} = frac{y – y_0}{p_2}$

В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:

$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$

Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:

$A(x – x_0) + B(y – y_0) = 0$

Аналитическая геометрия. Уравнение линии на плоскости.

Как известно, любая
точка на плоскости определяется двумя
координатами в какой- либо системе
координат. Системы координат могут быть
различными в зависимости от выбора
базиса и начала координат.

Определение.
Уравнением линии
называется соотношение y
= f(x)
между координатами точек, составляющих
эту линию.

Отметим,
что уравнение линии может быть выражено
параметрическим способом, то есть каждая
координата каждой точки выражается
через некоторый независимый параметр
t.

Характерный
пример – траектория движущейся точки.
В этом случае роль параметра играет
время.

Уравнение прямой на плоскости.

Определение.
Любая прямая на плоскости может быть
задана уравнением первого порядка

Ах
+ Ву + С = 0,

причем
постоянные А, В не равны нулю одновременно,
т.е. А²
+ В²

0. Это уравнение первого порядка называют
общим
уравнением прямой.

В
зависимости от значений постоянных А,В
и С возможны следующие частные случаи:

• C
  = 0, А 
  0, В 
  0 – прямая проходит через начало
  координат

• А
  = 0, В 
  0, С 
  0 { By
  + C
  = 0}- прямая параллельна оси Ох

• В
  = 0, А 
  0, С 
  0 { Ax
  + C
  = 0} – прямая параллельна оси Оу

• В
  = С = 0, А 
  0 – прямая совпадает с осью Оу

• А
  = С = 0, В 
  0 – прямая совпадает с осью Ох

Уравнение прямой
может быть представлено в различном
виде в зависимости от каких – либо
заданных начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение.
В декартовой прямоугольной системе
координат вектор с компонентами (А, В)
перпендикулярен прямой , заданной
уравнением Ах + Ву + С = 0.

Пример.
Найти уравнение прямой, проходящей
через точку А(1, 2) перпендикулярно вектору

(3,
-1).

Составим
при А = 3 и В = -1 уравнение прямой: 3х – у
+ С = 0. Для нахождения коэффициента С
подставим в полученное выражение
координаты заданной точки А.

Получаем:
3 – 2 + C
= 0, следовательно С = -1.

Итого:
искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть
в пространстве заданы две точки M₁(x₁,
y₁,
z₁)
и M₂(x_2,
y₂,
z₂),
тогда уравнение прямой, проходящей
через эти точки:

Если
какой- либо из знаменателей равен нулю,
следует приравнять нулю соответствующий
числитель.

На
плоскости записанное выше уравнение
прямой упрощается:

если
х₁ 
х₂
и х = х₁,
еслих₁
= х₂.

Дробь
=k
называется угловым
коэффициентом
прямой.

Пример.
Найти уравнение прямой, проходящей
через точки А(1, 2) и В(3, 4).

Применяя
записанную выше формулу, получаем:

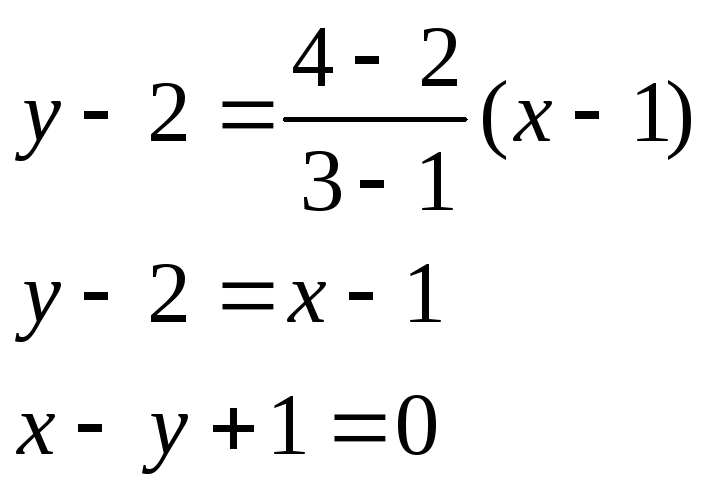
Уравнение прямой по точке и угловому коэффициенту.

Если
общее уравнение прямой Ах + Ву + С = 0
привести к виду:

и
обозначить
,
то полученное уравнение называетсяуравнением
прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом,
рассматривающим уравнение прямой через
вектор нормали можно ввести задание
прямой через точку и направляющий вектор
прямой.

Определение.
Каждый ненулевой вектор
(₁,
₂),
компоненты которого удовлетворяют
условию А₁
+ В₂
= 0 называется направляющим вектором
прямой

Ах
+ Ву + С = 0.

Пример.
Найти уравнение прямой с направляющим
вектором
(1,
-1) и проходящей через точку А(1, 2).

Уравнение
искомой прямой будем искать в виде: Ax
+ By
+ C
= 0. В соответствии с определением,
коэффициенты должны удовлетворять
условиям:

1A
+ (-1)B
= 0, т.е. А = В.

Тогда
уравнение прямой имеет вид: Ax
+ Ay
+ C
= 0, или x
+ y
+ C/A
= 0.

при
х = 1, у = 2 получаем С/A
= -3, т.е. искомое уравнение:

х
+ у – 3 = 0

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.

Здесь будет калькулятор

Уравнение прямой с угловым коэффициентом

Уравнения данного вида составляются следующим образом по формуле:

Общее уравнение прямой

Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:

y−x−1=0y-x-1=0

Уравнение прямой по двум точкам

Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:

Уравнение прямой при помощи точки и вектора нормали

Прямая в пространстве

Уравнение прямой, заданной в пространстве имеет такой вид:

Тест по теме “Составление уравнения прямой”

2.2.5. Нормальный вектор прямой

Или вектор нормали.

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:

Если прямая задана общим уравнением  в декартовой системе координат, то вектор  является вектором нормали данной прямой.

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2  работают и в общем аффинном случае.

Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:

И тут всё ещё проще: если координаты направляющего вектора  приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали  достаточно просто «снять».

Приведу примеры с теми же уравнениями, что и для направляющего вектора:

Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».

2.2.6. Как составить уравнение прямой по точке и вектору нормали?

2.2.4. Как составить уравнение прямой по двум точкам?

| Оглавление |



Автор: Aлeксaндр Eмeлин