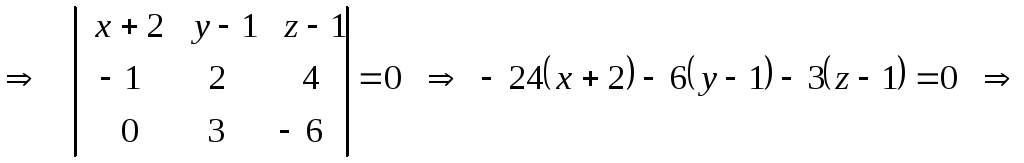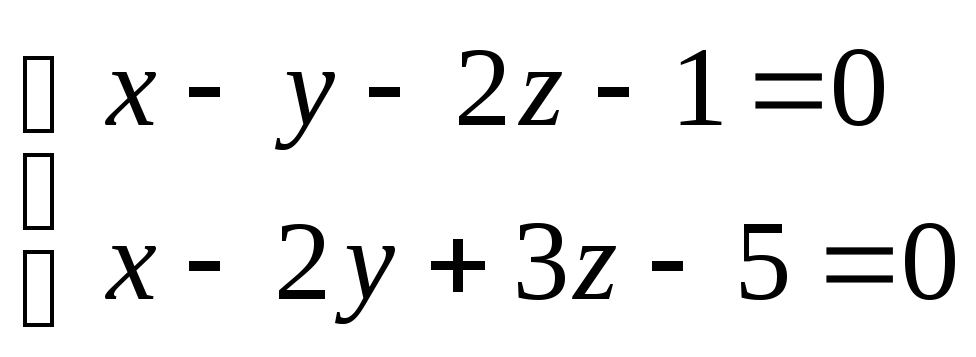Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
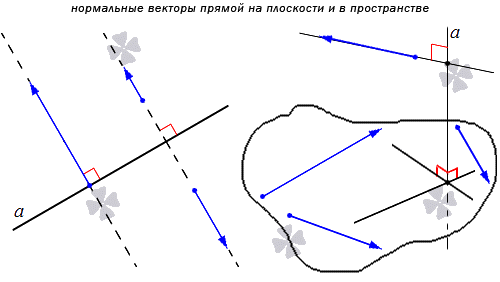
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1. Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·j→, t∈R, t≠0.
Прямоугольная система Oxyz имеет нормальный вектор i→, относящийся к прямой Оz. Вектор j→ также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный Оz, считается нормальным для Oz.
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат Оху выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2x+7y-4=0_, найти координаты нормального вектора.
Решение
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2, 7.
Ответ: 2, 7.
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y-3=0.
Решение
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0·x+1·y-3=0. Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0, 1.
Ответ: 0, 1.
Если дано уравнение в отрезках вида xa+yb=1 или уравнение с угловым коэффициентом y=k·x+b, тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x13-y=1.
Решение
Для начала необходимо перейти от уравнения в отрезках x13-y=1 к уравнению общего вида. Тогда получим, что x13-y=1 ⇔3·x-1·y-1=0.
Отсюда видно, что координаты нормального вектора имеют значение 3, -1.
Ответ: 3, -1.
Если прямая определена каноническим уравнением прямой на плоскости x-x1ax=y-y1ay или параметрическим x=x1+ax·λy=y1+ay·λ, тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a→=(ax, ay). Возможность нахождения координат нормального вектора n→ возможно, благодаря условию перпендикулярности векторов n→ и a→.
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔ay·x-ax·y+ax·y1-ay·x1x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔ay·x-ax·y+ax·y1-ay·x1=0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x-27=y+3-2.
Решение
Из прямой x-27=y+3-2 понятно, что направляющий вектор будет иметь координаты a→=(7, -2). Нормальный вектор n→=(nx, ny) заданной прямой является перпендикулярным a→=(7, -2).
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a→=(7, -2) и n→=(nx, ny) запишем a→, n→=7·nx-2·ny=0.
Значение nx – произвольное , следует найти ny. Если nx=1, отсюда получаем, что 7·1-2·ny=0⇔ny=72.
Значит, нормальный вектор имеет координаты 1, 72.
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x-27=y+3-2⇔7·(y+3)=-2·(x-2)⇔2x+7y-4+73=0
Полученный результат координат нормального вектора равен 2, 7.
Ответ: 2, 7 или 1, 72.
Указать координаты нормального вектора прямой x=1y=2-3·λ.
Решение
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x=1y=2-3·λ⇔x=1+0·λy=2-3·λ⇔λ=x-10λ=y-2-3⇔x-10=y-2-3⇔⇔-3·(x-1)=0·(y-2)⇔-3·x+0·y+3=0
Отсюда видно, что координаты нормального вектора равны -3, 0.
Ответ: -3, 0.
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат Охуz.
Когда прямая задается при помощи уравнений пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, тогда нормальный вектор плоскости относится к A2x+B2y+C2z+D2=0 и A2x+B2y+C2z+D2=0, тогда получаем запись векторов в виде n1→=(A1, B1, C1) и n2→=(A2, B2, C2).
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x-x1ax=y-y1ay=z-z1az или параметрического, имеющего вид x=x1+ax·λy=y1+ay·λz=z1+az·λ, отсюда ax, ay и az считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a→=(ax, ay, az). Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a→=(ax, ay, az).
Добрый день.
Подскажите пожалуйста. Допустим, две точки A(4, 2, 7) и B(3, 6, 5). Как найти нормаль к прямой, образуемой ими? Я правильно понимаю, ведь нормаль всегда перпендикулярна этой прямой?
1
Нормалей к прямой в пространстве имеется бесконечно много. Вас устраивает любая из них, или надо описать, как выглядят все?
Мне хотелось бы понять, они все перпендикулярны направлению прямой или я неправильно представляю?)
Нормаль — это и есть перпендикуляр. Это слова-синонимы.
Я просто хочу понять) В двух измерениях допустим у формулы Ax+By+C=0 нормаль N(A,B), то есть A – x нормали, B – y. В пространстве Ax+By+Cz+D=0. Нормаль N(A,B,C) – или нет?
Причем я не пойму, как получить общее уравнение из симметричного (хотя из общего симметрич. умею получать). Для примера x-4/3-4 = y-2/6-2 = z-7/5-7 а как получить общее уравнение из этого не знаю. Чтобы потом получить перпендикуляр.
1
@Neumann: конечно, для уравнения плоскости в пространстве вида Ax+By+Cz+D=0, вектор (A,B,C) будет нормалью к этой плоскости. А нахождение нормали к прямой естественно для плоского, а не пространственного случая. У Вас в примере рассматривается каноническое уравнение прямой. Какое общее уравнение Вы хотите получить? Ответ на Ваш вопрос наверняка очень прост, но я пока не могу осознать, чего именно Вы хотите. Осознаёте ли Вы, что у прямой в пространстве нет какой-то одной “выделенной” нормали? Если в пространстве дана прямая, естественной будет задача нахождения нормальной плоскости к ней.
Осознаю) пускай их много, мне нужна любая. Представьте, что вы смотрите, как в теннис играют два ваших друга. Вы хотите подбодрить одного из них большим пальцем вверх. Вы вытягиваете руку в его направлении (это будет прямая), сжимаете 4 пальца вместе и поднимаете большой палец вверх (он перпендикулярен движению прямой). Потом другой рукой – другому игроку. Тот палец уже перпендикулярен той руке(прямой). http://s.fishki.net/upload/users/2015/11/26/365176/c391014cbc5a19630abd4a1d6f0bfc48.jpg
1
@Neumann: если нужна какая-нибудь прямая, то это тривиально. У Вас есть вектор с координатами (u,v,w). Вам нужен перпендикулярный с координатами (a,b,c). Это значит, что au+bv+cw=0. Годятся, например, числа a=v, b=-u, c=0. Или a=w, b=0, c=-u. Вообще, если w не равно нулю, то a,b задаём как угодно, а c выражаем из уравнения. У Вас есть вектор BA с координатами (u,v,w)=(1,-4,2). Поэтому годятся любые три числа, для которых a-4b+2c=0. Задайте b,c как угодно, и пусть a=4b-2c. Это даст бесконечно много направлений, перпендикулярных прямой AB.
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y – 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y – 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y – 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 – y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 – y = 1 к уравнению общего вида. Тогда получим, что x 1 3 – y = 1 ⇔ 3 · x – 1 · y – 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , – 1 .
Ответ: 3 , – 1 .
Если прямая определена каноническим уравнением прямой на плоскости x – x 1 a x = y – y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x – 2 7 = y + 3 – 2 .
Из прямой x – 2 7 = y + 3 – 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , – 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , – 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , – 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x – 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 – 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x – 2 7 = y + 3 – 2 ⇔ 7 · ( y + 3 ) = – 2 · ( x – 2 ) ⇔ 2 x + 7 y – 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 – 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 – 3 · λ ⇔ x = 1 + 0 · λ y = 2 – 3 · λ ⇔ λ = x – 1 0 λ = y – 2 – 3 ⇔ x – 1 0 = y – 2 – 3 ⇔ ⇔ – 3 · ( x – 1 ) = 0 · ( y – 2 ) ⇔ – 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны – 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x – x 1 a x = y – y 1 a y = z – z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Метод координат в пространстве: формулы и комментарии репетитора
Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.
Угол между прямыми а и b
Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).
Какой алгоритм использует репетитор по математике для поиска угла?
1) Выбираем любые вектора 

2) Определяем координаты векторов 

3) Подставляем найденный координаты в формулу: 
Нормаль к плоскости
Нормалью 
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов 



Замечание репетитора по математике : Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).
Угол между прямой и плоскостью
Допустим, что нам заданы прямая и плоскость координатами направляющего вектора 

Угол 
Угол между плоскостями
Пусть 


Уравнение плоскости в пространстве
Точки, удовлетворяющие равенству 





Расстояние от точки до плоскости
Для вычисления расстояния 




В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке
Комментарий репетитора по математике :
Методом координат можно находить не только углы и расстояния в пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).
Для понимания таких формул нужно изучить понятия векторного и смешанного произведения векторов, а также определителя матрицы. В скором времени я сделаю для вычисления объемов соответствующую справочную страничку.
Средства аналитической геометрии репетитор по математике практически не использует в работе со средним и тем более слабым учеником. И очень жаль, что загруженность среднестатистического сильного школьника не позволяет репетитору провести более-менее серьезную работу на уровне определений из высшей математики и с соответствующей практикой решения задач. Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного – двух примеров их использования. В школьной программе не предусмотрено время для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная подготовка к ЕГЭ по математике с изучением приемов аналитической геометрии даст Вам мощное и универсальное средство для решения огромного класса задач типа С2. Пользуйтесь этой страничкой на здоровье!
Колпаков А.Н. Репетитор по математике Москва (Строгино).
Спасибо Вам за этот материал,все наглядно и понятно.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
http://ankolpakov.ru/metod-koordinat-v-prostranstve-formuly-i-kommentarii-repetitora/
[/spoiler]
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ – в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} – p = 0$
где $alpha$ – угол между прямой и осью абсцисс, а $p$ – расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y – y_0 = k cdot (x – x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой – самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x – x_n) + n_2 cdot (y – y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора “снимаются” с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x – x_0}{p_1} = frac{y – y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x – x_0) + B(y – y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x – x_0) + B cdot (y – y_0) = 0$
Подставив значения, получаем:
$3 cdot (x – (-1)) – (-1) cdot (y – (-3)) = 0$
$3 cdot (x + 1) – (y + 3) = 0$
$3x + 3 – y – 3 = 0$
$3x – y = 0$
Проверить правильность общего уравнения прямой можно “сняв” из него координаты для нормального вектора:
$3x – y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x – y = 0$:
$3 cdot (-1) – (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x – y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
8
Занятие 9.
Плоскость
и прямая в пространстве.
9.1. Общее уравнение плоскости. Нормальный
вектор.
9.2. Прямая в пространстве: канонические,
параметрические уравнения.
9.3. Расстояние от точки до плоскости.
Взаимное расположение двух плоскостей,
прямой и плоскости двух прямых в
пространстве.
9.1. Общее уравнение плоскости. Нормальный
вектор.
Общее уравнение плоскости в пространстве
имеет вид
,
где
– числовые коэффициенты,
– координаты произвольной точки плоскости.
Это уравнение получается при решении
следующей задачи.
Задача 1. Найти уравнение плоскости,
проходящей через заданную точку
перпендикулярно вектору
.
Решение. Обозначим искомую плоскость
через
.
Используем далее такую цепочку выводов:
,
где
.
Отметим полную аналогию между общим
уравнением прямой на плоскости
и общим уравнением плоскости в
пространстве.
Из решения задачи видно, что из общего
уравнения плоскости сразу же можно
найти вектор
перпендикулярный плоскости. Этот
вектор называется нормалью (или
нормальным вектором) к плоскости.
Например, из общего уравнения плоскости
( в этом уравнении
)
получаем такой нормальный вектор
.
Коэффициент
не имеет особой смысловой нагрузки,
относительно него можно только сказать,
что при
плоскость проходит через начало координат
,
а при
не проходит через начало координат.
Следует также отметить, что уравнение
задает в пространстве
плоскость с нормалью
,
которая показывает, что данная плоскость
проходит параллельно оси
.
Это же уравнение
на плоскости
определяет прямую.
Аналогично, уравнение
в пространстве
представляет общее уравнение координатной
плоскости
.
Нормалью к этой плоскости служит орт
– единичный вектор положительного
направления оси
.
При нахождении уравнений плоскостей
часто используются условие ортогональности
двух векторов (как это делается в задаче
1) и условие компланарности трех векторов.
Пример 1. Найти уравнение плоскости,
проходящей через три точки
.
Решение. Сначала убедимся, что данные
три точки не лежат на одной прямой (если
эти точки лежат на одной прямой, то
существует бесконечно много плоскостей,
содержащих данные точки). Найдем векторы
.
Их координаты не пропорциональны.
Значит, точки
не лежат на одной прямой и через них
проходит только одна плоскость. Найдем
эту плоскость, которую обозначим
,
двумя способами.
1)
– компланарны
смешанное
произведение векторов
равно нулю
– общее уравнение плоскости
.
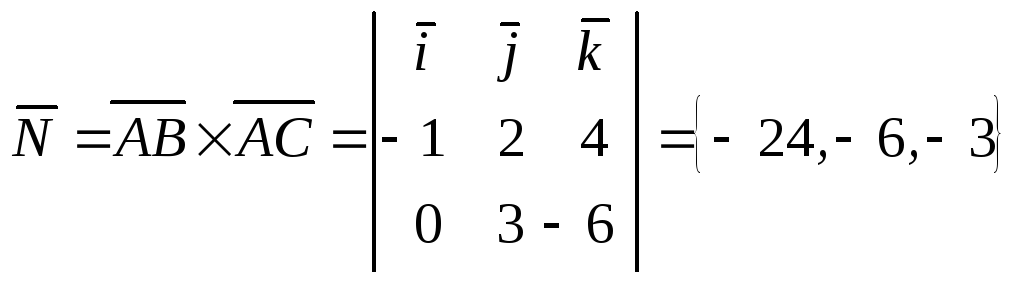
2)
– вектор нормали к плоскости
,
т.к. по определению векторного произведения
перпендикулярен векторам
,
параллельным
.
Дальнейшие рассуждения повторяют
решение задачи 1.
– общее уравнение плоскости
.
Пример 2. Найти уравнение плоскости
,
проходящей через точку
параллельно плоскости
:
.
Решение.
:
– вектор нормали к плоскости
.
Этот же вектор служит вектором нормали
к плоскости
.
Остается повторить решение задачи 1.
– общее уравнение плоскости
.
Пример 3.Найти двугранный угол, под
которым пересекаются плоскостии
.
:
,
:
.
Решение. Двугранный угол
(тупой или острый) между плоскостями
равен углу между их нормалями.
:
,
:
.
–
тупой угол,
. Острый двугранный угол между
и
равен
.
9.2. Прямая в пространстве
:
канонические, параметрические уравнения.
1). Прямую в пространстве
можно определить как линию пересечения
двух плоскостей. Следовательно, система
из двух уравнений плоскостей
,
(1)
задает прямую в пространстве
при обязательном условии, что нормали
,
к этим плоскостям не параллельны.
Если
и
параллельны, то плоскости
,
либо параллельны, либо совпадают. И в
том и другом случае система (1) уже не
будет давать прямую.
Замечание. Задание прямой системой (1)
не совсем удобно, т.к. из него не видно
ни направления прямой, ни одной из точек
на этой прямой. Эту информацию можно
добыть из системы (1) лишь посредством
дополнительных вычислений.
Более предпочтительными в плане
сделанного замечания являются канонические
и параметрические уравнения прямой в
.
2). Канонические уравнения прямой в
пространстве
имеют
вид
.
(2)
Здесь
– заданные числа, они имеют следующий
геометрический смысл:
– координаты фиксированной точки
на прямой;
– координаты направляющего вектора
прямой.
– координаты произвольной точки прямой.
Параметрические уравнения прямой в
имеют вид
(3)
Геометрический смысл величин
и величин
тот же, что и выше.
Уравнения (2),(3) получаются при решении
пространственного варианта задачи 2
из занятия 8.
Замечание. У прямой на плоскости
есть нормаль, которая также как и
направляющий вектор прямой, позволяет
установить направление этой прямой.
Для прямой в пространстве вектор
нормали не имеет смысла, т.к. существует
бесконечно много перпендикулярных к
пространственной прямой векторов с
разным направлением, и один заданный
перпендикулярный к этой прямой вектор
не дает однозначного ответа о ее
направлении.
Пример 4. Найти канонические уравнения
прямой
,
заданной как пересечение двух плоскостей
:
и
:
.
Решение.
Система уравнений
задает прямую
в пространстве, т.к. нормальные векторы
к плоскостям
и
,
а это векторы
и
не параллельны. Найдем две фиксированные
точки
на прямой
.
1. Подставим в систему значение
,
получим
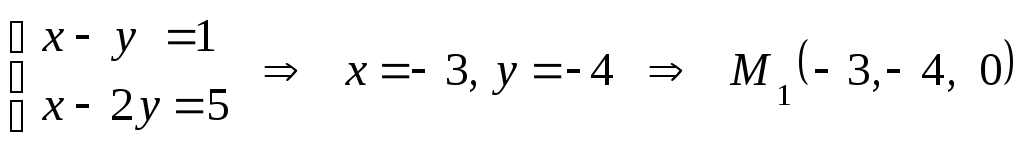
Геометрический смысл точки
:
это – точка пересечения прямой
с плоскостью
.
2. Подставим в систему значение
,
получим

Точка
,
это точка пересечения прямой
с плоскостью
.
3.
– направляющий вектор прямой
.
4.
координаты
векторов
пропорциональны
.
Это и есть каноническое уравнение
прямой
.
5. Замечание. Направляющий вектор прямой
можно было найти по векторам
и
.
Для этого надо вычислить векторное
произведение
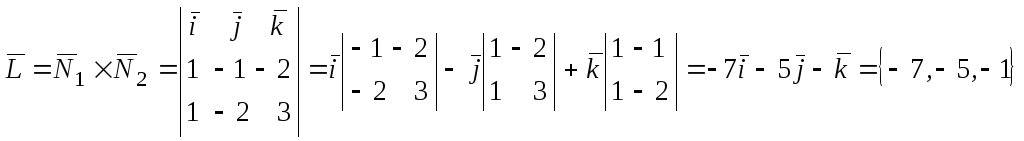
Вектор
перпендикулярен векторам
и
одновременно. Следовательно,
параллелен прямой
и служит другим (по сравнению с вектором
)
направляющим вектором этой прямой.
Кстати:
,
что тоже указывает на параллельность
вектора
прямой
.
При таком подходе канонические уравнения
прямой
получаются после выполнения пунктов
1., 4. и 5. изложенного решения. Только
ответ уже получится в виде
.
Пример 5. Найти параметрические
уравнения прямой
,
проходящей через точку
перпендикулярно плоскости
:
.
Решение.
– вектор нормали к плоскости
.
Этот вектор параллелен прямой
и, значит, является ее направляющим
вектором. Следовательно,
– ответ.
Пример 6. Найти канонические и
параметрические уравнения прямой
,
проходящей через точку
параллельно прямой
:
.
Решение.
– направляющий вектор прямой
.
Этот же вектор является направляющим
вектором искомой прямой
.
Следовательно,
координаты
векторов
пропорциональны
– канонические уравнения прямой
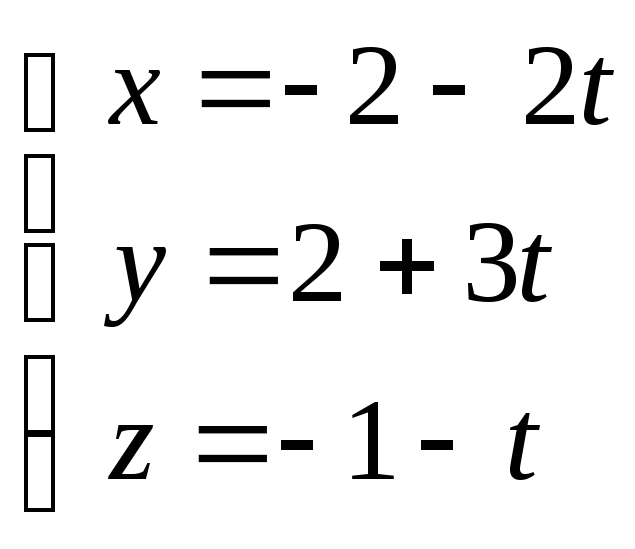
параметрические уравнения прямой
.
9.3. Расстояние от точки до плоскости.
Взаимное расположение двух плоскостей,
прямой и плоскости, двух прямых в
пространстве.
Расстояние
от точки
до плоскости
находится по формуле
.
Наиболее полезную информацию о взаимном
расположении двух плоскостей, прямой
и плоскости, двух прямых в пространстве
можно извлечь из направляющих векторов
прямых и нормалей к плоскостям.
Пример 8. Найти расстояние
от точки
до плоскости
.
Решение.
.
Пример 9. При каком значении параметра
плоскость
:
параллельна плоскости
:
?
Решение. Плоскости параллельны тогда
и только тогда, когда коллинеарны их
нормальные векторы
и
,
т.е. должно быть
.
Это двойное равенство не выполняется
ни при каком
,
т.к.
.
Следовательно, плоскости
и
не параллельны при всех значениях
параметра
.
Пример 10. При каких значениях
параметров
прямая
:
лежит в плоскости
:
?
Решение.
По каноническим уравнениям прямой
запишем ее параметрические уравнения

все точки прямой
удовлетворяют уравнению плоскости

ответ:
.
Можно эту задачу решить по другому.
– направляющий вектор прямой
и
– фиксированная точка этой прямой.
– вектор нормали к плоскости
.
Далее строим такую цепочку рассуждений.
.
Пример 11. Выяснить взаимное
расположение двух прямых
:
и
:
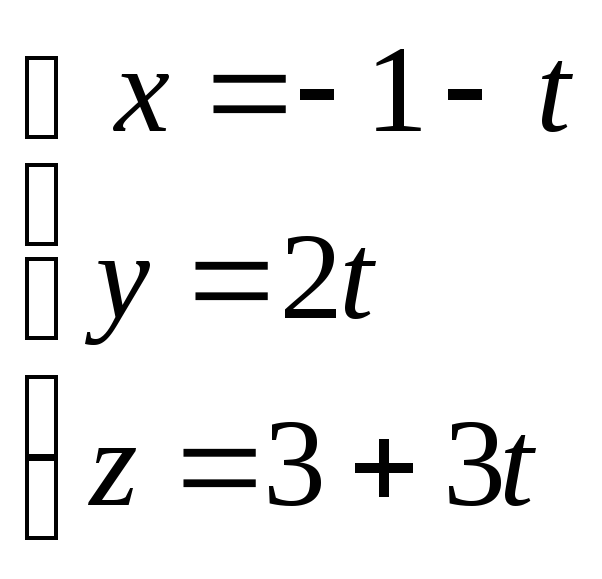
Решение. Прямые в пространстве могут
скрещиваться, могут пересекаться в
одной точке, могут быть параллельны,
могут совпадать. Выясним, какой из
указанных четырех случаев реализуется
в этом примере.
Из уравнения
выводим:
и
.
Из уравнения
выводим:
и
.
.
Если прямые
и
пересекаются или параллельны, или
совпадают, то тройка векторов
– компланарна. А если прямые
и
скрещиваются, то тройка векторов
-некомпланарна. Найдем смешанное
произведение этих трех векторов.
тройка
-некомпланарна
прямые
и
скрещиваются.
Приведенные в занятиях 8, 9 примеры
наглядно демонстрируют мощь векторных
методов и исключительную роль условий:
коллинеарности двух векторов;
ортогональности двух векторов;
компланарности трех векторов при
нахождении уравнений прямых и плоскостей.
Домашнее задание.
1. Найти общее
уравнение плоскости, проходящей через
три точки
.
2. Найти канонические и параметрические
уравнения прямой, являющейся пересечением
плоскостей
.
3. Найти точку
пересечения прямой, проходящей через
точку
перпендикулярно плоскости
,
с этой плоскостью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #