Как найти нормаль стороны

Применения:
Для 1) существует немного вариантов применения в области 3D-Графики (в отличии от Физики).
Через 2) рассчитывается соединительный вектор между вершинами.
Через 3) рассчитывается угол падения света на плоскость = Face = как правило треугольник.
Через 4) рассчитывается нормаль к плоскости = Face = обычно треугольник.
Через 5) рассчитывается длина, а если длина не играет роли, то она приравнивается к 1.0 = нормированный Вектор v = < v.X/Length, v.Y/Length, v.Z/Length>

Вывод: используйте простое определение Вертекса, а когда вам нужны углы, нормали и нормировки, переключайтесь на Векторные понятия.

Нормаль

2D-поверхности имеют только лицевую сторону, но в 3D нужно также различать тыльную сторону и общую ориентацию.
3D-поверхности = Faces обычно нуждаются в рассчете нормали = “Face Normal” = перпендикулярный к плоскости вектор. Направление наружу. См: Face and Vertex Normal Vectors .

Расчет нормали треугольника p0,p1,p2:
1) v0 = p0 – p1 // Вектор из p1 в p0
2) v1 = p2 – p1 // Вектор из p1 в p2
3) n0 = векторное произведение v0 и v1 // Нормаль без нормировки
4) Length = Math.Sqrt( n0. X 2 + n0.Y 2 + n0.Z 2 ) // Длина вектора n0
5) n = < n0.X/Length, n0.Y/Length, n0.Z/Length >// Нормированная нормаль

см: Cross Product Applet www.phy.syr.edu/courses/java-suite/crosspro.html

Нормаль определяет, где внешняя и где внутренняя сторона треугольника и под каким углом alpha находится поверхность относительно источника света. Из скалярного произведения нормированной нормали треугольника (Face) и нормированного вектора Света вычисляется cos(alpha), что определяет интенсивность освещенности (яркость отображения). Face наиболее освещен, когда направление Света совпадает с направлением нормали Фейса (треугольника).

alpha [Grad]	0	30	45	60	90	120	180	360
cos(alpha)	1.0	0.87	0.71	0.5	0.0	-0.5	-1.0	1.0
Освещенность (Яркость)	100%	87%	71%	50%	0%	0%	0%	100%

Для определения направления нормали вручную можно использовать метод левой руки – находясь на второй вершине (Вертексе) p[1], направляем большой палец левой руки на первый Вертекс p[0], а указательный на Вертекс p[2] . Нормаль Фейса будет совпадать с отогнутым перпендикулярно ладони средним пальцем.

В DirectX3D и в OpenGL у каждого Фейса, принято работать не с одной нормалью, а тремя Вертексными нормалями = “Vertex Normal”. То есть один треугольник содержит три параллельные “Vertex Normals”, что на первый взгляд – избыточно и бессмысленно для одного треугольника.
Однако, когда несколько треугольников образуют объемную фигуру, сводя свои вершины в одну, например на вершине пирамиды, то можно в этой точке посчитать среднюю нормаль, которая будет хорошо представлять данную вершину.
Преимущество такого подхода видно на краях поверхностей, где треугольники резко сталкиваются друг с другом – вместо резкого скачка цвета (Flat Shading), сглаженные нормали дают мягкий переход – Gouraud-Shading.

Shading (затенение) – это метод симуляции глубины сцены через эффект комбинации света и тени.
Gouraud-Shading опубликован в 1971-м году и назван по имени студента Henri Gouraud (произносится: Гуро).
Близкие методы: Phong-Shading, Metal Shading

3D своими руками. Часть 4: треугольник невидимка

Все части

Часть 2: оно трехмерное
( система координат, точка, вектор, матрица, вершина, индекс, конвейер визуализации )

Часть 4: треугольник невидимка
( треугольный полигон, нормаль )

В этой части мы разберем как и зачем строить модель при помощи треугольников. А также научимся не рисовать те части модели, которые не смотрят в камеру и не должны быть видны.

Для начала возьмите код с усеченной пирамидой из прошлой части бонусного раздела ( 25.01.22 в прошлую часть я внес исправления ошибок в код и текст, и если вы скачивали код раньше, нужно его сказать заново, какие именно правки указаны в конце прошлой части ). Всю пирамиду мы построили при помощи вершин ( массив vertices ) и ребер ( массив edges ). У этого подхода есть минус, у нас в коде у фигуры нету граней, т.е., у пирамиды неясно какие ребра ( или просто линии ) нужно соединить, чтобы в коде стало понятно что это грань, давайте посмотрим на такой пример

Индексы вершин усеченной пирамиды

По картинке видно что верхняя грань пирамиды это 0, 1, 2, 3 , лицевая грань: 3, 2, 6, 7 и т.д. Т.е. визуально мы эти грани различаем, но в коде у нас это никак не определено, т.к. мы рисуем фигуру линиями ( ребра ). Вы можете подумать, зачем нам вообще нужны грани, ведь и так красиво. Вопрос хороший и тут есть много причин, мы разберем некоторые из них.

Нам нужно знать грани, чтобы закрашивать модель в цвет, освещать её, или накладывать текстуры ( это будет в след. частях ). Ведь мы сейчас можем поменять цвет линии которой рисуем. А для того чтобы что-то закрасить, у нас должна быть замкнутая фигура в коде, которую будем заливать цветом.

Также грани нужны чтобы удалять невидимые части фигуры и немного оптимизировать скорость вывода и модель на экране была более реалистична ( посмотрим в этой части ).

Многие из моделей которые делают в других редакторах, состоят не просто из линий как наша текущая пирамида, а из множества граней ( полигонов ), которые стоят рядом и создают фигуру. Умение работать с такими моделями позволит нам в коде не создавать модели вручную ( их вершины и полигоны ), а загружать их из файлов, который были экспортированы из 3D-редакторов или скачаны из сайтов с 3D-моделями.

Давайте разберемся как нашу текущую модель и код переписать так, чтобы она имела понятия полигона. Первое что нам нужно это придумать систему, по которой мы будем выводить любую другую фигуру, а не только пирамиду. Ведь мы же не будем писать отдельную программу для пирамиды, сферы, или игрового персонажа… Например, смотря на пирамиду, мы видим что она состоит из 6 четырехугольных граней, у которых есть общие вершины. Все эти четырехугольники мы видим на картинке выше, там где пронумерованы вершины. Эти четырехугольники можно еще назвать четырехугольными полигонами. Но в 3D программировании на первых этапах нам проще использовать треугольные полигоны ( треугольники ), потому что такие полигоны будут в моделях, которые мы будем загружать из файлов. Плюс треугольники создают одну плоскость, в отличии от четырехугольника, и нам по треугольнику будет проще считать нормали ( узнаем что это в этой части ) и проще текстурировать ( разберем в следующих частях ). Вот пример треугольного и четырехугольного полигона:

Слева – треугольный полигон, справа – четырехугольный.

Из картинки можно увидеть что четырехугольный полигон, может создавать 2 плоскости. С треугольником такого не произойдет.

Для того чтобы начать использовать треугольники, нам много менять в уже имеющемся коде не придется.

Первое что нужно понять, что вершины никуда не деваются, все те же 8 штук, только теперь мы их соединим не просто линиями независимыми друг от друга, а каждую линию будем объединять в треугольник, так, чтобы получилась желаемая нам фигура. Принцип объединения такой-же как и был в массиве edges , т.е. при помощи индексов вершин, только теперь в массиве у нас будут не пары вершин ( пара т.к. у каждой линии есть начала и конец ), а по 3 вершины, например, чтобы описать 1 треугольник нам нужно указать 3 вершины, соединив которые мы получим треугольник. Мы уже упоминали что для построения усеченной пирамиды нам нужно 6 четырехугольников, а вот треугольников нам нужно в 2 раза больше, т.к. для вывода одного четырехугольника ( четырехугольного полигона ) нужно 2 треугольника. На картинке ниже в верхней части мы выводим 1 сторону пирамиды при помощи линий ( как у нас сейчас ), а ниже при помощи треугольников ( так сделаем ). В результате и там и там у нас визуально получился четырехугольник ( например, грань пирамиды ). Но в случае треугольников, у нас еще есть линия по диагонали, т.к. по сути это 2 приставленных к друг другу треугольника. Эта линия видна только потому что мы рисуем линиями. Когда мы научимся закрашивать в цвет, а потом и текстурировать фигуры и отключим линии, их не будет видно, и все будет выглядеть красиво, без ненужных стыков:

Сверху прямоугольник из линий, снизу – из треугольников.

Кажется что использование треугольников – избыточно. Конкретно в этом случае так и есть, т.к. пирамида состоит из четырехугольников и тут они конечно больше подходят. Но вспомните о преимуществах, которые описаны выше. А также о том, что мы не будем все время выводить одни пирамиды, будут другие, более сложные фигуры, где треугольники уже покажутся лучшим выбором и чтобы в коде все было просто и все фигуры выводились одинаково, мы все их будем выводить при помощи треугольников, хоть это и будет иногда не самым идеальным вариантом.

Давайте закомментируем массив edges и заменим его на массив indices , в котором будут подмассивы по 3 индекса:

В этом массиве каждая строчка ( подмассив из 3х элементов ) – это 3 индекса из массива вершин ( vertices ) которые если мы соединим линиями между собой – получим треугольник. Таким образом мы описали все стороны усеченной пирамиды, их у нее 6, но они прямоугольные, и для каждого прямоугольника приходится использовать по 2 треугольника.

Теперь нужно переписать код отрисовки линий, т.к. теперь мы рисуем не по одной линии используя массив edges , а сразу будем выводить по треугольнику ( массив indices ).

Давайте закомментируем целиком цикл работы с edges :

И вместо него будем перебирать массив indices :

Внутри этого цикла при помощи записи indices[i] мы можем достать строчку с 3мя индексами конкретного выводимого треугольника, эти индексы указывают на вершины в массиве sceneVertices ( т.к. мы сохранили порядок вершин из оригинального массива indices ). Поэтому при помощи такой записи мы можем достать координаты всех вершин:

И последним шагом перехода на треугольники — отрисовка 3х линий по 3м точкам:

В каком порядке рисовать линии не имеет значения, главное чтобы все 3 точки были соединены между собой и на экране получился треугольник.

Для того чтобы видеть пирамиду в динамике, давайте вернем ей вращение по оси Y , сразу после вращени по X ( хоть там сейчас и 0 стоит для X ):

Если все сделали правильно, то у вас должна быть на экране вращающаяся пирамида состоящая из треугольников:

Модель усеченной пирамиды из треугольников

Как видите, она отличается от предыдущей наличием диагональных линий, как я уже упоминал ранее это потому что каждый четырехугольник в пирамиде состоит из рядом стоящих 2 треугольников. Такой артефакт мы позднее уберем, в следующих частях.

Теперь давайте посмотрим еще раз что не так. У пирамиды которая получилась как и всех моделей выводимых ранее видны сразу все её грани ( технически мы видим линии ребер, т.к. их рисуем ), ранее это нас устраивало, т.к. нужно было видеть что происходит с каждой стороны, настраивать перспективу и т.д.

Предлагаю сделать оптимизацию и скрыть те грани фигуры, которые нам не должны быть видны. Это даст более реалистичную картинку ( сделает пирамиду непрозрачной ), также мы немного ускорим приложение, т.к. не будем рисовать линии тех треугольников, что сейчас не должны быть видны.

Для того чтобы эти треугольники скрыть, давайте подумаем как вообще это можно сделать. Сейчас когда мы используем треугольники, мы знаем что у него есть одна плоскость с 2мя сторонами, если бы мы вырезали треугольник из бумаги, то можно было бы его покрутить то одно стороной то другой. В жизни мы конечно видим треугольник независимо от того какой стороной он к нам повернут, но в 3D графике мы можем настроить так, чтобы была видна только одна сторона. Как определить какая сторона должна быть лицевой и видимой? Вообще обе стороны имеют право на звание лицевой и тут свобода выбора, поэтому мы как разработчики этой модели сами должны решить, какая сторона какой будет. Сейчас мы не оперируем понятием сторона в коде, у нас есть только индексы 3х вершин, по которым мы рисуем линии. Для того чтобы это понятие появилось нам поможет очень полезная штука — нормаль. Нормаль это вектор перпендикулярный треугольнику и откуда исходит нормаль, та сторона и считается лицевой:

Нормаль видимой грани.

Синяя стрелка это вектор нормали для какого-то треугольника. Поскольку выше упоминалось что сторон у треугольника 2, то и нормали тоже может быть 2, но нам нужна только 1 нормаль, та которая будет исходить из видимой стороны треугольника. когда мы будем считать нормаль ( ниже покажу как это делать ) то мы будем считать ее при помощи уже имеющихся у нас 3х вершин треугольника и порядок расстановки вершин будет влиять на то в какую сторону указывает нормаль. Например, если бы точки a, b, c дали бы нам одну нормаль, то c, b, a дали бы уже другую, возможно, в противоположную сторону. Следить за массивом indices вручную очень сложно, ведь у нас очень простая фигура и там уже 12 записей по 3 индекса. Поэтому все это за нас уже давно делают 3D редакторы, когда мы экспортируем модели из них, они уже расставляют вершины в правильном всегда одинаковом порядке, так что мы сможем по ним посчитать правильные нормали. Но пока мы с 3D-редакторов еще не умеем что либо загружать, я правильную расстановку вершин в массиве indices уже сделал заранее, тот массив что мы использовали выше расставлен так, что все индексы вершин в нем дают нам правильные нормали.

Для того чтобы посчитать сами нормали нам никаких новых методов добавлять не придется, более того, мы уже делали их в прошлой части в секции бонуса, когда считали вектор для движения в сторону по отношению к положению к камере.

Для того чтобы посчитать нормаль. нам нужно получить 2 вектора треугольника, именно эти вектора образуют плоскость, перпендикуляр к которой мы хотим получить — это и будет нормалью, чтобы получить из 3х точек 2 вектора, нам нужно применить уже известную функцию substruct , ведь если вычесть одну точку из другой, мы получим вектор направления от одной точки к другой. Добавьте следующий код ниже получения v1, v2, v3 в цикле перебора indices :

И теперь вектора t1 и t2 образуют плоскость, если мы перемножим их при помощи векторного произведения векторов, то получим вектор перпендикулярный обоим векторам — это и будет нашей нормалью:

Порядок вычитания точек играет роль, в примере выше если бы я отнимал v2 и v1 ( вот так: let t1 = Vector.substruct(v2, v1); ) то вектор был бы у меня в другом направлении, и это могло бы дать нормаль в другом направлении, в таком случае я увижу внутреннюю часть пирамиды. Вообще тут строго запоминать какие вектора от каких отнимать и не нужно, вы всегда можете подобрать порядок вычитания так — как вам нужно. Получили не тот результат и фигура наизнанку, поменяйте вектора местами и получить то что вам нужно. Ведь тут нельзя говорить что если нормаль повернута в другую сторону то это неправильно, т.к. вполне может быть что мы хотим такое отображение для игры, например, если нам нужно сделать простенький горизонт в игре, для этого мы можем поместить сферу вокруг нашей камеры и наложить текстуру на внутреннюю сторону сферы, т.к. мы видим её изнутри, и тут нормали, возможно, нам придется направить в другую сторону переставив вектора местами или любым другим способом. В тоже время эту же модель сферы мы можем переиспользовать для других объектов в игре и там уже нам нужно отрисовывать наружную часть сферы, где нормали повернуты в противоположную сторону от тех что нужны были для горизонта. Таким образом для одной модели нам может понадобиться считать нормали направленные как в одну сторону, так и в другую, зависимо от того что мы хотим получить на экране. А может нам и вовсе не нужно делать какую-то часть треугольника невидимой, если мы хотим чтобы были видны обе его стороны.

Нормали нужны далеко не для того чтобы можно было посчитать какие полигоны ( треугольники ) модели видны, с помощью нормалей, например, можно освещать модели, но это мы сделаем в следующих частях.

Теперь, когда у нас есть нормаль треугольника, нужно посчитать должен ли этот треугольник быть видимым по отношению к камере ( с нашего ракурса ). Для этого мы можем воспользоваться новой операцией над векторами: скалярным произведением векторов. Для этой операции нам нужно 2 вектора и в результате этой операции мы получим число, которое на первый взгляд не понятно как применить к нашей задаче. Определение результата скалярного произведения векторов звучит так: результатом называется число, равное произведению длин этих векторов на косинус угла между ними. Что за длины, что за косинус и как нам все это поможет? Давайте разбираться, добавим код этого самого скалярного произведения в класс Vector :

Код не сложный, а вот определение результата так себе. На самом деле нам в результате этой операции само число и не нужно, нам нужен лишь знак этого числа. Ведь в формулировке говорится что результат это длины векторов и косинус угла между ними перемноженные между собой, вот длины векторов нам не особо нужны, они всегда положительные, а вот косинус угла как раз интересный, т.к. если вспомним чуть математику или просто брутфорсом начнем подставлять углы в косинус, то увидим, что косинус угла 90 градусов = 0 , а косинус 89 градусов равен примерно 0.017 , а косинус 91 градуса -0.017 . Т.е. если угол который мы передадим в косинус более 90 градусов то мы будем получать отрицательные числа, а если менее — положительные. Таким образом, если результат скалярного произведения векторов окажется положительным, то значит что угол между ними ( в нашем случае между вектором камеры и нормалью треугольника ) менее 90 градусов и такой треугольник нам нужно рисовать, а если отрицательный – не нужно. Т.е. мы не зная углов между камерой и нормалью все равно можем принимать решения по отрисовке, т.к. в результате хоть и нету угла, но есть косинус угла, который даст нам правильный знак в результате скалярного произведения. Давайте попробуем это теперь применить в коде, ниже строчки в которой мы посчитали нормаль, добавим скалярное произведения вектора камеры на нормаль:

И следующей строчкой, поместим всю отрисовку пирамиды в проверку:

Если все сделали правильно, у Вас должна получиться пирамида, у которой видна только часть смотрящая в камеру, а остальные грани отброшены условием.:

Такое отсечение невидимых граней еще называют отбраковкой обратной стороны ( или backface culling ). Для теста, можете заменить в условии res > 0 на res и увидите внутреннюю часть пирамиды, т.к. теперь мы рисуем отвернутые от камеры треугольники.

На этом часть заканчивается, но приключение продолжается! В этот раз мы научились выводить модель при помощи треугольников. Посмотрели как считать нормали и как при помощи этих нормалей скрывать невидимую часть фигуры, воспользовавшись новой операцией, скалярным произведением векторов.

В следующей части мы посмотрим как можно закрашивать треугольники в интересующий нас цвет, научимся отсекать слишком близкие и далекие пиксели ( используем near / far параметры матрицы перспективы ) а также познакомимся с z-буфером, при помощи которого будем рисовать пиксели нескольких моделей на экране так, чтобы они правильно перекрывали друг друга. И даже сделаем первую игру, используя уже имеющиеся знания и наработки.

Как вычислить нормальный вектор отрезка?

предположим,что у меня есть отрезок линии,идущий от (x1, y1) до (x2, y2). Как вычислить нормальный вектор, перпендикулярный линии?

Я могу найти много вещей о том, как это сделать для самолетов в 3D,но не 2D.

пожалуйста, полегче с математикой (ссылки на отработанные примеры, диаграммы или алгоритмы приветствуются), я программист больше, чем математик;)

4 ответов

Если мы определим dx=x2-x1 и dy=y2-y1, то нормали будут (- dy, dx) и (dy, – dx).

обратите внимание, что деление не требуется, и поэтому вы не рискуете делением на ноль.

другой способ подумать об этом-вычислить единичный вектор для данного направления, а затем применить 90-градусное вращение против часовой стрелки, чтобы получить нормальный вектор.

матричное представление общего 2D-преобразования выглядит следующим образом:

где (x,y) – компоненты исходного вектора и (x’, y’) – преобразованные компоненты.

Если t = 90 градусов, то cos (90) = 0 и sin(90) = 1. Подстановка и умножение дает:

тот же результат, что и ранее, но с немного большим объяснением того, откуда он берется.

этот вопрос был размещен давно, но я нашел альтернативный способ ответить на него. Поэтому я решил поделиться им здесь.
Во-первых, надо знать, что: если два вектора перпендикулярны, то их скалярное произведение равно нулю.
Нормальный вектор (x’,y’) перпендикулярно линии, соединяющей (x1,y1) и (x2,y2) . Эта линия имеет направление (x2-x1,y2-y1) или (dx,dy) .
Итак,

множество пар (x’, y’), удовлетворяющих приведенному выше уравнению. Но лучше пара, которая всегда удовлетворяет, либо (dy,-dx) или (-dy,dx)

Если перпендикулярно две строки:

b-это что-то, если вы хотите передать его из точки, которую вы определили

[spoiler title=”источники:”]

http://habr.com/ru/post/647171/

http://askdev.ru/q/kak-vychislit-normalnyy-vektor-otrezka-12835/

[/spoiler]

Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.

Угол между прямыми а и b

Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов и по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
. Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль к плоскости

Нормалью к плоскости называется любой вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные произведение векторов к нулю, составляем систему уравнений с тремя переменными, из которой можно найти координаты нормали.

Замечание репетитора по математике: Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).

Угол между прямой и плоскостью

Допустим, что нам заданы прямая и плоскость координатами направляющего вектора и нормали
Угол между прямой и плоскость вычисляется по следующей формуле:

Угол между плоскостями

Пусть и  — две любые нормали к данным плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между нормалями:

Уравнение плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью . Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль (как это описано выше), а затем подставить координаты любой точки плоскости вместе с координатами найденной нормали в уравнение и найти коэффициент .

Расстояние от точки до плоскости

Для вычисления расстояния от точки до плоскости , заданной уравнением можно использовать следующую формулу:

В знаменателе стоит длина нормали, а числителе — значение выражения из левой части уравнения плоскости в точке

Комментарий репетитора по математике:

Методом координат можно находить не только углы и расстояния в пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).

Для понимания таких формул нужно изучить понятия векторного и смешанного произведения векторов, а также определителя матрицы. В скором времени я сделаю для вычисления объемов соответствующую справочную страничку.

Средства аналитической геометрии репетитор по математике практически не использует в работе со средним и тем более слабым учеником. И очень жаль, что загруженность среднестатистического сильного школьника не позволяет репетитору провести более-менее серьезную работу на уровне определений из высшей математики и с соответствующей практикой решения задач. Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного – двух примеров их использования. В школьной программе не предусмотрено время для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная подготовка к ЕГЭ по математике с изучением приемов аналитической геометрии даст Вам мощное и универсальное средство для решения огромного класса задач типа С2. Пользуйтесь этой страничкой на здоровье!

Колпаков А.Н. Репетитор по математике Москва (Строгино).

Как найти нормаль плоскости

Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.

Инструкция

Если задано общее уравнение плоскости – AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ – n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.

Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] – одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)

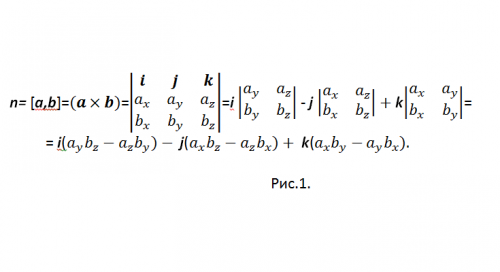
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.

Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена – n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

В самом общем случае нормаль к поверхности
представляет ее локальную кривизну, и,
следовательно, направление зеркального
отражения (рис. 3.5). Применительно к нашим
знаниям можно сказать, что нормалью
называется вектор, определяющий
ориентацию грани (рис. 3.6).

Рис. 3.5 Рис. 3.6

Во многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра и вершины, поэтому, для
того чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.
Пусть заданы уравнения плоскостей
полигональных граней, тогда нормаль к
их общей вершине равна среднему значению
нормалей ко всем многоугольникам,
сходящимся к этой вершине. Например, на
рис. 3.7 направление приближенной нормали
в точке V₁есть:

n_v1
= (a₀
+ a₁
+ a₄)i
+ (b₀
+ b₁
+ b₄)j
+ (c₀
+ c₁
+ c₄)k,
(3.15)

где a₀, a₁,
a₄, b₀, b₁,
b₄, c₀, c₁,
c₄– коэффициенты уравнений
плоскостей трех многоугольниковP₀,
P₁, P₄,окружающихV₁. Отметим, что
если требуется найти только направление
нормали, то делить результат на количество
граней необязательно.

Если же уравнения плоскостей не заданы,
то нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Еще
раз, рассматривая вершину V₁на
рис. 3.7, найдем направление приближенной
нормали:

n_v1
= V₁V₂

V₁V₄
+V₁V₅

V₁V₂
+ V₁V₄

V₁V₅
(3.16)

Рис. 3.7 – Аппроксимация
нормали к полигональной поверхности

Следует
обратить внимание на то, что необходимы
только внешние нормали. Кроме того, если
полученный вектор не нормируется, то
его величина зависит от количества и
площади конкретных многоугольников, а
также от количества и длины конкретных
ребер. Сильнее проявляется влияние
многоугольников с большей площадью и
более длинными ребрами.

Когда
нормаль к поверхности используется для
определения ин­тенсивности и для
изображения объекта или сцены выполняется
перспективное преобразование, то нормаль
следует вычислять до перспективного
деления. В противном случае направление
нор­мали будет искажено, а это приведет
к тому, что интенсивность, задаваемая
моделью освещения, будет определена
неправильно.

Если известно аналитическое описание
плоскости (поверхности), то нормаль
вычисляется непосредственно. Зная
уравнение плоскости каждой грани
многогранника, можно найти направление
внешней нормали.

Если
уравнение плоскости имеет вид:

, (3.17)

то вектор нормали к этой плоскости
записывается следующим образом:

, (3.18)

где
– единичные векторы осейx,y,zсоответственно.

Величина dвычисляется с помощью
произвольной точки, принадлежащей
плоскости, например, для точки ()

. (3.19)

Пример.Рассмотрим 4-х сторонний
плоский многоугольник, описываемый
4-мя вершинами V1(1,0,0), V2(0,1,0), V3(0,0,1) и
V4(1,1,1) (см. рис. 3.7).

Уравнение
плоскости имеет вид:

x
+ y
+ z
– 1 = 0.

Получим нормаль к этой плоскости,
используя векторное произведение пары
векторов, являющихся смежными ребрами
к одной из вершин, например, V1:

Во
многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра или вершины, поэтому, для
того, чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.

Пусть
заданы уравнения плоскостей граней
многогранника, тогда нормаль к их общей
вершине равна среднему значению нормалей
ко всем граням, сходящимся в этой вершине.

Например, на рис.3.7 направление приближенной
нормали в точке
есть

,

где
– коэффициенты уравнений плоскостей
3-х многоугольниковP0,P1иP4,
окружающих.

Если
же уравнение плоскостей не заданы, то
нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Опять,
выбирая вершину
(см.
рис. 3.7), найдем направление приближенной
нормали:

Замечания:

1. нам необходимы только внешние нормали;

2. вычисление нормали осуществляется до
   перспективных преобразований, в
   противном случае направление нормали
   будет искажено, что приведет к неправильной
   модели освещения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #