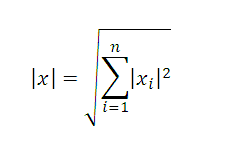Онлайн калькулятор для нахождения длины (нормы) вектора.
Найти нормированный вектор, норма вектора – длина вектора на линейном пространстве.
Построить вектор в двухмерном и трехмерном пространстве.
Скачать калькулятор
Рейтинг: 3.1 (Голосов 15)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Сообщить об ошибке
Смотрите также
| Действия с векторами | Cкалярное произведение | Векторное произведение | Длина, модуль вектора | Угол между векторами |
| Векторный калькулятор | Сложение и вычитание | Разложить вектор по базису | Сумма векторов | Середина отрезка |
Search for a tool
Vector Norm
Tool to calculate the norm of a vector. The vector standard of a vector space represents the length (or distance) of the vector.
Results
Vector Norm –
Tag(s) : Matrix
Share
dCode and more
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
- Mathematics
- Matrix
- Vector Norm
Vector’s Norm Calculator
Answers to Questions (FAQ)
What is the norm of a vector? (Definition)
The norm of a vector is its length. If $ A $ and $ B $ are two points (of a space of $ n $ dimensions) then the norm of the vector, noted with a double bar $ |overrightarrow{AB}| $, is the distance between $ A $ and $ B $ (the length of the segment $ [AB] $).
The absolute value is the special case of the norm for a real number (one dimension).
How to calculate the norm of a vector?
In a vector space of dimension $ n $, a vector $ vec{v} $ of components $ x_i $ : $ vec{v} = (x_1, x_2, …, x_n) $ is computed by the square root of the sum of the squares of the components: $$ left|vec{v}right| = sqrt{x_1^2 + x_2^2 + cdots +x_n^2} $$
The norm of a vector can also be computed from the scalar product of the vector with itself: $ | vec{v} | = sqrt{ vec{v} cdot vec{v} } $.
How to calculate the norm of a 2D vector?
In the 2D plane, for a vector $ vec{v} = (x,y) $ the formula is simplified $$ |vec{v}|= sqrt{x^2+y^2} $$
Example: $ vec{v} = left( begin{array}{c} 1 2 end{array} right) $ so $ |vec{v}| = sqrt{1^2+2^2} = sqrt{5} $
How to calculate the norm of a 3D vector?
In 3D space, for a vector $ vec{u} = (x,y,z) $ the formula is simplified $$ |{vec{u}}|= sqrt{x^2+y^2+z^2} $$
How to calculate the components of a vector from the points?
From the coordinates of the points $ A (x_A,y_A) $ and $ B (x_B,y_B) $ of the vector $ overrightarrow{AB} $, the components of the vector are $ {overrightarrow {AB}} = { (x_B-x_A), (y_B-y_A) } $ and therefore the norm is $ |overrightarrow {AB}| = sqrt{(x_B-x_A)^2+(y_B-y_A)^2} $
Source code
dCode retains ownership of the “Vector Norm” source code. Except explicit open source licence (indicated Creative Commons / free), the “Vector Norm” algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the “Vector Norm” functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for “Vector Norm” are not public, same for offline use on PC, mobile, tablet, iPhone or Android app!
Reminder : dCode is free to use.
Cite dCode
The copy-paste of the page “Vector Norm” or any of its results, is allowed (even for commercial purposes) as long as you cite dCode!
Exporting results as a .csv or .txt file is free by clicking on the export icon
Cite as source (bibliography):
Vector Norm on dCode.fr [online website], retrieved on 2023-05-20, https://www.dcode.fr/vector-norm
Summary
https://www.dcode.fr/vector-norm
© 2023 dCode — The ultimate ‘toolkit’ to solve every games / riddles / geocaching / CTF.
▲
Калькулятор онлайн.
Составить уравнение плоскости
Этот калькулятор онлайн составляет (находит) уравнение плоскости по трем точкам, лежащим на плоскости или по нормали и одной точке лежащей на плоскости.
Онлайн калькулятор для нахождения уравнения плоскости не просто даёт ответ задачи, он приводит подробное
решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Общее уравнение плоскости
Пусть заданы:
прямоугольная система координат Oxyz,
произвольная плоскость ( pi );
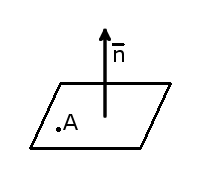
точка ( M_0(x_0;y_0;z_0) in pi );
вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости ( pi ) (смотри рисунок).
Рассмотрим произвольную точку М(х; у; z). Точка М лежит на плоскости ( pi ) тогда и только тогда, когда векторы
( vec{M_0M} ) и ( vec{N} ) взаимно перпендикулярны. Так как координаты вектора ( vec{M_0M} )
равны ( x-x_0, ; y-y_0, ; z-z_0 ) , то в силу условия перпендикулярности двух векторов (скалярное произведение
должно быть равно нулю) получаем, что точка М (х; у; z) лежит на плоскости ( pi ) тогда и только тогда, когда
( A(x-x_0)+B(y-y_0)+C(z-z_0)=0 tag{1} )
Это и есть искомое уравнение плоскости ( pi ), так как ему удовлетворяют координаты х; у; z любой точки М, лежащей на плоскости ( pi ),
и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.
Раскрывая скобки, приведем уравнение (1) к виду
( Ax+By+Cz+(-Ax_0-By_0-Cz_0)=0 )
Далее, обозначая число ( -Ax_0-By_0-Cz_0 ) через ( D ), получаем
( Ax +By+Cz+D=0 tag{2} )
Уравнение (2) называется общим уравнением плоскости. Таким образом, плоскость является поверхностью первого порядка, так как
определяется уравнением первой степени.
Верно и обратное: всякое уравнение первой степени вида (2) определяет в заданной прямоугольной системе координат плоскость.
Действительно, пусть заданы прямоугольная система координат Oxyz и уравнение ( Ax+By+Cz+D=0 ) с произвольными коэффициентами
А, В, С и D, причем из коэффициентов А, В и С хотя бы один отличен от нуля. Данное уравнение заведомо имеет хотя бы одно решение
( x_0, ; y_0, ; z_0 ) ( если, например, ( C neq 0 ), то, взяв произвольные х0, и y0, из уравнения получим:
( z_0 = -frac{A}{C}x_0 – frac{B}{C}y_0-frac{D}{C} ) ).
Таким образом, существует хотя бы одна точка M0(x0; y0; z0), координаты которой
удовлетворяют уравнению, т.е. Ax0+By0+Cz0+D=0. Вычитая это числовое равенство из уравнения
Ax+By+Cz+D=0, получаем уравнение
A(x-x0) + B(y-y0) + C(z-z0) + D=0,
эквивалентное данному. Полученное уравнение (а стало быть, и уравнение Ax+By+Cz+D=0 ) совпадает с уравнением (1) и, значит, определяет
плоскость ( pi ), проходящую через точку M0(x0 и перпендикулярную вектору ( vec{N}(A;B;C) ).
Вектор ( vec{N}(A;B;C) ), перпендикулярный плоскости, называется нормальным вектором или нормалью этой плоскости.
Теорема
Если два уравнения ( A_1x+B_1y+C_1z+D_1=0 ) и ( A_2x+B_2y+C_2z+D_2=0 ) определяют одну и ту же плоскость, то их коэффициенты
пропорциональны, т.е.
$$ frac{A_2}{A_1} = frac{B_2}{B_1} = frac{C_2}{C_1} = frac{D_2}{D_1} $$
Угол между двумя плоскостями
Рассмотрим две плоскости ( pi_1 ), и ( pi_2 ), заданные соответственно уравнениями
( A_1x+B_1y+C_1z+D_1=0, ;; A_2x+B_2y+C_2z+D_2=0 )
При любом расположении плоскостей ( pi_1 ), и ( pi_2 ) в пространстве один из углов ( varphi )
между ними равен углу между их нормалями ( vec{N_1}(A_1;B_1;C_1) ) и ( vec{N_2}(A_2;B_2;C_2) ) и вычисляется по
следующей формуле:
$$ cos varphi = frac{ vec{N_1} cdot vec{N_2}}{ |vec{N_1}| |vec{N_2}| } =
frac{A_1 A_2 + B_1 B_2 + C_1 C_2}{sqrt{A_1^2 + B_1^2 + C_1^2} ; sqrt{A_2^2 + B_2^2 + C_2^2} } tag{3} $$
Второй угол равен ( 180^circ -cos varphi )
Условие параллельности плоскостей
Если плоскости ( pi_1 ) и ( pi_2 ) параллельны, то коллинеарны их нормали ( vec{N_1} ) и
( vec{N_2} ), и наоборот. Но тогда
$$ frac{A_1}{A_2} = frac{B_1}{B_2} = frac{C_1}{C_2} tag{4} $$
Условие (4) является условием параллельности плоскостей ( pi_1 ) и ( pi_2 )
Условие перпендикулярности плоскостей
Если плоскости ( pi_1 ) и ( pi_2 ) взаимно перпендикулярны, то их нормали ( vec{N_1} ) и
( vec{N_2} ) также перпендикулярны, и наоборот. Поэтому из формулы (3) непосредственно получаем условие
перпендикулярности плоскостей ( pi_1 ) и ( pi_2 ):
( A_1 A_2 + B_1 B_2 + C_1 C_2 = 0 )
Уравнение плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через три точки
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы 
и 
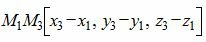не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M1, M2, M3 тогда и тольно тогда, когда векторы M1M2, M1M3 и 
компланарны. Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M1M2, M1M3, M1M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:
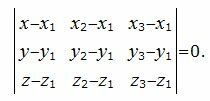
Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M1, M2, M3:
Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).
|
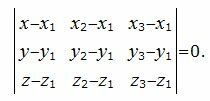(1) |
Подставляя координаты точек A, B, C в (1), получим:
Разложим определитель по первому столбцу:
Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:
Уравнение плоскости, проходящей через одну точку и имеющий нормаль n
Пример 2. Построить плоскость, проходящую через точку M0(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).
 |
(2) |
Подставляя координаты векторов M0 и n в (2), получим:
Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
-
Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x – x 1 | y – y 1 | z – z 1 | = 0 |
| x 2 – x 1 | y 2 – y 1 | z 2 – z 1 | |
| x 3 – x 1 | y 3 – y 1 | z 3 – z 1 |
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой
В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.
Как найти уравнение плоскости, которая проходит через 3 заданные точки
Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:
Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.
Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.
Допустим, у нас имеется прямоугольная система координат. Обозначим ее O x y z . В ней лежат три точки M с координатами M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , которые нельзя соединить прямой линией. Исходя из этих условий, мы можем записать уравнение необходимой нам плоскости. Есть два подхода к решению этой задачи.
1. Первый подход использует общее уравнение плоскости. В буквенном виде оно записывается как A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . С его помощью можно задать в прямоугольной системе координат некую плоскость альфа, которая проходит через первую заданную точку M 1 ( x 1 , y 1 , z 1 ) . У нас получается, что нормальный вектор плоскости α будет иметь координаты A , B , C .
Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.
Из этого мы и будем исходить в дальнейшем.
Таким образом, согласно условиям задачи, мы имеем координаты искомой точки (даже трех), через которую проходит плоскость. Чтобы найти уравнение, нужно вычислить координаты ее нормального вектора. Обозначим его n → .
Вспомним правило: любой не равный нулю вектор данной плоскости является перпендикулярным нормальному вектору этой же плоскости. Тогда мы имеем, что n → будет перпендикулярным по отношению к векторам, составленным из исходных точек M 1 M 2 → и M 1 M 3 → . Тогда мы можем обозначить n → как векторное произведение вида M 1 M 2 → · M 1 M 3 → .
Поскольку M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) а M 1 M 3 → = x 3 – x 1 , y 3 – y 1 , z 3 – z 1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора по координатам точек), тогда получается, что:
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1
Если мы вычислим определитель, то получим необходимые нам координаты нормального вектора n → . Теперь мы можем записать нужное нам уравнение плоскости, проходящей через три заданные точки.
2. Второй подход нахождения уравнения, проходящей через M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , основан на таком понятии, как компланарность векторов.
Если у нас есть множество точек M ( x , y , z ) , то в прямоугольной системе координат они определяют плоскость для заданных точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) только в том случае, когда векторы M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) будут компланарными.
На схеме это будет выглядеть так:
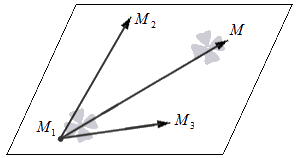
Это будет означать, что смешанное произведение векторов M 1 M → , M 1 M 2 → , M 1 M 3 → будет равно нулю: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , поскольку это является основным условием компланарности: M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) .
Запишем полученное уравнение в координатной форме:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
После того, как мы вычислим определитель, мы сможем получить нужное нам уравнение плоскости для трех не лежащих на одной прямой точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) .
От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.
В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.
Примеры задач на составление уравнения плоскости, проходящих через 3 точки
Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.
Есть три точки, не лежащие на одной прямой, с координатами M 1 ( – 3 , 2 , – 1 ) , M 2 ( – 1 , 2 , 4 ) , M 3 ( 3 , 3 , – 1 ) . Составьте уравнение плоскости, проходящей через них.
Решение
Используем поочередно оба способа.
1. Найдем координаты двух нужных нам векторов M 1 M 2 → , M 1 M 3 → :
M 1 M 2 → = – 1 – – 3 , 2 – 2 , 4 – – 1 ⇔ M 1 M 2 → = ( 2 , 0 , 5 ) M 1 M 3 → = 3 – – 3 , 3 – 2 , – 1 – – 1 ⇔ M 1 M 3 → = 6 , 1 , 0
Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →
У нас получился нормальный вектор плоскости, которая проходит через три искомые точки: n → = ( – 5 , 30 , 2 ) . Далее нам нужно взять одну из точек, например, M 1 ( – 3 , 2 , – 1 ) , и записать уравнение для плоскости с вектором n → = ( – 5 , 30 , 2 ) . Мы получим, что: – 5 · ( x – ( – 3 ) ) + 30 · ( y – 2 ) + 2 · ( z – ( – 1 ) ) = 0 ⇔ – 5 x + 30 y + 2 z – 73 = 0
Это и есть нужное нам уравнение плоскости, которая проходит через три точки.
2. Используем другой подход. Запишем уравнение для плоскости с тремя точками M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
Сюда можно подставить данные из условия задачи. Поскольку x 1 = – 3 , y 1 = 2 , z 1 = – 1 , x 2 = – 1 , y 2 = 2 , z 2 = 4 , x 3 = 3 , y 3 = 3 , z 3 = – 1 , в итоге мы получим:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73
Мы получили нужное нам уравнение.
Ответ: – 5 x + 30 y + 2 z – 73 .
А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.
У нас есть прямоугольная система координат в трехмерном пространстве, в которой размещены три точки с координатами M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) . Необходимо составить уравнение плоскости, проходящей через нее.
Решение
Используем первый способ и начнем с вычисления координат двух векторов M 1 M 2 → и M 1 M 3 → . Подсчитаем их координаты: M 1 M 2 → = ( – 4 , 6 , 2 ) , M 1 M 3 → = – 6 , 9 , 3 .
Векторное произведение будет равно:
M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →
Поскольку M 1 M 2 → × M 1 M 3 → = 0 → , то наши векторы будут коллинеарными (перечитайте статью о них, если забыли определение этого понятия). Таким образом, исходные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой, и наша задача имеет бесконечно много вариантов ответа.
Если мы используем второй способ, у нас получится:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0
Из получившегося равенства также следует, что заданные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой.
Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:
1. Записать уравнение прямой М 1 М 2 , М 1 М 3 или М 2 М 3 (при необходимости посмотрите материал об этом действии).
2. Взять точку M 4 ( x 4 , y 4 , z 4 ) , которая не лежит на прямой М 1 М 2 .
3. Записать уравнение плоскости, которая проходит через три различных точки М 1 , М 2 и M 4 , не лежащих на одной прямой.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/plane/
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-kotoraja-prohodit-cherez-tri-z/
[/spoiler]
Норма вектораФормулы, примеры, калькулятор нормы вектора Определение 1. Норма вектора ( эвклидова норма, модуль вектора, длина вектора) x=(x1,x2, …xn)
Пример 1. Найти норму вектора a = (5,-2,7) Решение. Подставляем координаты вектора, получаем норму вектора
Как нормировать векторНормированный вектор – это единичный вектор по направлению. То есть, сохраняется информация только о направлении вектора:
Для того чтобы получить нормированный вектор, необходимо каждую координату исходного вектора разделить на норму вектора. Пример 2. Нормировать вектор a = (5,-2,7) Решение. Подставляем координаты вектора, получаем нормированный вектор
Проверить правильность вычисления нормы вектора, а также найти нормированный вектор можно с помощью калькулятора. |
Категория: Аналитическая геометрия | Просмотров: 12351 | | Теги: вектор | Рейтинг: 0.0/0 |
