Нормалью грани (face normal) называется вектор, определяющиий ориентацию лицевой грани многоугольника (рис. 5.1).
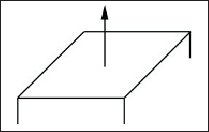 |
Рис. 5.1. Лицевая нормаль поверхности |
Нормали вершин (vertex normals) основаны на той же самой идее, но в этом случае задается не нормаль для всего многоугольника, а отдельная нормаль для каждой образующей его вершины (рис. 5.2).
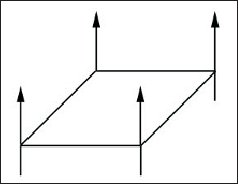 |
Рис. 5.2. Нормали вершин поверхности |
Direct3D необходимо знать нормали вершин, поскольку они необходимы чтобы оперделить под каким углом свет падает на грань. Кроме того, поскольку вычисление освещенности выполняется для каждой из вершин, Direct3D необходимо знать ориентацию грани (нормаль) для каждой вершины. Обратите внимание, что нормаль вершины не всегда совпадает с нормалью грани. Наиболее распростарненным примером объекта у которого нормали треугольных граней не совпадают с нормалями вершин является сфера или цилиндр (рис. 5.3).
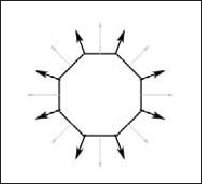 |
Рис. 5.3. Пример объекта, у которого нормали вершин не совпадают с нормалями граней. Векторы нормалей вершин выделены черным цветом, а векторы нормалей граней — серым |
Для описания нормалей вершин нам необходимо добавить соответствующие члены в структуру данных вершины:
struct Vertex
{
float _x, _y, _z;
float _nx, _ny, _nz;
static const DWORD FVF;
}
const DWORD Vertex::FVF = D3DFVF_XYZ | D3DFVF_NORMAL;
Обратите внимание, что мы убрали члены данных, задающие цвет вершины, которые использовали в предыдущей главе. Дело в том, что теперь для вычисления цвета вершин мы будем использовать данные освещения.
Для простых объектов, таких как кубы и сферы, нормали вершин можно оперделить путем осмотра. Для сложных сеток необходим более алгоритмизированный способ. Предположим, что треугольник образован вершинами p0, p1 и p2, и нам необходимо вычислить нормали n0, n1 и n2 для каждой из вершин.
Простейший подход заключается в том, чтобы вычислить нормаль грани для треугольника и использовать ее в качестве нормали для всех трех вершин. Сперва вычислим два вектора, лежащих в полскости треугольника:
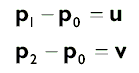
Тогда нормаль грани вычисляется по формуле:
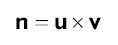
Поскольку нормаль каждой вершины совпадает с нормалью грани:
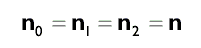
Ниже приведена функция, которая вычисляет нормаль треугольной грани на основании координат трех ее вершин. Обратите внимание, что функция предполагает, что вершины перечислены по часовой стрелке. Если это не так, нормаль будет указывать в противоположном направлении.
void ComputeNormal(D3DXVECTOR3* p0,
D3DXVECTOR3* p1,
D3DXVECTOR3* p2,
D3DXVECTOR3* out)
{
D3DXVECTOR3 u = *p1 - *p0;
D3DXVECTOR3 v = *p2 - *p0;
D3DXVec3Cross(out, &u, &v);
D3DXVec3Normalize(out, out);
}
Использование нормали грани в качестве нормалей вершин не позволяет добиться гладкого изображения состоящих из треугольных граней сложных кривых поверхностей. Лучшим методом вычисления нормалей вершин является усреднение нормалей (normal averaging). Чтобы вычислить вектор нормали vn для вершины v, мы вычисляем нормали граней всех треугольников сетки, в которые входит данная вершина v. Затем вектор нормали вершины vn получается путем вычисления среднего значения всех этих нормалей граней. Давайте разберем конкретный пример. Предположим, вершина v входит в три треугольника, для которых известны их нормали граней n0, n1 и n2. Тогда vn вычисляется путем усреднения нормалей граней:
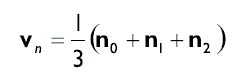
В процессе преобразований может получиться так, что векторы нормалей станут денормализованными. Так что лучше всего предусмотреть возможность подобной ситуации и приказать Direct3D заново нормализовать все векторы нормалей после преобразований, включив режим визуализации D3DRS_NORMALIZENORMALS:
Device->SetRenderState(D3DRS_NORMALIZENORMALS, true);
Сайт управляется системой uCoz

Нормали вершин додекаэдральной поверхности.
Нормаль вершины в вершине многогранника — это вектор, ассоциированный с вершиной, предназначенный для замены истинной геометрической нормали к поверхности. Обычно нормаль вычисляется как нормализованное среднее нормалей поверхности граней, содержащих вершину[1][2]. Среднее может быть взвешенным, например по площади грани, а может и не быть взвешенным[3][4]. Нормали вершин могут быть вычислены для приближений поверхностей многогранниками, таких как NURBS, или предназначены явно для художественных целей. Нормали вершин используются в методе тонирования Гуро, в затенении по Фонгу и других моделях освещения[en]. Используя нормали вершин, можно достичь более гладкого тонирования, чем при плоском тонировании. Однако без некоторых модификаций резкие края получить нельзя[5].
См. также[править | править код]
- Зеркальный световой блик[en]
- Попиксельное освещение
Примечания[править | править код]
- ↑ Gouraud, 1971, с. 623—629.
- ↑ Glassner, 1994, с. 60-74.
- ↑ Max, 1999, с. 1-6.
- ↑ Thürrner, Wüthrich, 1998, с. 43-46.
- ↑ Max Wagner. Generating Vertex Normals (англ.) // EmeyeX.com : сайт. — 2004. — 12 September. — P. 7. Архивировано 31 мая 2013 года.
Литература[править | править код]
- Henri Gouraud. Continuous Shading of Curved Surfaces // IEEE Transactions on Computers, C-20(6). — 1971. — С. 623—629.
- Andrew Glassner. I.6 Building vertex normals from a unstructured polygon list // Graphics Gems IV / Paul S. Heckbert, Morgan Kaufmann. — 1994. — С. 60—74.
- Nelson Max. Weights for Computing Vertex Normals from Facet Normals // Journal of Graphics Tools. — 1999. — Т. 4, вып. 2. — С. 1-6.
- Grit Thürrner, Charles A. Wüthrich. Computing Vertex Normals from Polygonal Facets // Journal of Graphics Tools. — 1998. — Т. 3, вып. 1. — С. 43-46.
В этом уроке мы будем учиться освещать и затенять наши 3д модели. Вот список того, что мы изучим:
- Как
сделать так, чтобы объект был ярче когда находится ближе к источнику света. - Как
сделать отблески когда мы видим отраженный свет на предмете(specular lighting) - Как сделать, чтобы объект был немного затененный, когда свет падает не прямо на объект(diffuse lighting)
- Подсветка сцены(ambient lighting)
В этом уроке мы не будем рассматривать.
- Тени. Эта тема заслуживает отдельного урока(или уроков, если даже не книг).
- Зеркальное отражение(например, вода)
- Подповерхностное рассеивание(например, как у воска)
- Анизотропные материалы(окрашенный металл, например)
- Затенение основанное на физических процессах, чтобы имитировать реальность еще лучше.
- Преграждение света(Ambient Occlusion если что-то
преграждает свет, то становится темнее) - Отражение цвета(красный ковер будет делать белый потолок слегка слегка красноватым)
- Прозрачность
- Глобальное освещение(в принципе все что мы указали выше можно назвать этим термином)
Другими словами, самое простое освещение и затенение.
Нормали
В прошлом уроке мы работали с нормалями, но без особого
понимания, зачем они вообще нужны.
Нормали Треугольников
Нормаль к плоскости — это единичный вектор который направлен
перпендикулярно к этой плоскости.
Нормаль к треугольнику — это единичный вектор направленный
перпендикулярно к треугольнику. Нормаль очень просто рассчитывается с помощью
векторного произведения двух сторон треугольника(если вы помните, векторное
произведение двух векторов дает нам перпендикулярный вектор к обоим) и
нормализованный: его длина устанавливается в единицу.
Вот псевдокод вычисления нормали:
треугольник( v1, v2, v3 )
сторона1 = v2-v1
сторона2 = v3-v1
треугольник.нормаль = вектПроизведение(сторона1, сторона2).нормализировать()
Вершинная Нормаль
Это нормаль введенная для удобства вычислений. Это
комбинированная нормаль от нормалей окружающих данную вершину треугольников.
Это очень удобно, так как в вершинных шейдерах мы имеем дело с вершинами, а не
с треугольниками. В любом случае в OpenGL
у мы почти никогда и не имеем дела с треугольниками.
вершина v1, v2, v3,
….
треугольник tr1,
tr2, tr3 // они все используют вершину v1
v1.нормаль =
нормализовать( tr1.нормаль + tr2.нормаль + tr3.нормаль)
Использование нормалей вершин
в OpenGL
Использовать нормали в
OpenGL очень просто. Нормаль — это просто атрибут вершины, точно так же, как и
позиция, цвет или UV координаты…Тоесть ничего нового учить не придется…даже
наша простенькая функция loadOBJ уже загружает нормали.
GLuint normalbuffer;
glGenBuffers(1,
&normalbuffer);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glBufferData(GL_ARRAY_BUFFER, normals.size() *
sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);
и
// Третий атрибутный
буфер : нормали
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glVertexAttribPointer(
2, // атрибут
3, // размер
GL_FLOAT, // тип
GL_FALSE, // нормализованный ли?
0, // шаг
(void*)0 // смещение в буфере
);
И этого достаточно
чтобы начать:
Диффузное освещение
Важность нормали к
поверхности
Когда световой луч
попадает на поверхность, большая его часть отражается во все стороны. Это
называется «диффузная компонента». Остальные компоненты мы рассмотрим чуть
позже.

После падения луча,
поверхность отражает свет по разному, в зависимости от угла под которым падает
этот луч к поверхности. Если луч падает перпендикулярно к поверхности, то он
концентрируется на маленьком участке, если по касательной, то рассеивается на
гораздо большей поверхности:

Это значит, что под
непрямым светом поверхность будет слегка темнее(и хотя общее количество света
будет тем же, просто он рассеивается на большей поверхности)
С точки зрения
компьютерной графики, цвет пикселя очень зависит от разности углов направления
света и нормали поверхности.
// Косинус угла
между нормалью и направлением света
// 1 — если свет перпендикулярен к треугольнику
// 0 — если свет параллелен к треугольнику
float cosTheta = dot( n,l );
color = LightColor
* cosTheta;
В этом коде «n» – это
нормаль, а «l» – единичный вектор который идет от поверхности к источнику света(а
не наоборот, хотя это может показаться
непонятным)
Будьте внимательны со знаком
Иногда наша формула
будет не работать. Например, когда свет будет находиться за треугольником, n и
l будут противоположны, поэтому n.l будет отрицательным. И в итоге у нас будет
какой-то отрицательный цвет, и в итоге какой-то бред. Поэтому мы приведем все
отрицательный числа к 0 с помощью функции clamp.
// Косинус угла
между нормалью и направлением света
// 1 — если свет перпендикулярен к треугольнику
// 0 — если свет параллелен к треугольнику
// 0 — если свет
позади треугольника
float cosTheta =
clamp( dot( n,l ), 0,1 );
color = LightColor
* cosTheta;
Цвет
материала
Конечно цвет предмета
должен очень сильно зависеть от цвета материала. Белый свет состоит из трех
компонент — красного, синего и зеленого. Когда свет падает на красную
поверхность, то зеленая и синяя компоненты поглощаются, а красная отражается.

Мы можем
промоделировать это простым умножением:
color =
MaterialDiffuseColor * LightColor * cosTheta;
Моделирование света
Давайте предположим,
что у нас есть точечный источник света, который излучает свет во все
направления, как, например, свечка.
С таким источником
света, уровень освещения поверхности будет зависеть от расстояния до источника
света: чем дальше, тем темнее. Эта зависимости рассчитывается так:
color =
MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);
Вскоре нам понадобится
еще один параметр чтобы управлять уровнем силы света — цвет света, но пока,
давайте предположим, что у нас есть лампочка белого света с определенной
мощностью(например, 60 ватт).
color = MaterialDiffuseColor * LightColor * LightPower
* cosTheta / (distance*distance);
Объединяем все вместе
Чтобы этот код работал
нам нужен определенный набор параметров(цвета и мощности) и немного
дополнительного кода.
MaterialDiffuseColor —
мы можем взять прямо из текстуры.
LightColor и
LightPower нужно будет выставить в шейдере с помощью GLSL uniform.
CosTheta будет
зависеть от векторов n и l. Его можно вычислять для любого из пространств, угол
будет одним и тем же. Мы будем использовать пространство камеры, так как тут
очень просто посчитать положение светового источника:
// Нормаль
фрагмента в пространстве камеры
vec3 n = normalize( Normal_cameraspace );
// Направление света(от фрагмента к источнику
света
vec3 l = normalize(
LightDirection_cameraspace );
Normal_cameraspace и LightDirection_cameraspace подсчитываются в вершинном шейдере и передаются
во фрагментный для дальнейшей обработки:
// Позиция вершины в пространстве камеры :МВП *
положение
gl_Position = MVP * vec4(vertexPosition_modelspace,1);
// Положение вершины в мировом пространстве: M * положение
Position_worldspace =
(M * vec4(vertexPosition_modelspace,1)).xyz;
// Вектор который идет от вершины камере в пространстве камеры
// В пространстве камеры, камера находится по
положению (0,0,0)
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace
= vec3(0,0,0) – vertexPosition_cameraspace;
// Вектор который идет от вершины к источнику
света в пространстве камеры.
//Матрица M пропущена, так как она в в этом пространстве единичная.
vec3
LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace
= LightPosition_cameraspace +
EyeDirection_cameraspace;
// Нормаль вершины в пространстве камеры
Normal_cameraspace = (
V * M * vec4(vertexNormal_modelspace,0)).xyz; // Будет работать лишь в том случае, когда матрица модели не изменяет её размер.
На первый взгляд код
может показаться довольно сложным и запутанным, но на самом деле, тут нет
ничего нового чего не было в уроке 3: Матрицы. Я старался давать каждой
переменной осмысленные имена, чтобы вам было легко понять что и как тут
происходит.
Обязательно попробуйте!!!
M и V – это матрицы
Модели и Вида, которые передаются в шейдер точно так же, как и наша старая
добрая MVP.
Время испытаний
Я рассказал вам все
что нужно, чтобы сделать диффузное освещение. Вперед, попробуйте.
Результат
Только лишь с одной
диффузной компонентой у нас получается вот такая вот картинка(простите меня за
некрасивые текстуры).

Вроде бы как получше,
чем было раньше, но многого еще не хватает. Особенно заметна проблема с
неосвещенными частями. Затылок нашей дорогой мартышки Сюзанны полностью
черный(мы ведь использовали clamp()).
Окружающее освещение(ambient lighting)
Окружающее освещение –
это чистой воды читерство.
Затылок Сюзанны не
должен быть полностью черным, так как в реальной жизни свет от лампы должен
упасть на стену, пол, потолок, частично отразиться от него, и осветить теневую
часть объекта.
Однако это слишком
вычислительно затратно делать в реальном времени. И именно поэтому мы будем
добавлять некую постоянную составляющую. Как будто сам объект излучает немного
света, чтобы не быть полностью черным.
vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) *
MaterialDiffuseColor;
color =
// Окружающее освещение :симулируем непрямое освещение
MaterialAmbientColor +
// Диффузное : “цвет” самого объекта
MaterialDiffuseColor * LightColor * LightPower
* cosTheta /
(distance*distance);
Результат
Вот так вот будет
немного лучше. Вы можете по играться с
коефициентами (0.1, 0.1, 0.1) чтобы попробовать добиться лучшего результата.
Отраженный свет(Specular light)
Часть света которая
отражается, в основном отражается в сторону отраженного луча к поверхности.

Как мы видим на
рисунке, отраженный свет формирует световое пятно. В некоторых случаях, когда
диффузная компонента равна нулю, это световое пятно очень очень узкое(весь свет
полностью отражается в одном направлении) и мы получаем зеркало.
(однако, хотя вы можете подправить параметры
чтобы получить зеркало, в нашем случае оно будет принимать во внимание лишь
отражение нашего источника света. Так что получится странное зеркало)
// вектор взгляда(в сторону камеры)
vec3 E =
normalize(EyeDirection_cameraspace);
//Направление в котором треугольник отражает свет
vec3 R = reflect(-l,n);
// Косинус угла между вектором взгляда и
вектором отражения обрезанный до нуля если нужно
// – Смотрим
прям на отражение -> 1
// -Смотрим
куда-то в другую сторону -> < 1
float cosAlpha = clamp(
dot( E,R ), 0,1 );
color =
// Окружающее
освещение :симулируем непрямое освещение
MaterialAmbientColor +
// Диффузное : “цвет” самого объекта
MaterialDiffuseColor * LightColor *
LightPower * cosTheta /
(distance*distance) ;
// Отраженное
: отраженные отблески, как зеркало
MaterialSpecularColor * LightColor *
LightPower * pow(cosAlpha,5) / (distance*distance);
R – направление в которое отражается свет. E – инвертированный
вектор направления взгляда. Если угол между этими векторами маленький, мы
смотрим прямо на отражение.
pow(cosAlpha,5)
используется для того, чтобы контролировать размер светового пятна.
Увеличивайте 5, чтобы получить пятнышко меньше.
Финальный результат

Обратите внимание на
отблески на носу, глазах и бровях.
Этот метод затенения
использовался на протяжении многих лет, так как он очень простой. Однако он
обладает множеством недостатков, поэтому сейчас стали применять другие методы
затенения: например микрофасеточный BRDF, но об этом позже.
В следующем уроке мы
будем разбирать, как можно ускорить рендеринг нашего VBO.
В самом общем случае нормаль к поверхности
представляет ее локальную кривизну, и,
следовательно, направление зеркального
отражения (рис. 3.5). Применительно к нашим
знаниям можно сказать, что нормалью
называется вектор, определяющий
ориентацию грани (рис. 3.6).


Рис. 3.5 Рис. 3.6
Во многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра и вершины, поэтому, для
того чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.
Пусть заданы уравнения плоскостей
полигональных граней, тогда нормаль к
их общей вершине равна среднему значению
нормалей ко всем многоугольникам,
сходящимся к этой вершине. Например, на
рис. 3.7 направление приближенной нормали
в точке V1есть:
nv1
= (a0
+ a1
+ a4)i
+ (b0
+ b1
+ b4)j
+ (c0
+ c1
+ c4)k,
(3.15)
где a0, a1,
a4, b0, b1,
b4, c0, c1,
c4– коэффициенты уравнений
плоскостей трех многоугольниковP0,
P1, P4,окружающихV1. Отметим, что
если требуется найти только направление
нормали, то делить результат на количество
граней необязательно.
Если же уравнения плоскостей не заданы,
то нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Еще
раз, рассматривая вершину V1на
рис. 3.7, найдем направление приближенной
нормали:
nv1
= V1V2
V1V4
+V1V5
V1V2
+ V1V4
V1V5
(3.16)

Рис. 3.7 – Аппроксимация
нормали к полигональной поверхности
Следует
обратить внимание на то, что необходимы
только внешние нормали. Кроме того, если
полученный вектор не нормируется, то
его величина зависит от количества и
площади конкретных многоугольников, а
также от количества и длины конкретных
ребер. Сильнее проявляется влияние
многоугольников с большей площадью и
более длинными ребрами.
Когда
нормаль к поверхности используется для
определения интенсивности и для
изображения объекта или сцены выполняется
перспективное преобразование, то нормаль
следует вычислять до перспективного
деления. В противном случае направление
нормали будет искажено, а это приведет
к тому, что интенсивность, задаваемая
моделью освещения, будет определена
неправильно.
Если известно аналитическое описание
плоскости (поверхности), то нормаль
вычисляется непосредственно. Зная
уравнение плоскости каждой грани
многогранника, можно найти направление
внешней нормали.
Если
уравнение плоскости имеет вид:
![]() , (3.17)
, (3.17)
то вектор нормали к этой плоскости
записывается следующим образом:
![]() , (3.18)
, (3.18)
где
![]() – единичные векторы осейx,y,zсоответственно.
– единичные векторы осейx,y,zсоответственно.
Величина dвычисляется с помощью
произвольной точки, принадлежащей
плоскости, например, для точки (![]() )
)
![]() . (3.19)
. (3.19)
Пример.Рассмотрим 4-х сторонний
плоский многоугольник, описываемый
4-мя вершинами V1(1,0,0), V2(0,1,0), V3(0,0,1) и
V4(1,1,1) (см. рис. 3.7).
Уравнение
плоскости имеет вид:
x
+ y
+ z
– 1 = 0.
Получим нормаль к этой плоскости,
используя векторное произведение пары
векторов, являющихся смежными ребрами
к одной из вершин, например, V1:

Во
многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра или вершины, поэтому, для
того, чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.
Пусть
заданы уравнения плоскостей граней
многогранника, тогда нормаль к их общей
вершине равна среднему значению нормалей
ко всем граням, сходящимся в этой вершине.
Например, на рис.3.7 направление приближенной
нормали в точке
![]() есть
есть
![]() ,
,
где
![]() – коэффициенты уравнений плоскостей
– коэффициенты уравнений плоскостей
3-х многоугольниковP0,P1иP4,
окружающих![]() .
.
Если
же уравнение плоскостей не заданы, то
нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Опять,
выбирая вершину
![]() (см.
(см.
рис. 3.7), найдем направление приближенной
нормали:
![]()
Замечания:
-
нам необходимы только внешние нормали;
-
вычисление нормали осуществляется до
перспективных преобразований, в
противном случае направление нормали
будет искажено, что приведет к неправильной
модели освещения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-

Rustem
New Member
- Публикаций:
-
0
- Регистрация:
- 8 мар 2004
- Сообщения:
- 429
- Адрес:
- Russia
Приветствую.
В общем сабж.
Допустим имеются все вершины объекта в массиве и еще один массив индексов.
Как вычислить нормали для каждой вершины? -

_Serega_
New Member
- Публикаций:
-
0
- Регистрация:
- 18 июн 2006
- Сообщения:
- 288
Дык, нормали ведь обычно вычисляются для полигонов (а не вершин) ?!?!?
-

asd
New Member
- Публикаций:
-
0
- Регистрация:
- 12 мар 2005
- Сообщения:
- 952
- Адрес:
- Russia
Индексов чего?
Где-то на GameDev было про это. Нормаль к вершине, вроде, среднее что-то нормалей всех граней прилегающих к вершине.
-
да ну! все зависит от ваших целей. скажем есть у вас шар из полигонов вычесляя нормаль к полигону а стало быть и плоскости вы при освещении такого шара увидите что это не шар а многоугольник. а вот если вы каждой вершине посчитаете свою нормаль то свет ляжет очень даже красиво. вы это легко можете увидеть в 3дс макс убрав фишечку сглаженные нормали.
-

Rustem
New Member
- Публикаций:
-
0
- Регистрация:
- 8 мар 2004
- Сообщения:
- 429
- Адрес:
- Russia
asd
Дано:
1. Массив вершин, допустим float x,y,z
2. Массив индексов вершин, из которых строится примитивы(треугольники). Например: 0,1,2, 2,3,1надо: построить массив нормалей к каждой вершине
-
1. vertices x,y,z
2. face veritces a,b,c
3. normals for each face vertice aX, aY, aZ, bX, bY, bZ, cX, cY, cZ -

Kozyr__
New Member
- Публикаций:
-
0
- Регистрация:
- 28 янв 2005
- Сообщения:
- 213
- Адрес:
- Ukraine
Rustem
в начале находишь нормаль для каждой грани. потом для каждой вершины вычисляешь сумму нормалей тех граней, где присутствует эта вершина. нормируешь вектор – получаешь нормаль для вершины.для шарика можно обойтись точным вычислением

-

Rustem
New Member
- Публикаций:
-
0
- Регистрация:
- 8 мар 2004
- Сообщения:
- 429
- Адрес:
- Russia
Kozyr__
К сожалению не только шарик
А объект любой формы. Конкретно пишу риппер моделей из игр дх7-9, и опенгл
Возникла проблема что не у всех заданы нормали, а для конвертации в obj они необходимы -
Rustem
лови алгоритм выдрал его из своих старых кодов думаю все вполне понятно
это не сглаженная нормаль! тоесть нормаль для плоскости вы ее можете положить для каждого фейс вертекса.-
mov eax, d_w_p [ebx.EDGE_FACES_VERTEX_A]
-
mov edx, d_w_p [ebx.EDGE_FACES_VERTEX_B]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_X]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_X]
-
fst d_w_p [@CE_AB.offs_X]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_Y]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_Y]
-
fst d_w_p [@CE_AB.offs_Y]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_Z]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_Z]
-
fst d_w_p [@CE_AB.offs_Z]
-
fld d_w_p [@CE_AB.offs_X]
-
fstp d_w_p [@CE_oAB.offs_X]
-
fld d_w_p [@CE_AB.offs_Y]
-
fstp d_w_p [@CE_oAB.offs_Y]
-
fld d_w_p [@CE_AB.offs_Z]
-
fstp d_w_p [@CE_oAB.offs_Z]
-
mov edx, d_w_p [ebx.EDGE_FACES_VERTEX_C]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_X]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_X]
-
fst d_w_p [@CE_AC.offs_X]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_Y]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_Y]
-
fst d_w_p [@CE_AC.offs_Y]
-
fld d_w_p [esi.edx.PrimitiveVerticeCoord_Z]
-
fsub d_w_p [esi.eax.PrimitiveVerticeCoord_Z]
-
fst d_w_p [@CE_AC.offs_Z]
-
fld d_w_p [@CE_AC.offs_X]
-
fstp d_w_p [@CE_oAC.offs_X]
-
fld d_w_p [@CE_AC.offs_Y]
-
fstp d_w_p [@CE_oAC.offs_Y]
-
fld d_w_p [@CE_AC.offs_Z]
-
fstp d_w_p [@CE_oAC.offs_Z]
-
; calculate normal ortho vector
-
fld d_w_p [@CE_AC.offs_Y] ; (Yc-Ya)(Zb-Za)
-
fmul d_w_p [@CE_AB.offs_Z]
-
fld d_w_p [@CE_AC.offs_Z] ; (Zc-Za)(Yb-Ya)
-
fmul d_w_p [@CE_AB.offs_Y]
-
fsubp st(01), st(00) ; (Yc-Ya)(Zb-Za)-(Zc-Za)(Yb-Ya)
-
fstp d_w_p [edi.PrimitiveNormal_X]
-
fld d_w_p [@CE_AC.offs_Z] ; (Zc-Za)(Xb-Xa)
-
fmul d_w_p [@CE_AB.offs_X]
-
fld d_w_p [@CE_AC.offs_X] ; (Xc-Xa)(Zb-Za)
-
fmul d_w_p [@CE_AB.offs_Z]
-
fsubp st(01), st(00) ; (Zc-Za)(Xb-Xa)-(Xc-Xa)(Zb-Za)
-
fstp d_w_p [edi.PrimitiveNormal_Y]
-
fld d_w_p [@CE_AC.offs_X] ; (Xc-Xa)(Yb-Ya)
-
fmul d_w_p [@CE_AB.offs_Y]
-
fld d_w_p [@CE_AC.offs_Y] ; (Yc-Ya)(Xb-Xa)
-
fmul d_w_p [@CE_AB.offs_X]
-
fsubp st(01), st(00) ; (Xc-Xa)(Yb-Ya)-(Yc-Ya)(Xb-Xa)
-
fstp d_w_p [edi.PrimitiveNormal_Z]
-
fld d_w_p [edi.PrimitiveNormal_X]
-
fld d_w_p [edi.PrimitiveNormal_Y]
-
fld d_w_p [edi.PrimitiveNormal_Z]
-
fld d_w_p [edi.PrimitiveNormal_X]
-
fstp d_w_p [edi.PrimitiveNormal_X]
-
fld d_w_p [edi.PrimitiveNormal_Y]
-
fstp d_w_p [edi.PrimitiveNormal_Y]
-
fld d_w_p [edi.PrimitiveNormal_Z]
-
fstp d_w_p [edi.PrimitiveNormal_Z]
-
-

DARK_FURY
New Member
- Публикаций:
-
0
- Регистрация:
- 20 апр 2007
- Сообщения:
- 3
попробуй посчитать:
нужно чтоб было два вектора u и v
естественно нормаль это перпендикуляр этим векторам
тогда нормаль это произведение векторов UxV
nx=uy*vz-uz*vy;
ny=uz*vx-ux*vz;
nz=ux*vy-uy*vx;берем треугольник с точками ABC
берем точку А – это будет начало вектора
тогда векторы AB и AC
вот их производим
таким способом я находил нормали для чего угодноp.s.
UxV= -(VxU)
поэтому порядок перемножения может определить направления вектора прямо или в противоположную сторону

