Как найти нормальное распределение по выборке - Сайт, где вы сможете решить свои вопросы

Нормальное распределение

Время на прочтение
7 мин

Количество просмотров 35K

Автор статьи: Виктория Ляликова

Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение

$frac{1}{sigmasqrt{2pi}}e^left(-frac{(x-a)^2)}{2sigma^2}right)$

где a -математическое ожидание, – среднее квадратическое отклонение.

Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики

Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.

Можно выделить следующие этапы проверки выборочных значений на нормальность

Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения

При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.

Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.

График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.

Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.

Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают

H0 – Выборка подчиняется нормальному закону распределения

H1 – Выборка не подчиняется нормальному распределению

Установи уровень значимости alpha=0,05.

Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости

Критерий Шапиро-Уилка

Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид

$W=frac{1}{s^2}{sumlimits_{i=1}^n{a_{n-i+1}(x_{n-i+1}-x_{i})}} s^2=sumlimits_{i=1}^n(x_i-overline x^2) overline x=frac{1}{n}sumlimits_{i=1}^n{x}$

Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты ${a_{n-i+1}}$ и критические значения статистики являются табулированными значениями. Если , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .

В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом

Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если, , тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.

Критерий Д’Агостино

В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия

$D=frac{T}{n^2s} T=sumlimits_{i=1}^nbigg(i-frac{n+1}{2}bigg)x_i s^2=sumlimits_{i=1}^n(x_i-overline x^2), {x_1}leq...leq{x_n}$

В качестве статистики критерия Д’Агостино используется величина

$Y=sqrt{n}frac{(D-0,28209479)}{0,02998598}$

значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при

$limlimits_{x to infty}Pbigg(frac{D-M[D]}{sqrt{D[D]}}{<x}bigg)=Phi(x)$

гдестандартная нормальная случайная величина.

Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.

В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.

Критерий согласия– Пирсона

Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.

Для решения задачи используется статистика – Пирсона

$G=sumlimits_{k=1}^mfrac{(v_k-np_k)^2}{np_k}$

где – эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал), ${np_k}$ – теоретические частоты. Подсчитывается критическое значение $chi^2_{кр}$ . Если $Ggeq chi^2_{кр}$ , отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если $G< chi^2_{кр}$ .

Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.

Загружаем необходимые библиотеки

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

Загружаем датасет

data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')

Набор состоит из 5110 строк и 12 столбцов.

Посмотрим на основные характеристики, каждого признака.
data_healthcares.describe()

Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.

Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения

new_data=data_healthcares.dropna()

Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики

Выборочная характеристика	Код в python	Значение характеристики
Выборочное среднее	new_data.bmi.mean()	28,89
Выборочная медиана	new_data.bmi.median()	28,1
Выборочная мода	new_data.bmi.mode()	28,7
Выборочное среднеквадратическое отклонение	new_data.bmi.std()	7.854066729680458
Выборочный коэффициент асиметрии	new_data.bmi.skew()	1.0553402052962928
Выборочный эксцесс	new_data.bmi.kurtosis()	3.362659165623678

После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.

Строим гистограмму

fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()

Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .

Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.

from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
Pyplot.show

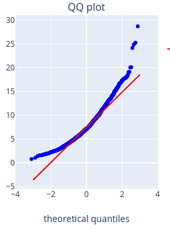
Что имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.

На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.

Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.

std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()

Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки

from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)

После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.

Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.

На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.

Источник

Нормальное распределение
Зеленая линия соответствует стандартному нормальному распределениюПлотность вероятности
Цвета на этом графике соответствуют графику наверхуФункция распределения
Обозначение	${displaystyle Nleft(mu ,sigma ^{2}right)}$
Параметры	`μ` — коэффициент сдвига (вещественный) `σ` > 0 — коэффициент масштаба (вещественный, строго положительный)
Носитель
Плотность вероятности	${displaystyle {frac {1}{sigma {sqrt {2pi }}}};exp left(-{frac {left(x-mu right)^{2}}{2sigma ^{2}}}right)}$
Функция распределения	${frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sqrt {2sigma ^{2}}}}right)right]$
Математическое ожидание
Медиана
Мода
Дисперсия	$sigma ^{2}$
Коэффициент асимметрии
Коэффициент эксцесса
Дифференциальная энтропия
Производящая функция моментов	$M_{X}left(tright)=exp left(mu ,t+{frac {sigma ^{2}t^{2}}{2}}right)$
Характеристическая функция	$phi _{X}left(tright)=exp left(mu ,i,t-{frac {sigma ^{2}t^{2}}{2}}right)$

Норма́льное распределе́ние^[1]^[2], также называемое распределением Гаусса или Гаусса — Лапласа^[3], или колоколообразная кривая — непрерывное распределение вероятностей с пиком в центре и симметричными боковыми сторонами, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

${displaystyle f(x)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x-mu }{sigma }}right)^{2}}}$

где параметр

— математическое ожидание (среднее значение), медиана и мода распределения, а параметр sigma

— среднеквадратическое отклонение, $sigma ^{2}$

— дисперсия распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений^[4]. Многомерный случай описан в статье «Многомерное нормальное распределение».

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием mu =0 и стандартным отклонением

Общие сведения[править | править код]

Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.

Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.

Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.

Определения[править | править код]

Стандартное нормальное распределение[править | править код]

Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда mu =0 и Его плотность вероятности равна:

${displaystyle varphi (x)={frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}x^{2}}.}$

Множитель ${displaystyle {frac {1}{sqrt {2pi }}}}$ в выражении обеспечивает условие нормировки интеграла ${displaystyle int limits _{-infty }^{+infty }varphi (x),dx=1}$ ^[5]. Поскольку множитель ${displaystyle {frac {1}{2}}}$ в экспоненте обеспечивает дисперсию равную единице, то и стандартное отклонение равно 1. Функция симметрична в точке x=0, её значение в ней максимально и равно ${displaystyle {frac {1}{sqrt {2pi }}}.}$ Точки перегиба функции: и

Гаусс называл стандартным нормальным распределение с ${displaystyle sigma ^{2}=1/2,}$ то есть:

${displaystyle varphi (x)={frac {e^{-x^{2}}}{sqrt {pi }}}.}$

Нормальное распределение с параметрами μ, σ[править | править код]

Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем sigma (стандартное отклонение) и переносится на (математическое ожидание):

${displaystyle f(xmid mu ,sigma ^{2})={frac {1}{sigma }}varphi left({frac {x-mu }{sigma }}right).}$

являются параметрами нормального распределения. Плотность вероятности должна нормироваться ${displaystyle {frac {1}{sigma }},}$ так что интеграл равен 1.

Если — стандартная нормальная случайная величина, то величина будет иметь нормальное распределение с математическим ожиданием и стандартным отклонением sigma. Наоборот, если — нормальная величина с параметрами и ${displaystyle sigma ^{2},}$ то ${displaystyle Z={frac {X-mu }{sigma }}}$ будет иметь стандартное нормальное распределение.

Если в экспоненте плотности вероятности раскрыть скобки и учитывать, что , то:

${displaystyle f(x)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x-mu }{sigma }}right)^{2}}=e^{-{frac {1}{2}}left(2ln sigma +ln 2pi +left({frac {x-mu }{sigma }}right)^{2}right)}=e^{-{frac {1}{2}}left({frac {x^{2}}{sigma ^{2}}}-2{frac {mu x}{sigma ^{2}}}+2ln sigma +ln 2pi +{frac {mu ^{2}}{sigma ^{2}}}right)}.}$

Таким образом, плотность вероятности каждого нормального распределения представляет собой экспоненту квадратичной функции:

${displaystyle f(x)=e^{ax^{2}+bx+c},}$

где ${displaystyle a=-{frac {1}{2sigma ^{2}}}, b={frac {mu }{sigma ^{2}}}, c=-left(ln sigma +{frac {1}{2}}ln 2pi +{frac {1}{2}}{frac {mu ^{2}}{sigma ^{2}}}right).}$

Отсюда можно выразить среднее значение как ${displaystyle mu =-{frac {b}{2a}},}$ а дисперсию как ${displaystyle sigma ^{2}=-{frac {1}{2a}}.}$ Для стандартного нормального распределения b=0 и ${displaystyle c=-{frac {1}{2}}ln 2pi .}$

Обозначение[править | править код]

Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой phi (фи)^[6]. Также достаточно часто используется альтернативная формы греческой буквы фи varphi .

Нормальное распределение часто обозначается ${displaystyle N(mu ,sigma ^{2}),}$ или ${displaystyle {mathcal {N}}(mu ,sigma ^{2})}$ ^[7]. Если случайная величина распределена по нормальному закону со средним и вариацией ${displaystyle sigma ^{2},}$ то пишут:

${displaystyle Xsim {mathcal {N}}(mu ,sigma ^{2}).}$

Функция распределения[править | править код]

Функция распределения стандартного нормального распределения (нормальное интегральное распределение) обычно обозначается заглавной греческой буквой Phi (фи) и представляет собой интеграл:

${displaystyle Phi (x)={frac {1}{sqrt {2pi }}}int limits _{-infty }^{x}e^{-x^{2}/2},dx.}$

С ней связана функция ошибок (интеграл вероятности) дающий вероятность того, что нормальная случайная величина со средним 0 и вариацией 1/2 попадёт в отрезок :

${displaystyle operatorname {erf} (x)={frac {2}{sqrt {pi }}}int limits _{0}^{x}e^{-x^{2}},dx.}$

Эти интегралы не выражаются в элементарных функциях и называются специальными функциями. Многие их численные приближения известны. См. ниже.

Функции связаны, в частности, соотношением:

${displaystyle Phi (x)={frac {1}{2}}left[1+operatorname {erf} left({frac {x}{sqrt {2}}}right)right]}$

Нормальное распределение с плотностью средним и отклонением sigma имеет следующую функцию распределения:

${displaystyle F(x)=Phi left({frac {x-mu }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right)right].}$

Можно использовать функцию — она даст вероятность того, что значение стандартной нормальной случайной величины превысит :

График стандартной нормальной функции распределения Phi имеет 2-кратную вращательную симметрию относительно точки (0;1/2), то есть Её неопределенный интеграл равен:

{displaystyle int Phi (x),dx=xPhi (x)+varphi (x)+C.}

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью метода интегрирования по частям в ряд:

${displaystyle Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2}left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1}}{(2n+1)!!}}+cdots right],}$

где знак означает двойной факториал.

Асимптотическое разложение функции распределения для больших может быть также произведено интегрированием по частям.

Стандартное отклонение[править | править код]

Правило 68-95-99,7.
Для нормального распределения количество значений, отличающихся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % выборок. В то же время количество значений, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.

Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.

Более точно, вероятность получить нормальное число в интервале между и равна:

{displaystyle F(mu +nsigma )-F(mu -nsigma )=}

${displaystyle Phi (n)-Phi (-n)=operatorname {erf} left({frac {n}{sqrt {2}}}right).}$

С точностью до 12 значащих цифр значения для приведены в таблице^[8]:

			${displaystyle {frac {1}{1-p}}}$	OEIS
1	0,682689492137	0,317310507863	3,15148718753	A178647
2	0,954499736104	0,045500263896	21,9778945080	A110894
3	0,997300203937	0,002699796063	370,398347345	A270712
4	0,999936657516	0,000063342484	15787.1927673
5	0,999999426697	0,000000573303	1744277,89362
6	0,999999998027	0,000000001973	506797345,897

Свойства[править | править код]

Моменты[править | править код]

Моментами и абсолютными моментами случайной величины называются математические ожидания случайных величин ${displaystyle X^{p}}$ и ${displaystyle left|Xright|^{p},}$ соответственно. Если математическое ожидание случайной величины то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых

Если имеет нормальное распределение, то для неё существуют (конечные) моменты при всех с действительной частью больше −1. Для неотрицательных целых центральные моменты таковы:

${displaystyle mathbb {E} left[X^{p}right]={begin{cases}0&p=2n+1,\sigma ^{p},left(p-1right)!!&p=2n.end{cases}}}$

Здесь — натуральное число, а запись означает двойной факториал числа то есть (поскольку p-1 в данном случае нечётно) произведение всех нечётных чисел от 1 до

Центральные абсолютные моменты для неотрицательных целых таковы:

${displaystyle mathbb {E} left[left|Xright|^{p}right]=sigma ^{p},left(p-1right)!!cdot left.{begin{cases}{sqrt {frac {2}{pi }}}&p=2n+1,\1&p=2n.end{cases}}right}=sigma ^{p}cdot {frac {2^{frac {p}{2}}Gamma left({frac {p+1}{2}}right)}{sqrt {pi }}}.}$

Последняя формула справедлива также для произвольных .

Преобразование Фурье и характеристическая функция[править | править код]

Преобразование Фурье нормальной плотности вероятности с математическим ожиданием стандартным отклонением sigma равно^[9]:

${displaystyle {hat {f}}(t)=int limits _{-infty }^{infty }f(x)e^{-itx},dx=e^{imu t-{frac {1}{2}}sigma ^{2}t^{2}},}$

где

есть мнимая единица.

Если математическое ожидание то первый множитель равен 1, и преобразование Фурье, с точностью до константы есть нормальная плотность вероятности на частотных интервалах, с математическим ожиданием равным 0 и стандартным отклонением В частности, стандартное нормальное распределение varphi есть собственная функция от преобразования Фурье.

В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины близко связано с характеристической функцией ${displaystyle varphi _{X}(t)}$ этой величины, которая определена как математическое ожидание от ${displaystyle e^{itX}}$ и является функцией вещественной переменной (частотный параметр преобразования Фурье). Определение может быть распространено и на комплексную переменную ^[10]. Соотношение записывается так:

${displaystyle varphi _{X}(t)={hat {f}}(-t).}$

Бесконечная делимость[править | править код]

Нормальное распределение является бесконечно делимым.

Если случайные величины $X_{1}$ и $X_{2}$ независимы и имеют нормальное распределение с математическими ожиданиями $mu _{1}$ и $mu _{2}$ и дисперсиями $sigma _{1}^{2}$ и $sigma _{2}^{2}$ соответственно, то $X_{1}+X_{2}$ также имеет нормальное распределение с математическим ожиданием $mu _{1}+mu _{2}$ и дисперсией $sigma _{1}^{2}+sigma _{2}^{2}.$

Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Максимальная энтропия[править | править код]

Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину^[11]^[12].

Правило трёх сигм для гауссовской случайной величины[править | править код]

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.

Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале:

{displaystyle left(mu -3sigma ;mu +3sigma right),}

где

— математическое ожидание и параметр нормальной случайной величины.

Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.

Моделирование нормальных псевдослучайных величин[править | править код]

При компьютерном моделировании, особенно при применении метода Монте-Карло, желательно использовать величины, распределенные по нормальному закону. Многие алгоритмы дают стандартные нормальные величины, так как нормальную величину ${displaystyle Xsim N(mu ,sigma ^{2})}$ можно получить как:

где Z — стандартная нормальная величина.

Алгоритмы также используют различные преобразования равномерных величин.
Простейшие приближённые методы моделирования основываются на центральной предельной теореме. Если сложить достаточно большое количество независимых одинаково распределённых величин с конечной дисперсией, то сумма будет иметь распределение, близкое к нормальному. Например, если сложить 100 независимых стандартно равномерно распределённых случайных величин, то распределение суммы будет приближённо нормальным.

Для программного генерирования нормально распределённых псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределённую величину на базе одной равномерно распределённой.

Также существует алгоритм Зиккурат, который работает даже быстрее преобразования Бокса — Мюллера. Тем не менее, сложнее в реализации, но его применение оправдано в случаях, когда требуется генерирование очень большого числа неравномерно распределённых случайных чисел.

Нормальное распределение в природе и приложениях[править | править код]

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

отклонение при стрельбе;
погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
некоторые характеристики живых организмов в популяции.

Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например биномиальное и пуассоновское. Этим распределением моделируются многие недетерминированные физические процессы^[13].

Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование параметров личности человека в психологии и психиатрии.

Связь с другими распределениями[править | править код]

${displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}})^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}$

${displaystyle F={frac {left(X_{1}^{2}+X_{2}^{2}+cdots +X_{n}^{2}right)/n}{left(Y_{1}^{2}+Y_{2}^{2}+cdots +Y_{m}^{2}right)/m}}sim F_{n,m}.}$

Отношение квадратов двух стандартных нормальных случайных величин имеет распределение Фишера со степенями свободы

История[править | править код]

Впервые нормальное распределение как предел биномиального распределения при ${displaystyle p={tfrac {1}{2}}}$ появилось в 1738 году во втором издании работы Муавра «Доктрина случайностей»^[en]^[18]. Это было первое доказательство частного случая центральной предельной теоремы. В 1809 году Гаусс в сочинении «Теория движения небесных тел» ввёл это распределение как возникающее в результате многократных измерений движения небесных тел. Однако Гаусс вывел формулу для действительных случайных величин из принципа достижения максимума совместной плотности всех измерений в точке с координатами, равными среднему всех измерений. Этот принцип впоследствии подвергался критике. В 1812 году Лаплас в теореме Муавра — Лапласа обобщил результат Муавра для произвольного биномиального распределения, то есть для сумм одинаково распределённых независимых бинарных величин^[3].

См. также[править | править код]

Аддитивный белый гауссовский шум
Логнормальное распределение
Равномерное распределение
Центральная предельная теорема
Двумерное нормальное распределение
Многомерное нормальное распределение
Распределение хи-квадрат
Статистический критерий
Частотное распределение

Примечания[править | править код]

↑ Вентцель Е. С. Теория вероятностей. — 10-е изд., стереотипное.. — М.: Academia, 2005. — 576 с. — ISBN 5-7695-2311-5.
↑ Ширяев А. Н. Вероятность. — М.: Наука, 1980.
↑ ¹ ² Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 139—140.
↑ Wasserman L. All of Statistics. — New York, NY: Springer, 2004. — С. 142. — 433 с. — ISBN 978-1-4419-2322-6.
↑ Доказательство см. Гауссов интеграл
↑ Halperin, Hartley & Hoel, 1965, item 7.
↑ McPherson (1990)
↑ Wolfram|Alpha: Computational Knowledge Engine. Wolframalpha.com. Дата обращения: 3 марта 2017.
↑ Bryc (1995, p. 23)
↑ Bryc (1995, p. 24)
↑ Cover, Thomas M.; Thomas, Joy A. Elements of Information Theory. — John Wiley and Sons, 2006. — С. 254.
↑ Park, Sung Y.; Bera, Anil K. Maximum Entropy Autoregressive Conditional Heteroskedasticity Model (англ.) // Journal of Econometrics (англ.) (рус. : journal. — Elsevier, 2009. — P. 219—230. Архивировано 7 марта 2016 года.
↑ Талеб Н. Н. Чёрный лебедь. Под знаком непредсказуемости = The Black Swan: The Impact of the Highly Improbable. — КоЛибри, 2012. — 525 с. — ISBN 978-5-389-00573-0.
↑ Королюк, 1985, с. 135.
↑ Галкин В. М., Ерофеева Л. Н., Лещева С. В. Оценки параметра распределения Коши // Труды Нижегородского государственного технического университета им. Р. Е. Алексеева. — 2014. — № 2(104). — С. 314—319. — УДК 513.015.2^(G).
↑ Lukacs, Eugene. A Characterization of the Normal Distribution (англ.) // The Annals of Mathematical Statistics (англ.) (рус. : journal. — 1942. — Vol. 13, no. 1. — P. 91—3. — ISSN 0003-4851. — doi:10.1214/aoms/1177731647. — JSTOR 2236166.
↑ Lehmann, E. L.^ru_en. Testing Statistical Hypotheses. — 2nd. — Springer (англ.) (рус., 1997. — С. 199. — ISBN 978-0-387-94919-2.
↑ The doctrine of chances; or, a method of calculating the probability of events in play, L., 1718, 1738, 1756; L., 1967 (репродуцир. изд.); Miscellanea analytica de scriebus et quadraturis, L., 1730.

Литература[править | править код]

Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (англ.) // The American Statistician (англ.) (рус. : journal. — 1965. — Vol. 19, no. 3. — P. 12—14. — doi:10.2307/2681417. — JSTOR 2681417.
McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (англ.). — Springer-Verlag, 1990. — ISBN 978-0-387-97137-7.
Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (англ.). — Springer-Verlag, 1995. — ISBN 978-0-387-97990-8.

Ссылки[править | править код]

Таблица значений функции стандартного нормального распределения
Онлайн расчёт вероятности нормального распределения

Источник

Как определить, является ли распределение нормальным?

Если
установлено, что исследуемые значения
имеют количественный характер, следует
проверить выборку на нормальность
распределения. Это можно сделать
несколькими способами.

Первый
способ проверки выборки на нормальность
распределения

Прежде
всего, нужно вычислить показатели
асимметрии и эксцесса, используя
программу Excel,
имеющуюся практически на всех компьютерах.
Для этого в таблицу программы следует
поместить результаты измерений. Пусть
это будет ряд значений, полученных на
выборке из 25 объектов: 9 10 10 10 11
11 11 11 12 12 12 12 12 12 12 13 13 13 13
14 14 15 15 16 17

Данные
могут располагаться как в виде строки,
так и в виде колонки. Далее, нажатием
кнопки с символами f_x,
расположенной
ниже панели инструментов, вызываем
мастер функций. В верхнем окне выбираем
категорию «Статистические», а в нижнем
– пункт «Скос». Возвращаемся к таблице
с результатами измерений, и, выделяя
набранные ранее цифры, помещаем их
значения в открывшееся окно «Аргументы
функций». На правой стороне окна
появляется результат вычислений –
0,579. Это и есть значение показателя
асимметрии, характеризующего степени
отклонения вершины кривой распределения
от его центра. Можно сказать, что
показатель асимметрии отражает отклонение
вершины реальной кривой распределения
от идеальной по оси абсцисс.

По
схожему алгоритму вычисляем величину
показателя эксцесса характеризующего
подъем или снижение вершины распределения,
то есть – отклонения по оси ординат.
Для того, чтобы произвести расчет данного
показателя, следует выбрать пункт
«эксцесс». В окне «Аргументы функций»
получим его значение – 0,116.

При
наличии статистических таблиц критических
значений асимметрии и эксцесса (в данном
учебном пособии это таблицы 9 и 10)
вычисленные значения сравниваются с
табличными. Если оба
(!) показателя окажутся меньше табличных
величин, то распределение может считаться
нормальным.

Для
нашего примера табличное значение
показателя асимметрии находим на
пересечении строки n
= 25 и колонки
р ≤ 0,01
(предположим,
что мы
анализируем
результаты
достаточно важных экспериментов и
считаем, что вероятность ошибки
статистического заключения не должна
превышать 1%). Это число составляет 1,061.
Так как вычисленное значение показателя
асимметрии 0,579 оказывается гораздо
меньше табличной величины 1,061, можно
сделать заключение, что отклонение
вершины распределения по оси абсцисс
не столь значительно, чтобы отказаться
от применения параметрических методов.

В
таблице 10 находим критическое значение
показателя эксцесса.
Для
n
= 26 (так как
в таблице
отсутствует строка для n
= 25, переходим
к ближайшей строке)
и

р
≤ 0,01 оно
составляет 0,869.
И снова
фактическое значение показателя 0,116
оказывается меньше табличного 0, 869.
Отсюда следует, что отклонение вершины
распределения по оси ординат также
несущественно и его можно считать
нормальным. То, что оба показателя
оказались меньше критических табличных
величин, дает основание для последующего
применения параметрических критериев.

Второй
способ проверки выборки на нормальность
распределения

При
отсутствии таблиц критических значений
асимметрии и эксцесса следует произвести
расчеты не только этих показателей, но
и их выборочных ошибок.

Ошибка
показателя асимметрии производится по
формуле:

Для
нашего примера
она составит:

Выборочная
ошибка эксцесса рассчитывается по
другой формуле:

в
результате получим:

Далее
следует разделить показатели асимметрии
и эксцесса на их ошибки.

Частное
от деления показателей асимметрии и
эксцесса на их ошибки определяется как
t_ф(фактическое
значение) и сравнивается с t_т_,табличное
значение),взятым из
таблицы Стьюдента (таблица 6), при
соответствующем уровне значимости и
числе степеней свободы. Если фактическое
значение критерия Стьюдента окажется
меньше табличного, распределение
признается нормальным, и, наоборот, если
фактическое значение окажется больше
табличного, следует сделать вывод о
несоответствии распределения нормальному
закону.

Для
показателя асимметрии получаем следующее
значение t-критерия:

Число
степеней свободы (df),
определяющее строку в таблице Стьюдента,
находим как n-1.
Следовательно, df
= 25-1=24. Уровень значимости (вероятность
ошибки статистического заключения),
определяющий колонку в таблице Стьюдента,
оставляем 1%. На пересечении строки df
=24 и колонки р
≤ 0,01 находим
табличное значение критерия t_т

=2,80_.
Так как t_ф(1,25)оказываетсягораздоменьше чем t_т(2,80), можно
заключить, что и второй способ проверки
указывает на незначительность асимметрии
кривой распределения.

Фактическое
значения t-критерия
для показателя эксцесса рассчитываем
по формуле
Таким образом, не только для асимметрии,
но и для эксцесса t_ф(0,129)оказываетсясущественноменьше чем t_т(2,80), что опять
же указывает на нормальность распределения.

Третий
способ проверки выборки на нормальность
распределения

Проще всего задача
решается, если имеется компьютер с
установленной на ней программой
Statistica. После ввода данных в таблицу
вызывается стартовая панель модуля
Основные
статистики и таблицы
(Basic
Statistics/Tables).
В средней части окна Descriptive
Statistics
(Описательные статистики) слева находится
блок проверки распределений (Distribution).
Чтобы проверить, относятся ли показатели
выбранной переменной к распределяемым
по нормальному закону, нужно поставить
галочку в окне возле пункта K-S
and Lilliefors test for normality (Критерий
Колмогорова-Смирнова и Лилиефорса для
нормальности)
и нажать на кнопку Histograms
(гистограммы). В появившемся окне
приводятся гистограмма распределения
значений переменной и наложенная на
нее кривая нормального распределения,
сопоставление которых позволяет
визуально оценить характер распределения.

В
верхней части окна указывается
достоверность отличия проверяемого
распределения от нормального,
характеризуемая уровнем значимости р
(вероятность неправильного отвержения
гипотезы, если она верна). Если уровень
значимости р<0,05, то распределение
отлично от нормального на основании
соответствующего критерия. И наоборот,
если р>0,05, как на рисунке, то наблюдаемая
величина распределена нормально. Зная
вид распределения, в дальнейшей обработке
можно применить оптимальные статистические
методы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Нормальное распределение

17 авг. 2022 г.
читать 3 мин

Нормальное распределение является наиболее распространенным в статистике распределением вероятностей.

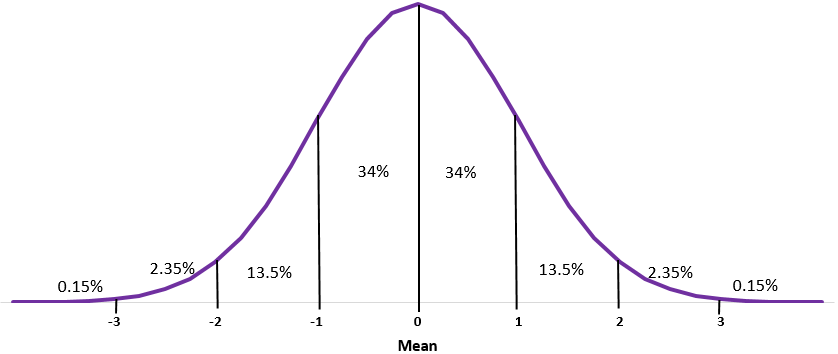
Нормальные распределения имеют следующие особенности:

Форма колокола
Симметричный
Среднее и медиана равны; оба расположены в центре распределения
Около 68% данных находятся в пределах одного стандартного отклонения от среднего
Около 95% данных находятся в пределах двух стандартных отклонений от среднего
Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.

Последние три пункта известны как эмпирическое правило , иногда называемое правилом 68-95-99,7 .

Связанный: Эмпирическое правило (практические задачи)

Как нарисовать нормальную кривую

Чтобы нарисовать нормальную кривую, нам нужно знать среднее значение и стандартное отклонение.

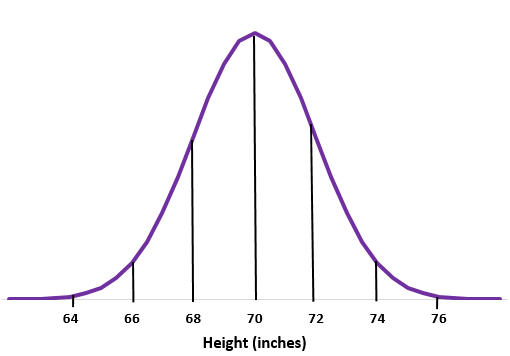
Пример 1. Предположим, что рост мальчиков в определенной школе распределен нормально со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма. Нарисуйте нормальную кривую.

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Среднее значение 70 дюймов находится посередине.

Шаг 3: Каждое стандартное отклонение равно расстоянию в 2 дюйма.

Пример 2: Предположим, что вес определенного вида выдр нормально распределен со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов. Нарисуйте нормальную кривую.

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Среднее значение 30 фунтов находится посередине.

Шаг 3: Каждое стандартное отклонение соответствует расстоянию в 5 фунтов.

Как найти проценты, используя нормальное распределение

Эмпирическое правило , иногда называемое правилом 68-95-99,7 , гласит, что для случайной величины с нормальным распределением 68 % данных находятся в пределах одного стандартного отклонения от среднего, 95 % — в пределах двух стандартных отклонений от среднего и 99,7% находятся в пределах трех стандартных отклонений от среднего значения.

Используя это правило, мы можем ответить на вопросы о процентах.

Пример: предположим, что рост мальчиков в определенной школе нормально распределен со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма.

Приблизительно какой процент мальчиков в этой школе выше 74 дюймов?

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма.

Шаг 2: Рост 74 дюйма на два стандартных отклонения выше среднего. Добавьте проценты выше этой точки в нормальное распределение.

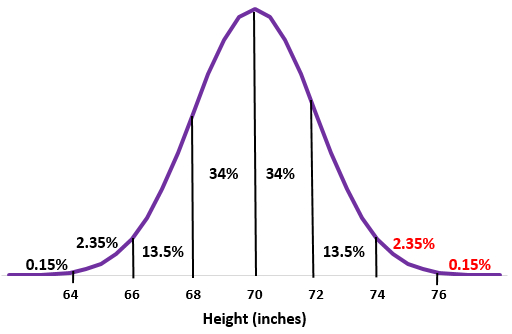
2,35% + 0,15% = 2,5%

Приблизительно 2,5% мальчиков в этой школе выше 74 дюймов.

Приблизительно какой процент мальчиков в этой школе имеет рост от 68 до 72 дюймов?

Решение:

Шаг 2: Высота 68 дюймов и 72 дюйма на одно стандартное отклонение ниже и выше среднего значения соответственно. Просто добавьте проценты между этими двумя точками в нормальном распределении.

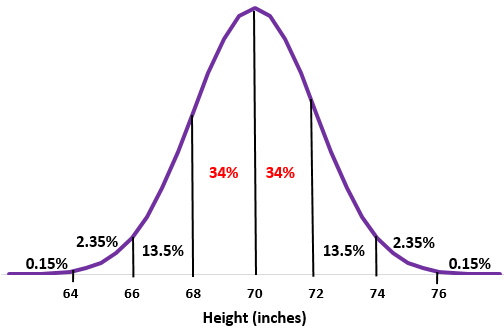
34% + 34% = 68%

Приблизительно 68% мальчиков в этой школе имеют рост от 68 до 72 дюймов.

Как найти количество, используя нормальное распределение

Мы также можем использовать эмпирическое правило, чтобы ответить на вопросы о подсчетах.

Пример: предположим, что вес определенного вида выдр распределен нормально со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов.

В одной колонии 200 таких выдр. Примерно сколько из этих выдр весят более 35 фунтов?

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов.

Шаг 2: Вес 35 фунтов превышает среднее значение на одно стандартное отклонение. Добавьте проценты выше этой точки в нормальное распределение.

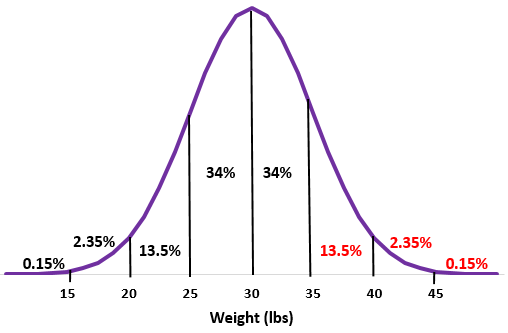
13,5% + 2,35% + 0,15% = 16%

Шаг 3: Поскольку в колонии 200 выдр, 16% от 200 = 0,16 * 200 = 32 .

Приблизительно 32 выдры в этой колонии весят более 35 фунтов.

Приблизительно сколько выдр в этой колонии весят менее 30 фунтов?

Вместо того, чтобы проходить все шаги, которые мы только что сделали выше, мы можем признать, что медиана нормального распределения равна среднему значению, которое в данном случае составляет 30 фунтов.

Это означает, что половина выдр весит более 30 фунтов, а половина – менее 30 фунтов. Это означает, что 50% из 200 выдр весят менее 30 фунтов, поэтому 0,5 * 200 = 100 выдр .

Дополнительные ресурсы

Следующие руководства предлагают дополнительную информацию о нормальном распределении:

6 реальных примеров нормального распределения
Нормальное распределение против t-распределения: разница
Как сделать кривую нормального распределения в Excel
Как сделать кривую нормального распределения в Python

Источник

Нормальное распределение (распределением Гаусса или Гаусса — Лапласа) – распространенная разновидность непрерывного распределения вероятностей для случайной величины.

Помните колоколообразную кривую? Вот эту:

Долгое время она служила главным критерием профессиональной оценки сотрудников американских учреждений, и равнодушных не оставляла, ведь от нее зависело, как себя позиционирует человек и его начальство.

Нормальное распределение – это ключевая концепция Статистики (Statistics) и основа Науки о данных (Data Science). При выполнении Разведочного анализа данных (EDA) мы сначала стремимся найти их распределение вероятностей, и наиболее распространенный ее вид – нормальное распределение.

Посмотрите на распределение вероятностей окупить инвестиции в фондовый индекс S&P 500:

Да-да, вероятность “выйти в ноль” выше остальных! Также справедливо утверждение, что вероятность потерять больше как бы тает вместе с отрицательным процентом возврата. Белой непрерывной линией обозначено предсказание кривой нормального распределения. Прочие наблюдения, такие как вес при рождении и показатель IQ, часто следуют нормальному распределению подобным образом.

Еще одна причина, по которой нормальное распределение становится важным для Дата-сайентистов (Data Scientist) – это Центральная предельная теорема (Central Limit Theorem). Эта теорема объясняет магию математики и является основой методов проверки гипотез.

В этой статье мы поймем важность и различные свойства нормального распределения, а изучим, как использовать эти свойства для проверки нормальности наших данных.

Свойства нормального распределения

Кривая стандартного нормального распределения симметрична относительно Среднего арифметического (Mean), Медианы (Median) и Моды (Mode). Более того, также являются нормальным распределением произведение двух нормальных распределений и их сумма. Магия, не правда ли? Существуют и другие, более сложные закономерности, пока обойдемся самыми понятными.

Эмпирическое правило

Вы слышали об эмпирическом правиле? Оно часто используется в статистике и гласит: “68,27% наблюдений случайной Выборки (Sample) лежат в пределах одного Стандартного отклонения (Standard Deviation), 95,45% – в пределах двух, а 99,73 – в пределах трех стандартных отклонений от среднего”:

Это правило позволяет нам идентифицировать Выбросы (Outlier) и очень полезно при Проверке на нормальность (Normality Test).

Стандартное нормальное распределение

Стандартное нормальное распределение – это частный случай нормального распределения, когда среднее значение равно нулю и стандартное отклонение равно единице. Любое нормальное распределение мы можем преобразовать его в стандартное, используя формулу:

$$z = frac{x – μ}{σ}, где$$
$$zspace{–}space{,}$$
$$xspace{–}space{значение выборки,}$$
$$μspace{–}space{среднее,}$$
$$σspace{–}space{стандартное}space{отклонение}$$

Пример. Есть два интерна: Левин и Ричардс. Левин набрал 65 баллов на экзамене по терапии, а Ричардс – 80 баллов на экзамене по кожной венерологии. Верно ли, что Ричардс учился лучше, чем Левин?

Нет, потому что манера поведения людей в терапии отличается от того, как люди проявляют себя в кожной венерологии. Таким образом, прямое сравнение простым сравнением оценок некорректно.

Теперь предположим, что отметки теста по терапии подчиняются нормальному распределению со средним значением 60 и стандартным отклонением 4. С другой стороны, отметки о кожвенерологии подчиняются нормальному распределению со средним значением 79 и стандартным отклонением 2.

Нам нужно будет вычислить Стандартизированную оценку (Z-score) путем стандартизации обоих этих распределений:

$$z_{Левин} = frac{65 – 60}{4} = 1,25$$
$$z_{Ричардс} = frac{80 – 79}{2} = 0,5$$

Таким образом, Левин набрал 1,25 стандартного отклонения выше среднего, в то время как Ричардс – только 0,5. Следовательно, Левин показал себя лучше:

Асимметричное распределение

Нормальное распределение – это симметрично, что означает, что его “хвосты” слева и справа – зеркальные отображения друг друга. Но это не относится к большинству реальных наборов данных. Как правило, мы будем иметь дело со скошенными асимметричными распределениями.

Визуальная оценка нормальности

Для таких целей принято использовать три вида графиков:

Гистограмма (Histogram), которая отображает частоту “попадания” наблюдения (Observation) в том или ином вертикальном “Ящике” (Bin). В этом примере распределение скошено вправо.
График Ядерного сглаживания (KDE). Является сглаженной версией гистограммы, где непрерывная кривая – ядро, также отображает каждое наблюдение.
График квантиль-квантиль (Q-Q Plot). Если значения располагаются по примерно прямой линии под углом 45 градусов, то данные распределяются нормально. На нашем графике видно, что значения данных имеют тенденцию немного отклоняться от линии под углом 45°, особенно на концах, что может указывать на то, что набор данных не распределяется нормально.

Слева направо: гистограмма, График KDE, Q-Q Plot

Для оценки нормальности распределения также используют Скошенность (Skewness) и Эксцесс (Kurtosis).

Нормальное распределение и Python

Посмотрим, как выглядит код, визуализирующий распределение и заодно рассчитывающий основные метрики Датасета (Dataset). Для начала импортируем необходимые библиотеки:

import numpy as np
import pandas as pd
import seaborn as sns

Загрузим данные:

df = pd.read_csv('https://www.dropbox.com/s/ezugw0xgfp8pzut/%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B8.csv?dl=1')
df.head()

Определим функцию, которая пройдется по всем столбцам датасета, рассчитает основные статистические метрики (среднее, минимум, максимум и т.д.):

def UVA_numeric(data):
    var_group = data.columns # Список столбцов
    size = len(var_group) # Количество столбцов (3)
    plt.figure(figsize = (7 * size, 3), dpi = 400) # Параметры графика

    # Применяем расчеты к каждому столбцу
    for j,i in enumerate(var_group):
        
        # Рассчитываем основные статистические метрики
        mini = data[i].min()
        maxi = data[i].max()
        ran = data[i].max()-data[i].min() # Диапазон значений
        mean = data[i].mean()
        median = data[i].median()
        st_dev = data[i].std() # Стандартное отклонение
        skew = data[i].skew() # Скошенность 
        kurt = data[i].kurtosis() # Эксцесс

        # Расчет точек стандартного отклонения
        points = mean - st_dev, mean + st_dev

        # Построим график с каждым из трех наборов даннных
        #Plotting the variable with every information
        plt.subplot(1, size, j+1)
        sns.distplot(data[i], hist = True, kde=  True)
        
        sns.lineplot(points, [0,0], color = 'black', label = "std_dev")
        sns.scatterplot([mini,maxi], [0,0], color = 'orange', label = "min/max")
        sns.scatterplot([mean], [0], color = 'red', label = "mean")
        sns.scatterplot([median], [0], color = 'blue', label = "median")
        plt.xlabel('{}'.format(i), fontsize = 20)
        plt.ylabel('density')
        plt.title('Стандартное отклонение = {}; Эксцесс = {};n Скошенность = {}; Разброс, шаг гистограммы = {}n Среднее = {}; Медиана = {}'.format((round(points[0],2),round(points[1],2)),
                                                                                 round(kurt,2),                             							round(skew,2),
        (round(mini,2),round(maxi,2),round(ran,2)),
        round(mean,2),
        round(median,2)))

Построим тройной график:

UVA_numeric(df)

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Фото: @changlisheng

Источник

Нормальное распределение

Общие сведения[править | править код]

Определения[править | править код]

Стандартное нормальное распределение[править | править код]

Нормальное распределение с параметрами μ, σ[править | править код]

Обозначение[править | править код]

Функция распределения[править | править код]

Стандартное отклонение[править | править код]

Свойства[править | править код]

Моменты[править | править код]

Преобразование Фурье и характеристическая функция[править | править код]

Бесконечная делимость[править | править код]

Максимальная энтропия[править | править код]

Правило трёх сигм для гауссовской случайной величины[править | править код]

Моделирование нормальных псевдослучайных величин[править | править код]

Нормальное распределение в природе и приложениях[править | править код]

Связь с другими распределениями[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Как определить, является ли распределение нормальным?

Нормальное распределение

Как нарисовать нормальную кривую

Как найти проценты, используя нормальное распределение

Как найти количество, используя нормальное распределение

Дополнительные ресурсы

Свойства нормального распределения

Эмпирическое правило

Стандартное нормальное распределение

Асимметричное распределение

Визуальная оценка нормальности

Нормальное распределение и Python

Вам также может понравиться

Как найти изменение импульса за четверть периода

0х80070035 не найден сетевой путь windows 10 0x80070035 как исправить

Как найти статистику авто по номеру кузова

Добавить комментарий Отменить ответ