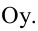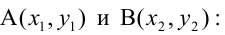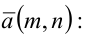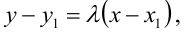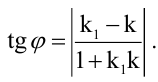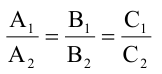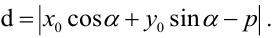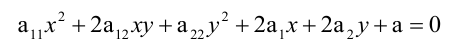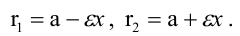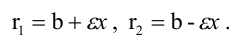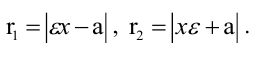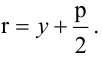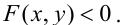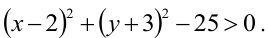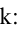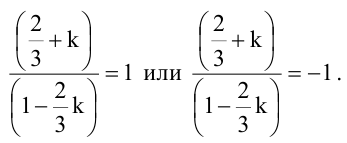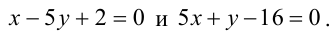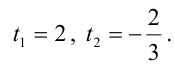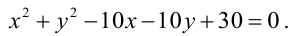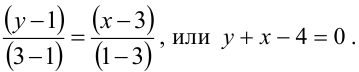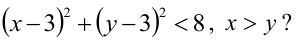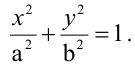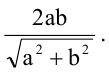VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x”(t_0) & y”(t_0) & z”(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
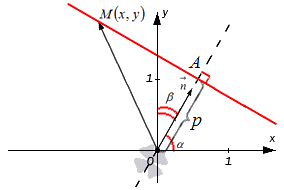
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y – p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y – p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y – p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
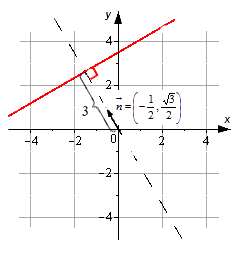
Если дано уравнение прямой вида – 1 2 · x + 3 2 · y – 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами – 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = – 1 2 , 3 2 .
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x – 4 y – 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = – 4 , С = – 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( – 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x – 4 y – 16 ) = 0 ⇔ 3 5 · x – 4 5 · y – 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x – 4 5 · y – 16 5 = 0 .
Уравнения прямых и кривых на плоскости с примерами решения
Содержание:
Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия – кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета – кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей – кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса – кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса – кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера – кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка – окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 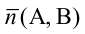
2. Уравнение прямой с угловым коэффициентом:
где 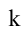
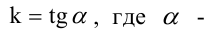
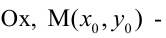
Уравнение (2.2) принимает вид 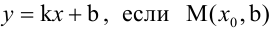
3. Уравнение прямой в отрезках:
где а и b – величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки –
5. Уравнение прямой, проходящей через данную точку 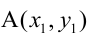
6. Нормальное уравнение прямой:
где 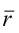
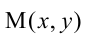
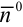
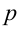
Нормальное уравнение прямой в координатной форме имеет вид:
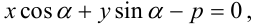
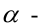
Уравнение пучка прямых с центром в точке 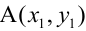
где 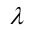
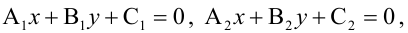
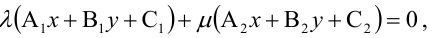
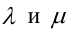
Величина угла между прямыми 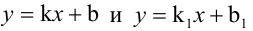
Равенство 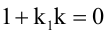
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 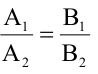
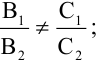
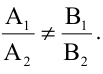
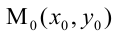
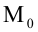
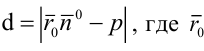
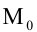
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 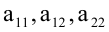
Уравнение окружности с центром в точке 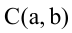

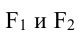
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 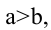
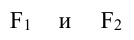
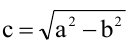
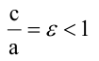
Расстояния от точки 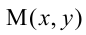
Если же 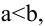
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 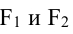
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 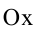
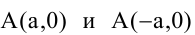
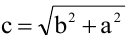
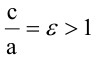
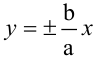
Расстояния от точки 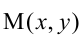
Гипербола, у которой а=b, называется равносторонней, ее уравнение 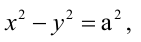
Гиперболы 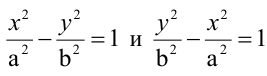
Каноническое уравнение параболы имеет два вида:
1. 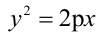
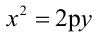
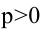
Парабола, уравнение которой 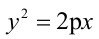
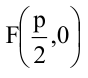
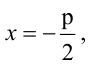
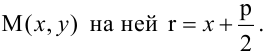
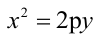
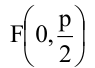
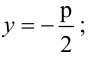
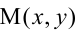
Уравнение 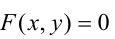
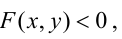
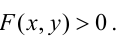
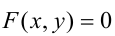
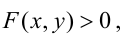
Прямая, уравнение которой 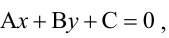
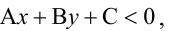
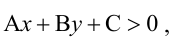
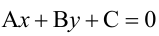
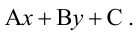
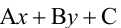
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 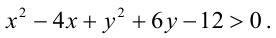
Уравнение 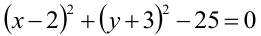
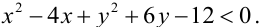
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 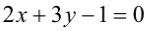
Решение:
Будем искать уравнение прямой в виде 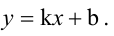
Величина угла между прямыми 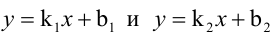
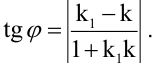
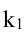
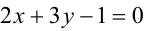
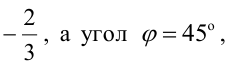
Имеем два значения 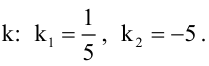
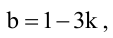
Пример:
При каком значении параметра t прямые, уравнения которых 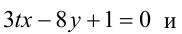
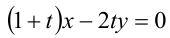
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 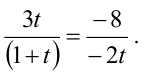
Пример:
Найти уравнение общей хорды двух окружностей: 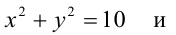
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 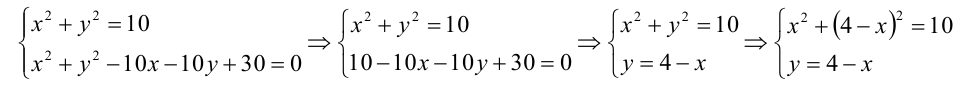
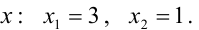
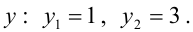
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 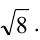
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 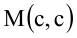
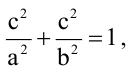
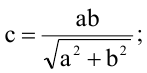
Пример:
Зная уравнение асимптот гиперболы 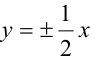
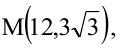
Решение:
Запишем каноническое уравнение гиперболы: 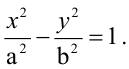
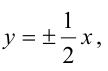
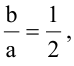
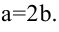
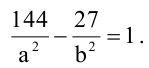
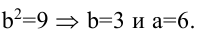
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 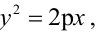
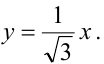
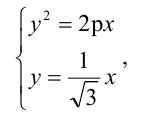
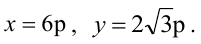
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnoe-normirovannoe-uravnenie-prjamoj/
http://www.evkova.org/uravneniya-pryamyih-i-krivyih-na-ploskosti
[/spoiler]
Содержание
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
-
Векторное уравнение $gamma:, vec{r}=vec{r}(t)$.
-
Параметрическое уравнение $gamma:,, x=x(t),, y=y(t),, z=z(t)$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin{equation*}
vec{r_0}=vec{r}(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0).
end{equation*}
Пусть в точке $M$ $ vec{r’}(t_0)neqvec{0}$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec{r’}(t_0)$.
Пусть $vec{R}$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
begin{equation*}
vec{R}=vec{r}(t_0)+lambdavec{r’}(t_0).
end{equation*}
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec{R}$).
Если $vec{R}={X,Y,Z}$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
begin{equation*}
frac{X-x(t_0)}{x'(t_0)}=frac{Y-y(t_0)}{y'(t_0)}=frac{Z-z(t_0)}{z'(t_0)}.
end{equation*}
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec{R}$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec{R}-vec{r}(t_0)$ и $vec{r’}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0))cdotvec{r’}(t_0)=0.
end{equation*}
Если расписать покоординатно, то получим следующее уравнение:
begin{equation*}
x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0.
end{equation*}
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec{r’}(t_0)$, $vec{r”}(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec{R}$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r”}(t_0)$:
begin{equation*}
(vec{R}-vec{r}(t_0), vec{r’}(t_0), vec{r”}(t_0))=0.
end{equation*}
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-x(t_0) & Y-y(t_0) & Z-z(t_0) \
x'(t_0) & y'(t_0) & z'(t_0)\
x”(t_0) & y”(t_0) & z”(t_0) \
end{array}
right|=0
end{equation*}
Плоская кривая лежит в своей соприкасающейся плоскости.
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec{r’}(t_0)timesvec{r”}(t_0)$, тогда ее уравнение можно записать в виде:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0)timesvec{r”}(t_0).
end{equation*}
Как и раньше, $vec{R}$ — радиус-вектор произвольной точки бинормали.
Каноническое уравнение прямой:
begin{equation*}
frac{X-x(t_0)}{left|
begin{array}{cc}
y'(t_0) & z'(t_0) \
y”(t_0) & z”(t_0) \
end{array}
right|
}=frac{Y-y(t_0)}{left|
begin{array}{cc}
z'(t_0) & x'(t_0) \
z”(t_0) & x”(t_0) \
end{array}
right|
}=frac{Z-z(t_0)}{left|
begin{array}{cc}
x'(t_0) & y'(t_0) \
x”(t_0) & y”(t_0) \
end{array}
right|
}.
end{equation*}
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r”}(t_0)right]$:
begin{equation*}
vec{R}=vec{r}(t_0)+lambda,vec{r’}(t_0) timesleft[vec{r’}(t_0),vec{r”}(t_0)right].
end{equation*}
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение:
Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec{R}-vec{r}(t_0)$, $vec{r’}(t_0)$, $vec{r’}(t_0)timesvec{r”}(t_0)$:
begin{equation*}
left(vec{R}-vec{r}(t_0),, vec{r’}(t_0),, vec{r’}(t_0)timesvec{r”}(t_0)right)=0.
end{equation*}
Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим:
$$ vec{tau}=frac{vec{r’}(t_0)}{|vec{r’}(t_0)|}. $$
Орт бинормали:
$$ vec{beta}=frac{vec{r’}(t_0)timesvec{r”}(t_0)}{|vec{r’}(t_0)timesvec{r”}(t_0)|}. $$
Орт главной нормали:
$$ vec{nu}=frac{vec{r’}(t_0) times[vec{r’}(t_0),,vec{r”}(t_0)]}{|vec{r’}(t_0) times [vec{r’}(t_0),,vec{r”}(t_0)]|}. $$
Правая тройка векторов $vec{tau}$, $vec{nu}$, $vec{beta}$ называется репером Френе.

Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
$$
x=t,,, y=t^2,,, z=e^t.
$$
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$.
Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin{gather*}
gamma: vec{r}(t)=left{ t,, t^2,, e^tright} ,, Rightarrow \
vec{r’}(t)=left{ 1,, 2t,, e^tright},\
vec{r”}(t)=left{ 0,, 2,, e^tright}.
end{gather*}
В точке $M(t_0=0)$:
begin{gather*}
vec{r}(t_0)={ 0,, 0,, 1},\
vec{r’}(t_0)={ 1,, 0,, 1},\
vec{r”}(t_0)={ 0,, 2,, 1}.
end{gather*}
-
Зная координаты точки $M(0,0,1)$ и направляющего вектора $ vec{r’}(t_0)={ 1,0,1 }$, можем записать уравнение касательной:
begin{equation*}
frac{X}{1}=frac{Y}{0}=frac{Z-1}{1}.
end{equation*}
-
Нормальная плоскость проходит через точку $M(0,0,1)$ перпендикулярно вектору $vec{r’}(t_0)={ 1,0,1 }$, поэтому ее общее уравнение имеет вид:
begin{equation*}
1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1.
end{equation*}
-
Запишем теперь уравнение соприкасающейся плоскости, определяемой точкой $M(0,0,1)$ и векторами: $vec{r’}(t_0)={ 1,, 0,, 1}$, $vec{r”}(t_0)={ 0,, 2,, 1}$:
begin{equation*}
left|
begin{array}{ccc}
X-0 & Y-0 & Z-1 \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|=0
end{equation*}
Раскрываем определитель, получаем уравнение:
begin{equation*}
-2X-Y+2Z-2=0
end{equation*}
-
Направление бинормали задается вектором $vec{r’}(t_0) times vec{r”}(t_0)$. Координаты этого вектора мы уже нашли, когда вычисляли миноры в определителе, задающем уравнение соприкасающейся плоскости.
$$
{ 1,, 0,, 1} times { 0,, 2,, 1}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
0 & 2 & 1 \
end{array}
right|= {-2,, -1,, 2}.
$$
Уравнение бинормали:
begin{equation*}
frac{X}{-2}=frac{Y}{-1}=frac{Z-1}{2}.
end{equation*}
-
Направление главной нормали задается вектором $vec{r’}(t_0) times (vec{r’}(t_0)timesvec{r”}(t_0))$.
$$
{ 1,, 0,, 1} times {-2,, -1,, 2}= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 1\
-2 & -1 & 2 \
end{array}
right|= {1,, -4,, -1} ,, Rightarrow ,,
frac{X}{1}=frac{Y}{-4}=frac{Z-1}{-1}.
$$
-
Спрямляющая плоскость перпендикулярна главной нормали, а значит, вектору ${1,, -4,, -1}$, поэтому можем сразу записать ее общее уравнение:
begin{equation*}
1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0.
end{equation*}
Орт касательной: $vec{tau} =frac{1}{sqrt{2}}{1,,0,,1}$,
Орт главной нормали: $vec{nu} =frac{1}{sqrt{18}}{1,,-4,,-1}$,
Орт бинормали: $vec{beta }=frac{1}{3}{-2,,-1,,2}$.
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ не будет правой (по определению векторного произведения вектор $vec{tau}timesvec{beta}$ направлен так, что тройка векторов $vec{tau}$, $vec{beta}$, $vec{nu}=vec{tau}timesvec{beta}$ — правая). Изменим направление одного из векторов. Например, пусть
$$ vec{nu} =frac{1}{sqrt{18}}{-1,,4,,1}.$$
Теперь тройка $vec{tau}$, $vec{nu}$, $vec{beta}$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой
$$
x=t,,, y=frac{t^2}{2},,, z=frac{t^3}{3},
$$
проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
begin{align*}
gamma: vec{r}(t)&=left{ t,, frac{t^2}{2},, frac{t^3}{3}right} ,, Rightarrow \
vec{r’}(t)&=left{ 1,, t,, 3t^2right},\
vec{r”}(t)&=left{ 0,, 1,, 6tright}.
end{align*}
В точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t_0,, frac{t_0^2}{2},, frac{t_0^3}{3}right} \
vec{r’}(t_0)&=left{1,, t_0,, 3t_0^2right},\
vec{r”}(t_0)&=left{0,, 1,, 6t_0right}.
end{align*}
Соприкасающаяся плоскость определяется векторами $vec{r’}(t_0)$, $vec{r”}(t_0)$, поэтому записываем определитель
begin{equation*}
left|
begin{array}{ccc}
X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \
&&\
1 & t_0 & t^2_0 \
&&\
0 & 1 & 2t_0
end{array}
right|=0 quad Rightarrow
end{equation*}
begin{equation*}
(X-t_0)cdot t_0^2 – (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0.
end{equation*}
Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$:
begin{equation*}
9-t_0^3/3=0 quad Rightarrow quad t_0=3.
end{equation*}
Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости:
$$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой:
$$
x=t^2,,, y=1+t,,, z=2t.
$$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec{r’}(t_0)$ и $vec{r’}(t_0)timesvec{r”}(t_0)$.
В произвольной точке $M(t=t_0)$:
begin{align*}
vec{r}(t_0)&=left{t^2_0,, 1+t_0,, 2t_0right} \
vec{r’}(t_0)&=left{2t_0,, 1,, 2right},\
vec{r”}(t_0)&=left{2,, 0,, 0right}.
end{align*}
begin{equation*}
vec{r’}(t_0)timesvec{r”}(t_0)= left|
begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
2t_0 & 1 & 2\
2 & 0 & 0
end{array}
right|= {0,, 4,, -2}
end{equation*}
Записываем уравнение спрямляющей плоскости:
begin{equation*}
left|
begin{array}{ccc}
X-t_0^2 & Y-1-t_0 & Z-2t_0 \
2t_0 & 1 & 2\
0 & 4 & -2
end{array}
right|= 0
end{equation*}
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$:
begin{equation*}
5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_{01}=2,, t_{02}=-frac25.
end{equation*}
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид:
begin{align*}
& 5X-4Y-8Z+24=0,\
& 25X+4Y+8Z=0.
end{align*}
-
Нормальная плоскость.
Начать изучение
-
Главная нормаль.
Начать изучение
Нормальная плоскость.
Плоскость (mathcal{P}), проходящую через точку (M_{0}) кривой (Gamma) и перпендикулярную касательной к этой кривой в точке (M_{0}), называют нормальной плоскостью кривой (Gamma) в точке (M_{0}).
Если кривая (Gamma) задана уравнением в векторной форме
$$
Gamma={textbf{r}=textbf{r}(t), alphaleq tleqbeta},label{ref3}
$$
где
$$
textbf{r}=(x,y,z),quad textbf{r}(t)=(x(t),y(t),z(t)),nonumber
$$
(t_{0}in[alpha,beta]), (overrightarrow{OM_0}=textbf{r}(t_0)) и (textbf{r}'(t_0)neq 0), то вектор (textbf{r}'(t_0)) параллелен касательной к кривой (Gamma) в точке (M_{0}). Пусть (M) — произвольная точка нормальной плоскости (mathcal{P}) (рис. 22.5), (overrightarrow{OM}=textbf{r}). Тогда вектор (overrightarrow{MM}_{0}=textbf{r}-textbf{r}(t_0)) перпендикулярен вектору (textbf{r}'(t_{0})), и поэтому уравнение нормальной плоскости (mathcal{P}) к кривой (Gamma) в точке (M_{0}) можно записать в виде
$$
(textbf{r}-textbf{r}(t_{0}),textbf{r}'(t_{0}))=0nonumber
$$
или
$$
(x-x(t_{0}))x'(t_0)+(y-y(t_{0}))y'(t_{0})+(z-z(t_0))z'(t_0)=0.nonumber
$$
Главная нормаль.
Любую прямую, лежащую в нормальной плоскости (mathcal{P}) к кривой (Gamma) в точке (M_{0}), называют нормалью кривой (Gamma) в точке (M_{0}). Среди всех нормалей выделяют одну — главную нормаль.
Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть (Gamma) — гладкая кривая, заданная уравнением eqref{ref3}, причем для всех (tin[alpha,beta]) существует (textbf{r}″(t)). В этом случае говорят, (Gamma) — дважды дифференцируемая кривая без особых точек.
Утверждение 1.
Если (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref{ref3}, (s) — переменная длина дуги кривой (Gamma), то существуют (displaystyle frac{dtextbf{r}}{ds}) и (displaystyle frac{d^{2}textbf{r}}{ds^{2}}) и справедливы равенства
$$
frac{dtextbf{r}}{ds}=frac{textbf{r}'(t)}{s'(t)},label{ref26}
$$
$$
frac{d^{2}rtextbf{}}{ds^{2}}=frac{s'(t)textbf{r}″(t)-s″(t)textbf{r}'(t)}{(s(t))^{3}}.label{ref27}
$$
Доказательство.
(circ) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу eqref{ref26}:
$$
frac{dtextbf{r}}{ds}=frac{dtextbf{r}}{dt}frac{dt}{ds}=frac{dtextbf{r}}{dt}frac{1}{s'(t)}=frac{textbf{r}'(t)}{s'(t)}.nonumber
$$
Используя формулу eqref{ref26} и правило дифференцирования произведения векторной функции на скалярную, находим
$$
frac{d^{2}textbf{r}}{ds^{2}}=frac{d}{dt}left(frac{dtextbf{r}}{ds}right)frac{dt}{ds}=frac{d}{dt}left(frac{textbf{r}'(t)}{s'(t)}right)frac{1}{s'(t)}=left(frac{textbf{r}″(t)}{s'(t)}-frac{s″(t)textbf{r}'(t)}{(s(t))^{2}}right)frac{1}{s'(t)},nonumber
$$
откуда следует формула eqref{ref27}.
Заметим, что (s″(t)) существует, так как (s'(t)=|textbf{r}'(t)|),
$$
s″(t)=frac{d}{dt}(|textbf{r}'(t)|)=frac{d}{dt}(textbf{r}'(t),textbf{r}'(t))^{1/2},nonumber
$$
а (textbf{r}″(t)) существует и (|textbf{r}'(t)|neq 0). (bullet)
Перейдем к определению главной нормали. Будем считать, что (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref{ref3}. Тогда существуют (displaystyle frac{dtextbf{r}}{ds}) и (displaystylefrac{d^{2}textbf{r}}{ds^{2}}), причем (displaystyle frac{dtextbf{r}}{ds}) — единичный вектор в силу данного утверждения. Обозначим этот вектор буквой (tau). Тогда
$$
frac{dtextbf{r}}{ds}=tau,quad |tau|=1,label{ref28}
$$
и поэтому (см. данный пример) вектор (displaystyle frac{dtau}{ds}=frac{d^{2}textbf{r}}{ds^{2}}) ортогонален вектору (tau).
Предположим, что
$$
frac{dtau}{ds}neq 0,label{ref29}
$$
и обозначим
$$
k=|frac{dtau}{ds}|.label{ref30}
$$
Пусть (nu) — единичный вектор, параллельный вектору (displaystyle frac{dtau}{ds}). Тогда
$$
frac{dtau}{ds}=knu,quad|nu|=1,label{ref31}
$$
причем вектор (nu) ортогонален вектору (tau).
Так как вектор (tau=displaystyle frac{dtextbf{r}}{ds}) параллелен вектору касательной (r'(t)) к кривой (Gamma) в силу равенства eqref{ref26}, то из eqref{ref31} следует, что вектор (nu) параллелен нормальной плоскости кривой (Gamma) в точке (M) ((overrightarrow{OM}=r(t))). Поэтому вектор (nu) параллелен одной из нормалей кривой (Gamma) в точке (M). Эту нормаль называют главной.
Итак, если в точке (MinGamma) выполняется условие eqref{ref29}, то нормаль к кривой (Gamma) в точке (M), параллельная вектору (nu) (формула eqref{ref31}), называется главной нормалью.
Найдем производную, дифференцируя функцию $ y(x) $ по переменной $ x $:
$$ (x^2)’_x+ (2xy^2)’_x + (3y^4)’_x = (6)’_x $$
Учитывая, что $ y^2 $ и $ y^4 $ сложные функции продолжаем:
$$ 2x + 2y^2 + 4xyy’ + 12y^3 y’ = 0 $$
Выражаем $ y’ $ из полученного уравнения:
$$ 4xyy’ + 12y^3 y’ = -2x – 2y^2 $$
Выносим $ y’ $ за скобки:
$$ y'(4xy + 12y^3) = -2x – 2y^2 $$
Делим обе части уравнения на выражение $ 4xy+12y^3 $:
$$ y’ = -frac{2x+2y^2}{4xy + 12y^3} = -frac{x+y^2}{2xy+6y^3} $$
Теперь вычисляем значение $ y’ $:
$$ y’ = -frac{1 + (-1)^2}{2cdot 1 cdot (-1) + 6cdot (-1)^3} = -frac{2}{-8} = frac{1}{4} $$
Зная, что $ y’ = frac{1}{4} $ и $ y(x_0) = y(1) = -1 $ составляем уравнения касательной и нормали к кривой в точке $ M(1;-1) $.
Получаем уравнение касательной:
$$ y – (-1) = frac{1}{4} (x – 1) $$
Записываем в красивой форме:
$$ y = frac{1}{4} x – frac{3}{4} $$
Получаем уравнение нормали:
$$ y – (-1) = -frac{1}{frac{1}{4}} (x – 1) $$
Раскрываем скобки и записываем в красивой форме, полученное уравнение:
$$ y+1 = -4(x-1) $$
$$ y = -4x + 3 $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Содержание:
Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия – кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета – кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей – кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса – кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса – кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера – кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка – окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 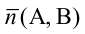
2. Уравнение прямой с угловым коэффициентом:
где 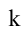
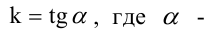
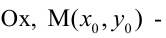
Уравнение (2.2) принимает вид 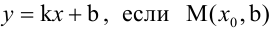
3. Уравнение прямой в отрезках:
где а и b – величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки –
5. Уравнение прямой, проходящей через данную точку 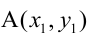
6. Нормальное уравнение прямой:
где 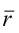
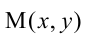
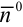
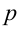
Нормальное уравнение прямой в координатной форме имеет вид:
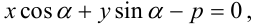
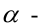
Уравнение пучка прямых с центром в точке 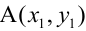
где 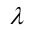
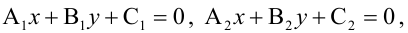
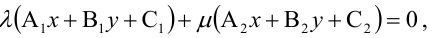
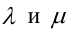
Величина угла между прямыми 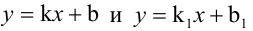
Равенство 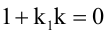
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 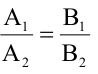
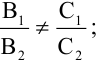
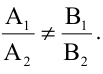
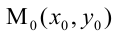
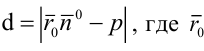
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 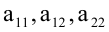
Уравнение окружности с центром в точке 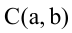

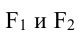
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 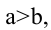
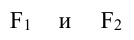
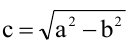
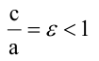
Расстояния от точки 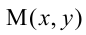
Если же 
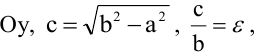
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 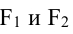
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 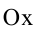
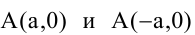
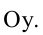
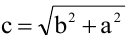
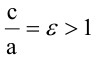
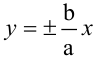
Расстояния от точки 
Гипербола, у которой а=b, называется равносторонней, ее уравнение 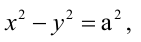
Гиперболы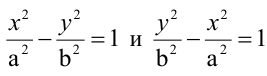
Каноническое уравнение параболы имеет два вида:
1. 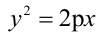
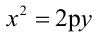
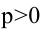
Парабола, уравнение которой 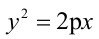
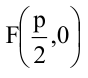
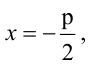
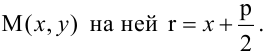
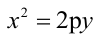
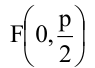
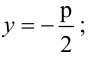
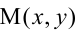
Уравнение 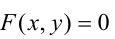
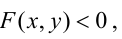
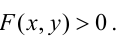
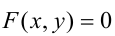
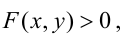
Прямая, уравнение которой 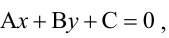
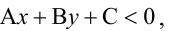
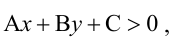
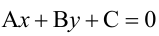
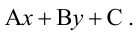
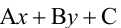
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 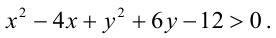
Уравнение 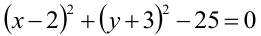
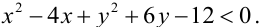
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 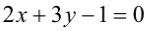
Решение:
Будем искать уравнение прямой в виде 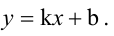
Величина угла между прямыми 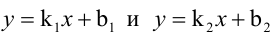
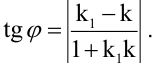
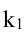
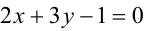
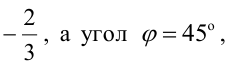
Имеем два значения 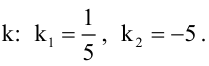
- Заказать решение задач по высшей математике
Пример:
При каком значении параметра t прямые, уравнения которых 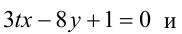
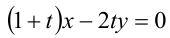
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 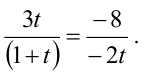
Пример:
Найти уравнение общей хорды двух окружностей: 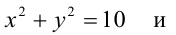
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 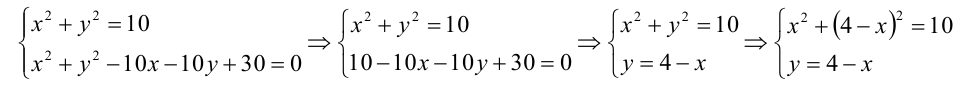
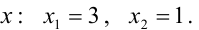
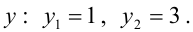
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 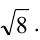
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 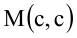
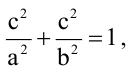
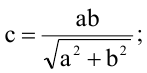
Пример:
Зная уравнение асимптот гиперболы 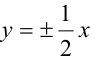
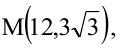
Решение:
Запишем каноническое уравнение гиперболы: 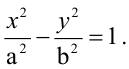
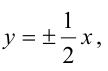
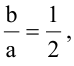
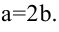
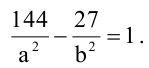
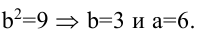
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 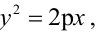
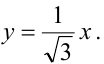
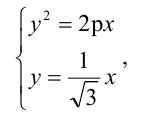
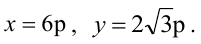
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных