Как найти нормальное ускорение зная тангенциальное
Содержание
- Этот видеоурок доступен по абонементу
- На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
- Ускорение. Нормальная и тангенциальная составляющие ускорения
- Пример нахождения тангенциальной и нормальной составляющей ускорения
- Задача 1
- Задача 2
- Нахождение закона изменения скорости от времени
- В физике
- Траектория движения и компоненты полного ускорения
- Ускорение тангенциальное
- Ускорение нормальное
- Ускорение полное, нормальное и тангенциальное
- Решение задачи
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
. Тангенциальное ускорение описывает степень изменения скорости по модулю:
Нормальное ускорение 
– это составляющая ускорения, которая направлена к центру кривизны траектории, то есть она является нормалью (направлена перпендикулярно) к скорости. Нормальное ускорение описывает степень изменения скорости по направлению:
Здесь R – это радиус кривизны траектории в заданной точке.
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:
.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
Ускорение. Нормальная и тангенциальная составляющие ускорения
Механическое движение по характеру подразделяется на поступательное, вращательное и колебательное; по виду траектории – прямолинейное и криволинейное. Также механическое движение можно подразделять по характеру изменения скорости.
Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени):  и нормальную (перпендикулярную вектору скорости).</p>
<p style=)
.</p>
<p style=)
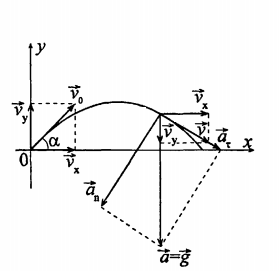
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Рис. 4. Направление нормального ускорения
Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением: 
При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).
Рис. 5. Прямолинейное движение
При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).
Рис. 6. Криволинейное движение
Пример нахождения тангенциальной и нормальной составляющей ускорения
Рассмотрим движение тела, брошенного под углом к горизонту (см. рис. 7). Найдём составляющие ускорения в тот момент, когда скорость тела направлена под углом 
к горизонту.
Рис. 7. Траектория движения тела
Касательная к траектории в точке A – это направление скорости 
Рис. 8. Проекции ускорения
На рисунке видно, что тангенциальная составляющая ускорения направлена против скорости, то есть скорость тела в данный момент уменьшается (см. рис. 8). Нормальная составляющая ускорения направлена перпендикулярно скорости, следовательно, скорость в следующий момент наклонится в сторону 
.
Величины составляющих ускорения находим геометрически.
Рис. 9. Геометрическое определение величины составляющих ускорения
Угол A в треугольнике разложения на составляющие (треугольник выделен жёлтым на рисунке) имеет взаимно перпендикулярные стороны с углом 
Следовательно, тангенциальная составляющая равна: 
.
Нормальная составляющая ускорения равна: 
.
Задача 1
Обод радиусом 1 метр катится по горизонтальной поверхности со скоростью 10 м/с. Найти радиус траектории точки поверхности обода при прохождении наивысшего положения.
Дано: 
Найти: 
.
Решение
Рис. 10. Иллюстрация к задаче
На рисунке изображён обод, который катится по горизонтальной поверхности со скоростью Скорость точки A относительно горизонтальной поверхности при движении обода без проскальзывания равна нулю. Это объясняется тем, что она движется вместе с ободом по горизонтали со скоростью Скорости точек в верхней части обода равны: 
. Эта скорость будет направлена по горизонтали в сторону движения обода.
С центром обода у всех точек, лежащих на её поверхности, связано нормальное ускорение, так как оно направлено перпендикулярно скорости движения точки по окружности в любой момент времени.
Ускорение остаётся неизменным для всех точек поверхности обода, так как при переходе к системе отсчёта, связанной с Землёй, центр обода движется равномерно: 
.
Тогда для точки 
В этой задаче заданное значение начальной скорости было лишним. Избыточные данные часто включают в задания ЕГЭ по физике.
Ответ: 
.
Задача 2
После удара футбольный мяч за 2 с пролетел 40 м и упал на землю. Чему равен радиус траектории мяча в верхней точке траектории?
Дано: Найти: 
.
Решение
Рис. 11. Иллюстрация к задаче
На рисунке изображена траектория полёта мяча (см. рис. 11). Точка A – верхняя точка траектории, скорость мяча в которой Скорость в точке A – это горизонтальная составляющая скорости, которая в процессе всего движения остаётся неизменной. Поэтому скорость в точке A равна отношению всего пути, пройденного по горизонтали, ко времени: 
.
Следовательно, радиус траектории в верхней точке равен: 
.
Ответ: 
.
Нахождение закона изменения скорости от времени
Сведения об ускорении необходимы для того, чтобы найти закон изменения скорости от времени. Например, зависимость скорости от времени находится как неопределённый интеграл от ускорения по времени: 
, где C – постоянная интегрирования.
При равноускоренном движении При 
- Вопросы в конце параграфа 13 (стр. 46); — Касьянов В.А. Физика. 10 кл. (см. список рекомендованной литературы) (Источник)
- Камень брошен со скоростью 20 м/c под углом
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.
В физике
Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:
Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.
Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:
Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.
Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с 2 ).
Траектория движения и компоненты полного ускорения
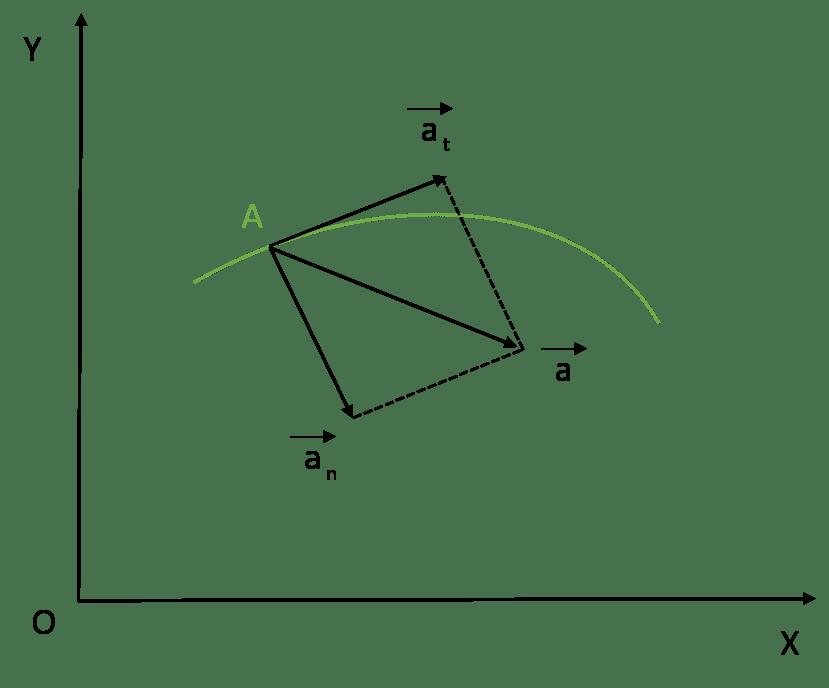
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?
Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:
Здесь ut¯ — вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.
Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:
Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.
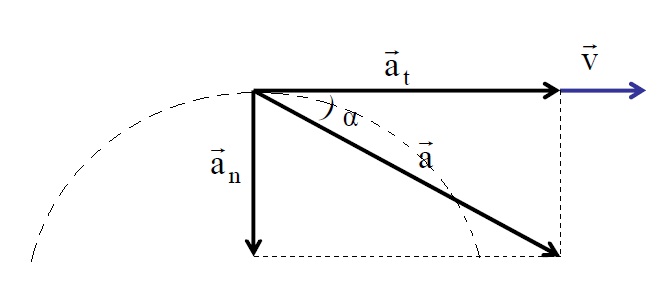
Ускорение тангенциальное
Запишем еще раз формулу для этой компоненты полного ускорения:
Это выражение позволяет описать свойства величины at¯:
- Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор ut¯.
- Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.
Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения — это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.
Ускорение нормальное
Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:
Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:
Здесь dL — это пройденный телом путь за промежуток времени dt, r — радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:
То есть величина an¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор an¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.
Ускорение полное, нормальное и тангенциальное
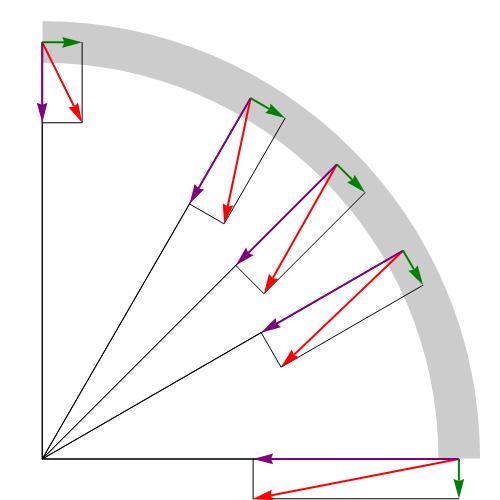
Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:
Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и an¯ вычисляется так:
Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.
Решение задачи
Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:
Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.
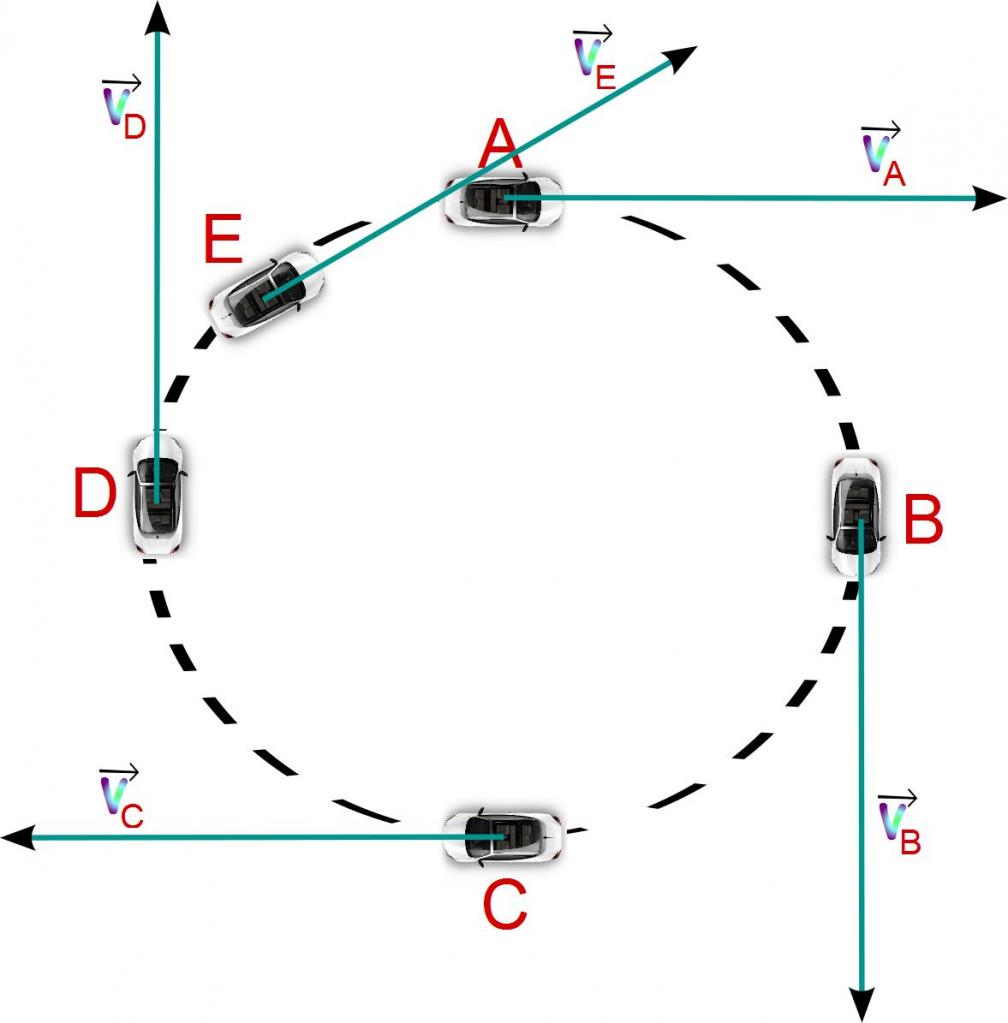
Для тангенциального имеем:
Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:
Теперь можно воспользоваться формулой для an:
Таким образом, мы определили все величины, которые требовалось найти для решения задачи.
.</li>
<li>Интернет-портал Gym1belovo.smartlearn.ru (Источник).</li>
<li>Интернет-портал Studopedia.info (Источник).</li>
</ol>
<p style=)
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта. 
Решение. Тело участвует в двух движениях:
Равномерном – относительно оси Ох и равнопеременном – относительно оси Оу с ускорением g = 10 м/с2.
Зная время движения, определим приблизительное положение тела в пространстве. Движение тела брошенного под углом к горизонту описывается формулами:
[ begin{align}
& x={{upsilon }_{0x}}cdot t,{{upsilon }_{0x}}={{upsilon }_{0}}cdot cos alpha ,x={{upsilon }_{0}}cdot cos alpha cdot t(1), \
& y={{upsilon }_{0y}}cdot t-frac{gcdot {{t}^{2}}}{2},{{upsilon }_{0y}}={{upsilon }_{0}}cdot sinalpha ,y={{upsilon }_{0}}cdot sinalpha cdot t-frac{gcdot {{t}^{2}}}{2}(2). \
end{align} ]
В конце полета координата y равна нулю, определим время полета:
[ begin{align}
& 0={{upsilon }_{0}}cdot sinalpha cdot t-frac{gcdot {{t}^{2}}}{2},tcdot ({{upsilon }_{0}}cdot sinalpha -frac{gcdot t}{2})=0,t=0,{{upsilon }_{0}}cdot sinalpha -frac{gcdot t}{2}=0, \
& frac{gcdot t}{2}={{upsilon }_{0}}cdot sinalpha ,t=frac{2cdot {{upsilon }_{0}}cdot sinalpha }{g}(3).t=frac{2cdot 15cdot 0,5}{10}=1,5. \
end{align}
]
Координата y равна нулю в начале полета (t = 0) и в конце.
Тело на весь путь затратит 1,5 с, на половину пути 0,75 с. Через 1,2 с тело будет находиться на второй половине пути. Покажем рисунок и определим скорость в указанной точке.
[ begin{align}
& {{upsilon }_{x}}={{upsilon }_{0}}cdot cos alpha (5),{{upsilon }_{y}}={{upsilon }_{0}}cdot sinalpha -gcdot t(6), \
& upsilon =sqrt{{{({{upsilon }_{0}}cdot cos alpha )}^{2}}+{{({{upsilon }_{0}}cdot sinalpha -gcdot t)}^{2}}}(7). \
end{align} ]
Запишем формулу для определения ускорений.
[ begin{align}
& {{a}_{n}}=frac{{{upsilon }^{2}}}{R} (2), {{a}_{n}}=gcdot cos varphi (3), cos varphi =frac{{{upsilon }_{x}}}{upsilon }, {{a}_{n}}=gcdot frac{{{upsilon }_{0}}cdot cos alpha }{sqrt{{{({{upsilon }_{0}}cdot cos alpha )}^{2}}+{{({{upsilon }_{0}}cdot sinalpha -gcdot t)}^{2}}}} (8,). \
& {{g}^{2}}=a_{n}^{2}+a_{tau }^{2}, a_{tau }^{2}={{g}^{2}}-a_{n}^{2}, {{a}_{tau }}=sqrt{{{g}^{2}}-{{(gcdot frac{{{upsilon }_{0}}cdot cos alpha }{sqrt{{{({{upsilon }_{0}}cdot cos alpha )}^{2}}+{{({{upsilon }_{0}}cdot sinalpha -gcdot t)}^{2}}}})}^{2}} }, \
& {{a}_{tau }}=gcdot sqrt{1-{{(frac{{{upsilon }_{0}}cdot cos alpha }{sqrt{{{({{upsilon }_{0}}cdot cos alpha )}^{2}}+{{({{upsilon }_{0}}cdot sinalpha -gcdot t)}^{2}}}})}^{2}} } (9). \
end{align} ]
[ begin{align}
& {{a}_{n}}=10cdot frac{15cdot frac{sqrt{3}}{2}}{sqrt{{{(15cdot frac{sqrt{3}}{2})}^{2}}+{{(15cdot frac{1}{2}-10cdot 1,2)}^{2}}}}=9,45. \
& {{a}_{tau }}=10cdot sqrt{1-{{(0,945)}^{2}}}=3,27. \
end{align}
]
[ a_{tau }^{2}={{g}^{2}}-a_{n}^{2},{{a}_{tau }}=sqrt{{{g}^{2}}-a_{n}^{2}}.{{a}_{tau }}=sqrt{{{10}^{2}}-{{(9,45)}^{2}}}=3,27. ]
Ответ: аn = 9,45 м/с2, аτ = 3,27 м/с2.
Для школьников.
Как будет двигаться тело, если ему сообщить начальную скорость, направленную под углом к горизонту?
Если телу сообщить начальную скорость, направленную под углом к горизонту, то оно будет двигаться по криволинейной траектории. Это значит, что вектор мгновенной скорости, направленный по касательной к траектории, будет постоянно менять своё направление. Будет меняться и величина (модуль) скорости.
В любой точке траектории тело будет находиться в состоянии свободного падения.
Как решать такие задачи?
Удобно разложить движение тела на движение по вертикали и движение по горизонтали. Тогда криволинейное движение заменится двумя прямолинейными и мы сможем пользоваться уже полученными ранее уравнениями.
Спроектировав вектор начальной скорости на вертикальное и горизонтальное направления, найдём начальную скорость тела в этих направлениях. Вектор текущей мгновенной скорости тоже можно разложить на горизонтальную и вертикальную составляющие.
Можно разложить на составляющие и вектор ускорения свободного падения, спроектировав его на касательную к траектории и на нормаль к касательной.
Тогда получим касательное (или тангенциальное) ускорение и нормальное (или центростремительное) ускорение. Модуль последнего определяется скоростью и радиусом кривизны траектории. Касательное и нормальное ускорения будут рассмотрены в следующем занятии.
Подробное решение этой задачи с добавлением вопросов смотрите в следующей записи “Продолжение занятия 7”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Задача 1; Задача 2; Задачи 3 и 4; Задачи 5 и 6; Задачи 7 и 8.
Предыдущая запись: Занятие 6
Следующая запись: Продолжение занятия 7
Первая запись: Занятие 1. Физика. Механика. Кинематика
Занятие 5. Подход к решению сложных задач на равнопеременное движение
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
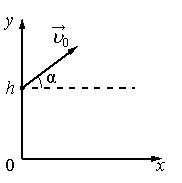
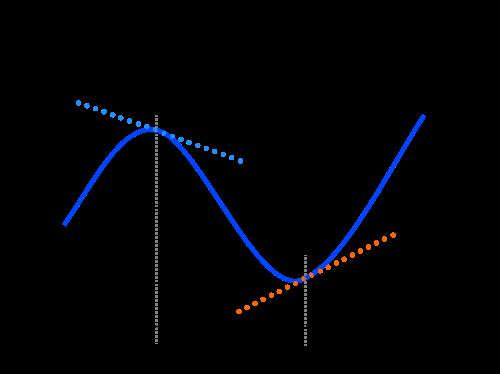
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.1k
Лучший ответ
|
|
 |
|
