- View Larger Image
Иногда возникает такая задача: есть фото небольшого разрешения и не очень хорошего качества, оно очень нужно, но не подходит для работы с ней.
Вот например из такой картинки банер не напечатать:
В такой ситуации есть три варианта действий:
1 вариант: Плюнуть и найти другое фото.
2 вариант: Работать с тем что есть. И закрыть глаза на артефакты и мутность фото при увеличении.
3 вариант: Найти это изображение в лучшем качестве по образцу той картинки которая у нас есть.
Сегодня я расскажу как реализовать третий вариант, т.к. первые два сделать никогда не поздно. :)))
Итак, у вас есть фото на вашем компьютере, или ссылка на фото на каком-то ресурсе в интернете. Что мы делаем дальше, чтобы найти изображение по картинке, которая у нас имеется.
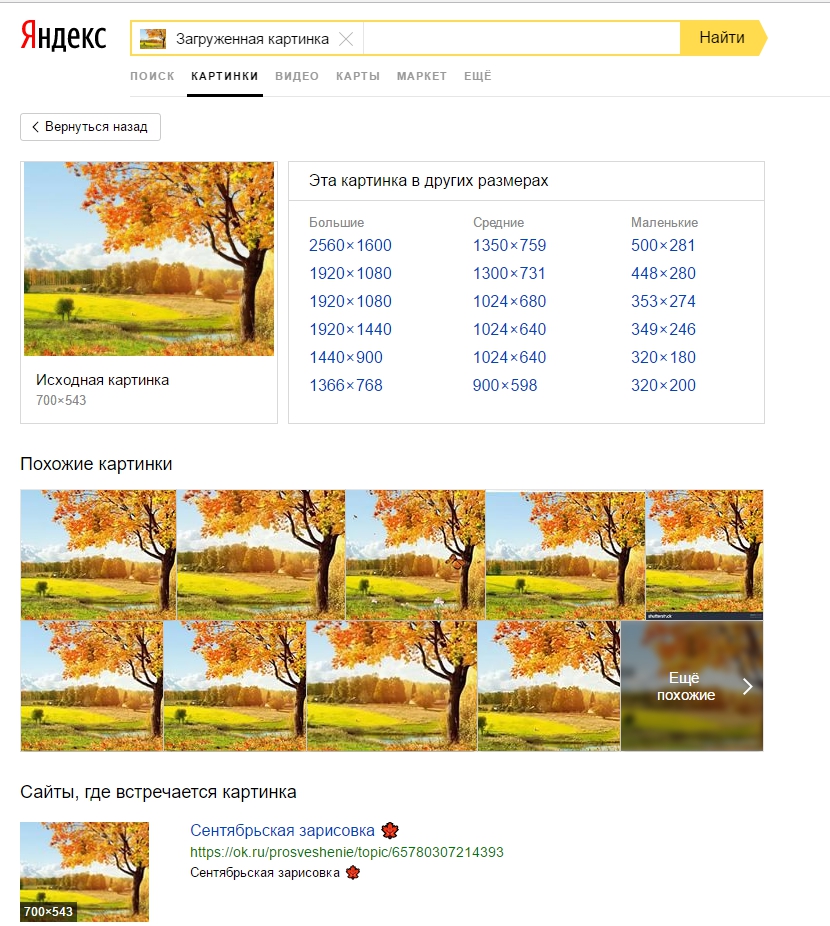
1. Используем сервис Яндекс Картинки.
- Переходим по ссылке: yandex.ru/images/
- В правом верхнем углу нажимаем на иконку фотоаппарата с лупой.
Выбираем файл на компьютере или вводим адрес картинки.
- Нажимаем «Найти» — и все готово.
Яндекс предложит нам все похожие картинки различных размеров. Нам остается только выбрать и скачать самую подходящую.
2. Используем сервис Google картинки
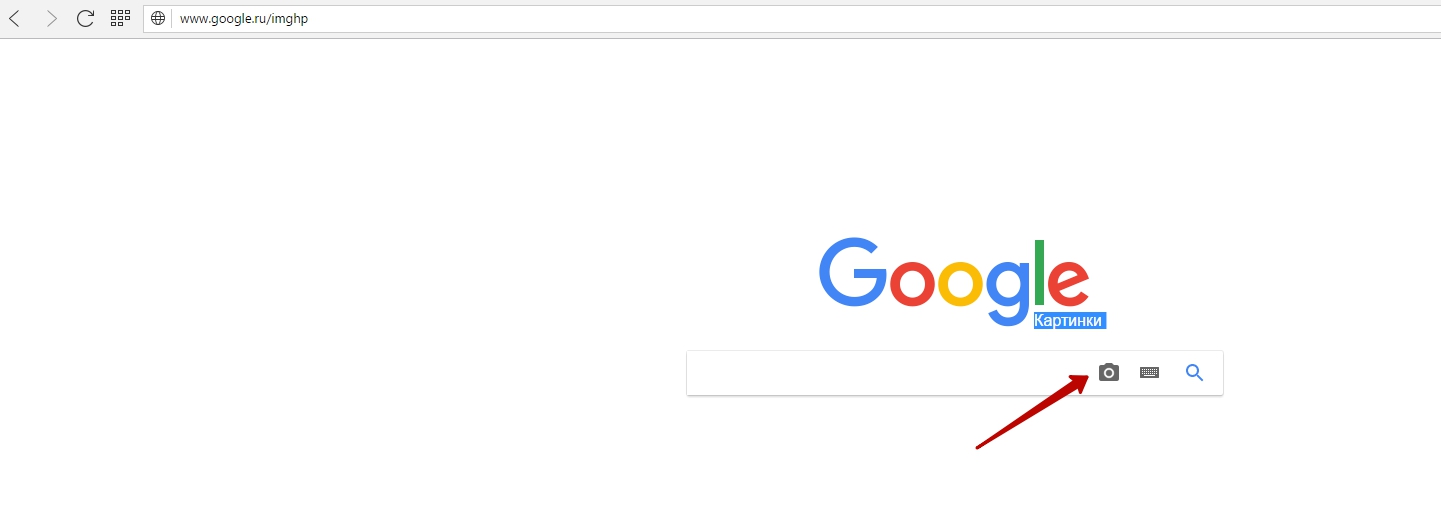
- Переходим по ссылке: www.google.ru/imghp
- Нажимаем на иконку фотоаппарата
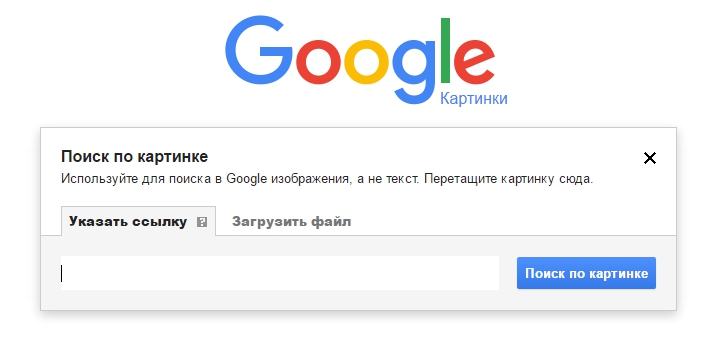
- Указываем ссылку на картинку или загружаем файл с компьютера
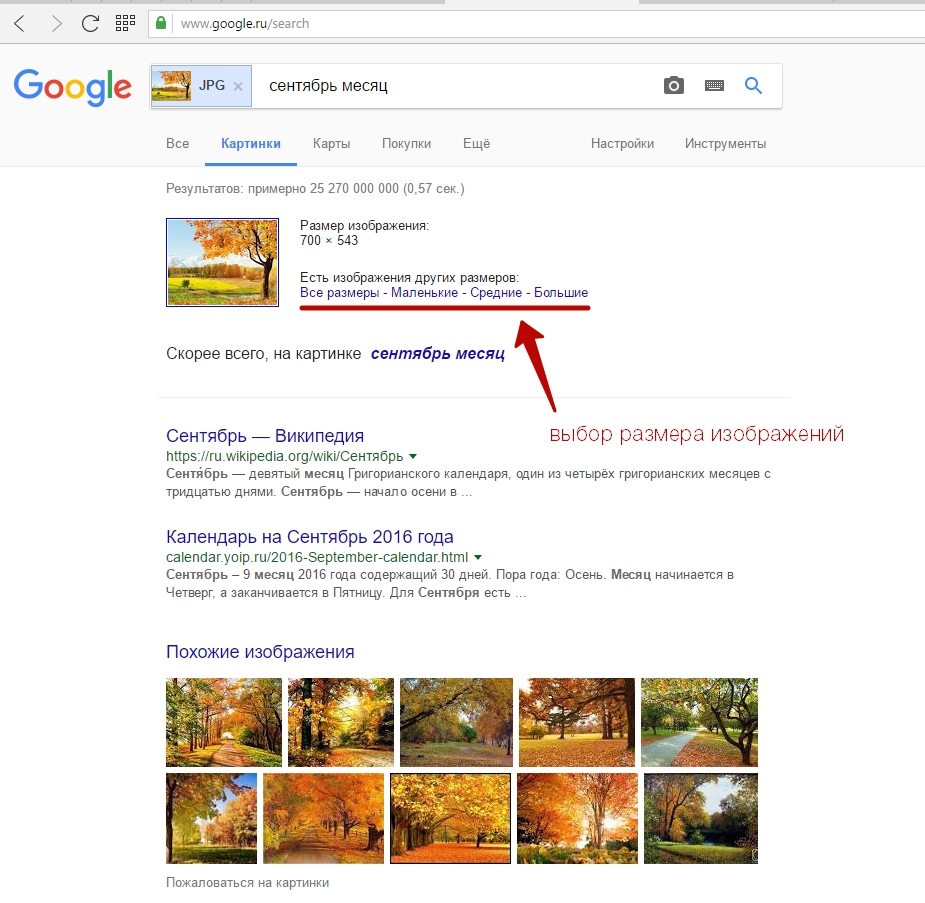
- Нажимаем «Поиск по картинке». Гугл предлагает нам различные варианты. Можно выбрать размеры картинок, которые будут нам наиболее интересны.
3. Способ. Сервис tineye.com
- Переходим на сервис www.tineye.com
- Загружаем картинку с компьютера или ссылку.
- Нажимаем найти.
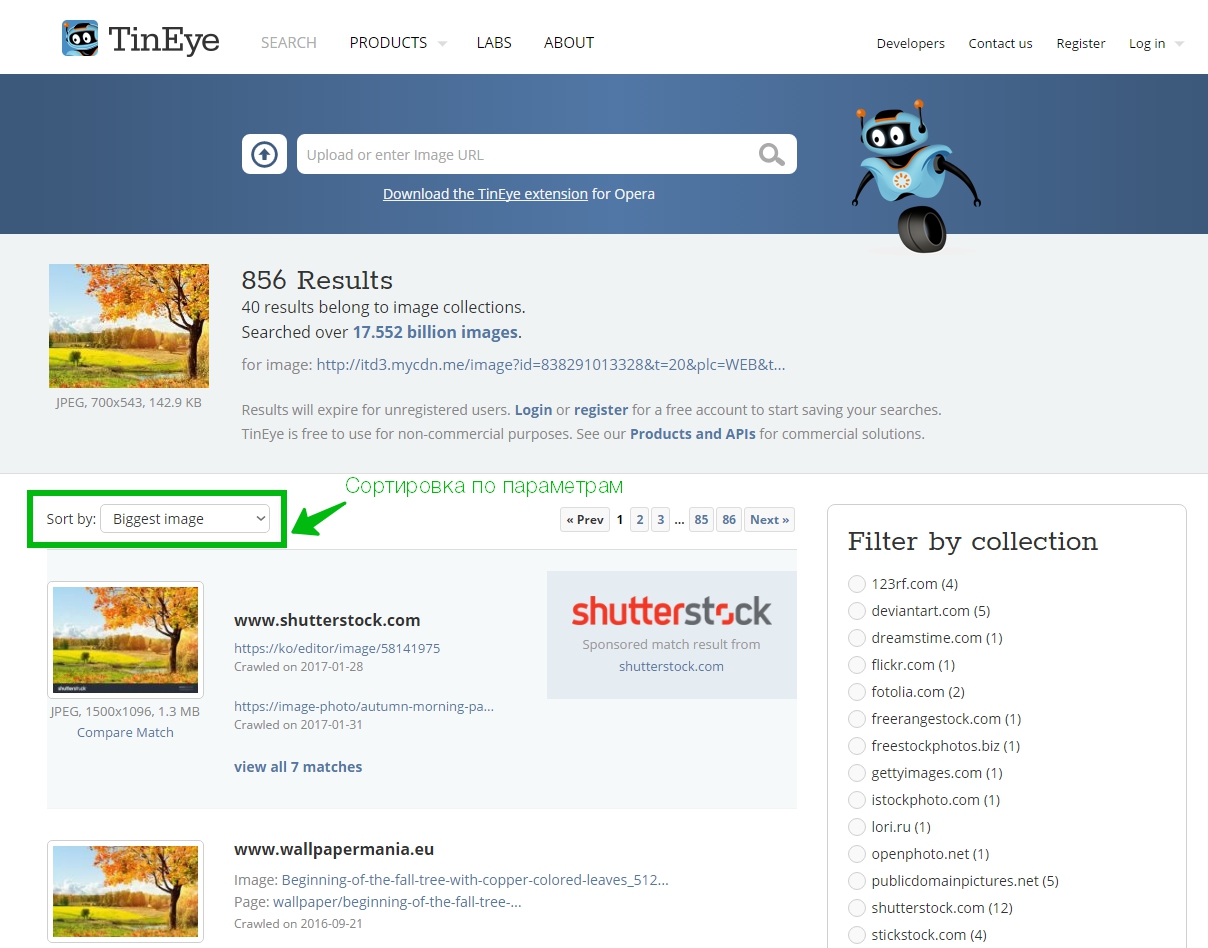
- Готово. Осталось только выбрать нужные настройки вывода результатов и выбрать подходящую нам картинку.
Вот такие нехитрые способы для поиска картинок лучшего качества.
Каждый из сервисов имеет свои алгоритмы поиска и вывода результатов поиска, поэтому если вас не устроят результаты одного из них, то обязательно попробуйте поиск через другие сервисы.
Бывает конечно, что найти лучшее фото не получается, но чем меньше результатов выдают данные поисковики по данной картинке, тем она уникальнее. А в некоторых случаях это тоже очень и очень хорошо.
По поиску данной картинки результаты получились такие: исходная картинка у нас была разрешением 700×543 пикселей, а мы нашли такую же картинку размером 3840×2400 пикселей. Думаю положительный результат очевиден и нам удалось найти изображение по картинке.
Спасибо за внимание. Если у вас есть какие либо вопросы, то задавайте их в комментариях, буду рад вам чем-нибудь помочь.
-
ВСЕ
-
Рисование
-
Советы художника
-
История искусств
-
Живопись
-
Рисунок
-
Цветоведение
-
Поэтапное рисование
-
Вдохновение
-
О художниках
-
Ученики
-
Композиция
-
Абстракция
-
Книги
Как проверить рисунок на ошибки? Как найти ошибки в рисунке?
15.03.2018 15:48
Бывало, в наших творческих буднях случалась такая история. Захожу я в большую комнату, где папа работал обычно над картиной, а он сидит метра за два от своего творения на любимом пуфике в позе роденовского мыслителя, а в глазах вся мировая скорбь.
– Вот, – говорит он, – вижу, что в работе что-то не так, а что именно – понять не могу. Может ты подскажешь.
Также и я просила папу помочь советом если, как говорят художники “глаз замылился” и уже совсем не видишь ошибок или неточностей, но знаешь определённо, что что-то тут не так. “Пальцы на левой руке коротковаты”, “Так у тебя дерево режет весь формат ровно пополам”, “этот цвет, по-моему, лишний здесь, он добавляет пестроты и мешает воспринимать картину целиком” – столько всего очевидного всплывает, если начать анализировать работу свежим взглядом. С подобной задачей сталкиваются все художники: от самых начинающих до профессионалов. Поэтому, давайте по-порядку исследуем основные способы диагностики “заболеваний” во время самостоятельной работы (в который раз напомню, что уроки рисунка и живописи с педагогом никто при этом не отменял!).
1) Не смотреть на рисунок какое-то время.
Очень часто профессиональные художники пишут сразу несколько картин, одновременно. Не в смысле, правой рукой – одну, а левой ногой – другую, конечно, а, например, одну начали, сделали первую прописку и оставили её на пару дней. А в это время дописываем последние мазки на другой картине, которая уже отдохнула от пристального внимания художника и тщательной прописки, просохла. На неё художник смотрит уже как будто на чужое творение, отвлекшись на другие задачи. Так становятся понятными многие вещи, появляются “слабые места” и недочёты. Свежий взгляд помогает увидеть то, чему не придал особого значения автор в пылу активного творческого горения. В некоторых случаях даже убирают картины и рисунки с глаз долой: лицом к стене, в папку, накрывают специальным покрывалом. Это можно наблюдать в фильмах о великих мастерах живописи. Ничего, пусть ваши работы постоят вот так, в углу, наказанными, зато будет над чем поработать после.
2) Повернуть рисунок вверх ногами.
Или положить на бок, но вниз головой лучше. Такой способ поиска ошибок часто применяют при обучении рисованию в художественной школе и профессиональной художественной студии. В перевёрнутом виде хорошо видны ошибки в перспективе, пропорциях, логике поворота и сокращения частей лица и тела, в компоновке. Человеческий глаз привыкает воспринимать реальность в определённом ракурсе и расслабляется. При изменении ракурса, нашему глазу снова приходится совершать необходимую работу, а мозгу – эту работу анализировать. Смена стандартного угла видения на нестандартный, расположение объектов в рисунке иным способом (например, в перевёрнутом виде) дают такую встряску, активизирующую аналитическую работу глаза и мозга.
3) Показать рисунок зеркалу.
Принцип такой же, как и при повороте рисунка вверх ногами, только отображение его меняется не по вертикали, а по горизонтали. Не так радикально, но не менее действенно.
4) Проверка замером соразмерности пропорций.
Не всегда все ошибки в рисунке видны на глаз, поэтому художники и пользуются разнообразными способами замера пропорций: от механического (подошёл и померил) до камеры обскура. Самый простой вариант – ещё, и ещё раз проверить соотношения, например, ширины к высоте предмета в натуре и у себя в рисунке, отследить разницу между большим и маленьким предметом в реале и в своей работе. Многие мои ученики, самые начинающие, нервничают и обижаются по поводу “непохожести” в портрете, а ведь всего дел-то – проверить лишний раз пропорции методом визирования. Чем точнее замеры, чем тщательнее сравнения и соотнесения реальных предметов с нарисованными, тем точнее рисунок. Не верите? Проверьте сами.
5) Уточнение частей друг относительно друга = сравнение.
Важно не только соотношение основных частей друг с другом и точное воспроизведение их в рисунке, но и правильная пропорция деталей по соотношению с основными формами. К примеру, основные пропорции чайника переданы в рисунке хорошо, а вот носик слишком большой или ручка слишком тонкая. И истинное положение вещей уже рушится. И рисунок не реалистичен. Даже мелочи стоит уделить должное внимание, чтобы изображение было правдивым, реалистичным.
6) Фотографирование рисунка.
Кое-какие ошибки становятся видны на фотографии, так как камера слегка обобщает изображение, удаляет некоторые полутона, обостряет главное. Сама я не всегда доверяю этому способу проверки на ошибки, но иногда он работает. Лучше использовать его вместе с некоторыми другими способами анализа правильности рисунка и соответствия его натурной точности. Особенно сильно фото привирает в передаче цветовых отношений. Будьте осторожны.
7) Конструктивная критика профи.
Если у вас есть знакомый профессиональный художник, а слово “профессиональный” подразумевает профильное образование не менее пяти лет и постоянную творческую деятельность, желательно и выставочную, можно обратиться за советом-подсказкой к нему. Обычно, художники-мастера с удовольствием отзываются на просьбу помочь, ведь они тоже когда-то были на вашем месте. Свежий взгляд + большой творческий и ученический опыт = грамотный многоходовый анализ вашей работы.
И, да, вам нужен именно профессиональный художник для этой цели, а не мама, муж, соседка или друг, которые так же далеки от изобразительной грамоты как лето от зимы. Иначе можно получить массу советов типа: “ Веточка на дальнем плане плохо прорисована”, “У мамы черты лица более красивые” или моё любимое – “Почему небо жёлтое? Оно же голубое!”
8) Диагональные линии, соединяющие ключевые точки.
Иногда этот метод я использую для обобщения построения и завершающего уточнения. Сам по себе он не работает, но хорошо ищет недочёты, например, вместе со способом механического замера пропорций или с методом визирования. Соединяя опорными линиями две точки, находящиеся в разных ключевых узлах рисунка, и соотнесение направления полученной диагонали с видимым направлением её в натуре с вашей точки зрения, можно обнаружить смещения или неточности, мешающие изобразительному правдоподобию. Этот метод также хорошо работает при рисовании по фото. Но, одно условие, не полагайтесь на него целиком и полностью: проверяйте рисунки ещё раз разными способами.
Рисунок ученика: Дмитрий Клюев. Курс”Техники рисунка”. Преподаватель: Екатерина Крюкова
9) Сверка контуров.
Сразу скажу, этот способ не имеет ничего общего с профессиональным рисованием. Лично я не одобряю подобный метод, хотя им очень часто пользуются художники-гиперреалисты и некоторые современные иллюстраторы. Это такое наложение реальных контуров объекта на рисунок и соотнесение их друг относительно друга. В некоторых случаях способ работает, например, при копировании или изображении один в один механически. Но, в большинстве своём, художники не копируют модель, как фотоаппарат, а усиливают главное, уменьшают второстепенное, отказываются от деталей, концентрируются на самом важном, создают художественный образ. Именно это отличает работу художника творца от ремесленника. Надеюсь, всё понятно.
Рисунок ученика: Кэри Майер. Курс”Техники рисунка”. Преподаватель: Екатерина Крюкова
10) Есть ошибки в рисунках, которые сложно исправить. Как вариант, почти невозможно исправить в процессе рисования огрехи компоновки или первоначально неудачно взятые пропорции, особенно когда большая часть рисунка уже проработана. В таких случаях, лучше отложить незавершённую работу и начать новую, аналогичную, с учётом предыдущего опыта. Неудавшийся рисунок – тоже работа, тоже результат, хоть и промежуточный. Это ваш творческий и ученический опыт, а значит, следующий рисунок будет точнее, лучше, убедительнее, реалистичнее.
Рисунок ученика. II Курс “Рисование с нуля до портрета на заказ”. Преподаватель: Екатерина Крюкова.
Применяйте эти способы, чтобы не чахнуть над рисунками, как Кощей над златом, в тщетной попытке отыскать “корень зла”. Ошибки в рисунках будут всегда – это нормально, а вот во время увидеть их и исправить – одна из основ деятельности художника. Точного вам глазомера и твёрдой руки, а всё остальное будет!
-
Назад -
Вперед
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
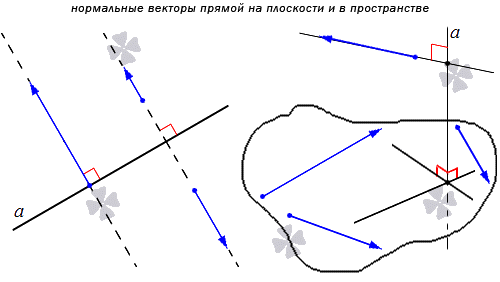
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y – 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y – 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y – 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 – y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 – y = 1 к уравнению общего вида. Тогда получим, что x 1 3 – y = 1 ⇔ 3 · x – 1 · y – 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , – 1 .
Ответ: 3 , – 1 .
Если прямая определена каноническим уравнением прямой на плоскости x – x 1 a x = y – y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x – x 1 a x = y – y 1 a y ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x – 2 7 = y + 3 – 2 .
Из прямой x – 2 7 = y + 3 – 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , – 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , – 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , – 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x – 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 – 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x – 2 7 = y + 3 – 2 ⇔ 7 · ( y + 3 ) = – 2 · ( x – 2 ) ⇔ 2 x + 7 y – 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 – 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 – 3 · λ ⇔ x = 1 + 0 · λ y = 2 – 3 · λ ⇔ λ = x – 1 0 λ = y – 2 – 3 ⇔ x – 1 0 = y – 2 – 3 ⇔ ⇔ – 3 · ( x – 1 ) = 0 · ( y – 2 ) ⇔ – 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны – 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x – x 1 a x = y – y 1 a y = z – z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
Вектор нормали: расчет и пример
Содержание:
В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.
Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:
Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.
Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.
Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.
Как получить вектор нормали к плоскости?
Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.
Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:
К этой плоскости есть два нормальных вектора: п1 Y п2. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:
ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.
Ну, нормальный вектор к указанной плоскости задается следующим образом:
N = а я + b j + c k
Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.
Вектор нормали из векторного произведения
Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.
Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.
Когда у вас есть векторы, векторный продуктили Икс v – операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.
Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:
N = или Икс v
На следующем рисунке показана описанная процедура:
пример
Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).
Решение
Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.
Вектор AB – вектор, начало которого – точка A, а конец – точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:
AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k
Таким же образом поступаем и находим вектор AC:
AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k
Расчет векторного произведения AB x AC
Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:
Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:
я Икс я = 0; j Икс j = 0; k Икс k = 0
А поскольку векторное произведение – это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:
я Икс j = k ; j Икс k = я; k Икс я = j
Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):
j Икс я = – k; k Икс j = –я; я Икс k = –j
Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.
AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k
Уравнение плоскости
Вектор N был определен с помощью предварительно рассчитанного векторного произведения:
N = 2я -8j-2k
Следовательно, a = 2, b = -8, c = -2, искомая плоскость:
ах + по + cz + d = 0 → 2x-8y-2z + d = 0
Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:
2,4 – 8,2 – 2,1 + d = 0
Вкратце, искомая карта:
Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.
Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.
Ссылки
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
- Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
- Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
- Линии и плоскости в R 3. Получено с: math.harvard.edu.
- Нормальный вектор. Получено с сайта mathworld.wolfram.com.
Выбор темы исследования: как это делается, важность, примеры
[spoiler title=”источники:”]
http://mathter.pro/angem/2_2_5_normalnyi_vektor_pryamoy.html
http://ru1.warbletoncouncil.org/vector-normal-6378
[/spoiler]
Перевод публикуется с сокращениями, автор оригинальной
статьи Anusha Saive.
Вы можете легко вывести свой проект или маркетинговую кампанию на новый уровень с помощью правильных изображений. Если знать, как использовать правильные фильтры для сортировки и ключевые слова, нетрудно получить изображение для любой цели.
Далеко не каждая
поисковая система предоставит вам лучшие изображения. Приступим к
рассмотрению.
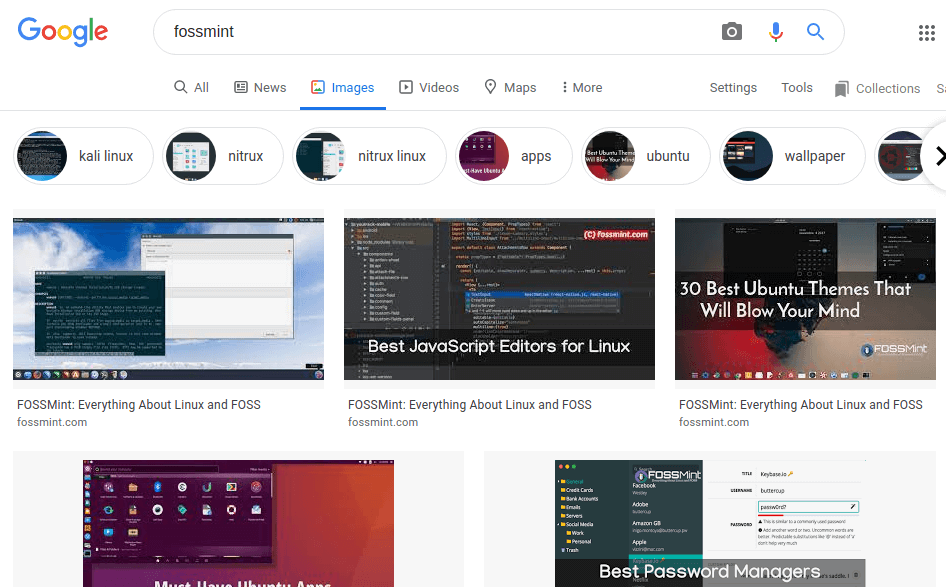
1. TinEye
TinEye – инструмент для поиска похожих на
оригинал изображений, требующий, чтобы вы либо ввели URL, либо загрузили картинку, чтобы узнать, откуда она появилась. Эта поисковая система проста в
использовании и отличается дружественным интерфейсом.
Можно также использовать расширение браузера TinEye для быстрого поиска: нажмите правой кнопкой мыши на любое изображение и найдите его.
2. Google Images
Никто не опережает Google Images,
когда дело доходит до поиска изображений. Все, что вам нужно сделать – ввести ключевое слово и нажать «Enter». Для более
детального поиска предлагаются определенные фильтры, предоставляющие широкий
выбор связанных изображений. Этот удобный инструмент дает именно то, что вам
необходимо.
Вы можете выбрать из
большого списка фильтров, представляющих изображения в виде клипарта,
мультфильма, иллюстраций и т. д. Фильтрация позволяет выбрать цвет,
размер, тематику и другую подобную информацию. Чтобы воспользоваться этим
инструментом, найдите значок камеры в поле поиска и нажмите на него.
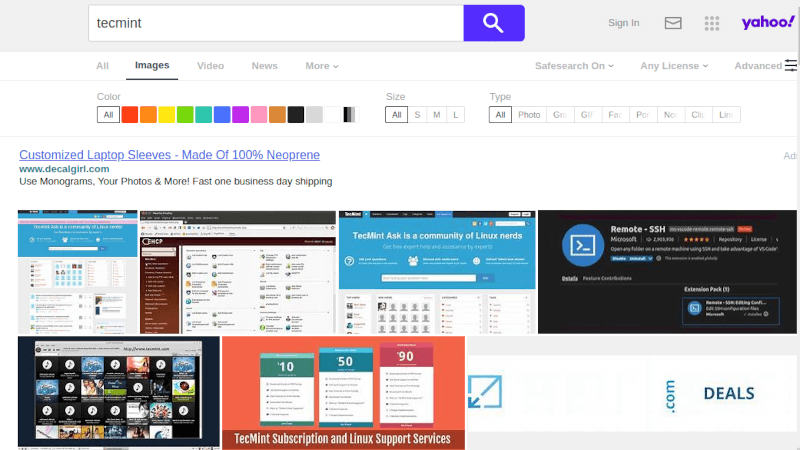
3. Yahoo Image Search
Yahoo Image Search – еще один удобный вариант для поиска изображений. Он похож на Google Images и дает отличные результаты. В этом продукте
фильтры менее сложны, но удобно расположены и находятся на виду.
4. Picsearch
Если хотите получить более разнообразные результаты по введенному ключевому слову, попробуйте Picsearch.
Эта поисковая система не показывает массу конкретных
результатов, как некоторые другие поисковики, но демонстрирует связанные
изображения по ключевому слову.
Расширенные опции поиска позволяют фильтровать
результаты по размеру, разрешению картинки, заднему фону и т. д.
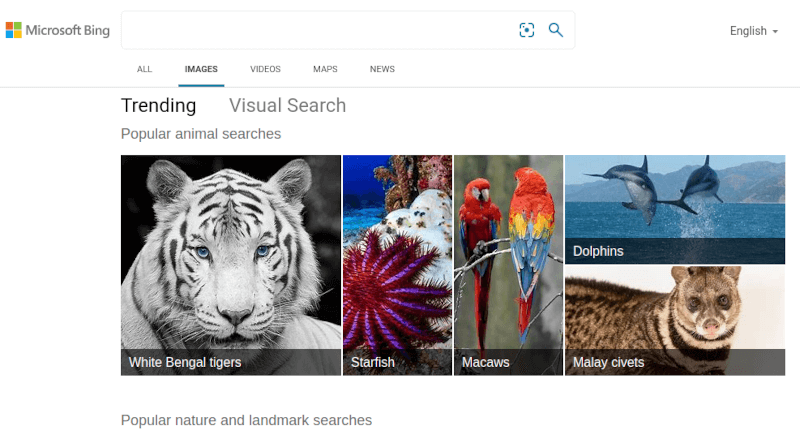
5. Bing Image Search
Bing IS является лучшей альтернативой Google Images,
поскольку выдает довольно похожие результаты. С точки зрения макета он также
довольно близок к сервису Google и обладает невероятными функциями для поиска людей,
используя параметры лица, головы и плеч.
Доступны многочисленные опции поиска и фильтры.
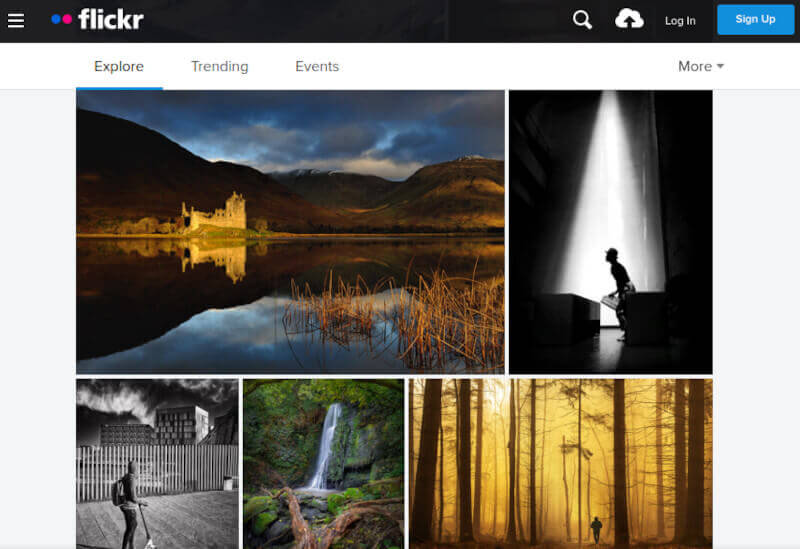
6. Flickr
Flickr работает несколько
иначе. Это своего рода платформа, где фотографы-любители и профессионалы делятся изображениями. В случае, если вы
находитесь на Flickr для поиска картинок на маркетинговую, брендовую или
коммерческую тематику, обязательно изучите лицензию.
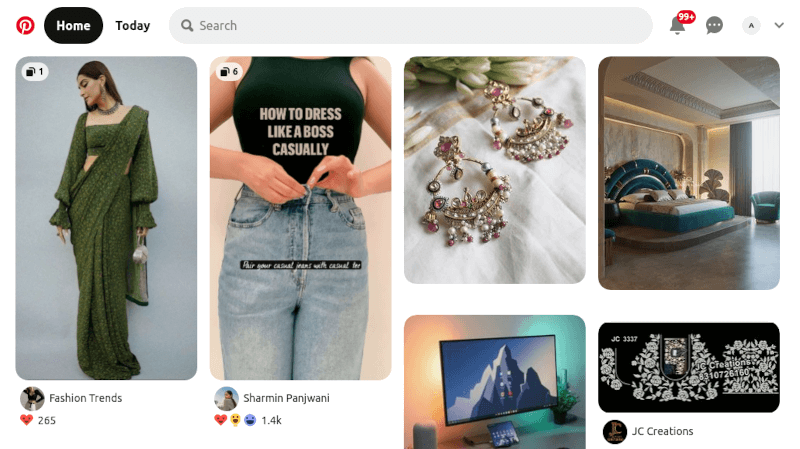
7. Pinterest Visual Search Tool
Pinterest давно всем знаком и многие жить без него не
могут из-за некоторых особенностей инструмента. Одна из них – встроенный
визуальный поиск. Чтобы получить доступ к этой платформе, вам нужно войти в
свою учетку, нажать на любой появившийся в ленте пин,
а затем щелкнуть по значку в правом нижнем углу, связанному с закрепленными в
системе изображениями.
Эта поисковая машина
имеет обширную базу данных и дает лучшие результаты,
соответствующие искомому изображению.
8. Getty Images
Getty
Images выполняет поиск по ключевым словам и по
изображению. Для поиска по ключевым словам существует
несколько вариантов с функциями автоматического предложения. Ресурс предлагает набор фильтров, гарантирующих, что вы получите именно то, что
ищете.
Сервис предоставляет
изображения в двух вариантах: творческие и редакционные, а также видео. Вам
придется заплатить за лицензию, чтобы использовать любую фотографию (ее можно купить в пакетах или поштучно с фиксированной ценой).
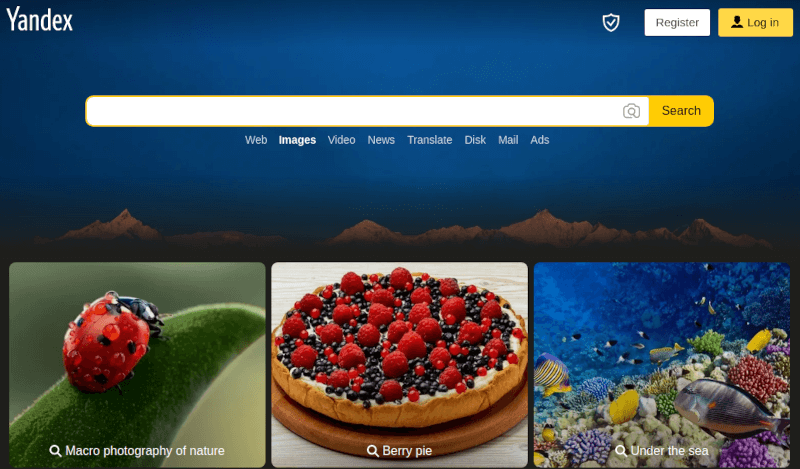
9. Яндекс
Яндекс позволяет искать изображения с помощью широкого
спектра фильтров и параметров сортировки по формату, ориентации,
размеру и т. д. Также доступен еще один
инструмент поиска, называемый «Похожие изображения».
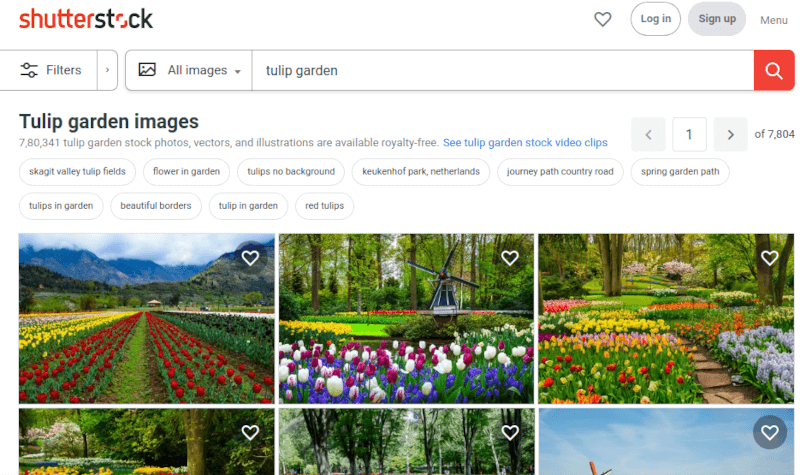
10. Shutterstock
Ищете бюджетный вариант с хорошим ассортиментом? Shutterstock – то что нужно. Он отобрал пальму первенства у Getty Images с помощью огромной
библиотеки изображений.
Ресурс позволяет
выполнять поиск изображений любым удобным для вас способом. Ежемесячные и
годовые тарифные планы предполагают варианты с предоплатой или с оплатой после покупки.
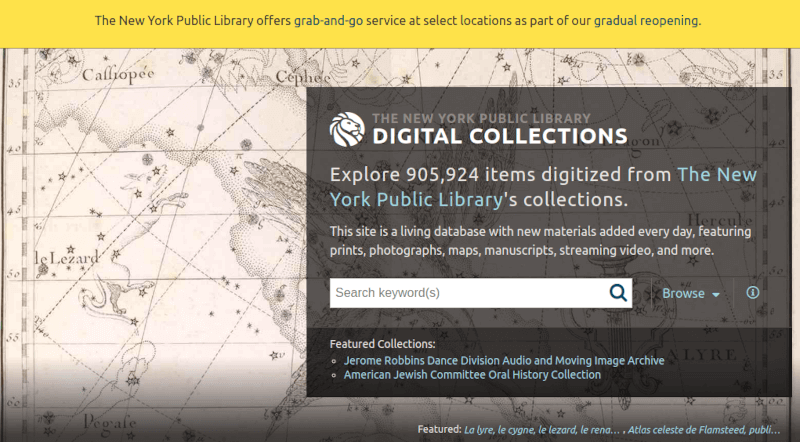
11. The New York Public Library Digital Collections
Последний, но не худший
источник. Если вам нужны изображения с высоким разрешением, относящиеся к
исторической эпохе, картам, книгам, бухгалтерской тематике, фотографии и т. д.,
не забудьте поискать в The New York Public Library! Огромный архив изображений – общественное достояние.
Этот инструмент поиска
исторических изображений позволяет уточнить условия, выбрав
результат в зависимости от жанра, коллекции, места, темы, издателя и т.д.
Дополнительные материалы:
- 10 лучших альтернатив YouTube, которые стоит попробовать в 2021 году
Источники
- https://www.fossmint.com/image-search-engines/
Оглавление:
-
Наиболее часто применяемые параметры для поиска изображений
-
Поиск картинок в Google
-
Открываем поиск изображений
-
Поиск изображений в Google по разным параметрам
-
Прозрачные изображения (без фона) или с выбранным цветом
-
Изображения определённого размера
-
Изображения с определёнными авторскими правами
-
-
-
Поиск картинок в Яндекс
-
Открываем поиск изображений
-
Поиск изображений в Яндекс по разным параметрам
-
Изображения без фона («прозрачные») и с выбранным цветовым оттенком
-
Изображения нужного размера
-
-
-
Заключение
Очень часто для разных целей требуется найти в интернете изображения на определённую тему и подходящие по каким-либо другим критериям, например: с прозрачным фоном (чтобы потом не вырезать); определённого размера; с правами на использование, изменение.
Подходящие изображения в интернете может потребоваться найти, например, для создания тизера к своим статьям на блоге, к новостям на сайте, к своим видео для канала в Youtube, а также для многих других задач. Потому что если нет своих подходящих фотографий, созданных вручную картинок, скриншотов, то остаётся только искать в интернете. И искать картинки в интернете ещё нужно уметь!
Поиск изображений в интернете отличается от обычного поиска по сайтам в Google и Яндекс, которым владеет подавляющее большинство. Каждому нужно найти какую-то информацию в интернете, бороздя различные сайты, а кому-то нужно найти товар для покупки или что-то ещё. Для этого пользуются обычным поиском по сайтам, как правило. А вот отдельно именно картинки ищут далеко не все и знаю, не все умеют их искать 🙂
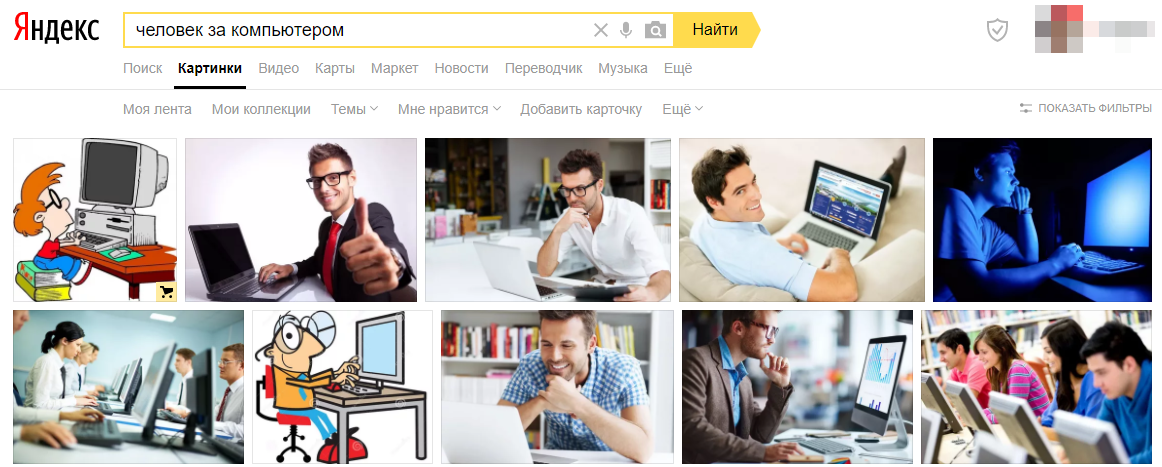
Изображения нужно искать через специальный поиск по картинкам в Google или Яндекс, вводя в поисковый запрос то, что хотели бы увидеть на картинке. Например, хотите найти картинку, где изображён человек, сидящий за компьютером, значит, вводите поисковый запрос “человек за компьютером” или аналогичный. Часто, чтобы найти хорошо подходящее изображение, нужно попробовать разные поисковые запросы.
Пробуйте обе поисковые системы. Если не можете найти какое-то изображение, например, в Google, то попробуйте поискать в Яндекс и наоборот. Результаты поиска по аналогичным запросам могут отличаться.
Наиболее часто применяемые параметры для поиска изображений
-
Поиск «прозрачных» изображений (без фона). Часто может потребоваться найти изображение без фона на заднем плане, чтобы его можно было вставить, например, поверх какого-то готового фона или картинки, не отрезая при этом фон вручную. Обрезка фона отнимет время, а для кого-то станет весьма непростой задачей. Для некоторых изображений — это действительно сложная задача.Пример “прозрачного” изображения (без фона):
Пример изображения с фоном:
Соответственно, если вы захотите такое изображение, как во втором примере (с фоном) наложить на какое-то другое, то придётся сначала его вырезать из фона. А в первом случае, ничего вырезать не потребуется, изображение изначально без фона.
Если вам нужно найти изображения именно без фона, то проще всего это сделать через поиск Google, поскольку там есть специальный поисковый фильтр для этого.
-
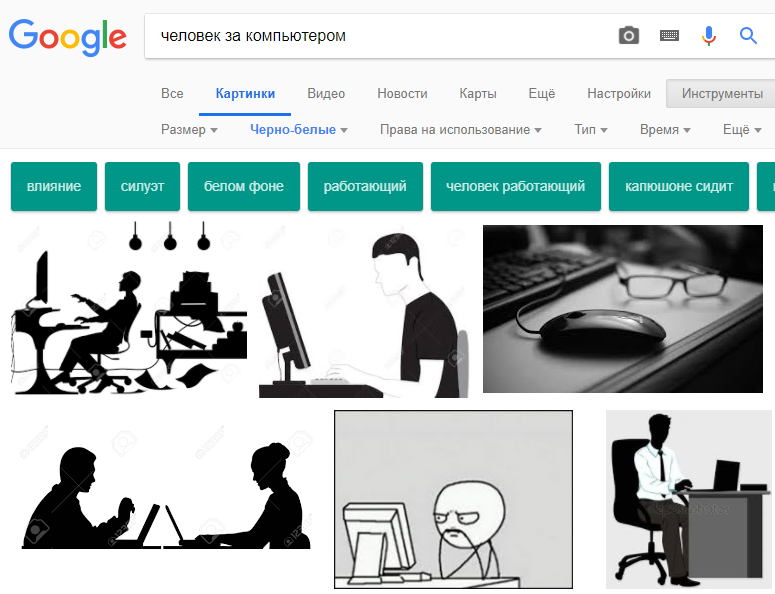
Поиск изображений определённых цветов. Через поисковики вы можете искать картинки определённого цвета или цветовых тонов, например: только чёрно-белые, только в синих тонах (или в любых других); любого цвета; только цветные. Пример. Поиск черно-белых изображений:
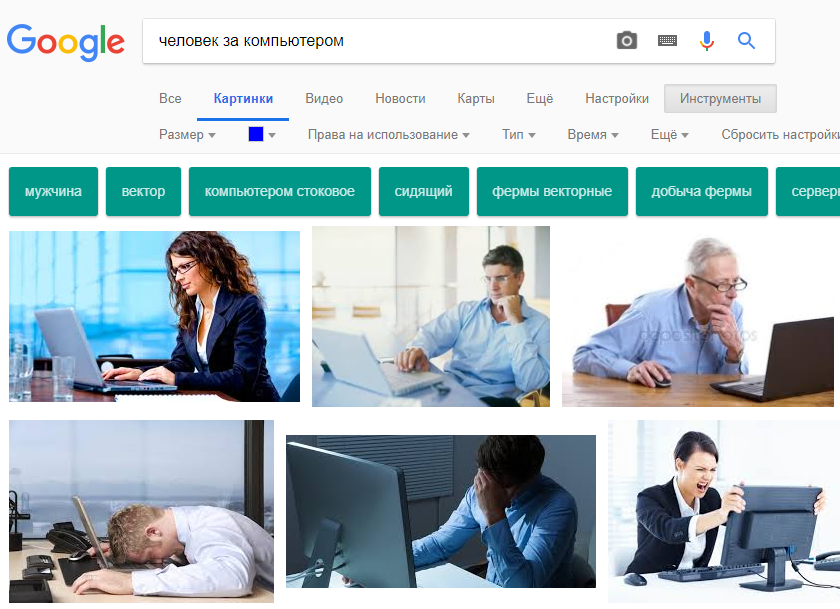
Пример. Поиск изображений с синеватым оттенком:
-
Определённого размера. Вы можете настроить поиск так, чтобы искать изображения точно указанного размера либо более широком диапазоне: большие, средние, маленькие или которые больше / меньше указанного размера.
-
С определёнными правами на использование. Например, хотите найти картинки, которые разрешено использовать на других сайтах (с лицензией на использование) или картинки, которые можно также изменять (с лицензией на использование и изменение). Такое может пригодиться, если вы, например, хотите найти картинку для использования на своём сайте, без нарушения чьих-то прав на это изображение.
Такой фильтр поиска доступен на данный момент только в Google.
Ниже рассмотрим как искать изображения по перечисленным выше параметрам в Google и Яндекс.
Поиск картинок в Google
В Google искать картинки чаще всего удобнее чем в Яндекс. Например, именно в Google можно выполнить поиск изображений без фона, потому что в Яндекс такой функции пока что нет, а может и не будет. Там есть лишь похожая функция, но которая работает не так качественно как в Google.
Открываем поиск изображений
Нужно открыть обычный поиск https://www.google.ru/ , после чего переходим в раздел “Картинки”.
Как обычно, вводим поисковый запрос, например:
И из появившегося списка изображений подбираем нужное.
Можно, открыв поиск, сразу ввести поисковый запрос. А уже после выдачи результатов перейти в “Картинки”. Разницы нет.
Поиск изображений в Google по разным параметрам
Прозрачные изображения (без фона) или с выбранным цветом
Под строкой поиска Google нужно открыть раздел “Инструменты” [1], выбрать “Цвет” [2] и нужный вариант, например, “Прозрачные” [3].
В этом случае картинки в поисковой выдаче сразу будут отфильтрованы и останутся только те, что с прозрачным фоном.
Если хотите найти картинки, например, только чёрно-белые, то выбираете соответствующий вариант. Аналогично и с поиском изображений других цветов.
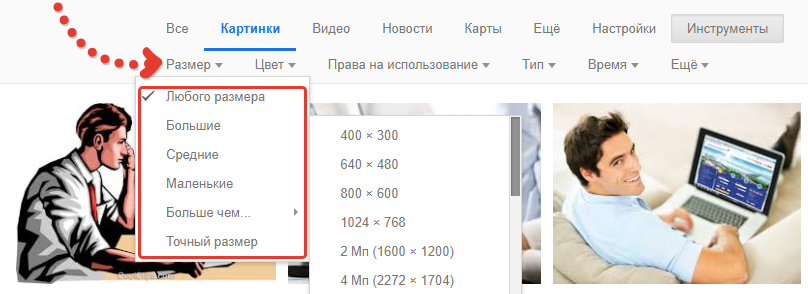
Изображения определённого размера
В разделе «Инструменты» под строкой поиска выберите «Размер». Из появившегося списка выберите один из готовых вариантов поиска, например, большие / средние / маленькие или можно настроить поиск так, чтобы подбирал изображения больше выбранного размера (пункт «больше чем» и укажите минимальный размер).
А если нужно найти изображения прямо определённого размера, то выберите пункт «Точный размер» и укажите значения ширины и высоты.
Помните, что чем точнее указываете размер, тем меньше результатов вам выдаст поиск. Это относится и ко всем остальным фильтрам поиска: чем тоньше настраиваете фильтры, тем меньше результатов выдаст поиск.
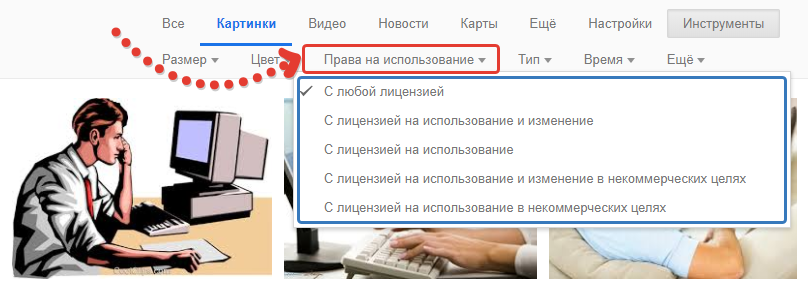
Изображения с определёнными авторскими правами
В разделе «Инструменты» выберите «Права на использование» и далее отметьте, изображения с какими авторскими правами вы хотите увидеть в результатах поиска.
Например, если хотите, чтобы отобразились только изображения с правами на использование, то и выбираете соответствующий пункт «С лицензией на использование». Такой вариант имеет место, если вы, к примеру, хотите разместить на своём блоге чужую фотографию и не беспокоиться по поводу того, что нарушили чьи-то права, ведь фотография с лицензией на использование.
Поиск картинок в Яндекс
Поиск изображений в Яндекс тоже со счетов сбрасывать нельзя. Он тоже хорошо ищет, но имеет свои нюансы и, на мой взгляд, недостатков в нём больше, по сравнению с Google. Так или иначе, в Яндекс вы сможете увидеть по одним и тем же запросам картинки, которые не видели через Google.
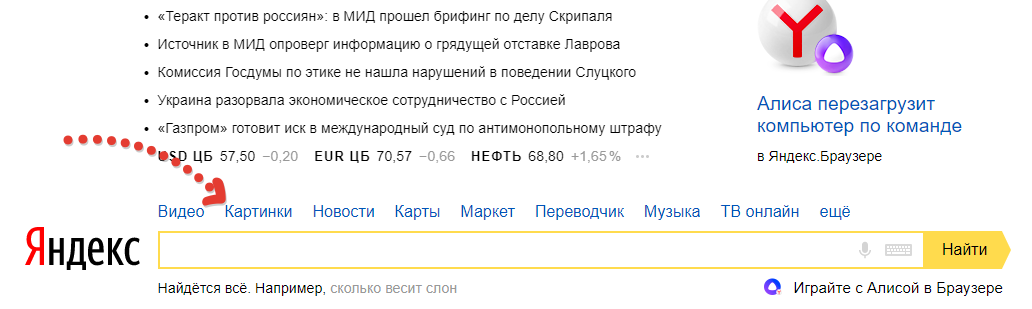
Открываем поиск изображений
Открываем стандартный поиск Яндекса и переходим в раздел поиска “Картинки”.
Остаётся ввести нужный поисковый запрос и выбрать подходящую картинку.
А можете сначала выполнить поиск, а потом уже перейти в раздел «Картинки».
Поиск изображений в Яндекс по разным параметрам
Изображения без фона («прозрачные») и с выбранным цветовым оттенком
Специального поискового фильтра, чтобы отсеять все картинки, кроме тех, что без фона, в поиске Яндекса нет. Но можно настроить поиск только по картинкам в формате PNG. Именно этот формат поддерживает прозрачность, а значит в поиске будут чаще встречаться изображения без фона.
Чтобы настроить поиск по картинкам формата PNG, под строкой поиска нужно нажать “Показать фильтры”.
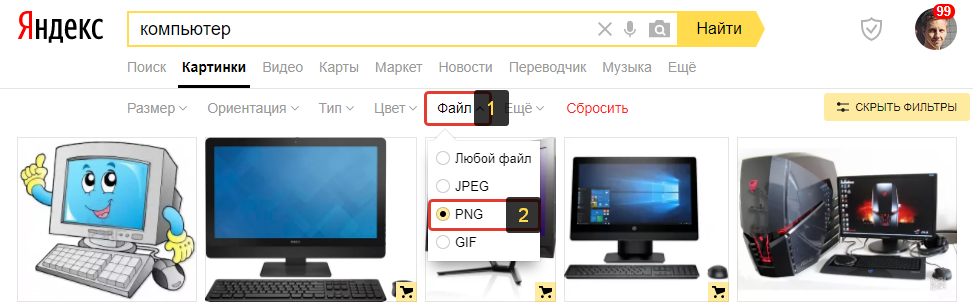
Затем выбираем фильтр “Файл” [1] и отмечаем “PNG” [2].
Всё, картинки отфильтруются и в результатах поиска будут отображаться только те, что в формате PNG, а из них будет много встречаться с прозрачным фоном.
Повторюсь, для поиска именно картинок без фона проще пользоваться поиском от Google.
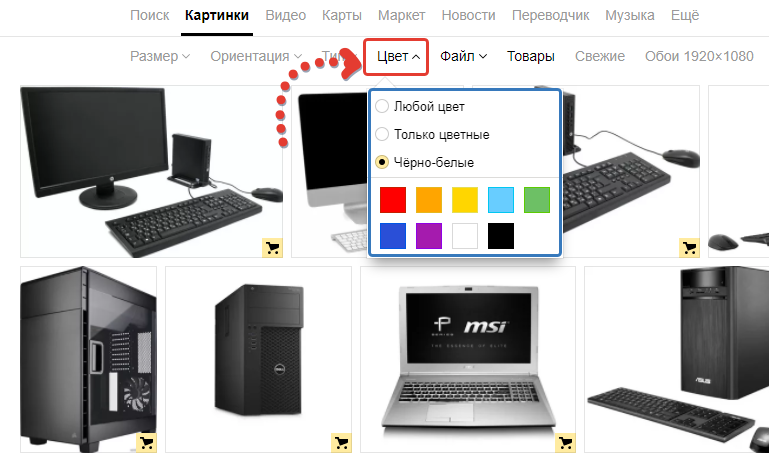
Если нужно найти картинки, где преобладает определённый цвет, то в фильтрах нужно открыть раздел «Цвет» и выбрать нужный цвет. Например, «черно-белые»:
Изображения нужного размера
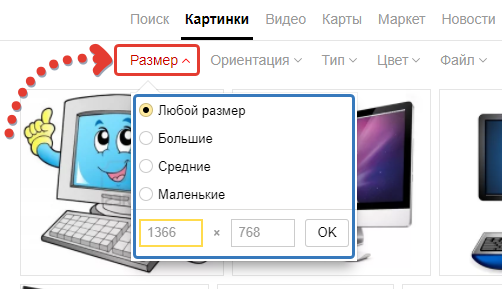
Если нужно в Яндексе найти картинки каких-то определённых размеров, то в фильтрах поиска выбираем «Размер» и либо внизу указываем точный размер по ширине и высоте, либо выбираем более широкие диапазоны фильтра: большие, средние или маленькие изображения.
Заключение
Найти нужную картинку в интернете под тот или иной случай — задача совсем несложная, если, конечно, требования ваши не слишком высоки. А то, порой, можно очень долго искать подходящее изображение или вовсе его не найти, потому что просто может не быть такой картинки, которая вам нужна по теме, с нужными размерами, фоном и правами на использование / изменение.
Но, пользуясь поиском Google и Яндекс по картинкам, чаще всего можно найти максимально подходящее изображение, если правильно искать!
А вы часто ищите для каких-либо целей изображения в интернете по определённым критериям? Буду рад любой обратной связи, с вопросами, предложениями и простыми комментариями к статье! 🙂