Как найти нормальный вектор плоскости по уравнению



5.2.3. Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.

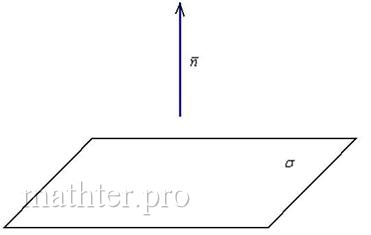
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением  в прямоугольной (!) системе координат, то вектор  является нормальным вектором данной плоскости.

Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:

Задача 134

Найти единичный нормальный вектор плоскости .

Решение: принципиально ситуация выглядит так:

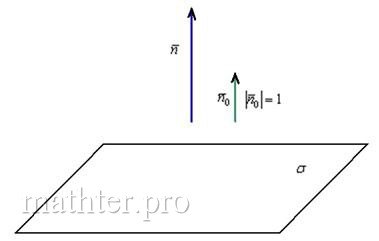
Сначала из уравнения плоскости «снимем» вектор нормали: .

И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора  разделить на длину вектора .

Вычислим длину вектора нормали:

Таким образом:

Контроль: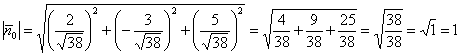, ОК

Ответ:

Вспоминаем, что координаты этого вектора  – есть в точности направляющие косинусы вектора : .

И, как говорится, обещанного три страницы ждут 🙂  – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке  и двум векторам , и в результате решения мы получили уравнение .

Проверяем:

Во-первых, подставим координаты точки  в полученное уравнение:

 – получено верное равенство, значит, точка  лежит в данной плоскости.

На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы  параллельны плоскости, а вектор  ей перпендикулярен, то должны иметь место следующие факты: . Ортогональность векторов элементарно проверяется с помощью скалярного произведения:

Вывод: уравнение плоскости найдено правильно.

В ходе проверки я фактически процитировал следующее утверждение теории: вектор  параллелен плоскости  в том и только том случае, когда .

Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:

5.2.4. Как составить уравнение плоскости по точке и вектору нормали?

5.2.2. Как составить уравнение плоскости по трём точкам?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Нормальный вектор плоскости – наиболее компактный и наглядный способ определить плоскость в трехмерной системе координат.

Для каждой плоскости существует бесконечное множество коллинеарных друг по отношению к другу нормальных векторов.

В качестве примера плоскостей, задаваемых нормальными векторами, можно рассматривать координатные плоскости системы координат $Oxyz$: $Oxy$, $Oxz$, $Oyz$. Для них нормальными векторами будут, векторы, направляющие оси, т.е., соответственно, $Oz$, $Oy$ и $Ox$ ($vec{k}, vec{j}, vec{i}$).

Рассмотрим основные математические закономерности, показываюшие как найти вектор нормали к плоскости.

Формула нормального вектора выводится из общего уравнения плоскости, которое имеет вид $Ax + By + Cz + D = 0$.

Плоскости, в уравнениях которых один из коэффициентов равен $0$, соответствуют базовым плоскостям системы координат ($Oxy, Oxz, Oyz$).

Уравнения вида

$Ax + D = 0 \ By + D = 0 \ Cz + D = 0$

описывают плоскости, параллельные $Oxy, Oxz, Oyz$ и отстоящие от них на расстояние, равное отношению свободного члена $D$ к соответствующему коэффициенту, например:

$x = frac{D}{A}$

Нормальный вектор плоскости $Ax + By + Cz + D = 0$ можно выразить как $bar{n}(A; B; C)$. Существует бесконечное множество плоскостей, перпендикулярных данному вектору. Для определения плоскости нужна еще точка на ней. Через любую точку также можно провести бесконечное количество плоскостей (их совокупность называется связкой). Нормальный вектор и точка взаимодополняют друг друга, определяя единственную плоскость.

«Нормальный вектор плоскости» 👇

Точку на плоскости можно обозначить как $M_1(x; y; z)$. Вектор, соединяющий ее с любой другой точкой $M$ данной плоскости, при скалярном умножении на вектор нормали к плоскости $N$ дает ноль:

$overline{M_1M} cdot N = 0$

Переписав уравнение через проекции, получим

$overline{M_1M} cdot N = A(x – x_1) + B(y – y_1) + C(z – z_1) = 0$

Это дает нам возможность выводить уравнение плоскости через координаты точки и параметры нормального вектора плоскости.

С помощью нормального вектора плоскости как ее определителя могут быть решены задачи на доказательство параллельности или перпендикулярности плоскостей, на составление уравнения плоскости, на нахождение угла между прямой и плоскостью, на нахождение угла между плоскостями.

Как найти нормальный вектор к плоскости

Нормальным вектором плоскости (или нормалью плоскости) называют вектор, перпендикулярный данной плоскости. Одним из способов задать плоскость является указание координат ее нормали и точки, лежащей на плоскости. Если плоскость задана уравнением Ax+By+Cz+D=0, то нормальным к ней является вектор с координатами (A;B;C). В других случаях для вычисления нормального вектора придется потрудиться.

Инструкция

Пусть плоскость задана тремя принадлежащими ей точками K(xk;yk;zk), M(xm;ym;zm), P(xp;yp;zp). Чтобы найти нормальный вектор, составим уравнение этой плоскости. Обозначьте произвольную точку, лежащую на плоскости, буквой L, пусть у нее будут координаты (x;y;z). Теперь рассмотрите три вектора PK, PM и PL, они лежат на одной плоскости (компланарны), поэтому их смешанное произведение равно нулю.

Найдите координаты векторов PK, PM и PL:
PK = (xk-xp;yk-yp;zk-zp)
PM = (xm-xp;ym-yp;zm-zp)
PL = (x-xp;y-yp;z-zp)
Смешанное произведение этих векторов будет равно определителю, представленному на рисунке. Этот определитель следует вычислить, чтобы найти уравнение для плоскости. Вычисление смешанного произведения для конкретного случая смотрите в примере.

Пример
Пусть плоскость задана тремя точками K(2;1;-2), M(0;0;-1) и P(1;8;1). Требуется найти нормальный вектор плоскости.
Возьмите произвольную точку L с координатами (x;y;z). Вычислите векторы PK, PM и PL:
PK = (2-1;1-8;-2-1) = (1;-7;-3)
PM = (0-1;0-8;-1-1) = (-1;-8;-2)
PL = (x-1;y-8;z-1)
Составьте определитель для смешанного произведения векторов (он на рисунке).

Теперь разложите определитель по первой строке, а затем подсчитайте значения определителей размера 2 на 2.
Таким образом уравнение плоскости -10x + 5y – 15z – 15 = 0 или, что то же, -2x + y – 3z – 3 = 0. Отсюда легко определить вектор нормали к плоскости: n = (-2;1;-3).

Источники:

• Уравнение плоскости, проходящей через три точки

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.

Общее уравнение плоскости принимает вид:

Общее уравнение плоскости

Ax+By+Cz+D=0Ax+By+Cz+D=0,

где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.

Здесь будет калькулятор

Составление уравнения плоскости по трем точкам

Текст цитаты

Заголовок

Текст цитаты

В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:

Уравнение плоскости через определитель

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,

где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.

Задача 1

Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).

Решение

Пусть:

x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0

Составляем определитель:

∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0

∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0

∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0

28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.

Ответ

28x−8y−22z−4=028x-8y-22z-4=0

Уравнение плоскости по точке и вектору нормали

Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:

Уравнение плоскости по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.

Задача 2

Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).

Решение

x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5

(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0

(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0

x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0

x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.

Проверка

Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:

8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0

0=00=0 — верно, значит ответ правильный.

Ответ

x+3y+5z−47=0x+3y+5z-47=0

1. Основные понятия.

Рассмотрим
прямоугольную систему координат Oxyz
в пространстве.

Уравнением
поверхности
называется такое уравнение F(x,y,z)=0,
которому удовлетворяют координаты
каждой точки, лежащей на поверхности,
и не удовлетворяют координаты точек,
не лежащих на поверхности.

Например, сфера
– это геометрическое место точек,
равноудаленных от некоторой точки,
называемой центром сферы. Так все точки,
удовлетворяющие уравнению
лежат на сфере с центром в точке О(0.0.0)
и радиусомR
(Рис.1).

Координаты любой
точки, не лежащей на данной сфере, не
удовлетворяют этому уравнению.

Линию в
пространстве
можно рассматривать как линию пересечения
двух поверхностей. Так на рисунке 1
пересечением сферы с плоскостью Oxy
является окружность с центром в точке
О и радиусом R.

Простейшей
поверхностью является плоскость,
простейшей линией в пространстве
является прямая.

2. Плоскость в пространстве.

2.1. Уравнение
плоскости по точке и нормальному вектору.

В системе
координат Oxyz
рассмотрим плоскость
(Рис.2). Ее положение определяется заданием
вектораперпендикулярного этой плоскости, и
фиксированной точкилежащей в этой плоскости. Вектор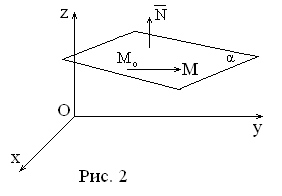перпендикулярный плоскостиназываетсянормальным
вектором
(вектором-нормалью). Рассмотрим
произвольную точку M(x,y,z)
плоскости
.
Векторлежащий в плоскостибудет перпендикулярен вектору-нормалиИспользуя условие ортогональности
векторовполучим уравнение:где

Уравнение
(2.2.1)

называется
уравнением плоскости по точке и
нормальному вектору.

Если в уравнении
(2.1.1) раскроем скобки и перегруппируем
члены, то получим уравнение
илиAx
+ By
+ Cz
+ D
= 0, где

D
= .

2.2. Общее
уравнение плоскости.

Уравнение
Ax
+ By
+ Cz
+D
= 0 (2.2.1)

называется общим
уравнением плоскости, где
– нормальный вектор.

Рассмотрим
частные случаи этого уравнения.

1).D
= 0. Уравнение имеет вид: Ax
+ By
+ Cz
= 0. Такая плоскость проходит через
начало координат. Ее нормальный вектор

2).
С = 0 :Ax
+ By
+ D
= 0

плоскость
параллельна оси oz
(Рис.3).

3). B
= 0 : Ax
+ Cz
+ D
= 0


плоскость параллельна оси oy
(Рис.4).

4). A
= 0 : By
+ Cz
+ D
= 0


плоскость параллельна оси ox
(Рис.5).

5). C
= D
= 0 : Ax
+ By
= 0


плоскость проходит через ось oz
(Рис.6).

6).B
= D
= 0 : Ax
+ Cz
= 0


плоскость проходит через ось oy
(Рис.7).

7). A
= D
= 0 : By
+ Cz
= 0


плоскость проходит через ось ox
(Рис.8).

8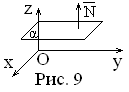).A
= B
= 0 : Cz
+ D
= 0

||oz

плоскость параллельна плоскостиOxy
(Рис.9).

9). B
= C
= 0 : Ax
+ D
= 0

||ox

плоскость

параллельна
плоскостиOyz
(Рис.10).

10).A
= C
= 0 : By
+ D
= 0

||oy

плоскость параллельна плоскостиOxz
(Рис.11).

Пример 1.
Составить уравнение плоскости, проходящей
через точку
перпендикулярно векторуНайти точки пересечения этой плоскости
с осями координат.

Решение.
По формуле (2.1.1) имеем

2x
– y
+ 3z
+ 3 = 0.

Для того, чтобы
найти пересечение этой плоскости с осью
ox,
подставим в полученное уравнение y
= 0, z
= 0. Имеем 2x
+ 3 = 0; x
= – 1,5.

Точка пересечения
искомой плоскости с осью ox
имеет координаты:

Найдем пересечение
плоскости с осью oy.
Для этого возьмем x
= 0; z
= 0. Имеем

– y
+ 3 = 0

y
= 3. Итак,

Для нахождения
точки пересечения с осью oz
возьмем x
= 0; y
= 0
3z
+ 3 = 0
z
= – 1. Итак,

Ответ:
2x
– y
+ 3z
+ 3 = 0, ,,.

Пример 2.
Исследовать
плоскости, заданные уравнениями:

a).
3x
– y
+ 2z
= 0

б). 2x
+ z
– 1 = 0

в). – y
+ 5 = 0

г). x
= 0.

Решение.
а). Данная плоскость проходит через
начало координат (D
= 0) и имеет нормальный вектор

б). В уравнении
коэффициентB
= 0. Следовательно,
Плоскость параллельна осиoy.

в). В уравнении –
y
+ 5 = 0 коэффициенты A
= 0, C
= 0. Значит

Плоскость параллельна
плоскости oxz.

г). Уравнение x
= 0 задает плоскость oyz,
так как при B
= 0, C
= 0 плоскость параллельна плоскости oyz,
а из условия D
= 0 следует, что плоскость проходит через
начало координат.

Пример 3.
Составить уравнение плоскости, проходящей
через точку A(2,3,1)
и перпендикулярной вектору
гдеB(1,0,
–1), C(–2,2,0).

Решение. Найдем
вектор

Вектор
является нормальным вектором искомой
плоскости, проходящей через точкуA(2,3,1).
По формуле (2.1.1) имеем:

– 3x
+ 2y
+ z
+ 6 – 6 – 1 = 0–
3x
+ 2y
+ z
– 1 = 0

3x
– 2y
– z
+ 1 = 0.

Ответ: 3x
– 2y
– z
+ 1 = 0.

2.3. Уравнение
плоскости, проходящей через три точки.

Три точки, не
лежащие на одной прямой, определяют
единственную плоскость (см. рис. 12). Пусть
точки
не лежат на одной прямой. Чтобы составить
уравнение плоскости, нужно знать одну
точку плоскости и нормальный вектор.
Точки, лежащие на плоскости, известны:

Можно взять любую. Для нахождения
нормального вектора воспользуемся
определением векторного произведения
векторов. Пусть
Тогдаследовательно,Зная координаты точкии нормального векторанайдем уравнение плоскости, применяя
формулу (2.1.1).

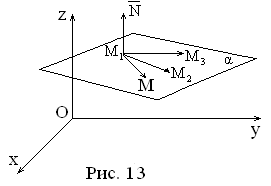Другим способом
уравнение плоскости, проходящей через
три заданные точки, можно получить,
используя условие компланарности трех
векторов. Действительно, векторы где M(x,y,z)
– произвольная точка искомой плоскости,
компланарны (см. рис.13). Следовательно,
их смешанное произведение равно 0:

.

Применив формулу
смешанного произведения в координатной
форме, получим:

(2.3.1)

Пример 1.
Составить
уравнение плоскости, проходящей через
точки

Решение.
По формуле (2.3.1) имеем

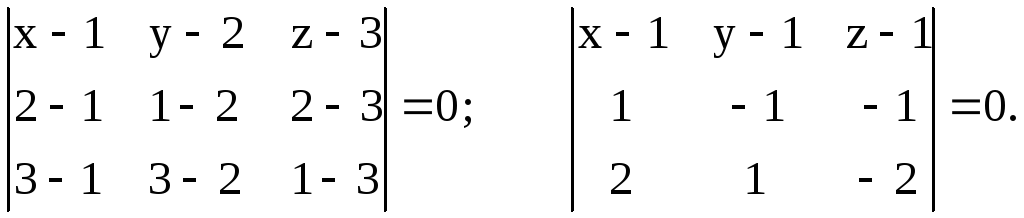
Раскрыв определитель,
получим:

Полученная плоскость
параллельна оси oy.
Ее нормальный вектор

Ответ:
x
+ z – 4 = 0.

2.4.
Угол между
двумя прямыми.

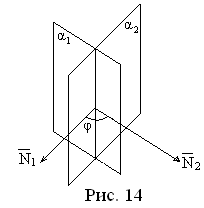Две плоскости,
пересекаясь, образуют четыре двугранных
угла, равных попарно (см. рис. 14). Один из
двугранных углов равен углу между
нормальными векторами этих плоскостей.

Пусть даны
плоскости:

и

Их нормальные
векторы имеют координаты:

Из векторной
алгебры известно, что
или

(2.4.1)

Пример: Найти
угол между плоскостями:

Решение:
Найдем
координаты нормальных векторов:
По формуле (2.4.1) имеем:

Один из двугранных
углов, полученных при пересечении данных
плоскостей, равен
Можно найти и второй угол:

Ответ:

2.5.
Условие
параллельности двух плоскостей.

Пусть даны две
плоскости:

и

Если эти плоскости
параллельны, то их нормальные векторы

коллинеарны (см.
рис.15).

Если векторы
коллинеарны, то их соответствующие
координаты пропорциональны:

(2.5.1)

Верно и обратное
утверждение: если нормальные векторы
плоскостей коллинеарны, то плоскости
параллельны.

Пример 1.
Какие из
указанных плоскостей
параллельны:

а).
,

б).
?

Решение:
а). Выпишем координаты нормальных
векторов.

Проверим их
коллинеарность:

Отсюда следует,
что

б). Выпишем
координаты

Проверим
коллинеарность:

Векторы не коллинеарны,
плоскости
не параллельны.

Пример 2.
Составить
уравнение плоскости, проходящей через
точку

M(2,
3, –2)
параллельно
плоскости

Решение:
Искомая плоскость параллельна данной
плоскости. Поэтому нормальный вектор
плоскости
можно взять за нормальный вектор искомой
плоскости.Применяя уравнение
(2.1.1), получим:

Ответ: .

Пример 3.
Определить
при каких a
и b
плоскости параллельны:

Решение:
Выпишем координаты нормальных векторов:

Так как плоскости
параллельны, то векторы коллинеарны.По условию (2.5.1)Отсюда b
= – 2 ; a
= 3.

Ответ: a
= 3; b
= –2.

2.6. Условие
перпендикулярности двух плоскостей.

Если плоскости

перпендикулярны, то их нормальные
векторытоже перпендикулярны
(см. рис.16)..
Отсюда следует, что их скалярное
произведение равно нулю, т.е. или в координатах:

(2.6.1)

Это условие
перпендикулярности двух плоскостей.
Обратное утверждение также верно, то
есть, если выполняется условие (2.6.1), то
векторы следовательно,

Пример 1.
Какие из указанных плоскостей
перпендикулярны:

а).
,

б).

Решение: а).
Запишем координаты нормальных векторов:

Проверим их
ортогональность:

Отсюда следует,
что

б). Запишем
координаты нормальных векторов:

Найдем их скалярное
произведение:

то есть плоскости
неперпендикулярны.

Пример 2.
При каком значении m
плоскости перпендикулярны

Решение:
Запишем
координаты нормальных векторов:

Найдем их скалярное
произведение:

Так как плоскости
перпендикулярны, то
Следовательно, 4 – 2m
= 0;

m
= 2.

Ответ:
m
= 2.

2.7. Расстояние
от точки до плоскости.

Пусть дана точка
и плоскость

Расстояние от
точки
(см. рис.17) находим по формуле:

(2.7.1)

Пример: Найти
расстояние от точки M(3,
9, 1) до плоскости

Решение:
Применяем формулу (2.7.1), где A
= 1, B
= – 2, C
= 2, D
= –3,

Ответ:

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.20154.96 Кб8Содержание OneNote.onetoc2

• #