Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M0(x0,y0,z0) имеет вид:
Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z – z0 = f’x(x0,y0,z0)(x – x0) + f’y(x0,y0,z0)(y – y0)
По условию задачи x0 = 0 , y0 = 1 , тогда z0 = 5
Найдем частные производные функции z = x^3+5*y :
f’x(x,y) = (x 3 +5•y)’x = 3•x 2
f’x(x,y) = (x 3 +5•y)’y = 5
В точке М0(0,1) значения частных производных:
f’x(0;1) = 0
f’y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z – 5 = 0(x – 0) + 5(y – 1) или -5•y+z = 0
Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f’x(1;0;1) = -3 /16
f’y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z – 1 = -3 /16(x – 1) + 0(y – 0) или 3 /16•x+z- 19 /16 = 0
Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
fx’(x, y) = (y/x + xy – 5x 3 )’x = – y/x 2 + y – 15x 2 ;
fy’ (x, y) = (y/x + xy – 5x 3 )’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
Пример №1 . Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z – z0 = f’x(x0,y0,z0)(x – x0) + f’y(x0,y0,z0)(y – y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x 2 +3•x•y•+y 2 )’x = 2•x+3•y 3
f’x(x,y) = (x 2 +3•x•y•+y 2 )’y = 9•x•y 2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z – 25 = 26(x – 1) + 36(y – 2)
или
-26•x-36•y+z+73 = 0
Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение
Нормальный вектор плоскости, координаты нормального вектора плоскости
Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
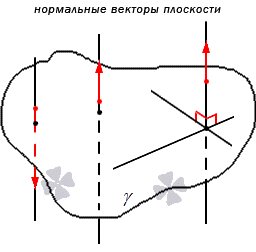
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2 x – 3 y + 7 z – 11 = 0 .
По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , – 3 , 7 ) – это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , – 3 · t , 7 · t , t является любым действительным числом не равным нулю.
Ответ: n → = ( 2 , – 3 , 7 ) .
Определить координаты направляющих векторов заданной плоскости x + 2 z – 7 = 0 .
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z – 7 = 0 к виду 1 · x + 0 · y + 2 z – 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Поверхности
Простые поверхности.
Будем говорить, что функция (f(u, v)) непрерывно дифференцируема на замкнутом множестве (E subset boldsymbol^<2>), если она определена и имеет непрерывные частные производные (partial f/partial u) и (partial f/partial v) на открытом множестве (G), содержащем замкнутое множество (E).
Пусть (Omega) — ограниченная область в (boldsymbol^<2>), а функции (varphi(u, v)), (psi(u, v)) и (chi(u, v)) непрерывно дифференцируемы на замкнутом множестве (overline <Omega>= Omega cup partial Omega), где (partial Omega) — граница области (Omega). Тогда отображение (F: overline <Omega>rightarrow boldsymbol^<3>), определяемое формулами
$$
x = varphi(u, v),quad y = psi(u, v),quad z = chi(u, v),quad (u, v) in overline<Omega>,label
$$
называется непрерывно дифференцируемым.
Если при этом в каждой точке ((u, v) in Omega) ранг функциональной матрицы
$$
beginvarphi_(u, v)&psi_(u, v)&chi_(u, v)\varphi_(u, v)&psi_(u, v)&chi_(u, v)endlabel
$$
равен двум, то отображение (F: rightarrow boldsymbol^<3>) называется гладким.
Если (overline<Omega>) есть замкнутое ограниченное множество в (boldsymbol^<2>), a (F: overline <Omega>rightarrow boldsymbol^<3>) есть такое гладкое отображение, что соответствие между множествами (overline<Omega>) и (Sigma = F(overline<Omega>)) является взаимно однозначным, то будем множество (Sigma) называть простой поверхностью в (boldsymbol^<3>), а уравнения eqref будем называть параметрическими уравнениями простой поверхности (Sigma).
Пусть область (Omega) ограничена простым гладким или кусочно гладким контуром (gamma). Образ кривой (gamma) при гладком отображении (F: overline <Omega>rightarrow boldsymbol^<3>) будем называть краем простой поверхности (Sigma) и обозначать через (partial Sigma).
Если уравнение кривой (gamma) имеет вид
$$
u = u(t),quad v = v(t),quad alpha leq t leq beta,nonumber
$$
то уравнение (partialSigma) задается следующими формулами:
$$
x = varphi(u(t), v(t)),quad y = psi(u(t), v(t)),quad z = chi(u(t), v(t)),quad alpha leq t leq beta.label
$$
График функции (z = f(x, y)), непрерывно дифференцируемой на замкнутом ограниченном множестве (overline <Omega>subset boldsymbol^<2>), есть простая поверхность, определяемая параметрическими уравнениями
$$
x = u,quad y = v,quad z = f(u, v),quad (u, v) in overline<Omega>.label
$$
В этом случае матрица (beginx_&x_\x_&y_end) является единичной, а поэтому ранг матрицы eqref равен двум.
Например, график функции (z = x^ <2>+ y^<2>), ((x, y) in overline<Omega>), где (overline <Omega>= <(x, y): x^<2>+ y^ <2>leq 1>), есть простая поверхность. Окружность, получаемая при пересечении параболоида вращения (z = x^ <2>+ y^<2>) и плоскости (z = 1), является краем рассматриваемой простой поверхности.
Уравнения eqref простой поверхности можно записать и в векторной форме:
$$
boldsymbol = boldsymbol(u, v),quad (u, v) in overline<Omega>,quad boldsymbol(u, v) = varphi(u, v) boldsymbol + psi(u, v) boldsymbol + chi(u, v) boldsymbol.label
$$
С механической точки зрения формулы eqref определяют гладкую (без разрывов и изломов) деформацию плоской области (Omega) в множество (Sigma) (простую поверхность в пространстве (boldsymbol^<3>)). Для практических целей только простых поверхностей недостаточно. Например, сфера (x^ <2>+ y^ <2>+ z^ <2>= a^<2>) не является простой поверхностью в (boldsymbol^<3>). Интуитивно ясно, что сферу нельзя получить никакой гладкой деформацией плоской области.
Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.
Пусть (Omega) — плоская область и (F: overline <Omega>rightarrow boldsymbol^<3>) — непрерывно дифференцируемое отображение. Будем множество (Sigma = F(overline<Omega>)) называть почти простой поверхностью в (boldsymbol^<3>), если найдется расширяющаяся последовательность ограниченных областей (<Omega_>) таких, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и поверхности (Sigma_ = F(overline<Omega>_)) простые.
Сфера (S = <(x, y, z): x^<2>+ y^ <2>+ z^ <2>= a^<2>>) есть почти простая поверхность.
(vartriangle) Введем сферические координаты. Тогда сфера (S) есть образ прямоугольника (overline <Omega>= displaystyleleft<(varphi, psi): 0 leq varphi leq 2pi, -frac<pi> <2>leq psi leq frac<pi><2>right>) при непрерывно дифференцируемом отображении (F: overline <Omega>rightarrow S), определяемом формулами
$$
x = a cos varphi cos psi,qquad y = a sin varphi cos psi,qquad z = a sin psi.nonumber
$$
Образами отрезков (varphi = varphi_<0>), (displaystyle-frac<pi> <2>leq psi leq frac<pi><2>) являются меридианы, а при (displaystyle|psi_<0>| Рис. 52.1
Конус (K = <(x, y, z): x^<2>+ y^ <2>= z^<2>>) есть почти простая поверхность.
(vartriangle) Введем цилиндрические координаты. Тогда конус (K) есть образ полуполосы
$$
overline <Omega>= <(r, varphi): 0 leq r Рис. 52.2
Легко проверить, что (overline<Omega>_ subset Omega_), (Omega = displaystylebigcup_^<infty>Omega_) и что поверхности (Sigma_ = F(overline<Omega>_)) являются простыми. Поэтому конус (K) — почти простая поверхность. (blacktriangle)
Если (Sigma) есть простая поверхность, заданная векторным уравнением eqref, а непрерывно дифференцируемые функции
$$
u = u(u’, v’), v = v(u’, v’), (u’, v’) in Omega’nonumber
$$
задают взаимно однозначное отображение замыкания области (Omega’) на замыкание ограниченной области (Omega), причем якобиан отображения
$$
frac<partial(u, v)> <partial(u’, v’)>= begindisplaystylefrac<partial u><partial u’>&displaystylefrac<partial u><partial v’>\displaystylefrac<partial v><partial u’>&displaystylefrac<partial v><partial v’>endnonumber
$$
отличен от нуля в (overline<Omega>’), то уравнение
$$
boldsymbol = boldsymbol (u(u’, v’), v(u’, v’)) equiv boldsymbol<rho>(u’, v’);quad (u’, v’) in Omega’,label
$$
определяет ту же простую поверхность, что и уравнение eqref. Уравнения eqref и eqref называют различными параметризациями поверхности (Sigma).
Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области (Omega).
(vartriangle) Переход от уравнений eqref к уравнениям eqref задается формулами
$$
u = a cos varphi cos psi,quad v = a sin varphi cos psi,quad (varphi, psi) in Omega’.label
$$
Якобиан отображения eqref равен (a^ <2>sin varphi cos psi) и обращается в нуль при (psi = 0), то есть на части границы области (Omega’). Это приводит к тому, что при переходе к параметризации eqref частные производные функции (z = sqrt-u^<2>-v^<2>>) стремятся к бесконечности при приближении точки (u, v) к окружности (u^ <2>+ v^ <2>= a^<2>). (blacktriangle)
Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.
Криволинейные координаты на поверхности.
Пусть простая поверхность (Sigma) задана векторным уравнением eqref. Предположим, что область (Omega) выпукла, ([a, b]) есть проекция области (Omega) на ось (u). Если (u_ <0>= in (a, b)), то прямая (u = u_<0>) будет пересекаться с областью (Omega) по отрезку (u = u_<0>), (alpha leq v leq beta) (рис. 52.3). Образ этого отрезка при отображении eqref есть кривая
$$
boldsymbol = boldsymbol (u_<0>, v), alpha leq v leq beta,label
$$
лежащая на поверхности (Sigma). Будем называть ее координатной кривой (u = u_<0>). Придавая (u_<0>) все значения из отрезка ([a, b]), получим семейство координатных кривых (u = operatorname). Аналогично строится и семейство координатных кривых (v = operatorname).
Рис. 52.3
В силу взаимной однозначности отображения eqref каждая точка (A) поверхности (S) однозначно определяется как пересечение двух координатных кривых, (u = u_<0>) и (v = v_<0>). Пара чисел ((u_<0>, v_<0>)) называется криволинейными координатами точки (A) поверхности. Запись (A(u_<0>, v_<0>)) означает, что точка (A) поверхности (Sigma) задана криволинейными координатами ((u_<0>, v_<0>)).
Например, в сферических координатах часть сферы (x^ <2>+ y^ <2>+ z^ <2>= a^<2>), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах (varphi), (psi) следующим образом:
$$
varphi_ <1>leq varphi leq varphi_<2>,quad psi_ <1>leq psi leq psi_<2>.nonumber
$$
На сфере координатные кривые (varphi = operatorname) — меридианы, а координатные кривые (psi = operatorname) — параллели.
На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.
Вектор-функция (boldsymbol (u_<0>, v)) есть непрерывно дифференцируемая функция параметра (v), и, следовательно, координатная кривая (u = u_<0>), определяемая равенством eqref, является непрерывно дифференцируемой. Вектор (boldsymbol_ (u_<0>, v_<0>)) является касательным к этой кривой в точке (A(u_<0>, v_<0>)). Аналогично, вектор (boldsymbol_ (u_<0>, v_<0>)) касателен к координатной кривой (v = v_<0>) в точке (A(u_<0>, v_<0>)). Заметим, что векторы (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_ (u_<0>, v_<0>)) не могут обратиться в нуль, так как в этом случае ранг матрицы eqref будет меньше двух. Следовательно, для простой поверхности координатные кривые являются гладкими.
Если область (Omega) не является выпуклой, а точка ((u_<0>, v_<0>)) лежит внутри (Omega), то нужно взять выпуклую окрестность точки ((u_<0>, v_<0>)), лежащую внутри (Omega). Тогда образ этой выпуклой окрестности будет куском поверхности (Sigma) и координатные кривые можно строить на этом куске поверхности (локально).
Касательная плоскость и нормаль к поверхности.
Пусть (Sigma) есть простая поверхность, заданная уравнениями eqref или векторным уравнением eqref. Рассмотрим точку (A(u, v)) на поверхности (Sigma), где ((u, v)) — внутренняя точка области (Omega). Построим координатные линии (u = operatorname) и (v = operatorname), проходящие через точку (A(u, v)). Векторы (boldsymbol_ (u, v)) и (boldsymbol_ (u, v)) будут касательными к соответствующим координатным линиям.
В любой точке (A(u, v)) простой поверхности (Sigma) векторы (boldsymbol_ (u, v)) и (boldsymbol_(u, v)) неколлинеарны. Направление вектора (N = [boldsymbol_, boldsymbol_]) при изменении способа параметризации или не меняется, или изменяется на противоположное.
(circ) Рассмотрим вектор (N = [boldsymbol_, boldsymbol_]) во всех точках поверхности (Sigma). Тогда
$$
boldsymbol=beginy_&z_\y_&z_endboldsymbol + beginz_&x_\z_&x_endboldsymbol + beginx_&y_\x_&y_endboldsymbol.nonumber
$$
Если (boldsymbol = boldsymbol<0>), то все компоненты вектора (boldsymbol) равны нулю, и ранг матрицы eqref будет меньше двух, что невозможно для простой поверхности. Пусть поверхность (Sigma) параметризована двумя способами, eqref и eqref. Тогда, воспользовавшись правилом нахождения частных производных сложной функции и аддитивностью и кососимметричностью векторного произведения, получаем
$$
boldsymbol’ = [boldsymbol<rho>_, boldsymbol<rho>_] = [boldsymbol_ frac<partial u> <partial u’>+ boldsymbol_ frac<partial v><partial u’>, boldsymbol_ frac<partial u> <partial v’>+ boldsymbol_ frac<partial v><partial v’>] =\= [boldsymbol_, boldsymbol_] left(frac<partial u><partial u’>frac<partial v><partial u’>-frac<partial u><partial v’>frac<partial v><partial v’>right) = [boldsymbol_, boldsymbol_] frac<partial(u, v)><partial(u’, v’)>,nonumber
$$
то есть
$$
boldsymbol’ = boldsymbol frac<partial(u, v)><partial(u’, v’)>.label
$$
Так как якобиан (J = displaystylefrac<partial(u, v)><partial(u’, v’)>) не обращается в нуль в области (Omega’), то векторы (boldsymbol’) и (boldsymbol) коллинеарны. Эти векторы сонаправлены, если (J > 0), и противоположно направлены, если (J Лемма 2.
Вектор нормали к простой поверхности (Sigma) в точке (A(u_<0>, v_<0>)) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку (A(u_<0>, v_<0>)).
(circ) В самом деле, такая кривая есть образ при отображении eqref некоторой гладкой кривой, лежащей в области (Omega) и задаваемой уравнениями (u = u(t)), (v = v(t)), (alpha leq t leq beta).
Уравнение кривой на поверхности тогда имеет вид
$$
boldsymbol = boldsymbol(u(t), v(t)), alpha leq t leq beta, u(t_<0>) = u_<0>, v(t_<0>) = v_<0>.
$$
Касательный вектор (boldsymbol<tau>) к этой кривой в точке (A) есть
$$
boldsymbol <tau>= frac
$$
Итак, (boldsymbol<tau>) есть линейная комбинация векторов (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)). Так как вектор (boldsymbol) ортогонален (boldsymbol_ (u_<0>, v_<0>)) и (boldsymbol_(u_<0>, v_<0>)), то он ортогонален и вектору (boldsymbol<tau>), то есть вектор нормали к поверхности в точке (A) ортогонален к любой гладкой кривой, лежащей на поверхности и проходящей через точку (A). (bullet)
Плоскость, проходящая через точку (A(u, v)) поверхности и ортогональная вектору (boldsymbol), называется касательной плоскостью к поверхности в точке (A). Пусть ((X, Y, Z)) — декартовы координаты точки касательной плоскости и пусть (boldsymbol = Xboldsymbol + Yboldsymbol + Zboldsymbol). Тогда векторы (boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) параллельны касательной плоскости, следовательно, их смешанное произведение равно нулю. Поэтому векторное уравнение касательной плоскости имеет вид
$$
(boldsymbol-boldsymbol(u, v), boldsymbol_(u, v), boldsymbol_(u, v)) = 0.nonumber
$$
В силу равенства eqref форма этого уравнения не зависит от выбора параметризации поверхности. Уравнение касательной плоскости в координатах имеет следующий вид:
$$
beginX-x(u, v)&Y-y(u, v)&Z-z(u, v)\x_(u, v)&y_(u, v)&z_(u, v)\x_(u, v)&y_(u, v)&z_(u, v)end = 0.nonumber
$$
Нормалью к поверхности в точке (A(u, v)) называется прямая, проходящая через точку (A) и параллельная вектору нормали в точке (A). Так как при изменении параметризации вектор нормали не меняет своего направления или изменяет его на противоположное в каждой точке поверхности, то нормаль не зависит от параметризации. Ее векторное уравнение имеет вид
$$
boldsymbol-boldsymbol(u, v) = k[boldsymbol_, boldsymbol_], -infty
Кусочно гладкие поверхности.
Из определения простой поверхности, данного в п. 1, следует, что она есть гладкий и взаимно однозначный образ некоторой плоской области, то есть получается из этой области при помощи гладких (без изломов) деформаций (отображений). Ясно, что многие объекты, которые мы привыкли называть поверхностями, не будут простыми поверхностями. Так, сфера не может быть непрерывным образом деформирована в плоскую область. Коническая поверхность не может быть получена гладкой деформацией плоской области.
Попытки дать общую классификацию поверхностей увели бы нас далеко в область высшей геометрии. Замечательным классом поверхностей в (boldsymbol^<3>) являются гладкие многообразия размерности 2, то есть связные множества, которые локально (в окрестности каждой своей точки) устроены, как простая гладкая поверхность. Например, сфера будет гладким многообразием. Если (A) есть точка сферы радиуса (a), то шар (S_<varepsilon>(A)) при (varepsilon Рис. 52.4
Из гладких кусков можно склеивать не только гладкие многообразия, но и связные поверхности, имеющие ребра и вершины (например, поверхности многогранников) (рис. 52.5).
Рис. 52.5
Мы не станем тут заниматься математической формализацией таких понятий, как разрезание и склеивание поверхностей, и тем более основанной на этом классификации поверхностей. Заметим только, что трудности возникают при построении общих теорий. В любом разумном частном случае нет проблем с разрезанием поверхности на простые куски. Поверхность, которую можно разрезать на конечное число простых кусков, будем называть кусочно гладкой.
Ориентируемые поверхности.
Будем говорить, что гладкая поверхность ориентируема, если можно построить на этой поверхности непрерывное поле единичных нормальных векторов. Говорят, что это поле единичных нормалей определяет ориентацию (или сторону) поверхности. Меняя направление всех единичных нормалей на противоположное, получим опять непрерывное поле единичных нормальных векторов. Говорят, что оно определяет противоположную ориентацию (другую сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>.label
$$
Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), так и неориентируемыми (односторонними).
Торы, изображенные на рис. 52.4, ориентируемы; бутылка Клейна — неориентируемая (односторонняя) поверхность. Легко построить лежащий на этой поверхности замкнутый гладкий контур такой, что, выбирая в какой-то точке контура вектор единичной нормали к поверхности и непрерывно изменяя его при движении по контуру, мы придем к начальной точке с противоположным направлением нормали. Следовательно, на бутылке Клейна построить непререрывное поле единичных нормальных векторов невозможно.
Заметим еще, что сфера, тор, тор с двумя дырами (рис. 52.4) делят пространство на ограниченную и неограниченную области, общей границей которых они являются. Бутылка Клейна таким свойством не обладает.
Можно доказать, что гладкая поверхность, являющаяся границей области в (boldsymbol^<3>), ориентируема. Ее внутренняя сторона задается нормальными векторами, направленными внутрь области (внутренними нормалями), внешняя сторона определяется внешними нормалями. Очевидно, что для построения поля внутренних нормалей к границе области достаточно построить внутреннюю нормаль к какой-то одной точке границы.
Рис. 52.6
Каждая плоскость делит пространство (boldsymbol^<3>) на два полупространства. Если плоскость рассматривать как границу полупространства, то внутренняя нормаль определяется естественным образом как направленная внутрь полупространства (рис. 52.6). Если (partial G) есть гладкая граница области (G), то касательная плоскость в точке (x in partial G) называется опорной, если область лежит по одну сторону от касательной плоскости, то есть в одном из полупространств, определяемых этой плоскостью. В точке (x in partial G) определена внутренняя нормаль (рис. 52.7).
Рис. 52.7
Границу области (G), ориентированную внешними нормалями, будем обозначать через (partial G), а внутренними — через (partial G^<->).
Несколько более сложно определяется ориентация кусочно гладких поверхностей.
Рис. 52.8
Пусть (Sigma) — простая поверхность (рис. 52.8), то есть гладкий и взаимно однозначный образ замыкания плоской области (Omega). В декартовых координатах отображение задается равенствами eqref. Прообразом гладкого простого контура (Gamma subset Sigma) будет простой гладкий контур (gamma subset Omega). Будем говорить, что контур (Gamma) ориентирован положительно, если его прообраз (gamma) ориентирован в плоскости ((u, v)) положительно (рис. 52.9), то есть при обходе контура (gamma) область, им ограничиваемая, остается слева (вектор касательной и вектор внутренней нормали образуют правую пару векторов в ориентированной плоскости ((u, v))). Будем говорить, что ориентация простой поверхности (Sigma), задаваемая полем единичных нормалей
$$
boldsymbol = frac<[boldsymbol_, boldsymbol_]><|[boldsymbol_, boldsymbol_]|>,nonumber
$$
согласована с положительной ориентацией простых контуров, лежащих на поверхности (Sigma).
Рис. 52.9
Покажем, что предложенное правило согласования ориентации поверхности с ориентациями простых контуров, лежащих на поверхности, совпадает с известным правилом правого винта. Пусть (A(u_<0>, v_<0>) in Sigma), то есть ((u_<0>, v_<0>) in Omega). Без ограничения общности можно считать, что (u_ <0>= 0), (v_ <0>= 0). Построим в точке (A)(0,0) касательную плоскость и ориентируем ее вектором нормали (boldsymbol) или, что то же самое, парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)). Возьмем в плоскости переменных (u), (v) окружность радиуса (varepsilon) с центром в точке (0,0):
$$
u = varepsilon cos t, v = varepsilon sin t, 0 leq t leq 2pi.nonumber
$$
Ее образ на поверхности есть простой замкнутый контур (Gamma):
$$
boldsymbol = boldsymbol (varepsilon cos t, varepsilon sin t), 0 leq t leq 2pi.nonumber
$$
С точностью до (boldsymbol(varepsilon)) при (varepsilon rightarrow 0) получаем, что
$$
boldsymbol = boldsymbol(0,0) + varepsilon boldsymbol_(0,0)cos t + varepsilon boldsymbol_(0,0)sin t + boldsymbol(varepsilon).nonumber
$$
С точностью до (boldsymbol(varepsilon)) кривая (Gamma) есть эллипс в касательной плоскости, ориентированной парой векторов ((boldsymbol_)(0, 0), (boldsymbol_)(0,0)).
Ориентация эллипса положительна (рис. 52.10). Если смотреть на касательную плоскость со стороны вектора нормали (boldsymbol), то движение по эллипсу происходит против часовой стрелки, от вектора (boldsymbol_)(0, 0) к вектору (boldsymbol_)(0, 0) (область, ограничиваемая эллипсом, остается слева).
Рис. 52.10
Пусть кусочно гладкая поверхность (Sigma) склеена из гладких простых кусков (Sigma_<1>, Sigma_<2>, ldots, Sigma_). Если склеивание происходит вдоль кривой (gamma), то после удаления концов кривой (gamma) она входит в края двух и только двух поверхностей (Sigma_). Кусочно гладкая поверхность (Sigma) называется ориентируемой, если можно так ориентировать гладкие куски (Sigma_), (i = overline<1, n>) что после согласования ориентации (Sigma_) с ориентациями (partial Sigma_) любая кривая склейки будет входить в состав краев соответствующих двух поверхностей с противоположными ориентациями (рис. 52.11).
Рис. 52.11
Можно показать, что кусочно гладкая поверхность, являющаяся границей ограниченной области, ориентируема, при этом каждый ее гладкий кусок можно ориентировать внутренними нормалями. В дальнейшем мы будем рассматривать только ориентируемые гладкие и кусочно гладкие поверхности.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-ploskosti-koordinaty-normalnogo-v/
http://univerlib.com/mathematical_analysis/curve_surface_integrals/surfaces/
[/spoiler]
Норма́ль в геометрии — обобщение понятия перпендикуляра к прямой или плоскости на произвольные гладкие кривые и поверхности.
В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.
Нормаль к кривой в заданной её точке — прямая, перпендикулярная к касательной прямой в указанной точке кривой. Плоская гладкая кривая имеет в каждой точке единственную нормаль, расположенную в той же плоскости. Пространственная кривая в каждой своей точке имеет бесконечное множество нормалей, формирующих так называемую нормальную плоскость. Две из этих нормалей выделяются особо: нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью, а нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью[1].
Нормаль к поверхности в заданной её точке — прямая, перпендикулярная к касательной плоскости в указанной точке поверхности. Нормаль для гладкой поверхности определяется однозначно[1].
Понятие нормали может быть легко распространено на многомерные многообразия. Кроме геометрии, нормали широко используются в геометрической оптике, механике, при создании трёхмерной компьютерной графики, в теории потенциала и в других естественных науках[2].
Вектор нормали[править | править код]
Векторы нормали в точках поверхности
Вектор нормали (или орт нормали) к поверхности в данной точке — единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Аналогично определяются векторы нормали к пространственной кривой в данной точке; среди них, соответственно сказанному выше, выбирают два, ортогональных друг к другу: вектор главной нормали и вектор бинормали.
Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным полем векторов нормали. В противном случае поверхность называют односторонней или неориентируемой. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.
Примерами односторонних и, следовательно, неориентируемых поверхностей являются бутылка Клейна или лист Мёбиуса.
Нормаль к пространственной кривой[править | править код]
Пусть 
![{displaystyle [[mathbf {r} ', mathbf {r} ''], mathbf {r} '].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ee7697e2619ae6eceeffeda8525c1fd2068d8ea)

Векторное уравнение бинормали в точке 
Уравнение нормальной плоскости[3] в точке 
Нормаль к плоской кривой[править | править код]
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке 
| Способ задания плоской кривой |
Уравнение кривой | Уравнение нормали |
|---|---|---|
| Параметрическое задание |  |

|
| Явное задание |  |

|
| Неявное задание |  |

|
Нормаль к поверхности[править | править код]
В дифференциальной геометрии исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Как правило, это — условия гладкости поверхности, то есть существования в каждой точке поверхности определённой касательной плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз дифференцируемыми или даже аналитическими функциями. При этом дополнительно накладывается условие регулярности (см. статью Поверхность). Примером точки поверхности, где нормаль не определена, является вершина конуса — в ней не существует касательной плоскости.
Координаты орта нормали для разных способов задания поверхности приведены в таблице:
| Координаты нормали в точке поверхности | |
|---|---|
параметрическое задание: 
|

|
неявное задание: 
|

|
явное задание: 
|

|
Здесь 


Сечение поверхности плоскостью, содержащей нормаль поверхности в заданной точке, образует некоторую кривую, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).
Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол 


Кривизна 
Примечания[править | править код]
- ↑ 1 2 Математическая энциклопедия, 1982, с. 1049—1050.
- ↑ Нормаль // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 416. — 847 с.
- ↑ 1 2 Рашевский, 1956, с. 146.
- ↑ Погорелов, 1974, с. 125—126.
- ↑ Погорелов, 1974, с. 132—133.
Литература[править | править код]
- Нормаль // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Погорелов А. И. Дифференциальная геометрия. — 6-е изд. — М.: Наука, 1974. — 176 с.
- Рашевский П. К. Курс дифференциальной геометрии. — 4-е изд. — М.: ГИТТЛ, 1956.
Ссылки[править | править код]
- Нормаль // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Касательная плоскость и нормаль к поверхности
Пусть M0(x0;
y0;
z0)
– фиксированная точка на поверхности,
заданной функцией z
= f(x;
y)
или уравнением F(x;
y;
z)
= 0.
Касательной
плоскостью к
поверхности в точке M0
называется плоскость, в которой
расположены касательные к всевозможным
кривым, проведенным на поверхности
через точку M0.
Нормалью называется
прямая, проходящая через точку M0
перпендикулярно касательной плоскости.
Из
определений следует, что нормальный
вектор касательной плоскости
и направляющий вектор нормали совпадают.
Если поверхность
задана уравнением z
= f(x;
y),
то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
к данной поверхности имеет вид
(1)
а
канонические
уравнения нормали,
проведенной через точку M0(x0;
y0;
z0)
поверхности, имеют вид
(2)
В случае, когда
уравнение гладкой поверхности задано
в неявном виде: F(x;
y;
z)
= 0 и F(x0;
y0;
z0)
= 0, то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
имеет вид
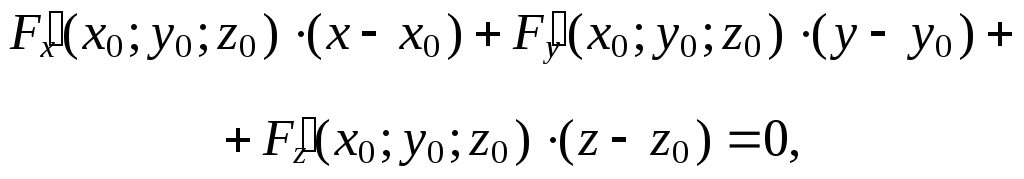
(3)
а уравнение
нормали
(4)
Пример 15.Найти уравнение касательной плоскости
и уравнения нормали к поверхностив точкеM0(1; 2;
–1).
Решение
Вычисляем значения
частных производных в точке M0(1;
2; –1)
Подставляя их в
уравнения (3) и (4), получаем соответственно
уравнение касательной плоскости:
канонические уравнения нормали:
Тест 11. Уравнение
касательной плоскости к поверхности
в точкеP0(2;
–3; 2) имеет следующий вид:
1)
2)
3)
4)
5)
Производная по направлению. Градиент
Частные производные
и
представляют собой производные от
функцииz
= f(x;
y)
по двум частным направлениям осей Ox
и Oy
(рисунок 43).
Рисунок 43
Пусть функция z
= f(x;
y)
определена в некоторой окрестности
точки М(х;
у),
– некоторое направление, задаваемое
единичным векторомгде
ибо
(или
);cos ,
cos
– косинусы углов, образуемых вектором
е
с осями координат и называемые
направляющими
косинусами.
При перемещении
в данном направлении
точкиM(x;
y)
в точку M1(x
+ x;
y
+ y)
функция z
получит приращение
z
= f(x
+ x;
y
+
+ y)
– f(x;
y),
называемое приращением
функции
в данном направлении
Если
то, очевидно, что
следовательно,
Производной
по направлению
функции двух переменных
z
= f(x;
y)
называется предел отношения приращения
функции в этом направлении к величине
перемещения
при стремлении последней к нулю, т. е.
Производная
характеризует
скорость
изменения функции в направлении
Формула для
производной функции z
= f(x;
y)
по
направлению
имеет вид
Пример 16.
Дана
функция z
= x2
+ y2,
в точке M(1;
1) направление составляет с осью Ox
угол
Найти производную функции по указанному
направлению в этой точке.
Решение
Так как
то угол
По формуле производной функции по
направлению получим
В точке M(1;
1) получаем:
Градиентом grad
z
функции z
= f(x;
y)
называется вектор с координатами
Рассмотрим скалярное
произведение векторов
и единичного вектора
Получим
Итак, производная
по направлению
есть скалярное произведение градиента
grad
z
и единичного вектора, задающего
направление
Градиент функции
grad
z
в данной точке характеризует направление
максимальной скорости изменения функции
в этой точке.
Пример 17.
Найти
градиент функции
в точкеM(0;
1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.2.3. Вектор нормали плоскости (нормальный вектор)
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением в прямоугольной (!) системе координат, то вектор
является нормальным вектором данной плоскости.
Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:
Задача 134
Найти единичный нормальный вектор плоскости .
Решение: принципиально ситуация выглядит так:
Сначала из уравнения плоскости «снимем» вектор нормали: .
И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора
разделить на длину вектора
.
Вычислим длину вектора нормали:
Таким образом:
Контроль: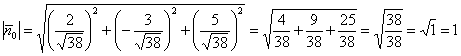
Ответ:
Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора :
.
И, как говорится, обещанного три страницы ждут 🙂 – вернёмся к Задаче 130, чтобы выполнить её проверку. Напоминаю, что там требовалось построить уравнение плоскости по точке и двум векторам
, и в результате решения мы получили уравнение
.
Проверяем:
Во-первых, подставим координаты точки в полученное уравнение:
– получено верное равенство, значит, точка
лежит в данной плоскости.
На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы
параллельны плоскости, а вектор
ей перпендикулярен, то должны иметь место следующие факты:
. Ортогональность векторов элементарно проверяется с помощью скалярного произведения:
Вывод: уравнение плоскости найдено правильно.
В ходе проверки я фактически процитировал следующее утверждение теории: вектор параллелен плоскости
в том и только том случае, когда
.
Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Как найти нормальный вектор
Перед тем как ответить на поставленный вопрос, требуется определить, нормаль чего именно необходимо искать. В данном случае, предположительно, в задаче рассматривается некая поверхность.
Инструкция
Приступая к решению поставленной задачи, следует помнить, что нормаль к поверхности определяется как нормаль к касательной плоскости. Исходя именно из этого и будет выбираться методика решения.
График функции двух переменных z=f(x, y)=z(x, y) – это поверхность в пространстве. Таким образом ее чаще всего и задают. В первую очередь необходимо найти касательную плоскость к поверхности в некоторой точке М0(x0, y0, z0), где z0=z(x0, y0).
Для этого следует вспомнить, что геометрический смысл производной функции одного аргумента, это угловой коэффициент касательной к графику функции в точке, где y0=f(x0). Частные производные функции двух аргументов находят, фиксируя «лишний» аргумент точно так же, как и производные обычных функций. Значит геометрический смысл частной производной по x функции z=z(x, y) в точке (x0,y0) состоит в равенстве ее углового коэффициента касательной, к кривой, образуемой пересечением поверхности и плоскости y=y0 (см. рис. 1).
Данные, отраженные на рис. 1, позволяют заключить, что уравнение касательной к поверхности z=z(x, y), содержащей точку М0(xo, y0, z0) в сечении при y=y0: m(x-x0)=(z-z0), y=y0. В каноническом виде можно записать:(x-x0)/(1/m)=(z-z0)/1, y=y0. Значит направляющий вектор этой касательной s1(1/m, 0, 1).
Теперь, если угловой коэффициент касательно для частной производной по y обозначить n, то совершенно очевидно, что аналогично предыдущему выражению, это приведет к (y-y0)/(1/n)=(z-z0), x=x0 и s2(0, 1/n, 1).
Далее продвижение решения в виде поиска уравнения касательной плоскости можно прекратить и перейти непосредственно к искомой нормали n. Ее можно получить как векторное произведение n=[s1, s2]. Вычислив его, будет определено, что в заданной точке поверхности (x0, y0, z0). n={-1/n, -1/m, 1/mn}.
Так как любой пропорциональный вектор также останется вектором нормали, удобнее всего ответ представить в виде n={-n, -m, 1} и окончательно n(дz/дx, дz/дx, -1).
Видео по теме
Обратите внимание
У незамкнутой поверхности имеется две стороны. В данном случае ответ дан для «верхней» стороны, там где нормаль образует острый угол с осью 0Z.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
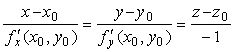
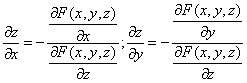
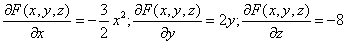
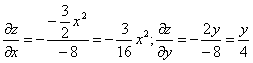


![{boldsymbol {r}}(lambda )={boldsymbol {r}}(t_{0})+lambda [{boldsymbol {r}}'(t_{0}),~{boldsymbol {r}}''(t_{0})].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b484d034092a7ddfd4f6cea0efa4b3f9f0cac69f)