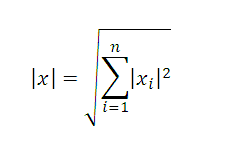Как найти нормальный вектор прямой онлайн - Сайт, где вы сможете решить свои вопросы

Онлайн калькулятор для нахождения длины (нормы) вектора.
Найти нормированный вектор, норма вектора – длина вектора на линейном пространстве.
Построить вектор в двухмерном и трехмерном пространстве.

Скачать калькулятор

Рейтинг: 3.1 (Голосов 15)

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке

Смотрите также

Действия с векторами	Cкалярное произведение	Векторное произведение	Длина, модуль вектора	Угол между векторами
Векторный калькулятор	Сложение и вычитание	Разложить вектор по базису	Сумма векторов	Середина отрезка

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

нормаль:y=x^2-x-1,:(2,:1)
нормаль:y=x^4+2e^x,:(0,:2)
нормаль:y=frac{x}{a}+frac{a}{x},::x=frac{a}{2}
нормаль:y=x^4+2x,:(1,:3)
нормаль:y=4x^2-6x,::x=2
нормаль:y=e^{-x}cdot ln (x),:(1,:0)
Показать больше

Описание

Поэтапное решение уравнения нормали

normal-line-calculator

Блог-сообщения, имеющие отношение к Symbolab

Slope, Distance and More

Ski Vacation? Nope, this is serious stuff; it’s about finding the slope of a line, finding the equation of a line…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

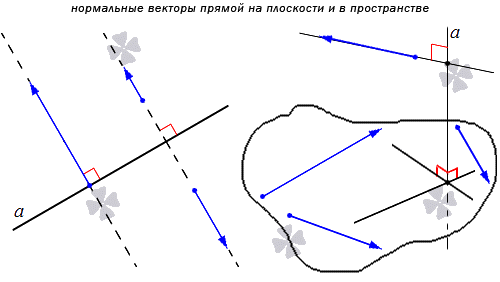
Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

Определение 1

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а1 параллельные, а n→ считается нормальным вектором прямой a, также считается нормальным вектором для прямой a1. Когда прямая а имеет прямой вектор, тогда вектор t·n→ является ненулевым при любом значении параметра t, причем также является нормальным для прямой a.

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость Оху, то множеством векторов для Ох является координатный вектор j→. Он считается ненулевым и принадлежащим координатной оси Оу, перпендикулярной Ох. Все множество нормальных векторов относительно Ох можно записать, как t·j→, t∈R, t≠0.

Прямоугольная система Oxyz имеет нормальный вектор i→, относящийся к прямой Оz. Вектор j→ также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный Оz, считается нормальным для Oz.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат Оху выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения Ax+By+C=0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Пример 1

Задана прямая вида 2x+7y-4=0_, найти координаты нормального вектора.

Решение

По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2, 7.

Ответ: 2, 7.

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Пример 2

Указать нормальный вектор для заданной прямой y-3=0.

Решение

По условию нам дано общее уравнение прямой, значит запишем его таким образом 0·x+1·y-3=0. Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0, 1.

Ответ: 0, 1.

Если дано уравнение в отрезках вида xa+yb=1 или уравнение с угловым коэффициентом y=k·x+b, тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Пример 3

Найти координаты нормального вектора, если дано уравнение прямой x13-y=1.

Решение

Для начала необходимо перейти от уравнения в отрезках x13-y=1 к уравнению общего вида. Тогда получим, что x13-y=1 ⇔3·x-1·y-1=0.

Отсюда видно, что координаты нормального вектора имеют значение 3, -1.

Ответ: 3, -1.

Если прямая определена каноническим уравнением прямой на плоскости x-x1ax=y-y1ay или параметрическим x=x1+ax·λy=y1+ay·λ, тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a→=(ax, ay). Возможность нахождения координат нормального вектора n→ возможно, благодаря условию перпендикулярности векторов n→ и a→.

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔ay·x-ax·y+ax·y1-ay·x1x=x1+ax·λy=y1+ay·λ⇔x-x1ax=y-y1ay⇔ay·x-ax·y+ax·y1-ay·x1=0

Для решения можно выбирать любой удобный способ.

Пример 4

Найти нормальный вектор заданной прямой x-27=y+3-2.

Решение

Из прямой x-27=y+3-2 понятно, что направляющий вектор будет иметь координаты a→=(7, -2). Нормальный вектор n→=(nx, ny) заданной прямой является перпендикулярным a→=(7, -2).

Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a→=(7, -2) и n→=(nx, ny) запишем a→, n→=7·nx-2·ny=0.

Значение nx – произвольное , следует найти ny. Если nx=1, отсюда получаем, что 7·1-2·ny=0⇔ny=72.

Значит, нормальный вектор имеет координаты 1, 72.

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

x-27=y+3-2⇔7·(y+3)=-2·(x-2)⇔2x+7y-4+73=0

Полученный результат координат нормального вектора равен 2, 7.

Ответ: 2, 7 или 1, 72.

Пример 5

Указать координаты нормального вектора прямой x=1y=2-3·λ.

Решение

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

x=1y=2-3·λ⇔x=1+0·λy=2-3·λ⇔λ=x-10λ=y-2-3⇔x-10=y-2-3⇔⇔-3·(x-1)=0·(y-2)⇔-3·x+0·y+3=0

Отсюда видно, что координаты нормального вектора равны -3, 0.

Ответ: -3, 0.

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат Охуz.

Когда прямая задается при помощи уравнений пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, тогда нормальный вектор плоскости относится к A2x+B2y+C2z+D2=0 и A2x+B2y+C2z+D2=0, тогда получаем запись векторов в виде n1→=(A1, B1, C1) и n2→=(A2, B2, C2).

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x-x1ax=y-y1ay=z-z1az или параметрического, имеющего вид x=x1+ax·λy=y1+ay·λz=z1+az·λ, отсюда ax, ay и az считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a→=(ax, ay, az). Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a→=(ax, ay, az).

Источник

Unit Converter

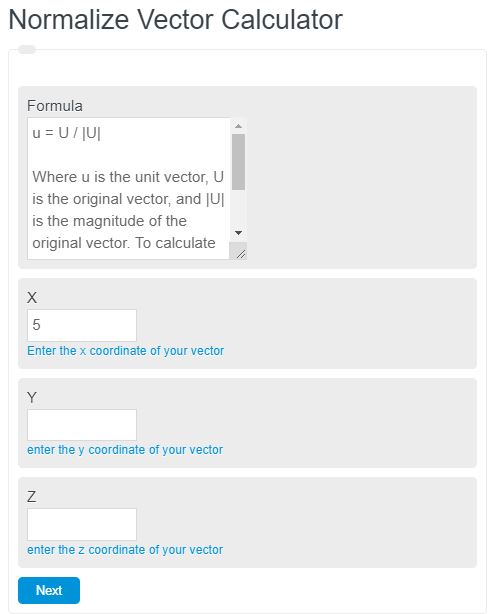
Enter any vector into the normalize vector calculator. The calculator will normalize this vector and display the unit vector.

Vector Subtraction Calculator
Vector Magnitude Calculator
Unit Vector Calculator
Resultant Vector Calculator

Normalizing a Vector Formula

The following formula is used to normalize a vector.

u = U / |U|

|U| = Square Root ( X^2 + Y^2+Z^2)

Where U is the original vector
|U| is the magnitude of the vector
u is the unit vector

Normalize Vector Definition

A vector normalization is a process of finding the unit vector of a given vector.

How to normalize a vector?

First, calculate the magnitude of the original vector
Using the formula above, calculate the magnitude of the original vector.
Next, divide each component of the vector by the magnitude.
For example, for a vector x,y,z, divide x by the magnitude, y by the magnitude, and z by the magnitude. The results of those divisions are your unit vector values.

Example Problem:

In the following example, a vector of (5,6,10) is given.

First, the magnitude of the vector must bed calculated. Using the formula above:

|U| = sqrt( 5^2 + 6^2+10^2)

|U| = 12. 688

Next, divide each individual component of the vector by the magnitude to normalize the vector.

X = 5 / 12.688 = .394

Y = 6 / 12.688 = .472

Z = 10 / 12.688 = .788

So the final normalized vector would be (.394,.472,.788).

FAQ

What is normalizing a vector?

Normalizing a vector is the process of turning a vector into its unit vector. This process involves dividing a vector by its magnitude. The result is a vector with the same direction, but with a magnitude of 1.

Why would you normalize a vector?

Normalizing a vector can simply problems. For example, if you want to multiply two vectors A and B, you can actually multiply their unit vectors to get the direction, then multiply that answer by the magnitudes to get the resulting vector of A * B.