Как найти нормальный вид квадратичной формы

КВАДРАТИЧНЫЕ ФОРМЫ
И ИХ ПРИМЕНЕНИЯ

Определение.
Квадратичной формой

переменных
,принимающих
числовые значения ,
называется числовая
функция вида

,

где
–
числа,
называемые коэффициентами квадратичной
формы.

Определение.
Матрицей квадратичной формы

переменных
,
называется симметрическая матрица
порядка
,
элементы главной диагонали которой
совпадают с коэффициентами при квадратах
переменных,
а каждый недиагональный элемент,
расположенный в
ой
строке
ом
столбце,
равен половине коэфициента при

в квадратичной форме.

Определение.
Рангом квадратичной формы называется
ранг её матри-цы.
Квадратичная форма может быть записана
в матричном виде

где

матрица
квадратичной формы и
.

Определение.
Квадратичная форма называется канонической
(имеет канонический вид),
если коэфициенты
при

,
то есть,
если матрица квадратичной формы
диагональная и следовательно

.,

где
не все коэффициенты

равны
нулю.

Теорема
(Лагранжа).
Для всякой квадратичной формы существует
такой базис,
в котором квадратичная форма имеет
канонический вид.

Определение.
Нормальным
видом квадратичной
формы называется такой канонический
вид,
в котором коэффициенты при квадратах
неизвестных (не считая нулевых) равны
.

Определение.
Квадратичная
форма

называется положительно

(отрицательно)
определённой, если

при всех

108

и
положительно (отрицательно)
полуопределённой,если

при всех
.

Теорема
(критерий
Сильвестра).
Для того чтобы квадратичная
форма

была положительно определённой,
необходимо и достаточно
чтобы все угловые миноры матрицы
квадратичной
формы
были положительны,то
есть,
чтобы

Здесь
-угловые
миноры матрицы квадратичной
формы.

Следствие.
Для того чтобы квадратичная
форма

была отрицательно определённой,
необходимо и достаточно,
чтобы знаки угловых миноров матрицы
квадратичной
формы чередовались следующим образом:

Примеры

1.
Привести квадратичную форму к каноническому
виду методом Лагранжа и записать
соответствующее преобразование

.

Решение.
Следуя алгоритму метода Лагранжа,
выделим вначале в квад-ратичной форме
все члены, содержащие
,
и дополним их до полного квадрата:

.

Сделаем
в этом выражении замену

и подставим его в квадратичную форму.
Получим:

.

Далее
выделим в

члены, содержащие

и проделаем с ними анало-гичную процедуру:

Если
положить
,
то квадратичная форма уже не будет
содержать смешанных произведений.
Примем также
,
тогда

109

канонический
вид квадратичной формы есть

.

Соответствующее
преобразование от переменных

к переменным

имеет вид:

.

2.
Найти ортогональное преобразование,
приводящее квадратичную форму к
каноническому виду, и записать
соответствующий канонический вид этой
формы:

.

Решение.
В исходном базисе

матрица оператора, соответствующая
данной квадратичной форме, есть

.

Эта
матрица будет определять
квадратичную форму канонического вида
в ортонормированном базисе
,
составленном из собственных векторов
матрицы
.
Найдем их.

Характеристическое
уравнение для матрицы

имеет вид

.

Откуда
следует

и
.

Как
известно собственные векторы матрицы
находятся из уравнений

.

Для
случая

имеем:

.

110

Ранг
матрицы этой системы уравнений
(относительно
)
равен 1. Следовательно, ФСР системы
состоит из двух линейно независимых
решений.

Как
видно из данной системы, величина

принимает произвольные значения, а
величины

связаны соотношением
.
В качестве собственных можно выбрать,
например, векторы

Эти
векторы ортогональны:

(если бы они оказались не ортогональными,
то их нужно было бы ортогонализировать
с помощью стандартной процедуры). Вектор

к тому же и нормирован. Откуда следует
–
.
Нормируем теперь вектор:

.

Для
случая

уравнение, определяющее собственный
вектор есть

.

Ранг
матрицы этой системы уравнений равен
2. Следовательно она имеет одно линейно
независимое решение, например,

Отнормируем этот вектор:
.

Теперь
можно составить искомую матрицу
ортогонального преобразования:

.

111

Исходная
квадратичная форма будет иметь следующий
канонический вид

.

При
этом переменные

связаны с переменными

соотношением

или

3.
Построить в прямоугольной системе
координат фигуру, определяемую следующим
уравнением, предварительно приведя его
к каноническому виду

.

Решение.
Выделим в этом выражении квадратичную
форму
.
Это три первых слагаемых уравнения
.

Матрица
квадратичной формы равна
.
Проведём процедуру приведения квадратичной
формы к каноническому виду с помощью
ортогонального преобразования.
Характеристическое уравнение матрицы
имеет вид

.

Его
корни таковы:
.

Найдём
теперь собственные векторы, соответствующие
этим корням и отнормрируем их. Для
вектора
,
соответствующего

,
имеем

112

В
итоге собственный вектор, соответствующий
,
можно выбрать в виде

.

Анологичная
процедура для собственного вектора
даёт:

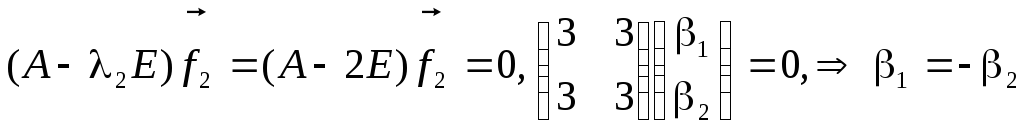
Откуда:

.

После
нормировки полученных векторов имеем:

.

Эти
векторы представляют собой ортонормированный
базис новой системы координат. Матрица
ортогонального оператора, приводящего
квадратичную форму

к каноническому виду
,
есть

Связь
старых

и новых

координат определяется соотношением

.

Учитывая
приведенные выражения, приведём заданную
квадратичную форму к каноническому
виду

113

Это
есть каноническое уравнение эллипса в
системе координат
,которая
получается из исходной её поворотом на
угол
и
переносом начала координат в точку
.

Задачи

Записать
матрицу квадратичной формы:

5.1.
;

5.2.
;

5.3.
;

5.4.
;

5.5.
;

5.6.
;

5.7.
;

5.8.
;

5.9.
;

5.10.
;

5.11.
.

Найти
ранг квадратичной формы:

5.12.
;

5.13.
;

5.14.
;

114

5.15.
;

5.16.
;

5.17.
;

5.18.
;

5.19.
;

5.20.
.

Записать
квадратичную форму в матричном виде:

5.21.

;

5.22.

;

5.23.

;

5.24.

;

5.25.

;

5.26.

;

5.27.

;

5.28.

;

5.29.

;

5.30.

.

Записать
квадратичную форму в виде

по
заданной

матрице
:

5.31.

;
5.32.
;

5.33.

;
5.34.
;

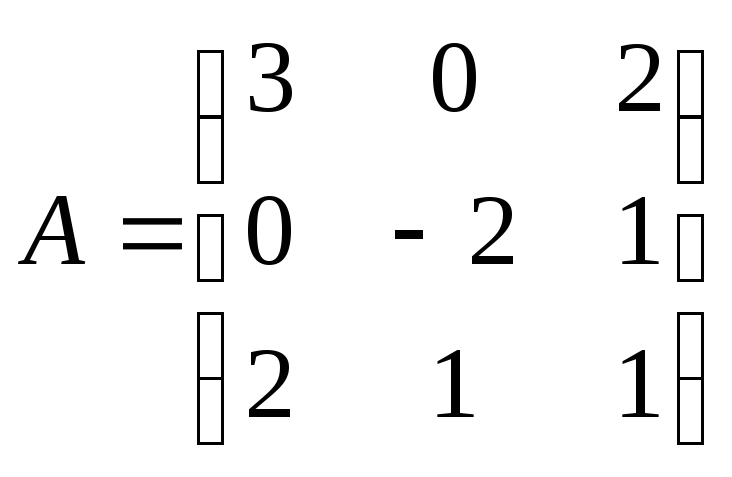115

5.35.

;
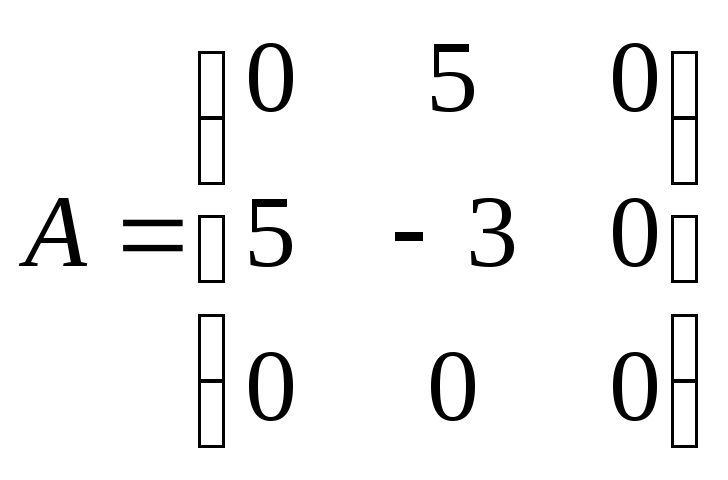5.36.
;

5.37.

;
5.38.
;

5.39.

;
5.40.
.

Привести
квадратичную форму к каноническому
виду методом

Лагранжа
и записать соответствующее преобразование:

5.41.

;

5.42.

;

5.43.

;

5.44.

;

5.45.

;

5.46.

;

5.47.

5.48.

5.49.

5.50.

5.51.

;

116

5.52.

.

Найти
ортогональное преобразование,
приводящее квадратичную

форму
к
каноническому
виду и записать соответствующий кано-

нический
вид квадратичной формы:

5.53.

;

5.54.

;

5.55.

;

5.56.

;

5.57.

;

5.58.

;

5.59.

;

5.60.

;

5.61.

;

5.62.

.

Записать
данное уравнение второго порядка в
матричном виде и

определить,
фигуру какого типа (эллиптического,
гиперболическо-

го,
параболического) оно определяет:

5.63.

5.64.

5.65.

5.66.

5.67.

5.68.

5.69.

5.70.

5.71.

5.72.

117

5.73.

5.74.

.

Построить
в прямоугольной системе координат Оху
(O;i,j)
фигуру,

определяемую
данным уравне-нием,
предварительно приведя его

к
каноническому виду:

5.75.

5.76.

5.77.

5.78.

5.79.

5.80.

5.81.

5.82.

5.83.

5.84.

.

Каждую
из квадратичных форм исследовать на
знакоопределённость

5.85.

5.86.

5.87.

5.88.

5.89.

5.90.

5.91.

5.92.

5.93.

;

5.94.

118

5.95.

;

5.96.

.

119

Соседние файлы в папке Анал_Геом

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

§ 1. Билинейные формы

Определение билинейной формы и ее различные формы записи

Определение. Билинейной формой на линейном пространстве над полем называется функция двух векторных аргументов, принимающая значения из поля , линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям:

1*. ;

2*. ;

3*. ;

4*. .

Рассмотрим N-мерное линейное пространство и выберем в нем какой-либо базис

(1)

Каждый вектор пространства можно разложить по этому базису: . Тогда

. (2)

Из (2) видно, Что значение билинейной формы для любых двух векторов и выражается через координаты этих векторов и некоторые числа , которые с аргументами и никаким образом не связаны, а зависят только от выбранного базиса. Обозначим

. (3)

Из (2) вытекает:

. (4)

Равенство (4) называется координатной формой записи билинейной формы.

Определение. Матрицей билинейной формы в базисе (1) называется матрица , где .

Обозначим, как обычно,

, —

Координатные столбцы векторов и соответственно в заданном базисе. Заметим, что — это число, которое можно рассматривать как матрицу размеров . В таком случае, (4) можно переписать и так: , откуда вытекает, что

. (5)

Равенство (5) называется матричной формой записи билинейной формы.

Итак, если в задан базис, то каждой билинейной форме на линейном пространстве соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.

Теорема 1. Пусть в линейном пространстве задан какой-либо базис (1). Тогда для любой квадратной матрицы , на линейном пространстве существует единственная билинейная форма , матрица которой в заданном базисе совпадает с В, то есть такая, для которой выполняется условие (3).

►Построение. Положим по определению:

Линейность.

;

.

Таким образом, линейность по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.

Выполнение условия (3). Так как (то есть I-я координата вектора равна , а J –я координата вектора — ). Поэтому .

Единственность. Предположим, что существует еще одна билинейная форма , не совпадающая с формой , для которой выполняется (3). Тогда

,

И мы пришли к противоречию.◄

Таким образом, если в задан какой-либо базис, то между множеством билинейных форм на линейном пространстве и множеством квадратных матриц N-го порядка с элементами из поля Р устанавливается взаимно однозначное соответствие.

Изменение матрицы билинейной формы при изменении базиса

Теорема 2. Пусть в линейном пространстве заданы два базиса:

(6)

И

, (7)

И пусть и — матрицы билинейной формы в базисах (6) и (7) соответственно. Тогда

, (8)

Где Т – матрица перехода от (6) к (7).

►Воспользуемся определением билинейной формы и ее матрицы:

. (9)

Заметим, что в правой части равенства (9) индекс должен соответствовать номеру строки, а индекс — номеру столбца (по согласованию с левой частью), поэтому из (9) и вытекает равенство (8).◄

Следствие. Если матрица билинейной формы в одном из базисов пространства невырождена, то в любом другом базисе матрица этой билинейной формы также невырождена.

Определение. Билинейная форма на линейном пространстве называется Невырожденной, если ее матрица в некотором, а значит, и в любом базисе пространства невырождена.

Определение. Квадратные матрицы и называются Конгруэнтными, если они связаны соотношением (8), где — невырожденная матрица.

Таким образом, матрицы одной и той же билинейной формы в различных базисах конгруэнтны.

Симметричные билинейные формы

Определение. Квадратная матрица называется Симметричной, если , или, если .

Лемма. Если матрица симметрична, то любая конгруэнтная ей матрица тоже симметрична.

►Пусть — симметричная матрица, — конгруэнтная ей. Тогда

.◄

Определение. Билинейная форма на линейном пространстве V называется Симметричной, если .

Теорема 3. Для того чтобы билинейная форма на линейном пространстве была симметричной, необходимо и достаточно, чтобы ее матрица в некотором, а значит, и в любом базисе пространства была симметричной.

►Докажем утверждение для некоторого базиса, а для произвольного оно будет вытекать из доказанной леммы. Обозначим матрицу билинейной формы в базисе.

Необходимость. Дано: — симметричная билинейная форма. Тогда и, таким образом, В — симметричная матрица.

Достаточность. Дано: В – симметричная матрица, то есть, . Тогда =.◄

Замечание. При доказательстве теоремы 3 мы также доказали, что преобразование конгруэнтности сохраняет свойство матрицы быть симметричной.

§ 2. Квадратичные формы

Определение. Квадратичной формой, соответствующей симметричной билинейной форме на линейном пространстве V, называется функция одного векторного аргумента .

Пусть задана квадратичная форма , — соответствующая ей симметричная билинейная форма. Тогда

,

Откуда вытекает, что по квадратичной форме соответствующая ей симметричная билинейная форма тоже определяется однозначно. Итак, между симметричными билинейными и квадратичными формами на линейном пространстве V устанавливается взаимно однозначное соответствие, поэтому квадратичные формы можно изучать с помощью симметричных билинейных.

Рассмотрим N-мерное линейное пространство . Матрицей квадратичной формы в заданном базисе линейного пространства называется матрица соответствующей ей симметричной билинейной формы в том же базисе. Матрица квадратичной формы всегда симметрична.

Обозначим матрицу квадратичной формы в некотором базисе пространства . Если, как обычно, обозначить Х координатный столбец вектора в том же базисе, то в матричном виде квадратичная форма запишется так:

. (1)

Теорема 1. Пусть в линейном пространстве заданы два базиса

(2)

И

, (3)

И пусть и – матрицы квадратичной формы В базисах (2) и (3) соответственно. Тогда , где Т — матрица перехода от (2) к (3).

Доказательство вытекает из теоремы 1 § 1 и определения матрицы квадратичной формы.

В связи с тем, что матрица перехода Т является невырожденной, то при переходе к новому базису ранг матрицы квадратичной формы не меняется. Поэтому можно сформулировать следующее

Определение. Рангом квадратичной формы, заданной на линейном пространстве , называется ранг ее матрицы в некотором, а значит, и в любом базисе пространства (обозначается ).

Теперь запишем квадратичную форму в координатном виде. Для этого вектор разложим по базису (2): . Если — матрица квадратичной формы в том же базисе, то, в соответствие с равенством (4) § 1 имеем:

— (4)

Координатная форма записи квадратичной формы. Распишем (4) подробно при N=3, учитывая, что

. (4′)

Итак, если в задан базис, то квадратичная форма в координатной записи выглядит как однородный многочлен второй степени от N переменных — координат вектора в данном базисе. Этот многочлен называется Видом квадратичной формы в заданном базисе. Но в приложениях часто такие многочлены возникают самостоятельно, без видимой связи с линейными пространствами (например, вторые дифференциалы функций), поэтому мы сформулируем еще одно определение квадратичной формы.

Определение. Квадратичной формой от N переменных называется однородный многочлен второй степени от этих переменных, т. е. функция вида (4). Матрицей квадратичной формы (4) называется симметричная матрица .

Пример составления матрицы квадратичной формы. Пусть

. (5)

Из (4) и (4′) видно, что коэффициент при совпадает с , т. е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что — половина коэффициента при произведении . Таким образом, матрица квадратичной формы (5) выглядит так:

.

Выберем теперь в пространстве опять два базиса (2) и (3) и обозначим, как обычно, — координатные столбцы вектора в базисах (2) и (3) соответственно. При переходе от базиса (2) к базису (3) координаты вектора меняются по закону:

, (6)

Где — матрица перехода от (2) к (3). Заметим, что матрица — невырожденная. Запишем равенство (6) в координатной форме:

, (7)

Или подробно:

. (8)

С помощью равенств (8) (или (7), что одно и то же) от переменных переходим к переменным .

Определение. Линейным невырожденным преобразованием переменных называется преобразование переменных, заданное системой равенств (7) или (8), или одним матричным равенством (6), при условии, что — невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.

Если в (4) вместо переменных подставить их выражения через переменные По формулам (8), раскрыть скобки и привести подобные, то получим другой однородный многочлен второй степени

.

В этом случае говорят, что линейное невырожденное преобразование переменных (8) переводит квадратичную форму в квадратичную форму . Значения переменных и , связанные соотношением (6) (или соотношениями (7) либо (8)) будем называть Соответствующими при заданном линейном невырожденном преобразовании переменных.

Определение. Набор переменных называется Нетривиальным, если в нем значение хотя бы одной из переменных отлично от нуля. В противном случае набор переменных называется Тривиальным.

Лемма. При линейном невырожденном преобразовании переменных тривиальному набору переменных соответствует тривиальный набор.

►Из равенства (6), очевидно, вытекает: если , то и . С другой стороны, используя невырожденность матрицы Т, опять же из (6) получаем , откуда видно, что при также и .◄

Следствие. При линейном невырожденном преобразовании переменных нетривиальному набору переменных соответствует нетривиальный набор.

Теорема 1′. Если линейное невырожденное преобразование (6) переводит квадратичную форму с матрицей А в квадратичную форму с матрицей А’, то (другая формулировка теоремы 1).

Следствие. При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака.

Замечание. В отличие от матрицы перехода и матрицы линейного оператора матрица линейного невырожденного преобразования переменных пишется не по столбцам, а по строкам.

Пусть заданы два линейных невырожденных преобразования переменных:

(9)

И

. (10)

Применим их последовательно:

. (11)

Композицией линейных невырожденных преобразований переменных (9) и (10) называется их последовательное применение, т. е. преобразование переменных Из (11) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.

Определение. Квадратичные формы называются Эквивалентными, если существует линейное невырожденное преобразование переменных, переводящее одну из них в другую.

§ 3 Канонический вид квадратичной формы

Мы уже говорили о том, что в каждом базисе линейного пространства квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.

Каноническим видом квадратичной формы называется такой ее вид, в котором коэффициенты при произведениях разноименных переменных равны 0, то есть при .

Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или -1. Все отличные от нуля коэффициенты при квадратах Нормального вида комплексной квадратичной формы равны 1.

Теорема 1. Для любой квадратичной формы, заданной на линейном пространстве в существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.

Или (другая формулировка этой же теоремы):

Для любой квадратичной формы от N переменных существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, и существует линейное невырожденное преобразование переменных, приводящее ее к нормальному виду.

Теорему 1 мы докажем позже, а сейчас только приведем пример приведения квадратичной формы к каноническому виду методом, который называется Методом Лагранжа или выделения полных квадратов. Он заключается в следующем: выбираем переменную, коэффициент при квадрате которой отличен от 0, и выделяем полный квадрат, включающий в себя все слагаемые с этой переменной. С этой целью записываем перед скобкой число, обратное выбранному коэффициенту, а в скобках — половину производной по выбранной переменной. За скобками остается квадратичная форма, количество переменных которой уже на единицу меньше. После конечного числа шагов получаем канонический вид.

Пример. ▼

Где . Матрица этого линейного преобразования запишется так:

.

Как видим, она невырождена, значит, и преобразование переменных является невырожденным. Вводя обозначения

,

Получаем нормальный вид квадратичной формы: .▲

Замечания. 1. На самом деле при применении метода Лагранжа получаем не прямое преобразование, приводящее квадратичную форму к каноническому виду, а обратное, т. е. преобразование, которое выражает не старые переменные через новые, а наоборот.

2.Если все коэффициенты при квадратах исходной квадратичной формы равны нулю, а отличен от нуля, например, коэффициент при произведении , применим вначале следующее преобразование: Матрица этого преобразования выглядит так:

.

Очевидно, она невырождена, и, поэтому, соответствующее преобразование переменных также будет невырожденным.

Заметим, что канонический вид квадратичной формы определяется неоднозначно, тем не менее, имеет место

Теорема 2 (Закон инерции). Все канонические виды одной квадратичной формы на действительном линейном пространстве имеют одинаковое число положительных коэффициентов и одинаковое число отрицательных коэффициентов. Нормальный вид квадратичной формы определяется однозначно с точностью до порядка следования коэффициентов.

►Доказательство достаточно провести для нормального вида.

Пусть в базисе линейного пространства квадратичная форма имеет вид

, (2)

А в базисе — вид

. (3)

Так как , то достаточно показать, что . Предположим, что это не так. Пусть, например, . Обозначим

, .

Так как а , то сумма не прямая, поэтому , следовательно, . Тогда, так как , то из (2) видно, что Но, так как , то из (3) видно, видно, что Итак, мы пришли к противоречию. Таким образом, . Аналогично доказывается, что , значит, .◄

Замечание. Для квадратичных форм на комплексном линейном пространстве нормальный вид, очевидно, определяется однозначно, т. к. количество отличных от нуля коэффициентов совпадает с рангом квадратичной формы.

§ 4. Знакоопределенные квадратичные формы

В этом параграфе и до конца главы мы будем рассматривать квадратичные формы только на действительных линейных пространствах.

Определения. Квадратичная форма называется Положительно определенной, если она принимает положительные значения для любого нетривиального набора переменных.

Квадратичная форма называется Отрицательно определенной, если она принимает отрицательные значения для любого нетривиального набора переменных.

Квадратичная форма называется Положительно (отрицательно) полуопределенной, если для любого нетривиального набора переменных она принимает либо положительное (отрицательное) значение, либо 0.

Квадратичная форма Знаконеопределена, если существует нетривиальный набор переменных, при которых она принимает положительное значение, и существует нетривиальный набор переменных, при котором она принимает отрицательное значение.

Лемма 1. Эквивалентные квадратичные формы принимают одинаковые значения при соответствующих наборах переменных.

►Пусть квадратичные формы

(1)

И

(2)

Эквивалентны. Это значит, что существует линейное невырожденное преобразование переменных , переводящее квадратичную форму в квадратичную форму . Тогда, по теореме 1′ § 2, , а значит,

.◄

Следствие. Если квадратичная форма положительно определена, то все эквивалентные ей квадратичные формы также положительно определены.

Лемма 2 (Необходимое условие знакоопределенности). Если квадратичная форма положительно (отрицательно) определена, то все ее коэффициенты при квадратах положительны (отрицательны).

►Пусть квадратичная форма

=

Положительно определена. Тогда (единица на M-ом месте), следовательно, все коэффициенты при квадратах положительны.◄

Теорема (Первый критерий знакоопределенности). Для того чтобы квадратичная форма была положительно (отрицательно) определенной необходимо и достаточно, чтобы все коэффициенты какого-либо ее канонического вида были положительными (отрицательными).

►Пусть задана квадратичная форма и пусть

=— (3)

Какой-либо ее канонический вид.

Необходимость. Дано: исходная квадратичная форма положительно определена. Тогда, по следствию к лемме 1, форма (3) тоже положительно определена, а значит, по лемме 2, .

Достаточность. Дано: . Тогда, очевидно, для любого нетривиального набора переменных форма (3) принимает только положи

Тельные значения, следовательно, форма (3) положительно определена, и поэтому, положительно определена и исходная квадратичная форма. ◄

Следствие. Матрица положительно определённой квадратичной формы имеет положительный определитель.

►Пусть А – матрица положительно определенной квадратичной формы, А’ – матрица ее канонического вида (3). При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака. Так как ,то и .◄

§ 5. Критерий Сильвестра знакоопределенности

Квадратичных форм

Назовем R— м усечением квадратичной формы

(1)

Квадратичную форму . Пусть

—

Матрица квадратичной формы (1). Главными минорами матрицы А называются ее миноры, расположенные в левом верхнем углу. Будем обозначать главный минор R-го порядка матрицы А. Очевидно, что совпадает с определителем матрицы квадратичной формы .

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной необходимо и достаточно, чтобы все главные миноры ее матрицы были положительными. Для того чтобы квадратичная форма была отрицательно определенной необходимо и достаточно, чтобы все главные миноры ее матрицы нечетного порядка были отрицательными, а четного – положительными.

►Доказательство для положительной определенности.

Необходимость. Дано: квадратичная форма K положительно определена. Тогда для любого нетривиального набора переменных , значит, положительно определена и квадратичная форма , и поэтому на основании следствия к теореме §4.

Достаточность. Дано: . Доказательство проведем методом математической индукции по количеству переменных.

A) Проверяем утверждение при . Имеем: , т. е. квадратичная форма K положительно определена.

В) Пусть утверждение верно для квадратичных форм от (N-1)-й переменной. Докажем его для квадратичных форм от N переменных.

Так как , то, по предположению индукции, квадратичная форма положительно определена, а значит, существует линейное невырожденное преобразование переменных

(2)

С матрицей , приводящее к нормальному виду . Рассмотрим следующее преобразование переменных:

. (3)

Если Т – матрица преобразования (3), то , а значит, (3) — линейное невырожденное преобразование переменных. Применив (3) к форме (1), получаем:

[(3)]

. (4)

Обозначим и положим

(5)

Очевидно, (5) – линейное преобразование переменных с матрицей

Так как , то (5) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (4) в квадратичную форму

. (6)

Применяя к форме (1) композицию преобразований (3) и (5), получаем квадратичную форму (6), и, таким образом, (6) эквивалентна исходной квадратичной форме (1).

Обозначим матрицу формы (6). Так как при линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака, и т. к. detA=, то

.

Поэтому квадратичная форма (6) положительно определена согласно теореме § 4, а значит, положительно определена и исходная квадратичная форма

Доказательство для отрицательной определенности. Обозначим , — матрицу квадратичной формы , — главные миноры матрицы . Тогда:

{K отрицательно определена}{ положительно определена}

◄

Замечание. Можно доказать, что, если хотя бы один минор четного порядка матрицы квадратичной формы есть число отрицательное, то эта квадратичная форма знаконеопределена.

Определение. Симметричная билинейная форма называется Положительно определенной, если положительно определена соответствующая ей квадратичная форма.

Упражнение. Сформулируйте критерий знакоопределенности для симметричной билинейной формы.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 сентября 2021 года; проверки требуют 3 правки.

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

Определение[править | править код]

Пусть есть векторное пространство над полем и — базис в .

Функция называется квадратичной формой,
если её можно представить в виде

где , а — некоторые элементы поля .

Связанные определения и свойства[править | править код]

.

где — матрица квадратичной формы в новом базисе.

• Из формулы следует, что определитель матрицы квадратичной формы не является её инвариантом (т.е. не сохраняется при замене базиса, в отличие, например, от матрицы линейного отображения), но её ранг — является. Таким образом, определено понятие ранга квадратичной формы.
• Если матрица квадратичной формы имеет полный ранг , то квадратичную форму называют невырожденной, в противном случае — вырожденной.
• Для любой квадратичной формы существует единственная симметричная билинейная форма , такая, что . Билинейную форму называют полярной к , если она может быть вычислена по формуле

• Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

Знакоопределённые и знакопеременные формы[править | править код]

В случае, когда (поле вещественных чисел), важную роль, в том числе, для различных приложений, играют понятия положительно и отрицательно определённой квадратичной формы.

Для решения вопроса о том, является ли данная квадратичная форма положительно (отрицательно) определённой, используется критерий Сильвестра:

• Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
• Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

Канонический вид[править | править код]

Вещественный случай[править | править код]

В случае, когда (поле вещественных чисел), для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид, то есть содержит только квадраты переменных:

где  — ранг квадратичной формы. . В этом случае коэффициенты называются каноническими коэффициентами. В случае невырожденной квадратичной формы , а в случае вырожденной — .

Существует также нормальный вид квадратичной формы:
.

Для приведения квадратичной формы к каноническому виду обычно используются метод Лагранжа или ортогональные преобразования базиса, причем привести данную квадратичную форму к каноническому виду можно не одним, а многими способами.

Число (отрицательных членов) называется индексом инерции данной квадратичной формы, а число (разность между числом положительных и отрицательных членов) называется сигнатурой квадратичной формы. Отметим, что иногда сигнатурой квадратичной формы называют пару . Числа являются инвариантами квадратичной формы, то есть не зависят от способа её приведения к каноническому виду (закон инерции Сильвестра).

Комплексный случай[править | править код]

В случае, когда (поле комплексных чисел), для любой квадратичной формы существует базис, в котором форма имеет канонический вид

где  — ранг квадратичной формы. Таким образом, в комплексном случае (в отличие от вещественного) квадратичная форма имеет один единственный инвариант — ранг, и все невырожденные формы имеют один и тот же канонический вид (сумма квадратов).

Примеры[править | править код]

См. также[править | править код]

• Теорема Витта
• Метод Лагранжа приведения квадратичной формы к каноническому виду

Примечания[править | править код]

Литература[править | править код]

• Беклемишев Д. В. Аналитическая геометрия и линейная алгебра.-М.: Высш. шк. 1998, 320с.
• Гельфанд И. М., Линейная алгебра. Курс лекций.
• Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
• Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М.: МЦНМО, 2008. — 144 с. — 1000 экз. — ISBN 978-5-94057-268-8.
• Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
• Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
• Кострикин А. И. Введение в алгебру, М.: Наука, 1977.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное
образовательное учреждение

высшего образования

«БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ АКАДЕМИКА И.Г. ПЕТРОВСКОГО»

Естественно-научный институт

Физико-математический факультет

Кафедра математического анализа, алгебры и
георметрии

КУРСОВАЯ РАБОТА

Нормальные квадратичные формы

Код, направление подготовки: 440301
Педагогическое образование

Направленность (профиль) программы:
Математика

Обучающийся

ФИО

2 курса

Заочная форма обучения

Даронина Анастасия Олеговна

Руководитель

Еловикова Юлия Александровна,

доцент кафедры математического анализа,
алгебры и геометрии,

кандидат физико-математических наук

______________

Брянск 2022

Оглавление.

Введение…………………………………………………………………3

Глава
1. Теоретическая часть…………………………………………5

Квадратичная
форма и ее матрица………………………………5

Преобразование
квадратичной формы при линейном однородном преобразовании
переменных………………………………9

Приведение
действительной квадратичной формы к нормальному виду…………………………………………………………11

Закон
инерции квадратичных форм……………………………14

Знакоопределенные
квадратичные формы……………………16

Упрощение
уравнений фигур второго порядка на плоскости и в пространстве……………………………………………………..19

Глава
2. Практическая часть…………………………………………23

Список
использованной литературы…………………………………28

Введение

Арифметическая
теория квадратичных форм берет свое начало с утверждения Ферма о представимости
простых чисел суммой двух квадратов.

Теория
квадратичных форм впервые была развита французским математиком Лагранжем,
которому принадлежат многие идеи в этой теории, в частности, он ввел важное
понятие приведенной формы, с помощью которого им была доказана конечность числа
классов бинарных квадратичных форм заданного дискриминанта. Затем эта теория
была значительно расширена Гауссом, который ввел много новых понятий, на основе
которых ему удалось получить доказательства трудных и глубоких теорем теории
чисел, ускользавших от его предшественников в этой области

Изучение
основ теории билинейных и квадратичных форм вызывает ряд трудностей методического
характера, обусловленных существованием нескольких различных подходов к
построению этой теории. Принятое изложение, основанное на теории унитарных и
евклидовых пространств и содержит единый подход к изучению симметричных и
эрмитовых форм.

При
изучении квадратичных форм необходимо знание классических понятий теории
унитарных и евклидовых пространств и основных свойств самосопряженных и
унитарных (ортогональных) линейных операторов. Общими обозначениями являются: P
– основное поле, под которым мы будем понимать поле комплексных чисел C или
поле действительных чисел R. α – комплексное число, сопряженное к комплексному
числу α ( α= α . α . R); |α| – модуль комплексного числа α. L – линейное
пространство над полем P. В случае, когда размерность линейного пространства L
равна n (L = Ln) будем считать L унитарным (при P = C ) или евклидовым (при P =
R ) пространством, так как на любом конечном пространстве Ln над полем C или R
можно определить скалярное произведение. Для любых векторов x, y . Ln (x, y)
обозначает их скалярное произведение. Остальные обозначения или являются
общепринятыми в линейной алгебре.

Целью
курсовой работы является рассмотрение квадратичной формы и ее свойств.

Перейдем
теперь к краткой характеристике содержания курсовой работы, посвященной
некоторым вопросам теории неопределенных бинарных квадратичных форм.

В
теоретической части работы приводятся предварительные общие сведения
квадратичных формах и ее свойств.

В
практической части курсовой работы представляется решение задач по заданной теме.

Глава 1.
Теоретическая часть

Квадратичная форма и ее
матрица.

Квадратичной
формой называется функция B(x) = A(x,x) из линейного пространства L над
произвольным полем F характеристики не 2 в поле F, которая получается из
билинейной формы A(x,y) при x = y.

При
фиксированном базисе в L квадратичная форма  имеет вид

(по
соглашению Эйнштейна), где , а aij =aji.

Квадратичной
формой f (x1,x2…,xn) п действительных переменных (x1,x2…,xn) называется сумма
вида:

(1.1)

или
f(x1,x2,…xn) = ∑i=1 ∑ j=1 aij xi xj, (1.2), где aij – некоторые числа,
называемые коэффициентами.

Не
ограничивая общ­ности, можно считать, что aij = aji. Квадратичная форма
называется действительной или комплексной в зависимости от того, являются ли ее
коэффициенты соответственно действительными или ком­плексными числами. Будем
рассматривать действительные квадратичные формы.

Квадратичная
форма обладает следующими свойствами:

1)
Симметричную билинейную форму A(x,y), называют полярной квадратичной форме
A(x,x). Матрица билинейной формы в произвольном базисе совпадает с матрицей
полярной ей билинейной формы в том же базисе.

2)
Если матрица квадратичной формы имеет полный ранг, то квадратичную форму
называют невырожденной, иначе – вырожденной.

3)
Квадратичная форма A(x,x) называется положительно (отрицательно) определённой,
если для любого x≠ 0 A(x,x) > 0 (A(x,x) < 0). Положительно определённые и
отрицательно определённые формы называются знакоопределёнными.

Квадратичная
форма является положительно определенной, тогда и только тогда, когда все
угловые миноры её матрицы строго положительны.

Квадратичная
форма является отрицательно определенной, тогда и только тогда, когда знаки
всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

4)
Квадратичная форма A(x,x) называется знакопеременной, если она принимает как
положительные, так и отрицательные значения.

5)
Квадратичная форма A(x,x) называется квазизнакоопределённой, если  , но форма 
не является знакоопределённой.

Для
приведения квадратичной формы к каноническому виду используется метод Лагранжа.
Метод приведения квадратичной формы к каноническому виду, указанный в 1759 году
Лагранжем.

Данный
метод состоит в последовательном выделении в квадратичной форме полных
квадратов. Пусть  есть данная квадратичная
форма. Возможны два случая:

–
хотя бы один из коэффициентов aii при квадратах отличен от нуля. Не нарушая
общности, будем считать a11≠0 (этого всегда можно добиться соответствующей
перенумерацией переменных);

–
все коэффициенты aii = 0,i = 1,2,…,n, но есть коэффициент,
отличный от нуля (для определённости пусть будет ) a12≠0.В первом случае
преобразуем квадратичную форму следующим образом:

 где
y1 = a11x1 + a12x2 + … + a1nxn, а через f2(x2, x3,…,xn) обозначены все
остальные слагаемые. f2(x2,…,xn) представляет собой квадратичную форму от n-1
переменных x2, x3,…,xn. С ней поступают аналогичным образом и так далее.
Заметим, что

Второй
случай заменой переменных x1 = y1 + y2, x2 = y1 − y2, x3 = y3,…,xn = yn
сводится к первому.

Матрицей
квадратичной формы называется матрица, составленная из ее коэффициентов.
Квадратичной форме (1.1) соответствует единственная симметрическая матрица

(1.3)

И
наоборот, всякой симметрической матрице (1.3) соответствует единственная
квадратичная форма с точностью до обозначения переменных.

Рангом
квадратичной формы называют ранг ее матрицы. Квадратичная форма n переменных
называется невырожденной, если ее матрица невырожденная, т. е. r = п, и
вырожденной, если r< п. При решении различных задач математики очень часто
приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц
удобно решать системы линейных уравнений, выполнять многие операции с
векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Матрицей
называется прямоугольная таблица из чисел, содержащая некоторое количество m
строк и некоторое количество п столбцов. Числа т и п называются порядками
матрицы. В случае, если т = п, матрица называется квадратной, а число m = n —
ее порядком.

В
дальнейшем для записи матриц будут применяться либо сдвоенные черточки, либо
круглые скобки

Квадратичную
форму (1.1) п переменных х1, х2,…,хn можно записать в мат­ричном виде.
Действительно, если Х- матрица-столбец из переменных (x1,x2…,xn), XT – матрица,
полученная транспонированием матрицы X, т.е. матрица-строка из тех же
переменных, то f (x1,x2…,xn)= XTAX (1.4), А определяется формулой (1.3).

Пример
1.

Пусть
e1, …, en — базис в L. И пусть для вектора x из L задано разложение x =
x1·e1+x2·e2+ …+ xn· en. Тогда для квадратичной формы k(x) справедливо
представление

Здесь
φ(ei , ej ) — значение полярной для k(x) билинейной формы φ(x , y). Матрица A =
{aij} называется матрицей квадратичной формы. Определённая таким образом
матрица квадратичной формы является симметричной матрицей. Пусть k(x) = x12 +
x22— квадратичная форма в пространстве R2. Пусть e1= (1, 0), e2= (0, 1) — базис
в R2. Вычислим матрицу A квадратичной формы. Поскольку симметричная билинейная
форма φ(x, y) = (x, y) — полярная для квадратичной формы k(x) = φ(x, x ) то
матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x , y):

Проверим.
Для этого подставим матрицу A в матричное представление квадратичной формы
k(x)=xT·A·x:

Матрица
квадратичной формы вычислена, верно.

Преобразование квадратичной
формы при линейном однородном преобразовании переменных.

Рассмотрим
квадратичную форму (1.1). Перейдем к новым переменным y1, y2….yn по формулам

(1.5)

или
в матричном виде X=BY (1.6), где. (1.7)

В
квадратичной форме (1.1) вместо (x1,x2…,xn) подставим их выражения через y1,
y2….yn определяемые формулами (1.5), получим квадратичную форму φ (y1, y2….yn)
п переменных с некоторой матрицей С. В этом случае го­ворят, что квадратичная
форма f(x1,x2,…xn) переводится в квадратичную форму φ (y1, y2….yn) линейным
однородным преобразованием (1.5). Линейное одно­родное преобразование (1.6)
называется невырожденным, если det B≠0.

Две
квадратичные формы называются конгруэнтными, если существует невы­рожденное
линейное однородное преобразование, переводящее одну форму в дру­гую. Если f
(x1,x2…,xn) и φ (y1, y2….yn) конгруэнтны, то будем писать f (x1,x2…,xn) ~ φ
(y1, y2….yn). Свойства конгруэнтности квадратичных форм:

f
(x1,x2…,xn) ~ φ (y1, y2….yn).

Если
f (x1,x2…,xn) ~ φ (y1, y2….yn), φ (y1, y2….yn)~ψ(z1, z2…zn)

Теорема
1. Квадратичная форма f (x1,x2…,xn) с матрицей А линей­ным однородным
преобразованием Х = ВУ переводится в квадратичную форму φ (y1, y2….yn) с
матрицей С=ВT АВ.

Следствие
1. Определители матриц конгруэнтных невырожденных действительных квадратичных
форм имеют одинаковые знаки.

Следствие
2. Конгруэнтные квадратичные формы имеют одинаковые ранги.

Приведение действительной
квадратичной формы к нормальному виду.

Квадратичная
форма f (x1,x2…,xn) называется канонической, если она не содержит произведений
различных переменных, т. е Каноническая
квадратная форма называется нормальной (или имеет нормаль­ный вид), если | an |
= 1 ( i= 1, 2, . . . , r), т. е. отличные от нуля коэффициенты при квадратах
переменных равны +1 или —1.

Например,
квадратичная форма f (x1,x2…,xn) = 6×21+4×23 – 3×24, для которой a11 =6, a22=0,
a33 = 4, a44= -3, имеет канонический вид; квадратная форма f (x1, x2, x3, x4) =
x21 – – x23 + x24 явля­ется нормальной, так как a11 =1, a22=0, a33 = – 1, a44=
1.

Теорема
2. Любая квадратичная форма некоторым невырожденным линейным преобразованием
может быть приведена к каноническому виду

,
где y1, y2….yn – новые переменные.

Некоторые
из коэффициентов bij могут оказаться равными нулю; число отличных от нуля
коэффициентов в этой формуле равно рангу r матрицы квадратичной формы φ.
Теорема 3. Любую действительную квадратичную форму линейным не­вырожденным
преобразованием можно привести к нормальному виду Число входящих сюда квадратов
равно рангу формы.

Пример
1. Привести к каноническому виду квадратичную форму Ф(х1, х2) = 27.
Коэффициенты: а11 = 27,   а12 = 5,   а22 = 3.

Составим
характеристическое уравнение:

(27
– l)(3 – l) – 25 = 0

l2
– 30l + 56 = 0

l1
= 2;   l2 = 28;

Пример
2. Привести к каноническому виду уравнение второго порядка: 17×2 + 12xy + 8y2 –
20 = 0. Коэффициенты а11 = 17, а12 = 6, а22 = 8. А=

Составим
характеристическое уравнение:

(17
– l)(8 – l) – 36 = 0

136
– 8l – 17l + l2 – 36 = 0

l2
– 25l + 100 = 0 l1 = 5,     l2 = 20.

Итого:–
каноническое уравнение эллипса.

Пример
3. Используя теорию квадратичных форм, привести к каноническому виду уравнение
линии второго порядка. Схематично изобразить график.

Решение:
Составим характеристическое уравнение квадратичной формы :при

Решив
это уравнение, получим l1 = 1, l2 = 11.

Найдем
координаты собственных векторов:

полагая
m1 = 1, получим  n1 =

полагая
m2 = 1, получим  n2 =

Собственные
векторы:

Находим
координаты единичных векторов нового базиса.

Имеем
следующее уравнение линии в новой системе координат:

Каноническое
уравнение линии в новой системе координат будет иметь вид:

Закон инерции квадратичных
форм.

Закон
инерции квадратичных форм выражает:

Теорема
4. Число положительных и число отрицательных квадратов в нормальном виде, к
которому приводится данная действительная квадратичная форма невырожденным
действительным линейным преобразованием, не зависит от выбора преобразования.

Число
положительных квадратов в нормальной форме, к которой приводится данная
действительная квадратичная форма, называют положительным индексом инерции этой
формы, число отрицательных квадратов – отрицательным индек­сом инерции,
разность между положительным и отрицательным индексами инер­ции – сигнатурой
формы f. Если известен ранг формы, то задание любого из трех указанных выше
чисел определяет два других.

Теорема
5. Две действительные квадратичные формы от n пере­менных тогда и только тогда
конгруэнтны, когда они имеют одинаковые ранги и одинаковые сигнатуры.

Пусть
k(x) = 3×12 − 2x2x1+ 3×22— квадратичная форма в пространствеR2. И пусть e1= (1,
0), e2= (0, 1) — базис в R2. Марица A квадратичной формы в этом базисе имеет
вид:Найдём канонический базис
квадратичной формы — собственный базис матрицы A и приведём её к диагональному
виду:

Имеем:
E1, E2 — канонический базис квадратичной формы. Канонический вид квадратичной
формы в этом базисе k(y) = 4y12 + 2y22. Числа 4, 2 — канонические коэффициенты
квадратичной формы. Положительный индекс инерции квадратичной формы равен 2.
Отрицательный индекс инерции квадратичной формы равен 0. Сигнатура квадратичной
формы равна 2 − 0 = 2. Ранг квадратичной формы равен 2.

Знакоопределенные квадратичные
формы.

Действительная
квадратичная форма f (x1,x2…,xn) называется положитель­но-определенной, если
она приводится к нормальному виду, состоящему из п по­ложительных квадратов: f
(x1,x2…,xn) ~ φ (y1, y2….yn), где (1.9)

т.
е. если ранг и положительный индекс инерции равны числу неизвестных.

Систему
значений x1,x2…,xn назовем нулевой, если x1= х2 = … = xn =0, и ненулевой,
если хотя бы одно из них отлично от нуля.

Теорема
6. Действительная квадратичная форма f (x1,x2…,xn) является
положительно-определенной тогда и только тогда, когда она принимает положительные
значения при любой ненулевой системе значений переменных x1, x2…,xn. Пусть дана
квадратичная форма f (x1,x2…,xn) с матрицей А = (ау). Глав­ными минорами
квадратичной формы f называются миноры

матрицы
А, расположенные в левом верхнем углу; последний из них совпадает с
определителем матрицы.

Теорема
7. Квадратичная форма f (x1,x2…,xn) с действительной матрицей
является положительно-определенной тогда и только тогда, когда все ее главные
миноры положительны.

Действительная
квадратичная форма называется отрицательно-определенной, ес­ли она является
невырожденной и приводится к нормальному виду, содержащему только отрицательные
квадраты всех переменных; эту форму можно привести к виду:

φ
(y1, y2….yn)= -y21 – y22 -…- y2n (1.10).

Теорема
8. Квадратичная форма является отрицательно-определенной тогда и только тогда,
когда ее главные миноры четного порядка положительны, а нечетного –
отрицательны.

Положительно-определенные
и отрицательно-определенные квадратичные формы называются знакоопределенными
квадратичными формами.

Вырожденные
квадратичные формы, нормальный вид которых состоит из квадратов одного знака,
называются полуопределенными. Неопределенными называются квадратичные формы,
нормальный вид которых содержит как положительные, так и отрицательные квадраты
переменных.

Пример.
Доказать, что квадратичная форма f (x1, x2, x3)

=
6×21+ 5х22 + 7х2/3 – 4х1х2 + 4х1×3 положительно-определенная.

Запишем
матрицу A этой квадратичной формы и определитель матрицы

е,
так и отрицательные квадраты переменных.

Так
как главные миноры матрицы a11=6,  все положительны, то данная квадратичная
форма является положительно-определенной.

Теорема
9. Если существует ортогональное преобразование с матри­цей С, приводящее
действительную квадратичную форму f (x1,x2…,xn) к ка­ноническому виду:

φ
(y1, y2….yn)= λ1y21+λ2y22+λny2n (1.11),

то
λ1, λ2,…. λn — характеристические числа матрицы А квадратичной формы f.

Теорема
10. Для любой действительной квадратичной формы сущест­вует ортогональное
преобразование, приводящее ее к каноническому виду.

Теорема
11. Для любой действительной симметрической матрицы А су­ществует такая
ортогональная матрица Т, что Т-1АТ – диагональная матрица.

С
помощью матрицы В записываем искомое ортогональное преобразование x1= √3/5 y1 +
√2/5 y2, x1= 1/√5(√3y1 + √2y2) или x2= √2/5 y1 + √3/5 y2, x2 = 1/√5 (- √2y1 +
√3y2).

Это
преобразование приводит данную квадратичную форму к каноническому виду φ (y1,
y2) = y21+ 11y22.

Упрощение уравнений фигур второго порядка на плоскости и в
пространстве

Глава 2.
Практическая часть.

Задание
1. Привести к каноническому виду уравнение линии в квадратичной форме.

Задание
2. Какую поверхность определяет уравнение 6×2+5y2+7z2– 4xy+4xz=18?

Решение
задания № 1.

Составим
характеристическое уравнение квадратичной формы 6×2 + 2√5xy + 2y2 – 21=0, при
a11=6, a12=√5, a22=2.

==(6
– λ)(2 – λ) -5 = 12 – 6λ – 2λ + λ2 – 5=λ2 – 8λ+ 7.

Находим
корни этого уравнения, λ1= 7, λ2= 1.

Найдем
координаты собственных векторов:

Полагая
m1 = 1, получим n1 = 1/√5

Полагая
m2 = 1, получим n2 = – √5

Ответ:
уравнение определяет эллипсоид с полуосями, а =√6, b =√3, c = √2.

Следствие
1. Определители матриц конгруэнтных невырожденных действительных квадратичных
форм имеют одинаковые знаки.

Следствие
2. Конгруэнтные квадратичные формы имеют одинаковые ранги.

Приведение
действительной квадратичной формы к нормальному виду.

Квадратичная
форма f (x1,x2…,xn) называется канонической, если она не содержит произведений
различных переменных, т. е. (1.8)

Каноническая
квадратная форма называется нормальной (или имеет нормаль­ный вид), если | an |
= 1 ( i= 1, 2, . . . , r), т. е. отличные от нуля коэффициенты при квадратах
переменных равны +1 или —1.

Например,
квадратичная форма f (x1,x2…,xn) = 6×21+4×23 – 3×24, для которой a11 =6, a22=0,
a33 = 4, a44= -3, имеет канонический вид; квадратная форма f (x1, x2, x3, x4) =
x21 – – x23 + x24явля­ется нормальной, так как a11 =1, a22=0, a33 = – 1, a44=
1.

Теорема
2. Любая квадратичная форма некоторым невырожденным линейным преобразованием
может быть приведена к каноническому видугде
y1, y2….yn – новые переменные.

Некоторые
из коэффициентов bij могут оказаться равными нулю; число отличных от нуля
коэффициентов в этой формуле равно рангу r матрицы квадратичной формы φ.
Теорема 3. Любую действительную квадратичную форму линейным не­вырожденным
преобразованием можно привести к нормальному виду

Число
входящих сюда квадратов равно рангу формы.

Пример
1. Привести к каноническому виду квадратичную форму Ф(х1, х2) = 27.
Коэффициенты: а11 = 27,   а12 = 5,   а22 = 3.

Составим
характеристическое уравнение:

(27
– l)(3 – l) – 25 = 0

l2
– 30l + 56 = 0

l1
= 2;   l2 = 28;

Пример
2. Привести к каноническому виду уравнение второго порядка: 17×2 + 12xy + 8y2 –
20 = 0. Коэффициенты а11 = 17, а12 = 6, а22 = 8.      А =

 .
Составим характеристическое уравнение:

(17
– l)(8 – l) – 36 = 0

136
– 8l – 17l + l2 – 36 = 0

l2
– 25l + 100 = 0 l1 = 5,     l2 = 20.

Итого:–
каноническое уравнение эллипса.

Пример
3. Используя теорию квадратичных форм, привести к каноническому виду уравнение
линии второго порядка. Схематично изобразить график.

Решение:
Составим характеристическое уравнение квадратичной формы :
при

Решив
это уравнение, получим l1 = 1, l2 = 11.

Найдем
координаты собственных векторов:

полагая
m1 = 1, получим  n1 =

полагая
m2 = 1, получим  n2 =

Собственные
векторы:

Находим
координаты единичных векторов нового базиса.

Имеем
следующее уравнение линии в новой системе координат:

Каноническое
уравнение линии в новой системе координат будет иметь вид:

Список
использованной литературы

Гусак
А. А., Гусак Г. М., Бричникова Е. А. Справочник по высшей математике. – М.:ТетраСистемс,
1999- 640 с.

Малугин
В. А. Математика для экономистов: Линейная алгебра. Курс лекций. – М.: Эксмо,
2006- 224 с.

Данко
П. Е. Высшая математика в упражнениях и задач. Ч.1. – М.: Высш. Шк., 2003.

Крутицкая
Н. Ч., Шишкин А. А. Линейная алгебра в вопросах и задачах: Учеб. Пособие для
вузов. – М.:Высш. шк.,1985.

Виноградов
И. М. Элементы высшей математики. (Аналитическая геометрия. Дифференциальное
исчисление. Основы теории чисел). Учебник для вузов. – М.: Высш. шк., 1999.

Щипачев
В. С. Высшая математика: Учебник для вузов. – Высш. шк., 2005.

В.А.Ильин,
Э.Г.Позняк. Линейная алгебра. М.: Наука, 1999.

И.В.Проскуряков.
Сборник задач по линейной алгебре. М.: Наука, 2000.

В.Л.Камынин,
Н.В.Шолохов. Элементы теории групп. М.:МИФИ, 1997.