Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: 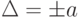
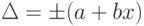
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, “Класс точности М”, а на приборе – буквой “М”. Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле 

Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
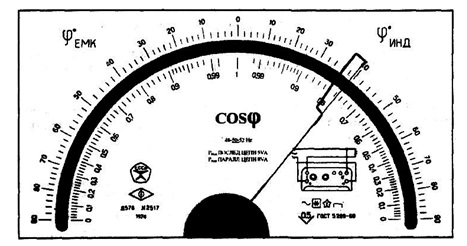
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 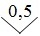
Рис.
3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
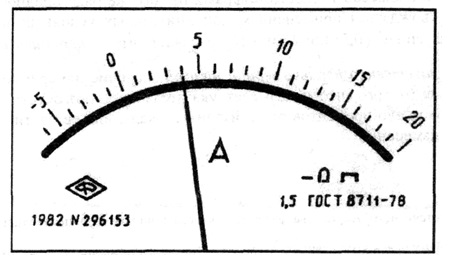
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
Рис.
3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой 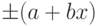
![delta=Delta/x=pm[c+d(|x_{k}/x|-1)]](https://intuit.ru/sites/default/files/tex_cache/3898a996678dab895193a1773d11ffc8.png) |
( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: 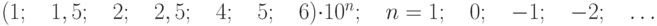
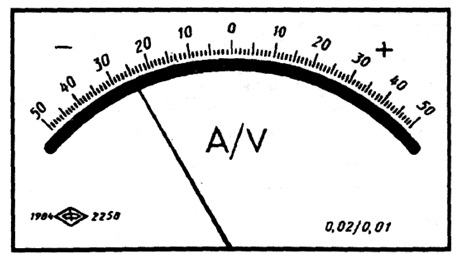
Рис.
3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле 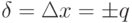
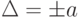
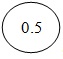
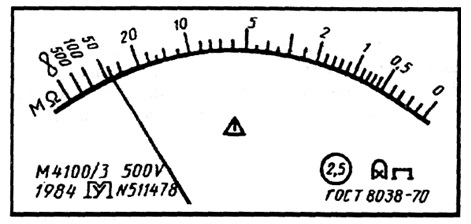
Рис.
3.4.
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?
.
Вместо неизвестного X используют
значение , определённое с помощью
образцовых приборов. Поэтому за абсолютную погрешность принимается следующая
разность:
.
Поправка к
показанию прибора представляет собой абсолютную погрешность, взятую с
противоположным знаком:
Приведенной погрешностью
называют отношение абсолютной
погрешности к нормирующему значению ,
выраженное в процентах:
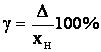
Нормирующим называется
условно принятое значение, равное:
а) для приборов с нулевой отметкой на краю или вне
шкалы – конечному значению диапазона измерений ;
б) для приборов, предназначенных измерять величины,
имеющие номинальное значение, – этому номинальному значению ;
в) для приборов с двусторонней шкалой, т. е. с нулевой
отметкой посредине, – арифметической сумме конечных значений диапазона
измерений .
Приведённая погрешность характеризует качество
измерительного прибора и обуславливается его метрологическими свойствами. В
связи с этим в зависимости от величины приведённой погрешности все
измерительные приборы относятся к различным классам точности. Все показывающие
электроизмерительные приборы (за исключением электронных и некоторых других) по
наибольшей приведённой погрешности, определённой в нормальных условиях,
относят к одному из восьми классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5
и 4,0.
Наибольшее значение приведённой погрешности прибора,
определённой в нормальных условиях его работы, не должно выходить за пределы,
допустимые для соответствующего класса точности, т. е.
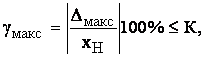
где
– наибольшее значение приведенной
погрешности, в %;
–
максимальное значение абсолютной погрешности, определенное в нормальных
условиях работы;
– нормирующее
значение величины;
К – класс точности прибора.
Согласно ГОСТ 13600-68 класс точности – это
обобщённая характеристика точности средств измерений, определяющая пределы допустимых
основной и дополнительной погрешностей. Таким образом, при отнесении
измерительного прибора к соответствующему классу учитывают не только его основную
погрешность, но и дополнительные, вызываемые различными влияющими величинами
(температура, электрическое и магнитное поля и т.д.). Эти погрешности
(дополнительные) также не должны выходить за пределы, установленные ГОСТом для
соответствующего класса.
Для каждого конкретного прибора по его классу точности
К и значению нормирующей величины можно согласно
(1.1) определить максимальное (предельное) значение абсолютной погрешности
измерения этим прибором в нормальных условиях:
.
Отсюда
предельное значение относительной погрешности измерения этим прибором в
нормальных условиях его применения будет равно:
(1.2)
где
X – истинное значение измеренной величины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Нормирующее значение
Cтраница 2
За нормирующее значение условно принимают значение, которое может быть равным верхнему пределу измерений, диапазону измерений, длине шкалы и др. При отсутствии специальных оговорок для измерительных приборов за нормирующее значение принимается диапазон шкалы прибора.
[16]
За нормирующее значение принимают разность конечных значений диапазона измерения. Нормирующее значение и диапазон измерения выражаются в единицах сопротивления.
[17]
Под нормирующим значением понимают некоторое установленное значение, по отношению к которому рассчитывается погрешность. Часто в качестве нормирующего значения в этом случае принимают верхний предел измерения прибора.
[18]
Под нормирующим значением параметра обычно принимают максимальное ( конечное) значение на шкале прибора.
[19]
Для потенциометров нормирующее значение измеряемой величины и диапазон измерения выражаются в единицах напряжения.
[20]
XN – нормирующее значение поверяемого прибора; – Д – поправка; увар – вариация показаний в процентах.
[22]
Для мостов за нормирующее значение принимают разность конечных значений диапазона измерения. Для потенциометров за нормирующее значение принимают: верхнее конечное значение диапазона измерения, если нулевое значение находится вне диапазона измерения; сумму абсолютных конечных значений диапазона измерения, если нулевое значение находится внутри диапазона измерения. Нормирующее значение и диапазон измерения выражаются в единицах входного сигнала.
[23]
Часто в качестве нормирующего значения для приведенной погрешности принимают верхний предел измерения прибора. Для многих средств измерений по приведенной погрешности устанавливают класс точности прибора.
[24]
Измерительным приборам с неравномерной шкалой нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений.
[25]
Помимо указанных, наиболее распространенных нормирующих значений, имеются и другие, устанавливаемые стандартами на отдельные типы средств измерений.
[26]
Помимо указанных, наиболее распространенных нормирующих значений, встречаются и другие, устанавливаемые в стандартах на отдельные виды приборов.
[27]
Помимо указанных, наиболее распространенных нормирующих значений, имеются и другие, устанавливаемые стандартами на отдельные типы средств измерений.
[28]
Условно принятое значение величины называют нормирующим значением. Часто за нормирующее значение принимают верхний предел измерений.
[29]
Разность хк – х называется нормирующим значением хир. В тех случаях, когда нулевое значение физической величины находится на краю диапазона измерения, как в рассмотренном примере, х р хк, если нулевое значение измеряемой величины находится внутри диапазона измерений, то хнр будет равен сумме абсолютных значений верхнего и нижнего пределов измерений.
[30]
Страницы:
1
2
3
4
Смыслова
А.Л. Лекции по дисциплине «Технически
средства автоматизации» спец.
21.01
Введение
Предмет
посвящен изучению тех технических
средств, на базе которых строятся
современные системы управления в самых
различных областях промышленности.
Трудно
переоценить роль информационно-измерительной
техники и измерительных технологий во
всех сферах деятельности и жизни
общества.
Ещё
великий Галилео Галилей утверждал:
«Надо измерять всё измеряемое и делать
измеримым то, что пока ещё не поддаётся
измерению». Измерение – один из важнейших
способов познания. Стало крылатой фразой
изречение Д.И.Менделеева: «Наука
начинается с тех пор, как начинают
измерять; точная наука немыслима без
меры».
В
различные исторические периоды состояние
мер и измерительной техники находилось
в зависимости от хозяйственной
деятельности, общественных, религиозных
и других факторов жизни общества.
Крупнейшие
строительные работы глубокой древности
на реке Ниле, строительство храмов,
дворцов, надгробий в Египте возможны
были только при достаточно хорошо
разработанной технике линейных,
поверхностных, объёмных измерений и
наличии точных узаконенных мер.
Широко
известны древние меры Египта, Вавилона
и Руси. Принципы построения вавилонской
системы мер проникли в другие страны.
Вавилоняне впервые в истории народов
установили единицы времени: год, час,
минуты, секунды. Им же принадлежит идея
построения кратных и дробных производных
однородных единиц измерения.
Наиболее ранняя
попытка создания узаконенных мер имела
место в Греции в период правления
Соломона (6 век до нашей эры). Мерой длины
в то время в Греции был фут, равный
приблизительно 297 мм.
В более позднее
время попытка введения мер, обязательных
для всех измерений и одинаковых во всей
стране, имела место в Англии в 1001 и 1215
гг., во Франции в 1321 г., в Австрии в 1438 г.
В 1790 г. в Учредительном
собрании Франции был поставлен вопрос
о создании и узаконении единой и для
всех обязательной, контролируемой
государственной системы мер.
Платиновые эталоны
метра и килограмма в1799 г. были переданы
на хранение в архив Французской
республики. Вся совокупность метрических
мер, созданных и узаконенных во Франции
в конце 18 века, легла в основу метрической
системы мер, некоторые единицы метрических
мер вошли в качестве основных единиц в
систему единиц СИ.
В связи с бурным
развитием науки об электричестве стали
создаваться электроизмерительные
приборы. Русский академик Г.В.Рихтер
изобрёл в 1745 г. электрометр, А.Ампер в
1820 г. демонстрировал первый гальванометр,
Карл Гаусс в 1832 г. изложил методику
составления системы магнитных единиц,
которую Вебер дополнил электрическими
единицами.
М.О.Доливо-Добровольскому
принадлежит первенство в создании
индукционных приборов – ваттметра,
фазометра и др.
В 1867 г. в Париже
бал организован Международный комитет
мер и весов, основная задача которого
состояла в тщательном изучении метрических
мер, сравнении их с другими мерами,
выявлении и разработке возможностей
использования их внутри каждой страны
и для международных отношений.
В России таким
учреждением было депо образцовых мер
и весов (1842); с 1893 г. – главная палата мер
и весов, которую возглавил Д.И.Менделеев.
Электроизмерительные
приборы, имеющие более 250-летнюю историю,
обязаны своим развитием работам Вольта,
Ампера, Фарадея. Им принадлежит первенство
в создании приборов прямого преобразования
– гальванометров, амперметров, вольтметров
и т.д. История создания приборов с
уравновешиванием измеряемой величины
начинается с 1841 г., когда предложены
четырехплечевой мост (Уитстон) и
компенсационный метод измерения
постоянного напряжения (компенсатор
Поггенорфа).
Кроме того, в 19
веке найдены основные принципы
преобразования неэлектрических величин
в электрические: термоэлектрический
эффект (Томас Зеетек, Уильям Томсон),
пьезоэффект, тензоэффект (О.Д.Хвольсон).
Дальнейшему
развитию электроизмерительных приборов
способствовало изобретение электронной
лампы: в 1904 г. появился диод, а в 1910 г. –
триод и пентод. Сочетание усилителей и
выпрямителей с магнитоэлектрическим
измерительным механизмом позволило
создать электронные вольтметры,
частотометры, фазометры. Изобретение
электронно-лучевой трубки в 1911 г. привело
к созданию электронно-лучевого
осциллографа, который становится
универсальным электроизмерительным
прибором. Развитие электроники дало
возможность разрабатывать автоматические
компенсаторы и мосты.
Таким образом,
классическая основа электроизмерительной
техники дополнилась приборами с
автоматическим уравновешиванием и
электронными измерительными приборами.
Создание микросхем,
микропроцессоров и ЭВМ способствовало
появлению измерительных устройств
нового типа – аналого-цифровых
преобразователей (АЦП), в результате
чего появились цифровые измерительные
приборы (ЦИП).
Интенсивное
развитие ЦИП, обладающих рядом преимуществ
по сравнению с «нецифровыми» приборами,
определило развитие измерительной
техники 20 века.
Усложнение
технологии производства, развитие
научных исследований в различных
областях жизни привело к необходимости
измерения сотен и тысяч параметров
одновременно. Появился новый класс
информационно-измерительной техники
– информационно-измерительные системы,
выполняющие роль сбора, обработки,
передачи, хранения, отображения и
воздействия на объект исследования или
управления.
Работы в области
информационно-измерительной техники
и измерительных технологий позволили
в последние годы создать новый раздел
теории и практики измерений – виртуальные
и интеллектуальные измерительные
приборы и системы. Информационно-измерительная
техника играет большую роль в информатизации
общества.
Сеть Интернет
является новой прогрессивной формой
использования распределённых
информационных и вычислительных
ресурсов. Некоторые организации
располагают уникальным или дорогостоящим
измерительным оборудованием, к которым
можно отнести, например, оптические
анализаторы спектра, часто требующие
размещения в специально оборудованных
помещениях. Ранее такое оборудование
использовалось, как правило, неэффективно
из-за низкой загрузки ввиду его доступности
для малого числа пользователей. С
появлением глобальных сетей открываются
новые перспективы для коллективного
использования таких измерительных
систем, в том числе в рамках международного
сотрудничества.
Перед наукой и
практикой в области измерений стоят
сложные задачи по развитию теории
виртуальных и интеллектуальных систем,
методов прогнозирования и исключением
погрешностей в реальном времени при
быстротекущем процессе, систем
автоматизированного проектирования
приборов и систем, по развитию общей
теории измерений и теории погрешностей,
по созданию средств измерений на основе
лазерной техники, оптоэлектроники,
оптоволоконной оптики.
Развитие
информационно-измерительной техники
и измерительных технологий будет
способствовать открытию новых областей
знаний и научно-инженерному прогрессу.
I.
Классификация
систем управления.
-
Локальные
системы контроля регулирования и
управления (ЛСКРиУ). -
Централизованные
системы контроля регулирования и
управления (ЦСКРиУ) -
Автоматизированные
системы управления технологическими
процессами (АСУ ТП)
Рис.
1. Схема ЛСКРиУ
ТОУ – технологический
объект управления
Д – датчик
УСО – устройство
связи с оператором
ЛПР – лицо,
принимающее решение
ЛР – локальный
регулятор
ИУ – исполнительное
устройство, изменяет величину регулирующего
параметра
РУ – ручное
управление
Локальные
системы управления эффективны при
следующих условиях:
1)
при технологически независимых ОУ.
2)
при несложных целях управления.
3) когда хорошо
отработана технология.
4)
при стационарных условиях эксплуатации.
Централизованные
системы управления появились в результате
увеличения числа регулируемых и
контролируемых параметров, а также в
связи с территориальной рассредоточенностью
объектов управления.
Рис.2.Схема
централизованной системы управления.
ВП – вторичный
преобразователь
УОИ – устройство
отображения информации
ЦПКиУ – центральный
пульт контроля и управления
ЗУ – задающее
устройство
ДУ – дистанционное
управление
ЛКУ – логико-командное
управление
ИУ ИМ – исполнительное
устройство, механизм
Рис. 3 Схема централизованной системы
с многоканальным управлением
КК – коммутатор
каналов
МВП – многоканальный
вторичный преобразователь
МЛКУ – многоканальное
логико-командное управление
РК – распределитель
каналов
Для
сокращения технических средств и
оборудования, а также для уменьшения
эксплуатационных расходов в
централизованных системах управления
стали применять многоканальные средства.
РК и КК подключается к индивидуальным
устройствам канала, образуя при этом
замкнутый контур управления. Цели и
задачи те же: поддержание заданного
параметра и оптимальное управление.
Следующий
уровень управляющих систем – АСУ ТП
может включать в себя как локальные,
так и централизованные системы управления,
состав и конфигурация такой системы
зависят от уровня сложности и в каждом
случае индивидуальны. Такие системы
решают самые разнообразные задачи,
включая экстремальное и адаптивное
управление.
II.
Элементы систем автоматического
регулирования и управления.
Информация по мере
продвижения претерпевает изменения,
связанные с её получением, преобразованием,
хранением, отображением, передачей,
использованием.
В
системах управления используют:
-
Энергетические
информационные параметры. -
Вещественные
информационные параметры.
Изменение
информационного параметра – сигнал
информации.
1 – электрические,
гидравлические, пневматические.
2 – печатные
документы, перфокарты, информация на
дискетах.
Энергетические:
-
Аналоговые
(непрерывные). -
Дискретные
(подаются в определённые промежутки
времени).
Аналоговые сигналы
преобразуются в дискретные операцией
квантования. Помимо неё осуществляется
кодирование. Обратная операция –
декодирование. Эти два сигнала подвергаются
модуляции и демодуляции при передаче
по каналам связи средствами: модулятором
и демодулятором.
Классификация
средств автоматизации.
Все изменения,
происходящие с информацией во время её
движения, осуществляется в отдельных
частях автоматизированных систем
(отдельными техническими средствами).
Простейшее устройство, выполняющее
одну или несколько операций над
информационным сигналом – элемент
автоматизированных систем.
Все элементы
делятся:
-
Средства получения,
преобразования и нормирования первичной
технологической информации (1,2). -
Средства приёма,
преобразования и передачи информации
по каналам связи (8,9,10). -
Средства
хранения и обработки информации для
выработки сигналов управления
(3,4,5,6,7,11,12,13,15). -
Средства
преобразования и передачи командной
информации (8,9,10). -
Вспомогательные
средства, обеспечивающие функционирование
остальных групп (14,16).
-
Первичные
преобразователи. -
Нормирующие
преобразователи. -
Средства индикации
и сигнализации. -
Регистраторы.
-
Блоки памяти.
-
Устройства
запоминания и хранения информации для
оператора. -
Устройства
обработки информации (процессор). -
Передатчики
(шифраторы). -
Линии связи.
-
Приёмники
(дешифраторы). -
Ручные задатчики.
-
Регулирующие
блоки. -
Программные
задатчики. -
Усилители.
-
Анализаторы.
-
Исполнительные
устройства.
Рис. 4. Локальная система управления
В
локальных СУ информация о состоянии
объекта, процессах, протекающих в нём
и конечных результатах его работы,
собирается группой получения контрольной
информации; устройства 1и 2 расположены
на ОУ. Сигналы измерительных преобразователей
нормируются преобразователями «2» и по
каналам передачи информации (II)
с помощью передатчиков (8) каналов связи
(9) и приёмников (10) передаются группе
средств функциональной обработки (III)
с блоками сравнения и выработки
управляющих командных сигналов. В
соответствии с заданным алгоритмом
обработки и установленным заданием на
«11» и «13» регулирующиеся блоки (12) через
линии передачи управляющего сигнала
(IV)
передают командную информацию в блоки
воздействия на объект (V)
через усилитель «14» на исполнительное
устройство «16».
Информация о
результатах работы СУ и текущий контроль
процесса регулирования осуществляется
с помощью вторичных приборов, индикаторов
и сигнализаторов (3), регистраторов
параметров (4) и может храниться в блоках
памяти (5). Оператор (6) воздействует на
СУ по каналам связи через устройство
дополнительной информации (11, 13).
Рис.5. Схема ЦСКР и У
ЦСКР
и У: управление основывается на
использовании текущей информации об
ОУ, непосредственно поступающей от
блоков получения, преобразования и
передачи (I,
II)
в устройство обработки и выработки
командной информации (III),
в качестве которых могут быть использованы:
УВМ, ЭВМ, МП, которые управляют устройствами
воздействия на объект (V)
непосредственно через линии связи
командных сигналов.
-
Основные понятия
измерительной техники.
-
Определение
измерения.
Возможное
рабочее описание термина «измерение»,
согласующееся с нашей интуицией, звучит
так: «измерение – это получение
информации».
Одним из наиболее существенных аспектов
измерения является сбор информации;
измерения производятся для того, чтобы
что-то узнать об объекте измерения, то
есть об измеряемой
величине.
Это означает, что результат измерения
должен описывать то состояние или то
явление в окружающем нас мире, которое
мы измеряем. Между этим состоянием или
результатом измерения должно существовать
то или иное соотношение. Хотя получение
информации, очевидно, оно является лишь
необходимым, но не достаточным для
определения измерения: когда кто-то
читает учебник, он накапливает информацию,
но не выполняет измерения.
Второй
аспект измерения состоит в том, что оно
должно быть избирательным.
Оно может
снабдить нас сведениями только о том,
что мы хотим измерить (об измеряемой
величине), но ничего не говорит ни об
одном из многих других состояний или
явлений вокруг нас. Это обстоятельство
тоже необходимо, но не достаточно для
определения измерения. Любуясь картиной
в пустой комнате, где нет ничего другого,
вы получаете информацию только об этой
картине, но это не будет измерением.
Третьей,
и также необходимой стороной дела,
является тот факт, что измерение должно
быть объективным.
Исход измерения не должен зависеть от
наблюдателя. Любой наблюдатель должен
извлекать из измерения одну и ту же
информацию и приходить к одним и тем же
выводам. Таким образом, чтобы гарантировать
объективность измерения, мы должны
воспользоваться теми или иными
приспособлениями. Другими словами,
прибор преобразует исходное наблюдение
в такой вид, в котором оно доступно
любому наблюдателю и относительно
которого между наблюдателями не может
быть разногласия.
В
дальнейшем будем полагать, по определению,
что измерение – это получение с помощью
измерительных
систем (приборов) информации в форме
результата измерения, отражающего
характеристику, состояние или явление
окружающего нас мира (объект измерения).
В этом контексте измерительная система
должна гарантировать требуемые
наглядность описания, избирательность
и объективность измерения.
Конечной
целью любого измерения является получение
количественной информации об измеряемой
величине. В процессе измерения
устанавливается во сколько раз измеряемая
физическая величина больше или меньше
однородной с ней в качественном отношении
физической величины, принятой за единицу.
Число, выражающее отношение измеряемой
величины к единице измерения, называется
числовым
значением измеряемой величины.
Значение величины, принятое за единицу
измерения, называется размером
этой величины.
Q
– измеряемая физическая величина.
Q-
некоторый размер физической величины,
принятой за «1» измерения.
q-
числовое значение величины Q.
Результат
измерения величины Q
может быть представлен так:
Q=q*
Q
(1)
Уравнение (1)
называют основным уравнением измерения.
Сведения
о значении измеренных физических величин
называются измерительной
информацией.
Сигналом
измерительной информации – называется
сигнал, функционально связанный с
измеряемой величиной.
1.2. Виды измерений
обычно классифицируются по следующим
признакам:
-
Характеристике
точности – равноточные, неравноточные
(равнорассеяные, неравнорассеяные); -
Числу измерений
– однократные, многократные; -
Отношению к
изменению измеряемой величины –
статические, динамические; -
Метрологическому
назначению – метрологические,
технические; -
Выражению результата
измерений – абсолютные, относительные; -
По общим приемам
получения результатов измерений –
прямые, косвенные, совместные, совокупные.
Равноточные
измерения – ряд
измерений какой-либо величины, выполненные
одинаковыми по точности СИ и в одних и
тех же условиях.
Неравноточные
измерения –
ряд измерений какой-либо величины,
выполненные несколькими различными по
точности СИ и (или) в разных условиях.
Однократное
измерение –
измерение, выполненное один раз.
Многократные
измерения –
измерения одного и того же размера ФВ,
результат которого получен из нескольких
следующих друг за другом наблюдений,
т.е. состоящих из ряда однократных
измерений.
Прямое
измерение –
измерение ФВ, проводимое прямым методом,
при котором искомое значение ФВ получают
непосредственно из опытных данных.
Прямое измерение производится путем
экспериментального сравнения измеряемой
ФВ с мерой этой величины или путем
отсчета показаний средства измерения
по шкале или цифровому прибору (например,
измерения длины, высоты с помощью
линейки, напряжения – с помощью
вольтметра, массы – с помощью весов).
Косвенное
измерение –
измерение, проводимое косвенным методом,
при котором искомое значение ФВ находят
на основании результата прямого измерения
другой ФВ, функционально связанной с
искомой величиной известной зависимостью
между этой ФВ и величиной, получаемой
прямым измерением. Например, определение
площади, объема с помощью измерения
длины, ширины, высоты; электрической
мощности методом измерения силы тока
и напряжения и т.д.
Совокупные
измерения –
одновременно проводимые измерения
нескольких одноименных величин, при
которых искомые значения величин
определяются путем решения системы
уравнений, получаемых при измерениях
различных сочетаний этих величин.
Пример: значение массы отдельных гирь
набора определяют по известному значению
массы одной из гирь и по результатам
измерений (сравнений) масс различных
сочетаний гирь.
Совместные
измерения –
одновременно проводимые измерения двух
или нескольких неодноименных физических
величин для определения зависимости
между ними. Пример: определение
температурного коэффициента сопротивления
(ТКС) путем одновременного измерения
сопротивления R
и температуры t,
а затем определение зависимости (t)
=R/t
1.3.Средством
измерения – называют
техническое устройство, используемое
при измерениях и имеющее нормированные
метрологические свойства.
Сигнал
измерительной информации, поступающий
на вход измерительного устройства,
называют входным
сигналом. Сигнал,
получаемый на выходе, называют выходным
сигналом
средства измерения.
К средствам
измерений относятся меры, измерительные
преобразователи, измерительные приборы,
измерительные установки и
информационно-измерительные системы.
Мерой
называется
средство измерений, предназначенное
для воспроизведения заданного значения
физической величины (образцовая катушка
сопротивления, гиря). Меры подразделяют
на рабочие и образцовые.
Измерительные
преобразователи
– это
устройства, предназначенные для
преобразования одной формы информации
об измеряемой величине в другую форму.
Это преобразование должно выполнятся
с заданной точностью, и обеспечить
требуемую функциональную зависимость
между выходной и входной величинами
преобразователя.
В зависимости от
характера преобразуемых величин
различают следующие виды измерительных
преобразователей:
-
Преобразователи
электрических величин в электрические
(шунты, делители напряжения, измерительные
трансформаторы) -
Преобразователи
магнитных величин в электрические
(измерительные катушки, феррозонды,
преобразователи, основанные на эффектах
Холла, Гаусса, сверхпроводимости и т.
д.) -
Преобразователи
неэлектрических величин в электрические
(термо – и тензопреобразователи,
реостатные, индуктивные, емкостные).
В зависимости
от функций, выполняемых преобразователями
в измерительной цепи, их подразделяют
на первичные, промежуточные, передающие
и масштабные.
Измерительный
преобразователь, находящийся в цепи
измерений на первом месте, называется
первичным измерительным преобразователем.
К первичным
преобразователям относят и отборные
устройства.
Отборным
устройством (отбором) – называют
устройство, устанавливаемое на
трубопроводах и технологических
агрегатах и служащее для непрерывного
отбора контролируемой среды и передачи
ее параметров к измерительному
преобразователю или измерительному
прибору.
Измерительные
приборы
– это
устройства, представляющие собой
совокупность измерительных преобразователей,
выполняющих определённые функции, и
отсчётного устройства, предназначены
для выработки сигнала измерительной
информации, доступной для непосредственного
восприятия наблюдателем. В практике,
для измерительных приборов, установленных
на щитах контроля и управления, применяется
термин «вторичный
прибор».
По физическим
явлениям, положенным в основу работы,
измерительные приборы можно разделить
на электроизмерительные (электромеханические,
электротепловые, электрохимические) и
электронные приборы.
По назначению их
подразделяют на приборы для измерения
электрических и неэлектрических
(магнитных, тепловых, химических и др.)
физических величин.
По способу
представления результатов – на
показывающие и регистрирующие.
По методу
преобразования измеряемой величины –
на приборы непосредственной оценки
(прямого преобразования) и сравнения.
По способу применения
и по конструкции – на щитовые, переносные,
стационарные.
В зависимости от
регистрации измеряемой величины
различают аналоговые и цифровые
измерительные приборы.
Аналоговым
называют измерительный прибор, показания
которого являются непрерывной функцией
измеряемой величины, например стрелочный
вольтметр, ртутно-стеклянный термометр.
В
цифровом
приборе осуществляется преобразование
аналогового сигнала измерительной
информации в цифровой код, и результат
отражается на цифровом табло.
По защищенности
от воздействия внешних условий
измерительные приборы подразделяют на
обыкновенные, влаго -, газо- и пылезащищенные,
герметичные, взрывобезопасные и др.
Измерительные
установки
– это комплекс
средств измерений, включающий в себя
меры, измерительные приборы и
преобразователи, вспомогательные
устройства, объединённые одной схемой,
с помощью которой можно измерить одну
или несколько физических величин.
Все средства
измерений имеют общие свойства,
позволяющие сопоставлять их между
собой: метрологические, эксплуатационные,
информационные и др. Отдельные виды и
типы средств измерений обладают своими
специфическими свойствами. Наиболее
важными являются метрологические
характеристики средств измерений.
Диапазон
измерений
– область
значений измеряемой величины, для
которой нормированы допускаемые
погрешности средства измерений. Он
ограничивается наибольшим и наименьшим
значениями. С целью повышения точности
измерений диапазон измерений может
быть разбит на несколько поддиапазонов.
При переходе с одного поддиапазона на
другой, некоторые составляющие основной
погрешности уменьшаются, что приводит
к повышению точности измерений. При
нормировании допускают для каждого
поддиапазона свои предельные погрешности.
Область
значений шкалы, ограниченную начальными
и конечными значениями шкалы, называют
диапазоном
показаний.
Для средств
измерений, выдающих результаты измерений
в цифровом коде, указывают цену единицы
младшего разряда (единицы младшего
разряда цифрового отсчётного устройства),
вид выходного кода (двоичный,
двоично-десятичный) и число разрядов
кода.
Для
оценки влияния средства измерения на
режим работы объекта исследования
указывают входное
полное сопротивление Zвх.
Входное сопротивление влияет на мощность,
потребляемую от объекта исследования
средством измерения.
Допустимая
нагрузка на средство измерения зависит
от его выходного
полного
сопротивления
Zвых.
Чем меньше выходное сопротивление, тем
больше допустимая нагрузка на средство
измерений.
Вариация
выходного сигнала
– разность
между значениями выходного сигнала,
соответствующими одному и тому же
действительному значению входной
величины при медленном подходе слева
и справа к выбранному значению входной
величины.
Вариация
показаний прибора
– наибольшая
вариация выходного сигнала прибора при
неизменных внешних условиях. Она является
следствием трения и люфтов в узлах
приборов, механического и магнитного
гистерезиса элементов и др.
Кроме метрологических
характеристик при эксплуатации средств
измерений важно знать и неметрологические
характеристики – показатели надежности,
электрическую прочность, сопротивление
изоляции, устойчивость к климатическим
и механическим воздействиям, время
установленного рабочего режима и др.
Под
надежностью
средства измерения понимают его
способность сохранять нормированные
характеристики при определенных условиях
работы в течение заданного времени.
Основными критериями надежности приборов
являются вероятность безотказной работы
и средняя продолжительность безотказной
работы.
Вероятность
безотказной
работы
определяется вероятностью отсутствия
отказов прибора в течение определенного
промежутка времени, средняя
продолжительность безотказной работы
– отношением продолжительности
безотказной работы к числу отказов за
это время.
Погрешность
– это отклонение результата измерения
от истинного значения измеренной
величины.
Погрешности
измерения, в зависимости от их
происхождения, делятся на три группы:
систематические погрешности, случайные
погрешности, субъективные погрешности.
Системные погрешности
имеют постоянный характер и по причинам
возникновения делятся:
-
Инструментальные
-
Погрешности
от неправильной установки средств
измерения -
Возникающие
от внешних влияний -
Методические
(теоретические)
Инструментальные
погрешности могут вызываться
конструктивными особенностями, а также
износом и старением средств измерения.
Конструктивные
погрешности вызываются несовершенством
конструкции или неправильной технологией
изготовления средства измерения (плохая
балансировка измерительного механизма,
неточность при нанесении отметок шкалы
и т.д.).
Погрешности от
неправильной установки вызываются
наклоном прибора, и т.д.
Погрешности внешних
влияний вызываются вибрацией,
электромагнитными полями, конвекцией
нагретого воздуха и т.д.
Методические
погрешности возникают в результате
несовершенства метода измерения и
теоретических допущений (использование
приближенной зависимости, вместо точной
и др.)
Исключение
погрешности достигается путем введения
соответствующей поправки в показания
прибора, численно равной системной
погрешности, но противоположной по
знаку.
Случайные
погрешности вызываются независимыми
друг то друга случайными факторами и
изменяются случайным образом при
повторных измерениях одной и той же
величины.
Проявляются
случайные погрешности в том, что при
измерении одной и той же неизменной
величины одним и тем же средством
измерения, получают различные показания.
Абсолютная
погрешность – это разность между
измеренным и истинным значением
измеряемой величины.
Δx=xизм
– хист,
Где Δx– погрешность измерения.
Строго
говоря, применение формулы для вычисления
погрешности измерения невозможно,
поскольку истинное значение измеряемой
величины неизвестно. На практике хист
заменяется
на его оценку – действительное значение
величины хд,
и погрешность рассчитывается по формуле
Δx=xизм–
хд
Относительная
погрешность – это отношение абсолютной
погрешности к истинному (действительному)
значению, выраженное в процентах
=Δх/
хд*100%
приведенная
погрешность измерительного прибора п
– это отношение абсолютной погрешности
к нормирующему значению прибора
п=Δх/хN*100
-
Средства
измерения и контроля.
-
Классификация
средств измерения и контроля по
определенным признакам.
Средства
измерения и контроля классифицируются
по различным признакам:
-
По типу и виду
контролируемых физических величин; -
Назначению –
универсальные и специальные; -
Числу проверяемых
параметров при одной установке объекта
измерения – одномерные и многомерные; -
Степени механизации
и автоматизации процесса измерений –
ручного действия, механизированные,
полуавтоматические, -
автоматические.
Классификация
средств измерения и контроля по типу
контролируемых физических величин
представлена на рис. 1.3.
Рис.1.3.
Универсальные
измерительные инструменты и приборы
нашли широкое применение в условиях
единичного и мелкосерийного производства,
а также для определения численных
величин и отклонений от правильной
геометрической формы и взаимного
расположения поверхностей, при наладке
станков, при особо ответственных
измерениях во всех видах производств,
включая массовое и крупносерийное
(рис.1.5.).
В условиях
расширяющейся автоматизации технологических
процессов, повышения требований к
производительности, точности и качеству
все большее значение приобретают
автоматические средства
контроля. Они классифицируются
по числу проверяемых параметров, степени
автоматизации, способу преобразования
измерительного импульса, воздействию
на технологический процесс (рис.1.6.).
Рис.1.5.
Классификация универсальных инструментов
и приборов
ИЗМЕРЕНИЕ
НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН.
В науке, технике
и производстве все чаще возникают задачи
точного измерения различных неэлектрических
величин. Внедрение механизации и
комплексной автоматизации в производство
требует быстрого и точного контроля
технологических процессов, т.е. измерения
самых разнообразных физических величин.
Особенно большое число различных
неэлектрических величин требуется
контролировать в металлургической,
химической и текстильной промышленностях.
Развитие измерительной техники показало,
что среди разнообразных методов измерения
неэлектрических величин наибольшими
преимуществами обладают электрические
методы. Их отличительными достоинствами
являются:
-
Возможность
измерения сигналов малой величины –
применение электронных усилителей
дает возможность измерять такие сигналы,
которые не могут быть измерены никакими
другими способами; -
Возможность
передачи измеренной величины на
расстояние, а, следовательно, и
дистанционного управления различными
процессами; -
Достаточно
высокая точность и малая инерционность
электроизмерительной аппаратуры; -
Быстрота
измерений; -
Возможность
комплектования измерительных и
управляемых ими автоматических установок
из блоков однотипной электрической
аппаратуры.
Для того чтобы
неэлектрическую величину можно было
измерить электрическим прибором,
необходимо эту величину преобразовать
в пропорциональный ей ток или напряжение.
С этой целью используют специальные
устройства, называемые измерительными
преобразователями. Схемы для измерения
неэлектрических величин могут быть
довольно сложными, так как кроме
измерительных преобразователей в схему
могут входить усилители, выпрямители,
источники питания, двигатели,
неэлектрические преобразователи
(например, пружины, оптические системы)
и т.д.
Нормиро́вочный мно́житель — фактор, на который домножается математическое выражение, чтобы после этого какой-либо значимый параметр оказался равным 1. Подбор нормировочного множителя называется нормированием (нормировкой).
Чаще всего имеется в виду ситуация, когда на нормировочный фактор домножаются неотрицательная функция или все члены числового ряда, чтобы интеграл от функции по области определения или сумма членов ряда равнялись единице. Тогда фактор представляет собой положительное число или алгебраическое выражение, не зависящее от аргументов функции. Подобная нормировочная процедура применяется в теории вероятностей и в различных областях физики (статфизике, квантовой механике, теории спектров и других). После нормировки функция может рассматриваться как плотность распределения, а ряд как ряд распределения.
Однако понятия «нормировочный множитель», «нормировка» используются и в иных, не связанных со статистикой ситуациях. Целью нормировки при этом может быть приведение данных к в чём-то более удобному виду.
Нормировочный множитель в статистике[править | править код]
Задачи, прямо или косвенно относящиеся к статистике, составляют основную сферу применения нормировочных множителей. Общий смысл состоит в наложении требования равенства суммарной вероятности всех возможных событий единице[1].
Процедура нормировки[править | править код]
Если 


,
при этом функция 
Если 


,
при этом последовательность 

Потребность в нормировке[править | править код]
Наиболее значимые и часто встречающиеся распределения, как правило, записываются уже с нормировкой, то есть никаких дополнительных процедур не требуется. Например, нормальное распределение величины 

,
Здесь предполагается область определения 

Однако в менее распространённых ситуациях подбор нормировочного множителя может потребоваться. Скажем, иногда нужно сузить область определения 




Примеры из области физики[править | править код]
Пример 1. Распределение Максвелла для модулей скоростей молекул идеального газа имеет вид 






Пример 2. Состояние частицы в квантовой механике задаётся волновой функцией 




Пример 3. Непрерывный электромагнитный или акустический спектр может быть задан в виде некоей функции 









Нормировочные факторы вне статистики[править | править код]
Нормировочные множители также используются, когда желательно добиться того, чтобы какая-то величина (не обязательно имеющая смысл полной вероятности) оказалась равной единице.
- Нормировка
(и, соответственно, подбор нормировочного множителя) могут потребоваться не только для вышеупомянутого физического случая волновой функции, но и для собственных функций в более широком классе задач[3].
Примечания[править | править код]
- ↑ А. И. Волковец, А. Б. Гуринович Теория вероятностей и математическая статистика. Минск, БГУИР (2003), см. ф-лы: (4.9), (8.7), (10.8).
- ↑ П. С. Парфенов Квантовая механика. Методическое пособие к практикуму по квантовой физике. СПб: ИТМО (2012), см. 1.1.4. Нормирование волновых функций.
- ↑ Н. Н. Воробьев Теория рядов. М.: Наука (1979), см. гл. 8, § 3: Нормированные и ортогональные функции.
- ↑ И. Мальцевская Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач, см. на образовательном сервисе Zaochnik.
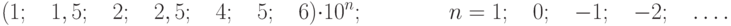








![{displaystyle A=left[int _{x_{1}}^{x_{2}}phi (x),dxright]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0fcca8f170a090edda6c2d612c11b340ce4f64d)
![{displaystyle A=left[sum limits _{n}p(x_{n})right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4fd74d778c97c0ea3fd48c4a7c67c5406b8047)


